수학 표기법의 역사
History of mathematical notation수학적[1] 표기법의 역사는 수학적 기호의 시작, 진행 및 문화적 확산과 표기가 대중화되거나 눈에 띄지 않게 이동하는 과정에서 직면하는 표기법의 상충을 포함한다.수학[2] 표기법은 수학 방정식과 공식을 쓰는 데 사용되는 기호로 구성됩니다.일반적으로 표기법은 수량 및 기호 [3]연산자의 잘 정의된 표현 집합을 의미합니다.역사는 힌두-아랍 숫자, 로마자, 그리스어, 히브리어, 독일어 알파벳 문자, 그리고 지난 몇 세기 동안 수학자들에 의해 발명된 수많은 기호들을 포함합니다.
수학 표기법의 발달은 [4][5]단계별로 나눌 수 있다."법적" 단계는 말로 계산을 수행하며 기호는 [6]사용되지 않습니다."동기화된" 단계는 자주 사용되는 연산과 양이 상징적인 구문 약어로 나타나는 단계입니다.고대로부터 고전기 이후의 [note 1]시대까지, 수학적 창의성의 폭발은 종종 수 세기의 침체 뒤에 이어졌다.초기 근대 시대가 열리고 지식의 전 세계적인 확산이 시작되면서 수학 발전의 기록된 예가 드러났다."상징적" 단계는 포괄적인 표기법이 수사학을 대체하는 단계입니다.16세기 이탈리아를 시작으로, 새로운 과학적 발견과 상호작용하는 새로운 수학적 발전이 오늘날까지 계속된 증가된 속도로 이루어졌다.이 상징 체계는 17세기 [7]중반부터 중세 인도 수학자들과 유럽에서 사용되었고, 현대에도 계속 발전해왔다.
수학의 역사로 알려진 연구 분야는 주로 수학에서의 발견의 기원에 대한 조사이며, 여기서의 초점은 과거의 수학적 방법과 표기법에 대한 조사이다.
수사 단계
역사가 이오니아 학파의 역사로 시작되기는 하지만, 그것에 관심을 기울였던 고대 그리스인들이 고대 이집트인들과 고대 페니키아인들의 이전 조사에 크게 힘입은 것은 분명하다.숫자 표기법의 특징, 즉 고유의 값(산술)뿐만 아니라 지역적인 값을 가진 기호들은 그 발명 당시의 문명 상태를 암시한다.이 섹션이 할애된 이러한 초기 사람들의 수학적 성취에 대한 우리의 지식은 불완전하며, 다음의 간단한 메모는 가장 가능성이 있어 보이는 결론의 요약으로 간주되며, 수학의 역사는 기호 섹션으로부터 시작된다.
수학의 많은 영역은 근본적인 규칙과 개념이 추상적인 구조로 확인되고 정의되기 전에 현실 세계의 문제에 대한 연구로 시작되었다.예를 들어, 기하학은 실제 세계에서의 거리와 면적의 계산에서 기원을 가지고 있다; 대수학은 산술에서 문제를 푸는 방법에서 시작되었다.
기록을 남긴 대부분의 초기 사람들은 수치와 역학을 알고 있었고, 소수의 사람들은 육지 탐사의 요소들에 대해서도 알고 있었다는 것은 의심의 여지가 없다.특히 이집트인들은 기하학과 숫자에, 페니키아인들은 실용적인 산수, 부기, 항해, 육지 탐사에 주목했다.이 사람들이 얻은 결과는 여행자들이 특정한 조건하에서 접근할 수 있었던 것으로 보인다.이집트인과 페니키아인에 대한 지식은 주로 관찰과 측정의 결과였을 가능성이 높으며, 여러 시대의 축적된 경험을 대표한다.
표기 시작
쓰여진 수학은 각각의 집계가 하나의 단위를 나타내며 집계 표시로 표현된 숫자로 시작되었다.숫자 기호는 아마도 나무나 돌로 잘린 획이나 칼집으로 구성되었고,[note 2] 모든 국가가 똑같이 이해할 수 있었다.예를 들어, 뼈의 한 부분은 하나의 동물, 사람, 또는 다른 어떤 것을 나타냅니다.누구와 그리스 소 아시아(서부 역사의 표기법이 시작된다 사이)의 잦은 접촉하게 될 가능성이 있는 국민. 사람들의 동부 지중해 연안에 거주하는:그리스 전통의 반응은 한결같이 이집트 사람들 기하학의 특별한 개발. 그리고 numbers[주 3]eithe의 과학에 달한다.r에 찾았다고이집트인 또는 페니키아인에게.
고대 이집트인들은 상형문자에 [8][9]의한 숫자라는 상징적인 표기법을 가지고 있었다.이집트 수학은 1, 10, 100, 1,000, 10,000, 10만, 100만을 나타내는 기호를 가지고 있었다.숫자의 왼쪽에는 힌두-아랍 숫자처럼 작은 숫자가 배치되었다.나중에 이집트인들은 숫자를 나타내기 위해 상형문자 대신 상형문자를 사용했다.히에라틱은 필기체에 가까웠고 여러 그룹의 기호를 개별 기호로 대체했다.예를 들어, 4개를 나타내기 위해 사용된 4개의 수직선은 단일 수평선으로 대체되었습니다.이것은 진드 수학 파피루스(기원전 2000년–1800년)와 모스크바 수학 파피루스(기원전 1890년)에서 발견된다.이집트인들이 사용한 시스템은 지중해의 많은 다른 문명들에 의해 발견되고 수정되었다.이집트인들은 또한 기본 연산을 위한 기호를 가지고 있었다: 앞으로 가는 다리는 덧셈을 나타내고 뒤로 걷는 다리는 뺄셈을 나타낸다.
메소포타미아인들은 10의 [10]각 거듭제곱에 대한 상징을 가지고 있었다.나중에, 그들은 현대와 거의 똑같은 방식으로 그들의 숫자를 썼다.각 10의 거듭제곱에 대한 기호가 있는 대신 이 숫자의 계수를 입력합니다.각 자릿수는 띄어쓰기로만 구분되어 있었지만 알렉산더 대왕의 시대에는 0을 나타내는 기호와 자리 표시자가 되었다.메소포타미아인들은 또한 60진법이라는 60진법을 사용했다.현대에서 시간과 각도를 측정할 때 사용되는 시스템입니다.바빌로니아 수학은 1850년대 [11]이후 발굴된 400개 이상의 점토판에서 파생되었다.쐐기꼴 문자로 쓰인 이 명판은 점토가 촉촉할 때 새겨졌고 오븐이나 태양의 열기에 의해 단단하게 구워졌다.이것들 중 일부는 채점된 숙제로 보인다.쓰여진 수학의 가장 초기의 증거는 기원전 3000년의 고대 수메르인들과 도량형 체계로 거슬러 올라간다.기원전 2500년경부터 수메르인들은 점토판에 곱셈표를 쓰고 기하학적 운동과 분할 문제를 다루었다.바빌로니아 숫자의 초기 흔적 또한 이 [12]시대로 거슬러 올라간다.
대부분의 메소포타미아 점토판은 기원전 1800년부터 1600년까지 거슬러 올라가며, 분수, 대수, 2차 방정식, 입방정식, 그리고 규칙, 역수,[13] 쌍의 계산을 포함하는 주제를 다룬다.태블릿에는 곱셈표와 선형 방정식과 이차 방정식을 푸는 방법도 포함되어 있습니다.바빌로니아 태블릿 YBC 7289는 소수점 이하 5자리까지 정확히 2파운드입니다.바빌로니아 수학은 60진법으로 작성되었다.이를 통해 1분당 60초, 1시간당 60분, 원 안에서 360도(60×6)의 현대적 용법뿐만 아니라 1도의 분수를 나타내기 위해 분, 초의 호를 사용한다.바빌로니아 수학의 발전은 60이 많은 제수를 가지고 있다는 사실에 의해 촉진되었다: 60의 제수의 배수인 정수의 역수는 60의 밑변에서 유한한 팽창을 가진다. (십진수 산술에서, 2와 5의 배수만이 유한한 십진수 팽창을 가지고 있다.또한 이집트인, 그리스인, 로마인들과 달리, 바빌로니아인들은 진정한 자리 가치 체계를 가지고 있었는데, 왼쪽 열에 쓰여진 숫자는 십진법에서처럼 더 큰 가치를 나타낸다.그러나 그들은 소수점에 상당하는 것이 부족했고, 그래서 종종 문맥에서 기호의 자리값을 추론해야 했다.
동기 단계
수학의 역사는 확실히 이오니아 그리스 이전의 어느 학파나 시대로 거슬러 올라갈 수 없지만, 이후의 역사는 그 구별이 충분히 잘 나타나는 시기로 나눌 수 있다.기하학 연구로 시작된 그리스 수학은 시작부터 연역적이고 과학적인 경향을 보였다.서기 4세기 이후, 피타고라스는 일반적으로 직각 삼각형에서 빗변의 정사각형 면적 (직각 반대쪽 변)이 다른 두 [note 5]변의 정사각형 면적 합계와 같다는 것을 나타내는 기하학상의 정리인 피타고라스 정리를 발견했다는 공로를 인정받았다.고대 수학 텍스트는 앞서 언급한 고대 이집트 표기법과 플림프턴 322(바빌로니아 수학 c. 1900 BC)와 함께 사용할 수 있습니다.수학 자체의 과목으로서의 연구는 기원전 6세기에 고대 그리스어 μμα (mathema)에서 "[14]수학적"이라는 용어를 만든 피타고라스인들과 함께 시작되었는데, 그는 "교육의 과목"을 의미한다.
플라톤의 영향력은 특히 수학과 과학에서 강했다.그는 현재 숫자 이론이라고 불리는 "산술"과 현재 산술이라고 불리는 "논리학적" 사이의 차이를 넓힘으로써 순수 수학과 응용 수학 사이의 차이를 구별하는 데 도움을 주었다.그리스 수학은 방법(특히 연역적 추론과 증명에서의 수학적 엄격함의 도입을 통해)을 크게 개선했고 [15]수학의 주제를 확장했다.아리스토텔레스는 나중에 배제의 법칙이라고 불리게 된 것에 대해 공로를 인정받고 있다.
추상 Mathematics[16]magnitude[노트 6]이나 양의 간식, 절대적이고 일반적으로, 특정 크기의 기하학과 산수 같은 어떤 종들,와 관계 없이 이런 의미에서, 추상적 수학 혼합 수학, 거기에 단순하고 추상적인 속성, 뇌의 관계를 소박하게에 반대한다 주어진다.여겨진다수학에서, 는 감각적인 물체에 적용되며, 그 수단에 의해 유체정역학, 광학, [16]항법 등과 같은 물리적 고려사항과 혼합된다.
아르키메데스는 일반적으로 고대의 가장 위대한 수학자이며 [17][18]역사상 가장 위대한 수학자 중 한 명으로 여겨진다.그는 포물선의 원호 아래 면적을 무한 급수의 합으로 계산하기 위해 소진 방법을 사용했고,[19] 놀라울 정도로 정확한 파이 근사치를 제공했습니다.그는 또한 자신의 이름이 새겨진 나선형, 혁명의 수량을 나타내는 공식, 그리고 매우 많은 수를 표현하는 기발한 체계를 정의했다.
기하학의 역사적 발전에서 기하학의 추상화 단계는 고대 그리스에 의해 이루어졌다.유클리드의 원소는 평면 기하학의 공리에 대한 현존하는 최초의 문서이다.프로쿠스는 [20]키오스의 히포크라테스에 의한 초기 공리화를 말한다.유클리드의 원소(기원전 300년경)는 현존하는 가장 오래된 그리스 수학 논문[note 7] 중 하나이며 알렉산드리아어로 쓰여진 13권의 책으로 구성되어 있다. 다른 수학자들이 증명한 정리들을 모아 몇몇 독창적인 [note 8]작품들에 의해 보충되었다.이 문서는 정의, 공식(축), 명제(이론과 구성) 및 명제의 수학적 증명에 대한 성공적인 모음입니다.유클리드의 첫 번째 정리는 소수의 성질을 갖는 보조정리이다.영향력 있는 13권의 책은 유클리드 기하학, 기하학 대수학, 그리고 고대 그리스 버전의 대수 체계와 초등수 이론을 다룬다.그것은 쿼드리비움 어디에나 있었고 논리학, 수학, 과학의 발전에 중요한 역할을 한다.
알렉산드리아의 디오판토스는 산술메티카라고 불리는 일련의 책을 썼는데, 그 책들 중 많은 것들이 지금은 사라졌습니다.이 텍스트들은 대수 방정식을 푸는 것을 다룬다.보에티우스는 6세기 산수, 기하학, 천문학, 그리고 음악의 연구를 설명하기 위해 쿼드리비움이라는 용어를 만들었을 때 교과 과정에 수학을 위한 장소를 제공했습니다.그는 니코마치 산술 입문서의 그리스어 번역본인 De institutione 산술메티카, 또한 그리스 자료에서 파생된 De institutione musica, 그리고 유클리드의 요소에서 발췌한 일련의 발췌본을 썼다.그의 작품들은 실용적이기보다는 이론적인 것이었고 그리스와 아랍의 수학 [21][22]작품들이 회복될 때까지 수학 연구의 기초가 되었다.
아크로포닉과 마일즈 수
그리스인들은 이집트인들의 체계에 기초하고 나중에 로마에 의해 개조되고 사용된 아티케 [23]번호를 사용했다.그리스 숫자 1부터 4까지는 상형문자와 같이 세로줄이었다.5의 기호는 그리스 문자 δ (pi)로, 5를 뜻하는 그리스 단어의 글자 펜테이다.6번부터 9번까지는 펜테 옆에 세로줄이 그려져 있었다.10은 10을 나타내는 글자(δ), 데카(deka), 100을 나타내는 글자( etc) 등으로 표현되었다.
이오니아 숫자는 세 개의 고대 문자를 포함한 알파벳 전체를 사용했다.그리스인의 숫자 표기법은 현재 사용되고 있는 것보다 훨씬 덜 편리했지만, 완벽하게 규칙적이고 과학적인 [24]계획으로 형성되었고, 로마체제는 전혀 적용되지 않는 계산수단으로 충분히 효과적으로 사용될 수 있었다.그리스인들은 알파벳의 24자를 세 가지 등급으로 나누었고, 각 등급에 다른 기호를 추가함으로써, 그들은 단위, 10, 그리고 수백을 나타내는 문자를 가지고 있었다.(Jean Bestice Joseph Delambre의 천문학자 Ancien, t. 2).
| α(α) | β(β) | г()) | δ()) | ε()) | ϝ()) | ζ()) | η()) | § (표준) | ι()) | κ()) | λ()) | μ(μ) | ν()) | ξ()) | op ( op ) | π()) | ϟ()) | ρ()) | σ()) | τ()) | υ()) | φ()) | χ()) | ψ()) | ω()) | ϡ()) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
이 체계는 디감마(am), 카파(ppa), 샘피(i)가 없어지기 전인 기원전 3세기에 나타났다.소문자가 대문자와 구별되면 소문자가 표기 기호로 사용되었습니다.앞에 획을 긋는 9개의 숫자에 1,000의 배수가 쓰여졌다. 즉, 1,000은 ",α", 2,000은 ",β" 등이었다. M은 10,000을 곱하는 데 사용되었다.예를 들어 88,888,888은 M으로 표기됩니다[25].
그리스의 수학적 추론은 거의 전적으로 기하학적이었고, 그래서 그리스인들은 대수적 기호에 관심이 없었다.큰 예외는 위대한 대수학자 [26]알렉산드리아의 디오판토스였다.그의 산술메티카는 방정식에서 기호를 사용하는 텍스트 중 하나였다.그것은 완전히 상징적이지는 않았지만, 이전의 책들보다 훨씬 더 그랬다.알 수 없는 번호가 [27]s로 호출되었습니다.s의 제곱은 y \ \^ {}, 큐브는 K y{ 은 y 은 y \ \[28][note 9]。
중국인들은 집계 [29]시스템과 매우 흡사한 숫자를 사용했다.1번부터 4번까지는 가로줄이었어요.5는 두 가로줄 사이의 X로, 10의 로마 숫자와 거의 똑같아 보였다.오늘날 화목제는 중국 시장이나 전통적인 수기 송장에 가격을 표시하는 데만 사용된다.
중국 역사에는 산수, 기하학, 역학, 광학, 항해, 천문학 등의 과학에 정통한 사람들이 있었다.중국의 수학은 기원전 [30]11세기에 독립적으로 등장했다.중국인들이 몇몇 기하학적 혹은 다소 건축적인 [note 10]도구들, 기계 기계들,[note 11] 자기 바늘의 특징적인 특성에 대해 알고 있었고 천문학적 사건들이 주기적으로 일어난다는 것을 알고 있었다는 것은 거의 확실하다.당시 중국인들은 그들이 알고 있던 산수나 기하학의 법칙을 분류하거나 확장하여 그들이 알고 있던 현상의 원인을 설명하려고 시도했다.중국은 독립적으로 매우 크고 음의 숫자, 십진수, 자리값 십진수, 이진법, 대수, 기하학, 삼각법을 개발했다.
중국의 수학은 자리값 [31][32]체계를 포함한 초기 공헌을 했다.고대 중국인들이 알고 있던 기하학적 정리는 어떤 경우(즉 [note 12]변의 비율)에 적용할 수 있었다.준실험적 중첩 방식으로 증명될 수 있는 기하학적 이론도 그들에게 알려져 있었다는 것이다.산수에서 그들의 지식은 백조판을 통한 계산술과 그 결과를 글로 표현하는 힘에 국한된 것으로 보인다.중국인들의 초기 성취에 대한 우리의 지식은 비록 미미하지만, 대부분의 동시대인들의 경우보다 더 완전하다.한 국가가 응용 예술에 상당한 기술을 가지고 있다고 알려질 수 있지만, 그러한 예술의 기초가 되는 후기 수학에 대한 우리의 지식은 부족할 수 있다는 것은 따라서 유익하고 사실을 보여주는 역할을 한다.기원전 254년 이전의 중국 수학에 대한 지식은 다소 단편적이며, 심지어 이 날짜 이후에도 원고 전통은 모호하다.중국 학자들은 확인된 고고학적 증거가 동반되지 않는 한 고전시대 이전 수세기 동안을 일반적으로 추측으로 간주한다.
다른 초기 사회와 마찬가지로 농업 달력을 완성하기 위해 천문학에 초점을 맞췄고, 공식적인 시스템을 구축하는 데 초점을 맞추지 않았다.중국 수학원의 의무는 연감, 연감, 연감, 일자와 예측에 한정되었다.고대 중국의 수학자들은 자명한 접근법을 개발하지 않고 알고리즘 개발과 대수학에 있어 진보했다.중국 대수의 업적은 13세기에 주석제가 4개의 미지수를 발명하면서 절정에 달했다.
언어적·지리적 장벽과 내용적 장벽이 뚜렷해 중국 수학과 고대 지중해의 수학은 수학예술 9장이 완성될 때까지 다소 독립적으로 발전한 것으로 추정된다.나는 고전 그리스 수학과 대략 동시대적이다.적어도 로마 시대부터 알려진 문화 교류를 통해 아시아 전역에서 어떤 의견 교환이 있을 것 같다.종종, 초기 사회의 수학의 요소들은 기하학이나 수 이론과 같은 현대 수학의 분과에서 나중에 발견되는 기초적인 결과에 대응합니다.예를 들어 피타고라스의 정리는 주공 시대에 증명되었다.파스칼의 삼각형에 대한 지식은 또한 심궈에 의해 [33]파스칼보다 수세기 전에 중국에 존재했던 것으로 나타났다.

중국의 삼각법 상태는 송 왕조(960–1279) 동안 서서히 변화하고 발전하기 시작했고, 송 왕조(960–1279)는 중국의 수학자들이 달력 과학과 천문 [34]계산에서 구면 삼각법의 필요성을 강조하기 시작했다.박식한 중국의 과학자, 수학자 그리고 관리인 Shen Kuo (1031–1095)는 화음과 [34]호의 수학 문제를 풀기 위해 삼각함수를 사용했습니다.Sal Restivo는 원의 호 길이에 대한 Shen의 연구가 수학자이자 천문학자 Guo Shoujing (1231–1316)[35]에 의해 13세기에 개발된 구면 삼각법의 기초를 제공했다고 쓰고 있다.역사학자 L. Gauchet과 Joseph Needham이 말했듯이, Guo Shoujing은 달력 체계와 중국 [36][37]천문학을 개선하기 위해 구면 삼각법을 계산에서 사용했습니다.중국의 수리 과학은 13세기 동안 중국에 온 구면 삼각법에 대한 지식을 가진 아랍 선교사들의 작업과 가르침을 포함시켰다.
인도 및 아라비아 숫자와 표기법
비록 우리의 현재 숫자 표기법의 기원이 고대이긴 하지만, 그것이 2천 년 전에 힌두교인들 사이에서 사용되었음은 의심의 여지가 없다.인도 수학자 브라흐마굽타의 대수 표기법은 동기화되었다.덧셈은 숫자를 나란히 배치하고, 뺄셈은 서브헨드(뺄셈할 수 있는 수) 위에 점을 배치하고, 나눗셈은 우리의 표기법과 비슷하지만 막대가 없는 배당금 아래에 제수를 배치하여 표시하였다.곱셈, 진화 및 미지의 양은 적절한 [38]용어의 약어로 표현되었다.오늘날 전 세계에서 사용되고 있는 힌두-아랍 숫자 체계와 그 운영의 사용 규칙은 아마도 서기 1천년의 과정 동안 진화했고 이슬람 [39][40]수학을 통해 서양으로 전달되었을 것이다.
이름에도 불구하고 아라비아 숫자는 인도에 뿌리를 두고 있다.이러한 잘못된 명칭의 이유는 유럽인들이 모홈메드 이븐 무사 알 크와리즈미의 아랍어 책 "힌두교 계산에 대하여"에서 사용된 숫자들을 보았기 때문이다.알-크와리즈미는 힌두-아랍 숫자와 방정식을 푸는 방법에 대한 몇 가지 중요한 책을 썼습니다.알-킨디의 [note 13]연구와 함께 약 825년에 쓰여진 그의 책 "힌두 숫자를 사용한 계산에 대하여"는 인도의 수학과 인도 숫자를 서양에 전파하는 데 중요한 역할을 했다.알-크와리즈미는 숫자를 아랍어라고 주장하지 않았지만, 몇몇 라틴어 번역에 따르면 숫자들이 인도어라는 사실은 사라졌다.알고리즘이라는 단어는 Al-Khwarizmi의 이름인 Algoritmi와 Al-Kitab al-mukhtaarar f h hīsabr wa'l-muqabala(계산 및 계산에 의한 완료에 관한 포괄적인 책)의 제목에서 유래했다.
이슬람 수학은 중앙아시아 [41]문명에 알려진 수학을 발전시키고 확장시켰다.알-크와리즈미는 양의 [42]근을 갖는 2차 방정식의 대수적 해법에 대해 철저한 설명을 했고, 알-크와리즈미는 대수학을 기초적인 형태로 그리고 그 자체를 [43]위해 가르치는 것이었다.Al-Khawarizm also는 또한 "축소"와 "균형"의 근본적인 방법에 대해 논의했으며, 감산된 항이 방정식의 반대쪽, 즉 방정식의 반대쪽에서 유사한 항을 상쇄하는 것을 언급하였다.이것은 원래 알-크와리즈미가 [44]알-자브르라고 묘사한 작전이다.그의 대수학은 또한 더 이상 "해결되어야 할 일련의 문제에 관한 것이 아니라, 조합이 방정식을 위한 모든 가능한 프로토타입을 제공해야 하는 원시적인 용어로 시작하는 설명"에 관한 것이었고, 따라서 분명히 진정한 연구 대상을 구성합니다.Al-Khawarizm also는 또한 방정식을 그 자체로 연구했고 "단순히 문제를 푸는 과정에서 나타나는 것이 아니라 무한한 종류의 [45]문제를 정의하도록 특별히 요구받는 한 일반적인 방식으로"를 연구했다.
Al-Karaji는 그의 논문 al-Fakhri에서 방법론을 확장하여 정수 검정력과 [note 14][46]미지의 양의 정수 루트를 통합한다.수학사학자 F.Woepcke는 [47]알-Karaji가 "대수 미적분 이론을 최초로 도입한 사람"이라고 칭찬했다.또한 10세기에 Abul Wafa는 디오판투스의 작품을 아랍어로 번역했다.Ibn al-Haytham은 해석 기하학을 발전시켰다.Al-Haytham은 적분력의 합에 대한 일반 공식을 결정하기 위해 쉽게 일반화할 수 있는 방법을 사용하여 4제곱의 합에 대한 공식을 도출했다.알-헤이담은 포물체의 부피를 구하기 위해 적분을 수행했고, 4차까지 [note 15][48]다항식의 적분에 대한 그의 결과를 일반화 할 수 있었다.11세기 후반에, 오마르 카이얌은 대수기하학을 발전시켰고, 유클리드의 [note 16]난관에 대한 토론을 썼으며, 입방정식의 일반적인 기하학적 해법에 대해 썼다.나시르 알-딘 투시는 구면 삼각법을 발전시켰다.이 기간 동안 무슬림 수학자들은 아라비아 숫자에 소수점 표기법을 추가하는 것을 포함한다.
전 세계에서 사용되는 현대 아랍 숫자 기호는 10세기에 이슬람 북아프리카에서 처음 나타났다.서양 아라비아 숫자의 독특한 변형은 10세기 경 마그레브와 알-안달루스에서 나타나기 시작했는데, 이것은 [49]전 세계에서 사용되는 현대 아라비아 숫자의 직접적인 조상이다.
그리고 나서 수학에 관한 많은 그리스어와 아랍어 텍스트들이 라틴어로 번역되었고, 이것은 중세 유럽에서 수학의 발전을 이끌었다.12세기에 학자들은 알 크와리즈미의 책과[note 17] 유클리드의 [note 18][50][51]원소 전문을 포함한 과학적인 아랍어 문헌을 찾아 스페인과 시칠리아를 여행했다.숫자 사용을 주창했던 유럽 책들 중 하나는 피보나찌로 더 잘 알려진 피사의 레오나르도가 쓴 리버 아바치였다.Liber Abaci는 피보나찌가 토끼 집단에 대해 쓴 수학적인 문제로 더 잘 알려져 있다.모집단의 성장은 결국 피보나치 수열로 끝났는데, 여기서 항은 앞의 두 항을 합한 것이다.
기호 단계
- 인기 소개 날짜별 기호
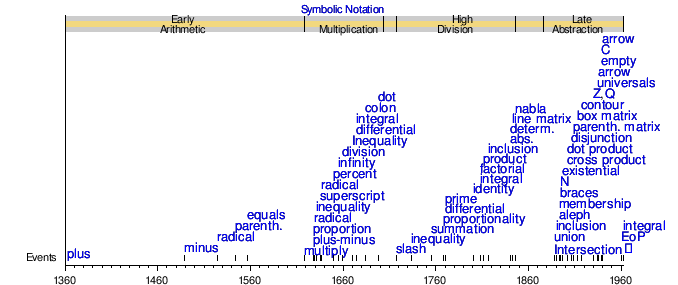
초기 산술 및 곱셈
기호만 사용되는 기호대수로의 전환은 이븐 알-반나의 알-마라쿠시(1256–1321)와 아부 알-하산 이븐 알-칼라ā(1412–1482)[52][53]의 연구에서 처음 볼 수 있다.알칼라사드는 중세 아랍의 마지막 대수학자로, 이븐 알-반나에 [54]의해 마그레브에서 초기에 사용된 대수 표기법을 개선했다.수학 [55]연산을 위한 기호가 부족했던 그들의 전임자인 디오판투스와 브라흐마굽타의 동시 표기와는 대조적으로, 알칼라디의 대수 표기법은 이러한 함수에 대한 기호를 가진 최초의 것이었고, 따라서 "대수 상징의 도입을 향한 첫 단계"였다.그는 아랍 [54]알파벳의 문자를 사용하여 수학적 기호를 표현했다.
14세기는 광범위한 [56]문제를 조사하기 위한 새로운 수학적 개념의 발전을 보았다.널리 사용되는 두 가지 산술 기호는 더하기와 빼기, +와 -입니다.플러스 부호는 니콜 오렘이[57][note 19] 1360년에 그의 작품인 알고리스무스 프로페셔널툼에서 [58]사용했다.라틴어로 "그리고"를 뜻하는 "et"의 줄임말로 생각되는데, 앰퍼샌드 기호도 "et"로 시작하는 것과 거의 같은 방식으로.파리 대학의 Oresme와 이탈리아의 Giovanni di Casali는 독립적으로 일정한 가속도를 나타내는 선 아래의 영역이 [59]이동된 총 거리를 나타낸다고 주장하면서 균일하게 가속되는 물체에 의해 커버되는 거리를 그래픽으로 표현했다.빼기 부호는 1489년 요하네스 비드만(Johannes Widmann)이 상업 산술 또는 베헨데 und Hüpsche Rechenung auff Allen Kauffmanschafft에서 사용했다.[60]Widmann은 마이너스 기호와 플러스 기호를 사용하여 각각 [61]결손과 잉여를 나타냅니다.Summa de arcemetica, geometria, propotioni e propotioni [note 20][62]e propotialita에서 Luca Pacioli는 플러스 기호와 마이너스 기호를 사용했고 [note 21]대수를 포함했다.
15세기에 기야트 알 카시는 computed의 값을 소수점 16위까지 계산했다.Kashi는 n번째 [note 22]루트를 계산하는 알고리즘도 가지고 있었다.1533년에 레지오몬타누스의 사인표와 코사인표가 출판되었다.[63]Scipione del Ferro와 Niccol font Fontana Tartaglia는 입방정식의 해법을 발견했다.제롤라모 카르다노는 그의 제자 로도비코 페라리가 발견한 4차 방정식에 대한 해법과 함께 1545년 저서 아르스 마그나에 그것들을 실었다.제곱근의 급진적[note 23] 기호는 크리스토프 [note 24]루돌프에 의해 도입되었다.마이클 스티펠의 중요한 작품인 산술적분학은 수학 표기법의[64] 중요한 혁신을 포함하고 있다.1556년 Niccol®Tartaglia는 우선 순위 그룹화에 괄호를 사용했습니다.1557년 로버트 레코드는 등호(=)와 영어 독자를 위한 플러스 기호와 마이너스 기호를 도입한 위트의 휘트스톤을 출판했다.1564년, Gerolamo Cardano는 확률론의 초기 단계를 시작하는 우연의 게임을 분석했습니다.1572년 라파엘 봄벨리는 입방정식을 푸는 카르다노의 공식에 나타날 수 있는 상상의 양을 다루는 방법을 보여주는 그의 라알게브라를 출판했다.1585년 네덜란드어로 출판된 사이먼 스테빈의 책 De Thiende ('10분의 1의 예술')는 십진법 표기의 체계적인 처리를 포함하였고, 이는 이후 모든 실수 체계에 영향을 미쳤다.프랑수아 비에트의 새로운 대수학 (1591)은 대수적 표현의 현대적 표기 조작을 도입했다.넓은 지역을 탐색하고 정확한 지도를 만들기 위해 삼각법은 수학의 주요 분야로 성장했다.바르톨로마이우스 피티스쿠스는 1595년에 그의 삼각법을 발표하면서 "트리고메트리"라는 단어를 만들었다.
존 네이피어는 대수의[note 25][65] 발명가로 가장 잘 알려져 있으며 산수와 [66][67]수학에서 소수점을 사용하는 것을 보편화했다.네이피어 이후 에드먼드 건터는 슬라이드 규칙의 기초가 되는 로그 척도(선 또는 규칙)를 만들었고, 윌리엄 코스트레드는 직접 곱셈과 나눗셈을 수행하기 위해 서로 미끄러지는 두 척도를 사용했다. 그리고 그는 1622년 슬라이드 규칙의 발명가로 인정받는다.1631년 소레드는 곱셈 기호(×)를 도입했고, [note 26]사인 함수와 코사인 함수를 [68]위해 sin과 cos를 약자로 쓴다.Albert Girard는 또한 그의 논문에서 삼각함수에 'sin', 'cos', 그리고 'tan'의 약어를 사용했다.
요하네스 케플러는 무한수의 [note 27]수학적 응용의 선구자 중 한 명이었다.르네 데카르트는 해석기하학의 아버지로서 대수학과 [note 28]기하학을 잇는 가교로서 미적분학과 해석학의 발견에 중요한 역할을 했다.17세기에 데카르트는 해석 [note 29]기하학의 발전을 가능하게 하는 데카르트 좌표를 도입했다.블레즈 파스칼은 평생 수학에 영향을 미쳤다.1653년에 그가 쓴 "산술 삼각형에 대한 처리"는 이항 [note 30]계수에 대한 편리한 표 형식의 표현을 묘사했다.Pierre de Fermat와 Blaise Pascal은 [note 31]확률을 조사할 것이다.존 월리스는 무한대 기호를 [note 32]도입했다.그는 마찬가지로 이 표기법을 [note 33]무한소수에 사용했다.1657년 Christiaan Huygens는 확률에 관한 논문 "운명의 [note 34][69]게임에서의 추론에 대하여"를 출판했다.
요한 란(Johann Rahn)은 1659년에 분할 기호(,, 오벨루스 변종)와 그에 따른 기호를 도입했다.윌리엄 존스는 1706년 시놉시스 팔마리오룸 마테시오스에서[70] in를 사용했는데, 이는 그리스어로 둘레를 뜻하는 페리메트론(imetεμμδο)의 첫 글자이기 때문이다.이 용법은 1737년 오일러에 의해 대중화 되었다.1734년, 피에르 부게르는 부등호 [71]아래에 이중 수평 막대를 사용했다.
도함수 표기법:라이프니츠와 뉴턴
| 파생 표기법 | |
|---|---|
| |
선형대수의 연구는 선형방정식의 체계를 풀기 위해 사용된 결정인자의 연구에서 비롯되었다.미적분학에는 두 가지 주요 표기법이 있었는데, 각각 창안자 중 한 명이 창안했다: 아이작 뉴턴이 개발한 표기법과 고트프리드 라이프니츠가 개발한 표기법은 각각 아이작 뉴턴과 고트프리드 라이프니츠입니다.라이프니츠는 오늘날 가장 자주 사용되는 표기법이다.뉴턴의 것은 단순히 함수 [note 35]위에 있는 점이나 대시였다.현대 용법에서, 이 표기법은 일반적으로 시간에 관한 물리량의 도함수를 나타내며, 역학의 과학에서 자주 사용된다.반면 라이프니츠는 d를 접두사로 사용해 미분화를 나타내며 미분수를 나타내는 표기법을 [note 36]도입했다.이 표기법은 함수의 도함수가 취해지는 변수를 명시합니다.라이프니츠는 또한 적분 [note 37]기호를 만들었다.기호는 "sum"을 뜻하는 라틴어 Suma를 나타내는 길쭉한 S입니다.곡선 아래의 영역을 찾을 때, 종종 면적을 무한히 많은 높고 얇은 직사각형으로 분할하여 통합이 설명됩니다. 이 직사각형은 면적이 추가됩니다.따라서 적분 기호는 합계의 경우 길쭉한 s입니다.
고분할 연산자 및 함수
이 시기에 알파벳의 문자는 양의 상징으로 사용되었고, 문자의 선택과 관련하여 많은 다양성이 존재했지만, 다음 [24]역사에는 보편적으로 인정된 몇 가지 규칙이 있었다.따라서 방정식의 역사에서 알파벳의 첫 글자는 계수로 알려졌고, 마지막 글자는 알려지지 않은 용어(inserti orderis)로 알려졌습니다.대수기하학에서도 마찬가지로 알파벳의 마지막 글자가 변수 또는 현재 좌표를 나타낸다. { e { e 등과 같은 특정 문자는 보편적 동의에 의해 자주 발생하는 숫자 3.14159 및 2.7182818 [note 38]등의 기호로 지정되었으며,[24] 다른 문자는 가급적 사용하지 않도록 하였다.문자는 조작 기호로 사용되어야 하며, 앞서 언급한 임의의 조작 문자와 함께 사용되어야 한다.미적분 및 적분에서는 문자d\displaystyle d S\S, 차분에서는 \를 [24]수술 기호로 사용하기로 했다.기능적 표기법에서 문자는 조작의 기호로서 [24][note 39]수량의 기호로 간주되는 문자와 조합된다.
1718년부터 토마스 트윈인은 분할 슬래시(solidus)를 사용하여 초기 아랍어 수평 분수 막대에서 파생했습니다.피에르-시몽 드 라플라스 후작은 널리 사용되는 라플라스 미분 [note 40]연산자를 개발했습니다.1750년, 가브리엘 크레이머는 선형 시스템을 풀기 위한 "크래머의 법칙"을 개발했습니다.
오일러와 소수 표기법
레온하르트 오일러는 역사상 가장 다작의 수학자 중 한 명이었고, 정준 표기법의 다작 발명가이기도 했다.그의 공헌은 자연 로그의 밑수를 나타내기 위해 e를 사용하는 것을 포함한다.e를 는 정확히 알려지지 않았지만, 아마도 알파벳의 네 글자가 변수와 다른 상수를 나타내기 위해 이미 일반적으로 사용되었기 때문일 것입니다.오일러는 파이를 일관되게 나타내기 위해 {\를 사용했습니다.displaystyle의 사용은 William Jones에 의해 제안되었습니다. William Jones는 이것을 경계선의 약어로 사용했습니다.오일러는 음수 [note 41][note 42][note 43]1의 제곱근을 나타내기 위해했지만, 이전에는 무한대로 사용했다.합계를 위해 오일러는 시그마 [note 44]δ를 사용했다.함수의 경우, 오일러는의 를 나타내기 위해 (x) {f 을 사용했다. 1730년에 오일러는 감마 [note 45]함수를 썼다.1736년, 오일러는 그래프 이론의 연구를 시작한 쾨니히스베르크의[72] 일곱 다리에 관한 논문을 작성했습니다.
수학자 윌리엄[73] 에머슨은 비례 [note 46][note 47][74][75]부호를 발달시킬 것이다.다양한 비례 현상의 값에 대한 추상적 표현에서 훨씬 후에, 표기법 당 부품은 다양한 차원 없는 양의 작은 값을 설명하는 의사 단위 집합으로서 유용하게 사용될 것이다.1768년 콘도르세 후작은 부분 미분 부호를 [note 48]발전시켰다.1771년 알렉상드르 테오필 반데르몽드는 위치 기하학과 관련된 매듭의 특성을 논할 때 위상 특성의 중요성을 추론했다.1772년과 1788년 사이에, 조셉 루이 라그랑주는 라그랑주 역학이라고 불리는 고전적인 "뉴턴" 역학의 공식과 계산을 다시 공식화했다.파생상품의 주요 기호 또한 라그랑주에 의해 만들어졌다.
그러나 우리의 견해로는 이런 종류의 진실은 표기가 아닌 개념에서 도출되어야 한다.
--
가우스, 해밀턴 및 매트릭스 표기법
19세기 초에 카를 프리드리히 가우스는 일치 관계에 대한 동일 부호를 개발했고, 2차 상호주의에서는 적분 부분을 개발했습니다.가우스는 기하학 및 급수의 수렴에 복잡한 변수의 함수를 기여했다.그는 대수학의 기본정리와 2차상호법칙에 대한 만족스러운 증거를 제시했다.가우스는 처음에 측지학의 [76]발전으로 등재된 가우스 소거를 이용하여 선형 시스템을 푸는 이론을 개발했습니다.그는 또한 제품 간판을 개발할 것이다.또한 이 시기에 닐스 헨리크 아벨과 에바리스[note 50] 갈로아는 군 이론과 장이론을 연결하는 방정식의 용해성에 대한 연구를 수행하였다.
1800년대 이후, Christian Kramp는 정수 [77]이외의 사람들에게 적용되는 일반화 요인 함수를 연구하는 동안 요인 표기법을 장려했습니다.Joseph Diaz Gergonne은 세트 포함 사인을 [note 51]소개했다.피터 구스타프 르준 디리클레는 산술 급수에 대한 디리클레의 정리를 증명하기 위한 디리클레 L-함수를 개발했고 해석적 수 [note 52]이론을 시작했습니다.1828년, 가우스는 표면의 특성을 확립하면서 그의 이론(라틴어로 주목할 만한 정리)을 증명했다.1830년대에 George Green은 Green의 기능을 개발했다.1829년에.Carl Gustav Jacobi는 그의 타원 세타 함수와 함께 Fundama nova evertioniae functionum ellipticarum을 출판했다.1841년까지, "현대 분석의 아버지"인 칼 바이어스트래스는 절대 가치의 개념과 행렬의 결정 인자에 대해 상세히 설명했습니다.
매트릭스 표기법은 아서 케일리가 라그랑주의 메카니크 분석서와[78] 라플라스의 작품 중 일부를 읽음으로써 제안된 주제에 대해 그의 세 논문에서 더욱 완전하게 개발될 것이다.케일리가 정의한 행렬 곱셈과 행렬 역수.케일리는 [79]행렬을 나타내기 위해 하나의 문자를 사용했고, 따라서 행렬을 집합체로 취급했습니다.그는 또한 행렬과 [80]행렬의 연관성을 깨닫고, "이 행렬 이론에 대해, 내가 보기에, 행렬 이론보다 앞서야 할 많은 말들이 있을 것이다."[81]라고 썼다.
[...] 수학 사분원은 4차원을 가지거나 적어도 참조를 포함한다.
--
William Rowan [82][83]Hamilton은 벡터 미분 기호인 nabla[note 54] 기호를 도입할 것이다.이것은 해밀턴에 의해 범용 연산자 [84]기호로 이전에 사용되었습니다.해밀턴은 현재 해밀턴 역학이라고 불리는 뉴턴 역학을 재구성했다.이 연구는 전자기학과 같은 고전장 이론의 현대 연구의 중심인 것으로 입증되었다.이것은 또한 양자역학의 [note 55]발전에 중요했다.수학에서, 그는 아마도 4분위[note 56] 표기법과 4분위수의 발명가로 가장 잘 알려져 있다.해밀턴은 또한 [85][note 57]1846년에 "텐서"라는 단어를 도입했습니다.제임스 코클은 테사린과[note 58] 1849년에 코쿼티온을 개발했다.1848년 제임스 조셉 실베스터는 행렬 대수학에 [note 59]행렬이라는 용어를 도입했다.
Maxwell, Clifford 및 Ricci 표기법
1864년 제임스 클러크 맥스웰은 당시 전자기학에 대한 모든 지식을 20개의 변수에서 20개의 방정식을 가진 연결된 미분 방정식의 집합으로 줄였다.[87]이 계산법은 라그랑주(Lagrange)에 의해 제시되었으며, 이후 해밀턴의 방정식에 의해 약간의 수정과 함께 개발되었다.이것은 보통 해밀턴의 원리로 언급된다; 원래의 형태의 방정식이 사용될 때 그들은 라그랑주 방정식으로 알려져 있다.1871년에 리처드 데데킨드는 4개의 산술 연산에서 닫힌 실수 또는 복소수 집합을 필드라고 불렀다.1873년 맥스웰은 전기와 자성에 관한 논문을 발표했다.
1878년, 윌리엄 킹든 클리포드는 그의 [88]역동적인 요소를 출판했다.클리포드는 그가 대수적 모터라고 부르는 분할 [note 60]비쿼터니언을 개발했다.클리포드는 완전한 4분위 [note 61]표기법에서 두 벡터의 점곱과 교차곱을 분리함으로써 4분위 연구를 배제했다.이 접근방식은 3차원으로 작업하는 엔지니어와 다른 사람들이 벡터 미적분을 사용할 수 있게 [note 63]했고 4차원의 납-래그[note 62] 효과에 회의적이었다.공통 벡터 표기법은 벡터 공간의 공간적 또는 추상적 구성원인 벡터를 다룰 때 사용되는 반면 각도 표기법(또는 위상 표기법)은 전자 공학에서 사용되는 표기법입니다.
1881년 레오폴드 크로네커는 그가 "합리성의 영역"이라고 부르는 것을 정의했는데, 이것은 현대 [89]용어로 유리수 영역의 확장이다.1882년 휘세인 테브픽는 "선형 대수"[90][91]라는 책을 썼다.켈빈 경의 에테르 원자론은 1885년 피터 거스리 타이트를 타이트 추측으로 알려진 최대 10개의 교차가 있는 매듭의 위상 표를 발표하도록 이끌었다.1893년 하인리히 M. 웨버는 추상적인 [note 64]분야에 대한 명확한 정의를 내렸다.텐서 미적분은 1887년과 1896년 사이에 그레고리오 리치-쿠르바스트로에 의해 개발되었고, 1892년에 절대미분학이라는 제목으로 제시되었고, "텐서"[92]의 현대 용법은 1898년에 [93]월드마르 보이트에 의해 언급되었다.1895년에 앙리 푸앵카레는 Analysis Situs를 [94]출판했다.1897년, 찰스 프로테우스 스타인메츠는 에른스트 [95]버그의 도움을 받아 교류 현상의 이론과 계산을 출판했다.
공식 수학에서 텐서까지
위의 제안은 때때로 유용하다.
--
1895년, 주세페 페아노는 특별한 기호를 바탕으로 수학을 간결한 텍스트로 소화하려는 노력인 그의 공식적 수학을 [96]발표했다.그는 벡터 공간과 선형 지도의 정의를 제공할 것이다.그는 또한 교차로 기호, 결합 기호, 멤버십 기호(요소) 및 실존적 수량화[note 66](존재)를 도입할 것이다.페아노는 1900년 파리 컨퍼런스에서 버트런드 러셀에게 그의 작품을 넘겼다; 그것은 러셀에게 깊은 인상을 주었기 때문에 러셀 역시 수학을 보다 간결하게 표현하려는 의욕에 사로잡혔다.그 결과는 알프레드 노스 화이트헤드와 함께 쓴 프린키피아 매스매티카였다.이 논문은 상징이 지배적인 현대 [note 67]문학의 분수령이다.
Ricci-Curbastro와 Tullio Levi-Civita는 1900년경 텐서 지수 [97]표기법을 대중화했다.
수학적 논리와 추상화
| 추상화 | |
|---|---|
이 기간의 시작에서, 펠릭스 클라인의 "에를랑겐 프로그램"은 다양한 기하학의 기본 테마를 확인하였고, 각각의 테마를 주어진 대칭 그룹 하에서 불변의 성질에 대한 연구로 정의하였다.이 추상화 수준은 기하학과 추상 대수학 사이의 연관성을 드러냈습니다.Georg[note 68] Cantor는 초한집합 [note 69]기수를 위해 알레프 기호를 도입할 것이다.그의 기수 표기법은 자연수 첨자를 가진 히브리 였다. 서수 표기법에는 그리스 문자 ((오메가)를 사용했다.이 표기법은 언어에 의미를 부여하는 체계에 따라 서수를 명명하는 유한 알파벳에서 기호의 유한한 서수 표기법에서 오늘날에도 여전히 사용되고 있다.그의 이론은 많은 논란을 일으켰다.칸토르는 푸리에 급수를 연구할 때 유클리드 공간의 점 집합을 고려했다.
20세기 이후, 조시아 윌러드 깁스는 물리 화학에서 도트 곱셈의 중간점과 교차 곱셈의 곱셈 기호를 도입했다.그는 벡터 분석에서 소개된 스칼라와 벡터 곱에 대한 표기법도 제공했습니다.1904년, 에른스트 체르멜로는 선택 공리와 질서 [98]정리에 대한 그의 증명을 장려했다.버트랜드 러셀은 그 직후인 1906년에 논리분할(OR)을 도입했다.또한 1906년에 푸앵카레는 "전자의 역학[99]"을 출판했고 모리스 프레셰는 미터법을 [100]도입했다.나중에 게르하르트 코왈레스키와 커스베르트 에드먼드[101][102][103] 컬리스는 각각 행렬 표기법, 상위행렬 및 상자행렬 표기법을 순차적으로 도입했다.1907년 이후 수학자들은[note 70] 매듭군의 관점에서 매듭을, 호몰로지 [note 71]이론에서 불변량을 연구했다.1908년, 조지프 웨더번의 구조 정리는 한 분야에 걸친 유한 차원 대수학을 위해 공식화되었습니다.1908년, 에른스트 체르멜로는 "확정한" 속성과 최초의 공리 집합론인 체르멜로 집합론을 제안했다.1910년에 에른스트 스타이니츠는 영향력 있는 논문인 '장 [note 72][note 73]대수론'을 발표했다.1911년, 스타인메츠는 일시적인 전기 현상과 진동의 이론과 계산론을 발표했다.
1916년에 알버트 아인슈타인은 공식에서 색인화된 일련의 용어들을 합한 아인슈타인[note 74] 표기법을 도입하여, 이를 통해 국가적인 간결성을 발휘했다.Arnold Sommerfeld는 1917년에 등고선 적분 기호를 만들었다.1917년, 디미트리 미리마노프는 규칙성의 공리를 제안한다.1919년, 테오도르 칼루자는 5차원을 사용하여 일반 상대성 방정식을 풀었고, 그 결과 전자기 방정식이 나타났다.[104]이것은 1921년에 "Zum Unitéts problem der Physik"[105]에 발표될 것이다.1922년 아브라함 프렝켈과 토랄프 스콜렘은 독립적으로 사양의 공리 스키마를 대체의 공리 스키마로 대체할 것을 제안했다.또한 1922년에는 체르멜로-프랭켈 집합론이 개발되었다.1923년, 스타인메츠는 상대성과 공간에 대한 네 가지 강의를 출판했다.1924년경, Jan Arnoldus Schouten은 20세기 [note 75][106][107][108]초에 일반상대성이론과 미분기하학에 절대미분을 적용하는 동안 리치 미적분 체계를 위한 현대 표기법과 형식주의를 발전시켰다.1925년, 엔리코 페르미는 파울리 배타 원리를 따르는 많은 동일한 입자로 이루어진 시스템을 설명하였고, 그 후 확산 방정식(페르미 나이 방정식)을 개발하였다.1926년 오스카 클라인은 칼루자-클레인 이론을 발전시켰다.1928년 에밀 아르틴은 아르티니아 고리로 고리 이론을 추상화했다.1933년, 안드레이 콜모고로프는 콜모고로프 공리를 도입했다.1937년 브루노 드 피네티는 "운영 주관적" 개념을 추론했다.
수학적 상징성
수학적 추상화는 수학적 [109][110]개념의 근본적인 본질을 추출하는 과정으로 시작되었고, 그것이 원래 [111]연결되어 있었을 수 있는 현실 세계의 물체에 대한 의존성을 제거하고, 동등한 현상에 대한 다른 추상적 기술들 사이에서 더 폭넓게 적용되거나 일치하도록 그것을 일반화했다.현대 수학의 두 가지 추상적인 영역은 범주 이론과 모델 이론이다.버트런드 [112]러셀은 "일반 언어는 일상 생활의 단어들이 충분히 추상적이지 않기 때문에 물리학이 실제로 주장하는 것을 표현하는데 전혀 적합하지 않습니다. 오직 수학과 수학 논리만이 물리학자가 말하고자 하는 것만큼 적게 말할 수 있다.그러나 수학은 실세계의 사물을 대체하고 방정식을 거치면서 [113]현실과 무관한 개념구조를 만들 수 있다.
기호논리는 기호열의 순수 형식적 특성을 연구한다.이 지역에 대한 관심은 두 가지 근원에서 나온다.첫째, 기호논리에서 사용되는 표기법은 철학논리에서 사용되는 단어를 나타내는 것으로 볼 수 있다.둘째, 심볼 로직에서 발견된 심볼을 조작하기 위한 규칙을 컴퓨팅 머신에서 구현할 수 있다.기호논리는 보통 명제논리와 술어논리의 두 개의 하위 필드로 나뉩니다.다른 관심 논리에는 시간 논리, 모달 논리 및 퍼지 논리가 포함됩니다.명제 미적분이라고도 불리는, 명제 논리학이라고 불리는 상징 논리학의 영역은 상수와 논리[note 76] 연산자로 형성된 문장의 특성을 연구합니다.대응하는 논리연산은 각각 접속, 접속해제, 물질조건부, 바이콘디셔널 및 부정으로 알려져 있다.이러한 연산자는 키워드 및 기호 표기로 표시됩니다[note 77].
이 기간 동안 도입된 수학 논리 표기법 중 일부는 부울 대수에서 사용되는 기호 집합을 포함했다.이것은 1854년 조지 불에 의해 만들어졌습니다.불 자신은 논리를 수학의 한 분야로 보지 않았지만, 어쨌든 논리는 포함되게 되었다.부울 대수에서 볼 수 있는 \land), \lor) 및 displaystyle\비표시)가 있습니다.이러한 기호와 서로 다른 진실 값을 나타내는 문자를 사용하여 (\ \1 즉 "a가 참" 또는 "a가 참이 아님"과 논리적인 진술을 할 수 있습니다. 즉, a는 참이거나 참이 아님(즉, 거짓)을 의미합니다.부울대수는 많은 실용성을 가지고 있지만 [note 78]논리학에서 사용되는 큰 기호 집합의 시작이기도 했다.원래 술어 미적분이라고 불리는 술어 논리는 변수의 도입과[note 79] [note 80]술어라고 불리는 변수를 포함하는 문장으로 명제 논리를 확장합니다.또한 술어 로직은 [note 81]수량자를 허용합니다.이러한 논리 기호와 술어 [note 82]논리로부터의 추가 수량자를 통해 비합리적으로 [note 83]인위적이지만 구문적인 유효한 [note 84]증거를 만들 수 있습니다.
괴델 불완전 표기법
공식의 모든 "일관된 재귀 클래스"에는 v Genr도 Neg(v Genr)도 Flg(θ)에 속하지 않는 재귀 클래스 부호 r이 대응한다(여기서 v는 r의 자유 변수이다).
--
그의 불완전성을 [note 85]증명하는 동안, Kurt Gödel은 논리학에서 일반적으로 사용되는 기호들에 대한 대안을 만들었다.그는 Gödel 수, 즉 정해진 숫자와 10보다 큰 소수를 가진 변수들을 사용했다.Gödel 숫자를 사용하면 논리문을 숫자 시퀀스로 나눌 수 있습니다.그리고 나서 괴델은 이것을 한 걸음 더 나아가 n개의 소수들을 수열 속 숫자들의 거듭제곱에 대입했다.그리고 이 숫자들을 곱하여 최종 산출물을 얻음으로써 모든 논리문에 고유한 [115][note 86]번호를 부여했습니다.
현대 표기법 및 토픽
20세기 초 표기법
표기법의 추상화는 진행 중인 과정이며 많은 수학적 주제들의 역사적 발전은 구체에서 추상화로의 진보를 보여준다.기본 객체 집합을 위해 다양한 집합 표기가 개발됩니다.1924년경, 데이비드 힐버트와 리처드 쿠랑은 "수학 물리학의 방법"을 출판했다. 편미분방정식"[116]입니다.1926년 오스카 클라인과 월터 고든은 상대론적 [note 87]입자를 설명하기 위해 클라인-고든 방정식을 제안했다.방사선과 물질 상호작용을 설명하는 양자 이론의 첫 공식은 1920년 동안 [117]원자의 자연 방출 계수를 처음으로 계산할 수 있었던 폴 아드리엔 모리스 디락 때문이다.1928년, 상대론적 디랙 방정식은 상대론적으로 움직이는 [note 88]전자의 행동을 설명하기 위해 디랙에 의해 공식화 되었다.Dirac은 전자기장의 정량화를 입자의 생성 및 소멸 연산자의 개념을 도입하면서 조화 진동자의 합체라고 설명했다.로 볼프강 파울리, 유진 위그너, 파스쿠알 요르단, 그리고 베르너 하이젠베르크 및 양자 전기 역학 엔리코 Fermi,[118]물리학자들로 인해 우아한 공식화에서 기고, 원칙적으로 어떤 물리적 과정 광자와 관련한 어떤 계산을 수행할 수 있을 것이다 믿고 왔다 그 다음 해에, pa. 부과rtic레즈
1931년 알렉산드루 프로카는 핵력의 벡터 중간자 이론과 상대론적 양자장 방정식을 위한 프로카 방정식(울러-라그랑주 방정식)[note 89]을 개발했다.1937년 John Archibald Wheeler는 S 매트릭스를 개발했습니다.1937년과 1939년에 펠릭스 블로흐와 아놀드 노드시크,[119] 그리고 빅터 와이스코프의 [120]연구는 그러한 계산이 로버트 오펜하이머가 [121]이미 지적한 문제인 섭동 이론의 첫 번째 순서에서만 믿을 수 있다는 것을 밝혀냈다.급수에서 더 높은 차수의 무한대가 나타나면서, 그러한 계산이 무의미해지고 이론 자체의 내부 일관성에 심각한 의문을 제기했습니다.그 당시에는 이 문제에 대한 해결책이 알려지지 않았기 때문에, 특수 상대성 이론과 양자 역학 사이에 근본적인 양립불가능성이 존재하는 것으로 보였다.
1930년대에 에드먼드 란다우가 정수 집합의 이중 대문자 Z를 만들었다.니콜라스 부르바키는 합리적인 숫자 집합을 위해 이중으로 된 자본 Q를 만들었다.1935년에 게르하르트 겐젠은 만능 수량화기를 만들었다.1936년, 타르스키의 정의 불능 정리는 알프레드 타르스키에 의해 발표되었고 [note 90]증명되었다.1938년, 괴델은 "선택의 공리와 일반화된 연속체의 일관성"이라는 논문에서 구성 가능한 우주를 제안한다.앙드레 베일과 니콜라 부르바키는 1939년에 빈 세트 사인을 개발하였다.같은 해, Nathan Jacobson은 복소수 집합의 이중 대문자 C를 만들 것입니다.
1930년대 무렵, Voigt[note 91] 표기법은 그 순서를 줄임으로써 대칭 텐서를 표현하는 방법으로 다선형 대수학을 위해 개발되었다.쇤파리[note 92] 표기법은 점군을 기술하는 데 사용되는 두 가지 규칙 중 하나가 되었다(다른 하나는 헤르만-마우귄 표기법).또한 이 시기에는 2성분 스피너(와일 스피너)를 4차원 시공간으로 사용하는 데 판 데르 바덴[122][123] 표기법이 유행했다.아렌드 헤이팅은 헤이팅 대수와 헤이팅 산수를 소개할 것이다.
화살표(예: →)는 1936년 öystein Ore에 의해 특정 [note 93][note 94]요소의 이미지를 나타내기 위해 함수 표기용으로 개발되었다.이후 1940년에 비톨드 휴레비츠의 연구를 통해 f: X → Y와 같은 현재의 형태를 띠게 되었다.1941년 베르너 하이젠베르크는 입자 상호작용에 대한 S 매트릭스 이론을 제안했다.
브라-케트 표기법(디락 표기법)은 양자 상태를 설명하기 위한 표준 표기법으로, 각도 괄호와 수직 막대로 구성됩니다.또한 추상 벡터와 선형 함수를 나타낼 때도 사용할 수 있습니다.2개의 상태의 내적(복소 벡터 공간상의 도트적)을 왼쪽 부분인 β와 오른쪽 부분인 β로 이루어진 [note 95]β브라케트로 나타내기 때문에 이렇게 불린다.이 표기법은 1939년 Paul Dirac에 [124]의해 도입되었지만, Grassmann이 약 100년 [125]전에 그의 내적 산물에 [φ ψ ] 표기법을 사용한 선구자가 있다.
브라켓 표기법은 양자역학에서 널리 퍼져있다: 현대 물리학의 많은 부분을 포함하여 양자역학을 사용하여 설명되는 거의 모든 현상은 보통 브라켓 표기법의 도움을 받아 설명된다.이 표기법은 부호화된 추상 표현 독립성을 확립하여 관련된 선형 공간의 특성에 대한 과도한 의존 없이 다용도 특정 표현(예: x, p 또는 고유 함수 기반)을 생성한다.오버랩 표현 「」은, 통상, 상태 「」가 붕괴해 상태 「」가 될 확률 진폭으로 해석됩니다.파인만 슬래시 표기법(디락 슬래시[126] 표기법)은 리처드 파인만이 양자장 이론에서 디락장을 연구하기 위해 개발한 것입니다.
1948년, 발렌타인 바르그만과 유진 위그너는 자유 입자를 설명하기 위해 상대론적 바르그만-위그너 방정식을 제안했고, 그 방정식은 다성분 스피너 전계 파동 함수의 형태이다.1950년 윌리엄 발란스 더글라스 호지는 국제 수학자 회의에서 "대수 변종의 위상 불변량"을 발표했다.1954년에서 1957년 사이에, Eugenio Calabi는 Kéhler 측정지표와 칼라비의 개발에 대한 칼라비 추측을 연구했다.야우다양체1957년 툴리오 레게는 슈뢰딩거 [note 96]방정식으로 전위 산란의 수학적 특성을 공식화했다.스탠리 만델스탐은 레지(Regge)와 함께 강력한 상호작용 현상에 대한 레지(Regge) 이론을 최초로 개발했다.1958년 머레이 겔만과 리처드 파인만은 조지 수다르샨과 로버트 마샤크와 함께 물리학에서 약한 상호작용의 키랄 구조를 추론했다.Geoffrey Chu는 다른 사람들과 함께 1960년에 강력한 상호작용과 관련된 부트스트랩 원리에 대한 매트릭스 표기법을 장려했다.1960년대에 집합 빌더 표기법은 집합의 구성원들이 만족해야 하는 속성을 기술함으로써 집합을 기술하기 위해 개발되었다.또한 1960년대에 텐서는 모노이드 범주의 개념에 의해 범주 이론 내에서 추상화되었습니다.나중에, 다중 지수 표기법은 정수 지수의 개념을 지수의 순서 있는 태플에 추상화함으로써 다변수 미적분, 편미분 방정식, 그리고 분포 이론에서 사용되는 전통적인 개념을 제거한다.
현대 수학 표기법
특수 상대성 이론, 전자기학, 파동 이론의 현대 수학에서 달랑베르[note 97][note 98] 연산자는 민코프스키 공간의 라플라스 연산자이다.Levi-Civita[note 99] 기호는 텐서 미적분에 사용된다.
양자전기역학의 섭동 계열에서 어떤 순서로든 유한한 완전한 로렌츠 공분산 공식 후에,[127] 신이티로 토모나가, 줄리안 슈윙거, 리처드 파인만은 1965년에 공동으로 노벨 물리학상을 수상했습니다.그들의 공헌과 프리먼 다이슨의 공헌은 어떤 섭동 이론의 순서에서도 관측 가능성의 계산을 가능하게 하는 양자 전기 역학의 공변 및 게이지 불변 공식에 관한 것이었다.그의 도표를 바탕으로 한 파인만의 수학적 기법은 처음에는 슈윙거와 토모나가의 장 이론, 연산자 기반 접근법과 매우 다르게 보였지만, 프리먼 다이슨은 나중에 두 접근법이 동등하다는 것을 보여주었다.적분을 통해 이론에서 나타나는 특정 분기에 물리적 의미를 부여할 필요성인 재규격화는 이후 양자장 이론의 기본 측면 중 하나가 되었고 이론의 일반적인 수용성의 기준으로 간주되었다.양자 전기역학은 후속 양자장 이론의 모델이자 템플릿 역할을 해왔다.피터 힉스, 제프리 골드스톤, 그리고 다른 사람들, 셸던 글래쇼, 스티븐 와인버그, 그리고 압두스 살람은 어떻게 약한 핵력과 양자 전기 역학을 하나의 약한 힘으로 통합할 수 있는지를 독립적으로 보여주었다.1960년대 후반, 입자 동물원은 쿼크가 발견되기 전에 당시 알려진 소립자로 구성되었다.
스탠다드 모델을 향한 첫걸음은 1960년 셸던 글래쇼가 전자기 상호작용과 [128]약한 상호작용을 결합하는 방법을 발견한 것이다.1967년 스티븐 와인버그와[129] 압두스[130] 살람은 글래쇼의 전기 약자 이론에 힉스[131][132][133] 메커니즘을 접목시켜 현대적 형태를 만들어냈다.힉스 메커니즘은 표준 모델에 있는 모든 소립자의 질량을 발생시키는 것으로 알려져 있습니다.여기에는 W와 Z 보손의 질량, 그리고 페르미온의 질량, 즉 쿼크와 렙톤이 포함됩니다.1967년 브라이스 드윗은 "아인슈타인-슈뢰딩거 방정식" (나중에 "휠러-드윗 방정식"[134]으로 개명)이라는 이름으로 방정식을 발표했다.1969년에는 난부 요이치로, 닐슨 홀저, 서스킨드 등이 시공간을 현으로 표현했다.1970년, 피에르 라몽은 2차원 초대칭을 개발하였다.그 후, 미치오 카쿠와 키카와 게이지가 현악 변주곡을 만들어 낸다.1972년, 마이클 아르탱, 알렉상드르 그로텐디크, 장 루이 베르디에가 그로텐디크 [135]우주를 제안합니다.
1973년 [136][137][138][139]CERN에서 Z보손 교환에 의한
중성 약전류가 발견된 후, 이 약전류가 널리 받아들여졌고 글래쇼, 살람, 와인버그는 이를 발견한 공로로 1979년 노벨 물리학상을 공동 수상했다.많은 사람들이 기여했던 강한 상호작용 이론은 1973-74년 경에 현대적인 형태를 얻었다.양자 색역학의 확립에 의해, 기본 입자와 교환 입자의 집합이 완성되어 게이지 불변성의 수학에 근거한 「표준 모델」의 확립이 가능하게 되어 중력을 제외한 모든 힘을 성공적으로 기술해, 그것이 설계되고 있는 영역내에서 일반적으로 받아들여지고 있다.적용됩니다.1970년대 후반, 윌리엄 서스턴은 쌍곡기하학을 쌍곡선 기하학을 쌍곡선화 정리와 함께 매듭 연구에 도입했다.서스턴에 의해 발명된 오비폴드 표기법은 일정한 곡률의 2차원 공간에서 대칭 그룹의 유형을 표현하기 위해 개발되었습니다.1978년, Sing-Tung Yau는 칼라비 추측이 Ricci 플랫 메트릭을 가지고 있다고 추론했다.1979년, 다니엘 프리단은 끈 이론의 운동 방정식이 일반 상대성 이론의 아인슈타인 방정식의 추상화라는 것을 보여주었다.
첫 번째 초끈 혁명은 1984년과 1986년 사이에 개발된 수학 방정식으로 구성되어 있다.1984년, Vaughan Jones는 Jones 다항식을 추리하고 에드워드 위튼, Maxim Kontsevich, 그리고 다른 사람들로부터 그 이후의 공헌을 추론하여 통계 역학 및 양자장 이론에서 매듭 이론과 수학적 방법 사이의 깊은 연관성을 밝혀냈습니다.끈 이론에 따르면, "입자 동물원"에 있는 모든 입자들은 공통의 조상, 즉 진동하는 끈을 가지고 있다.1985년, 필립 Candelas, 게리 Horowitz,[140]앤드루 스트로 민저, 에드워드 위튼 나중에"superstrings에 진공 구성"[141]을 출판할 것이다, 4형식 주의(사분자 지수 표기법)일반 상대성 이론이 좌표 기준에 대한 국내 기준의 덜 제한적인 선택에 따라 선택을 대신하는 접근 방식 도입될 예정이다.그 싸한 맛ent [note 102][142]번들
1990년대에 Roger Penrose는 펜로즈 그래픽 표기법(텐서 다이어그램 표기법)을 다선형 함수 또는 [143]텐서의 시각적 표현으로 제안했습니다.Penrose는 또한 추상 [note 103]색인 표기법을 도입할 것이다.1995년 에드워드 위튼은 M이론을 제안하고 이후 관찰된 이중성을 설명하기 위해 M이론을 사용하여 제2의 초끈 [note 104]혁명을 일으켰다.
존 콘웨이는 또한 콘웨이 연쇄 화살표 표기법, 매듭 이론의 콘웨이 표기법, 콘웨이 다면체 표기법을 포함한 다양한 표기법을 추가했다.콕서터 표기법은 대칭군을 분류하며, 콕서터 그룹의 기본 반사와 사이의 각도를 설명한다.특정 서브그룹을 나타내는 수식어와 함께 괄호로 둘러싸인 표기법을 사용합니다.이 표기법은 H. S. M. 콕서터와 Norman Johnson이 보다 포괄적으로 정의한 것을 따서 명명되었다.
조합 LCF 표기법은[note 105] 해밀턴식 [144][145]입방체 그래프를 표현하기 위해 개발되었습니다.주기 표기법은 구성 [146]주기의 관점에서 순열을 기록하기 위한 규칙입니다.이것은 순환 표기법이라고도 하며 순환 또는 순환 [147]순열이라고도 합니다.
컴퓨터 및 마크업 표기법
1931년 IBM은 IBM 601 Multiplying Punch를 생산했습니다. IBM 601 Multiplying Punch는 카드에서 최대 8자리 길이의 두 숫자를 읽고 동일한 [148]카드에 해당 제품을 삽입할 수 있는 전기 기계입니다.1934년 Wallace Eckert는 IBM 601 Multipling Punch를 사용하여 미분 [149]방정식의 통합을 자동화했습니다.1936년, 앨런 튜링은 "계산 가능한 숫자에 대하여, entscheidungsproblem에 대한 응용"[150][note 106]을 출판했다.디지털 컴퓨터와 컴퓨터 [note 107]과학의 선구자인 존 폰 노이만은 1945년에 EDVAC에 대한 불완전한 보고서 초안을 작성했습니다.1962년, 케네스 E. Iverson은 학생들에게 가르친 배열을 조작하기 위해 APL이 된 통합 부품 표기법을 개발했고 그의 책 A Programming Language에서 설명했습니다.1970년에 에드거 F. Codd는 데이터베이스 쿼리 언어에 대한 데이터의 관계형 모델로 관계형 대수를 제안했다.1971년 Stephen Cook은 "정리 증명 절차의 [151]복잡성"을 출판했다. 1970년대 컴퓨터 아키텍처 내에서 Quote 표기법은 유리수의 대표수 체계를 위해 개발되었다.또한 이 10년 동안 Z 표기법(APL 언어와 마찬가지로 훨씬 이전)은 많은 비 ASC를 사용합니다.II 기호, 사양은 ASCII 및 LaTeX에서 Z 표기 기호를 렌더링하기 위한 제안을 포함합니다.현재 다양한 C 수학 함수(Math.h)와 숫자 라이브러리가 있습니다.수치 계산을 수행하기 위한 소프트웨어 개발에 사용되는 라이브러리입니다.이러한 계산은 심볼 실행으로 처리할 수 있습니다. 즉, 프로그램을 분석하여 프로그램의 각 부분을 실행하는 원인이 되는 입력을 결정합니다.매스매티카와 SymPy는 기호 수학에 기초한 컴퓨터 소프트웨어 프로그램의 예입니다.
수학 표기법의 미래
수학 표기법의 역사에서, 표의 기호 표기법은 컴퓨터 시각화 시스템의 출현과 함께 완전히 순환되어 왔다.표기는 칼라비의 투영을 렌더링하는 등 추상적인 시각화에 적용할 수 있습니다.야우 매니폴드수학적 상상력에 적절히 속하는 추상적 시각화의 예는 컴퓨터 그래픽스에서 찾을 수 있다.예를 들어, 연구 주제에 대한 측정이 실제로 무작위 변수이고 실제로 일반적인 수학 함수가 아닌 경우, 그러한 모델의 필요성은 풍부하다.
「 」를 참조해 주세요.
- 주요 관련성
- 표기법 남용, 잘 형성된 공식, 빅 O 표기법(L-표기), 다우커 표기법, 헝가리 표기법, 인픽스 표기법, 위치 표기법, 폴란드 표기법(역 폴란드 표기법), 부호 값 표기법, 숫자 기록
- 수와 수량
- 무리수, 무리수 및 의심수, irr, ics(3), 22, 33, 55, ,, αS, e, ,, ,, ,, 물리상수, c0, ,, h, G, 수학, 과학, 공학에서 사용되는 그리스 문자 목록
- 화살표 표기법
- 크누스의 위 화살표 표기법, 무한 조합법(화살표 표기법(램지 이론))
- 목록 및 개요
- 수학의 개요(수학 역사 주제 및 수학 주제(수학 범주), 수학 이론(일차 이론, 이론 및 반증된 수학 사상), 수학 증명(불완전한 증명), 수학 정체성, 수학 시리즈, 수학 참조표, 수학 논리 주제, 수학 기초)ed 방법, 수학적 함수, 변환과 연산자, 수학의 점, 수학적 형상, 매듭(수학적 매듭과 수학적인 매듭과 링크), 부등식, 장소의 이름을 딴 수학적 개념, 고전 역학의 수학적 주제, 양자 이론의 수학적 주제, 상대성 이론의 수학적 주제, 끈 이론의 수학적인 주제그림, 수학의 미해결 문제, 수학 전문 용어, 수학 예제, 수학 약어, 수학 기호 목록
- 사람
- 수학자(아마추어 수학자 및 여성 수학자), 토마스 브래드워딘, 토마스 해리오트, 펠릭스 하우스도르프, 가스톤 줄리아, 헬게 폰 코흐, 폴 레비, 알렉산드르 랴푸노프, 베누아 만델브로, 루이스 프라이 리처드슨, 바츠와프 시에르스키 H. 하디, E. M. 라이트, 제임스 R. 뉴먼, 칼 구스타프 제이콥 자코비, 로저 조셉 보스코비치, 에릭 W. Weisstein, 수학적 확률학자, 통계학자
메모들
- ^ 아니면 중세시대.
- ^ 사실 이러한 문자는 존 레슬리의 산술 철학에서 찾을 수 있는 로마 표기법의 거의 변화 없이 보존되어 있다.
- ^ 수론은 주로 정수 연구에 전념하는 순수 수학의 한 분야이다.수 이론가들은 소수뿐만 아니라 정수(예: 유리수)로 만들어지거나 정수(예: 대수 정수)의 일반화로서 정의되는 물체의 특성도 연구한다.
- ^ 그리스어: μμο μο ο υ greek greek greek greek τ τ ε greek
- ^ , a + 2 2 ({ a})2
- ^ 크기(수학), 물체의 상대적 크기(벡터), 벡터의 크기 또는 길이를 나타내는 용어, 스칼라(수학), 크기만으로 정의되는 수량, 유클리드 벡터, 크기와 방향에 의해 정의되는 수량, 크기 순서, 이전 등급에 대한 고정 비율을 갖는 척도 종류.
- ^ 오토라이커스'는 그 시대의 또 다른 고대 수학 필사본이다.
- ^ 유클리드 이후 몇 세기 동안 살았던 그리스 수학자 프로클로스는 원소 해설에서 다음과 같이 썼다: "유클리드, 원소를 종합하고, 에우독소스의 많은 이론들을 수집하며, 테에테토스의 많은 이론들을 완성시키고, 또한 그의 전임자들에 의해 약간 느슨하게 증명된 것들도 회복할 수 없는 증명들을 가져왔다."
- ^ 표현:
다음과 같이 기술됩니다.
SS2 C3 x 5 M S4 u6
를 클릭합니다.[citation needed] - ^ 예를 들어, 규칙, 정사각형, 나침반, 수위(레드 레벨), 플럼밥 등이 있습니다.
- ^ 바퀴나 차축과 같은
- ^ 직각 삼각형의 빗변에서 묘사된 정사각형의 면적은 변에서 묘사된 정사각형의 면적 합계와 같다.
- ^ 알 킨디는 암호 해독과 주파수 분석도 도입했다.
- ^ 서기 1000년경에 알-카라지가 쓴 책에 수학 귀납에 의한 증명에 가까운 것이 등장하는데, 그는 그것을 사용하여 이항 정리, 파스칼의 삼각형, 적분 입방체의 합을 증명한다.
- ^ 따라서 그는 다항식의 적분에 대한 일반 공식을 찾는 데 거의 근접했지만, 그는 4차 이상의 다항식에는 관심이 없었다.
- ^ 그가 유클리드 원소의 결점으로 인식한 것, 특히 평행한 가설에 관한 책
- ^ 체스터의 로버트에 의해 라틴어로 번역된
- ^ 바스의 아델라드, 카린시아의 헤르만, 크레모나의 제라드에 의해 다양한 버전으로 번역된
- ^ 그의 개인적인 사용은 1351년경에 시작되었다.
- ^ Summa de Salcemetica:Geometria Propotioni et Propactionita.제3절 산술의 합계:비례와 비례의 기하학.
- ^ 작품의 대부분은 피에로 델라 프란체스카에서 비롯되어 그가 유용하고 정제했다.
- ^ 이것은 수 세기 후에 루피니와 호너가 준 방법의 특별한 경우였다.
- ^ 즉입니다.
- ^ 소문자 r(기수)과 비슷하다고 생각했기 때문입니다.
- ^ 경이로운 로그 캐논에 실리다.
- ^ 그것은,∷
- ^ '연속성의 법칙'을 참조하십시오.
- ^ 평면에서 데카르트 좌표를 사용하여 두 점(x1, y1)과 (x2, y2) 사이의 거리는 다음 공식으로 정의됩니다.
이것은 피타고라스 정리의 한 버전이라고 볼 수 있다. - ^ 추상화의 추가 단계는 비유클리드 기하학을 발전시키기 위해 기하학의 개념을 일반화한 로바체프스키, 볼야이, 리만, 그리고 가우스에 의해 이루어졌다.
- ^ 지금은 파스칼의 삼각형이라고 불립니다.
- ^ 예를 들어, "포인트의 문제"입니다.
- ^ 즉, 입니다.
- ^ 를 들어 1. { \ 。
- ^ 원제목 '루도알레에의 라티오키니'
- ^ 예를 들어 함수 x의 도함수는 x 로 됩니다.x의 두 번째 도함수는 x{\(\ 등으로 됩니다.
- ^ 예를 들어, Leibniz 표기법에서 변수 t에 대한 함수 x의 도함수는 t { \ dt 로 됩니다.
- ^ " - ( ) x { _ { - } ) , } 。
- ^ 다음 항목도 참조하십시오.e 표현 목록
- ^ f { f는 x x에 대한 연산f{f(x)}의 수행에 대한 수학적 결과를 나타냅니다. 이 결과에서 동일한 연산이 반복되면 새로운 결과는f [(로됩니다.() { f 등입니다.다른 함수에 대해 동일한 f f의 결과로 간주되는 x의 양 적절한 기호는f -이다. 따라서f { f과f - f은 역연산의 기호이다.이온은 x(\ x . {f및 - 에 대한 후자의 영향을 유사한 방법으로 상쇄하는 전자를 역함수라고 한다.
- ^ 즉, f ( \ f
- ^ - {-
- ^ 오늘날 John Wallis가 만든 기호 는 무한대에 사용됩니다.
- ^ 과 같이 n 1 {\ _}{
- ^ 대문자 시그마 표기법은 많은 유사한 용어의 합계를 압축적으로 나타내는 기호를 사용한다. 즉, 그리스 문자 시그마의 확대된 형태인 합계 기호 δ.이것은 다음과 같이 정의됩니다.
여기서 i는 합계의 지수를 나타냅니다.a는i 급수의 연속된 각 항을 나타내는 지수 변수입니다.m은 합계의 하한, n은 합계의 상한입니다.합산 기호 아래의 "i = m"은 지수 i가 m과 동일하게 시작됨을 의미한다.지수 i는 연속항마다 1씩 증가하며 i = n일 때 멈춘다.
- ^ , n 01( - s ) s\ n !1}(-\s
n > 0 에 유효합니다. - ^ 그것은,∝
- ^ 비례성은 한 수량과 다른 수량의 비율이며, 특히 전체와 비교한 부품의 비율입니다.수학적인 맥락에서, 비율은 두 비율 사이의 평등에 대한 진술입니다. 비율이 일정한 두 변수의 관계인 비례성(수학)을 참조하십시오.종횡비, 기하학적 비율도 참조하십시오.
- ^ 곱슬곱슬한 d 또는 자코비의 델타.
- ^ 윌슨 정리의 증명에 대해서요제76조 산술(1801)의 발췌
- ^ 갈로아 이론과 갈로아 기하학은 그의 이름을 따서 지어졌다.
- ^ 즉, "subset of"과 "superset of"이다. 이것은 나중에 에른스트 슈뢰더에 의해 재개발되었다.
- ^ 정수에 대한 문제를 해결하기 위해 수학적 분석 방법을 사용하는 숫자의 과학입니다.
- ^ 로버트 퍼시벌 그레이브스의 윌리엄 로완 해밀턴 경의 생애에 인용됨 (3권, 1882년, 1885년, 1889년)
- ^ 즉, 나중에 del로 불림)
- ^ 해밀턴(양자 역학)을 참조하십시오.
- ^ , k - { i} = }
- ^ 비록 그의 용도는 현재 텐서가 의미하는 것과 다른 무언가를 묘사하고 있지만.즉, 특정 유형의 대수 체계(현재는 클리포드 대수라고 알려져 있음)에서의 표준 연산이다.
- ^ 그것은,
어디에
- ^ 이것은 라틴어로 "웜"을 뜻한다.
- ^ , w + i + j + k { q
- ^ 클리포드는 헤르만 그라스만의 규칙pp ee = 0을 규칙pp ee = 1로 대체함으로써 해밀턴의 4분의 1과 대수학을 교차시켰다.자세한 내용은 외부 대수를 참조하십시오.
- ^ 참고 항목: 위상, 그룹(수학), 신호 속도, 다상 시스템, 고조파 발진기 및 RLC 직렬 회로
- ^ 아니면 네 번째 공간 차원에 대한 개념도요참고 항목: 4차원 연속체로서의 시공간 통합, 그리고 특수 상대성 이론의 수학적 설정인 민코프스키 공간.
- ^ 다음 항목도 참조하십시오.수학 필드 및 필드 확장
- ^ 알프레드 노스 화이트헤드...와 버트랜드 러셀이 프린키피아 수학에서 완성한 1+1=2의 증명 후에 코멘트합니다.제2권 제1판(1912년)
- ^ 이것은 순수한 존재론에 대한 의문을 제기한다.
- ^ 페아노의 '포뮬라리오 매스매티코'는 러셀의 작품보다는 덜 인기가 있었지만, 다섯 판까지 계속되었다.다섯 번째는 1908년에 나타났고 4200개의 공식과 정리를 포함했다.
- ^ 집합론의 발명자
- ^ 초한산술은 기본연산을 무한집합과 같은 무한량으로 일반화한 것입니다. 초한수, 초한유도 및 초한보간법을 참조하십시오.순서 산술도 참조하십시오.
- ^ 예를 들어 맥스 덴, J. W. 알렉산더 등.
- ^ 알렉산더 다항식처럼요
- ^ (독일어:Algebraische Theory der Körper)
- ^ 이 논문에서 스타이니츠는 필드의 특성을 공리적으로 연구했고, 소수장, 완전장, 필드 확장의 초월도와 같은 많은 중요한 필드 이론 개념을 정의했다.
- ^ 인덱스의 범위는 집합 {1, 2, 3)을 초과합니다.
규약에 의해 다음과 같이 감소한다.
상위 지수는 지수가 아니라 좌표, 계수 또는 기준 벡터의 지수입니다.
다음 항목도 참조하십시오.리치 미적분 - ^ 리치 미적분은 텐서와 텐서장에 대한 지수 표기 및 조작 규칙을 구성합니다.다음 항목도 참조하십시오.Synge J.L.; Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 6–108.
- ^ 여기서 논리 상수는 기호 논리학의 기호로 모든 모델에서 동일한 의미를 갖습니다. 예를 들어, 기호 "="는 "변수"를 의미합니다.
상수는 수학적인 맥락에서 θ나 e와 같이 수학에서 자연적으로 발생하는 수치입니다. 이러한 수학 상수 값은 변하지 않습니다.이는 다항식 상수 항(차수 0의 항) 또는 적분 시 발생하는 자유 모수인 적분 상수를 의미할 수 있습니다.
이와 관련하여, 물리 상수는 일반적으로 보편적이고 변하지 않는 것으로 여겨지는 물리량이다.프로그래밍 상수는 변수와 달리 다른 값과 다시 연결할 수 없는 값입니다. - ^ 인덱스 용어는 아니지만 키워드는 정보를 나타내는 용어입니다.키워드는 특별한 의미를 가진 단어(이것은 의미적 정의)이며, 구문적으로는 문법의 말단 기호입니다.관련 개념은 예약어를 참조하십시오.
- ^ 이들 기호의 대부분은 L ( , , ,) ( \ { \ {L } = { L } \ ( \ , \ \ \ { Z } , \ \{ Z )로 기술되는 공식 미적분학에서 찾을 수 있습니다위의 올레인 대수. is the set that contains the subsets that contain operations, such as or . contains the inference rules, which are the rules dictating how inferences may be logically made, and 에는 공리가 포함되어 있습니다.'기본 및 파생 인수 양식'도 참조하십시오.
- ^ 보통 x, y, z 또는 기타 소문자로 표시됩니다.
여기에서는 수학식으로 수량을 나타내는 기호, 즉 많은 과학에서 사용되는 수학 변수입니다.
변수는 값과 관련된 기호 이름일 수 있으며, 관련 값은 컴퓨터 과학에서 변수 참조로 알려져 있습니다.변수는 추가 데이터 처리를 위해 속성이 표현되는 작동 방식(예를 들어 논리적 속성 세트)일 수도 있습니다.다음 항목도 참조하십시오.통계량에서 종속 및 독립 변수입니다. - ^ 일반적으로 대문자 뒤에 P(x) 또는 Q(y,z)와 같은 변수 목록이 표시됩니다.
여기 수학 논리 술어 1차 논리학의 기본 개념입니다.문법적 술어는 문장의 문법적 구성요소이다.
관련된 것은 파서 프로세스의 가이드라인인 파서 테크놀로지의 구문 술어입니다.컴퓨터 프로그래밍에서 분기 술어는 기계 레지스터의 내용에 근거하여 주어진 명령을 실행할지 여부를 선택할 수 있도록 한다. - ^ EXISTES는 과 같습니다.
- ^ 들어 있다 ' 있다', '모두 있다', '모두 있다', '모두 있다', '모두 있다', '모두 있다', '있다', '있다', '있다', '있다'와 같이요.
- ^ 다음 항목도 참조하십시오.디알테히즘, 모순, 역설
- ^ 관련된, 익살스러운 추상적 난센스는 코믹한 문학적 비순서적 장치(비논리적 비순서적 장치가 아닌)와 유사한 범주 이론과 관련된 특정 종류의 논쟁과 방법을 기술한다.
- ^ 괴델의 불완전성 정리는 힐베르트의 모든 수학에 대한 완전하고 일관된 공리 집합을 찾는 프로그램이 불가능하다는 것을 보여주며 힐베르트의 두 번째 문제에 대한 부정적인 답을 준다.
- ^ 예를 들어, "Y가 아닌 숫자 x가 존재합니다."라는 문구를 예로 들어 보겠습니다.명제 미적분 기호를 사용하면 다음과 같이 됩니다. ( x) ( ) \ ( \ displaystyle ( \ x ) ( x= \ y )}
Gödel 번호가 기호를 대체하는 경우{,, , ,, {displaystyle 4,9, 8, , 1,, 9{ \} 이 됩니다.
10개의 숫자가 있으므로 10개의 소수점을 찾을 수 있습니다,,5, 23 } { \ { 2, 3 、 、、 、 17 、 、 、 }。
그런 다음 각 소수의 거듭제곱을 하여 곱한다: × 4 × 7× × × × × ×× { 2 3 7}\ 17
결과는 약.× 3. 10입니다. - ^ 클라인-고든 방정식은 다음과 같다.
- ^ Dirac이 원래 제안한 형태의 Dirac 방정식은 다음과 같습니다.
여기서 δ = δ(x, t)는 전자에 대한 파동 함수이고, x와 t는 공간과 시간 좌표이고, m은 전자의 나머지 질량이고, p는 운동량이며, 슈뢰딩거 이론에서 운동량 연산자로 이해되며, c는 빛의 속도이고, δ = h/2θ는 감소 플랑크 상수이다. - ^ 그것은,
- ^ 이 정리는 시스템 표준 모델의 진실이 시스템 내에서 정의될 수 없다는 것을 보여주며, 충분히 강력한 공식 시스템에 더 일반적으로 적용됩니다.
- ^ 보이트의 1898년 업적을 기리기 위해 붙여진 이름입니다.
- ^ Arthur Moritz Schoenflys의 이름을 딴
- ^ Galois 연결을 참조하십시오.
- ^ Oystein Ore는 또한 "숫자 이론과 그것의 역사"를 썼다.
- ^
- ^ 산란 진폭은 각 운동량의 해석 함수로 간주할 수 있으며 극의 위치는 산란 각도의 코사인 큰 값의 순수 수학 영역에서 진폭의 멱함수 증가율을 결정한다.
- ^ 즉, {\
- ^ 달랑베리안 또는 웨이브 연산자로도 알려져 있습니다.
- ^ "변환 기호"(순열 참조), "반대칭 기호"(반대칭 참조) 또는 "교체 기호"라고도 합니다.
- ^ 입자의 "매스"(예: 일관성 있는 비확정 체형)는 과학계에 의해 주기적으로 재평가된다.값이 조정되었을 수 있습니다. 측정량의 주어진 값에 해당하는 지정된 표시를 제공하기 위해 계측기에 대해 수행된 작업에 의해 조정됩니다.공학, 수학 및 측지학에서 데이터 세트에 가장 적합하도록 수학 모델을 추정하는 것과 같은 최적의 매개 변수입니다.
- ^ 자세한 내용은 입자 데이터 그룹을 참조하십시오.
- ^ 사각형이라고 하는 4개의 선형 독립 벡터장으로 이루어진 국소 정의 집합
- ^ 그가 아인슈타인 합계를 사용한 것은 현대 추상 텐서 표기법에서 수축과 공변 분화를 기술하는 불편함을 상쇄하고 관련된 표현들의 명시적인 공분산을 유지하기 위해서였다.
- ^ 다음 항목도 참조하십시오.현악기 이론의 풍경과 수영장
- ^ Joshua Lederberg가 고안하고 Coxeter와 Frucht가 확장했습니다.
- ^ 그리고 1938년에.
- ^ 폰 노이만의 다른 업적들 중에는 양자역학, 함수 분석의 개발, 그리고 다양한 형태의 연산자 이론의 적용이 포함된다.
레퍼런스 및 인용문
- 일반
- Florian Cajori (1929) 수학 표기사, 2권.도버, 1993년 1권으로 전재.ISBN 0-486-6776-4.
- 인용문
- ^ 플로리안 카조리수학적 표기법 역사:2개의 볼륨인원주식회사 코시모, 2011년 12월 1일
- ^ 과학, 문학, 예술 사전, 제2권.William Thomas Brande 편집, George William Cox. 683 페이지
- ^ "Notation – from Wolfram MathWorld". Mathworld.wolfram.com. Retrieved 24 June 2014.
- ^ 알렉산드리아의 디오판토스:그리스 대수학의 역사 연구토마스 리틀 히스 경에 의해.페이지 77.
- ^ 수학:파워와 유틸리티Karl J. Smith 지음.86페이지.
- ^ 1300-1500년 르네상스 플로렌스에서의 상업 혁명과 서양 수학의 시작.워렌 밴 에그몬드 1976년233쪽.
- ^ 솔로몬 간즈.알-코와리즈미 대수학의 근원
- ^ 아메리카나 백과사전토마스 가말리엘 브래드포드 지음.페이지 314
- ^ 수학 Excursion, 확장판:강화된 Web Assign Edition By Richard N.오프만, 조앤 록우드, 리처드 D.네이션, 다니엘 K.분류 186페이지
- ^ 이집트와 메소포타미아의 수학[데드링크]
- ^ Boyer, C. B. A 수학사, 제2판 Uta C. 개정판. 메르즈바흐뉴욕: Wiley, 1989년 ISBN 0-471-09763-2(1991년판).ISBN 0-471-54397-7)."메소포타" 페이지 25
- ^ 던컨 J. 멜빌(2003)세 번째 밀레니엄 연대기, 세 번째 밀레니엄 수학.세인트로렌스 대학교
- ^ Aaboe, Asger (1998). Episodes from the Early History of Mathematics. New York: Random House. pp. 30–31.
- ^ Heath (1931). "A Manual of Greek Mathematics". Nature. 128 (3235): 5. Bibcode:1931Natur.128..739T. doi:10.1038/128739a0. S2CID 3994109.
- ^ 토마스 L. 경그리스 수학 매뉴얼, 도버, 1963년 페이지 1: "수학의 경우, 수학을 과학으로 만든 것은 그리스인이었기 때문에 가장 알아야 할 것은 그리스인의 공헌입니다."
- ^ a b 새로운 백과사전, 또는 예술과 과학 유니버설 사전.Pertensi 백과사전 지음.49페이지
- ^ Calinger, Ronald (1999). A Contextual History of Mathematics. Prentice-Hall. p. 150. ISBN 0-02-318285-7.
Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity.
- ^ "Archimedes of Syracuse". The MacTutor History of Mathematics archive. January 1999. Retrieved 9 June 2008.
- ^ O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". University of St Andrews. Archived from the original on 15 July 2007. Retrieved 7 August 2007.
- ^ "Proclus' Summary". Gap.dcs.st-and.ac.uk. Archived from the original on 23 September 2015. Retrieved 24 June 2014.
- ^ Caldwell, John(1981) "The Institutione 산술메티카와 De Institutione Musica", 135-54페이지, 보에셔스, ed.: 그의 인생, 생각, 영향 (옥스포드: 바질 블랙웰).
- ^ Folkerts, Menso, "Boethius" Geometrie II, (비에스바덴: Franz Steiner Verlag, 1970).
- ^ 오스왈드 애쉬튼 웬트워스 딜크의 수학과 측정.페이지 14
- ^ a b c d e W.T. Brande의 과학, 문학, 예술 사전.683페이지
- ^ 보이어, 칼 B.A History of Mathematic, 제2판, John Wiley & Sons, Inc., 1991.
- ^ 디오판토스 방정식제출자: Aaron Zerhusen, Chris Rakes 및 Shasta Mece.MA 330-002칼 에버하트 박사 1999년 2월 16일
- ^ 그리스 수학의 역사:아리스타르코스에서 디오판토스까지.토마스 리틀 히스 경에 의해.페이지 456
- ^ 그리스 수학의 역사:아리스타르코스에서 디오판토스까지.토마스 리틀 히스 경에 의해.페이지 458
- ^ 미국 수학 월간지 제16권페이지 131
- ^ "Overview of Chinese mathematics". Groups.dcs.st-and.ac.uk. Retrieved 24 June 2014.
- ^ 조지 게버게세 조셉, 공작새의 문장: 비유럽 수학의 뿌리, 펭귄 북스, 런던, 1991, 페이지 140-148
- ^ George Ifrah, Universalgeschichte der Zahlen, 캠퍼스, 프랑크푸르트/뉴욕, 1986, 페이지 428-437
- ^ "Frank J. Swetz and T. I. Kao: Was Pythagoras Chinese?". Psupress.psu.edu. Retrieved 24 June 2014.
- ^ a b 니덤, 조셉(1986년).중국의 과학과 문명: 제3권 수학과 천지의 과학.타이베이: 케이브 북스 주식회사..
- ^ 살레스티보
- ^ 니덤, 조셉(1986년).중국의 과학과 문명: 제3권 수학과 천지의 과학.타이베이: 케이브 북스
- ^ 마르셀 고셰, 151세
- ^ Boyer, C. B. A 수학사, 제2판 Uta C. 개정판.메르즈바흐뉴욕: Wiley, 1989년 ISBN 0-471-09763-2(1991년판).ISBN 0-471-54397-7)."중국과 인도" 페이지 221. (cf.) "그는 선형 디오판토스 방정식의 a, b, c가 정수인 = c에 의한 일반적인 해답을 준 최초의 사람이다. [...] 디오판토스가 선형 디오판토스 방정식의 모든 적분해를 준 반면, 그는 자신을 특별히 만족시켰다.r 불확정 방정식의 해.브라흐마굽타가 디오판투스와 같은 예를 사용했기 때문에, 우리는 인도에서 그리스가 영향을 미쳤을 가능성, 혹은 둘 다 바빌로니아에서 온 공통의 원천을 사용했을 가능성을 다시 보게 된다.디오판투스의 대수처럼 브라흐마굽타의 대수학이 싱코페이트된 것도 흥미롭다.덧셈은 분할표기법에서와 같이 소분수 위에 점을 찍음으로써, 그리고 나눗셈으로 나타내어진다.알 수 없는 양뿐만 아니라 증식 및 진화(근원 획득)의 연산은 적절한 단어의 약어로 표현되었다.")
- ^ 로버트 카플란, "The Nothing That Is: A Natural History of Zero", 앨런 레인 / 펭귄 프레스, 런던, 1999
- ^ ""The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." – Pierre-Simon Laplace". History.mcs.st-and.ac.uk. Retrieved 24 June 2014.
- ^ A.P. Juschkewitsch, "Geschichte der Mathemik im Mittelalter", 라이프치히 테브너, 1964년
- ^ Boyer, C. B. A 수학사, 제2판 Uta C. 개정판.메르즈바흐뉴욕: Wiley, 1989년 ISBN 0-471-09763-2(1991년판).ISBN 0-471-54397-7)."아랍의 헤게모니" 페이지 230. (cf. "위의 6가지 방정식은 양의 근을 갖는 선형 및 2차 방정식의 모든 가능성을 소진한다.알 크와리즈미의 설명은 매우 체계적이고 철저해서 그의 독자들이 해결책을 숙달하는 데 큰 어려움이 없었을 것이다.")
- ^ 간즈와 살로만(1936) 콰리즈미 대수의 출처, 오시리스 i, 263-77페이지: "어떤 의미에서는, 콰리즈미는 디오판토스보다 "대수의 아버지"라고 불릴 자격이 더 있다. 왜냐하면 콰리즈미는 기초적인 형태로 대수를 가르친 최초의 사람이기 때문에 디오판토프스와 주로 관련이 있기 때문이다.
- ^ Boyer, C. B. A 수학사, 제2판 Uta C. 개정판.메르즈바흐뉴욕: Wiley, 1989년 ISBN 0-471-09763-2(1991년판).ISBN 0-471-54397-7)."아랍의 패권" 페이지 229. (cf. "알자브르와 무카발라라는 용어가 무엇을 의미하는지 확실하지 않지만, 일반적인 해석은 위의 번역에 내포된 것과 유사하다.al-jabr이라는 단어는 아마도 "복원"이나 "완료"와 같은 것을 의미하고 감산된 항이 방정식의 다른 쪽으로 옮겨지는 것을 가리키는 것으로 보인다; muqabalah라는 단어는 "축소" 또는 "균형"을 가리킨다고 한다 – 즉, 방정식의 반대쪽에서 유사한 항을 지우는 것이다.")
- ^ Rashed, R.; Armstrong, Angela (1994). The Development of Arabic Mathematics. Springer. pp. 11–12. ISBN 0-7923-2565-6. OCLC 29181926.
- ^ 빅터 J. 카츠(1998).수학의 역사: A 서론, 페이지 255-59.애디슨 웨슬리.ISBN 0-321-01618-1.
- ^ F. Woepcke(1853년).엑스트라잇 뒤 파흐리, 알제브르 파아 아부 베크르 모하메드 벤 알하칸 알카르키.파리.
- ^ Katz, Victor J. (1995). "Ideas of Calculus in Islam and India". Mathematics Magazine. 68 (3): 163–74. doi:10.1080/0025570X.1995.11996307.
- ^ Kunitzsch, Paul (2003), "The Transmission of Hindu-Arabic Numerals Reconsidered", in J. P. Hogendijk; A. I. Sabra (eds.), The Enterprise of Science in Islam: New Perspectives, MIT Press, pp. 3–22 (12–13), ISBN 978-0-262-19482-2
- ^ 마리 테레즈 달베르니, "번역과 번역가", 로베르 L. 페이지 421~62.벤슨과 자일즈 컨스터블, 12세기 르네상스와 리뉴얼(캠브리지:Harvard University Press, 1982).
- ^ Guy Beaujouan, "The Transformation of the Quadrivium", Robert L. 페이지 463–87.벤슨과 자일즈 컨스터블, 12세기 르네상스와 리뉴얼(캠브리지:Harvard University Press, 1982).
- ^ O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor History of Mathematics archive, University of St Andrews
- ^ Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 298. ISBN 0-393-04002-X.
- ^ a b O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews
- ^ Boyer, C. B. A 수학사, 제2판 Uta C. 개정판.메르즈바흐뉴욕: Wiley, 1989년 ISBN 0-471-09763-2(1991년판).ISBN 0-471-54397-7)."그리스 수학의 부활과 쇠퇴" 페이지 178 (cf. "디오판토스 동기법과 현대 대수 표기법의 주요 차이점은 지수 표기법뿐만 아니라 연산과 관계에 대한 특별한 기호가 없다는 것입니다.")
- ^ 그랜트, 에드워드, 존 E.Murdoch(1987), ed., 수학과 중세 과학 및 자연철학에 대한 응용(캠브리지:Cambridge University Press) ISBN 0-521-32260-X.
- ^ 수학 잡지 1권아르테마스 마틴, 1887년페이지 124
- ^ Der Algorismus procolationum des Nicolaus Oresme: 줌얼스텐 말레 나흐 데 레사르트 데 한슈리프트 R.40.2. der Königlichen 체조 비블리오텍 주 손.니콜 오렘S. Calvary & Company, 1868년
- ^ Clagett, Marshall (1961) 중세 기계학의 과학 (Madison:위스콘신 대학 출판부), 페이지 332~45, 382~91.
- ^ 후기 현대판: 새로운 상업 산술 체계:통상 무역에서 발생하는 회계 형태 및 기타 문서와 함께 국내외 관계에서 미국 상거래에 적합하다.마이클 월쉬의 작품.에드먼드 M. 블런트 (유형자), 1801년
- ^ Miller, Jeff (4 June 2006). "Earliest Uses of Symbols of Operation". Gulf High School. Retrieved 24 September 2006.
- ^ 인쇄의 발명으로부터 현대에 이르기까지의 산술서.아우구스투스 드 모건이 쓴 페이지 2
- ^ Grattan-Guinness, Ivor (1997). The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 0-393-32030-8.
- ^ 산술적 요소.마이클 스티펠, 필립 멜랑크톤.노림베르게: 아푸드 이오한 페트레이움, 1544년.
- ^ 앤 룬의 수학사페이지 40
- ^ 머치스톤의 존 네이피어의 회고록.마크 네이피어
- ^ 머치스톤의 존 네이피어의 인생, 글쓰기, 발명품 설명.작성자: 데이비드 스튜어트 Erskine Earl of Buchan, Walter Minto
- ^ Cajori, Florian (1919). A History of Mathematics. Macmillan. p. 157.
- ^ Jan Gullberg, 숫자의 탄생부터의 수학, W. W. Norton & Company; ISBN 978-0-393-04002-9. 페이지 963-965,
- ^ 시놉시스 팔마리오룸 마테서스.William Jones. 1706. (Alt: 개요: Palmariorum Matheseos: 또는 수학의 새로운 입문)archive.org )를 참조해 주세요.
- ^ 적은 것이 많을 때: 기본적인 불평등을 시각화한다.클라우디 알시나, 로저 B.넬스, 18페이지
- ^ 오일러, 레온하르트, 솔루티오 문제아디 지오메트리암 시투스 관련
- ^ 지오메트리의 요소.윌리엄 에머슨 지음
- ^ 비례, 산술, 기하학의 원칙. 일반적인 비례수량별 배치 방법과 함께.윌리엄 에머슨에 의해.
- ^ 수학 특파원.조지 배런 지음 83
- ^ Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Archived from the original on 10 September 2012. Retrieved 24 January 2012.
- ^ "Kramp biography". History.mcs.st-and.ac.uk. Retrieved 24 June 2014.
- ^ Mécanique analytique: 제1권, 제2권.조셉 루이스 라그랑쥬의 작품.베 쿠시어 씨, 1811년
- ^ 아서 케일리의 수학 논문 모음집.제11권페이지 243.
- ^ 자연 수리 과학 역사 백과사전 제1권.Ari Ben-Menahem에 의해.2070쪽
- ^ 비툴리, 마리"선형 대수학과 행렬 이론의 간략한 역사"수학과입니다.오리건 대학교원래 주소는 darkwing.uoregon.edu/~vituli/441.sp04/LinAlgHistory.html 입니다.
- ^ 수학의 단어.스티븐 슈워츠먼의 작품.6.
- ^ 전자파:이론과 응용 프로그램A. Pramanik에 의해.38
- ^ 나블라와 다른 수학 기호들의 역사.homepages.math.uic.edu/~hanson.
- ^ Hamilton, William Rowan (1854–1855). Wilkins, David R. (ed.). "On some Extensions of Quaternions" (PDF). Philosophical Magazine (7–9): 492–499, 125–137, 261–269, 46–51, 280–290. ISSN 0302-7597.
- ^ "James Clerk Maxwell". IEEE Global History Network. Retrieved 25 March 2013.
- ^ Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London. 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. S2CID 186207827. (이 기사는 1864년 12월 8일 맥스웰이 왕립학회에 제출한 프레젠테이션에 첨부되었다.)
- ^ 인터넷 아카이브의 제1권, 제2권, 제3권(1878), 인터넷 아카이브의 제4권(1887)
- ^ Cox, David A. (2012). Galois Theory. Pure and Applied Mathematics. Vol. 106 (2nd ed.). John Wiley & Sons. p. 348. ISBN 978-1118218426.
- ^ "TÜBİTAK ULAKBİM DergiPark". Journals.istanbul.edu.tr. Archived from the original on 16 March 2014. Retrieved 24 June 2014.
- ^ "Linear Algebra : Hussein Tevfik : Free Download & Streaming : Internet Archive". A.H. Boyajian. 1882. Retrieved 24 June 2014.
- ^ Ricci Curbastro, G. (1892). "Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique". Bulletin des Sciences Mathématiques. 2 (16): 167–189.
- ^ Voigt, Woldemar (1898). Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung. Leipzig: Von Veit.
- ^ Poincaré, Henri, "Analysis situs", 저널 de l'cole Polytecique ser 2, 1 (1895) 페이지 1~123
- ^ Whitehead, John B., Jr. (1901). "Review: Alternating Current Phenomena, by C. P. Steinmetz" (PDF). Bull. Amer. Math. Soc. 7 (9): 399–408. doi:10.1090/s0002-9904-1901-00825-7.
- ^ 여러 가지 판이 있습니다.다음 두 가지가 있습니다.
- 1901년 파리 고티에 빌라르 출판.230p. OpenLibrary OL15255022W, PDF.
- (이탈리아어) 1960년 로마 에디조네 크레모네즈 출판.463p. OpenLibrary OL165867658M.
- ^ Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications", Mathematische Annalen, Springer, 54 (1–2): 125–201, doi:10.1007/BF01454201, S2CID 120009332
- ^ Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann" (reprint). Mathematische Annalen. 59 (4): 514–16. doi:10.1007/BF01445300. S2CID 124189935.
- ^ – via Wikisource.
- ^ Fréchet, Maurice, "Surquelques points du calculate functionnel", 박사학위논문, 1906년
- ^ Cuthbert Edmund Cullis (Author) (5 June 2011). Matrices and determinoids Volume 2: Cuthbert Edmund Cullis: Amazon.com: Books. Ulan Press. Retrieved 24 June 2014.
{{cite book}}:author=범용명(도움말)이 있습니다. - ^ 주어진 행렬을 할당할 수 있다: 행렬의 클래스에 대하여(Gr.Ueber eine Klasse von Matrizen: die sich einer geveen matrix zuordn lassen) (이세이 슈어)
- ^ 현대 방정식 이론의 입문Florian Cajori의 작품.
- ^ 프러시아 과학아카데미(1918년).966쪽.
- ^ Sitzungsberichte der Preussischen Akademie der Vissenschaften(1918년) (프러시아 과학아카데미 회보(1918년).archive.org; "Kaluza-Klein 이론"도 참조하십시오.
- ^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 85–86, §3.5. ISBN 0-7167-0344-0.
- ^ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ^ Schouten, Jan A. (1924). R. Courant (ed.). Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus – An introduction in the latest methods and problems in multi-dimmensional differential geometry). Grundlehren der mathematischen Wissenschaften (in German). Vol. 10. Berlin: Springer Verlag.
- ^ 로버트 B.애쉬 추상수학의 입문서죠케임브리지 대학 출판부, 1998년 1월 1일
- ^ 새로운 미국 백과사전.Edward Thomas Roe, Le Roy Hooker, Thomas W. Handford 편집자페이지 34
- ^ 자연철학의 수학적 원리, 제1권.아이작 뉴턴 경, 존 머신.페이지 12.
- ^ 과학적 전망(1931)
- ^ 수학은 단순화되고 매력적으로 변했습니다. 즉, 운동의 법칙이 설명되었습니다.토마스 피셔의 작품.페이지 15. (참조)그러나 추상화는 기초가 되지 않고 자연과 일치하지 않으며 (논리적인) 진실은 거짓, 광기가 될 것이다.)
- ^ 발의안 제6호, 수학 원리 및 관련 시스템 I의 공식적 결정 불가능한 명제에 대하여(1931년)
- ^ 카스티, 존 L. 5 황금률뉴욕: MJF Books, 1996.
- ^ Methoden Der Mathischen Physik
- ^ P.A.M. Dirac (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society of London A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
- ^ E. Fermi (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4 (1): 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
- ^ F. Bloch; A. Nordsieck (1937). "Note on the Radiation Field of the Electron". Physical Review. 52 (2): 54–59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
- ^ V. F. Weisskopf (1939). "On the Self-Energy and the Electromagnetic Field of the Electron". Physical Review. 56 (1): 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
- ^ R. Oppenheimer (1930). "Note on the Theory of the Interaction of Field and Matter". Physical Review. 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
- ^ Van der Waerden B.L. (1929). "Spinoranalyse". Nachr. Ges. Wiss. Göttingen Math.-Phys. 1929: 100–109.
- ^ Veblen O. (1933). "Geometry of two-component Spinors". Proc. Natl. Acad. Sci. USA. 19 (4): 462–474. Bibcode:1933PNAS...19..462V. doi:10.1073/pnas.19.4.462. PMC 1086023. PMID 16577541.
- ^ Dirac, P.A.M. (1939). "A new notation for quantum mechanics". Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 35, no. 3. pp. 416–418. Bibcode:1939PCPS...35..416D. doi:10.1017/S0305004100021162.
- ^ H. Grassmann (1862). Extension Theory. History of Mathematics Sources. American Mathematical Society, London Mathematical Society, 2000 translation by Lloyd C. Kannenberg.
- ^ Weinberg, Steven (1964), The quantum theory of fields, Volume 2, Cambridge University Press, 1995, p. 358, ISBN 0-521-55001-7
- ^ "The Nobel Prize in Physics 1965". Nobel Foundation. Retrieved 9 October 2008.
- ^ S.L. Glashow (1961). "Partial-symmetries of weak interactions". Nuclear Physics. 22 (4): 579–588. Bibcode:1961NucPh..22..579G. doi:10.1016/0029-5582(61)90469-2.
- ^ S. Weinberg (1967). "A Model of Leptons". Physical Review Letters. 19 (21): 1264–1266. Bibcode:1967PhRvL..19.1264W. doi:10.1103/PhysRevLett.19.1264.
- ^ A. Salam (1968). N. Svartholm (ed.). Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. p. 367.
- ^ F. Englert; R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters. 13 (9): 321–323. Bibcode:1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321.
- ^ P.W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters. 13 (16): 508–509. Bibcode:1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508.
- ^ G.S. Guralnik; C.R. Hagen; T.W.B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
- ^ http://www.physics.drexel.edu/~vkasli/phys676/주의%20 for%20a%20brief%20history%20 of%20quantum%20gravity%20-%20Carlo%20Rovelli.pdf[베어 URL PDF]
- ^ Bourbaki, Nicolas (1972). "Univers". In Artin, Michael; Grothendieck, Alexandre; Jean-Louis Verdier (eds.). Séminaire de Géométrie Algébrique du Bois Marie - 1963-64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - vol. 1 (Lecture notes in mathematics 269) (in French). Berlin; New York: Springer-Verlag. pp. 185–217.
- ^ F.J. Hasert; et al. (1973). "Search for elastic muon-neutrino electron scattering". Physics Letters B. 46 (1): 121. Bibcode:1973PhLB...46..121H. doi:10.1016/0370-2693(73)90494-2.
- ^ F.J. Hasert; et al. (1973). "Observation of neutrino-like interactions without muon or electron in the gargamelle neutrino experiment". Physics Letters B. 46 (1): 138. Bibcode:1973PhLB...46..138H. doi:10.1016/0370-2693(73)90499-1.
- ^ F.J. Hasert; et al. (1974). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Nuclear Physics B. 73 (1): 1. Bibcode:1974NuPhB..73....1H. doi:10.1016/0550-3213(74)90038-8.
- ^ D. Haidt (4 October 2004). "The discovery of the weak neutral currents". CERN Courier. Retrieved 8 May 2008.
- ^ "Mainpage".
- ^ Candelas, P. (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.
- ^ De Felice, F.; Clarke, C.J.S. (1990), Relativity on Curved Manifolds, p. 133
- ^ V. G. Turaev(1994년)의 "노트와 3-매니폴드의 양자 불변량", 71페이지
- ^ Pisanski, Tomaž; Servatius, Brigitte (2013), "2.3.2 Cubic graphs and LCF notation", Configurations from a Graphical Viewpoint, Springer, p. 32, ISBN 9780817683641
- ^ Frucht, R. (1976), "A canonical representation of trivalent Hamiltonian graphs", Journal of Graph Theory, 1 (1): 45–60, doi:10.1002/jgt.3190010111
- ^ 프레일리 2002:89; 헝거포드 1997:230
- ^ 덴, 에드거대수 방정식, 도버. 1930:19
- ^ "The IBM 601 Multiplying Punch". Columbia.edu. Retrieved 24 June 2014.
- ^ "Interconnected Punched Card Equipment". Columbia.edu. 24 October 1935. Retrieved 24 June 2014.
- ^ 런던 수학회 의사록 42 (2)
- ^ Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158. doi:10.1145/800157.805047. ISBN 9781450374644. S2CID 7573663.
추가 정보
- 일반
- 수학의 역사에 대한 짧은 설명.Walter William Rouse Ball 지음.
- 수학사의 입문서.Walter William Rouse Ball 지음.
- 초등 수학의 역사:교수법에 대한 힌트 포함.Florian Cajori의 작품.
- 초등 수학의 역사Florian Cajori의 작품.
- 수학의 역사Florian Cajori의 작품.
- A Short History of Greek Mathematics. By James Gow.
- On the Development of Mathematical Thought During the Nineteenth Century. By John Theodore Merz.
- A New Mathematical and Philosophical Dictionary. By Peter Barlow.
- Historical Introduction to Mathematical Literature. By George Abram Miller
- A Brief History of Mathematics. By Karl Fink, Wooster Woodruff Beman, David Eugene Smith
- History of Modern Mathematics. By David Eugene Smith.
- History of modern mathematics. By David Eugene Smith, Mansfield Merriman.
- Other
- Principia Mathematica, Volume 1 & Volume 2. By Alfred North Whitehead, Bertrand Russell.
- The Mathematical Principles of Natural Philosophy, Volume 1, Issue 1. By Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
- General investigations of curved surfaces of 1827 and 1825. By Carl Friedrich Gaus.
External links
- Mathematical Notation: Past and Future
- History of Mathematical Notation
- Earliest Uses of Mathematical Notation
- Finger counting. files.chem.vt.edu.
- Some Common Mathematical Symbols and Abbreviations (with History). Isaiah Lankham, Bruno Nachtergaele, Anne Schilling.




















 사용했다. 1730년에 오일러는
사용했다. 1730년에 오일러는 





 OR
OR

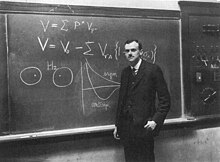














![f[f(x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f54da4ffd78a97e0493340583f3157015327436)


























