다항식
Polynomial수학에서 다항식은 변수의 덧셈, 뺄셈, 곱셈, 양의 정수 거듭제곱의 연산만을 포함하는 불확정 변수(변수라고도 함)와 계수로 구성된 표현입니다.단일 불확정 x의 다항식의 예는 x2 - 4x + 7입니다.3개의 불확정자가 있는 예는3 x + 2xyz2 - yz + 1입니다.
다항식은 수학과 과학의 많은 분야에서 나타납니다.예를 들어, 그것들은 기초 단어 문제부터 복잡한 과학 문제까지 광범위한 문제를 부호화하는 다항식을 형성하는 데 사용됩니다. 그것들은 다항식 함수를 정의하는 데 사용됩니다.그것들은 기초 화학과 물리학에서 경제학과 사회과학에 이르는 범위의 환경에서 나타납니다; 그것들은 미적분학과 수치 분석에서 대략적인 다른 함수들에 사용됩니다.고급 수학에서 다항식은 대수와 대수기하학의 중심 개념인 다항식 고리와 대수적 다양성을 구성하는 데 사용됩니다.
어원
다항식이라는 단어는 "많은"을 의미하는 그리스어 폴리와 라틴어 명사, 즉 "이름"이라는 두 가지 다양한 어근을 결합합니다.라틴어 근 bi-를 그리스어 poly-로 대체하여 이항이라는 용어에서 유래했습니다.즉, 여러 항(여러 단칭)의 합을 의미합니다.다항식이라는 단어는 17세기에 처음 사용되었습니다.[1]
표기법과 용어

다항식에서 발생하는 x를 일반적으로 변수 또는 불확정자라고 합니다.다항식이 식으로 간주될 때 x는 값이 없는 고정 기호입니다(값은 "불확정"입니다).그러나 다항식에 의해 정의된 함수를 고려할 때 x는 함수의 인수를 나타내므로 "변수"라고 불립니다.많은 작가들이 이 두 단어를 혼용하고 있습니다.
불확정 x의 다항식 P는 일반적으로 P 또는 P(x)로 표시됩니다.형식적으로는 다항식의 이름은 P가 아니라 P이지만 함수 표기법 P(x)를 사용하는 것은 다항식과 관련 함수의 구별이 불분명했던 때부터입니다.또한 함수 표기법은 종종 다항식과 그 불확정식을 단일 구문으로 지정하는 데 유용합니다.예를 들어, "P(x)를 다항식이라고 하자"는 "P를 불확정 x의 다항식이라고 하자"의 축약어입니다.반면에, 불확정자의 이름을 강조할 필요가 없을 때, 많은 공식들은 다항식의 각 발생 때마다 불확정자의 이름이 나타나지 않는다면 훨씬 더 간단하고 읽기 쉽습니다.
다항식에 대한 함수 표기의 일반적인 의미를 고려하면 단일 수학적 대상에 대해 두 개의 표기를 갖는 것의 모호성을 공식적으로 해결할 수 있습니다.a가 숫자, 변수, 다른 다항식, 또는 더 일반적으로 임의의 식을 나타내는 경우, P(a)는 관례에 따라 P의 x를 a로 치환한 결과를 나타냅니다.따라서 다항식 P는 함수를 정의합니다.
보다 구체적으로, a가 불확정한 x일 때, 이 함수에 의한 x의 상은 다항식 P 그 자체입니다 (x를 x로 치환해도 아무것도 변하지 않습니다).즉,
정의.
다항식은 변수라고 불리는 상수와 기호로 구성하거나 음수가 아닌 정수 거듭제곱에 대한 덧셈, 곱셈, 지수화를 통해 결정할 수 있는 표현입니다.상수는 일반적으로 숫자이지만, 불확정자를 포함하지 않는 모든 표현일 수 있으며, 덧셈과 곱셈이 가능한 수학적 대상을 나타냅니다.두 다항식은 덧셈과 곱셈의 교환성, 연관성 및 분배성의 일반적인 특성을 적용하여 하나에서 다른 하나로 변환될 수 있는 경우 동일한 다항식을 정의하는 것으로 간주됩니다.예를 들어 (- )( - 2) ( 및 x - + 2 는 동일한 다항식을 나타내는 두 개의 다항식이므로 하나는 동일한 다항식 (- ) x- 2) = 2 - + () = x입니다
단일 불확정 x의 다항식은 항상 다음과 같은 형태로 쓰여질 수 있습니다.
이는 합산 표기법을 사용하여 보다 간결하게 표현할 수 있습니다.
분류
항의 불확정치에 있는 지수를 항의 불확정치의 차수라고 합니다. 항의 차수는 해당 항의 불확정치의 차수의 합이고, 다항식의 차수는 0이 아닌 계수를 갖는 모든 항의 가장 큰 차수입니다.[3]x = x이기 때문에 서면 지수가 없는 불확정자의 정도는 1입니다.
불확정항이 없는 항과 불확정항이 없는 다항식을 각각 상수항과 상수다항식이라고 합니다.[b]상수항과 0이 아닌 상수 다항식의 차수는 0입니다.0 다항식 0(항이 전혀 없음)의 정도는 일반적으로 정의되지 않은 것으로 취급됩니다(아래 참조).[4]
예를 들어,
여러 항의 합을 형성하면 다항식이 생성됩니다.예를 들어, 다음은 다항식입니다.
작은 차수의 다항식에 특정한 이름이 붙여졌습니다.차수 0의 다항식은 상수 다항식 또는 단순히 상수입니다.차수 1, 차수 2 또는 차수 3의 다항식은 각각 선형 다항식, 이차 다항식 및 입방 다항식입니다.[3]높은 차수의 경우 일반적으로 특정 이름이 사용되지 않지만 4차 다항식(4차)과 5차 다항식(5차)이 사용되는 경우도 있습니다.차수의 이름은 다항식 또는 다항식의 항에 적용할 수 있습니다.예를 들어, x2 + 2x + 1의 2x 항은 2차 다항식의 선형 항입니다.
항이 전혀 없는 것으로 간주될 수 있는 다항식 0을 영 다항식이라고 합니다.다른 상수 다항식과 달리 그 차수는 0이 아닙니다.오히려 영 다항식의 정도는 명확하게 정의되지 않은 상태로 남겨지거나 음(-1 또는 -∞)으로 정의됩니다.영다항식은 한 불확정체에서 무한한 수의 근을 갖는 유일한 다항식이라는 점에서도 독특합니다.영다항식 f(x) = 0의 그래프는 x축입니다.
두 개 이상의 불확정한 다항식의 경우, 0이 아닌 모든 항이 degree n을 가지면 다항식을 degree n의 동차라고 합니다.영 다항식은 동차이며, 동차 다항식으로서 그 정도는 정의되지 않습니다.[c]예를 들어 xy32 + 7xy23 - 3x는5 5도의 균질입니다.자세한 내용은 동차 다항식을 참조하십시오.
덧셈의 교환 법칙은 용어를 원하는 순서로 재정렬하는 데 사용될 수 있습니다.하나의 불확정자가 있는 다항식에서, 항들은 보통 "x의 내림차순", 가장 큰 차수가 먼저인 항 또는 "x의 오름차순"에서 정도에 따라 순서가 정해집니다.다항식 3x2 - 5x + 4는 x의 내림차순으로 작성됩니다.첫 번째 항은 계수 3, 불확정 x 및 지수 2를 갖습니다.두 번째 항에서 계수는 -5입니다.세 번째 항은 상수입니다.0이 아닌 다항식의 차수가 어느 한 항의 차수 중 가장 크기 때문에 이 다항식은 차수 2를 갖습니다.[6]
동일한 거듭제곱에 대하여 동일한 불확정성을 갖는 두 항을 "유사항" 또는 "유사항"이라고 하며, 이들은 분배 법칙을 이용하여 결합된 항들의 계수의 합인 단일 항으로 결합될 수 있습니다.이렇게 되면 계수가 0이 될 수 있습니다.[7]다항식은 계수가 0이 아닌 항의 개수로 분류할 수 있으므로 1항 다항식은 일항, [d]2항 다항식은 이항, 3항 다항식은 삼항이라고 합니다.
실수 다항식은 실수 계수가 있는 다항식입니다.함수를 정의하는 데 사용될 때 도메인은 제한을 받지 않습니다.그러나 실수 다항 함수는 실수 다항식에 의해 정의되는 실수에서 실수까지의 함수입니다.마찬가지로 정수 다항식은 정수 계수를 갖는 다항식이고 복소수 다항식은 복소수 계수를 갖는 다항식입니다.
하나의 불확정치에 있는 다항식을 일변량 다항식이라고 하고, 둘 이상의 불확정치에 있는 다항식을 다변량 다항식이라고 합니다.불확정자가 두 개인 다항식을 이변량 다항식이라고 합니다.[2]이러한 개념은 개별 다항식보다는 일반적으로 작업하는 다항식의 종류를 나타냅니다. 예를 들어, 일변량 다항식을 사용할 때, 비록 엄밀하게 말하면, 상수 다항식을 제외하지는 않습니다.상수 다항식에 불확정치가 전혀 포함되지 않습니다.다변량 다항식을 허용되는 불확정치의 최대 수에 따라 이변량, 삼변량 등으로 추가로 분류할 수 있습니다.다시 말해서, 고려 중인 대상의 집합을 뺄셈 하에서 닫기 위해, 삼변수 다항식의 연구는 일반적으로 이변량 다항식 등을 허용합니다.허용되는 불확정치를 나열하여 간단히 "x, y, z의 다항식"이라고 말하는 것도 일반적입니다.
작전
덧셈과 뺄셈
다항식은 덧셈의 연관 법칙(모든 항을 하나의 합으로 묶는 것)을 사용하여 추가할 수 있으며, 그 뒤에 순서를 바꾸거나(교환 법칙을 사용하여) 같은 항을 결합할 수 있습니다.[7][8]예를 들어, 만약
- 3 - +5 - 2 P = -3 + x +4 + Q=-
그 다음에 합
다항식의 뺄셈도 비슷합니다.
곱셈
다항식을 곱할 수도 있습니다.두 다항식의 곱을 항들의 합으로 확장하기 위해, 분포 법칙이 반복적으로 적용되고, 이는 한 다항식의 각 항에 다른 다항식의 각 항을 곱하는 결과를 가져옵니다.[7]예를 들어, 만약
구성.
단일 변수의 다항식 와 임의 수의 변수의 다른 다항식 g가 주어지면, 구성 ∘ g는 첫 번째 다항식의 변수의 각 복사본을 두 번째 다항식으로 치환함으로써 얻어집니다.예를 들어, ( )= + {\) = + 2 이고 g( = 3 + ) = 인 경우
나누기
한 다항식을 다른 다항식으로 나누는 것은 일반적으로 다항식이 아닙니다.대신 이러한 비율은 상황에 따라 합리적 분수, 합리적 표현 또는 합리적 함수라고 불리는 보다 일반적인 객체 계열입니다.[11]이것은 두 정수의 비율이 반드시 정수가 아닌 유리수라는 사실과 유사합니다.[12][13]예를 들어 분수 1/(x + 12)은 다항식이 아니며 변수 x의 거듭제곱의 유한합으로 쓸 수 없습니다.
한 변수의 다항식의 경우, 정수의 유클리드 분할을 일반화하는 다항식의 유클리드 분할 개념이 있습니다.[e]이러한 분할 a(x)/b(x)의 개념은 a = b q + r 및 차수(r) < 도(b)와 같이 몫 q(x)와 나머지 r(x)의 두 다항식을 만듭니다.몫과 나머지는 다항식 긴 나눗셈과 합성 나눗셈을 포함한 여러 알고리즘 중 하나로 계산될 수 있습니다.[14]
분모 b(x)가 단성이고 선형일 때, 즉 어떤 상수 c에 대하여 b(x) = x - c일 때, 다항식 나머지 정리는 a(x)를 b(x)로 나눈 나머지가 평가 a(c)임을 주장합니다.이 경우, 몫은 합성 분할의 특별한 경우인 Ruffini의 규칙에 의해 계산될 수 있습니다.[15]
팩토링
고유한 인수분해 영역(예: 정수 또는 필드)에 계수가 있는 모든 다항식에는 다항식이 축소 불가능한 다항식과 상수의 곱으로 쓰여지는 인수 형태도 있습니다.이 인수 형태는 요인의 순서와 가역 상수의 곱셈까지 고유합니다.복소수 필드의 경우 축소 불가능한 인자는 선형입니다.실제 숫자보다 그들은 1~2개 정도의 학위를 가지고 있습니다.정수와 유리수에 걸쳐 감소 불가능한 요인은 정도를 가질 수 있습니다.[16]예를 들어, 요인화된 형태의
인수분해라고 불리는 인수 형태의 계산은 일반적으로 손으로 쓴 계산으로 하기에는 너무 어렵습니다.그러나 대부분의 컴퓨터 대수 시스템에서는 효율적인 다항식 인수분해 알고리즘을 사용할 수 있습니다.
미적분학.
다항식의 미분과 적분을 계산하는 것은 다른 종류의 함수에 비해 특히 간단합니다.다항식의 도함수
계수가 더 추상적인 설정(예를 들어 계수가 정수 모듈로인 경우 소수 p 또는 임의의 환의 원소)에서 나오는 다항식의 경우, 계수 ka는k a의k k개 복사본의 합을 의미하는 것으로 이해되어 도함수에 대한 공식은 여전히 형식적으로 해석될 수 있습니다.예를 들어, 정수 모듈로프에서 다항식 xp + x의 도함수는 다항식 1입니다.[17]
다항 함수
다항 함수는 다항식을 평가하여 정의할 수 있는 함수입니다.더 정확하게 말하면, 주어진 정의역에서 하나의 인수의 함수 f는 다항식이 존재할 경우 다항식 함수입니다.
예를 들어, 함수 f는 다음과 같이 정의됩니다.
다항식의 평가는 해당 다항식 함수의 계산입니다. 즉, 평가는 각 불확정한 것에 수치 값을 대입하고 표시된 곱셈과 덧셈을 수행하는 것으로 구성됩니다.
하나의 불확정자에 있는 다항식의 경우, 평가는 일반적으로 다음과 같이 다항식을 다시 쓰는 호너의 방법을 사용하여 더 효율적입니다(수행할 산술 연산의 수가 적음).
그래프
-
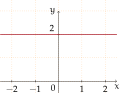
차수 0의 다항식:
f(x) = 2 -
차수 1의 다항식:
f(x) = 2x + 1 -
차수 2의 다항식:
f(x) = x - x - 2
= (x + 1)(x - 2) -
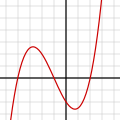
차수 3의 다항식:
f(x) = x/4 + 3x/4 - 3x/2 - 2
= 1/4(x + 4)(x + 1)(x - 2) -
차수 4의 다항식:
f(x) = 1/14 (x + 4)(x + 1)(x - 1)(x - 3)
+ 0.5 -
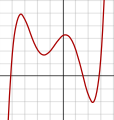
차수 5의 다항식:
f(x) = 1/20 (x + 4)(x + 2)(x + 1)(x - 1)
(x − 3) + 2 -
차수 6의 다항식:
f(x) = 1/100 (x - 2x - 26x + 28x)
+ 145x2 - 26x - 80) -
차수 7의 다항식:
f(x) = (x - 3)(x - 2)(x - 1)(x + 1)(x + 2)
(x + 3)
하나의 실제 변수에 있는 다항 함수는 그래프로 나타낼 수 있습니다.
- 영다항식의 그래프f(x) = 0는 x축입니다.
- 차수 0 다항식의 그래프f(x) = a, 여기서 ≠ 0,는 y intercept a인 수평선입니다.
- 차수 1 다항식(또는 선형 함수)의 그래프f(x) = a + ax, 여기서 ≠ 0,는 y intercept a와 기울기 a를 갖는 사선입니다.
- 차수 2 다항식의 그래프f(x) = a + ax + ax, 여기서 ≠ 0포물선입니다.
- 차수 3 다항식의 그래프f(x) = a + ax + ax + ax, 여기서 ≠ 0입방 곡선입니다.
- 차수가 2 이상인 다항식의 그래프f(x) = a + ax + ax + ax + ⋯ + ax, 여기서 ≠ 0과 n은 2 ≥는 연속형 비선형 곡선입니다.
변수가 무한대로 증가할 때(절대값에서) 비 상수 다항식 함수는 무한대로 증가하는 경향이 있습니다.차수가 1보다 높으면 그래프에 점근점이 없습니다.수직 방향을 가진 두 개의 포물선 가지(양의 x를 나타내는 가지와 음의 x를 나타내는 가지)가 있습니다.
다항식 그래프는 절편, 기울기, 오목 및 끝 거동을 사용하여 미적분학적으로 분석됩니다.
방정식
다항식은 대수 방정식이라고도 불리며, 다음과[18] 같은 형태의 방정식입니다.
방정식을 고려할 때 다항식의 불확정치(변수)는 미지수라고도 하며, 해는 동일성이 참인 미지수의 가능한 값입니다(일반적으로 해가 둘 이상 존재할 수 있습니다).다항식은 (x + y)(x - y) = x - y와 같은 다항식 항등식과 대조를 이루며, 두 식을 서로 다른 형태로 동일한 다항식을 나타내므로, 결과적으로 두 구성원의 평가는 모두 유효한 동일성을 갖습니다.
기본 대수학에서는 1차 다항식과 2차 다항식을 모두 하나의 변수로 풀기 위해 2차 공식과 같은 방법을 가르칩니다.입방정 방정식과 사분위 방정식에 대한 공식도 있습니다.아벨-루피니 정리는 더 높은 차수의 경우 라디칼에는 일반적인 공식이 존재할 수 없다고 주장합니다.그러나, 루트 찾기 알고리즘은 임의의 차수의 다항식의 루트의 수치 근사치를 찾는 데 사용될 수 있습니다.
실수 계수가 있는 다항식의 해의 수는 정도를 초과할 수 없으며, 복소수 해를 다중도로 셀 때의 정도와 같습니다.이 사실을 대수학의 기본 정리라고 합니다.
방정식 풀기
0이 아닌 일변량 다항식 P의 근은 P(a) = 0이 되는 x의 값 a입니다. 즉, P의 근은 다항식 P(x) = 0의 해 또는 P로 정의된 다항식 함수의 0입니다.영다항식의 경우 모든 수는 해당 함수의 영이며, 근의 개념은 거의 고려되지 않습니다.
선형 다항식 x - a가 P를 나누는 경우, 즉 P = (x - a) Q가 되는 또 다른 다항식 Q가 있는 경우에만 수 a는 다항식 P의 근이 됩니다.x - a의 거듭제곱(1보다 큰)이 P를 나눌 수 있습니다. 이 경우 a는 P의 배수근이고, 그렇지 않으면 a는 P의 단순근입니다.만약 P가 0이 아닌 다항식이라면, (x - a)m가 P를 나누는 것과 같은 가장 높은 거듭제곱 m이 존재하며, 이를 P의 근으로서 a의 곱이라고 합니다.각각의 다중도로 계산된 0이 아닌 다항식 P의 근 수는 P의 정도를 초과할 수 없으며,[19] 모든 복소수 근을 고려한다면 이 정도와 같습니다(이것은 대수학의 기본 정리의 결과입니다).다항식의 계수와 다항식의 근은 비에타의 공식과 관련이 있습니다.
x2 + 1과 같은 일부 다항식에는 실수 중에 근이 없습니다.그러나 만약 수용된 해의 집합이 복소수로 확장된다면, 모든 비정수 다항식은 적어도 하나의 근을 갖습니다. 이것이 대수학의 기본 정리입니다.인자 x - a를 연속적으로 분할함으로써 복소수 계수를 갖는 다항식은 상수(그 선행 계수) 곱하기 차수 1로 기록될 수 있음을 알 수 있습니다. 결과적으로, 다중도로 계산된 (복소수) 근의 수는 다항식의 정도와 정확히 일치합니다.
"방정식을 푸는 것"에는 여러 가지 의미가 있을 수 있습니다.솔루션을 명시적인 숫자로 표현하고 싶을 수 있습니다. 예를 들어 2x - 1 = 0의 고유 솔루션은 1/2입니다.불행히도, 이것은 일반적으로 1보다 큰 차수의 방정식에서는 불가능하며, 고대 이래로 수학자들은 해를 대수적 표현으로 표현하기 위해 탐구해 왔습니다. 예를 들어, 황금 비율 (+ )/ 2 1 + 은 - - = 의 유일한 양의 해입니다 x 고대에는 1도와 2도 정도만 성공했습니다.2차 방정식의 경우, 2차 공식은 해의 표현을 제공합니다.16세기 이래로, (제곱근 외에 입방체근을 사용하는) 유사한 공식들은, 훨씬 더 복잡하기는 하지만, 3차 방정식과 4차 방정식에 대해서도 알려져 있습니다 (입방체 방정식과 4차 방정식 참조).하지만 5도 이상의 공식들은 몇 세기 동안 연구자들을 피했습니다.1824년 닐스 헨리크 아벨은 수학 연산과 라디칼만으로 해를 (무한) 공식으로 표현할 수 없는 5차 방정식이 있다는 놀라운 결과를 증명했습니다(아벨-루피니 정리 참조).1830년에 에바리스트 갈루아는 4보다 높은 도의 방정식은 대부분 라디칼로 풀 수 없다는 것을 증명했고, 각각의 방정식에 대해 라디칼로 풀 수 있는지 여부를 결정하고, 풀 수 있다면 풀 수 있다는 것을 보여주었습니다.이 결과는 현대 대수학의 두 중요한 분야인 갈루아 이론과 군론의 시작을 나타냅니다.갈루아 자신은 그의 방법에 의해 암시된 계산이 실행 불가능하다는 것에 주목했습니다.그럼에도 불구하고, 5도와 6도의 해결 가능한 방정식에 대한 공식이 발표되었습니다(5차 함수 및 6차 방정식 참조).
근에 대한 대수적 표현이 없을 때, 그리고 그러한 대수적 표현이 존재하지만 너무 복잡해서 유용하지 않을 때, 그것을 해결하는 독특한 방법은 해의 수치 근사치를 계산하는 것입니다.[20]이를 위한 여러 가지 방법이 있습니다. 일부 방법은 다항식으로 제한되고 다른 방법은 연속 함수에 적용될 수 있습니다.가장 효율적인 알고리즘은 1,000도 이상의 다항식을 컴퓨터에서 쉽게 풀 수 있습니다(루트 찾기 알고리즘 참조).
불확정자가 두 개 이상인 다항식의 경우 다항 함수가 값 0을 취하는 변수에 대한 값의 조합을 일반적으로 "근" 대신 0이라고 합니다.다항식의 0 집합에 대한 연구는 대수기하학의 대상입니다.몇 가지 알 수 없는 다항식 집합의 경우, 유한한 수의 복잡한 해를 갖는지 여부를 결정하는 알고리즘이 있으며, 이 수가 유한한 경우 해를 계산하기 위한 알고리즘이 있습니다.다항식 시스템을 참조하십시오.
모든 다항식이 1등급인 특수한 경우를 선형 방정식 체계라고 하며, 이를 위해 고전 가우스 제거를 포함한 또 다른 범위의 다른 해 방법이 존재합니다.
정수인 해에만 관심이 있는 다항식을 디오판토스 방정식이라고 합니다.디오판토스 방정식을 푸는 것은 일반적으로 매우 어려운 일입니다.해결을 위한 일반적인 알고리즘은 존재할 수 없으며, 해의 집합이 비어 있는지 여부를 결정하는 것조차 불가능하다는 것이 증명되었습니다(힐버트의 열 번째 문제 참조).지난 50년 동안 해결된 가장 유명한 문제 중 일부는 페르마의 마지막 정리와 같은 디오판토스 방정식과 관련이 있습니다.
다항식
불확정자가 다른 수학적 대상에 대입되는 다항식은 종종 고려되며, 때로는 특별한 이름을 갖기도 합니다.
삼각 다항식
삼각 다항식은 n이 하나 이상의 자연수의 값을 가지는 함수 sin(nx)과 cos(nx)의 유한한 선형 조합입니다.[21]실제 값 함수의 경우 계수를 실수로 사용할 수 있습니다.
sin(nx)과 cos(nx)를 sin(x)과 cos(x)로 확장하면 삼각 다항식은 sin(x)와 cos(x) 두 변수에서 다항식이 됩니다 (삼각 항등식 목록 사용)#다각 공식).반대로, sin(x) 및 cos(x)의 모든 다항식은 곱 대 합 항등식과 함께 sin(nx) 및 cos(nx) 함수의 선형 조합으로 변환될 수 있습니다.이 등가성은 선형 조합을 다항식이라고 부르는 이유를 설명합니다.
복잡한 계수의 경우, 그러한 함수와 유한 푸리에 급수 사이에는 차이가 없습니다.
삼각 다항식은 주기 함수의 보간에 적용되는 삼각 보간에 널리 사용됩니다.이산 푸리에 변환에도 사용됩니다.
행렬 다항식
행렬 다항식은 제곱 행렬을 변수로 하는 다항식입니다.[22]주어진 보통의 스칼라 값 다항식
행렬 다항식은 문제의 특정 행렬에 대해 성립하는 두 행렬 다항식 사이의 등식입니다.행렬 다항식 항등식은 지정된 행렬 고리 Mn(R)의 모든 행렬 A에 대해 성립하는 행렬 다항식입니다.
지수 다항식
두 번째 변수가 첫 번째 변수에 적용되는 지수 함수(예: P(x, ex)로 대체되는 이변량 다항식을 지수 다항식이라고 할 수 있습니다.
관련개념
유리함수
유리 분수는 두 다항식의 몫(대수 분수)입니다.유리분수로 다시 쓸 수 있는 모든 대수적 표현은 유리함수입니다.
다항 함수는 변수의 모든 값에 대해 정의되지만, 유리 함수는 분모가 0이 아닌 변수의 값에 대해서만 정의됩니다.
유리 분수는 로랑 다항식을 포함하지만 분모를 불확정자의 거듭제곱으로 제한하지는 않습니다.
로랑 다항식
로랑 다항식은 다항식과 같지만 변수의 음의 거듭제곱이 발생할 수 있습니다.
멱급수
형식 멱급수는 다항식과 같지만 0이 아닌 항이 무한히 많이 발생하여 유한한 정도를 갖지 않습니다.다항식과 달리 이들은 일반적으로 명확하고 완전히 적을 수 없지만(비이성적인 수가 적을 수 없는 것처럼), 이들의 항을 조작하는 규칙은 다항식과 동일합니다.비정형 멱급수도 다항식을 일반화하지만, 두 멱급수의 곱셈은 수렴하지 않을 수 있습니다.
다항식환
교환환 R 위의 다항식 f는 계수가 모두 R에 속하는 다항식입니다.R에 대해 주어진 불확정치 집합의 다항식이 이 불확정치에서 다항식 링이라고 불리는 교환 링을 형성하는지 확인하는 것은 단변량 경우에서 [ x] 다변량 에서 R x 을(를) 나타냅니다.
한명은
R에서 R[x]을 상수 다항식으로 간주하는 자신으로 보내는 맵은 R[x]의 하위 링으로 간주되는 주입 링 동형입니다.특히 R[x]는 R 위의 대수입니다.
고리 R[x]는 R에 하나의 새로운 원소 x를 추가하고, x가 의무적인 것 외에는 다른 관계를 만족하지 않는 고리로 최소한의 방법으로 확장되며, R의 모든 원소와의 교호작용(즉, xr = rx)을 갖는다고 생각할 수 있습니다.이를 위해서는 x의 모든 거듭제곱과 그 선형 조합을 더해야 합니다.
다항식 고리의 형성은 이상을 인수분해하여 요인 고리를 형성하는 것과 함께 알려진 고리를 새로운 고리로 구성하는 중요한 도구입니다.예를 들어, 다항식 x + 1의2 배수의 이상을 인수분해하여 실수 위에 다항식 링 R[x]로부터 구성할 수 있는 복소수의 링(사실 필드).또 다른 예는 유한장의 구성인데, 이는 정수 모듈로의 필드에서 시작하여 계수 링 R로 소수를 시작합니다(모듈러 산술 참조).
만약 R이 가환이면, R[x]의 모든 다항식 P와 R과 같은 정의역과 치역을 갖는 다항식 함수 f를 연관시킬 수 있습니다. (더 일반적으로, R에 대해 정의역과 치역을 취할 수 있습니다.)하나는 P의 기호 x에 대한 값 r을 대체하여 f(r) 값을 얻습니다.다항식과 다항식 함수를 구별하는 한 가지 이유는 일부 링에서 다른 다항식이 동일한 다항식 함수를 생성할 수 있기 때문입니다(예를 들어 R이 정수 모듈 p인 경우 페르마의 작은 정리 참조).R이 실수이거나 복소수인 경우에는 그렇지 않으며, 분석에서 두 개념이 항상 구분되지는 않습니다.다항식과 다항식 함수를 구별하는 더 중요한 이유는 (유클리드 나눗셈과 같이) 다항식에 대한 많은 연산이 x에 대한 일정한 값으로 다항식을 평가하는 것보다 수식으로 구성된 것을 보아야 하기 때문입니다.
가감성
만약 R이 적분 도메인이고, R[x]에 f와 g가 다항식이면, f를 g로 나눈다든지 f를 g로 나눈다든지 f를 g로 나눈다든지, 만약 R[x]에 f q = g가 되는 다항식 q가 존재한다면. 만약 ∈ 이면 a는 f의 근이고, x -만 f를 나눈다.이 경우 다항식 긴 분할을 사용하여 몫을 계산할 수 있습니다.[24][25]
만약 F가 필드이고 f와 g가 g ≠ 0인 F[x]의 다항식이라면, F[x]에는 다음과 같은 고유한 다항식 q와 r이 존재합니다.
마찬가지로, 소수 다항식(더 정확하게는 줄일 수 없는 다항식)은 0이 아닌 다항식으로 정의될 수 있으며, 이는 두 개의 비 상수 다항식의 곱으로 인수분해될 수 없습니다.링의 계수의 경우 "비 상수"는 "비 상수 또는 비 단위"로 대체해야 합니다(두 정의 모두 필드의 계수의 경우 동일).임의의 다항식은 환원 불가능한 다항식의 곱에 의해 가역 상수의 곱으로 분해될 수 있습니다.계수가 필드 또는 고유 인자화 도메인에 속하는 경우 이 분해는 인자의 순서와 단위로 비단위 인자를 곱하는 것까지 고유합니다(그리고 단위 인자를 같은 단위로 나눕니다).계수가 정수, 유리수 또는 유한 필드에 속할 경우 축소불가능성을 검정하고 축소불가능한 다항식으로 인수분해를 계산하는 알고리즘이 있습니다(다항식 인수분해 참조).이 알고리즘들은 손으로 쓴 계산에는 사용할 수 없지만 모든 컴퓨터 대수 시스템에서 사용할 수 있습니다.Eisenstein의 기준은 환원불가능성을 결정하는 데에도 사용될 수 있습니다.
적용들
위치표기
십진법과 같은 현대적인 위치수 체계에서 정수의 숫자와 그들의 위치는 기수 또는 기저의 다항식에 대한 축약 표기이며, 이 경우 4 × 101 + 5 × 10입니다0.다른 예로, 기수 5에서 132와 같은 숫자열은 (decimal) 숫자 1 × 5 + 3 × 5 + 2 × 5 = 42를 나타냅니다.이 표현은 독특합니다.b를 1보다 큰 양의 정수라고 합니다.그러면 모든 양의 정수 a는 다음과 같은 형태로 유일하게 표현될 수 있습니다.
i = 0, 1, ..., m - 1의 경우 0 < r < b 및 0 ≤ r < b.
보간 및 근사
다항 함수의 단순한 구조는 다항식 근사를 사용하여 일반 함수를 분석하는 데 상당히 유용합니다.미분적분학에서 중요한 예로는 테일러 정리가 있는데, 테일러 정리는 미분 가능한 모든 함수가 국소적으로 다항 함수처럼 보인다는 것과 스톤-바이어스트라스 정리가 있습니다.이것은 실수축의 콤팩트 구간에 정의된 모든 연속 함수가 다항 함수에 의해 원하는 만큼 전체 구간에서 근사화될 수 있다는 것을 의미합니다.근사의 실용적인 방법으로는 다항식 보간법과 스플라인의 사용이 있습니다.[27]
기타 어플리케이션
다항식은 다른 개체에 대한 정보를 인코딩하는 데 자주 사용됩니다.행렬 또는 선형 연산자의 특성 다항식에는 연산자의 고유 값에 대한 정보가 들어 있습니다.대수적 요소의 최소 다항식은 해당 요소가 만족하는 가장 간단한 대수적 관계를 기록합니다.그래프의 색다항식은 해당 그래프의 적절한 착색 횟수를 계산합니다.
형용사로서 "다항식"이라는 용어는 다항식 형태로 쓸 수 있는 양이나 함수에도 사용될 수 있습니다.예를 들어, 계산 복잡도 이론에서 다항 시간이란 알고리즘을 완료하는 데 걸리는 시간이 입력의 크기와 같은 일부 변수의 다항 함수에 의해 제한됨을 의미합니다.
역사
다항식의 근을 결정하는 것, 즉 대수 방정식을 푸는 것은 수학에서 가장 오래된 문제 중 하나입니다.그러나 오늘날 우리가 사용하는 우아하고 실용적인 표기법은 15세기에 들어서야 발전했습니다.그 전에는 방정식들이 단어로 쓰여졌습니다.예를 들어, 기원전 200년 중국 산술의 대수 문제는 "풍작 3개, 평작 2개, 흉작 1개를 29더우에 판다"고 시작합니다.우리는 3x + 2y + z = 29 라고 적을 것입니다.
표기법의 역사
등호를 사용한 최초의 사례는 로버트 레코드의 '위트의 숫돌', 1557년에 있습니다.뺄셈을 위한 기호 + for addition, -와 미지의 글자를 사용하는 기호는 Michael Stifel의 Arithemetica integra, 1544에 나타납니다.1637년 라게오메트리의 르네 데카르트는 다항식의 그래프의 개념을 소개했습니다.그는 한 변수의 다항식에 대한 일반적인 공식에서 위에서 볼 수 있는 것처럼 알파벳의 시작부터 상수를 나타내기 위해 문자를 사용하고 변수를 나타내기 위해 알파벳의 끝부터 문자를 사용하는 것을 대중화했습니다. 여기서 a's는 상수를 나타내고 x는 변수를 나타냅니다.데카르트는 지수를 나타내기 위해 위첨자를 사용하는 것을 도입했습니다.[28]
참고 항목
메모들
- ^ 컴팩트 옥스포드 영어 사전의 "다항식" 및 "이항식" 참조
- ^ a b Weisstein, Eric W. "Polynomial". mathworld.wolfram.com. Retrieved 2020-08-28.
- ^ a b "Polynomials Brilliant Math & Science Wiki". brilliant.org. Retrieved 2020-08-28.
- ^ a b c Barbeau 2003, pp. 1-2
- ^ Weisstein, Eric W. "Zero Polynomial". MathWorld.
- ^ Edwards 1995, 페이지 78
- ^ a b c Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.
- ^ Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.
- ^ a b Introduction to Algebra. Yale University Press. 1965. p. 621.
Any two such polynomials can be added, subtracted, or multiplied. Furthermore , the result in each case is another polynomial
- ^ Kriete, Hartje (1998-05-20). Progress in Holomorphic Dynamics. CRC Press. p. 159. ISBN 978-0-582-32388-9.
This class of endomorphisms is closed under composition,
- ^ Marecek, Lynn; Mathis, Andrea Honeycutt (6 May 2020). Intermediate Algebra 2e. OpenStax. §7.1.
- ^ Haylock, Derek; Cockburn, Anne D. (2008-10-14). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers. SAGE. p. 49. ISBN 978-1-4462-0497-9.
We find that the set of integers is not closed under this operation of division.
- ^ a b Marecek & Mathis 2020, §5.4]
- ^ Selby, Peter H.; Slavin, Steve (1991). Practical Algebra: A Self-Teaching Guide (2nd ed.). Wiley. ISBN 978-0-471-53012-1.
- ^ Weisstein, Eric W. "Ruffini's Rule". mathworld.wolfram.com. Retrieved 2020-07-25.
- ^ Barbeau 2003, pp. 80–2
- ^ Barbeau 2003, 페이지 64–5
- ^ Proskuryakov, I.V. (1994). "Algebraic equation". In Hazewinkel, Michiel (ed.). Encyclopaedia of Mathematics. Vol. 1. Springer. ISBN 978-1-55608-010-4.
- ^ Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.
- ^ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
- ^ Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.
- ^ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-681-8. Zbl 1170.15300.
- ^ 호른 & 존슨 1990, 페이지 36.
- ^ Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. p. 129. ISBN 978-0-387-20172-6.
- ^ Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. p. 143. ISBN 978-0-7503-0329-3.
- ^ 맥코이 1968, 페이지 75
- ^ de Villiers, Johann (2012). Mathematics of Approximation. Springer. ISBN 9789491216503.
- ^ Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN 0-03-029558-0.
- ^ 항의 계수는 지정된 집합의 임의의 숫자일 수 있습니다.만약 그 집합이 실수의 집합이라면, 우리는 "실수 위의 다항식"이라고 말합니다.다른 일반적인 유형의 다항식은 정수 계수를 갖는 다항식, 복소수 계수를 갖는 다항식, 정수 모듈로 일부 소수 p인 계수를 갖는 다항식입니다.
- ^ 이 용어는 다항식과 그것이 정의하는 함수의 구별이 명확하지 않았던 때로부터 시작됩니다. 상수항과 상수 다항식은 상수 함수를 정의합니다.[citation needed]
- ^ 사실, 동질적인 함수로서, 그것은 모든 정도의 동질적입니다.[citation needed]
- ^ 어떤 저자들은 "단항형"을 "단항형"이라는 뜻으로 사용합니다. 참조
- ^ 이 단락에서는 다항식이 필드에 계수를 갖는다고 가정합니다.
참고문헌
- Barbeau, E.J. (2003). Polynomials. Springer. ISBN 978-0-387-40627-5.
- Bronstein, Manuel; et al., eds. (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Springer. ISBN 978-3-540-27357-8.
- Cahen, Paul-Jean; Chabert, Jean-Luc (1997). Integer-Valued Polynomials. American Mathematical Society. ISBN 978-0-8218-0388-2.
- Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6..
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556이 고전은 이 글의 대부분의 내용을 다루고 있습니다.
- Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. ISBN 9789622092716.
- Mayr, K. (1937). "Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen". Monatshefte für Mathematik und Physik. 45: 280–313. doi:10.1007/BF01707992. S2CID 197662587.
- McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68015225
- Prasolov, Victor V. (2005). Polynomials. Springer. ISBN 978-3-642-04012-2.
- Sethuraman, B.A. (1997). "Polynomials". Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Springer. ISBN 978-0-387-94848-5.
- Toth, Gabor (2021). "Polynomial Expressions". Elements of Mathematics. Undergraduate Texts in Mathematics. pp. 263–318. doi:10.1007/978-3-030-75051-0_6. ISBN 978-3-030-75050-3.
- Umemura, H. (2012) [1984]. "Resolution of algebraic equations by theta constants". In Mumford, David (ed.). Tata Lectures on Theta II: Jacobian theta functions and differential equations. Springer. pp. 261–. ISBN 978-0-8176-4578-6.
- von Lindemann, F. (1884). "Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen". Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1884: 245–8.
- von Lindemann, F. (1892). "Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen. II". Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1892: 245–8.
외부 링크
- Markushevich, A.I. (2001) [1994], "Polynomial", Encyclopedia of Mathematics, EMS Press
- "Euler's Investigations on the Roots of Equations". Archived from the original on September 24, 2012.



 다항식의 계수라고 불리는 상수이고,
다항식의 계수라고 불리는 상수이고,  불확정입니다.
불확정입니다.






















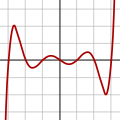
 구간
구간  다항식
다항식 ![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)




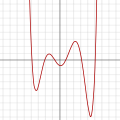




![R[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)
![{\displaystyle R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c388e003e234e12fb55533e35a211c8cf295e5) R
R ![{\displaystyle R[x_{1},\ldots ,x_{n}]=\left(R[x_{1},\ldots ,x_{n-1}]\right)[x_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0bbfe1bccac6aa10e3a7daba9b95381c6f05bd)




