벡터 표기법

수학과 물리학에서 벡터 표기법은 유클리드 벡터 또는 더 일반적으로 벡터 공간의 구성원일 수 있는 벡터를 나타내기 위해 일반적으로 사용되는 표기법입니다.^[1][2]

벡터를 표현할 때 일반적인^[3] 타이포그래픽 규칙은 v와 같이 소문자 직립 굵은 글씨체입니다.국제 표준화 기구(ISO)는 v와 같이 굵은 이탤릭체 세리프 또는${\displaystyle \stackrel{}{}}v$→${\displaystyle {\vec {v}}$과 같이 오른쪽 화살표로 강조된 굵은 이탤릭체 세리프를 권장합니다$.$

고급 수학에서 벡터는 다른 변수와 마찬가지로 단순한 이탤릭체로 표현되는 경우가 많습니다.

역사

1835년 주스토 벨라비티스는 등분의 방향 선분 ${\displaystyle \mathrm{AB}}$ ≏ ${\displaystyle \mathrm{CD}}$ ${\displaystyle AB\bumpeq CD}$의 아이디어를 도입하여 그러한 세그먼트의 등가 클래스로서 벡터의 개념을 만들었습니다.

벡터라는 용어는 1843년경에 W. R. 해밀턴이 4차원 공간에 벡터와 스칼라를 사용하는 계인 쿼터니언을 발표하면서 만들어졌습니다.쿼터니언 q = a + bi + cj + dk에 대하여 해밀턴은 q의 스칼라 부분에 대하여 Sq = a와 벡터 부분인 Vq = bi + cj + dk의 두 개의 투영을 사용했습니다.두 벡터 p, q의 4차곱은 현대적 용어인 교차곱(x)과 점곱(x)을 사용하여 pq = –p.q + pxq로 표기할 수 있습니다.1878년, W. K. Clifford는 그의 교과서 Elements of Dynamic에서 쿼터니언 연산을 학생들에게 유용하게 만들기 위해 두 제품을 절단했습니다.예일 대학교에서 강의를 하던 Josiah Willard Gibbs는 벡터 분석에 소개된 스칼라 곱과 벡터 곱에 대한 표기법을 제공했습니다.^[5]

1891년 올리버 헤비사이드는 클라렌던이 스칼라로부터 벡터를 구별할 것을 주장했습니다.그는 테이트의 그리스 문자와 맥스웰의 고딕 문자 사용을 비판했습니다.^[6]

1912년 J.B. 쇼는 "벡터 표현에 대한 비교 표기법"을 쿼터니언 협회 회보에 기고했습니다.^[7]그 후 알렉산더 맥팔레인은 같은 출판물에서 벡터로 명확한 표현을 위한 15가지 기준을 설명했습니다.^[8]

벡터 아이디어는 1841년에 헤르만 그라스만에 의해 발전되었고, 1862년에 다시 독일어로 발전되었습니다.하지만 독일 수학자들은 영어를 사용하는 수학자들만큼 사분위수를 가지고 있지는 않았습니다.펠릭스 클라인이 독일 수학 백과사전을 정리하고 있을 때, 그는 아르놀트 조머펠트에게 벡터 표기법을 표준화하는 일을 맡겼습니다.^[9]1950년, 아카데믹 프레스(Academical Press)가 G. 쿠어티(G. Kuerti)의 조머펠트의 이론물리학 강의 2권 번역본을 출판했을 때, 벡터 표기법은 각주의 주제가 되었습니다: "원문 독일어 텍스트에서 벡터와 그 구성 요소는 동일한 고딕 형식으로 인쇄됩니다.이 번역에는 양자를 일반적으로 구분하는 방법이 채택되었습니다."^[10]

사각좌표

데카르트 좌표계가 주어지면 벡터는 숫자의 튜플인 데카르트 좌표로 지정될 수 있습니다.

순서 집합 표기법

${\displaystyle {}^{}}$ ${\$의 벡터는 괄호 또는 각괄호로 둘러싸인 정렬된 구성 요소 집합을 사용하여 지정할 수 있습니다$$.

일반적인 의미에서 n차원 벡터 v는 다음 형태 중 하나로 지정할 수 있습니다.

• ${\displaystyle \mathbf {v} =(v_{1},v_{2},\dots,v_{n-1},v_{n})}$
• ${\displaystyle \mathbf {v} =\langle v_{1},v_{2},\dots,v_{n-1},v_{n}\rangle }$ ^[11]

여기서 v₁, v₂, …, v_{n − 1}, v는_n v의 구성 요소입니다.^[12]

행렬 표기법

${\displaystyle {}^{}}$ ${\$의 벡터는 성분 순서 집합을 포함하는 행 또는 열 행렬로 지정할 수도$$ 있습니다.행 행렬로 지정된 벡터를 행 벡터라고 하고 열 행렬로 지정된 벡터를 열 벡터라고 합니다.

다시 행렬을 사용하여 $n차원{\displaystyle \mathbf{}}$벡터 v {\$displaystyle$ \mathbf {$v}}을($를) 다음 형태 중 하나로 지정할 수 있습니다$$.

• ${\displaystyle \mathbf {v} = {\begin{bmatrix}v_{1}&v_{2}&\cdots &v_{n-1}&v_{n}\end{bmatrix} = {\begin{pmatrix}v_{1}&v_{2}&\cdots &v_{n-1}&v_{n}\end{pmatrix}}$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}v_{1}\v_{2}\\\vdots \\v_{n-1}\v_{n}\end{bmatrix}}={\begin{pmatrix}v_{1}\v_{2}\\vdots \\v_{n-1}\end{pmatrix}}$

여기서 v₁, v₂, …, v_{n − 1}, v는_n v의 성분입니다. 일부 고급 맥락에서 행과 열 벡터는 다른 의미를 갖습니다. 자세한 내용은 벡터의 공분산 및 반변성을 참조하십시오.

단위 벡터 표기법

R ${\displaystyle {\mathrm{}}^{}}$ ${\$$$\$mathbb {R} ^{3}$ 의 벡터($$${\displaystyle {\mathrm{}}^{}}$ R$$2 {\$displaystyle$ \$mathbb${R} ^{$2}$와 같이 아래 v가_z 0인 경우)는$$R 3 {\$displaystyle$ \$mathbb${R$}$^{$3}$ 의 표준 기저의 멤버와 벡터의 성분의 스칼라 배수의 합으로 지정할 수 있습니다$.$기본은 단위 벡터 ı ^$$=${\displaystyle }$(${\displaystyle 1,}$ 0${\displaystyle ,}$ ${\displaystyle 0}$) ${\displaystyle {\hat {\imath$}}}=($1, 0, 0),$ȷ ^${\displaystyle \stackrel{}{\mathbf{}}}$=${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 1,}$ ${\displaystyle 0)}$ ${\displaystyle {\hat {\jmath$}}= ($0, 1, 0)$ $\{\backslash$displaystyle {\hat {\jmath}}=${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 0,}$ 1) {\displaystyle ${\hat {$k}}= ($0, 0, 1) {\displaystyle$ {\hat {k}}}.

단위 벡터 표기법을 사용하여 다음과 같은 $형태$로$$3차원 $벡터$ v {\$displaystyle {\boldsymbol$ {v}}을(를$)$ 지정할 수 있습니다$$.

여기서 v_x, v_y, v는_z v의 스칼라 성분입니다. 스칼라 성분은 양수일 수도 있고 음수일 수도 있습니다. 스칼라 성분의 절대값은 크기입니다.

극좌표

평면에 있는 점의 두 극좌표는 2차원 벡터로 간주될 수 있습니다.이러한 벡터는 크기(또는 길이)와 방향(또는 각도)으로 구성됩니다.일반적으로 r로 표시되는 크기는 시작점, 원점에서 표시되는 점까지의 거리입니다.일반적으로 θ(그리스 문자 theta)로 표시되는 각도는 일반적으로 시계 반대 방향으로 측정되는 고정된 방향(일반적으로 양의 x축)과 원점에서 점까지의 방향 사이의 각도입니다.각도는 일반적으로 θ< 2 π ${\displaystyle 0\leq \theta <2\pi }$ 라디안 또는 θ< ∘ ${\displaystyle 0\leq \theta <360^{\circ}}$ 범위 내에 있도록 줄어듭니다

순서 집합 및 행렬 주석

벡터는 직사각형 좌표와 마찬가지로 순서 쌍 표기법(성분 두 개만 사용하는 순서 집합 표기법의 부분 집합) 또는 행렬 표기법을 사용하여 지정할 수 있습니다.이러한 형태에서 벡터의 첫 번째 성분은 r(v 대신)이고 두 번째 성분은 θ(v 대신)입니다.극좌표를 직사각형 좌표와 구별하기 위해 각도 기호 ∠ ${\displaystyle \angle}$을(를) 접두사로 붙이면 됩니다$.$

v에 대한 2차원 극좌표는 순서쌍 또는 행렬 표기법을 사용하여 다음 중 하나로 나타낼 수 있습니다.

• ${\displaystyle \mathbf {v} =(r,\angle \theta )}$
• ${\displaystyle \mathbf {v} =\langler,\angle \theta \rangle }$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}r&\angle \theta \end{bmatrix}}$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}r\\\angle \theta \end{bmatrix}}$

여기서 r은 크기, θ는 각도, 각도 기호$$∠ ${\displaystyle \angle$는 옵션입니다.

직기법

벡터는 r과 θ를 명시적으로 정의하는 단순화된 자율 방정식을 사용하여 지정할 수도 있습니다.이것은 다루기 힘들 수 있지만 순서 쌍 또는 행렬 표기법을 사용하여 발생하는 2차원 직사각형 벡터와의 혼동을 방지하는 데 유용합니다.

크기가 5 단위이고 방향이 π/9 라디안(20°)인 2차원 벡터는 다음 형태 중 하나를 사용하여 지정할 수 있습니다.

• ${\displaystyle r=5,\theta ={\pi \over 9}}$
• ${\displaystyle r=5,\theta =20^{\circ}}$

원통벡터

원통형 벡터는 극좌표의 개념을 3차원으로 확장한 것입니다.이것은 원통 좌표계에 있는 화살표와 같습니다.원통형 벡터는 xy 평면에서의 거리, 각도 및 xy 평면으로부터의 거리(높이)에 의해 지정됩니다.일반적으로 r 또는 ρ(그리스 문자 rho)로 표시되는 첫 번째 거리는 xy 평면에 대한 벡터 투영의 크기입니다.일반적으로 θ 또는 φ(그리스 문자 pi)로 표시되는 각도는 x축과 양의 방향으로 공선을 이루는 선으로부터의 오프셋으로 측정됩니다. 각도는 일반적으로 θ< π ${\displaystyle 0\leq \theta <2\pi }$ 범위 내에 놓이도록 감소됩니다 일반적으로 h 또는 z로 표시되는 두 번째 거리,xy 평면에서 벡터의 끝점까지의 거리입니다.

순서 집합 및 행렬 주석

원통형 벡터는 극좌표를 사용하는데, 여기서 두 번째 거리 성분은 세 번째 성분으로 연결되어 순서가 매겨진 삼중항(다시 순서가 매겨진 집합 표기법의 부분 집합)과 행렬을 형성합니다.각도는 각도 기호( ∠ ${\displaystyle \angle}$ )로 접두사가 붙을 수 있습니다. 거리-각도-거리 조합은 이 표기법의 원통형 벡터와 유사한 표기법의 구형 벡터를 구별합니다.

3차원 원통형 벡터 v는 순서가 매겨진 삼중항 또는 행렬 표기법을 사용하여 다음 중 하나로 나타낼 수 있습니다.

• ${\displaystyle \mathbf {v} =(r,\angle \theta,h)}$
• ${\displaystyle \mathbf {v} =\langler,\angle \theta,h\rangle }$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}r&\angle \theta &h\end{bmatrix}}$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}r\\\angle \theta \h\end{bmatrix}}}$

여기서 r은 xy 평면에 대한 v 투영 크기이고, θ는 양의 x축과 v 사이의 각도이며, h는 xy 평면에서 v의 끝점까지의 높이입니다. 다시 각도 기호( ∠ ${\displaystyle \angle$는 선택 사항입니다.

직기법

원통형 벡터는 r(또는 ρ), θ(또는 φ), h(또는 z)를 정의하는 단순화된 자율 방정식을 사용하여 직접 지정할 수도 있습니다.변수에 사용할 이름을 선택할 때는 일관성을 사용해야 하며, ρ는 θ 등과 함께 사용해서는 안 됩니다.

xy 평면에 대한 투영의 크기가 5 단위이고, 양의 x축으로부터의 각도가 π/9 라디안(20°)이고, xy 평면으로부터의 높이가 3 단위인 3차원 벡터는 다음 형태 중 하나로 지정될 수 있습니다.

• ${\displaystyle r=5,\theta = {\pi \over 9},\ h=3}$
• ${\displaystyle r=5,\theta =20^{\circ},\ h=3}$
• ${\displaystyle \rho = 5,\ \phi = {\pi \over 9},\ z=3}$
• ${\displaystyle \rho =5, \phi =20^{\circ },\ z=3}$

구면벡터

구형 벡터는 극벡터의 개념을 3차원으로 확장하는 또 다른 방법입니다.이것은 구면 좌표계에 있는 화살표와 같습니다.구면 벡터는 크기, 방위각 및 진각으로 지정됩니다.규모는 보통 ρ으로 표시됩니다.방위각은 일반적으로 θ로 표시되며, 양의 x축에서 (시계 반대 방향으로) 오프셋입니다.일반적으로 φ로 표시되는 제니스 각도는 양의 z 축으로부터의 오프셋입니다.두 각도는 일반적으로 0(포함)에서 2 π(단독) 범위 내에 놓이도록 줄어듭니다.

순서 집합 및 행렬 주석

구형 벡터는 극성 벡터처럼 지정되며, 여기서 제니스 각도는 세 번째 성분으로 연결되어 순서가 지정된 삼중항과 행렬을 형성합니다.방위각 및 제니스 각도는 모두 각도 기호( ∠ ${\displaystyle \angle})$로 접두사가 붙여질 수 있습니다. 접두사는 구면 벡터와 원통형 벡터를 구별하는 거리-각-각 조합을 생성하는 데 일관되게 사용되어야 합니다.

3차원 구면 벡터 v는 순서가 매겨진 삼중항 또는 행렬 표기법을 사용하여 다음 중 하나로 나타낼 수 있습니다.

• ${\displaystyle \mathbf {v} = (\rho,\angle \theta,\angle \phi )}$
• ${\displaystyle \mathbf {v} =\langle \rho ,\angle \theta ,\angle \phi \angle }$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}\rho &\angle \theta &\angle \phi \end{bmatrix}}$
• ${\displaystyle \mathbf {v} = {\begin{bmatrix}\rho \\\angle \theta \\\angle \phi \end{bmatrix}}$

여기서 ρ은 크기, θ은 방위각, φ은 제니스 각도입니다.

직기법

극 및 원통형 벡터와 마찬가지로 구면 벡터는 단순화된 자율 방정식을 사용하여 지정할 수 있으며, 이 경우 ρ, θ 및 φ에 대해 지정할 수 있습니다.

크기가 5 단위이고 방위각이 π/9 라디안(20°)이며, 제니스각이 π/4 라디안(45°)인 3차원 벡터는 다음과 같이 지정할 수 있습니다.

• ${\displaystyle \rho = 5,\theta = {\pi \over 9},\pi = {\pi \over 4}}$
• ${\displaystyle \rho = 5,\theta = 20^{\circ },\phi = 45^{\circ }$

작전

주어진 벡터 공간에서 벡터 덧셈과 스칼라 곱셈의 연산이 정의됩니다.노름 벡터 공간은 노름(또는 크기 결정)으로 알려진 연산을 정의하기도 합니다.내부 제품 공간은 내부 제품이라고 하는 작업을 정의하기도 합니다.${\displaystyle {}^{}}$ ${\$에서 내부곱을 점곱이라고 합니다$.$$R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$ 및 $R$ ${\displaystyle {\mathrm{}}^{}}$ ${\$에서 교차곱이라고 하는 추가 연산도 정의됩니다$.$

벡터 덧셈

벡터 덧셈은 두 벡터 사이의 연산자로 사용되는 더하기 기호로 표시됩니다.두 벡터 u와 v의 합은 다음과 같이 표현됩니다.

스칼라 곱셈

스칼라 곱셈은 대수적 곱셈과 같은 방식으로 표현됩니다.벡터 옆의 스칼라(둘 중 하나 또는 둘 다 괄호 안에 있을 수 있음)는 스칼라 곱셈을 의미합니다.두 개의 공통 연산자인 점과 회전된 십자가도 사용할 수 있지만(회전된 십자가는 거의 사용되지 않음에도 불구하고), 점 곱과 두 벡터에서 작동하는 교차 곱과 혼동할 위험이 있습니다.벡터 v를 갖는 스칼라 k의 곱은 다음과 같은 방식으로 나타낼 수 있습니다.

• ${\displaystyle k\mathbf {v}}$
• ${\displaystyle k\cdot \mathbf {v}}$

벡터 뺄셈과 스칼라 나눗셈

뺄셈과 나눗셈의 대수적 특성과 스칼라 곱셈을 사용하면 두 벡터를 " 뺄셈"하고 스칼라로 벡터를 "나눗셈"하는 것도 가능합니다.

벡터 뺄셈은 첫 번째 벡터 피연산자에 두 번째 벡터 피연산자가 있는 -1의 스칼라 배수를 더함으로써 수행됩니다.이것은 연산자로서 마이너스 부호를 사용하는 것으로 나타낼 수 있습니다.두 벡터 u와 v 사이의 차이는 다음 방식 중 하나로 나타낼 수 있습니다.

• ${\displaystyle \mathbf {u} +-\mathbf {v}}$
• ${\displaystyle \mathbf {u} -\mathbf {v}}$

스칼라 분할은 벡터 피연산자에 스칼라 피연산자의 숫자 역을 곱하여 수행됩니다.이는 분율 막대 또는 분할 기호를 연산자로 사용하는 것으로 나타낼 수 있습니다.벡터 v와 스칼라 c의 몫은 다음과 같은 형태로 나타낼 수 있습니다.

• ${\displaystyle {1 \over c}\mathbf {v}}$
• ${\displaystyle {\mathbf {v} \over c}}$
• ${\displaystyle {\mathbf {v} \div c}$

노름

벡터의 노름은 벡터의 양쪽에 이중 막대로 표시됩니다.벡터 v의 노름은 다음과 같이 나타낼 수 있습니다.

표준은 ${\displaystyle v\mathbf{}}$ $displaystyle \mathbf {v}$ }과 같은 단일 막대로 표현되기도 하지만$,$ 이는 표준의 한 유형인 절대값과 혼동될 수 있습니다.

내품

두 벡터(스칼라 곱이라고도 하며, 스칼라 곱과 혼동하지 않도록 함)의 내부 곱은 각괄호 안에 포함된 순서 쌍으로 표시됩니다.두 벡터 u와 v의 내적은 다음과 같이 표현됩니다.

도트상품

${\displaystyle {}^{}}$ ${\$에서 내부곱을 점곱이라고도 합니다$.$표준 내부 곱 표기법 외에도 (점을 연산자로 사용하는) 점 곱 표기법도 사용할 수 있습니다.두 벡터 u와 v의 점곱은 다음과 같이 나타낼 수 있습니다.

일부 오래된 문헌에서 점 곱은 나란히 쓰여진 두 벡터 사이에 암시되어 있습니다.이 표기법은 두 벡터 사이의 다이애딕 곱과 혼동될 수 있습니다.

크로스 상품

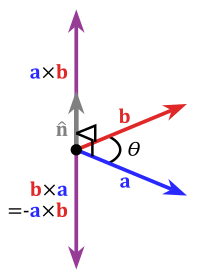
두 벡터(${\displaystyle {\mathrm{}}^{}}$ ${\$의 교차곱을 연산자로 사용하여 표현합니다.두 벡터 u와 v의 교차곱은 다음과 같이 표현됩니다.

일부 규약(예: 프랑스와 고등 수학의 일부 영역)에 따르면, 이는 쐐기로도 표시되며,^[13] 쐐기곱은 3차원에서 기능적으로 동일하므로 쐐기곱과의 혼동을 방지합니다.

일부 오래된 문헌에서는 u와 v 사이의 교차곱에 대해 다음과 같은 표기법이 사용됩니다.

나블라

벡터 표기법은 나블라 연산자를 통해 미적분학과 함께 사용됩니다.

스칼라 함수 f를 사용하면 기울기는 ∇ ${\displaystyle f}$,${\displaystyle \nabla$ f$\..}$로 표기됩니다.

벡터 필드를 사용하면, 발산 F는 ∇ ⋅ ${\displaystyle F,}$ ${\displaystyle \nabla \cdot$ F$,}$로 표기됩니다.

그리고 벡터 필드를 사용하면, F 컬은 ∇${\displaystyle }$× ${\displaystyle F}$로 표기됩니다$.$ {\$displaystyle \nabla \times$ F$.}$

참고 항목

• 유클리드 벡터
• ISO 31-11 § 벡터 및 텐서
• 파소르

참고문헌