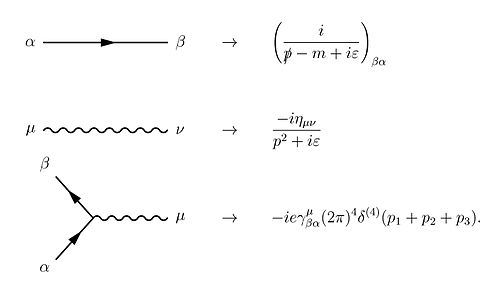양자전기역학

양자장 이론
파인만 도표
역사
배경 장 이론 전자기학 약한 힘 강한 힘 양자역학 특수상대성 일반상대성 게이지 이론
대칭 양자역학의 대칭 C대칭 P-대칭 T-대칭 공간 번역 대칭 시간 변환 대칭 회전 대칭 로렌츠 대칭 푸앵카레 대칭 게이지 대칭 명시적 대칭 깨짐 자연대칭파단 양-밀스 이론 노에더 전하 위상 전하
도구들 변칙 교차 유효장 이론 기대값 파데예프-포포프 유령 파인만 도표 격자 게이지 이론 LSZ 환원식 파티션 함수 전파자 수량화 정규화 리노말화 진공 상태 윅의 정리 와이트먼 공리
방정식 디라크 방정식 클라인-고든 방정식 프로카 방정식 휠러-드위트 방정식 바그만-위그너 방정식
표준 모델 양자전기역학 전기와크 상호작용 양자 색역학 힉스 메커니즘
불완전 이론 위상 양자장 이론 끈 이론 초대칭 테크니컬러 만물론 양자 중력
과학자들 앤더슨 안셀름 아티야 바그만 베치 벨라빈 벤더 베테 비요르켄 블뤼어 보골류보프 브로스키 브라우트 갈색 부홀츠 캘런 캐스웰 콜먼 콘스 다센 드위트 디락 도플리처 다이슨 잉글러트 파데예프 파딘 페르미 파인만 피에르즈 포크 프레덴하겐 프리츠슈 프롤리히 털로 덮인 글래쇼 글림 겔판트 겔만 골드스톤 그리보프 징그럽다 굽타 구랄니크 하그 하이젠베르크 헵 힉스 하겐 't 후프트' 일리오풀로스 잇직슨 이바넨코 재피 조나라시니오 조던 조스트 켈렌 카플란 카슬러 켄달 키블 클레바노프 콘체비치 쿠라예프 양고기 란다우 리 리 레만 르페이지 리파토프 낮음 뤼데르 마이아니 메이저나나 몰다세나 미그달 밀스 뮐러 나이마르크 남부 네베우 니시지마 오메 오펜하이머 오스터왈더 파리시 파울리 폴리티저 폴리아코프 포메란추크 포포프 프로카 루엘 살람 슈바르츠 슈윙거 시걸 세이베르크 세메노프 시르코프 스카이르메 스토라 슈테켈베르크 수다르산 시만지크 서링 토모나가 튜틴 벨트만 비라소로 병동 와인버그 바이스코프 갠젤 웨스 웨테리히 바일 윅 와이트먼 위그너 윌체크 윌슨 비튼 양 유카와 자몰로드치코프 자몰로드치코프 짐머만 진 저스틴 주버 주미노
v t

입자물리학에서 양자전기역학(QED)은 전기역학의 상대론적 양자장 이론이다.본질적으로 빛과 물질이 어떻게 상호작용을 하는지를 기술하고 있으며 양자역학과 특수상대성이론의 완전한 합치가 이루어지는 최초의 이론이다.QED는 광자의 교환을 통해 상호작용하는 전기 전하 입자와 관련된 모든 현상을 수학적으로 기술하며, 물질과 빛 상호작용에 대한 완전한 설명을 제공하는 고전 전자석의 양자적 대응력을 나타낸다.

기술 용어로 QED는 전자기 양자 진공의 섭동 이론으로 설명할 수 있다.리처드 파인만은 전자의 변칙적인 자기 모멘트나 수소의 에너지 수준의 양 이동과 같은 수량의 극히 정확한 예측을 위해 그것을 "물리학의 보석"이라고 불렀다.^{[1]: Ch1}

역사

방사선과 물질의 상호작용을 기술하는 양자 이론의 첫 번째 공식은 (1920년대 동안) 원자의 자발적 방출 계수를 계산할 수 있었던 영국의 과학자 폴 디락 덕분이다.^[2]

디락은 전자기장의 정량화를 입자의 생성과 소멸 연산자의 개념의 도입과 함께 조화 발진기의 앙상블이라고 묘사했다.그 다음 해에, 물리학자들은 볼프강 파울리, 유진 위그너, 파스쿠알 요르단, 베르너 하이젠버그의 기여와 엔리코 페르미의 양자 전자역학의 우아한 공식화 덕분에, 원칙적으로 광자와 전하 입자를 포함하는 어떤 물리적 과정에 대해서도 어떤 계산도 수행할 수 있을 것이라고 믿게 되었다.^[3]그러나 1937년과 1939년에 ^[5]아놀드 노르딕과 ^[4]함께 펠릭스 블로흐가 수행한 추가 연구는 그러한 연산이 로버트 오펜하이머가 이미 지적한 문제인 섭동 이론의 첫 번째 순서에서만 신뢰할 수 있다는 것을 밝혀냈다.^[6]일련의 부정행위에 더 높은 순서가 나타나면서 그러한 연산은 무의미하게 만들고 이론 자체의 내적 일관성에 심각한 의구심을 갖게 했다.당시 이 문제에 대한 해결책이 알려지지 않은 상태에서 특수상대성이론과 양자역학 사이에 근본적인 비호환성이 존재하는 것으로 나타났다.

그 이론에 대한 어려움은 1940년대 말까지 증가했다.전자레인지 기술의 발전은 현재 전자의 램 시프트와 자기 모멘트라고 알려진 ^[7]수소 원자의 수준 이동에 대한 더 정확한 측정을 할 수 있게 했다.^[8]이 실험들은 이론이 설명할 수 없는 불일치를 드러냈다.

탈출 가능성에 대한 첫 징후는 1947년 ^[9]한스 베테에 의해 보호소 섬 회의에 참석한 후 나왔다.^[10]그가 컨퍼런스에서 쉐넥타디로 기차를 타고 이동하는 동안 그는 람과 레서포드가 측정한 수소 원자의 선들의 이동에 대한 최초의 비-상대론적 계산을 했다.^[9]연산의 한계에도 불구하고, 합의는 훌륭했다.그 생각은 단순히 실험에 의해 실제로 유한한 값으로 고정된 질량과 전하 교정에 불의를 붙이는 것이었다.이렇게 해서, 그 불순물들은 그 상수에 흡수되어 실험과 좋은 합치를 이루는 유한한 결과를 낳게 된다.이 절차는 리노멀라이제이션이라고 명명되었다.

토모나가 신이치로,^[11] 줄리안 슈윙거,^[12][13] 리처드^[14][15][16] 파인만, 프리만 다이슨이 이 주제에 대해 베테의 직관과 기초적인 논문을 바탕으로 마침내 양자 전기역학의 섭동 시리즈에서 어떤 순서로든 유한한 완전한 공변량 형성을 얻을 수 있었다.^[17][18]토모나가 신이치로, 줄리안 슈윙거, 리처드 파인만은 이 분야에서 일한 공로로 1965년 노벨 물리학상을 공동 수상했다.^[19]그들의 기여와 프리먼 다이슨의 기여는 어떤 순서로든 섭동 이론에서 관측 가능성의 연산을 가능하게 하는 양자 전자역학의 공변량과 게이지 내 변이성 형성에 관한 것이었다.파인만의 도표를 바탕으로 한 수학적 기법은 처음에는 슈윙거와 토모나가의 현장 이데올로기적, 연산자 기반 접근법과는 매우 다른 것처럼 보였지만, 프리먼 다이슨은 나중에 두 접근법이 동등하다는 것을 보여주었다.^[17]결합을 통해 이론에 나타나는 특정 다이버전스에 물리적 의미를 부여해야 할 필요성인 리노말화는 이후 양자장 이론의 근본적인 측면 중 하나가 되어 이론의 일반적인 수용성의 기준으로 여겨지게 되었다.비록 리노말화가 실제로 매우 잘 작동한다고 해도 파인만은 리노말화를 "껍질 게임"과 "호쿠스 포커스"^{[1]: 128} 라고 언급하면서 수학적 타당성에 완전히 만족한 적이 없었다.

QED는 모든 후속 양자장 이론의 모델과 템플릿 역할을 해왔다.그러한 일련의 이론 중 하나는 양자 색역학으로, 1960년대 초에 시작되어 1970년대 H. 데이비드 폴리티저, 시드니 콜먼, 데이비드 그로스, 프랭크 윌크젝트에 의해 현재의 형태를 갖추게 되었다.슈윙거, 제럴드 구랄닉, 딕 하겐, 톰 키블,^[20][21] 피터 힉스, 제프리 골드스톤 등의 선구적 업적을 바탕으로 셸던 글래쇼, 스티븐 와인버그, 압두스 살람 등이 독자적으로 약한 핵력과 양자 전기역학이 어떻게 하나의 전기약력으로 융합될 수 있는지를 보여주었다.

파인만의 양자 전자역학 관점

소개

말년에 리처드 파인만은 일반 대중을 위한 QED에 대해 일련의 강의를 했다.이 강의들은 Feynman(1985년), QED: 이상한 빛과 물질의 이론은 QED의 전형적인 비수학적인 표현으로,^[1] 아래에 설명되어 있다.

파인만의 QED 발표의 핵심 구성 요소는 세 가지 기본 행동이다.^{[1]: 85}

광자는 한 장소에서 다른 시간과 장소로 간다.

전자는 한 장소와 시간에서 다른 장소와 시간으로 간다.

전자는 특정한 장소와 시간에 광자를 방출하거나 흡수한다.

이러한 작용은 파인만 다이어그램의 세 가지 기본 요소인 광자에 대한 웨이브 선, 전자에 대한 직선과 두 개의 직선의 교차점, 전자에 의한 광자의 방출이나 흡수를 나타내는 꼭지점에 대한 웨이브 선으로 시각적 속기 형태로 표현된다.이것들은 모두 인접한 도표에서 볼 수 있다.

파인만이 도입하는 행동의 시각적 속기뿐만 아니라 확률 진폭이라고 불리는 수량의 다른 종류의 속기를 소개한다.확률은 ${\displaystyle \text{전체}}$ 확률 진폭의 ${\displaystyle 절대값}$인 f$($) ${\displaystyle {}^{\mathrm{}}}$ $displaystyle{$probability}=$f({\text{$probability}=$f$$({\$text${amplitude}) ^2$ 광자가 한 장소와 시간 $A{\displaystyle }$ {\$displaystystyle A$$}$에서 다른 $장소$와 시간 B$\}$로 이동하는$$ 경우, 관련 qua.ntity는 파인만의 속기에 $P{\displaystyle }$(${\displaystyle A}$ ${\displaystyle \text{to}}$ B $){\displaystyle$P$(A{\text{{}}B)}$로 쓰여 있다$.$$C{\displaystyle }$ ${\displaystyle C}$에서 $D{\displaystyle }$ ${\displaystyle D}($으)로$$ 이동하는 전자에 대해 유사한 양이 $E{\displaystyle (\text{C}}$ to ${\displaystyle D)}$ ${\displaystyle E(C{\text{}~}D)}$로 기록되어$$ 있다$.$그가 j라고 부르는 광자의 방출 또는 흡수에 대한 확률 진폭에 대해 알려 주는 수량.이는 측정된 전자 전하 e와 관련이 있지만 동일하지는 않다.^{[1]: 91}

QED는 많은 전자와 광자의 복잡한 상호작용이 위의 세 가지 빌딩 블록의 적절한 컬렉션을 결합한 다음 확률 진폭을 사용하여 그러한 복잡한 상호작용의 확률을 계산함으로써 표현될 수 있다는 가정에 근거한다.위에서 언급한 확률 진폭(P(A~B), E(C~D), j)의 총 제곱이 우리의 일상적인 확률(Feynman의 책에서 만들어진 단순화)과 똑같이 작용한다고 가정하면서 QED의 기본이념을 전달할 수 있는 것으로 나타났다.나중에 파인만에 이어 양자형 수학을 구체적으로 포함하도록 수정될 것이다.

사용될 확률 진폭의 기본 규칙은 다음과 같다.^{[1]: 93}

기본 구성

우리는 특정한 장소와 시간에 하나의 전자(이 장소와 시간에는 임의의 라벨 A가 주어짐)와 다른 장소와 시간에 있는 광자(라벨 B가 주어짐)로 시작한다고 가정합시다.물리적인 관점에서 전형적인 질문은 "C(다른 장소와 나중의 시간)에서 전자를 찾을 확률은 얼마인가"이다.이 목적을 달성하기 위한 가장 간단한 과정은 전자가 A에서 C로 이동하는 것(기본 작용)과 광자가 B에서 D로 이동하는 것(다른 기초 작용)이다.이러한 각 하위 프로세스(E(A~C)와 P(B~D)의 확률 진폭에 대한 지식으로부터 위의 규칙 b)를 사용하여 두 가지 프로세스를 곱하여 두 가지 프로세스의 확률 진폭을 계산할 수 있을 것으로 예상한다.이것은 추정된 확률을 제공하기 위해 제곱된 단순 추정 전체 확률 진폭을 제공한다.^{[citation needed]}

그러나 최종 결과가 나올 수 있는 다른 방법들이 있다.전자는 광자를 흡수하는 장소와 시간 E로 이동한 다음 F에서 또 다른 광자를 방출하기 전에 움직인 다음, 새로운 광자가 D로 이동하는 동안 C로 이동할 수 있다.이 복잡한 과정의 확률은 세 가지 전자 작용, 두 개의 광자 작용, 두 개의 정점, 즉 한 개의 방출과 한 개의 흡수라는 각각의 개별 작용의 확률 진폭을 알면 다시 계산할 수 있다.E와 F의 선택된 위치에 대해 각 작용의 확률 진폭에 곱하여 총 확률 진폭을 찾을 수 있을 것으로 예상한다.그런 다음 위의 규칙 a)를 사용하여 E와 F의 모든 대안에 대해 이 모든 확률 진폭을 합산해야 한다(실제로는 초보적이지 않으며 통합을 수반함).그러나또다른 가능성이 있는데,그것은 전자가 먼저 G로 이동해서 광자를 방출하고, 여기서 D로 이어지는 반면, 전자는 첫 번째 광자를 흡수하는 H로 이동하다가 C로 이동한다는 것이다.다시, 이러한 가능성의 확률 진폭(모든 점 G와 H)을 계산할 수 있다.그런 다음 이 두 가지 가능성의 확률 진폭을 원래 단순 추정치에 추가함으로써 전체 확률 진폭에 대한 더 나은 추정치를 얻는다.우연히, 광자가 전자와 이런 방식으로 상호작용하는 이 과정에 주어진 이름은 콤프턴 산란이다.^{[citation needed]}

점점 더 많은 광자가 흡수되거나 방출되는 다른 중간 "가상" 프로세스가 무한히 많다.이러한 각 프로세스에 대해 파인만 다이어그램을 그릴 수 있다.이는 결과적인 확률 진폭에 대한 복잡한 계산을 의미하지만, 도표가 복잡할수록 결과에 기여하는 것이 적다는 점을 감안한다면, 본문에 대한 원하는 만큼 정확한 답을 찾는 것은 시간과 노력의 문제일 뿐이다.이것은 QED의 기본적인 접근법이다.전자와 광자 사이의 어떤 쌍방향 공정의 확률을 계산하기 위해서는 우선 파인만 도표와 함께 세 가지 기본 요소로부터 공정을 구성할 수 있는 가능한 모든 방법을 주목해야 한다.각 다이어그램은 관련된 확률 진폭을 찾기 위한 명확한 규칙을 포함하는 계산을 포함한다.

양자 서술로 옮겨갈 때 기본적인 비계는 남아있지만, 개념적인 변화가 필요하다.하나는 우리가 일상 생활에서 입자가 움직일 수 있는 지점에 약간의 제약이 있을 것이라고 예상하는 반면, 완전한 양자 전기역학에서는 그렇지 않다.A에는 전자, B에는 광자의 0이 아닌 확률 진폭이 있어 우주의 다른 장소와 시간에 대한 기본 작용으로 움직인다.그것은 빛의 속도보다 더 빠른 속도에서만 도달할 수 있는 장소를 포함한다.(시간에 역행하는 전자는 시간에 따라 전진하는 양전자라고 볼 수 있다.)^{[1]: 89, 98–99}

확률 진폭

양자역학은 확률 계산 방식에 중요한 변화를 도입한다.확률은 여전히 우리가 일상 세계에서 확률에 사용하는 일반적인 실제 숫자로 표현되지만, 확률은 복잡한 숫자인 확률 진폭의 제곱 계수로 계산된다.

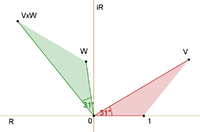
파인만은 종이나 화면에 화살표로 단순하지만 정확한 표현을 사용함으로써 복잡한 숫자의 수학에 독자를 노출시키는 것을 피한다.(이러한 것들은 공간의 3차원에서 점들 사이의 관계의 2차원에서 단순화된 표현인 파인만 다이어그램의 화살표와 혼동해서는 안 된다.그리고 한 번)진폭 화살표는 양자 이론에 의해 주어진 세계에 대한 설명에 기초한다.그것들은 사건의 확률이 해당 진폭 화살표의 길이의 제곱이라는 단순한 규칙에 의해 우리의 일상적인 확률 아이디어와 관련이 있다.따라서 주어진 공정의 경우, v와 w라는 두 개의 확률 진폭이 관련될 경우 공정의 확률은 다음 중 하나에 의해 부여된다.

${\displaystyle P= \mathbf {v} +\mathbf {w} ^{2}}$

또는

${\displaystyle P= \mathbf {v} \,\mathbf {w} ^{2}.}$

그러나 덧셈이나 곱셈에 관한 규칙은 위와 같다.그러나 확률을 추가하거나 곱할 것으로 예상할 경우, 대신 현재 복잡한 숫자인 확률 진폭을 추가하거나 곱할 수 있다.

덧셈과 곱셈은 복잡한 숫자의 이론에서 흔히 볼 수 있는 연산이며 수치로 주어진다.합계는 다음과 같다.두 번째 화살표의 시작은 첫 번째 화살표의 끝에 있게 하라.그러면 합은 제1의 시작부터 제2의 끝까지 직접 가는 제3의 화살이다.두 화살표의 곱은 길이가 두 길이의 곱인 화살이다.제품의 방향은 기준 방향에 대해 두 개 각각을 통과했다는 각도, 즉 기준 방향에 대해 제품이 회전한다는 각도를 추가함으로써 발견된다.

확률에서 확률 진폭으로의 변화는 기초적인 접근법을 바꾸지 않고 수학을 복잡하게 만든다.그러나 광자와 전자가 모두 양극화될 수 있다는 사실을 고려하지 못하기 때문에 그 변화는 여전히 충분치 않다. 즉, 공간과 시간에 대한 그들의 방향을 고려해야 한다는 것이다.따라서 P(A~B)는 16개의 복잡한 숫자 또는 확률 진폭 화살표로 구성된다.^{[1]: 120–121} 또한 수량 j와 관련된 약간의 사소한 변화도 있는데, 일부 편광의 경우 90°의 배수로 회전해야 할 수도 있는데, 이는 상세한 부기만을 위한 관심사일 뿐이다.

전자가 양극화될 수 있다는 사실과 관련, 또 하나의 작은 필요한 세부사항으로, 전자가 페르미온이라는 사실과 연관되어 페르미-디락 통계에 복종한다.기본 규칙은 만약 우리가 둘 이상의 전자와 관련된 주어진 복잡한 과정에 대한 확률 진폭을 가지고 있다면, 우리가 두 개의 전자 이벤트를 교환하는 보완적인 파인만 다이어그램을 포함시킬 때, 결과 진폭은 첫 번째의 역 - 음 -이다.가장 간단한 경우는 A와 B에서 시작하는 두 개의 전자가 C와 D에서 끝나는 것이다.진폭은 "차이", E(A~D) × E(B~C) - E(A~C) × E(B~D)로 계산될 것이다. 여기서 우리는 일상적인 확률 아이디어에서 합이 될 것으로 예상한다.^{[1]: 112–113}

전파자

마지막으로 광자와 전자의 확률 진폭에 해당하는 P(A~B)와 E(C~D)를 각각 계산해야 한다.이것들은 기본적으로 전자 확률 진폭의 동작을 설명하는 디락 방정식과 광자의 확률 진폭의 동작을 설명하는 맥스웰 방정식의 해법이다.이것들은 파인만 전파자라고 불린다.표준 문헌에서 일반적으로 사용되는 표기법에 대한 번역은 다음과 같다.

${\displaystyle P(A{\text{{}B}-x_{A})\to D_{F}(x_{B}-x_{A}),\quad E(C{\text{{{}D})\to S_{F}(x_{D}-x_{C}),},}}}}},}}$

$여기$서 x ${\displaystyle A_{}}$ ${\$와 같은 속기 기호$A}$은(는) A라고 표시된 점의 3차원으로 시간과 위치를 제공하는 네 개의 실수를 의미한다$$.

대량 재생성

20년 동안 진보를 지연시킨 역사적으로 문제가 발생했다: 비록 우리는 세 가지 기본적인 "단순" 행동의 가정으로부터 시작하지만, 게임의 규칙은 만약 우리가 A에서 B까지 도달하기 위해 전자에 대한 확률 진폭을 계산하려면 가능한 모든 방법들을 고려해야 한다고 말한다: 가능한 모든 방법들: 그것들과 함께 파인만 도표들.dpoints.따라서 전자가 C로 이동하여 거기서 광자를 방출한 다음 D에서 다시 흡수하여 B로 이동하는 방법이 있을 것이다.아니면 이런 일을 두 번, 아니 그 이상 할 수도 있다.요컨대 선을 자세히 보면 '단순' 선들의 집합으로 갈라지는 프랙탈과 같은 상황이 있는데, 이 선들을 자세히 보면 각각 '단순' 선으로 이루어져 있으며, 즉 애드 인피니텀으로 되어 있다.이것은 다루기 힘든 상황이다.만약 그 세부사항을 추가하면 사물이 약간만 변했을 뿐이라면 그리 나쁘지 않았을 텐데, 위에서 언급한 간단한 보정이 무한한 확률의 진폭으로 이어진다는 사실이 밝혀지면서 재앙이 닥쳤다.이 문제는 시간이 지남에 따라 새로이 나타나는 기법에 의해 "고정"되었다.그러나 파인만 자신은 "디피 프로세스"^{[1]: 128} 라며 불만스러워했다.

결론들

위의 프레임워크 내에서 물리학자들은 그 후 변칙적인 자기 쌍극자 모멘트와 같은 전자 속성의 일부를 높은 정확도로 계산할 수 있었다.그러나 파인만이 지적하듯이 전자와 같은 입자들이 왜 그들이 하는 질량을 가지고 있는지 설명하지 못한다."이 숫자들을 적절하게 설명하는 이론은 없다.우리는 우리의 모든 이론에 그 숫자를 사용하지만, 그것들이 무엇인지, 어디에서 왔는지 이해하지 못한다.나는 근본적인 관점에서 이것은 매우 흥미롭고 심각한 문제라고 생각한다."^{[1]: 152}

수학적 공식화

수학적으로 QED는 대칭군 U(1)를 가진 아벨계 게이지 이론이다.충전된 스핀-1/2장 사이의 상호작용을 매개하는 게이지장은 전자기장이다.전자장과 상호 작용하는 스핀-1/2장에 대한 QED 라그랑지안은 실제^{[22]: 78} 부품에 의해 자연 단위로 주어진다.

어디에

• ${\displaystyle {\gamma }^{}}$ ${\displaystyle {\mu }^{}}$ ${\$은(는) Dirac 행렬이다.
• ${\displaystyle ③}$스핀-1/2 입자의 비스파이너 장$($예: 전자-양전자장)
• ${\displaystyle \stackrel{}{}}$"psi-bar"라고 불리는$$${\displaystyle \stackrel{}{\psi }}$의${\displaystyle \stackrel{}{}{\equiv }^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {0\mathrm{}}^{}}$ 0 ${\$는 "psi-bar"라고 불리기도 한다.
• ${\$$A_{\mu }+ieB_$${\mu }}$은(는) 게이지 공변량 파생 모델이며,
• e는 연결 상수로, 비스파이너 장의 전기 전하와 동일하다.
• m은 전자 또는 양전자의 질량이다.
• ${\displaystyle {\mu }_{}}$ ${\$은 전자 자체에 의해 생성되는 전자기장의 공변량 4전위이다.
• ${\displaystyle B_{}}$ ${\displaystyle {\mu }_{}}$ ${\$은(는) 외부 선원에 의해 부과되는 외부장이다.
• ${\displaystyle F_{}}$ ${\displaystyle {\mu A}_{}}$ =${\displaystyle {}_{}{\mathrm{\mu A}}_{}}$ ${\displaystyle {\mu A}_{}}$ -${\displaystyle {}_{}}$μA${\displaystyle {\mathrm{}}_{}}$- μA ${\displaystyle {\mu A}_{}}$ -$$ -$μA {\mu \nu }=\partial _{\nu }-{\nu }-\$partial$_${\$nu }-{\nu }}}}}}}}}}}}}$은 전자기장 텐서이다.

운동 방정식

D의 정의를 라그랑지안이 주는 것으로 대체하는 것

${\displaystyle {\mathcal {L}}=i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma ^{\mu }(A_{\mu }+B_{\mu })\psi -m{\bar {\psi }}\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }.}$

이 라그랑지안으로부터 ψ과 A의 장의 운동 방정식을 얻을 수 있다.

• ψ에 대한 현장-이론적 오일러-라그랑주 방정식을 사용하여,

$${\displaystyle \partial _{\mu }\왼쪽({\frac {\partial {}\mathcal {L}}\오른쪽)-{\frac {\partial {\mathcal {L}{\partial \psi}}=0.}$$

(2)

ψ에 관한 라그랑지아의 파생상품은 다음과 같다.

이러한 항목을 (2)에 삽입하면

에르미트 콘게이트로

중기 수익률 우측으로 가져오기

왼쪽은 원래의 디락 방정식과 같고, 오른쪽은 전자기장과 상호작용을 하는 것이다.

• A 필드에 오일러-라그랑주 방정식을 사용하면

$${\displaystyle \partial _{\nu }\왼쪽({\frac {\partial {\mathcal{L}}}}{\partial _{\nu }A_{\mu }}}\partial {\mathcal {L}}{\partial A_{}}}}}}}=0,}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$

(3)

금번 파생상품은

(3) 리드로 다시 대체하면

로렌츠 게이지 조건을 적용하면

로 방정식이 감소하다.로렌츠 게이지에 있는 고전적인 맥스웰 방정식의 QED 버전인 4전위를 위한 파동 방정식이다.(제곱은 달랑베르 연산자 $,{\displaystyle }$=${\displaystyle {\mathrm{}}_{\alpha }{\mathrm{}}^{\alpha }}$ α ${\$를 나타낸다.$$

인터랙션 사진

이 이론은 보소닉 섹터와 페르미온 섹터를^{[clarification needed]} 공짜로 취급함으로써 단도직입적으로 정량화할 수 있다.이를 통해 우리는 서로 다른 공정의 확률 진폭 계산을 시작하는 데 사용할 수 있는 점증상 상태 세트를 구축할 수 있다.그러기 위해서는 진화 연산자를 계산해야 하는데, 주어진 초기 상태 ${\displaystyle i}$ $⟩$ {\$displaystyle i\rangle }$에 대해 최종 ${\displaystyle \mathrm{상태}}$ $⟨{\displaystyle }$ f $displaystyle \langle$f$}$이(가) 다음과^{[22]: 5} 같은 방식으로$$ 주어진다$$.

이 기법은 S-매트릭스로도 알려져 있다.진화 연산자는 상호 작용 그림에서 얻으며, 여기서 시간 진화는 위에서 주어진 라그랑지 밀도에서 두 번째 기간의 공간에 대한 적분인 상호 작용 해밀턴에 의해 주어진다.^{[22]: 123}

그래서, 한 사람이^{[22]: 86}

여기서 T는 시간 순서 연산자다.이 진화 연산자는 단지 연속적인 의미만을 가지고 있으며, 여기서 우리가 도달한 것은 미세구조가 개발 매개변수로 상수인 섭동 시리즈다.이 시리즈는 다이슨 시리즈라고 불린다.

파인만 도표

Feynman 접근방식이 QED에 대한 개념적 명확함에도 불구하고, 거의 초기 교과서는 그의 발표를 따르지 않는다.계산을 수행할 때 전파자의 푸리에 변환으로 작업하는 것이 훨씬 쉽다.양자 전자역학의 실험 실험은 전형적으로 산란 실험이다.산란 이론에서는 입자의 위치보다는 입자의 모멘텀a를 고려하며, 입자가 상호작용할 때 생성되거나 소멸되는 것으로 생각하면 편리하다.파인만 도표들은 똑같이 보이지만, 선들은 서로 다른 해석을 가지고 있다.전자 라인은 주어진 에너지와 운동량을 가진 전자를 나타내며, 광자 라인의 해석도 비슷하다.정점도는 특정 에너지와 모멘텀을 각각 가지고 있는 광자의 흡수 또는 생성과 함께 한 전자의 전멸과 다른 전자의 생성을 나타낸다.

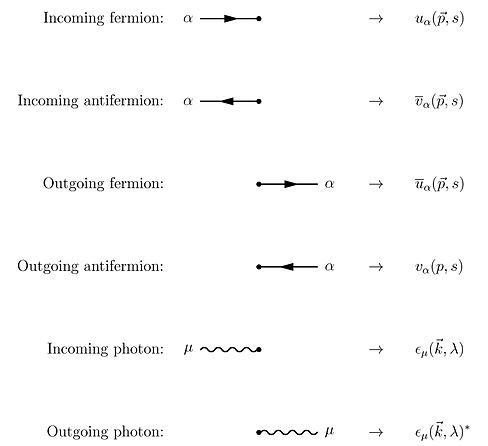
다이슨 시리즈의 용어에 대한 Wick의 정리를 이용하여 양자 전자역학에 대한 S-매트릭스의 모든 용어는 파인만 도표의 기법을 통해 계산할 수 있다.이 경우 그리기 규칙은 다음과^{[22]: 801–802} 같다.

이러한 내부("가상") 입자는 특정 에너지-모멘텀에 제약을 받지 않으므로$,$ 이러한 규칙에는 $\int$ ${}^{}$ ${4\mathrm{}}^{}$ ${}^{}$/$$($2$ $\pi {}^{}$) ${4\mathrm{}}^{}$ ${\$ d$^{4}p/(2\pi )^{4}}$에 대한 통합을 의미하는 폐쇄 루프에 대해 추가해야 한다(자세한 내용은 전파자 참조).

그것들로부터, 확률 진폭의 계산은 직접적으로 주어진다.예를 들어, 전자와 광자가 탄성 산란을 겪는 콤프턴 산란이 있다.파인만 다이어그램은 이 경우에^{[22]: 158–159} 해당된다.

S-매트릭스에 대한 섭동 시리즈의 첫 번째 순서로 해당하는 진폭을 얻을 수 있다.

이 산란을 위한 단면을 계산할 수 있다.

비고동현상

양자 전자역학의 예측 성공은 파인만 도표로 표현된 섭동 이론의 사용에 크게 의존한다.그러나 양자전기역학도 섭동 이론을 넘어서는 예측으로 이어진다.매우 강한 전기장이 있는 곳에서 전자와 양전자가 자연적으로 생성되어 전자의 붕괴를 초래할 것이라고 예측한다.Schwinger 효과라고 불리는 이 과정은 파인만 도표의 어떤 한정된 숫자의 관점에서 이해할 수 없으므로 비페테르부르크로 묘사된다.^[23]수학적으로, 그것은 양자 전자역학의 통합된 경로에 대한 반전추적 근사치에 의해 도출될 수 있다.

리노말리제이션성

고차 항은 진화 연산자를 위해 직접 계산할 수 있지만, 이 항들은 다음과 같은 간단한 항을^{[22]: ch 10} 포함하는 도표를 표시한다.

• 

  진공 양극화 기능 $\pi {\displaystyle \mathrm{}}$ ${\displaystyle \Pi }$에 대한 1루프 기여

• 

  전자 자가 에너지 함수 $\sigma$에 대한 1루프 기여 ${\displaystyle \Sigma }$

• 

  꼭지점 함수 $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma$}에 대한 단일 루프 기여

닫힌 루프라는 것은 수학적인 의미가 없는 분산된 통합의 존재를 암시한다.이러한 어려움을 극복하기 위해 리노말라이제이션이라는 기술이 고안되어 실험과 매우 밀접하게 일치하는 유한한 결과를 낳았다.리노멀라이제이션 후 이론의 의미가 있는 기준은 다이버깅 다이어그램의 수가 유한하다는 것이다.이 경우 이론은 "재론할 수 있다"고 한다.그 이유는 관측을 재개하기 위해서는 이론의 예측가치를 손대지 않고 유지하기 위해 한정된 수의 상수가 필요하기 때문이다.양자 전자역학에서 단 3개의 다이버싱 도표만 보이는 경우가 바로 여기에 해당한다.이 절차는 전자 자석 비율과 같이 실험과 매우 밀접하게 일치하는 관찰 결과를 제공한다.

재생가능성은 양자장 이론이 실행 가능한 이론으로 간주되기 위한 필수적인 기준이 되었다.양자상대가 추측에 불과하고 현재 매우 활발한 연구를 하고 있는 중력을 제외한 근본적인 상호작용을 기술하는 모든 이론은 이론화할 수 있는 이론들이다.

직렬의 비융합

프리먼 다이슨의 주장은 QED에서 섭동 시리즈의 수렴 반경이 0이라는 것을 보여준다.^[24]기본적인 주장은 다음과 같다:연결 상수가 음수인 경우 이는 쿨롱 힘 상수가 음수인 것과 같을 것이다.이것은 전자파 상호작용을 "역방향"하여 전하와 달리 전하를 유인하고 전하를 역방향으로 할 수 있다.이것은 붕괴에 대비한 진공을 우주의 한쪽에는 전자 군집, 반대쪽에는 양전자 군집으로 불안정하게 만들 것이다.이 이론은 연결 상수의 어떤 음수 값에 대해서도 "심장"하기 때문에, 연속체는 수렴하지 않고 기껏해야 점증적 연속이다.

현대적인 관점에서는 QED가 임의적으로 높은 에너지를 얻기 위한 양자장 이론으로 잘 정의되어 있지 않다고 말한다.^[25]연결 상수는 한정된 에너지로 무한대로 진행되며, 란다우 극에 신호를 보낸다.문제는 본질적으로 QED가 양자간 사소한 문제로 인해 어려움을 겪고 있는 것처럼 보인다는 점이다.이것은 대통합 이론에 QED를 포함시키기 위한 동기 중 하나이다.

참고 항목

참조

추가 읽기

책들

• De Broglie, Louis (1925). Recherches sur la theorie des quanta [Research on quantum theory]. France: Wiley-Interscience.
• Feynman, Richard Phillips (1998). Quantum Electrodynamics (New ed.). Westview Press. ISBN 978-0-201-36075-2.
• Jauch, J.M.; Rohrlich, F. (1980). The Theory of Photons and Electrons. Springer-Verlag. ISBN 978-0-387-07295-1.
• Greiner, Walter; Bromley, D.A.; Müller, Berndt (2000). Gauge Theory of Weak Interactions. Springer. ISBN 978-3-540-67672-0.
• Kane, Gordon, L. (1993). Modern Elementary Particle Physics. Westview Press. ISBN 978-0-201-62460-1.
• Miller, Arthur I. (1995). Early Quantum Electrodynamics: A Sourcebook. Cambridge University Press. ISBN 978-0-521-56891-3.
• Milonni, Peter W. (1994). The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Boston: Academic Press. ISBN 0124980805. LCCN 93029780. OCLC 422797902.
• Schweber, Silvan S. (1994). QED and the Men Who Made It. Princeton University Press. ISBN 978-0-691-03327-3.
• Schwinger, Julian (1958). Selected Papers on Quantum Electrodynamics. Dover Publications. ISBN 978-0-486-60444-2.
• Tannoudji-Cohen, Claude; Dupont-Roc, Jacques; Grynberg, Gilbert (1997). Photons and Atoms: Introduction to Quantum Electrodynamics. Wiley-Interscience. ISBN 978-0-471-18433-1.

저널스

• Dudley, J.M.; Kwan, A.M. (1996). "Richard Feynman's popular lectures on quantum electrodynamics: The 1979 Robb Lectures at Auckland University". American Journal of Physics. 64 (6): 694–98. Bibcode:1996AmJPh..64..694D. doi:10.1119/1.18234.

외부 링크

• QED의 진화와 그 안에서 그의 역할을 묘사한 파인만의 노벨상 강의.
• 파인만의 뉴질랜드 비피시스트들을 위한 QED 강의
• http://qed.wikina.org/ – QED를 시연하는 애니메이션