단면체 범주

수학에서 단일 범주(또는 텐서 범주)는 분기기가 장착된 범주 $\mathbf {C}$ $\mathbf {C}$ ${\$ 이다.

\displaystyle \otimes :\mathbf {C} \times \mathbf {C} \to \mathbf {C} }

그것은 자연 이소모르피즘과 연관성이 있고, ⊗의 좌우 정체성인 사물 I가 다시 자연 이소모르피즘에 연관되어 있다.관련된 자연 이형성은 모든 관련 도표가 통근하도록 보장하는 특정 일관성 조건에 따르게 된다.

일반적인 텐서 제품은 벡터 공간, 아벨리아 그룹, R-모듈 또는 R-알제브라를 단면체 범주로 만든다.모노이드 카테고리는 이것들과 다른 예들의 일반화로 볼 수 있다.모든 (작은) 단일 범주, 즉 범주의 객체의 이형성 등급인 단형의 "범주화"로 볼 수 있으며, 범주의 텐서 제품에 의해 이진 연산이 주어진다.

다소 다른 애플리케이션으로 추상화로 간주될 수 있는 것은 두 가지 유형을 취하고 Aggregate 유형을 구축하는 유형 생성자 아래에서 닫힌 데이터 유형 시스템이다 $\otimes$ 유형은 개체이고 and $\otimes$ 은 $\otimes$ Aggregate 생성자다.이소모르피즘까지의 연관성은 동일한 데이터를 집계하는 다른 방법( $((a,b),c)$ : $((a,b),c)$ ) $((a,b),c)$ , $((a,b),c)$ ) {\ $디스플레이$ 스타일 $($ a $,b),c)$ 및 $((a,b),c)$ $(a,(b,c))$ $(a,(b,c))$ c $(a,(b,c))$ ) {\ $디스플레이 스타일(a, (b,$ c)})을 표현하는 방법이다 $(a,(b,c))$ 즉, 집계 값이 동일할 필요는 없더라도 동일한 정보를 저장한다.집계 유형은 덧셈(타입 합계) 또는 곱셈(타입 제품)의 작동과 유사할 수 있다.타입 제품의 경우, 아이덴티티 객체는 단위 $()$ ( $()$ ) ${\displaystyle$ 이므로 타입의 거주자는 단 한 명뿐이며, 그것이 있는 제품은 항상 다른 피연산자에게 이형성이 있는 것이다.유형 합계의 경우, ID 개체는 어떤 정보도 저장하지 않는 보이드 유형이며 거주자를 대상으로 하는 것은 불가능하다.단면체 범주의 개념은 그러한 집계 유형의 값이 분리될 수 있다고 가정하지 않는다. 반대로 고전적 및 양자적 정보 이론을 통합하는 프레임워크를 제공한다.^[1]

카테고리 이론에서, 단일 카테고리를 사용하여 카테고리 오브젝트에 대한 모노이드 오브젝트 및 관련 작용의 개념을 정의할 수 있다.그것들은 또한 농축된 범주의 정의에도 사용된다.

단일 범주에는 적절한 범주 이론 이외의 수많은 적용이 있다.직관적 선형 논리의 곱셈 파편 모델을 정의하는데 사용된다.그것들은 또한 응축 물질 물리학의 위상학적 질서에 대한 수학적 기초를 형성한다.땋은 단면체 범주에는 양자 정보, 양자장 이론, 끈 이론에 응용이 있다.

형식 정의

단일 범주(monoidal category)는 단일 구조를 갖춘 $\mathbf {C}$ 범주 $\mathbf {C}$ ${\$ 이다 $.$ 단면체 구조는 다음과 같이 구성된다.

tensor 제품 또는 단일 제품이라고 하는 $\otimes \colon \mathbf {C} \times \mathbf {C} \to \mathbf {C}$ bifunctor $\otimes \colon \mathbf {C} \times \mathbf {C} \to \mathbf {C}$ → C ${\$ \colon $\mathbf {C} \to \mathbf {$ C} \ $to$ \mathbf {C} $}$
단위 개체 또는 ID 개체라고 하는 $I$ $개체$ I ${\displaystyle$ I $},$
텐서 연산의 사실을 나타내는 특정 일관성 조건의 영향을 받는 세 가지 자연 이형성
- is associative: there is a natural (in each of three arguments $A$ , $B$ , $C$ ) isomorphism $\alpha$ , called associator, with components ${\displaystyle \alpha _{A,B,C}\colon A\otimes (B\otimes C)\cong$ $(A\time$ B $)\time$ C $\alpha _{A,B,C}\colon A\otimes (B\otimes C)\cong (A\otimes B)\otimes C$
- has $I$ as left and right identity: there are two natural isomorphisms $\lambda$ and $\rho$ , respectively called left and right unitor, with components $\lambda _{A}\colon I\otimes A\cong A$ and ${\displaystyl$ $e \rho _{A}\colon A\time I\cong A$

$\lambda$ 과 $\lambda$ $\rho$ $\rho$ 이 $\rho$ 가) 어떻게 작용하는지를 $\rho$ 기억하는 좋은 방법은 반복에 의한 것이며, 람다, $\lambda$ ${\displaystyle$ $\lambda$ $}$ 은 $\lambda$ 가) 왼쪽의 ID를 취소하고, $\rho$ 는 $\rho$ 오른쪽의 ID를 $취소$ 한다는 점에 유의한다.

이러한 자연적 변환에 대한 일관성 조건은 다음과 같다.

$\mathbf {C}$ ${\$ ${C$ }의 모든 A {\ $displaystyle$ B}, C {\ $D$ $C$ } 및 D {\displaystyle $D$ $}$ 에 대해 $\mathbf {C}$ 펜타곤 다이어그램

통근자;

$\mathbf {C}$ ${\$ 의 $B$ $모든$ A $A$ 및 $A$ $B$ $B$ 에 대해 $\mathbf {C}$ 삼각형 다이어그램

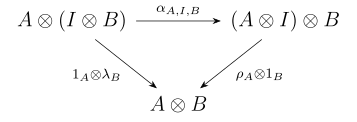
This is one of the diagrams used in the definition of a monoidal cateogory. It takes care of the case for when there is an instance of an identity between two objects.

통근하다

엄격한 단모형 범주는 자연 이형성 α, α, ρ, ρ이 정체성인 범주를 말한다.모든 모노이드 카테고리는 엄격한 모노이드 카테고리와 단노이드로 동등하다.

예

유한 제품을 가진 모든 범주는 제품을 단면제품으로 하고 단자 물체를 단품으로 하는 단면체로 간주할 수 있다.그러한 범주를 데카르트 단면체 범주라고 부르기도 한다.예를 들면 다음과 같다.
- 세트, 데카르트 제품이 포함된 세트 범주, 유닛으로 사용되는 특정 1개 요소 세트.
- 제품 범주가 있는 작은 범주의 범주인 Cat. 여기서 하나의 개체와 그 ID 맵만 있는 범주가 단위다.
한 달에 한정된 코프로덕트를 가진 모든 범주는 단면체로서 코프로덕트를 단면체로 하고, 초기 물체를 단위로 한다.그러한 단면체 범주를 코코아체 단면체라고 한다.
R-Mod는 조합형 링R을 통한 모듈의 범주로서, 단일형 제품으로서의 역할을 하는 모듈 ⊗_R과 단위로서의 링 R(자체적으로 모듈로서 생각되는 모듈)의 텐서 제품을 가지는 단일형 범주다.특별한 경우 다음과 같이 처리한다.
- K-벡트는 필드 K에 걸친 벡터 공간의 범주로서, 1차원 벡터 공간 K가 단위 역할을 한다.
- 아벨 그룹들의 범주인 아브, 정수 Z 그룹이 유닛으로 활동한다.
모든 조합형 링 R의 경우, R-알제브라의 범주는 알제브라의 텐서 제품을 제품, R을 단위로 하여 단면적이다.
뾰족한 공간 범주(예를 들어, 압축적으로 생성된 공간에는 제한됨)는 스매시 제품이 제품 역할을 하고, 뾰족한 0-sphere(두 점 이산 공간)가 유닛 역할을 하는 단면이다.
범주 C에 있는 모든 내분자 범주는 엄격한 단면체 범주로, 제품은 펑터의 구성, 유닛은 아이덴티티 펑터의 구성을 가지고 있다.
어떤 범주 E와 마찬가지로, 주어진 개체에 의해 확장되는 전체 하위 범주가 단노이드인 경우, 어떤 2-범주 E와 Ob(E)의 모든 개체 C의 경우, {C}이(가) 확장한 E의 전체 2-범주가 단노이드 범주인 경우다.E = Cat의 경우, 위의 Endofunctors 예제를 얻는다.
경계-위-준위-준위-준위-준위-대칭 단원형 범주로, 제품이 충족되고 식별성이 상위 요소다.
모든 일반 모노이드 $(M,\cdot ,1)$ , $(M,\cdot ,1)$ , $(M,\cdot ,1)$ ) ${\displaystyle (M,\cdot ,1$ )은 객체 $집합$ M ${\displaystyle M$ 형태론에 대한 ID만, $\cdot$ ${\displaysty \cdot }$ 을(를 $\cdot$ ) 텐서 제품으로, $1$ ${\displaystystystyone }$ 을 ID $1$ 객체로 하는 작은 단일 범주다 $(M,\cdot ,1)$ .반대로, 단성 범주의 이형성 등급 집합(그런 것이 타당하다면)은 텐서 제품인 단성 w.r.t.이다.

모노이드 선주문

"예약된 모노이드"로도 알려진 모노이드 사전 주문은 모노이드 카테고리의 특별한 경우다.이런 구조는 끈 재작성 체계론에서는 나오지만 순수한 수학에서도 풍부하다.For example, the set $\mathbb {N}$ of natural numbers has both a monoid structure (using + and 0) and a preorder structure (using ≤), which together form a monoidal preorder, basically because $m\leq n$ and $m'\leq n'$ implies ${\d$ $isplaystyle m+m'\leq n+n$ 우리는 이제 일반적인 사례를 제시한다.

사전 주문은 범주 $c,c'\in \mathrm {Ob} (\mathbf {C} )$ 로 간주될 수 있다는 것은 잘 알려져 있다. 예를 들어, 두 개체 $c,c'\in \mathrm {Ob} (\mathbf {C} )$ $c,c'\in \mathrm {Ob} (\mathbf {C} )$ c, $\displaystyle$ c $,c'\$ in \ $mathrm$ {Ob $}(\mathbf$ {C $})$ 에 $c\to c'$ 대해, $c,c'\in \mathrm {Ob} (\mathbf {C} )$ C에는 최대 하나의 $c\to c'$ c $c\to c'$ → c → c → c $c\to c'$ { ${\$ c $'$ 가 $c,c'\in \mathrm {Ob} (\mathbf {C} )$ 한다.If there happens to be a morphism from c to c' , we could write $c\leq c'$ , but in the current section we find it more convenient to express this fact in arrow form $c\to c'$ . Because there is at most one such morphism, we never have to give it a name, such as ${\di$ $splaystyle f\put c\to$ c $f\colon c\to c'$ 주문의 반사성 및 전이성 특성은 각각 C의 신원 형태론과 구성 공식에 의해 설명된다. $c\cong c'$ $c\leq c'$ $c\leq c'$ $c\cong c'$ c $c\leq c'$ $c\cong c'$ $\$ {\ $displaystyle c$ \ $cong$ c $c'\leq c$ $c'\leq c$ if $c\leq c'$ $c'\leq c$ if c $c'\leq c$ c ${\$ $displaystyle c'\leq$ c $},$ C에서 이형인 경우.부분적인 순서로 보면, 두 개의 이형체 물체는 사실상 동일하다는 점에 유의한다.

앞으로, 사전 주문 C에 단면 구조를 추가하고 싶다고 가정합시다.그렇게 하는 것은 우리가 선택해야 한다는 것을 의미한다.

개체 $I\in \mathbf {C}$ $I\in \mathbf {C}$ $I\in \mathbf {C}$ ${\$ 모노이드 단위라고 하는 개체
functor $\mathbf {C} \times \mathbf {C} \to \mathbf {C}$ $\mathbf {C} \times \mathbf {C} \to \mathbf {C}$ $\mathbf {C} \times \mathbf {C} \to \mathbf {C}$ → $\mathbf {C} \times \mathbf {C} \to \mathbf {C}$ ${\$ \mathbf ${C} \to \mathbf$ {C} \to \mathbf { $C}$ $\;\cdot \;$ 에 대한 \mathbf는 단순히 점 $"{\$ 로 표시되며, $\;\cdot \;$ 단면 다음과 같다.

따라서 어떤 두 물체 $c_{1},c_{2}$ 1, $c_{1},c_{2}$ c $c_{1},c_{2}$ ${\$ }}개의 $c_{1},c_{2}$ 물체 c $c_{1}\cdot c_{2}$ $c_{1}\cdot c_{2}$ c $c_{1}\cdot c_{2}$ ${\$ $I$ 는 I $I$ 와 $I$ $⋅{\displaystystysty \cdot$ }을 이형상까지 연관성 및 일률적으로 선택해야 한다 $\cdot$ .이는 다음을 충족해야 함을 의미한다.

(c_{1}\cdot c_{2})\cdot c_{3}\cong c_{1}\cdot (c_{2}\cdot c_{3})

and

I\cdot c\cong c\cong c\cdot I

.

더욱이 ·가 functor가 되어야 한다는 사실은 (현재의 경우, C가 사전주문인 경우) 다음을 의미하지 않는다.

if

c_{1}\to c_{1}'

and

c_{2}\to c_{2}'

then

(c_{1}\cdot c_{2})\to (c_{1}'\cdot c_{2}')

.

이 경우 모든 다이어그램이 사전 주문으로 통용되기 때문에 단일형 범주에 대한 추가 일관성 조건은 비어 있다.

C가 부분 순서인 경우 연상성 및 일이태성 이형성이 동등해지기 때문에 위의 설명은 더욱 단순화된다.Another simplification occurs if we assume that the set of objects is the free monoid on a generating set $\Sigma$ . In this case we could write $\mathrm {Ob} (\mathbf {C} )=\Sigma ^{*}$ , where * denotes the Kleene star and the monoidal unit I stands for the empty string.형태론(≤體論, ≤에 관한 팩트)을 생성하는 R의 집합으로부터 출발하면, R을 「재작성 규칙」이라고 하는 세미투에 시스템의 통상적인 개념을 회복한다.

본 예시로 돌아가려면, $i\leq j$ 이 단일 형태론 $i\to j$ → j ( $i\to j$ i에서 j까지의 형태론 없음)를 $i\leq j$ 가진 자연수 0, 1, 2, ...을 가진 범주가 되도록 한다. i $i\leq j$ mon $i\leq j$ $i\leq j$ 과 $i\to j$ 0으로 주어진 단면체 단위와 단면체 곱셈 구조를 가진 단일 형태론 i.일반적인 덧셈에 의해 $i\cdot j:=i+j$ i $i\cdot j:=i+j$ j $i\cdot j:=i+j$ + $i\cdot j:=i+j$ ${\displaystyle i\cdot$ j $:=i+j$ .그 다음 N은 단일 사전 주문이다. 사실 그것은 단일 물체 1에 의해 자유롭게 생성되는 것이고, 단일 형태론 0 ≤ 1이며, 여기서 다시 0은 단일 단위다.

속성 및 관련 개념

큰 종류의 다이어그램(즉, $\lambda$ ${\displaystyle \alpha },$ , ${\displaystyle \lambda$ $\lambda$ $\rho$ ${\displaystyle \rho$ $\rho$ identity and tensor product)이 통근하는 세 가지 정의 일관성 조건으로부터 따르게 된다. 이것이 맥 레인의 "일 것이다.때때로 그러한 모든 도표는 부정확하게 통근한다고 언급된다.

단면체 범주에는 단면체 물체에 대한 일반적인 개념이 있는데, 추상 대수학에서 단면체라는 통상적인 개념을 일반화한다.일반 모노이드들은 정확하게 데카르트 모노이드 범주 세트에 있는 모노이드 물체들이다.또한 어떤 (소형) 엄격한 단면체 범주는 Cat 범주(카테시안 제품이 유도하는 단면체 구조 포함)에서 단면체로 볼 수 있다.

단면체 펑커스는 텐서 제품을 보존하는 단면체 범주 간의 펑커스와 단면체 자연 변환은 텐서 제품과 "호환성"인 이들 펑커 사이의 자연스러운 변환이다.

모든 단면체 범주는 ∗으로 표시된 하나의 개체만을 가진 바이카테고리 B의 범주 B(∗, ∗)로 볼 수 있다.

단일 범주 M에서 농축된 범주 C의 개념은 C에서 개체 쌍 사이의 형태 집합의 개념을 C에서 두 개체 사이의 형태론의 M-개념으로 대체한다.

자유엄격한단면분류

모든 범주 C에 대해 다음과 같이 엄격한 단일 범주 σ(C)를 자유롭게 구성할 수 있다.

그 물체는 목록(마지막 순서) A₁, ..., C의 물체 A이다_n.
두 물체 A₁, ..., A_m, B₁, m = n인 경우에만 B_n, 화살표가 f₁ → B, ..., f_n : A_n → B₁, C의₁ 화살표_n 목록(마인릿 시퀀스)이 된다.
두 물체 A₁, ..., A_n, B의₁ 텐서 곱, B는_m 두 목록의 연결 A₁, ..., A_n₁, B, ..., B이며_m, 마찬가지로 두 형태론의 텐서 곱은 리스트의 결합에 의해 주어진다.ID 개체는 빈 목록이다.

σ 매핑 범주 C에서 σ(C)까지의 이 작업은 Cat에서 엄격한 2-모나드로 확장할 수 있다.

전문화

단면체 $A\otimes B$ 에서 $A\otimes B$ $A\otimes B$ B $A\otimes B$ 및 $B\otimes A$ $B\otimes A$ $B\otimes A$ $B\otimes A$ 이 $B\otimes A$ (가) 결합 조건과 호환되는 방식으로 자연적으로 이형성인 경우, 우리는 땋은 단면체 범주를 말한다.더욱이 이러한 자연 이형성이 그 자체의 역행이라면, 우리는 대칭적인 단모형 범주를 가지고 있다.
A closed monoidal category is a monoidal category where the functor $X\mapsto X\otimes A$ has a right adjoint, which is called the "internal Hom-functor" $X\mapsto \mathrm {Hom} _{\mathbf {C} }(A,X)$ . Examples include cartesian closed categories such as Set, the ca유한 차원 벡터 공간의 범주인 FdVect와 같은 세트의 티고리와 컴팩트한 닫힘 범주.
자율 범주(또는 콤팩트하게 닫힌 범주 또는 엄격한 범주)는 좋은 속성을 가진 듀얼이 존재하는 단일 범주로서 FdVect의 아이디어를 추상화한다.
단도 대칭 단도 범주는 FdHilb, 유한 차원 Hilbert 공간의 아이디어를 추상화하며 여분의 단도 펑터를 장착한다.여기에는 단도 콤팩트한 범주가 포함된다.
탄나키어 범주는 한 분야에 걸쳐 농축된 단면체 범주로, 선형 대수 집단의 표현 범주와 매우 유사하다.

참고 항목

참조

^ Baez, John; Stay, Mike (2011). "Physics, topology, logic and computation: a Rosetta Stone". In Coecke, Bob (ed.). New Structures for Physics. Lecture Notes in Physics. Vol. 813. Springer, Berlin. pp. 95–172. arXiv:0903.0340. ISBN 9783642128219. ISSN 0075-8450.

Joyal, Andre; Street, Ross (1993년)."Braided Tensor Categories".수학 102, 20-78의 진보.
Joyal, Andre; Street, Ross (1988년)"평면도 및 텐서 대수"
켈리, G. 맥스(1964)"맥레인의 자연 연관성, 공통성 등의 일치조건에 관한 연구." 대수학 제1, 397–402호 저널
Kelly, G. Max (1982). Basic Concepts of Enriched Category Theory (PDF). London Mathematical Society Lecture Note Series No. 64. Cambridge University Press.
맥 레인, 선더스(1963년)."자연적 연관성과 공동체성"라이스 대학 연구 49, 28–46.
Mac Lane, Sunders(1998), Categories for the Working Mathister (2차 개정)뉴욕: 스프링거-베를라크.
nLab의 단일 범주

외부 링크

Wikimedia Commons의 모노이드 카테고리와 관련된 미디어

[1] Baez, John; Stay, Mike (2011). "Physics, topology, logic and computation: a Rosetta Stone". In Coecke, Bob (ed.). New Structures for Physics. Lecture Notes in Physics. Vol. 813. Springer, Berlin. pp. 95–172. arXiv:0903.0340. ISBN 9783642128219. ISSN 0075-8450.

[1]

Search