페르미-디랙 통계

통계역학
열역학 동역학 이론
입자통계 스핀통계정리 동일입자 맥스웰-볼츠만 보스-아인슈타인 페르미-디랙 파라통계학 애니온 통계 땋은 통계
열역학적 앙상블 NVE 마이크로캐노니컬 NVT 정준의 µVT 그랜드 캐노니컬 NPH 이소텐탈픽-이소바릭 NPT 등온-등온성
모델들 데비 아인슈타인 이싱 포츠
가능성 내부에너지 엔탈피 헬름홀츠 자유 에너지 깁스 자유 에너지 그랜드 포텐셜 / 란다우 자유 에너지
사이언티스트 맥스웰 볼츠만 보스 깁스 아인슈타인 에렌페스트 폰 노이만 톨만 데비 페르미
v t

페르미-디랙 통계학은 파울리 배제 원리를 따르는 상호 작용하지 않는 동일한 많은 입자로 구성된 시스템의 물리학에 적용되는 일종의 양자 통계학입니다. 결과적으로 에너지 상태에 대한 입자의 페르미-디랙 분포입니다. 엔리코 페르미(Enrico Fermi)와 폴 디랙(Paul Dirac)의 이름을 따서 명명되었으며, 이들은 각각 1926년에 독립적으로 분포를 도출했습니다.^[1][2] 페르미-디랙 통계학은 통계역학 분야의 일부이며 양자역학의 원리를 사용합니다.

페르미-디랙 통계는 열역학적 평형 상태에서 페르미온이라고 불리는 반정수 스핀(1/2, 3/2 등)을 가진 동일하고 구별할 수 없는 입자에 적용됩니다. 입자 사이의 상호작용이 무시할 수 있는 경우, 시스템은 단일 입자 에너지 상태로 설명될 수 있습니다. 결과적으로 두 입자가 동일한 상태를 차지할 수 없는 이러한 상태에 대한 입자의 페르미-디랙 분포가 시스템의 특성에 상당한 영향을 미칩니다. 페르미-디랙 통계는 스핀이 1/2인 페르미온의 일종인 전자에 가장 일반적으로 적용됩니다.

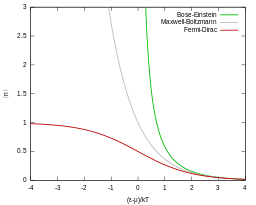
페르미-디랙 통계에 대응하는 것은 보스-아인슈타인 통계로, 보손이라고 불리는 정수 스핀(0, 1, 2 등)을 가진 동일하고 구별할 수 없는 입자에 적용됩니다. 고전물리학에서 맥스웰-볼츠만 통계는 동일하고 구별 가능한 것으로 취급되는 입자를 설명하는 데 사용됩니다. 보스-아인슈타인 통계와 맥스웰-볼츠만 통계 모두 페르미-디랙 통계와 달리 둘 이상의 입자가 동일한 상태를 차지할 수 있습니다.

역사

1926년 페르미-디랙 통계가 발표되기 전에는 겉보기에는 모순적인 현상으로 인해 전자 행동의 일부 측면을 이해하는 것이 어려웠습니다. 예를 들어 상온에서 금속의 전자 열용량은 전류보다 100배나 적은 전자에서 나오는 것처럼 보였습니다.^[3] 상온에서 금속에 높은 전기장을 가해 발생하는 방출 전류가 왜 온도와 거의 무관한지도 이해하기 어려웠습니다.

당시 금속의 전자이론인 드루드 모형이 직면한 어려움은 전자가 모두 동등하다는 것을 고려했기 때문입니다. 즉, 각각의 전자는 볼츠만 상수 k의_B 순서로 비열에 기여한다고 믿었습니다. 이 문제는 페르미-디랙 통계가 개발될 때까지 해결되지 않은 채로 남아 있었습니다.

페르미-디랙 통계는 1926년 엔리코^[1] 페르미와 폴 디랙에 의해 처음 발표되었습니다.^[2] 맥스 보른(Max Born)에 따르면 파스쿠알 요르단(Pascual Jordan)은 1925년에 파울리(Pauli) 통계라고 부르는 동일한 통계를 개발했지만 적시에 발표되지 않았습니다.^[4][5][6] 디랙에 따르면, 페르미에 의해 처음 연구되었고, 디랙은 이를 "페르미 통계학", 그리고 이에 대응하는 입자를 "페르미온"이라고 불렀습니다.^[7]

페르미-디랙 통계는 1926년 랄프 파울러가 별이 백색 왜성으로 붕괴하는 것을 설명하기 위해 적용했습니다.^[8] 1927년 아놀드 소머펠트는 금속의 전자에 응용하여 자유 전자 모델을 개발하였고,^[9] 1928년 파울러와 로타어 노드하임은 금속의 전계 전자 방출에 응용하였습니다.^[10] 페르미-디랙 통계는 물리학의 중요한 부분을 계속해서 차지하고 있습니다.

페르미-디랙 분포

열역학적 평형 상태에 있는 동일한 페르미온 계의 경우, 단일 입자 상태 i에 있는 평균 페르미온 수는 페르미-디랙(F–D) 분포에 의해 주어집니다.^{[11][nb 1]}

여기서 k는 볼츠만 상수, T는 절대온도, ε은 단일입자 상태 i의 에너지, μ는 전체 화학 퍼텐셜입니다. 조건에 의해 분포가 정규화됩니다.

${\displaystyle \sum_{i}{\bar {n}}_{i}=N}$

$\mu$ ${\displaystyle \mu$ =\$mu$(T,$N)}$를 표현하는 데 사용할 ${\displaystyle 수}$ 있습니다$.$ ${\displaystyle \{\backslash }$displaystyle \mu $}$는 양 또는 음의 값을 가정할 수 있습니다.

절대 온도 0에서 μ는 양의 스펙트럼 밀도 근처에 있다면 페르미 에너지에 페르미온당 퍼텐셜 에너지를 더한 값과 같습니다. 반도체의 전자와 같은 스펙트럼 갭의 경우 대칭점인 μ는 일반적으로 페르미 준위 또는 전자의 경우 전기화학 퍼텐셜로 불리며 갭의 중간에 위치합니다.^[13][14]

페르미-디랙 분포는 계의 페르미온 수가 충분히 많아서 계에 페르미온을 하나 더 추가하면 μ에 미치는 영향이 미미할 때만 유효합니다.^[15] 페르미-디랙 분포는 최대 하나의 페르미온이 각 가능한 상태를 차지할 수 있는 파울리 배제 원리를 사용하여 유도되었기 때문에 결과적으로 < ¯ i < 1 {\$displaystyle 0<{\bar${n$}$_{i}<1}입니다.

• 페르미-디랙 분포
• 
  에너지 의존. ε =$$ {\displaystyle \varepsilon =\mu }일 때 높은 T. $n$ ¯ = 0.5 {\displaystyle {\n}}= 0.5}일 때 더 점진적입니다. 표시되지 않은 것은 μ {\displaystyle \mu }이(가) 높은 T일 때 감소한다는 것입니다.
• 
  ε> μ ${\$displaystyle \varepsilon >\mu}에 대한 온도 의존성입니다.

${\displaystyle {n개}_{}}$의 ¯$i {\displaystyle {\n$_{i}에 대한 상기 식으로부터 i 상태의 입자 수의 분산을 계산할 수 있습니다.

${\displaystyle V(n_{i})=k_{\rm {B}}T{\frac {\partial }{\mu partial}}{\bar {n}}_{i}={\bar {n}}_{i}(1-{\bar {n}}_{i})}$

에너지에 따른 입자의 분포

상태에 따른 입자의 페르미-디랙 분포로부터 에너지에 대한 입자의 분포를 알 수 있습니다.^{[nb 3]} 에너지$$ε i ${\displaystyle \varepsilon_${i}}를 갖는 페르미온의 평균 수는 ${\displaystyle {페르미-디랙}_{}}$분포 n ¯ i ${\displaystyle$ {n}_{i}에$$축퇴 $gi {\displaystyle$ g_{i}}를 곱하면 알 수 있습니다. ${\displaystyle {에너지}_{}}$εi ${\displaystyle \varepsilon$_{i}},

${\displaystyle {\bar {aligned}{\bar {n}}(\varepsilon _{i})&=g_{i}{\bar {n}}_{i}\&={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}+1}}.\end{align}}}$

$gi$ ≥ 2 ${\displaystyle g_{i$geq 2}일 때,$동일한 에너지$ε$$i {\$displaystyle {\bar {n$varepsilon _{i}) > 1 ${\displaystyle${\displaystyle {bar}}(\varepsilon _{i}) > 1 가능성이 있습니다.

$에너지$의$$준연속$$ε {\displaystyle \varepsilon}이${\displaystyle (}$가) 상태 g$($ε) {\displaystyle$$g(\varepsilon)}의 관련 밀도를 가질 때(즉, 단위 부피당 단위 에너지 범위당 상태 수), 단위 부피당 단위 에너지 범위당 평균 페르미온 수는

${\displaystyle {\bar {\mathcal {N}}(\varepsilon)=g(\varepsilon)F(\varepsilon),}$

$여기$서 F$($ε$)$ {\$displaystyle F(\$varepsilon)}는 페르미 함수라고 불리며, 페르미-디랙 ${\displaystyle {분포}_{}}$n ¯ i ${\displaystyle${\n}_{i}에 사용되는 것과 동일한 함수입니다.

${\displaystyle F(\varepsilon )={\frac {1}{e^{(\varepsilon -\mu )/k_{\rm {B}}T}+1},}$

하도록

${\displaystyle {\bar {\mathcal {N}}(\varepsilon )={\frac {g(\varepsilon )}{e^{(\varepsilon -\mu )/k_{\rm {B}}T}+1}}.$

양자 체제와 고전 체제

페르미-디랙 분포는 특별한 가정 없이 고온과 낮은 입자 밀도의 한계에서 맥스웰-볼츠만 분포에 접근합니다.

• ${\displaystyle {입자}_{}}$ 밀도가 낮은 한계에서 $n$ ¯ i = 1${\displaystyle \frac{{{}_{}}^{}}{}e}$( ε i - μ ) / k BT + 1 ≪ 1$${\displaystyle {\bar {n}}_{i}={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}$T}+1}}\ll$ 1$\},$ 따라서 $e{\displaystyle {(}^{}}$$ε$${\displaystyle {}^{}}$i - ${\displaystyle {{}_{}}^{}}$)${\displaystyle {}^{}}$/ ${\displaystyle \mathrm{k}}$B ${\displaystyle \mathrm{T}}$+ 1 $≫$ 1${\displaystyle e^{(\varepsilon _{i}-\$mu )/k_{\rm {B}}$T}+1\gg1}$ 또는 이와 $동등$한 e${\displaystyle {(}^{}}$$ε$${\displaystyle {}^{}}$i - μ)${\displaystyle {}^{}}$/ ${\displaystyle \mathrm{k}}$B T $≫$$1$ {\$displaystyle e^{(\varepsilon$_{$i}-\$mu )/k_{\rm {B}}$T}\gg 1$ $이$ 경우 ${\displaystyle \frac{{}^{}}{}}$ $¯$${\displaystyle \frac{i^{}}{}}$ $≈$ ${\displaystyle \frac{1^{}}{}}$ e ($ε$ i - ${\displaystyle \mu }$)${\displaystyle {}^{}}$/ ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {B_{}{T}_{}}^{}}$ $=$ N $Ze$ - $ε$ i $/$ k $B T$ {\$displaystyle${\$bar${n}}_{i}\$approx$ ${\frac {1}{e^{(\$varepsilon _{i}-\mu )/k_{\rm {B}}$T}}}={\frac {N}{Z}}e^{-\varepsilon _{i}/k_{\rm {B}}$$T$ Maxwell-Boltzmann 통계량의 결과입니다.
• 고온의 한계에서 입자는 큰 범위의 에너지 값에 걸쳐 분포되어 있으며, 따라서 각 상태${\displaystyle {(}_{}}$ ≫ i - μ$$ε k B T {\$displaystyle \varepsilon$ _${i$ \g k_{\rm {B}T})의 점유율은 다시 매우 작습니다. $¯$$T}+1}}\ll1$ 맥스웰-볼츠만 통계량으로 다시 줄어듭니다.

맥스웰-볼츠만 통계가 페르미-디랙 통계의 근사치로 사용될 수 있는 고전적 체계는 입자의 위치와 운동량에 대한 하이젠베르크 불확정성 원리에 의해 부과된 한계와 거리가 먼 상황을 고려함으로써 발견됩니다. 예를 들어 반도체의 물리학에서 전도대 상태의 밀도가 도핑 농도보다 훨씬 높을 때, 전도대와 페르미 레벨 사이의 에너지 갭은 맥스웰-볼츠만 통계를 사용하여 계산할 수 있었습니다. 그렇지 않으면, 도핑 농도가 전도 대역의 상태 밀도에 비해 무시할 수 없을 경우, 정확한 계산을 위해 대신 페르미-디랙 분포를 사용해야 합니다. 그러면 입자의 농도가 입자의 평균 드브로이 $파장$λ ¯ ${\displaystyle$ {\lambda}}보다 훨씬 큰 평균 입자 간 분리 $R$ ¯ {\displaystyle ${\bar$ {\lambda}}에 해당할 때 고전적인 상황이 우세함을 알 수 있습니다.

${\displaystyle {\bar {R}}\gg {\bar {\lambda }}\approx {\frac {h}{\sqrt {3mk_{\rm {B}}T}}},}$

여기서 h는 플랑크 상수이고 m은 입자의 질량입니다.

전형적인 금속의 전도 전자의 경우, T = 300 K (약 실온)에서 계는 $R{\displaystyle }$¯ ≈ λ ¯ / ${\displaystyle 25}${\$displaystyle {\bar$ {R}\약 {\bar {\lambda }/25}이기 때문에 고전적인 계와는 거리가 있습니다. 이것은 전자의 질량이 작고 농도가 높기 때문입니다. $금속$ 내 전도 $전자의 작은$ R ¯ {\$displaystyle$bar {R}}). 따라서 전형적인 금속의 전도 전자에는 페르미-디랙 통계가 필요합니다.^[22]

고전 체제에 없는 계의 또 다른 예는 백색 왜성으로 붕괴한 항성의 전자로 구성된 계입니다. 백색 왜성의 온도는 높지만(일반적으로 표면에 T = 10000 K), 높은 전자 농도와 각 전자의 작은 질량은 고전적인 근사를 사용하지 않으며, 페르미-디랙 통계가 필요합니다.

도함수

그랜드카노니컬 앙상블

상호 작용하지 않는 페르미온의 양자 시스템에만 적용되는 페르미-디랙 분포는 그랜드 표준 앙상블에서 쉽게 도출됩니다.^[24] 이 앙상블에서 시스템은 저장소(온도 T 및 저장소에 의해 고정된 화학 퍼텐셜 μ)와 에너지를 교환하고 입자를 교환할 수 있습니다.

상호작용하지 않는 품질로 인해 사용 가능한 각 단일 입자 레벨(에너지 레벨 ϵ)은 저장기와 접촉하는 별도의 열역학 시스템을 형성합니다. 즉, 각각의 단일 입자 수준은 별개의 아주 작은 표준 앙상블입니다. 파울리 배제 원리에 의해 단일 particle 수준에 대해 가능한 미세 상태는 입자가 없거나(에너지 E = 0), 또는 하나의 입자(에너지 E = ε) 두 가지뿐입니다. 따라서 단일 입자 수준에 대한 결과 분할 함수는 단 두 개의 항을 갖습니다.

${\displaystyle {\begin{aligned}{\mathcal {Z}}&=\exp {\big(}0(\mu -\varepsilon )/k_{\rm {B}}T{\big )}+\exp {\big(}1(\mu -\varepsilon )/k_{\rm {B}}T{\big )}\\&=1+\exp {\big(}(\mu -\varepsilon )/k_{\rm {B}}T{\big )},\end{aligned}}$

그리고 그 단일 particle 수준 기질의 평균 입자 수는 다음과 같이 주어집니다.

${\displaystyle \ lang N\rangle = k_{\rm {B}}T{\frac {1}{\mathcal {Z}}\left({\frac {\partial {\mathcal {Z}}}{\partial \mu}}\right)_{V,T}={\frac {1}{\exp {\big (}(\varepsilon -\mu )/k_{\rm {B}}T{\big}}+1}}.$

이 결과는 각 단일 입자 수준에 적용되므로 시스템 전체 상태에 대한 페르미-디랙 분포를 제공합니다.^[24]

(열 변동으로 인한) 입자 수의 변화도 유도할 수 있습니다(입자 수는 단순한 베르누이 분포를 갖습니다).

${\displaystyle {\big \lang}(\Delta N)^{2}{\big \rangle}=k_{\rm {B}}T\left({\frac {d\langle N\rangle }{d\mu }}\right)_{V,T}=\langle N\langle {\big(}1-\lang N\langle {\big)}.$

이 양은 에너지 수준이 수송 현상에 기여하는 능력이 ⟨${\displaystyle {에}^{}}$ 비례하는 전기 전도도 및 전자 가스의 열전 계수에 대한 Mott 관계와 같은 수송 현상에서 중요합니다( δ N). 2 ⟩ ${\displaystyle$ {\big \$langle}(\$Delta$$N)^{\big \langle }}.

정준앙상블

표준 앙상블에서 페르미-디랙 통계를 도출하는 것도 가능합니다. 상호작용은 무시할 수 있고 열평형에 있는 N개의 동일한 페르미온으로 구성된 다입자계를 생각해 보자.^[15] 페르미온 사이에는 무시할 수 있는 상호작용이 있기 때문에 다입자계의 상태$$ $R{\displaystyle }$ ${\displaystyle R}$의 에너지 ${\displaystyle {ER}_{}}$ ${\$는 단일입자 에너지의 합으로 표현될 수 있고,

${\displaystyle E_{R}=\sum_{r}n_{r}\varepsilon_{r}}$

여기서 ${\displaystyle n_{}}$ ${\displaystyle n_{r}}$은 점유수라고 하며, ${\displaystyle {에너지}_{}}$ε가 ${\displaystyle$\$varepsilon_${r}인 단일 particle 상태$${\$displaystyle r$}의 입자 수이다. 합산은 가능한 모든 단일 $입자{\displaystyle }$상태 {\$displaystyler$}에 걸쳐 있습니다$.$

다입자 시스템이 $R{\displaystyle }$ ${\displaystyle R}$ 상태에 있을 확률은 정규화된 표준 분포에 의해 주어집니다$.$^[26]

${\displaystyle P_{R}={\frac {e^{-\beta E_{R}}}{\displaystyle \sum _{R'}e^{-\beta E_{R'}}}$

여기서 $\beta$ = ${\displaystyle 1}$/ k B T {\$displaystyle$ \beta = 1/k_{\rm {B}}, e는 볼츠만 인자라고 불리며, 합산은 다중 particle 시스템의 모든 가능한 상태 R' {\displaystyle R'}에 걸쳐 있습니다. ${\displaystyle {점유}_{}}$ 번호 $n{\displaystyle {}_{}}$ $displaystyle n_{i}\;}$의 평균값은 다음과$$^[26] 같습니다.

${\displaystyle {\bar {n}}_{i}\ =\ \sum _{R}n_{i}\ P_{R}}$

다입자 시스템의$$ 상태 $R{\displaystyle }$ ${\displaystyle$ R$}$은 단일 입자 상태의 입자 점유, 즉 $n{\displaystyle {}_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle {n\mathrm{}}_{}}$ ${\displaystyle {2\mathrm{}}_{}\dots ,}$ ${\displaystyle n_{1},\,n_{2},\ldots \;,}$를 지정하여 다음과 같이 지정할 수 있습니다.

${\displaystyle P_{R}=P_{n_{1},n_{2},\ldots }={\frac {e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots )}}{\displaystyle \sum _{{n_{1}}',{n_{2}}',\ldots }e^{-\beta ({n_{1}}'\varepsilon _{1}+{n_{2}}'\varepsilon _{2}+\cdots )}}}}$

$그리고$ n ¯ i ${\displaystyle {\n}_${i}에 대한 방정식은

${\displaystyle {\begin{alignat}{\bar {n}}_{i}&=\sum _{n_{1}}, n_{2},\dots }n_{i}\P_{n_{1}, n_{2},\dots}\\\\&={\frac {\displaystyle \sum _{n_{1}, n_{2},\dots }n_{i}\e^{-\beta(n_{1})\varepsilon _{1}+\cdots +n_{i}\varepsilon _{i}+\cdots )}}{\displaystyle \sum _{n_{1}, n_{2}, n_cdots )}}\\n\displaystyle \sum _{n_{1}, n_{2}, n_cdots )}\dots }e^{-\beta(n_{1})\varepsilon_{1}+n_{2}\varepsilon_{2}+\cdots +n_{i}\varepsilon_{i}+\cdots)}}\\\\end{alignat}}}$

여기서 합산은 파울리 배제 원칙을 따르는 $n$ ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 2_{}}$… ${\displaystyle n_{1}, n_{2},\dots },$ n ${\displaystyle n_{r}$ = 각 $r$ ${\display r}$에 대해 0 또는 1의 값의 각 조합에 걸쳐 있습니다$.$ 또한 ${\displaystyle n_{}}1$, ${\displaystyle n_{}}$2${\displaystyle ,}$ …$${\$displaystyle n_{1}$의 값의 각 조합입니다.$n_{2},\ldots }$은(는) 총 입자 수가$N{\displaystyle }$ {\$displaystyle$ N$}$이라는 제약 조건을 만족합니다$.$

${\displaystyle \sum_{r}n_{r}=N.}$

요약들을 다시 정리하면서

${\displaystyle {\bar {n}}_{i}={\displaystyle \sum_{n_{i}=0}^{1}n_{i}\e^{-\beta(n_{i}\varepsilon_{i})}\quad \sides세트 {}{^{(i)}}\sum_{n_{1}}\n_{2}\dots }e^{-\beta(n_{1})\varepsilon_{1}+\cdots)}{\displaystyle \sum_{n_{i}=0}^{-\beta(n_{i}\varepsilon_{i})}\qquad \sides세트 {^{(i)}}}\sum_{n_{1}}}\sum_{n_{2}}\sum_{n_{2}}\dots }e^{-\beta(n_{1}\varepsilon_{1}+n_{2}\varepsilon_{2}+\cdots)}}}}$

여기서${\displaystyle {}^{}}$합 ${\displaystyle {\mathrm{기호}}^{}}$의${\displaystyle {}^{}}$($i$$)$ {\displaystyle$$$^{($i)}}는 합이$$n을 넘지 않음을 나타내며, 합과 관련된 총 입자 수가 ${\displaystyle {Ni}_{}}$ = ${\displaystyle N}$-$$n i {\displaystyle $N_{i$}= N-n_{i}}라는 제약 조건에 따릅니다. Note that ${\displaystyle \Sigma ^{(i)}}$ still depends on ${\displaystyle n_{i}}$ through the ${\displaystyle N_{i}}$ constraint, since in one case ${\displaystyle n_{i}=0}$ and ${\displaystyle \Sigma ^{(i)}}$ is evaluated with ${\displaystyle N_i=N,}$${\displaystyle N_{i$}=$N,}$ 반면 다른 경우$$${\displaystyle {}^{}}$ $=$ $1$ {\$displaystyle$ n_${$$i$}=1}$$및 σ (i) {\displaystyle \Sigma ^{(i)}}은 $N$i = N-1로 평가됩니다. {\displaystyle N_${$i}= N-1.$}$표기법을 단순화하고$$$σ$(i) ${\displaystyle \Sigma$^{(i)}}가 $여전히$ ni ${\displaystyle$ n_{i$ni${\$displaystyle$N-n_{i}}에$$하고 있음을 명확히 나타내려면 다음을 정의합니다.

${\displaystyle Z_{i}(N-n_{i})\equiv \ \sideset {}{^{(i)}}\sum _{n_{1},n_{2},\ldots }e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots )}\;}$

$n$¯i ${\displaystyle$$$${\n}_${i}에 대한 이전 표현식을$Zi {\displaystyle$ Z_{i}로 다시 ${\displaystyle {쓰고}_{}}$ 평가할 수 있도록,

${\displaystyle {\begin{alignedat}{3}{\bar {n}}_{i}\ &={\frac {\displaystyle \sum _{n_{i}=0}^{1}n_{i}\ e^{-\beta (n_{i}\varepsilon _{i})}\ \ Z_{i}(N-n_{i})}{\displaystyle \sum _{n_{i}=0}^{1}e^{-\beta (n_{i}\varepsilon _{i})}\qquad Z_{i}(N-n_{i})}}\\[8pt]&=\ {\frac {\quad 0\quad \;+e^{-\beta \varepsilon _{i}}\;Z_{i}(N-1)}{Z_{i}(N)+e^{-\beta \varepsilon _{i}}\;Z_{i}(N-1)}}\\[6pt]&=\ {\frac {1}{[Z_{i}(N)/Z_{i}(N-1)]\;e^{\beta \varepsilon _{i}}+1}}\quad .\end{alignedat}}}$

${\displaystyle {Zi}_{}N)}$/ ${\displaystyle {Zi}_{}\mathrm{N-1})}$ ${\displaystyle Z_{i}(N)/Z_{i}(N-1)}$를 대체할 식을 찾는 데 다음 근사값이^[27] 사용됩니다.$$

${\displaystyle {\begin{alignat}{2}\ln Z_{i}(N-1)&\simeq \ln Z_{i}(N)-{\frac {\ln Z_{i}(N)}{\partial N}\&=\ln Z_{i}(N)-\alpha_{i}\;\end{alignat}}}$

여기서 ${\displaystyle \frac{\mathrm{\alpha i}}{}}$≡ ∂ ${\displaystyle \frac{\ln }{}}$ ⁡ Zi ($N$) ∂ $N. {\displaystyle \alpha_{i}\equiv {\frac {\partial$ \$ln$Z_${$i}(N))}{\partial N}\.}

$입자$가 시스템에 추가될 때 $화학 퍼텐셜$ μ ${\displaystyle \mu \;}$의 변화가 매우 작을 정도로 입자의 $수$ N ${\$displaystyle N$}$이 충분히 크다면, ${\displaystyle \alpha i}$ ≃ - ${\displaystyle {\mu }_{}}$/ ${\displaystyle k_{}}$ B $T$. ${\displaystyle \alpha _{i}\simeq -\mu /k_{\rm$ {B}T\.} 양변의 기본 전자 로그를 취하면, ${\displaystyle {\alpha i}_{}}$ $displaystyle \alpha_{i}\,}$를 대체하고 재배열합니다$.$

${\displaystyle Z_{i}(N)/Z_{i}(N-1)=e^{-\mu /k_{\rm {B}}T}.}$

위의 내용을 $n개의$¯i ${\displaystyle$}_{i}에 대한 방정식에 대입하고, β${\displaystyle$\beta \;}의 이전$정의$를 사용하여 ${\displaystyle 1_{}}$/ k $BT {\displaystyle 1/k_{\$rm {B}}를${\displaystyle }$대체합니다.$\beta {\displaystyle }$ ${\displaystyle$ \$beta \;}$에 대한$$ T$}$는$$페르미-디랙 분포를 초래합니다.

${\displaystyle {\bar {n}}_{i}=\{\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}+1}}$

맥스웰-볼츠만 분포와 보스-아인슈타인 분포와 마찬가지로 페르미-디랙 분포도 평균 값의 다윈-폴러 방법으로 유도할 수 있습니다.^[30]

미소정통합주

시스템의 다중도를 직접 분석하고 라그랑주 승수를 사용하면 결과를 얻을 수 있습니다.^[31]

지수 i로 표시된 에너지 준위가 여러 개 있고, 각 준위는 에너지 ε을 가지며 총 n개의 입자를 포함한다고 가정합니다. 각 수준이 g개의_i 서로 다른 부분 수준을 포함하고 있으며, 이들은 모두 동일한 에너지를 가지며 구별할 수 있다고 가정합니다. 예를 들어, 두 입자의 운동량은 서로 다를 수 있지만(즉, 그들의 운동량은 서로 다른 방향을 따라 있을 수 있습니다), 이 경우 그들은 서로 구별될 수 있지만 여전히 같은 에너지를 가질 수 있습니다. 레벨 i와 관련된 g의_i 값을 해당 에너지 레벨의 "퇴행성"이라고 합니다. 파울리 배타원리는 페르미온 하나만이 그러한 하위 수준을 차지할 수 있다고 말합니다.

에너지 준위들 중_i 구별할 수 없는_i n개의 입자들을 분배하는 방법들의 수는, 그것의 조합적 해석을 사용하여, 이항 계수에 의해 주어집니다.

${\displaystyle w(n_{i},g_{i})={\frac {g_{i}!}{n_{i}! (g_{i}-n_{i})!}}\ .}$

예를 들어, 두 개의 입자를 세 부분군에 분포시키면 총 세 가지 방법으로 3!/(2!1!)과 같은 110, 101 또는 011의 모집단 번호가 부여됩니다.

직업 번호 n의_i 집합이 실현될 수 있는 방법의 수는 각 개인의 에너지 수준이 충족될 수 있는 방법의 곱입니다.

${\displaystyle W=\prod _{i}w(n_{i},g_{i})=\prod _{i}{\frac {g_{i}!}{n_{i}! (g_{i}-n_{i})!}}.}$

맥스웰-볼츠만 통계를 유도할 때 사용된 것과 동일한 절차에 따라 입자의 수가 고정되어 있고 에너지가 고정되어 있다는 제약 조건 하에 W가 최대화되는 n의_i 집합을 찾고자 합니다. 함수를 구성하는 라그랑주 승수를 사용하여 솔루션을 제한합니다.

${\displaystyle f(n_{i})=\ln(W)+\alpha \left(N-\sum n_{i}\right)+\beta \left(E-\sum n_{i}\varepsilon_{i}\right)}$

요인에 대한 스털링의 근사를 사용하여 n에_i 대한 도함수를 취하고, 결과를 0으로 설정하고, n에_i 대해 풀면 페르미-디랙 모집단 수가 산출됩니다.

${\displaystyle n_{i}={\frac {g_{i}}{e^{\alpha +\beta \varepsilon _{i}+1}}}$

맥스웰-볼츠만 통계 기사에 설명된 것과 유사한 과정을 통해 $\beta$ = $1$ k $\frac{B_{}}{}$ T${\$textstyle \ beta =${\$frac {1}{k_{\$rm${B}}임을 열역학적으로 보여줄 수 있습니다.$T}}$ 및 $\alpha$ $=$$$-$$ B T {\textstyle \alpha $=$-{\frac {\mu}{k_{\rm {B$}$$T$ 따라서 최종적으로 상태가 점유될 확률은 다음과 같습니다.

${\displaystyle {\bar {n}}_{i}={\frac {n_{i}}{g_{i}}}={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}+1}}.$

참고 항목

메모들

참고문헌

더보기

• Reif, F. (1965). Fundamentals of Statistical and Thermal Physics. McGraw–Hill. ISBN 978-0-07-051800-1.
• Blakemore, J. S. (2002). Semiconductor Statistics. Dover. ISBN 978-0-486-49502-6.
• Kittel, Charles (1971). Introduction to Solid State Physics (4th ed.). New York: John Wiley & Sons. ISBN 978-0-471-14286-7. OCLC 300039591.