양자 상태
Quantum state| 에 관한 일련의 기사의 일부 |
| 양자역학 |
|---|
양자 물리학에서 양자 상태는 시스템에서 가능한 각 측정의 결과에 대한 확률 분포를 제공하는 수학적 실체이다.양자 상태에 대한 지식은 시스템의 진화에 대한 규칙과 함께 시스템의 동작에 대해 예측할 수 있는 모든 것을 소진합니다.양자 상태의 혼합은 다시 양자 상태입니다.다른 상태의 혼합으로 쓸 수 없는 양자 상태를 순수한 양자 상태라고 하는 반면, 다른 모든 상태를 혼합 양자 상태라고 합니다.순수한 양자 상태는 복소수 [1][2]위의 힐버트 공간의 광선에 의해 표현될 수 있는 반면, 혼합 상태는 힐버트 [3][4]공간에 작용하는 양의 반정의 연산자인 밀도 행렬에 의해 표현된다.
순수한 상태는 상태 벡터 또는 파동 함수라고도 하며, 특히 위치 또는 운동량의 함수로 표현될 때 적용되는 후자 용어입니다.예를 들어 수소원자 중 전자의 에너지 스펙트럼을 취급할 때 주양자수 n, 각운동량 양자수 θ, 자기양자수 m 및 스핀 z성분z s로 관련 상태 벡터를 동정한다.다른 예로, 예를 들어 스턴-게라크 실험으로 전자의 스핀을 어떤 방향으로 측정하면, 두 가지 가능한 결과가 있다: 위 또는 아래.그러므로 전자의 스핀을 위한 힐버트 공간은 큐비트를 구성하는 2차원이다.여기서 순수한 상태는 길이가 1인 2차원 복소벡터 ( β) {로 나타납니다.
혼합 양자 상태는 순수 상태의 확률론적 혼합에 해당하지만, 순수 상태의 다른 분포는 등가(즉 물리적으로 구별할 수 없는) 혼합 상태를 생성할 수 있다.슈뢰딩거-HJW 정리는 주어진 혼합 상태를 쓰는 여러 가지 방법을 [6]순수한 상태의 볼록한 조합으로 분류합니다.양자 시스템에서 특정 측정을 수행하기 전에 이 이론은 결과에 대한 확률 분포만을 제공하며, 이 분포가 취하는 형태는 양자 상태와 측정을 기술하는 선형 연산자에 의해 완전히 결정된다.다른 측정에 대한 확률 분포는 불확실성 원리에 의해 예시된 트레이드오프를 나타낸다. 즉, 한 실험에 대해 가능한 결과의 좁은 확산을 암시하는 상태는 다른 실험에 대한 가능한 결과의 광범위한 확산을 반드시 의미한다.
개념 설명
순수한 상태
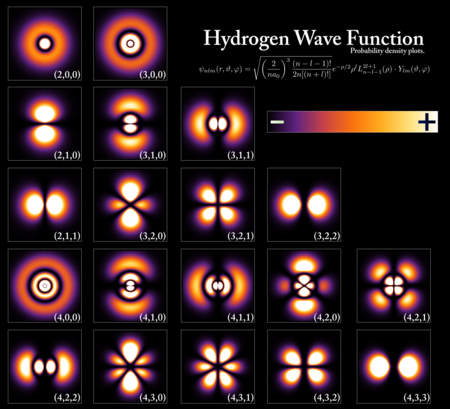
양자역학의 수학적 공식에서, 순수한 양자 상태는 힐베르트 공간의 벡터에 대응하는 반면, 각각의 관측 가능한 양(입자의 에너지 또는 운동량)은 수학적 연산자와 관련된다.연산자는 시스템 상태에 작용하는 선형 함수 역할을 합니다.측정 시스템의 고유값은 관측 가능한 값에 해당합니다.예를 들어 운동량 연산자의 고유값 중 하나가 1kgµm/s인 경우에만 운동량이 1kgµm/s인 입자를 관찰할 수 있다.고유값이 1kgµm/s인 해당 고유 벡터(물리학자가 고유 상태라고 함)는 양자 불확실성 없이 운동량의 확실하고 잘 정의된 값이 1kgµm/s인 양자 상태일 것이다.운동량을 측정하면 1kgµm/s가 된다.
반면, 여러 고유 상태의 중첩에 있는 시스템은 일반적으로 주어진 관측 가능에 대한 양자 불확실성을 갖는다.이 고유 상태의 선형 조합을 다음과 같이 나타낼 수 있습니다.
선형 조합의 특정 상태에 해당하는 계수는 복소수이므로 상태 간의 간섭 효과를 허용합니다.계수는 시간에 따라 달라집니다.양자 상태가 시간에 어떻게 변화하는지는 시간 진화 연산자에 의해 제어됩니다.를 둘러싼[a] 기호와 le(\displaystyle\은 브라켓 표기법의 일부입니다.
상태의 통계적 혼합은 선형 조합의 다른 유형입니다.상태들의 통계적 혼합은 독립적인 시스템들의 통계적 합체이다.통계적 혼합은 지식의 정도를 나타내며, 양자역학 내의 불확실성은 기본이다.수학적으로 통계적 혼합은 복잡한 계수를 사용하는 조합이 아니라 다른 상태의 실제 값, 양의 확률을 사용하는 이다. nn \ 은 무작위로 선택된 시스템이 상태에 있을 확률을 나타낸다. _ 선형 조합의 경우와 달리 각 시스템은 명확한 고유 [7][8]상태에 있습니다.
관측대상 A의 기대치 A A display ( \ \ A \ }{ \ )는 관측대상 측정치의 통계평균이다.이 평균과 확률의 분포는 물리 이론에 의해 예측됩니다.
모든 관측 가능성의 고유 상태가 동시에 존재하는 것은 아닙니다.예를 들어 위치측정 Q(t)와 운동량측정 P(t)를 모두 정확하게 알 수 있는 상태를 준비할 수 없으며, 적어도 1개는 가능한 [b]값의 범위를 가진다.하이젠베르크 불확도 관계의 내용입니다.
게다가 고전적인 역학과 달리, 시스템에 대한 측정을 수행하면 일반적으로 [9][10][c]시스템 상태가 바뀌는 것은 피할 수 없습니다.보다 정확하게: 관측 가능한 A를 측정한 후 시스템은 A의 고유 상태가 됩니다. 따라서 시스템이 이미 고유 상태에 있지 않는 한 상태가 변경됩니다.이는 일종의 논리적 일관성을 나타냅니다.같은 실험의 실행에서 A를 두 번 측정하면 측정값이 시간에 [d]따라 직접 연속되어 동일한 결과를 얻을 수 있습니다.그러나 이것은 다음과 같은 이상한 결과를 낳는다.
A가 [e]B보다 이른 시간에 측정값에 해당하는 호환되지 않는 두 관측치 A와 B를 고려합니다.실험을 시작할 때 시스템이 B의 고유 상태에 있다고 가정합니다.B만 측정하면 실험의 모든 런에서 동일한 결과가 나옵니다.실험의 같은 실행에서 먼저 A를 측정한 후 B를 측정하면 시스템은 첫 번째 측정 후 A의 고유 상태로 이행하며 일반적으로 B의 결과는 통계적이라는 것을 알 수 있습니다.따라서 양자역학적 측정이 서로 영향을 미치며, 측정이 수행되는 순서가 중요합니다.
양자 상태의 또 다른 특징은 여러 개의 하위 시스템으로 구성된 물리적 시스템을 고려한다면 관련성이 있습니다. 예를 들어, 하나의 입자가 아닌 두 개의 입자로 이루어진 실험입니다.양자물리학은 고전 이론으로 설명할 수 없는 두 입자에 대한 측정 사이의 특정한 통계적 상관관계를 보여주는 뒤엉킨 상태라고 불리는 특정한 상태를 허용합니다.자세한 내용은 얽힘을 참조하십시오.이러한 얽힌 상태는 양자 이론과 대체 고전(비양자) 모델을 구별할 수 있게 하는 실험적으로 테스트 가능한 특성(벨의 정리)으로 이어집니다.
슈뢰딩거 사진 vs.하이젠베르크 그림
실험 시작 시 상태 was가 한 번 고정된 상태에서 시간에 의존할 수 있는 관측값을 얻을 수 있습니다.이 접근방식은 하이젠베르크 그림이라고 불립니다.(이 접근방식은 시간에 따라 변화하는 관측가능성 P(t), Q(t)와 함께 위의 논의 후반부에서 채택되었습니다.) 관측가능성을 동일하게 취급할 수 있는 반면, 시스템의 상태는 시간에 따라 달라집니다. 이는 슈뢰딩거 그림으로 알려져 있습니다.(이 접근방식은 상기의 논의의 초기 에서 되었으며, 개념적으로 n n () n n {\ \ _ { } _ { ( ) \ _ { } \ 。
두 관점 양자 이론에 사용된다.반면non-relativistic 양자 역학은 슈뢰딩거 묘사의 관점에서 공식화한 것, 하이젠베르크의 묘사는 종종 상대론적 맥락에서 장의 양자 이론에 대한, 즉 선호된다.디랙 사진과 비교해 보라.[12]:65
양자 물리학의 형식론
복잡한 힐베르트 공간에서의 광선으로서의 순수한 상태
양자 물리학 가장 일반적으로 선형 대수학의 관점에서 다음과 같이 제조되어 있다.어떤 제도가 몇몇 finite-, 5힐베르트 공간으로 간주되고 있다.그 순수한 국가 표준 1의 요인에 해당한다.때문에 단위 영역 모든 벡터의 표준 1과 세트로 정의된다 그러므로 모든 순수한 국가들의 집합은 힐베르트 공간에 있는 부대 구에, 해당합니다.
한 scalar에 의해 순수한 상태 Multiplying 신체적으로(한 국가 그 자체로 여겨진다)가 작다.만약 복잡한 힐베르트 공간의 벡터 H{H\displaystyle} 다른 벡터에서 0이 아닌 복소수로 곱하여 얻어질 수 있는, 두 벡터 H{H\displaystyle}[1]에서 같은"광선":50과 또한 H{H\displaystyle}의 사영 힐베르트 공간에서 같은 부분에 해당하는 것으로 알려졌다.
브라켓 표기법
양자 역학에 계산 선형 사업자, scalar 제품, 이중 공간과 에르 미트 접합을 자주 사용하고 있다.에서 이 같은 계산이 원활하게 흘러가면서 입원이 불필요하거나(은 어떤 상황에서)완전히 내부 선형 대수학 이해하기만 해도, 폴 디랙은 표기법 양자 상태들을 묘사하는 데 bra–ket 표기법으로 알려져를 발명했다.비록 이것의 세부 사항 이 기사의 범위에 포함되지 않는다, 이것의 몇가지 결과들: 있다.
- 그 표현⟩{\displaystyle \psi \rangle}(는"ψ{\displaystyle \psi}" 다른 기호, 문자, 숫자, 말이라도 대체될 수 있는)ψ( 깨끗한 양자 상태에 해당합니다)형태는 상태 벡터를 나타내곤 했다.이곳에서 벡터는 보통 소문자로 된 라틴 편지는 늘 수학적 표기법 그리고는 문맥은 그들이 정말로 경로로부터 분명하다 대조적일 수 있다.
- 디락은 두 종류의 벡터를 정의했다. 브라와 케트, 서로 [f]쌍대이다.
- 각 케트 는 동일한 물리 양자 상태에 해당하는 브라(와 고유하게 관련지어진다엄밀히 말하면 브래지어는 주방의 부속품이다.이것은 이중 공간의 요소이며, Riesz 표현 정리에 의한 케트와 관련이 있다.기저를 선택한 유한 차원 공간에서 열 벡터로 }을 쓰면 {\ \은 행 벡터이므로 이를 얻으려면 {\ \rangle의 전치 복소 활용을 취하기만 하면 된다.
- 스칼라 제품[g][h](브래킷이라고도 함)은 브라와 케트를 나란히 하여 2 { style \_ {_ { \ 로 표기합니다.('브래킷'은 브라켓과 비슷합니다).
스핀
각운동량은 플랑크 상수와 같은 차원(M·L2·T−1)을 가지며 양자 스케일에서는 양자계의 [which?]이산 자유도처럼 작용한다.대부분의 입자는 고전 역학에서는 전혀 나타나지 않는 일종의 고유 각운동량을 가지고 있으며 디락의 상대론적 이론 일반화에 의해 발생합니다.수학적으로 그것은 스피너로 설명된다.비상대론적 양자역학에서 Lie 그룹 SU(2)의 군표현은 이 추가 자유도를 설명하기 위해 사용된다.주어진 입자에 대해 표현 선택(따라서 관측 가능한 스핀 값의 범위)은 플랑크의 환원 상수 θ 단위로 정수(0, 1, 2 ...) 또는 반정수(1/2, 3/2, 5/2 ...)인 비음수 S로 지정된다.스핀 S를 가진 거대한 입자의 경우, 스핀 양자수 m은 항상 집합에서 가능한 2S + 1 값 중 하나를 가정한다.
그 결과, 스핀을 가지는 입자의 양자 상태를 C의 값을2S+1 가지는 벡터치 파동 함수로 기술한다.마찬가지로, 이것은 4개의 변수의 복소수 함수로 표현된다. 즉, 하나의 이산 양자수 변수(스핀용)가 일반적인 세 개의 연속 변수(공간 내 위치용)에 추가된다.
다체 상태 및 입자 통계
각각 스핀이 있을 수 있는 N개의 입자 시스템의 양자 상태는 입자당 4개의 변수를 갖는 복소수 함수로 설명되며, 이는 3개의 공간 좌표 및 스핀에 해당한다.
여기서 스핀 변수ν m은 집합의 값을 가정한다.
동일한 입자의 처리는 보손(정수 스핀을 가진 입자)과 페르미온(반정수 스핀을 가진 입자)에 대해 매우 다릅니다.위의 N-입자 함수는 입자 수에 대해 대칭(보손의 경우) 또는 반대칭(페르미온의 경우)이어야 한다.모든 N개의 입자가 동일하지는 않지만 일부 입자가 동일할 경우, 그 통계(보소닉 또는 페르미온)에 따라 동일한 변수의 각 그룹에 대응하는 변수에 대해 함수는 별도로 (반)대칭되어야 한다.
전자는 S = 1/2인 페르미온이고, 광자는 S = 1인 보손이다(비록 진공 상태에서는 질량이 없고 슈뢰딩거 역학으로는 설명할 수 없음).
대칭화 또는 반대칭화가 불필요할 경우, N-입자 공간은 단순히 1-입자 공간의 텐서 곱에 의해 얻을 수 있으며, 나중에 다시 그 값으로 돌아간다.
원입자 시스템의 기본 상태
다른 힐베르트 공간과 마찬가지로, 시스템의 힐베르트 공간에 대한 기저가 선택되면, 어떤 케트도 그러한 기초 요소의 선형 조합으로 확장될 수 있다.기호적으로 기본 {\({이면 모든 ({ \rangle을 쓸 수 있습니다.
주의할 점은 정규화된 상태 는 다음과 같은 특징이 있다는 것입니다.
이런 종류의 팽창은 양자역학에서 측정에 중요한 역할을 한다.특히, 만약 내 ⟩은 k개의{\displaystyle{k_{나는}}\rangle}은 eigenstates은 식별할 수 있는. 그건 관측 가능한 정규화된 상태에서 측정한다(eigenvalues ki과)⟩{\displaystyle \psi \rangle}ψ, 그때 mand 위의 측정 값의 결과가 ki은 확률은 2.ci(정상화 조건이다.먹었다.s 확률의 합계가 1인 경우).
특히 중요한 예는 위치 기준이며, 이는 측정 [i]위치에 해당하는 관측치의 r를) 갖는 고유 r \ \r} \구성된 기준이다.이러한 고유 상태가 비이성적인 경우(예를 들어 시스템이 단일 스핀리스 입자일 경우), 임의의 케트 는 3차원 공간의 복소값 함수와 관련지어집니다.
순수 상태의 중첩
위와 같이 양자상태는 중첩될 수 있다.α { } β{\ { 이 양자 상태에 대응하는 2개의 ket일 ket은
중첩의 한 가지 실제적인 예는 겹침이 양자 간섭으로 이어지는 이중 슬릿 실험입니다.광자 상태는 왼쪽 슬릿을 통과하는 광자와 오른쪽 슬릿을 통과하는 광자 이동에 해당하는 두 가지 상태의 중첩이다.이 두 상태의 상대 위상은 두 슬릿으로부터의 거리 차이에 따라 달라집니다.이 단계에 따라 간섭은 일부 위치에서는 건설적이고 다른 위치에서는 파괴적이며 간섭 패턴을 생성합니다.우리는 다른 파동 현상의 일관성과 유추함으로써 중첩된 상태가 일관성 있는 중첩 상태에 있다고 말할 수 있다.
양자 중첩에서 상대 위상의 중요성의 또 다른 예는 라비 진동으로, 두 상태의 상대 위상이 슈뢰딩거 방정식으로 인해 시간에 따라 변화합니다.결과적으로 발생하는 중첩은 두 가지 다른 상태 사이에서 앞뒤로 진동하게 됩니다.
혼합 상태
순수 양자 상태는 위에서 설명한 것과 같이 단일 케트 벡터로 기술할 수 있는 상태를 말한다.혼합 양자 상태는 순수 상태의 통계적 앙상블입니다(양자 통계 역학 참조).
혼합 상태는 양자역학에서 두 가지 다른 상황에서 발생합니다. 첫째, 시스템의 준비가 완전히 알려져 있지 않을 때, 따라서 가능한 준비의 통계적 앙상블을 다루어야 하며, 둘째, 다른 시스템과 얽혀 있는 물리적 시스템을 순수한 상태로 설명할 수 없는 것처럼 설명하고자 할 때.첫 번째 경우, 이론적으로 시스템의 전체 역사를 알고 있는 다른 사람이 있을 수 있으며, 따라서 같은 시스템을 순수한 상태로 기술할 수 있습니다. 이 경우, 밀도 매트릭스는 양자 상태에 대한 제한된 지식을 나타내기 위해 사용됩니다.그러나 두 번째 경우 양자 얽힘의 존재는 이론적으로 서브시스템에 대한 완전한 지식의 존재를 방해하며, 어떤 사람도 얽힌 쌍의 서브시스템을 순수한 상태로 묘사하는 것은 불가능하다.
혼합상태는 H_}\ H_})가 얽힌 상태에서 관찰자가 H_에 접근할 수 없는 순수한 상태에서 발생할 수밖에 없다. H_{의 상태는 H_ 위의 트레이스로 표현됩니다.
혼합 상태는 단일 케트 벡터로 설명할 수 없습니다.대신, 일반적으로 ρ로 표기되는 관련 밀도 행렬(또는 밀도 연산자)에 의해 설명된다.밀도 행렬은 혼합 상태와 순수 상태를 모두 설명할 수 있으며, 이러한 상태를 동일한 기반에서 취급할 수 있습니다.또한, 공간H(\H)에 의해 기술된 주어진 양자 시스템상의 혼합 양자 상태는 충분히 큰 공간 K(\ K에 대해 더 큰 초당 H K(\ H\otimes K 상의 순수 양자 상태의 부분 트레이스로 항상 표현될 수 있다.
혼합 상태를 설명하는 밀도 행렬은 형식의 연산자로 정의됩니다.
밀도 매트릭스가 순수 또는 혼합 상태를 나타내고 있는지 여부를 확인하는 간단한 기준은 θ의2 트레이스가 순수 상태일 경우 1, [l][14]혼합 상태일 경우 1 미만이라는 것입니다.또 다른 동등한 기준은 폰 노이만 엔트로피가 순수 상태일 경우 0이고 혼합 상태일 경우 엄격하게 양수라는 것입니다.
양자역학에서의 측정 규칙은 밀도 행렬의 관점에서 특히 말하기 쉽다.예를 들어 관측 가능한 A에 대응하는 측정의 앙상블 평균(기대치)은 다음과 같이 구한다.
유진 위그너에 [15]따르면, 혼합물의 개념은 Lev Landau에 [16][13]: 38–41 의해 제안되었다.
수학적 일반화
상태는 벡터 공간의 벡터가 아니라 관측 가능성의 관점에서 공식화할 수 있습니다.이는 C*-대수의 양의 정규화 선형 함수이거나 관측 가능한 대수의 다른 클래스입니다.자세한 내용은 C*-대게브라 및 Gelfand-Naimark-Segal 구조에 대한 상태를 참조하십시오.
「 」를 참조해 주세요.
메모들
- ^ 때때로 ">"라고 쓰기도 합니다. "각 괄호"를 참조하십시오.
- ^ 오해를 피하기 위해:여기서 Q(t)와 P(t)는 동일한 상태에서 측정되지만 동일한 실험 실행에서는 측정되지 않습니다.
- ^ Dirac(1958년),[11] 페이지 4: "시스템이 작으면 심각한 장애를 일으키지 않고는 관측할 수 없다."
- ^ 즉, 제로 지연으로 구분됩니다.시간을 멈추고 두 가지 측정을 차례로 한 후 시간을 재개하는 것으로 볼 수 있습니다.따라서 동시에 측정이 이루어졌지만 여전히 어떤 측정이 먼저인지 구분할 수 있습니다.
- ^ 구체적으로는 위의 예에서 A = Q(t1) 및 B = P(t2)를 t > t1 > 0으로2 가정합니다.
- ^ Dirac(1958년)[11] 페이지 20: "브래지어 벡터는 여기서 소개된 바와 같이 케트와는 상당히 다른 종류의 벡터이며, 지금까지 브래지어와 케트의 스칼라 곱이 존재하는 것 외에는 그들 사이에 어떠한 연관성도 없다."
- ^ Dirac(1958년),[11] 페이지 19: "스칼라 제품 "B A"가 완전한 괄호 표현으로 나타납니다."
- ^ Gottfried (2013)[12] 페이지 31: "스칼라 제품을 브라와 킷 사이에 있는 것으로 정의한다."
- ^ 상태 \rangle는 서로 다른 기본 r \의 중첩이므로 상태 r과 r \은 동일한 Hilbert 공간의 요소입니다.r 의입자는 r ( , ,) { = ( , )} 에 정확히 배치되어 있으며, r 의 입자는 r { \ 의 다른 위치에 대응하는 확률로 배치되어 있습니다.
- ^ 란다우(Landau),[13] 페이지 17: "∫ ψf′f q * dq = fδ ( " - )" (왼쪽은 ⟨f ′ "에 해당), "∫ ( ′f - ) df = 1"
- ^ 연속되는 경우 기본 r \ \은 ( \\rangle과는 ) 단위 kets가 아닙니다.그들은 ∫ d3r′⟨ rr′⟩)1,{\textstyle\int d^{3}\mathbf{r}'\,\langle}[j]즉,⟨ rr′ ⟩)δ(r′ − r){\displaystyle\langle \mathbf{r}\mathbf{r}'\rangle =\delta(\mathbf{r}'-\mathbf{r})}(는 디랙 델타 함수),\mathbf{r}'\rangle =1,{r}\mathbf 따라 정상화 시킨다. which는 r .。{ } \ { \ = \ . }
- ^ 이 기준은 밀도 매트릭스가 정규화되었을 때 이 섹션에 제시된 표준 정의와 마찬가지로 θ의 트레이스가 1이 되도록 기능한다.밀도 매트릭스가 다르게 정규화되는 경우가 있는데, 이 경우 기준은 δ ( 2) ( δ )2 (\^{2}) = (\ \이다.
레퍼런스
- ^ a b Weinberg, S. (2002), The Quantum Theory of Fields, vol. I, Cambridge University Press, ISBN 978-0-521-55001-7
- ^ Griffiths, David J. (2004), Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, ISBN 978-0-13-111892-8
- ^ Holevo, Alexander S. (2001). Statistical Structure of Quantum Theory. Lecture Notes in Physics. Springer. ISBN 3-540-42082-7. OCLC 318268606.
- ^ Peres, Asher (1995). Quantum Theory: Concepts and Methods. Kluwer Academic Publishers. ISBN 0-7923-2549-4.
- ^ Rieffel, Eleanor G.; Polak, Wolfgang H. (2011-03-04). Quantum Computing: A Gentle Introduction. MIT Press. ISBN 978-0-262-01506-6.
- ^ Kirkpatrick, K. A. (February 2006). "The Schrödinger-HJW Theorem". Foundations of Physics Letters. 19 (1): 95–102. arXiv:quant-ph/0305068. Bibcode:2006FoPhL..19...95K. doi:10.1007/s10702-006-1852-1. ISSN 0894-9875. S2CID 15995449.
- ^ "Statistical Mixture of States". Archived from the original on September 23, 2019. Retrieved November 9, 2021.
- ^ "The Density Matrix". Archived from the original on January 15, 2012. Retrieved January 24, 2012.
- ^ 하이젠베르크, W. (1927년)über den anschaulicheen Inhalt der quantheoretischen Kinematik und Mechanik, Z. 신체 43: 172~198.번역은 '양자 이론 운동학 및 역학의 실제 내용'이다.또한 편집자 John Wheeler와 Wojciech Zurek에 의해 62-84페이지에서 '양자 운동학 및 역학의 물리적 내용'으로 번역되었으며, 프린스턴 뉴저지주 프린스턴 대학 출판부의 양자 이론 및 측정(1983)에 수록되었다.
- ^ 노스캐롤라이나 주 보어(1927/1928)양자 공식과 원자 이론의 최근 발전, Nature Supplement 1928년 4월 14일 121: 580–590.
- ^ a b c 디락, P.A.M.(1958)The Principle of Quantum Mechanics, 제4판, 옥스포드 대학 출판부, 영국 옥스포드.
- ^ a b Gottfried, Kurt; Yan, Tung-Mow (2003). Quantum Mechanics: Fundamentals (2nd, illustrated ed.). Springer. ISBN 9780387955766.
- ^ a b Lev Landau; Evgeny Lifshitz (1965). Quantum Mechanics — Non-Relativistic Theory (PDF). Course of Theoretical Physics. Vol. 3 (2nd ed.). London: Pergamon Press.
- ^ 39페이지, 밀도 매트릭스 이론과 응용.
- ^ Eugene Wigner (1962). "Remarks on the mind-body question" (PDF). In I.J. Good (ed.). The Scientist Speculates. London: Heinemann. pp. 284–302. 페이지 180의 각주 13
- ^ Lev Landau (1927). "Das Dämpfungsproblem in der Wellenmechanik (The Damping Problem in Wave Mechanics)". Zeitschrift für Physik. 45 (5–6): 430–441. Bibcode:1927ZPhy...45..430L. doi:10.1007/bf01343064. S2CID 125732617. 영어 번역본 (p.8 ~18)
추가 정보
양자 상태의 개념, 특히 위의 양자 물리학의 형식주의 섹션의 내용은 양자 역학의 대부분의 표준 교과서에서 다루어진다.
개념적 측면 및 고전적 상태와의 비교에 대한 자세한 내용은 다음을 참조하십시오.
- Isham, Chris J (1995). Lectures on Quantum Theory: Mathematical and Structural Foundations. Imperial College Press. ISBN 978-1-86094-001-9.
수학적 측면에 대한 자세한 내용은 다음을 참조하십시오.
- Bratteli, Ola; Robinson, Derek W (1987). Operator Algebras and Quantum Statistical Mechanics 1. Springer. ISBN 978-3-540-17093-8. 2nd edition. 특히 2.3항을 참조한다.
혼합 양자 상태의 정화에 대한 논의는 Caltech에서 물리학 219에 대한 John Preskill의 강의 노트 2장을 참조하십시오.
기하학적 측면에 대한 자세한 내용은 다음을 참조하십시오.
- Bengtsson I; Życzkowski K (2006). Geometry of Quantum States. Cambridge: Cambridge University Press., 제2판 개정판(2017년)





 둘러싼
둘러싼
 le(\displaystyle\
le(\displaystyle\
 무작위로 선택된 시스템이
무작위로 선택된 시스템이 


 동일한 물리 양자 상태에 해당하는
동일한 물리 양자 상태에 해당하는 








 ) 갖는 고유
) 갖는 고유 




 양자 상태에 대응하는 2개의 ket일
양자 상태에 대응하는 2개의 ket일 

 진폭과 위상(
진폭과 위상(


 모든
모든 동일한 물리 상태에 대응합니다.이것은 때때로 "전지구적" 위상 요인은 비물리적이지만 "상대적" 위상 요인은 물리적이고 중요하다라는 말로 설명된다.
동일한 물리 상태에 대응합니다.이것은 때때로 "전지구적" 위상 요인은 비물리적이지만 "상대적" 위상 요인은 물리적이고 중요하다라는 말로 설명된다. 
 접근할 수 없는 순수한 상태에서 발생할 수밖에 없다.
접근할 수 없는 순수한 상태에서 발생할 수밖에 없다.













