군론

대수구조 → 군론 군론
기본 개념 서브그룹 정규 부분군 몫군 (반쪽-)다이렉트 프로덕트 군 동형사상 커널 이미지 직접 합계 화환 제품 간단하죠. 유한한 인피니트 계속되는 곱셈의 첨가물 순환의 아벨리안 이면체 무효 해결 가능한 액션. 군론 용어집 그룹 이론 토픽 목록
유한군 유한단순군분류 순환의 번갈아 거짓말형 산발적인 코시의 정리 라그랑주 정리 시로우 정리 홀의 정리 p그룹 초등 아벨 군 프로베니우스군 슈어 승수 대칭군n S 클라인 4족 V 이면체군n D 사분위수 Q 쌍환기n Dic
개별 그룹 격자 ${\displaystyle \mathbb{}}$($$Z \$displaystyle \mathbb {Z$$$) 자유 그룹 모듈러 그룹 PSL(2,$Z{\displaystyle \mathbb{}}$ \$style \mathbb {Z$ 표시$)$ SL(2,$Z{\displaystyle \mathbb{}}$ \$displaystyle \mathbb {Z$ 산술군 격자 쌍곡선 군
토폴로지 그룹 및 Lie 그룹 솔레노이드 원형 일반 선형 GL(n) 특수 선형 SL(n) 직교 O(n) 유클리드 E(n) 특수 직교 SO(n) 유니터리 U(n) 특수 유니터리 SU(n) 심플렉틱 Sp(n) G2 에프4 E6. E7. E8. 로렌츠 푸앵카레 컨포멀 미분 동형 고리 무한 차원 리 군 O()) SU()) Sp())
대수군 선형 대수군 환원군 아벨 변종 타원 곡선
v t

추상 대수학에서, 그룹 이론은 그룹으로 알려진 대수 구조를 연구한다.군의 개념은 추상대수의 중심이다: 고리, 필드, 벡터 공간과 같은 다른 잘 알려진 대수 구조는 모두 추가 연산과 공리를 가진 군으로 볼 수 있다.군들은 수학 전반에 걸쳐 반복되며, 군 이론의 방법들은 대수의 많은 부분에 영향을 끼쳤다.선형 대수군과 리군은 진보를 경험하고 그들 자신의 권리로 주어 영역이 된 두 개의 군 이론 분야이다.

결정과 수소 원자, 그리고 우주에서 알려진 네 가지 기본 힘 중 세 가지는 대칭 그룹에 의해 모델링될 수 있습니다.따라서 집단 이론과 밀접하게 연관된 표현 이론은 물리학, 화학, 재료 과학에서 많은 중요한 응용 분야를 가지고 있다.그룹 이론은 공개 키 암호화에 있어서도 핵심입니다.

집단 이론의 초기 역사는 19세기부터 시작되었다.20세기의^[1] 가장 중요한 수학적 업적 중 하나는 10,000페이지 이상의 저널 페이지를 차지하고 1960년과 2004년 사이에 대부분 출판된 협력적 노력이었고, 이는 유한한 단순 그룹의 완전한 분류로 끝이 났다.

역사

군 이론은 세 가지 주요 역사적 원천을 가지고 있다: 수 이론, 대수 방정식 이론, 그리고 기하학.수이론적 가닥은 레온하르트 오일러에 의해 시작되었고, 2차장과 관련된 모듈식 산술 및 가법 및 곱셈 그룹에 대한 가우스의 연구에 의해 개발되었다.라그랑주, 루피니, 아벨은 높은 수준의 다항식 일반 해법을 찾기 위해 치환 그룹에 대한 초기 결과를 얻었다.Evariste Galois는 "집단"이라는 용어를 만들었고, 초기 그룹 이론과 필드 이론 사이에 현재 갈로아 이론으로 알려진 연결을 확립했습니다.기하학에서, 그룹은 투영 기하학에서, 그리고 나중에는 비유클리드 기하학에서 중요해졌다.펠릭스 클라인의 에를랑겐 프로그램은 군 이론을 기하학의 조직 원리라고 선언했다.

1830년대에 갈로아는 다항식의 용해성을 결정하기 위해 그룹을 처음으로 사용했다.Arthur Cayley와 Augustin Louis Cauchy는 치환 그룹의 이론을 만들어냄으로써 이러한 조사를 더욱 추진했다.그룹의 두 번째 역사적 원천은 기하학적 상황에서 비롯된다.군 이론을 사용하여 가능한 기하학(유클리드, 쌍곡선 또는 투영 기하학)을 파악하려는 시도로, 펠릭스 클라인은 에를랑겐 프로그램을 시작했습니다.1884년에 소푸스 리는 분석적 문제에 관련된 그룹(현재는 Lie 그룹이라고 불린다)을 사용하기 시작했다.셋째, 군들은 처음에는 암묵적으로 그리고 나중에는 명시적으로 대수적 수 이론에서 사용되었다.

이러한 초기 소스의 다른 범위는 집단의 다른 개념을 낳았다.집단 이론은 1880년경부터 통일되었다.그 이후로, 집단 이론의 영향은 20세기 초에 추상 대수학, 대표 이론, 그리고 훨씬 더 영향력 있는 분사 영역의 탄생을 야기하면서 계속 커져 왔다.유한 단순 그룹의 분류는 모든 유한 단순 그룹을 분류하는 20세기 중반의 방대한 작업체이다.

그룹의 주요 클래스

고려 대상 그룹의 범위는 유한 치환 그룹 및 매트릭스 그룹의 특수한 예에서 생성자와 관계에 의한 프레젠테이션을 통해 지정될 수 있는 추상 그룹으로 점차 확대되었다.

치환 그룹

체계적인 연구를 받은 그룹의 첫 번째 클래스는 치환 그룹이었다.어떤 집합 X와 그 자체에 대한 X의 분사의 집합 G가 구성 및 반전 하에서 닫힌 경우, G는 X에 작용하는 군이다.X가 n개의 원소로 구성되고 G가 모든 순열로 구성되면 G는 대칭 그룹_n S이며, 일반적으로 모든 순열 그룹 G는 X의 대칭 그룹의 부분군입니다.케일리로 인한 초기 구성에서는 왼쪽 정규 표현에 의해 스스로 작용(X = G)하는 치환 군으로서 어떤 군도 나타났다.

많은 경우, 치환 그룹의 구조는 대응하는 집합에 대한 작용의 속성을 사용하여 연구할 수 있다.예를 들어, 이 방법으로 n 5 5에 대해 교대군_n A가 단순하다는 것을 증명한다. 즉, 적절한 정규 부분군을 인정하지 않는다.이 사실은 라디칼에서 차수 n in 5의 일반 대수 방정식을 푸는 것이 불가능하다는 데 중요한 역할을 한다.

매트릭스 그룹

다음으로 중요한 그룹의 클래스는 행렬 그룹 또는 선형 그룹에 의해 지정됩니다.여기서 G는 곱과 역수로 닫힌 필드 K 위에 주어진 차수 n의 가역행렬로 이루어진 집합이다.이러한 그룹은 선형 변환에 의해 n차원 벡터 공간ⁿ K에 작용한다.이 액션은 매트릭스 그룹을 개념적으로 치환 그룹과 유사하게 만듭니다.액션의 지오메트리를 유용하게 이용하여 그룹 G의 속성을 확립할 수 있습니다.

변환 그룹

치환 그룹과 행렬 그룹은 변환 그룹의 특별한 경우입니다. 즉, 특정 공간 X에 작용하여 고유한 구조를 보존하는 그룹입니다.치환 그룹의 경우 X는 집합이고 행렬 그룹의 경우 X는 벡터 공간입니다.변환 그룹의 개념은 대칭 그룹의 개념과 밀접하게 관련되어 있습니다. 변환 그룹은 종종 특정 구조를 보존하는 모든 변환으로 구성됩니다.

변환군 이론은 군 이론과 미분 기하학을 연결하는 가교를 형성합니다.Lie와 Klein에서 시작된 긴 연구 라인은 동형사상 또는 미분동형사상에 의한 다양체에 대한 집단 행동을 고려한다.그룹 자체는 이산형 또는 연속형일 수 있습니다.

추상 그룹

군 이론의 발전의 첫 단계에서 고려된 대부분의 그룹은 "구체적"이었고, 숫자, 순열 또는 행렬을 통해 실현되었다.19세기 후반이 되어서야 추상집단을 특정한 공리 체계를 만족시키는 연산과 함께 집합으로 삼는다는 생각이 자리잡기 시작했다.추상 그룹을 지정하는 전형적인 방법은 생성자와 관계에 의한 프레젠테이션을 통해서이다.

$(\displaystyle G=\langle S R\rangle .}$

추상 그룹의 중요한 출처는 정규 하위 그룹 H에 의한 그룹 G의 인자 그룹 또는 몫 그룹 G/H의 구성에 의해 주어진다. 대수적 숫자 필드의 클래스 그룹은 숫자 이론에 많은 관심을 가진 요인 그룹의 초기 예시 중 하나였다.그룹 G가 집합 X의 치환 그룹인 경우 요인 그룹 G/H는 더 이상 X에 작용하지 않지만 추상 그룹이라는 개념을 사용하면 이러한 불일치를 걱정할 필요가 없습니다.

구체적인 집단에서 추상적인 집단으로의 시각의 변화는 특정 실현으로부터 독립한 집단의 속성, 또는 현대 언어에서 동형 하에서의 불변성, 그리고 그러한 속성을 가진 집단의 클래스: 유한 집단, 주기적 집단, 단순 집단, 해결 가능한 집단 등을 고려하는 것을 자연스럽게 만든다.개별 그룹의 속성을 탐구하기보다는 전체 그룹의 클래스에 적용되는 결과를 확립하려고 합니다.새로운 패러다임은 수학의 발전에 가장 중요했다: 그것은 힐버트, 에밀 아르탱, 에미 노에더, 그리고 그들의 ^{[citation needed]}학교의 수학자들의 작품에서 추상 대수학의 창조를 예시했다.

추가 구조를 가진 그룹

G가 위상 공간, 미분 가능한 다양체 또는 대수적 다양성의 추가 구조를 부여받으면 군 개념의 중요한 정교화가 발생한다.그룹이 m(곱셈)과 i(반전)를 조작하는 경우,

${\displaystyle m:G\times G\to G, (g,h)\map to gh,\quad i:G\to G,g\mapsto g^{-1}$

는 이 구조와 양립할 수 있다. 즉, 연속, 평활 또는 규칙(대수 기하학의 의미) 맵이다. 그러면 G는 위상군,^[2] Lie 그룹 또는 대수군이 된다.

추가 구조의 존재는 이러한 유형의 그룹을 다른 수학 분야와 연관시키고 연구에 더 많은 도구를 사용할 수 있음을 의미한다.위상군은 추상적 조화 분석을 위한 자연 영역을 형성하는 반면, 라이 군(변환 군으로 종종 실현됨)은 미분 기하학과 단일 표현 이론의 주요 단계이다.일반적으로 해결할 수 없는 특정 분류 문제는 그룹의 특별한 하위 분류에 접근하여 해결할 수 있습니다.따라서 콤팩트하게 연결된 Lie 그룹은 완전히 분류되었습니다.무한 추상군과 위상군 사이에는 알찬 관계가 있다: 군 δ이 위상군 G의 격자로 실현될 수 있을 때마다 G와 관련된 기하학과 분석은 δ에 대한 중요한 결과를 산출한다.유한군 이론의 비교적 최근의 경향은 콤팩트 위상군(프로파일군)과의 관련성을 이용한다.예를 들어, 단일 p-adic 분석군 G는 다양한 차수의 유한 p-군인 지수군을 가지며, G의 특성은 그 유한 지수의 속성으로 변환된다.

그룹 이론의 분파

유한군 이론

20세기 동안, 수학자들은 유한군의 이론, 특히 유한군의 국부적인 이론과 해결가능하고 무능력한 ^{[citation needed]}그룹의 이론의 몇 가지 측면을 매우 깊이 있게 조사했다.그 결과, 유한 단순 그룹의 완전한 분류가 이루어졌고, 이는 모든 유한 그룹이 만들어질 수 있는 모든 단순 그룹이 현재 알려져 있다는 것을 의미한다.

20세기 후반 동안, 체발리와 스타인버그와 같은 수학자들은 또한 고전 그룹들과 다른 관련 그룹의 유한한 유사체들에 대한 우리의 이해를 증가시켰다.그러한 그룹의 한 패밀리는 유한장 위에 있는 일반 선형 그룹의 패밀리다.유한 그룹은 수학적 또는 물리적 객체의 대칭을 고려할 때 종종 발생하며, 이러한 객체가 한정된 수의 구조 보존 변환만 허용할 때 발생합니다."연속 대칭"을 다루는 것으로 간주될 수 있는 거짓말 그룹의 이론은 연관된 바일 그룹에 의해 강한 영향을 받는다.이것들은 유한 차원 유클리드 공간에 작용하는 반사에 의해 생성된 유한 그룹이다.따라서 유한 그룹의 특성은 이론 물리학과 화학과 같은 과목에서 역할을 할 수 있다.

그룹의 표현

그룹 G가 집합 X에 작용한다고 하는 것은, 집합 X상에 그룹 구조에 대응하도록 G의 모든 요소가 생물적 맵을 정의한다는 것을 의미한다.X가 더 많은 구조를 가지고 있을 때, 이 개념을 더 제한하는 것이 유용하다. 벡터 공간 V 위의 G의 표현은 군 동형사상이다.

${\displaystyle\rho:G\to\operatorname{GL}(V),}$

여기서 GL(V)은 V의 가역 선형 변환으로 구성됩니다.즉, G 내의 임의의 h에 대해 θ(g) θ(h) = θ(gh)가 되도록 모든 그룹 요소 g에 자기동형성 θ(g)를 할당한다.

이 정의는 두 가지 방향으로 이해될 수 있으며, 둘 다 완전히 새로운 ^[3]수학 영역을 만들어낸다.한편으로, G군에 대한 새로운 정보를 얻을 수 있다: 종종 G에서의 군 연산은 추상적으로 주어지지만, θ를 통해 행렬의 곱셈에 대응하며, 이는 매우 ^[4]명시적이다.한편, 복잡한 물체에 대해 잘 이해된 그룹이 행동할 경우, 이것은 문제의 물체에 대한 연구를 단순화합니다.예를 들어 G가 유한하다면 위의 V는 환원 불가능한 부분으로 분해되는 것으로 알려져 있다(마슈케의 정리 참조).또한 이러한 부분은 전체 V보다 훨씬 쉽게 관리할 수 있습니다(슈어의 보조를 통해).

그룹 G가 주어졌을 때, 표현 이론은 G의 어떤 표현이 존재하는지 묻는다.몇 가지 설정이 있으며, 채택된 방법과 얻어진 결과는 모든 경우에 다소 다르다: 유한 그룹의 표현 이론과 리 그룹의 표현은 이론의 두 가지 주요 하위 영역이다.표현의 전체는 그룹의 캐릭터에 의해 관리됩니다.예를 들어 푸리에 다항식은 주기함수의 L공간에² 작용하는 절대값 1의 복소수군인 U(1)의 문자로 해석할 수 있다.

거짓말 이론

Lie 그룹은 그룹 연산이 부드러운 구조와 호환된다는 특성을 가진 차별화 가능한 다양체이기도 한 그룹입니다.리 그룹은 연속 변환 그룹의 이론의 기초를 닦은 소푸스 리의 이름을 따서 명명되었다.groupes de Lie라는 용어는 1893년 프랑스어로 리의 제자 Arthur Tresse의 ^[5]논문 3페이지에 처음 등장했습니다.

리 군(Lie groups)은 수학적 대상과 구조의 연속 대칭에 대한 가장 잘 발달된 이론을 나타내며, 이것은 현대 수학의 많은 부분과 현대 이론 물리학에 필수적인 도구입니다.그들은 미분 방정식의 연속 대칭을 분석하기 위한 자연스러운 틀을 제공합니다. 이는 갈로아 이론에서 대수 방정식의 이산 대칭을 분석하기 위해 치환 그룹이 사용되는 것과 거의 같은 방식으로 사용됩니다.연속 대칭군의 경우로 갈로아 이론을 확장한 것이 리의 주요 동기 중 하나였다.

조합 및 기하학적 군론

그룹은 다양한 방법으로 설명할 수 있습니다.유한 그룹은 가능한 모든 곱셈 g • h로 구성된 그룹 표를 적어 설명할 수 있다. 그룹을 정의하는 보다 간단한 방법은 생성자와 관계(그룹의 표시라고도 함)에 의한 것이다.생성기${\displaystyle }${${\displaystyle {gi}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {ii}_{}}$I { $displaystyle$\ {$g$_ { i }$_ {$ i \ $in$I$\}$ } の f F f generated f generated G에 투영됩니다.이 맵의 커널은 일부 하위 집합 D에 의해 생성된 관계의 하위 그룹이라고 불립니다.프레젠테이션은 보통${\displaystyle }$"${\displaystyle Fd}$ D . D ${\displaystyle .}$。{ $displaystyle \langle$ F$\mid$ D$\rangle$}로$$ 표시됩니다.예를 들어 그룹 프레젠테이션 ${\displaystyle "a}$ , ${\displaystyle b{\mathrm{aa}}^{}}$ -${\displaystyle {}^{}{}^{}{}^{}}$ b - ${\displaystyle 1^{}}$" { $displaystyle \langle$a ,$b$ \ $mid aba ^$ { - $1$} b^ { - 1 \ $langle$ } 。이 그룹은 다음과 같습니다$$$.$발전기 기호와 그 반대로 이루어진 고리를 단어라고 한다.

조합군론은 생성자와 ^[6]관계의 관점에서 그룹을 연구합니다.이는 특히 유한성 가정이 충족되는 경우(예: 최종 생성된 그룹 또는 최종 제시된 그룹)에 유용하다(즉, 관계가 유한하다).이 영역은 기본 그룹을 통한 그래프 연결을 활용합니다.예를 들어, 자유 그룹의 모든 부분군이 자유롭다는 것을 보여줄 수 있습니다.

그룹을 발표함으로써 생기는 몇 가지 자연스러운 질문들이 있다.단어 문제에서는 두 단어가 효과적으로 동일한 그룹 요소인지 여부를 묻습니다.튜링 기계와 문제를 연관시킴으로써, 일반적으로 이 과제를 해결하는 알고리즘이 없다는 것을 보여줄 수 있다.일반적으로 더 어렵고 알고리즘적으로 해결할 수 없는 또 다른 문제는 그룹 동형 문제인데, 이 문제는 서로 다른 프레젠테이션에 의해 주어진 두 그룹이 실제로 동형인지 여부를 묻는다.${\displaystyle 예}$를 들어$,{\displaystyle }$ ${\displaystyle ,}$ ${\displaystyle x}$ , ${\displaystyle yx}$ x y ${\displaystyle x}$ x x x e ${\displaystyle =}$ $⟩$ , {$display$ \ $syle$ x $, y$ \ $mid xyxxy$=$$e \ rangle $,$ }를$$ 가진 그룹은 정수의 가법군 Z와 동형입니다. ($쓰기{\displaystyle }$ z ${\displaystyle =}$ ${\displaystyle x}$ \$displaystyle zxy$ , $1$은 ${\displaystyle {3xyxyxy\mathrm{}}^{}}$ ${\displaystyle ）。}$$gle$ z$,y\mid$ z$^{3}=y\rangle \cong \signle$ z$\rangle$ $.\})$

기하학적 그룹 이론은 기하학적 관점에서, 그룹을 기하학적 개체로 보거나, 그룹이 ^[7]작용하는 적절한 기하학적 개체를 찾음으로써 이러한 문제들을 공격합니다.첫 번째 아이디어는 케일리 그래프를 사용하여 정밀하게 작성됩니다. 케일리 그래프에서는 정점은 그룹 요소에 대응하고 가장자리는 그룹 내 오른쪽 곱셈에 대응합니다.2개의 요소가 주어졌을 때, 하나는 요소 간의 최소 경로 길이에 의해 주어진 단어 메트릭을 구성합니다.밀너와 스바르크의 정리는 예를 들어 콤팩트 다양체처럼 미터법 공간 X에서 합리적인 방식으로 작용하는 군 G가 주어진다면, G는 공간 X에 대해 준등각(즉, 멀리서 보면 유사해 보인다)이라고 말한다.

군과 대칭의 연결

어떤 종류의 구조화 객체 X가 주어졌을 때, 대칭은 구조를 보존하는 객체 그 자체에 대한 매핑이다.예를 들어, 이 문제는 많은 경우에 발생합니다.

• X가 추가 구조가 없는 집합일 경우 대칭은 집합에서 그 집합으로 가는 바이젝티브 맵으로 치환 그룹을 발생시킵니다.
• 객체 X가 미터법 구조 또는 다른 미터법 공간의 평면 내 점 집합인 경우 대칭은 각 점 쌍 사이의 거리를 유지하는 집합의 분사(등각도)입니다.대응하는 그룹을 X의 등각군이라고 합니다.
• 대신 각도가 유지된다면 등각도라고 할 수 있다.예를 들어 컨포멀 맵은 클라이니아 그룹을 일으킨다.
• 대칭은 기하학적 객체에 국한되지 않고 대수적 객체도 포함한다.${\displaystyle {예}^{}}$를 들어 x 2${\displaystyle {}^{}}$- ${\displaystyle 3}$ $0$ { $displaystyle$$x$$$^ { } - 3$$ $=$0 } $3$ 、 2 is$$、 ${\displaystyle 3\sqrt{\mathrm{}}}$（ $displaystyle$ - { \ $displayrt$ {$}$$）{\displaystyle }$ 。이 경우, 두 근을 교환하는 그룹은 방정식에 속하는 갈로아족이다.한 변수의 모든 다항식 방정식은 그 근에 특정 치환군인 갈로아 군을 가지고 있습니다.

집단의 공리는 대칭의 본질적인 측면을 공식화한다.대칭은 그룹을 형성합니다.물체의 대칭을 취하고 다른 대칭을 적용해도 결과는 대칭이 되기 때문에 닫혀 있습니다.물체를 고정시키는 정체성은 항상 물체의 대칭입니다.대칭을 되돌림으로써 역의 존재를 보증하고, 연상성은 대칭이 공간상의 함수이며, 함수의 구성이 연상성이라는 사실에서 나온다.

Frucht의 정리는 모든 그룹이 그래프의 대칭 그룹이라고 말한다.그래서 모든 추상 그룹은 실제로 어떤 명시적인 개체의 대칭입니다.

오브젝트의 "구조 유지"라는 말은 카테고리에서 작업함으로써 정확하게 할 수 있습니다.구조를 보존하는 지도는 형태론이며 대칭군은 문제의 물체의 자기동형군이다.

군론의 응용

집단 이론의 응용은 풍부하다.추상대수의 거의 모든 구조들은 군의 특별한 경우이다.예를 들어 링은 두 번째 연산(곱셈에 대응)과 함께 아벨 군(더하기 대응)으로 볼 수 있다.그러므로 집단 이론 주장은 그러한 실체들의 이론의 많은 부분을 기초한다.

갈로아 이론

갈로아 이론은 다항식의 근의 대칭을 설명하기 위해 그룹을 사용한다.갈로아 이론의 기본 정리는 대수적 장 확장과 군 이론 사이의 연결을 제공한다.그것은 대응하는 갈로아 그룹의 용해성의 관점에서 다항식의 용해성에 대한 효과적인 기준을 제공한다.예를 들어, 5개의 원소의 대칭군인 S는₅ 분해할 수 없으며, 이는 일반 5차 방정식이 저차 방정식이 할 수 있는 방식으로 라디칼에 의해 풀릴 수 없다는 것을 의미한다.집단 이론의 역사적 뿌리 중 하나인 그 이론은 계급장 이론과 같은 분야에서 새로운 결과를 도출하기 위해 여전히 잘 적용되고 있다.

대수 위상

대수적 위상학은 이론이 관심을 갖는 대상과 그룹을 두드러지게 연관짓는 또 다른 영역이다.여기서 그룹은 위상 공간의 특정 불변량을 설명하기 위해 사용됩니다.공간이 변형되어도 변하지 않는 방식으로 정의되기 때문에 "불변량"이라고 불립니다.예를 들어, 기본 그룹은 공간 내 경로의 수를 "카운트"합니다.그리고리 페렐만이 2002/2003년에 증명한 푸앵카레 추측은 이 아이디어의 두드러진 적용이다.그러나 그 영향은 단방향은 아니다.예를 들어, 대수 위상은 규정된 호모토피 그룹이 있는 공간인 에일렌버그-맥레인 공간을 이용한다.마찬가지로 대수적 K이론은 어떤 면에서 그룹의 공간을 분류하는 데 의존한다.마지막으로, 무한 그룹의 비틀림 부분군의 이름은 군 이론에서 위상의 유산을 보여준다.

대수기하학

대수기하학도 마찬가지로 여러 가지 방법으로 군이론을 사용한다.아벨의 변종들은 위에서 소개되었다.그룹 조작의 존재에 의해서, 이러한 다양성에 특히 액세스 할 수 있는 추가 정보가 생성됩니다.그것들은 종종 새로운 추측을 위한 테스트 역할을 한다. (예를 들어, (특정 경우) 호지 추측)1차원 사례, 즉 타원 곡선이 특히 상세하게 연구된다.그것들은 이론적으로나 실질적으로나 ^[8]흥미롭다.다른 방향에서, 토릭 품종은 토러스에 의해 작용되는 대수 품종이다.트로이덜 임베딩은 최근 대수 기하학, 특히 특이점 ^[9]분해능의 발전을 이끌었다.

대수적 수론

대수적 수 이론은 몇몇 중요한 응용 분야에 군을 이용한다.예를 들어, 오일러의 곱 공식은

${\displaystyle {n\sum _{n\geq 1}{\frac {1}{n^{s}}&=\frac {1-p^{-s}},\\end {aligned}}\!}$

는 모든 정수가 고유한 방식으로 소수점으로 분해된다는 사실을 캡처합니다.더 일반적인 고리에 대한 이 진술의 실패는 페르마의 마지막 정리에 대한 쿠머의 처리에서 특징인 클래스 군과 규칙적인 소수를 발생시킵니다.

고조파 분석

Lie 그룹 및 기타 특정 그룹에 대한 분석을 조화 분석이라고 합니다.Haar 측정값, 즉 Lie 그룹의 변환에 불변 적분값이 패턴 인식 및 기타 이미지 처리 ^[10]기술에 사용됩니다.

조합

조합론에서, 치환 그룹의 개념과 그룹 동작의 개념은 종종 객체 집합의 카운트를 단순화하기 위해 사용됩니다. 특히 번사이드의 보조항목을 참조하십시오.

음악

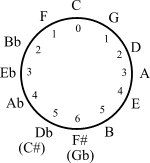
5분의 1 원에서 12주기성이 존재하면 음악 집합론에서 소그룹 이론의 적용을 얻을 수 있다.변환 이론은 수학적 그룹의 요소로서 음악적 변환을 모델링합니다.

물리

물리에서 그룹은 물리 법칙이 따르는 것처럼 보이는 대칭을 묘사하기 때문에 중요하다.노에터의 정리에 따르면 물리적 시스템의 모든 연속 대칭은 시스템의 보존 법칙에 해당합니다.물리학자들은 집단 표현, 특히 리 집단 표현에 매우 관심이 있는데, 이러한 표현들이 종종 "가능한" 물리 이론을 가리키기 때문입니다.물리학에서 그룹을 사용하는 예로는 표준 모형, 게이지 이론, 로렌츠 군, 푸앵카레 군 등이 있습니다.

그룹 이론은 의미 있는 해결책을 ^[11]도출하기 위해 무한한 수의 확률의 합계와 관련하여 윌러드 깁스에 의해 개발된 역학의 통계적 해석의 불완전성을 해결하기 위해 사용될 수 있다.

화학 및 재료 과학

화학 및 재료 과학에서 점군은 규칙적인 다면체, 분자의 대칭, 공간 그룹은 결정 구조를 분류하는 데 사용됩니다.할당된 그룹은 물리적 특성(예: 화학적 극성 및 키라리티), 분광 특성(특히 라만 분광학, 적외선 분광학, 원형 이색성 분광학, 자기 원형 이색성 분광학, UV/Vis 분광학, 형광 분광학)을 결정하는 데 사용될 수 있다.ct 분자 궤도

분자대칭은 화합물의 많은 물리적 및 분광학적 특성에 책임이 있으며 화학반응이 일어나는 방법에 대한 관련 정보를 제공합니다.주어진 분자에 대해 점군을 할당하기 위해서는 점군에 존재하는 대칭 연산 세트를 찾아야 합니다.대칭 연산은 축을 중심으로 회전하거나 거울 평면을 통해 반사하는 것과 같은 동작입니다.즉, 원래의 구성과 구별되지 않게 분자를 움직이는 조작이다.그룹 이론에서 회전축과 거울 평면을 "대칭 요소"라고 합니다.이러한 요소는 대칭 연산이 수행되는 점, 선 또는 평면이 될 수 있습니다.분자의 대칭 연산에 따라 이 분자의 특정 점군이 결정됩니다.

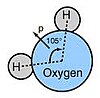
화학에는 다섯 가지 중요한 대칭 연산이 있다.동일운전(E), 회전운전 또는 적정회전(C_n), 반사운전(θ), 반전(i) 및 회전반사운전 또는 부적절한 회전(S_n)이 그것이다.동일성 연산(E)은 분자를 그대로 두는 것으로 구성됩니다.이는 모든 축을 중심으로 한 모든 전체 회전 횟수에 해당합니다.이것은 모든 분자의 대칭인 반면, 키랄 분자의 대칭 그룹은 오직 항등 연산으로만 구성됩니다.항등 연산은 대칭이 없어도 모든 분자의 특성이다.축(C_n)을 중심으로 한 회전은 분자를 특정 축을 중심으로 특정 각도만큼 회전시키는 것으로 구성됩니다.360°/n의 각도를 통해 회전하는 것입니다. 여기서 n은 회전 축을 중심으로 한 정수입니다.예를 들어 물 분자가 산소 원자를 통과하는 축과 수소 원자 사이를 180° 돌면 시작과 같은 형태다.이 경우 n = 2이므로 2번 적용하면 아이덴티티 연산이 생성됩니다.둘 이상의 회전축을 가진 분자에서 가장 큰 값 n을 갖는 C축은 가장_n 높은 차수의 회전축 또는 주축이다.예를 들어 삼불화붕소(BF₃)는 회전축의 최고순위가 C이므로₃ 회전축은 C이다₃.

반사 연산( ()에서 많은 분자는 명백하지는 않지만 거울 평면을 가진다.반사 연산은 각 점이 평면을 통해 평면에서 정확히 시작할 때와 같은 위치로 수직으로 이동한 것처럼 왼쪽과 오른쪽으로 교환합니다.평면이 회전축에 수직일 때 θ_h(수평)라고 한다.회전 주축을 포함하는 다른 평면에는 수직()) 또는_v 이면체(σ_d)라는 레이블이 붙습니다.

반전(i)은 보다 복잡한 조작입니다.각 점은 분자의 중심을 통과하여 원래 위치와 반대되는 위치로 이동하며 시작 지점과 같은 중심점에서 멀리 떨어져 있습니다.얼핏 보면 반전 중심이 있는 것처럼 보이는 많은 분자들은 그렇지 않다. 예를 들어, 메탄과 다른 사면체 분자들은 반전 대칭이 부족하다.이를 보려면 오른쪽 수직면에 수소 원자가 2개, 왼쪽 수평면에 수소 원자가 2개 있는 메탄 모델을 잡습니다.반전은 오른쪽의 수평면에 두 개의 수소 원자가 생기고 왼쪽의 수직면에 두 개의 수소 원자가 생긴다.따라서 반전 동작 후의 분자의 방향이 원래의 방향과 다르기 때문에 반전 동작은 메탄의 대칭 동작이 아니다.그리고 마지막 동작은 부적절한 회전 또는 회전반사 동작(S_n)으로 360°/n의 회전이 필요하며, 그 후 회전축에 수직인 평면을 통한 반사가 필요하다.

암호화

타원곡선암호법으로 구성된 매우 큰 수의 주요 그룹은 공개키 암호화에 사용됩니다.이런 종류의 암호화 방법은 기하학적 객체의 유연성, 즉 그 그룹 구조, 그리고 이산 로그를 계산하기 매우 어렵게 만드는 복잡한 그룹의 구조로부터 이익을 얻는다.초기 암호화 프로토콜 중 하나인 시저의 암호는 (매우 쉬운) 그룹 작업으로 해석될 수도 있습니다.대부분의 암호화 방식은 어떤 방식으로든 그룹을 사용합니다.특히 Diffie-Hellman 키 교환은 유한 순환 그룹을 사용합니다.따라서 그룹 기반 암호화라는 용어는 주로 브레이드 그룹과 같은 무제한 비벨 그룹을 사용하는 암호화 프로토콜을 의미합니다.

「 」를 참조해 주세요.

• 그룹 이론 토픽 목록
• 그룹의 예

메모들

레퍼런스

• Borel, Armand (1991), Linear algebraic groups, Graduate Texts in Mathematics, vol. 126 (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0941-6, ISBN 978-0-387-97370-8, MR 1102012
• Carter, Nathan C. (2009), Visual group theory, Classroom Resource Materials Series, Mathematical Association of America, ISBN 978-0-88385-757-1, MR 2504193
• Cannon, John J. (1969), "Computers in group theory: A survey", Communications of the ACM, 12: 3–12, doi:10.1145/362835.362837, MR 0290613, S2CID 18226463
• Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe", Compositio Mathematica, 6: 239–50, ISSN 0010-437X, archived from the original on 2008-12-01
• Golubitsky, Martin; Stewart, Ian (2006), "Nonlinear dynamics of networks: the groupoid formalism", Bull. Amer. Math. Soc. (N.S.), 43 (3): 305–364, doi:10.1090/S0273-0979-06-01108-6, MR 2223010 그룹 간 일반화의 장점을 보여줍니다.
• Judson, Thomas W. (1997), Abstract Algebra: Theory and Applications Gallian 또는 Herstein의 텍스트 정신에 입문한 학부 텍스트로, 그룹, 고리, 통합 영역, 필드 및 Galois 이론을 다룹니다.오픈 소스 GFDL 라이선스를 사용하여 무료로 다운로드 가능한 PDF.
• Kleiner, Israel (1986), "The evolution of group theory: a brief survey", Mathematics Magazine, 59 (4): 195–215, doi:10.2307/2690312, ISSN 0025-570X, JSTOR 2690312, MR 0863090
• La Harpe, Pierre de (2000), Topics in geometric group theory, University of Chicago Press, ISBN 978-0-226-31721-2
• Livio, M. (2005), The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry, Simon & Schuster, ISBN 0-7432-5820-7 물리 및 기타 과학에서 대칭을 어떻게 가리키는지 설명함으로써 그룹 이론의 실질적인 가치를 전달합니다.
• Mumford, David (1970), Abelian varieties, Oxford University Press, ISBN 978-0-19-560528-0, OCLC 138290
• 로난 M., 2006.대칭과 괴물.옥스퍼드 대학 출판부ISBN 0-19-280722-6.일반 독자를 위한.유한 그룹의 기본 구성 요소를 찾는 탐색을 설명합니다.
• Rotman, Joseph (1994), An introduction to the theory of groups, New York: Springer-Verlag, ISBN 0-387-94285-8 표준 동시대의 레퍼런스입니다.
• Schupp, Paul E.; Lyndon, Roger C. (2001), Combinatorial group theory, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41158-1
• Scott, W. R. (1987) [1964], Group Theory, New York: Dover, ISBN 0-486-65377-3 저렴하고 읽기 쉽지만 강조점, 스타일 및 표기법에 있어 다소 시대에 뒤떨어져 있습니다.
• Shatz, Stephen S. (1972), Profinite groups, arithmetic, and geometry, Princeton University Press, ISBN 978-0-691-08017-8, MR 0347778
• Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38, Cambridge University Press, ISBN 978-0-521-55987-4, MR 1269324, OCLC 36131259

외부 링크

• 추상 그룹 개념의 이력
• 고차원 그룹 이론 이것은 모든 차원으로 확장되고 호모토피 이론과 국소 대 지구 문제에 대한 고차원 노벨식 방법에 적용되는 이론의 수준 1로서의 그룹 이론을 제시합니다.
• 또한 교사 및 학생 패키지: 군 이론 이 패키지는 캠브리지 대학의 밀레니엄 수학 프로젝트에 의해 제작된 온라인 수학 잡지 플러스의 군 이론에 대한 모든 기사들을 모아 응용 프로그램과 최근의 돌파구를 탐색하고 그룹에 대한 명확한 정의와 예를 제공합니다.
• Burnside, William (1911), "Groups, Theory of" , in Chisholm, Hugh (ed.), Encyclopædia Britannica, vol. 12 (11th ed.), Cambridge University Press, pp. 626–636 이것은 그 분야의 초기 연구자에 의한 그룹 이론의 동시적 이해에 대한 상세한 설명입니다.