Page semi-protected

끈 이론

String theory
이 기사는 물리학에 관한 것이다.문자열 알고리즘에 대해서는 문자열(컴퓨터 과학)을 참조하십시오.그 외의 용도는, 「문자열(동음이의구분)을 참조해 주세요.
이 주제에 대한 보다 쉽게 접근할 수 있고 덜 기술적인 소개는 M-이론 소개를 참조하십시오.
끈 이론
Calabi yau formatted.svg
기본 객체
섭동 이론
자극적이지 않은 결과
현상학
수학
관련 개념
이론가

물리학에서 끈 이론은 입자 물리학의 점 같은 입자들이 끈이라고 불리는 1차원 물체로 대체되는 이론적인 틀이다.끈 이론은 이 끈들이 공간을 통해 어떻게 전파되고 서로 상호작용하는지를 설명합니다.스트링 스케일보다 큰 거리 스케일에서 스트링은 일반 입자와 똑같이 보이며 질량, 전하 및 기타 특성은 스트링의 진동 상태에 따라 결정됩니다.끈 이론에서 끈의 많은 진동 상태 중 하나는 중력을 전달하는 양자 기계 입자인 중력자에 해당합니다.그러므로 끈 이론은 양자 중력의 이론이다.

끈 이론은 기초 물리학의 많은 깊은 질문들을 다루려고 시도하는 광범위하고 다양한 주제이다.끈 이론은 블랙홀 물리학, 초기 우주 우주론, 핵 물리학, 응집 물질 물리학 등의 다양한 문제에 적용되어 온 수학 물리학에 많은 진보를 기여했고, 순수 수학의 많은 주요 발전을 자극했다.끈 이론은 잠재적으로 중력과 입자 물리학에 대한 통일된 설명을 제공하기 때문에, 모든 것의 이론, 물질의 모든 기본 힘과 형태를 설명하는 자급자족한 수학적 모델의 후보입니다.이러한 문제에 대한 많은 연구에도 불구하고, 끈 이론이 현실 세계를 어느 정도까지 묘사하고 있는지, 혹은 그 이론이 세부 사항의 선택에 있어서 얼마나 많은 자유를 허용하고 있는지는 알려져 있지 않다.

끈 이론은 1960년대 후반에 강한 핵력에 대한 이론으로 처음 연구되었고, 양자 색역학을 위해 포기되었다.그 후 끈이론을 핵물리학 이론으로 적합하지 않게 만든 바로 그 특성이 그것을 양자 중력 이론의 유망한 후보로 만들었다는 것을 깨달았다.끈 이론의 초기 버전인 보손 끈 이론은 보손이라고 알려진 입자의 종류만을 통합했습니다.그것은 나중에 초끈 이론으로 발전했는데, 이것은 보손과 페르미온이라고 불리는 입자의 종류 사이의 초대칭이라고 불리는 연결을 가정한다.슈퍼스트링 이론의 5가지 일관된 버전이 1990년대 중반 M 이론으로 알려진 11차원의 단일 이론의 다른 제한 사례라는 추측이 나오기 전에 개발되었습니다.1997년 말, 이론가들은 끈 이론을 양자장 이론이라고 불리는 다른 유형의 물리 이론과 연관짓는 반 드 시터/적합장 이론 대응이라고 불리는 중요한 관계를 발견했습니다.

끈 이론의 도전 중 하나는 완전한 이론이 모든 상황에서 만족스러운 정의를 가지고 있지 않다는 것이다.또 다른 쟁점은 이 이론이 가능한 우주의 거대한 풍경을 묘사하는 것으로 생각된다는 것인데, 이 이론은 끈 이론에 기초한 입자 물리학 이론을 발전시키기 위한 복잡한 노력을 가지고 있다.이러한 문제들은 지역사회에서 물리학에 대한 이러한 접근 방식을 비판하고 끈 이론 통일에 대한 지속적인 연구의 가치에 의문을 제기하게 만들었다.

초초

A wavy open segment and closed loop of string.
끈 이론의 근본적인 대상은 열린 끈과 닫힌 끈이다.

★★★

20세기에, 물리 법칙을 공식화하기 위한 두 가지 이론적인 틀이 등장했다.첫 번째는 알버트 아인슈타인의 일반 상대성 이론으로, 중력의 힘과 시공간 구조를 거시적으로 설명하는 이론이다.다른 하나는 양자역학으로, 완전히 다른 공식으로, 알려진 확률 원리를 사용하여 물리적 현상을 미시적 수준에서 기술합니다.1970년대 후반, 이 두 개의 틀은 소립자에서 원자, 그리고 별과 우주의 [1]진화까지 우주의 관측된 특징의 대부분을 설명하기에 충분하다는 것이 입증되었다.

이러한 성공에도 불구하고, 여전히 해결해야 할 많은 문제들이 남아 있다.현대 물리학에서 가장 심각한 문제 중 하나는 양자 [1]중력의 문제이다.일반 상대성 이론은 고전 물리학의 틀 안에서 공식화되는 반면, 다른 기본 힘들은 양자 역학의 틀 안에서 설명된다.일반 상대성 이론과 양자역학 원리를 조화시키기 위해서는 양자 중력 이론이 필요하지만, 양자 이론의 일반적인 법칙을 [2]중력에 적용하려고 할 때 어려움이 발생한다.양자 중력의 일관된 이론을 개발하는 문제 외에도, 원자핵, 블랙홀, 그리고 초기 [a]우주의 물리학에는 많은 다른 근본적인 문제들이 있다.

끈 이론은 이러한 질문들과 다른 많은 것들을 다루려고 시도하는 이론적인 틀이다.끈 이론의 출발점은 입자 물리학의 점 같은 입자들도 끈이라고 불리는 1차원 물체로 모델링될 수 있다는 생각이다.끈 이론은 끈이 어떻게 공간을 통해 전파되고 서로 상호작용하는지를 설명합니다.주어진 버전의 끈 이론에는, 작은 고리나 보통의 끈의 세그먼트처럼 보일 수 있고, 그것은 다른 방식으로 진동할 수 있는 하나의 종류의 끈만이 있다.스트링 스케일보다 큰 거리 스케일에서는 스트링은 일반 입자와 똑같이 보이며 질량, 전하 및 기타 특성은 스트링의 진동 상태에 따라 결정됩니다.이와 같이, 모든 다른 소립자는 진동하는 끈으로 볼 수 있다.끈 이론에서, 끈의 진동 상태 중 하나는 중력을 전달하는 양자 기계 입자인 중력자를 발생시킨다.그러므로 끈 이론은 양자 중력의 [3]이론이다.

끈 이론의 지난 수십 년 동안 주요한 발전 중 하나는 물리 이론을 다른 이론과 동일시하는 수학적인 변환인 특정한 '이중성'의 발견이었다.끈이론을 연구하는 물리학자들은 끈이론의 다른 버전들 사이에서 이러한 이중성을 발견했고, 이것은 끈이론의 모든 [4]일관된 버전이 M-이론으로 알려진 하나의 틀에 포함된다는 추측을 이끌어냈다.

끈 이론의 연구들은 또한 블랙홀의 본질과 중력 상호작용에 대한 많은 결과를 낳았다.블랙홀의 양자적 측면을 이해하려고 할 때 나타나는 어떤 모순이 있으며 끈이론을 연구하여 이러한 문제들을 명확히 할 수 있다.1997년 말, 이 연구 라인은 반(反)-de Sitter/conformal 필드 이론 대응 또는 AdS/CFT의 [5]발견으로 절정에 달했다.이것은 끈 이론을 이론적으로 더 잘 이해되는 다른 물리 이론과 연관짓는 이론적 결과이다.AdS/CFT 대응은 블랙홀과 양자 중력의 연구에 영향을 미치며, 핵과 응집 물질 [7][8]물리학을 포함한[6] 다른 과목에 적용되어 왔다.

끈 이론이 중력을 포함한 모든 근본적인 상호작용을 포함하고 있기 때문에, 많은 물리학자들은 끈 이론이 결국 우리의 우주를 완전히 묘사할 정도로 발전되어 모든 것의 이론이 될 것이다.끈 이론에서 현재 연구의 목표 중 하나는 암흑 물질을 포함하고 우주 팽창을 위한 그럴듯한 메커니즘을 포함하는 작은 우주 상수로 관측된 소립자의 스펙트럼을 재현하는 이론의 해답을 찾는 것입니다.이러한 목표를 향한 진보는 있었지만, 끈 이론이 현실 세계를 어느 정도까지 묘사하고 있는지,[9] 또는 그 이론이 세부 사항의 선택에 얼마나 많은 자유를 허용하고 있는지는 알려지지 않았다.

끈 이론의 도전 중 하나는 완전한 이론이 모든 상황에서 만족스러운 정의를 가지고 있지 않다는 것이다.끈의 산란은 섭동 이론의 기법을 사용하여 가장 직접적으로 정의되지만, 일반적으로 끈 이론을 [10]비강동적으로 정의하는 방법은 알려져 있지 않다.끈 이론이 우주의 [11]특성을 결정하는 물리적 상태인 진공 상태를 선택하는 원리가 있는지도 명확하지 않다.이러한 문제들은 지역 사회 일각에서 물리학의 통일에 대한 이러한 접근 방식을 비판하고 [12]이러한 문제에 대한 지속적인 연구의 가치에 의문을 제기하도록 만들었다.

strings

주요 기사:문자열(물리학)
양자 세계에서의 상호작용: 점 같은 입자의 세계선 또는 끈 이론의 닫힌 끈에 의해 휩쓸린 세계판.

시공간에서 확장되는 전자기장과 같은 물리적 물체에 양자역학을 적용하는 것은 양자장 이론으로 알려져 있다.입자 물리학에서 양자장 이론은 기본 분야의 [13]들뜸으로 모델링된 소립자에 대한 이해의 기초를 형성합니다.

양자장 이론에서는 일반적으로 섭동 이론의 기법을 사용하여 다양한 물리적 사건의 확률을 계산합니다.리처드 파인만과 다른 사람들에 의해 20세기 초에 개발된 섭동 양자장 이론은 계산을 구성하기 위해 파인만 도표라고 불리는 특별한 도표를 사용합니다.사람들은 이 그림들이 점 같은 입자의 경로와 [13]그 상호작용을 묘사한다고 상상한다.

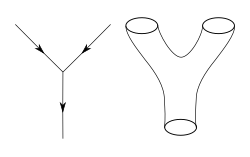
끈 이론의 출발점은 양자장 이론의 점 같은 입자도 [14]끈이라고 불리는 1차원 물체로 모델링될 수 있다는 생각이다.문자열의 상호작용은 일반 양자장 이론에서 사용되는 섭동 이론을 일반화함으로써 가장 쉽게 정의된다.파인만 도표 수준에서 이는 [15]점 입자의 경로를 나타내는 1차원 도표를 끈의 움직임을 나타내는 2차원(2D) 표면으로 대체하는 것을 의미한다.양자장 이론과 달리 끈 이론은 완전한 비교란적 정의를 가지고 있지 않기 때문에 물리학자들이 대답하고 싶어하는 많은 이론적인 질문들은 [16]도달 불가능한 상태로 남아 있다.

끈이론에 기초한 입자물리학 이론에서 끈의 특징적인 길이 척도는 양자 중력의 영향이 [15]클 것으로 생각되는 플랑크 길이, 즉−35 10미터 정도라고 가정한다.물리학 실험실에서 볼 수 있는 눈금과 같이 훨씬 더 큰 길이의 눈금으로, 그러한 물체는 0차원 점 입자와 구별할 수 없을 것이고, 끈의 진동 상태에 따라 입자의 종류가 결정될 것이다.끈의 진동 상태 중 하나는 [3]중력을 전달하는 양자역학 입자인 중력자에 해당합니다.

끈 이론의 원래 버전은 보손 끈 이론이었지만, 이 버전은 물질 입자 사이에 힘을 전달하는 입자의 종류인 보손 또는 페르미온만을 묘사했다.보스닉 스트링 이론은 결국 슈퍼스트링 이론이라고 불리는 이론으로 대체되었다.이 이론들은 보손과 페르미온 모두를 묘사하고, 그들은 초대칭이라고 불리는 이론적인 생각을 통합한다.초대칭 이론에서, 각각의 보손은 페르미온인 대항체를 가지고 있고,[17] 그 반대도 마찬가지입니다.

슈퍼스트링 이론에는 타입 I, 타입 IIA, 타입 IIB, 그리고 2가지 맛의 이종 끈 이론(SO(32)과8 E×E8)이 있습니다.다른 이론들은 다른 종류의 끈을 허용하고, 낮은 에너지에서 발생하는 입자들은 다른 대칭을 보입니다.예를 들어 타입 I 이론에는 오픈스트링(엔드포인트가 있는 세그먼트)과 클로즈드스트링([18]클로즈드루프를 형성한다)이 모두 포함되며 타입 IIA, IIB 및 헤테로틱에는 클로즈드스트링만 포함됩니다.

추가 치수

A tubular surface and corresponding one-dimensional curve.
압축의 예:원거리에서는 원형의 2차원 표면이 1차원처럼 보인다.

일상생활에서는 높이, 폭, 길이 등 익숙한 3차원(3D) 공간이 있습니다.아인슈타인의 일반 상대성 이론은 시간을 세 개의 공간 차원과 동등한 차원으로 취급한다; 일반 상대성 이론에서, 공간과 시간은 분리된 실체로 모델링되지 않고 대신에 4차원 시공간으로 통합된다.이 틀에서 중력 현상은 [19]시공간 기하학의 결과로 보인다.

우주가 4D 시공간으로 잘 묘사되어 있음에도 불구하고, 물리학자들이 다른 차원의 이론을 고려하는 데는 몇 가지 이유가 있습니다.경우에 따라서는 시공간을 다른 차원으로 모델링함으로써 이론이 수학적으로 다루기 쉬워지고 계산을 수행하고 일반적인 통찰력을 더 [b]쉽게 얻을 수 있다.또한 2~3개의 시공간 차원의 이론이 응집물질 [13]물리학에서 현상을 설명하는 데 유용한 상황도 있다.마지막으로,[20] 실제로 4D 이상의 시공간이 존재할 수 있는 시나리오가 있습니다. 그럼에도 불구하고 검출을 피할 수 있었습니다.

끈 이론은 수학적 일관성을 위해 추가적인 시공간 차원을 필요로 한다.보스닉 스트링 이론에서 시공간은 26차원이고, 슈퍼스트링 이론에서는 10차원이며, M 이론에서는 11차원이다.그러므로 끈 이론을 사용하여 실제 물리적 현상을 설명하기 위해서는 이러한 추가 차원이 실험에서 [21]관찰되지 않는 시나리오를 상상해야 한다.

Visualization of a complex mathematical surface with many convolutions and self intersections.
5종 칼라비의 단면-야우 다양체

콤팩트화는 물리 이론에서 차원 수를 수정하는 한 가지 방법입니다.콤팩트화에서는 추가 차원 중 일부는 스스로 [22]원을 형성하기 위해 "닫히는" 것으로 가정합니다.이러한 컬업 치수가 매우 작아지는 한계에서는 시공간이 실질적으로 더 적은 수의 치수를 갖는 이론을 얻을 수 있다.이에 대한 표준적인 유추는 정원 호스와 같은 다차원 물체를 고려하는 것입니다.호스가 충분한 거리에서 보이는 경우, 호스의 치수는 1치수, 즉 길이입니다.그러나 호스에 접근할 때 호스에 두 번째 치수인 둘레가 포함되어 있음을 알게 됩니다.따라서 호스 표면을 기어다니는 개미는 2차원으로 움직인다.

콤팩트화는 시공간이 효과적으로 4차원인 모델을 구축하는 데 사용될 수 있습니다.그러나 추가 치수를 압축하는 모든 방법이 자연을 설명하는 올바른 속성을 가진 모델을 생성하는 것은 아닙니다.소립자 물리학의 실행 가능한 모델에서는 콤팩트한 추가 치수는 칼라비 모양이어야 합니다.야우 [22]매니폴드칼라비-Yau 다지관은 끈 이론에서 일반적으로 6차원으로 간주되는 특별한 공간입니다.그것은 수학자 유제니오 칼라비와 신퉁 [23]야우의 이름을 따서 지어졌다.

차원 수를 줄이기 위한 또 다른 접근방식은 소위 브레인 월드 시나리오입니다.이 접근법에서, 물리학자들은 관측 가능한 우주가 더 높은 차원 공간의 4차원 부분 공간이라고 가정합니다.이러한 모형에서, 입자 물리학의 힘을 전달하는 보손은 4차원 부분 공간에 연결된 끝점이 있는 열린 끈에서 발생하는 반면, 중력은 더 큰 주변 공간을 통해 전파되는 닫힌 끈에서 발생합니다.이 생각은 끈이론에 기초한 실제 물리학의 모델을 개발하려는 시도에 중요한 역할을 하며, 다른 [24]기본력에 비해 중력의 약점에 대한 자연스러운 설명을 제공한다.

★★★★

A diagram indicating the relationships between M-theory and the five superstring theories.
끈 이론의 이중성에 대한 다이어그램입니다.파란색 가장자리는 S 이중성을 나타냅니다.빨간색 가장자리는 T-듀얼리티를 나타냅니다.
주요 기사: S-Duality 및 T-Duality

끈 이론에 대한 주목할 만한 사실은 이론의 다른 버전들은 모두 매우 사소한 방식으로 연관되어 있다는 것이다.서로 다른 끈 이론 사이에 존재할 수 있는 관계 중 하나는 S-이중성이라고 불립니다.이것은 하나의 이론에서 강하게 상호작용하는 입자의 집합이 어떤 경우에는 완전히 다른 이론에서 약하게 상호작용하는 입자의 집합으로 보일 수 있다는 것을 말해주는 관계입니다.대략적으로 말하면, 입자 집합은 결합과 부패가 잦으면 강하게, 드물게 일어나면 약하게 상호작용하는 것으로 알려져 있다.타입 I 스트링 이론은 SO(32)의 이질적인 스트링 이론과 S-이중성에 의해 동등하다는 것이 판명되었습니다.마찬가지로 타입 IIB 스트링 이론은 S-이중성에 [25]의해 중요하지 않은 방법으로 자신과 관련지어집니다.

다른 끈 이론들 사이의 또 다른 관계는 T-이중성이다.여기서는 원형의 추가 차원을 중심으로 전파되는 문자열을 고려합니다.T-duality는 반지름 R의 원을 중심으로 전파되는 문자열은 하나의 설명에서 관측 가능한 모든 양이 이중 설명의 양으로 식별된다는 점에서 반지름 1/R의 원을 중심으로 전파되는 문자열과 동등함을 나타냅니다.예를 들어, 끈은 원을 돌 때 운동량이 있고 원을 한 바퀴 이상 감을 수도 있습니다.끈이 원을 감는 횟수를 와인딩 수라고 합니다.스트링이 하나의 설명에 운동량 p와 권선 번호 n을 가지고 있는 경우, 듀얼 설명에 운동량 n과 권선 번호 p를 가집니다.예를 들어 타입 IIA 스트링 이론은 타입 IIB 스트링 이론과 동등하며, 헤테로틱스트링 이론의 2가지 버전도 타입 IIB [25]스트링 이론과 관련되어 있습니다.

일반적으로 이중성이라는 용어는 겉으로 보기에 서로 다른 두 개의 물리적 시스템이 중요하지 않은 방식으로 동등하게 판명되는 상황을 말합니다.이원성에 관련된 두 이론이 끈 이론일 필요는 없다.예를 들어, 몬토넨-올리브 이중성은 양자장 이론 사이의 S-이중성 관계의 한 예이다.AdS/CFT 대응은 끈 이론을 양자장 이론과 연관짓는 이중성의 한 예이다.만약 두 이론이 이중성에 의해 연관되어 있다면, 그것은 하나의 이론이 어떤 식으로든 변형될 수 있다는 것을 의미한다.그리고 그 두 이론은 변환 하에서 서로 이중적이라고 한다.달리 말하면, 두 이론은 수학적으로 같은 [26]현상을 다르게 기술한 것이다.

분기

주요 기사: Brane
A pair of surfaces joined by wavy line segments.
한 쌍의 D-브랜스에 연결된 문자열을 엽니다.

끈 이론과 다른 관련 이론에서, 브레인(brane)은 점 입자의 개념을 더 높은 차원으로 일반화하는 물리적 물체이다.예를 들어 점입자는 치수 0의 브레인, 끈은 치수 1의 브레인이라고 볼 수 있다.또한 고차원적인 브레인도 고려할 수 있다.차원 p에서는, 이것들을 p-브레인이라고 부릅니다.브레인이라는 단어는 2차원 브레인([27]brane)을 가리키는 "membrane"에서 유래했다.

분지는 양자역학 법칙에 따라 시공간을 통해 전파될 수 있는 동적 물체이다.질량이 있고 전하와 같은 다른 속성을 가질 수 있습니다.p-브레인(p+1)은 세계 부피라고 불리는 시공간에서 (p+1)차원 부피를 쓸어낸다.물리학자들은 종종 [27]브레인 세계 부피 위에 사는 전자기장과 유사한 분야를 연구한다.

끈 이론에서, D-브랜은 열린 끈을 고려할 때 생기는 중요한 종류의 브런이다.열린 문자열이 시공간을 통해 전파될 때 해당 끝점은 D-브레인 상에 있어야 합니다.D-브레인에서 문자 "D"는 디리클레 경계 조건으로 알려진 시스템의 특정 수학적 조건을 나타냅니다.끈 이론에서 D-브랜에 대한 연구는 AdS/CFT 대응과 같은 중요한 결과를 이끌어 냈고, 이것은 양자장 [27]이론의 많은 문제점들을 밝혀냈다.

브랜드는 순수 수학적인 관점에서 자주 연구되며, 복잡한 대수적 다양성의 일관성 있는 단층의 파생 범주나 심플렉틱 [28]다양체의 후카야 범주 등 특정 범주의 대상으로 기술된다.브레인(brane)의 물리적 개념과 범주의 수학적 개념 사이의 연관성은 대수학 및 심플렉틱[29] 기하학 및 표현 [30]이론 분야에서 중요한 수학적 통찰력을 이끌어냈다.


M이론

주요 기사 : M이론

1995년 이전에, 이론가들은 초끈 이론의 5가지 일관된 버전이 있다고 믿었다.이 이해는 1995년 에드워드 위튼이 5가지 이론이 M 이론이라고 불리는 11차원 이론의 특별한 제한 사례일 뿐이라고 제안하면서 바뀌었다.위튼의 추측은 아쇼크 센, 크리스 헐, 폴 타운젠드, 그리고 마이클 더프를 포함한 많은 다른 물리학자들의 연구에 기초했다.그의 발표는 현재 제2의 슈퍼스트링 [31]혁명으로 알려진 수많은 연구 활동으로 이어졌다.

초끈 이론의 통일

A star-shaped diagram with the various limits of M-theory labeled at its six vertices.
M이론, 5개의 초끈 이론, 11차원 초중력 간의 관계를 개략적으로 나타낸 그림.음영 영역은 M 이론에서 가능한 다른 물리적 시나리오의 집합을 나타낸다.커스에 해당하는 특정 제한 사례에서는 여기에 표시된 6가지 이론 중 하나를 사용하여 물리학을 설명하는 것이 자연스럽다.

1970년대에 많은 물리학자들은 일반 상대성 이론과 초대칭 이론을 결합한 초중력 이론에 관심을 갖게 되었다.일반상대성이론은 어떤 차원에서도 타당하지만, 초중력은 [32]차원 수에 상한을 둔다.1978년, 베르너 나옴의 연구는 일관된 초대칭 이론을 공식화할 수 있는 최대 시공간 차원이 [33]11이라는 것을 보여주었다.같은 해, 에콜 노르말 수페리외의 유진 크레머, 베르나르 줄리아, 그리고 조엘 셰르크는 초중력이 최대 11개의 차원을 허용할 뿐만 아니라 사실 이 최대 차원 [34][35]수에서 가장 우아하다는 것을 보여주었다.

처음에, 많은 물리학자들은 11차원 초중력을 압축함으로써, 우리의 4차원 세계의 사실적인 모형을 만드는 것이 가능할 것이라고 희망했다.그러한 모델들이 자연의 네 가지 기본 힘, 즉 전자기력, 강하고 약한 핵력, 그리고 중력에 대한 통일된 설명을 제공하는 것이 희망이었다.이 계획의 다양한 결함이 발견되면서 11차원 초중력에 대한 관심은 곧 시들해졌다.문제들 중 하나는 물리 법칙이 시계방향과 시계반대방향으로 구분하는 것으로 보인다는 것인데, 이것은 키랄리티로 알려진 현상이다.에드워드 위튼과 다른 사람들은 이 키랄리티 특성을 11차원에서 [35]압축하여 쉽게 도출할 수 없다고 관찰했다.

1984년 첫 번째 슈퍼스트링 혁명에서 많은 물리학자들은 입자 물리학과 양자 중력의 통합 이론으로 끈 이론으로 눈을 돌렸다.초중력 이론과 달리 끈 이론은 표준 모형의 키라리티를 수용할 수 있었고, 양자 [35]효과와 일치하는 중력 이론을 제공했습니다.1980년대와 1990년대에 많은 물리학자들이 끌렸던 끈 이론의 또 다른 특징은 그것의 높은 독특함이었다.일반 입자 이론에서는 임의의 라그랑지안에 의해 묘사되는 고전적인 행동을 가진 소립자의 집합을 생각할 수 있다.끈 이론에서, 가능성은 훨씬 더 제한적이다: 1990년대까지, 물리학자들은 이론의 [35]일관된 초대칭 버전이 5개 밖에 없다고 주장했다.

비록 소수의 일관된 초끈 이론이 있었지만, 왜 하나의 일관된 [35]공식만 존재하지 않는지는 미스터리로 남아있었다.그러나 물리학자들이 끈 이론을 더 면밀히 조사하기 시작하면서, 그들은 이 이론들이 복잡하고 사소한 방식으로 연관되어 있다는 것을 깨달았다.그들은 강하게 상호작용하는 문자열의 시스템이, 경우에 따라서는 약하게 상호작용하는 문자열의 시스템으로 간주될 수 있다는 것을 발견했다.이 현상을 S-이중성이라고 합니다.이것은 4차원의[36][37] 이질적인 문자열의 맥락에서 아쇼크 센에 의해 연구되었고, IIB [38]이론의 맥락에서 크리스 헐과 폴 타운센드에 의해 연구되었다.이론가들은 또한 다른 끈 이론들이 T-이중성과 관련이 있을 수 있다는 것을 발견했다.이 이중성은 완전히 다른 시공간 지오메트리로 전파되는 문자열이 물리적으로 [39]동등할 수 있음을 의미합니다.

비슷한 시기에 많은 물리학자들이 현의 성질을 연구하고 있었기 때문에 소수의 물리학자들이 더 높은 차원의 물체의 가능한 응용을 조사하고 있었다.1987년 에릭 버그슈프, 에린 세즈긴, 폴 타운센드는 11차원 초중력이 2차원 브랜치를 [40]포함한다는 것을 보여주었다.직관적으로 이 물체들은 11차원 시공간을 전파하는 시트나 막처럼 보입니다.이 발견 직후 마이클 더프, 폴 하우, 타케오 이나미, 켈로그 스텔은 11차원 초중력의 특별한 콤팩트화를 [41]고려했다.이 설정에서는, 원형 치수를 감싸고 있는 막을 상상할 수 있습니다.원의 반지름이 충분히 작으면 이 막은 10차원 시공간에서 끈처럼 보입니다.더프와 그의 협력자들은 이 구조가 IIA 초끈 [42]이론에서 나타나는 현들을 정확하게 재현한다는 것을 보여주었다.

1995년 끈 이론 컨퍼런스에서 에드워드 위튼은 다섯 개의 초끈 이론 모두가 사실 11개의 시공간 차원으로 단일 이론의 다른 제한 사례라는 놀라운 제안을 했다.위튼의 발표는 끈 [43]이론에서 S-T-이중성과 고차원 브랜의 출현에 대한 이전의 모든 결과를 모았다.위튼의 발표 이후 몇 달 동안, 그의 [44]제안의 다른 부분을 확인하는 수백 개의 새로운 신문들이 인터넷에 게재되었다.오늘날 이러한 일의 난립은 제2의 슈퍼스트링 [45]혁명으로 알려져 있다.

처음에, 몇몇 물리학자들은 새로운 이론이 막의 기본 이론이라고 제안했지만, 비튼은 그 이론에서 막의 역할에 대해 회의적이었다.1996년 논문에서 호아바와 위튼은 "11차원 이론이 초막 이론이지만 그 해석을 의심할 만한 몇 가지 이유가 있기 때문에 우리는 M이론과 [46]막 사이의 미래 관계를 남겨두고 M이론이라고 부를 것이다"라고 썼다.M 이론의 진정한 의미와 구조에 대한 이해가 부족할 때, 비튼은 M이 취향에 따라 "마법", "신비" 또는 "막"을 의미해야 하며, 제목의 진정한 의미는 이론의 보다 근본적인 공식이 알려졌을 [47]때 결정되어야 한다고 제안했다.

행렬 이론

주요 기사 : 매트릭스 이론 (물리학)

수학에서 행렬은 숫자나 다른 데이터의 직사각형 배열입니다.물리학에서 행렬 모형은 수학 공식화가 행렬의 개념을 중요한 방식으로 포함하는 특정한 종류의 물리 이론이다.매트릭스 모델은 양자역학 [48]프레임워크 내에서 일련의 매트릭스의 동작을 기술합니다.

매트릭스 모델의 중요한 예로는 1997년 톰 뱅크스, 윌리 피슐러, 스티븐 셴커, 레너드 서스킨드가 제안한 BFSS 매트릭스 모델이 있다.이 이론은 9개의 큰 행렬 집합의 동작을 설명합니다.저자들은 원본 논문에서 무엇보다도 이 매트릭스 모델의 낮은 에너지 한계가 11차원 초중력에 의해 설명된다는 것을 보여주었다.이러한 계산을 통해 그들은 BFSS 행렬 모델이 M 이론과 정확히 동등하다는 것을 제안하게 되었다.따라서 BFSS 매트릭스 모델은 M 이론의 정확한 공식화를 위한 프로토타입 및 비교적 단순한 [48]환경에서 M 이론의 특성을 조사하기 위한 도구로 사용할 수 있다.

M 이론의 행렬 모형 공식의 발전은 물리학자들이 끈 이론과 비교환 기하학이라고 불리는 수학의 한 분야 사이의 다양한 연관성을 고려하도록 이끌었다.이 과목은 수학자들이 비가환대수의 [49]도구를 사용하여 새로운 기하학적 개념을 정의하는 일반 기하학의 일반화이다.1998년 신문에서 알랭 콘스, 마이클 R. 더글러스, 알버트 슈워츠는 행렬 모델과 M 이론의 일부 측면이 비가환 양자장 이론, 즉 시공간이 비가환 [50]기하학을 사용하여 수학적으로 묘사되는 특별한 종류의 물리 이론에 의해 설명된다는 것을 보여주었다.이것은 한편으로는 행렬 모델과 M 이론, 그리고 다른 한편으로는 비가환 기하학 사이의 연결을 확립했다.그것은 빠르게 비가동 기하학과 다양한 물리 [51][52]이론 사이의 다른 중요한 연결고리의 발견으로 이어졌다.

블랙홀

일반 상대성 이론에서 블랙홀은 중력장이 너무 강해서 입자나 방사선이 빠져나갈 수 없는 시공간 영역으로 정의된다.현재 받아들여지고 있는 항성진화 모형에서 블랙홀은 거대한 별들이 중력붕괴를 겪을 때 발생하는 것으로 생각되며, 많은 은하들은 그 중심에 초거대 블랙홀을 포함하고 있는 것으로 생각됩니다.블랙홀은 중력의 양자적 측면을 이해하려는 이론가들에게 심오한 도전을 제시하기 때문에 이론적인 이유로도 중요하다.끈 이론은 이론가들이 그들의 열역학을 [53]연구할 수 있는 틀을 제공하기 때문에 블랙홀의 이론적 특성을 조사하는데 중요한 도구임이 증명되었다.

베켄슈타인-호킹 공식

통계역학이라 불리는 물리학 분야에서 엔트로피는 물리적 시스템의 무작위성 또는 무질서의 척도이다.이 개념은 1870년대에 오스트리아의 물리학자 루드비히 볼츠만에 의해 연구되었는데, 그는 가스의 열역학 특성이 많은 구성 분자들의 결합된 특성으로부터 도출될 수 있다는 것을 보여주었다.볼츠만은 기체 안에 있는 모든 다른 분자들의 행동을 평균화함으로써, 사람은 부피, 온도, 압력과 같은 거시적 특성을 이해할 수 있다고 주장했다.게다가, 이 관점은 그가 엔트로피의 정확한 정의를 동일한 거시적 [54]특징을 발생시키는 분자들의 다른 상태들의 숫자에 대한 자연 로그로 제공하도록 이끌었습니다.

20세기에, 물리학자들은 같은 개념을 블랙홀에 적용하기 시작했다.기체와 같은 대부분의 시스템에서 엔트로피는 부피와 함께 확장됩니다.1970년대에, 물리학자 제이콥 베켄스타인은 블랙홀의 엔트로피는 대신 물질과 방사선이 중력에 [55]의해 손실되는 경계인 사건 지평선의 표면적에 비례한다고 제안했다.물리학자 스티븐 [56]호킹의 생각과 결합했을 때, 베켄스타인의 연구는 블랙홀의 엔트로피에 대한 정확한 공식을 산출했습니다.베켄슈타인-호킹 공식은 엔트로피 S를 다음과 같이 표현한다.

여기서 c는 빛의 속도, k는 볼츠만의 상수, θ는 축소된 플랑크 상수, G는 뉴턴의 상수, A는 사건 [57]지평선의 표면적이다.

다른 물리적 시스템과 마찬가지로, 블랙홀은 동일한 거시적 특징을 이끌어내는 다른 미세 상태의 수로 정의된 엔트로피를 가지고 있습니다.베켄슈타인-호킹 엔트로피 공식은 블랙홀의 엔트로피의 예상값을 제공하지만, 1990년대까지 물리학자들은 양자 중력 이론에서 미세 상태를 세는 것에 의한 이 공식의 도출이 여전히 부족했다.이 공식의 그러한 파생물을 찾는 것은 [58]끈 이론과 같은 양자 중력 이론의 생존 가능성에 대한 중요한 테스트로 여겨졌다.

끈 이론 내에서의 파생

1996년의 논문에서 앤드류 스트로밍거와 컴런 바파는 끈 [59]이론의 특정 블랙홀에 대한 베켄슈타인-호킹 공식을 도출하는 방법을 보여주었다.이들의 계산은 D-브랜(약하게 상호작용할 때 막이 변동하는 것처럼 보이는)이 상호작용이 강할 때 사건의 지평을 가진 밀도가 높고 무거운 물체가 된다는 관찰에 기초했다.즉 끈 이론에서 강하게 상호작용하는 D-브랜 시스템은 블랙홀과 구별할 수 없다.스트로밍거와 바파는 이러한 D-브레인 시스템을 분석하여 D-브랜을 시공간에서 배치하는 다양한 방법을 계산하여 이들의 질량과 전하를 합친 블랙홀이 주어진 질량과 전하가 되도록 했다.이들의 계산은 1/4 [60]계수를 포함하여 정확히 베켄스타인-호킹 공식을 재현했다.Strominger, Vafa, 그리고 다른 사람들의 후속 연구는 원래의 계산을 개선하고 매우 작은 블랙홀을 [61][62]묘사하는 데 필요한 "양자 보정"의 정확한 값을 제시했습니다.

스트로밍거와 바파가 그들의 원래 연구에서 고려했던 블랙홀은 실제 천체물리 블랙홀과는 상당히 달랐다.한 가지 차이점은 스트로밍거와 바파는 계산을 쉽게 하기 위해 극단의 블랙홀만을 고려했다는 것이다.이들은 주어진 [63]전하와 호환되는 가능한 가장 낮은 질량을 가진 블랙홀로 정의됩니다.스트로밍거와 바파는 또한 물리적인 초대칭성이 [64]없는 5차원 시공간에서 블랙홀에 대한 관심을 제한했다.

스트로밍거와 바파의 엔트로피 계산은 원래 끈 이론에서 매우 특이하고 물리적으로 비현실적인 맥락에서 개발되었지만, 양자 중력 이론에서 블랙홀 엔트로피가 어떻게 설명될 수 있는지에 대한 질적인 이해를 이끌어냈다.실제로, 1998년에 스트로밍거는 원래의 결과가 끈이나 [65]초대칭에 의존하지 않고 양자 중력에 대한 임의의 일관된 이론으로 일반화될 수 있다고 주장했다.그는 2010년 몇몇 다른 저자들과 협력하여 블랙홀 엔트로피에 대한 일부 결과가 극단이 아닌 천체물리 [66][67]블랙홀로 확대될 수 있다는 것을 보여주었다.

AdS/CFT 대응

주요 기사: AdS/CFT 대응

끈이론을 공식화하고 그 특성을 연구하기 위한 한 가지 접근방식은 반(反)-de Sitter/compormal field theory(AdS/CFT) 대응에 의해 제공됩니다.이것은 끈 이론이 어떤 경우에는 양자장 이론과 동등하다는 것을 암시하는 이론적 결과이다.끈 이론의 수학적 구조에 대한 통찰력을 제공할 뿐만 아니라, AdS/CFT 대응은 전통적인 계산 기법이 [6]효과적이지 않은 체제에서 양자장 이론의 많은 측면을 밝혀냈습니다.AdS/CFT 대응은 1997년 [68]말 후안 말다세나에 의해 처음 제안되었다.통신의 중요한 측면은 스티븐 굽서, 이고르 클레바노프, 알렉산더 마르코비치 [69]폴랴코프와 에드워드 [70]비튼의 기사에서 상세히 설명되었다.2010년까지, Maldacena의 기사는 7,000개 이상의 인용문을 보유하여 고에너지 [c]물리학 분야에서 가장 많이 인용된 기사가 되었습니다.

서신의 개요

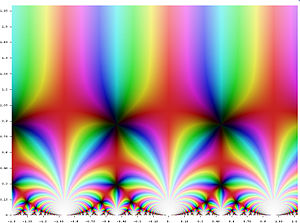
A disk tiled by triangles and quadrilaterals which become smaller and smaller near the boundary circle.
쌍곡 평면 삼각형 및 정사각형 테셀레이션

AdS/CFT 대응에서 시공간 기하학은 반 드 시터 [6]공간이라고 불리는 아인슈타인 방정식의 진공해로 묘사된다.매우 기초적인 용어로, 반 드 시터 공간은 점 사이의 거리에 대한 개념이 일반적인 유클리드 기하학의 거리에 대한 개념과 다른 시공간 수학적 모델이다.이것은 왼쪽 [71]그림과 같이 디스크로 볼 수 있는 쌍곡선과 밀접한 관련이 있습니다.이 이미지에서는 삼각형 및 정사각형별로 디스크의 테셀레이션을 보여 줍니다.모든 삼각형과 정사각형의 크기가 같고 원형 외부 경계가 내부 어느 [72]점으로부터도 무한히 멀도록 이 디스크의 점 사이의 거리를 정의할 수 있습니다.

사람들은 각각의 원반이 주어진 시간에 우주의 상태를 나타내는 쌍곡 원반 더미를 상상할 수 있다.결과 기하학적 객체는 3차원 안티-de-시터 [71]공간입니다.단면이 쌍곡선 원반의 복사본인 솔리드 실린더처럼 보입니다.이 그림에서는 시간이 세로 방향으로 흐릅니다.이 실린더의 표면은 AdS/CFT 대응에 중요한 역할을 합니다.쌍곡면과 마찬가지로 반 드 시터 공간은 내부 점들이 실제로 이 경계 [72]표면에서 무한히 멀리 떨어져 있는 방식으로 곡선화됩니다.

A cylinder formed by stacking copies of the disk illustrated in the previous figure.
3차원 반데시터 공간은 마치 쌍곡 원반 더미와 같으며, 각각은 주어진 시간의 우주 상태를 나타냅니다.결과적으로 발생하는 시공간은 솔리드 실린더처럼 보입니다.

이 구성은 2개의 공간 차원과 1개의 시간 차원으로만 구성된 가상 우주를 설명하지만, 임의의 수의 차원으로 일반화할 수 있습니다.실제로 쌍곡선 공간은 2차원 이상의 차원을 가질 수 있으며 쌍곡선 공간의 복사본을 "스택"하여 반 드 시터 [71]공간의 고차원 모델을 얻을 수 있습니다.

안티 드 시터 공간의 중요한 특징은 경계(3차원 안티 드 시터 공간의 경우 실린더처럼 보인다)입니다.이 경계의 한 가지 특성은, 주어진 점 주변의 표면의 작은 영역 안에서, 그것은 비중력 [73]물리학에서 사용되는 시공간 모델인 민코프스키 공간과 똑같이 보인다는 것입니다.따라서 반 드 시터 공간의 경계에 의해 "공간"이 주어지는 보조 이론을 고려할 수 있다.이 관측은 반 드 시터 공간의 경계를 양자장 이론의 "공간적 시간"으로 간주할 수 있다는 AdS/CFT 대응의 시작점이다.이 양자장 이론은 하나의 이론에서 실체와 계산을 다른 이론에서 그것의 상대 이론으로 번역하는 "사전"이 있다는 점에서 벌크 반 드 시터 공간에서의 끈 이론과 같은 중력 이론과 동등하다는 주장이다.예를 들어, 중력 이론의 단일 입자는 경계 이론의 입자 집합과 일치할 수 있습니다.또한 두 이론의 예측은 양적으로 동일하기 때문에 중력 이론에서 두 입자가 충돌할 확률이 40%라면 경계 이론에서 대응하는 집합도 [74]충돌할 확률이 40%가 된다.

양자 중력에 대한 응용

AdS/CFT 대응의 발견은 끈 이론과 양자 중력에 대한 물리학자들의 이해에 있어 큰 발전이었다.이에 대한 한 가지 이유는 대응이 양자장 이론의 관점에서 끈 이론의 공식을 제공하고, 이는 비교에 의해 잘 이해되기 때문이다.또 다른 이유는 이것이 물리학자들이 블랙홀의 [53]역설들을 연구하고 해결할 수 있는 일반적인 틀을 제공한다는 것이다.

1975년, 스티븐 호킹은 블랙홀이 완전히 검은 것은 아니지만 사건의 [56]지평선 근처의 양자 효과로 인해 희미한 방사선을 방출한다는 계산을 발표했다.처음에, 호킹의 결과는 블랙홀이 정보를 파괴한다는 것을 암시했기 때문에 이론가들에게 문제가 되었다.좀 더 정확히 말하면, 호킹의 계산은 물리 시스템이 슈뢰딩거 방정식에 따라 시간에 따라 진화하는 양자 역학의 기본 가설 중 하나와 충돌하는 것처럼 보였다.이 속성은 보통 시간 진화의 단일성이라고 합니다.호킹의 계산과 양자역학의 단일성 가설 사이의 명백한 모순은 블랙홀 정보의 [75]역설로 알려지게 되었다.

AdS/CFT 대응은 블랙홀이 어떤 맥락에서 양자 역학과 일치하는 방식으로 어떻게 진화할 수 있는지를 보여주기 때문에 적어도 어느 정도 블랙홀 정보의 모순을 해결합니다.실제로 AdS/CFT 대응의 맥락에서 블랙홀을 고려할 수 있으며, 이러한 블랙홀은 반 드 시터 [76]공간의 경계에 있는 입자의 구성에 해당된다.이러한 입자들은 양자 역학의 일반적인 법칙에 따르고 특히 단일 방식으로 진화하기 때문에, 블랙홀은 양자 [77]역학의 원리를 존중하면서 단일 방식으로 진화해야 합니다.2005년, 호킹 박사는 AdS/CFT 통신에 의해 이 역설은 정보 보존에 유리하게 정착되었다고 발표하면서 블랙홀이 정보를 [78]보존할 수 있는 구체적인 메커니즘을 제안했다.

핵물리학의 응용

주요 기사 : AdS/QCD 대응
A magnet levitating over a superconducting material.
고온 초전도체 위에서 자기부상하는 것.오늘날 일부 물리학자들은 AdS/CFT [7]대응법을 사용하여 고온 초전도도를 이해하기 위해 노력하고 있습니다.

AdS/CFT 대응은 양자 중력의 이론적인 문제에 대한 적용 외에도 양자장 이론의 다양한 문제에 적용되어 왔다.AdS/CFT 대응 관계를 사용하여 연구된 물리적 시스템 중 하나는 입자 가속기에서 생성된 물질의 이국적인 상태인 쿼크-글루온 플라스마이다.이러한 물질의 상태는 금이나 납 핵과 같은 무거운 이온이 높은 에너지로 충돌할 때 잠깐 동안 발생합니다.이러한 충돌로 인해 원자핵을 구성하는 쿼크는 빅뱅 이후 약 10초 후에 존재하는 것과 유사한 [79]약 2조−11 켈빈의 온도에서 결합이 해제됩니다.

쿼크-글루온 플라즈마의 물리학은 양자 색역학이라고 불리는 이론에 의해 지배되지만, 이 이론은 쿼크-글루온 [d]플라즈마와 관련된 문제에서는 수학적으로 다루기 어렵다.2005년에 등장한 기사에서, 탐 탄 선과 그의 협력자들은 끈 이론의 언어로 쿼크-글루온 [80]플라즈마를 설명함으로써 AdS/CFT 대응이 쿼크-글루온 플라즈마의 일부 측면을 이해하는 데 사용될 수 있다는 것을 보여주었다.AdS/CFT 대응관계를 적용함으로써, 선과 그의 협력자들은 5차원 시공간에서 블랙홀의 관점에서 쿼크-글루온 플라즈마를 설명할 수 있었다.계산 결과 쿼크-글루온 플라즈마와 관련된 두 가지 양의 비율, 즉 엔트로피의 전단 점도와 체적 밀도는 특정 보편 상수와 거의 동일해야 합니다.2008년 브룩헤이븐 국립 [7][81]연구소의 상대론적 중이온 충돌기에서 쿼크-글루온 플라즈마에 대한 이 비율의 예측 값이 확인되었다.

응집 물질 물리학에 대한 응용

주요 기사 : AdS/CMT 대응

AdS/CFT 대응은 응집 물질 물리학의 측면을 연구하는 데에도 사용되어 왔다.수십 년 동안, 실험 응축 물질 물리학자들은 초전도체와 초유체를 포함한 많은 이국적인 물질의 상태를 발견했다.이러한 상태는 양자장 이론의 형식주의를 사용하여 설명되지만, 일부 현상은 표준장 이론 기법을 사용하여 설명하기가 어렵습니다.Subir Sachdev를 포함한 몇몇 응집 물질 이론가들은 AdS/CFT 대응으로 끈 이론의 언어로 이러한 시스템을 기술하고 그들의 [7]행동에 대해 더 많이 배울 수 있기를 희망합니다.

지금까지 끈 이론 방법을 사용하여 초유체의 절연체로의 전이를 설명하는데 어느 정도 성공했습니다.초유체는 마찰 없이 흐르는 전기적으로 중성인 원자의 시스템이다.이러한 시스템은 종종 액체 헬륨을 사용하여 실험실에서 만들어지지만, 최근 실험자들은 수조 개의 차가운 원자를 십자형 레이저 격자 안에 부어 인공 초유체를 만드는 새로운 방법을 개발했다.이 원자들은 처음에는 초유체처럼 행동하지만, 실험자들이 레이저의 강도를 높이면, 이동성이 떨어지고 갑자기 절연 상태로 전환된다.과도기 동안, 원자들은 특이한 방식으로 행동한다.예를 들어, 원자는 온도와 플랑크의 상수에 의존하는 속도로 천천히 멈춥니다.플랑크의 상수는 양자역학의 기본 변수입니다.플랑크의 상수는 다른 위상을 설명하지 않습니다.이 동작은 최근 유체의 특성이 고차원 블랙홀의 [8]관점에서 설명되는 이중적인 설명을 통해 이해되고 있습니다.

현상학

주요 기사:현현상학

끈 이론은 상당한 이론적 관심을 갖는 아이디어일 뿐만 아니라 일반 상대성 이론과 입자 물리학을 결합한 실제 물리학의 모델을 구성하기 위한 프레임워크를 제공합니다.현상학은 물리학자들이 보다 추상적인 이론 아이디어로부터 자연의 현실적인 모델을 구성하는 이론 물리학의 한 분야이다.끈 현상학은 끈 이론을 바탕으로 현실적이거나 반현실적인 모델을 구성하려는 끈 이론의 한 부분이다.

부분적으로 이론과 수학적인 어려움과 부분적으로 이러한 이론들을 실험적으로 테스트하는 데 필요한 극도로 높은 에너지 때문에, 지금까지 이 모델들 중 어느 것이 자연에 대한 정확한 기본 기술임을 명백하게 지적할 수 있는 실험 증거는 없습니다.이것은 지역 사회 일각에서 통일에 대한 이러한 접근 방식을 비판하고 이러한 [12]문제에 대한 지속적인 연구의 가치에 의문을 제기하도록 만들었다.

입자 물리학

소립자와 소립자의 상호작용을 설명하는 현재 받아들여지고 있는 이론은 소립자 물리학의 표준 모델로 알려져 있다.이 이론은 자연의 세 가지 기본 힘, 즉 전자기력과 강하고 약한 핵력에 대한 통일된 설명을 제공한다.광범위한 물리적 현상을 설명하는 데 있어 주목할 만한 성공에도 불구하고, 표준 모델은 현실의 완전한 설명이 될 수 없다.이는 표준 모델이 중력을 통합하지 못하기 때문이며, 계층 문제 및 페르미온 질량 또는 암흑 물질의 구조를 설명할 수 없는 문제와 같은 문제 때문이다.

끈 이론은 표준 모델을 넘어 다양한 입자 물리학 모델을 구성하기 위해 사용되어 왔다.일반적으로 이러한 모델은 콤팩트화 개념을 기반으로 합니다.끈이나 M 이론의 10차원 또는 11차원 시공간에서 시작하여 물리학자들은 추가 차원에 대한 형태를 가정합니다.이 모양을 적절하게 선택함으로써, 그들은 발견되지 않은 추가적인 [82]입자와 함께 입자 물리학의 표준 모델과 거의 비슷한 모델을 만들 수 있다.끈 이론에서 현실적인 물리학을 도출하는 인기 있는 방법 중 하나는 10차원의 이질적인 이론에서 시작해서 시공간 6차원이 6차원의 칼라비처럼 생겼다고 가정하는 것이다.야우 매니폴드이러한 콤팩트화는 끈 이론에서 현실적인 물리학을 추출하는 많은 방법을 제공한다.M이론에 [83]기초한 4차원 세계의 현실적 또는 반현실적 모델을 구축하기 위해 다른 유사한 방법을 사용할 수 있습니다.

우주론

주요 기사:끈 우주론
윌킨슨 마이크로파 이방성 탐사선에 의해 생성된 우주 마이크로파 배경 지도

빅뱅 이론은 알려진 가장 이른 시기부터 이후의 대규모 진화에 이르는 우주의 지배적인 우주론적 모델이다.은하 적색편이, 수소와 헬륨과 같은 빛 원소의 상대적 풍부함, 그리고 우주 마이크로파 배경의 존재를 포함한 우주의 많은 관측된 특징들을 설명하는데 성공했음에도 불구하고, 몇 가지 의문점들이 남아 있습니다.예를 들어, 표준 빅뱅 모형은 왜 우주가 모든 방향에서 같은 것으로 보이는지, 왜 매우 큰 거리 척도로 평평하게 보이는지, 그리고 [84]왜 자기 단극과 같은 특정한 가설 입자가 실험에서 관찰되지 않는지를 설명하지 않는다.

현재 빅뱅을 뛰어넘는 이론의 유력한 후보는 우주 인플레이션 이론이다.1980년대에 앨런 거스와 다른 사람들에 의해 개발된 인플레이션은 표준 빅뱅 이론에 의해 묘사된 팽창 이전에 우주의 극도로 빠른 팽창 기간을 가정한다.우주 인플레이션 이론은 빅뱅의 성공을 보존하면서 우주의 [85]신비로운 특징 중 일부에 대한 자연스러운 설명을 제공한다.이 이론은 또한 빅뱅 [86]이후 약 38만 년 이후 하늘을 가득 채운 방사선인 우주 마이크로파 배경의 관측으로부터 놀라운 지지를 받았다.

인플레이션 이론에서, 우주의 빠른 초기 팽창은 팽창이라고 불리는 가상의 입자에 의해 야기된다.이 입자의 정확한 특성은 이론에 의해 고정된 것이 아니라 궁극적으로 끈 [87]이론과 같은 보다 근본적인 이론에서 도출되어야 한다.실제로 끈이론에 의해 기술된 입자의 스펙트럼 내에서 팽창을 확인하고 끈이론을 이용한 인플레이션을 연구하려는 많은 시도가 있었다.이러한 접근법은 결국 우주 마이크로파 배경의 측정과 같은 관측 자료에서 지지를 얻을 수 있지만, 우주론에 대한 끈 이론의 적용은 아직 초기 [88]단계에 있습니다.

수학과의 관계

이론 물리학 연구에 영향을 미치는 것 외에도 끈 이론은 순수 수학의 많은 주요 발전을 자극했다.이론 물리학에서 발전하는 많은 아이디어들처럼, 끈 이론은 현재 수학적으로 엄격한 공식을 가지고 있지 않다. 모든 개념을 정확하게 정의할 수 있다.결과적으로, 끈 이론을 연구하는 물리학자들은 종종 물리적인 직관에 의해 이론의 다른 부분을 공식화하기 위해 사용되는 겉보기에 다른 수학적 구조들 사이의 관계를 추측하도록 유도된다.이러한 추측은 나중에 수학자들에 의해 증명되고, 이런 식으로 끈 이론은 순수 [89]수학에서 새로운 아이디어의 원천이 된다.

거울 대칭

주요 기사:거울 대칭(끈 이론)
A complex mathematical surface in three dimensions.
클렙시 입방체는 대수적 다양성이라고 불리는 기하학적 물체의 한 예이다.열거형 기하학의 고전적인 결과에 따르면 이 표면에는 정확히 27개의 직선이 있습니다.

칼라비 이후-Yau 다지관은 끈 이론의 추가 차원을 압축하는 방법으로 물리학에 입문했고, 많은 물리학자들은 이러한 다지관을 연구하기 시작했습니다.1980년대 후반, 몇몇 물리학자들은 끈 이론의 그러한 콤팩트화를 고려할 때, 대응하는 칼라비를 독특하게 재구성하는 것은 불가능하다는 것을 알아챘다.야우 [90]매니폴드대신에, 타입 IIA와 타입 IIB의 2개의 다른 버전의 스트링 이론을 완전히 다른 칼라비 상에서 컴팩트화할 수 있습니다.Yau 다지관은 같은 물리학을 만들어냈다.이 상황에서 다양체는 거울 다양체라고 불리며, 두 물리 이론 사이의 관계는 거울 [28]대칭이라고 불립니다.

칼라비 여부에 관계없이...끈 이론의 Yau 콤팩트화는 자연에 대한 올바른 설명을 제공하며, 다른 끈 이론들 사이의 거울 이중성의 존재는 수학적으로 중요한 결과를 가져옵니다.칼라비-끈 이론에서 사용되는 Yau 다양체는 순수 수학에 관심이 있고, 거울 대칭은 수학자들이 기하학적 [28][91]질문에 대한 해법의 수를 세는 것과 관련된 수학의 한 분야인 열거형 기하학의 문제를 풀 수 있게 해준다.

열거형 기하학은 다항식의 소멸에 의해 정의되는 대수적 다양성이라고 불리는 기하학적 객체의 클래스를 연구한다.예를 들어 오른쪽의 Clebsch 입방체는 4개의 변수에서 3차 다항식을 사용하여 정의된 대수적 다양체이다.19세기 수학자 아서 케일리와 조지 살몬의 유명한 결과에 따르면, 그러한 [92]표면에는 정확히 27개의 직선이 있다고 한다.

이 문제를 일반화하면 5진수 칼라비에 몇 개의 선을 그릴 수 있는지 물어볼 수 있습니다.위에서 설명한 것과 같은 Yau 다양체로, 5차 다항식으로 정의됩니다.이 문제는 19세기 독일 수학자 헤르만 슈베르트(Hermann Schubert)에 의해 해결되었는데, 슈베르트(Hermann Schubert)는 그러한 선이 정확히 2,875개라는 것을 알아냈다.1986년, 지오미터 셸던 캣츠는 2차 다항식으로 정의되고 완전히 5진수 안에 있는 원과 같은 곡선의 수가 609,[93]250이라는 것을 증명했다.

1991년까지, 열거형 기하학의 고전적인 문제들은 대부분 해결되었고 열거형 기하학에 대한 관심은 [94]줄어들기 시작했다.이 분야는 1991년 5월 물리학자 Philip Candelas, Xenia de la Ossa, Paul Green 및 Linda Parks가 거울 대칭을 사용하여 칼라비에 대한 어려운 수학 질문을 번역할 수 있다는 것을 보여주면서 다시 활기를 띠게 되었다.Yau는 거울에 대한 [95]더 쉬운 질문들로 다양합니다.특히, 그들은 6차원 칼라비를 보여주기 위해 거울 대칭을 사용했다.Yau 매니폴드는 정확히 317,206,375도의 [94]3도 곡선을 포함할 수 있습니다.칸델라스와 그의 협력자들은 도수 3곡선을 세는 것 외에도 수학자들이 [96]얻은 결과를 훨씬 뛰어넘는 합리적인 곡선을 세는 데 있어 더 많은 일반적인 결과를 얻었다.

원래 칸델라스의 결과는 물리적인 이유로 정당화 되었다.그러나 수학자들은 일반적으로 물리적 직관에 호소하지 않는 엄격한 증거를 선호한다.따라서 수학자들은 거울 대칭에 대한 물리학자들의 연구에서 영감을 얻어 거울 [e]대칭의 열거적 예측을 증명하는 그들만의 주장을 구성했다.오늘날 거울 대칭은 수학에서 활발한 연구 분야이며, 수학자들은 물리학자들의 [102]직관에 기초하여 거울 대칭에 대한 보다 완전한 수학적 이해를 발전시키기 위해 노력하고 있다.거울 대칭에 대한 주요 접근법으로는 Maxim Kontsevich의[29] 호몰로지 거울 대칭 프로그램과 Andrew Strominger, Sing-Tung Yau 및 Eric Zaslow의 [103]SYZ 추측이 있습니다.

괴물 문샤인

주요 기사:괴물 문샤인
An equilateral triangle with a line joining each vertex to the midpoint of the opposite side
정삼각형은 120°, 240° 또는 360°로 회전할 수 있으며, 형상의 변화 없이 그림 3개의 선 중 하나에 반사될 수 있다.

군 이론은 대칭의 개념을 연구하는 수학의 한 분야이다.예를 들어 정삼각형과 같은 기하학적 형태를 생각할 수 있다.모양을 바꾸지 않고 이 삼각형에서 수행할 수 있는 연산은 다양하다.120°, 240°, 360°로 회전할 수도 있고, 사진의1 S, S, S2 중 하나의0 선에 반사시킬 수도 있습니다.각각의 연산은 대칭이라고 불리며, 이러한 대칭들의 집합은 수학자들이 그룹이라고 부르는 것을 만드는 특정한 기술적 특성을 충족시킵니다.이 예에서 그룹은 6개의 원소를 가지고 있기 때문에 순서 6의 이면체 그룹으로 알려져 있습니다.일반 그룹은 많은 대칭 또는 무한히 많은 대칭을 설명할 수 있습니다. 만약 대칭이 매우 많다면, 유한 [104]그룹이라고 불립니다.

수학자들은 종종 특정 유형의 모든 수학적 대상을 분류하기 위해 노력한다.일반적으로 유한 집단은 유용한 분류를 인정하기에는 너무 다양하다고 여겨진다.더 평범하지만 여전히 어려운 문제는 모든 유한 단순 그룹을 분류하는 것입니다.이들은 소수가 [f]곱을 취함으로써 임의의 정수를 구성하기 위해 사용될 수 있는 것과 같은 방식으로 임의의 유한 그룹을 구성하기 위한 구성 요소로 사용될 수 있는 유한 그룹이다.현대 그룹 이론의 주요 업적 중 하나는 가능한 모든 유한 단순 [104]그룹의 목록을 제공하는 수학적 정리인 유한 단순 그룹의 분류이다.

이 분류정리는 여러 그룹의 무한 패밀리뿐만 아니라 어떤 패밀리에도 맞지 않는 26개의 추가 그룹을 식별합니다.후자의 그룹은 "스포라딕" 그룹이라고 불리며, 각각의 그룹은 상황의 놀라운 조합에 의해 존재하게 됩니다.가장 큰 산발적인 그룹인 괴물 그룹은 지구상의 원자의 천 [105]배 이상인 10개 이상의53 원소를 가지고 있다.

복소 평면의 j-함수 그래프

겉으로 보기에 무관한 구성은 수 이론의 j-함수이다.이 오브젝트는 모듈러 함수라고 불리는 특별한 클래스의 함수에 속하며 그래프는 특정 종류의 반복 [106]패턴을 형성합니다.비록 이 함수는 유한군의 이론과 매우 다르게 보이는 수학의 한 분야에서 나타나지만, 두 과목은 밀접하게 연관되어 있는 것으로 드러난다.1970년대 후반, 수학자 존 맥케이와 존 톰슨은 괴물군의 분석에서 발생하는 특정 수([107]즉, 축소할 수 없는 표현들의 차원)가 j-함수의 공식에 나타나는 숫자와 관련이 있다는 것을 알아챘다.이 관계는 존 호튼 콘웨이와 사이먼[108] 노튼에 의해 더욱 발전되었는데,[109] 그는 이 문샤인을 괴물 같은 문샤인이라고 불렀다.

1992년, 리처드 보처스는 모듈러 함수의 이론과 유한군 사이의 가교를 건설했고, 그 과정에서 맥케이와 [110][111]톰슨의 관찰을 설명했다.보르체르스의 작품은 끈 [112]이론의 특정 버전의[which?] 대칭으로 괴물 집단을 깨달은 이고르 프렌켈, 제임스 레포스키, 그리고 아르네 뫼르만의 초기 결과를 확장하면서, 끈 이론의 아이디어를 본질적인 방법으로 사용했습니다.1998년, Borcherds는 그의 [113]업적으로 Fields 상을 받았다.

1990년대 이후, 끈 이론과 문샤인 사이의 연관성은 수학과 [105]물리학에 더 많은 결과를 가져왔다.2010년, 물리학자 에구치 토루, 우구리 히로시, 다치카와 유지는 다른 산발적인 그룹인 마티외 그룹24 M과 특정 버전의[which?] 끈 [114]이론 사이의 연관성을 발견했다.미란다 청, 존 던컨, 제프리 A. 하비는 추골 문샤인이라고 불리는 이 문샤인 [115]현상의 일반화를 제안했고, 그들의 추측은 던컨, 마이클 그리핀, 켄 [116]오노에 의해 수학적으로 증명되었다.위튼은 또한 거대한 달빛에 나타나는 끈 이론의 버전이 3개의 [117]시공간 차원으로 이루어진 특정한 단순화된 중력 모델과 관련이 있을 것이라고 추측했다.

★★★

주요 기사:끈 이론의 역사

★★★★★

끈이론에 의해 재도입된 구조들 중 일부는 알버트 아인슈타인에 의해 시작된 고전적 통일 프로그램의 일부로 훨씬 더 일찍 생겨났다.중력 이론에 5차원을 추가한 최초의 사람은 1914년 군나르 노르드스트롬으로, 그는 5차원의 중력이 4차원의 중력과 전자기학을 모두 설명한다고 언급했다.노드스트롬은 그의 중력 이론과 전자기학을 통합하려고 시도했지만 1919년 아인슈타인의 일반 상대성 이론으로 대체되었다.그 후, 독일 수학자 테오도르 칼루자는 5차원을 일반 상대성 이론과 결합했고, 칼루자만이 이 아이디어를 가지고 있다고 여겨진다.1926년 스웨덴의 물리학자 오스카 클라인은 관찰할 수 없는 추가 차원에 대한 물리적 해석을 내렸습니다. 즉, 작은 원 모양으로 감겨져 있습니다.아인슈타인은 비대칭 메트릭 텐서를 도입했고, 훨씬 후에 브랜스와 디케는 중력에 스칼라 성분을 추가했다.이러한 생각들은 끈 이론 안에서 부활할 것이며, 끈 이론에서는 일관성 조건에 의해 요구될 것이다.

끈 이론은 원래 강한 상호작용을 느끼는 양성자와 중성자와 같은 아원자 입자인 강입자의 완벽한 이론으로 1960년대 후반과 1970년대 초에 개발되었다.1960년대에, 제프리 츄와 스티븐 프라우츠키는 중간자가 회전하는 현으로부터 기대되는 관계로 나중에 요이치로 난부, 홀거 벡 닐슨, 레너드 서스킨드에 의해 이해된 방식으로 스핀과 관련된 질량을 가진 레게 궤적이라고 불리는 가족을 만든다는 것을 발견했다.Chuge는 기본 입자로 구성된다고 가정하지 않고 S-행렬의 자기 일관성 조건으로부터 그들의 상호작용을 구성하는 이러한 궤도의 상호작용에 대한 이론을 만들 것을 주장했습니다.S 매트릭스 접근방식은 1940년대에 Werner Heisenberg에 의해 시작되었는데, 하이젠베르크는 핵 규모에서 분해된다고 믿었던 공간과 시간의 국지적 개념에 의존하지 않는 이론을 구성하기 위한 방법이었다.저울이 여러 차례 어긋났지만, 그가 주장한 접근법은 양자 중력 이론에 이상적으로 적합했다.

실험 데이터 R. Dolen, D.경적과 C.Schmid는 하드론 교환에 대한 몇 가지 합계 규칙을 개발했습니다.입자와 반입자가 흩어질 때 가상 입자는 두 가지 질적으로 서로 다른 방식으로 교환될 수 있습니다.s채널에서는 2개의 입자가 소멸되어 최종 상태 입자로 분해되는 일시적인 중간 상태가 됩니다.T채널에서 입자는 방출과 흡수에 의해 중간상태를 교환한다.필드 이론에서, 두 가지 기여는 함께 추가되는데, 하나는 지속적인 배경 기여이고 다른 하나는 특정 에너지에서 피크를 제공합니다.데이터에서, 피크가 백그라운드에서 훔치고 있는 것이 분명했습니다. 저자들은 이것을 전체 진폭을 설명하고 다른 진폭을 포함하는 것을 의미하는 t 채널의 기여가 s 채널의 기여에 대해 이중적이라고 해석했습니다.

결과는 Murray Gell-Mann에 의해 널리 홍보되었고, Gabriel Veneziano는 Dolen-특성의 산란 진폭을 구성하도록 이끌었다.Horn-Schmid 이중성(나중에 World-Sheet Duality로 개명).입자가 직선 궤적으로 나타나는 곳에 극이 필요하고, 그 극이 실제 선의 절반에 균등하게 배치된 특별한 수학 함수(감마 함수)가 있는데, 이는 레지 이론에서 널리 사용되었다.감마 함수의 조합을 조작함으로써 베네치아는 거의 양의 잔류물이 있는 직선의 극과 일관된 산란 진폭을 찾을 수 있었고, 이는 이중성을 따르고 높은 에너지에서 적절한 레지 스케일링을 가지고 있었다.진폭은 근빔 산란 데이터뿐만 아니라 다른 Regge 유형 적합치에도 적합할 수 있으며 일반화에 사용할 수 있는 암시적 적분 표현을 가지고 있다.

이후 몇 년 동안 수백 명의 물리학자들이 이 모델의 부트스트랩 프로그램을 완성하기 위해 노력했지만 많은 놀라운 결과를 낳았다.베네치아노 자신은 이론에서 나타난 입자의 산란을 설명하는 산란 진폭을 발견했는데, 이는 명백한 자기 일관성 조건이며, 가장 가벼운 입자는 타키온이어야 한다는 것을 알아냈다.Miguel Virasoro와 Joel Shapiro는 현재 닫힌 현의 진폭으로 알려진 다른 진폭을 발견했고, Ziro Koba와 Holger Nielsen은 베네치아의 필수적인 표현을 다중 입자 산란으로 일반화했습니다.베네치아노와 세르히오 푸비니는 세계 시트 컨포멀 이론의 선구자였던 산란 진폭 계산을 위한 연산자 형식을 도입했고, 비라소로는 상태에 대한 제약을 사용하여 잘못된 부호 잔류물로 극을 제거하는 방법을 이해했다.Claud Lovelace는 루프 진폭을 계산했고, 이론의 차원이 26이 아니면 불일치가 있다고 언급했다.찰스 손, 피터 고다드, 리처드 브라우어는 26 이하의 차원으로 잘못된 부호를 전파하는 주가 없다는 것을 증명했다.

1969-70년에 난부 요이치로, 닐슨 홀거, 서스킨드는 이 이론을 끈의 관점에서 시공간으로 설명할 수 있다는 것을 인정했다.산란 진폭은 피터 고다드, 제프리 골드스톤, 클라우디오 레비, 찰스 손의 작용 원리에서 체계적으로 도출되었으며, 베네치아노와 푸비니에 의해 도입된 정점 연산자에 시공간 그림을 제공하고 비라소로 조건에 대한 기하학적 해석을 제공한다.

1971년, 피에르 라몽은 이 모델에 페르미온을 추가했고, 이로 인해 그는 잘못된 부호 상태를 상쇄하기 위해 2차원 초대칭 구조를 공식화했다.존 슈바르츠와 안드레 네베우는 잠시 후 페르미 이론에 또 다른 분야를 추가했다.페르미온 이론에서 임계 차원은 10이었다.스탠리 만델스탐은 보즈와 페르미 케이스 모두에 대해 세계 시트 컨포멀 이론을 공식화했고, 연산자 형식주의를 생성하기 위해 2차원 필드 이론 경로 적분을 제공했습니다.미치오 카쿠와 기카와 게이지 등은 현의 장 이론으로서 무한히 많은 입자형과 장에 포인트가 아닌 루프와 곡선의 값을 취하는 등 서로 다른 형태의 보손 현을 표현했다.

1974년, 타미아키 요네아는 알려진 모든 끈 이론이 중력자가 되기 위해 올바른 워드 정체성에 따르는 질량 없는 스핀 2 입자를 포함하고 있다는 것을 발견했다.존 슈워츠와 조엘 셰르크는 같은 결론에 도달했고 끈 이론은 강입자 이론이 아니라 중력 이론이라고 주장하기 위해 대담하게 도약했다.그들은 추가 차원을 이해하기 위한 방법으로 칼루자-클레인 이론을 재도입했다.동시에 양자 색역학은 강입자의 올바른 이론으로 인식되어 물리학자들의 관심을 옮기고 부트스트랩 프로그램을 역사의 휴지통에 남겨둔 것으로 보인다.

끈 이론은 결국 쓰레기통에서 나왔지만, 그 이후 10년 동안, 그 이론에 대한 모든 작업은 완전히 무시되었다.그럼에도 불구하고, 그 이론은 소수의 헌신자들의 노력 덕분에 꾸준한 속도로 발전했다.페르디난도 글리오지, 조엘 셰르크, 그리고 데이비드 올리브는 1977년에 원래의 라몬드와 네브 슈바르츠 스트링이 따로따로 일관성이 없고 결합될 필요가 있다는 것을 깨달았다.결과 이론은 타키온을 가지지 않았고 1984년 존 슈워츠와 마이클 그린에 의해 시공간 초대칭성이 있다는 것이 증명되었다.같은 해, 알렉산더 폴랴코프는 이 이론에 현대 경로 적분 공식을 주었고, 등각장 이론을 광범위하게 발전시켰다.1979년 다니엘 프리단은 아인슈타인 일반상대성이론 방정식의 일반화인 끈이론의 운동 방정식이 2차원 장론의 정규화 군 방정식에서 나온다는 것을 보여주었다.슈바르츠와 그린은 T-이중성을 발견하고 두 개의 초끈 이론을 구축했다.IIA 및 IIB는 T-duality에 의해 관련지어지며 타입 I 이론에는 오픈 스트링이 있습니다.일관성 조건은 매우 강했기 때문에, 이론 전체가 거의 유일하게 결정되어 몇 가지 개별적인 선택만이 가능했습니다.

번째 슈퍼스트링 1번

1980년대 초, 에드워드 위튼은 양자 중력의 대부분의 이론이 중성미자와 같은 키랄 페르미온을 수용할 수 없다는 것을 발견했다.이것은 루이스 알바레즈-가우메와 협력하여, I형 끈 이론이 일관성이 없다고 결론짓고, 중력 이론에서 보존 법칙의 위반을 연구하도록 이끌었습니다.그린과 슈바르츠는 비튼과 알바레즈-가우메가 놓쳤던 이상 현상에 대한 기여도를 발견했고, 이로 인해 제1형 끈 이론의 게이지군이 SO(32)로 제한되었다.이 계산을 이해하면서 에드워드 위튼은 끈 이론이 정말로 일관된 중력 이론이라고 확신하게 되었고, 그는 세간의 이목을 끄는 지지자가 되었다.1984년부터 1986년 사이에 수백 명의 물리학자들이 이 분야에서 일하기 시작했고, 이것은 때때로 최초의 슈퍼스트링 [citation needed]혁명으로 불린다.

이 기간 동안 데이비드 그로스, 제프리 하비, 에밀 마르티넥, 라이언 롬은 이질적인 끈을 발견했다.이러한 닫힌 문자열의 게이지 그룹은 E8의 두 복사본이었고, 두 복사본 모두 쉽고 자연스럽게 표준 모델을 포함할 수 있었습니다.필립 칸델라스, 게리 호로위츠, 앤드류 스트로밍거, 에드워드 위튼은 칼라비 가문이...야우 다양체는 초대칭성의 현실적인 양을 보존하는 콤팩트화이며, 랜스 딕슨과 다른 사람들은 끈 이론에서 허용되는 독특한 기하학적 특이점인 오비폴드의 물리적 특성을 알아냈다.Cumrun Vafa는 원에서 임의의 다양체로 T-이중성을 일반화하여 거울 대칭의 수학적 분야를 만들었습니다.다니엘 프리단, 에밀 마르티네크, 스티븐 셴커는 등각장 이론 기법을 사용하여 초끈의 공변 양자화를 더욱 발전시켰다.David Gross와 Vipul Periwal은 끈 섭동 이론이 서로 다르다는 것을 발견했다.스티븐 셴커는 그것이 필드 이론보다 훨씬 더 빨리 분화한다는 것을 보여주었고 새로운 비교란성 물체가 [citation needed]사라졌다는 것을 암시했다.

1990년대에, 조셉 폴친스키는 이 이론이 D-브레인이라고 불리는 고차원적인 물체를 필요로 한다는 것을 발견하고 초중력의 블랙홀 해법으로 그것들을 확인하였다.이것들은 섭동적 분산에 의해 제시된 새로운 개체로 이해되었고, 풍부한 수학적 구조를 가진 새로운 분야를 열었다.끈이 아닌 D-브랜과 다른 p-브랜이 끈 이론의 물질 내용을 형성한다는 것이 금방 밝혀졌고, 끈과 나뭇가지에 대한 물리적 해석은 블랙홀의 일종이라는 것이 밝혀졌다.Leonard Suskind는 Gerardus 't Hooft의 홀로그래픽 원리를 끈 이론에 접목시켜 오랫동안 매우 흥분된 끈 상태를 일반적인 열 블랙홀 상태와 동일시했다.'t Hooft'가 시사한 바와 같이, 블랙홀 지평선, 즉 세계 부피 이론의 변동은 블랙홀의 자유도뿐만 아니라 근처의 모든 물체도 묘사합니다.

번째 슈퍼스트링 2차 슈퍼스트링 혁명

1995년 남캘리포니아대학(USC)에서 열린 끈이론자 연례회의에서 에드워드 위튼은 끈이론에 대한 연설을 통해 당시 존재했던 5가지 끈이론을 통합하고 M-이론이라는 새로운 11차원 이론을 탄생시켰다.M이론은 또한 대략 같은 시기에 폴 타운센드의 작품에서 전조였다.이 시기에 시작된 일련의 활동은 때때로 제2의 슈퍼스트링 [31]혁명으로 불린다.

이 기간 동안 톰 뱅크스, 윌리 피슐러, 스티븐 셴커, 레너드 서스킨드는 IIA D0 브랜들을 [48]이용한 M 이론의 완전한 홀로그래픽 기술인 매트릭스 이론을 공식화했다.이것은 홀로그래픽 원리의 완전한 비교란적이고 구체적인 수학적 실현을 위한 끈 이론의 첫 번째 정의였다.이것은 게이지-중력 이중성의 한 예이며, 현재는 AdS/CFT 대응의 특수한 경우로 이해되고 있습니다.Andrew Strominger와 Cumrun Vafa는 D-브랜의 특정 구성의 엔트로피를 계산하여 극단적으로 대전된 [59]블랙홀에 대한 반고전적 해답과 일치함을 발견했다.페트르 호차바와 위튼은 오르비폴드가 키랄리티 문제를 해결한다는 것을 보여주면서 이질적인 끈 이론의 11차원 공식을 발견했다.위튼은 낮은 에너지에서 D-브랜의 물리학을 효과적으로 기술하는 것은 초대칭 게이지 이론에 의한 것이라고 언급했고, 그와 네이선 세이버그가 일찍이 나뭇가지 위치 측면에서 발견한 게이지 이론에서 수학적 구조의 기하학적 해석을 발견했다.

1997년, 후안 말다세나는 블랙홀 근처의 이론의 낮은 에너지 들뜸은 지평선에 가까운 물체들로 구성되어 있으며, 극단적으로 충전된 블랙홀은 반 드 시터 [68]공간처럼 보인다고 언급했다.그는 이 한계에서 게이지 이론은 지느러미 근처의 끈 들뜸을 설명한다는 점에 주목했다.그래서 그는 반드 시터 공간에 플럭스를 곱한 거의 극한의 하전 블랙홀 기하학에 대한 끈 이론이 저에너지 한계 게이지 이론인 N = 4 초대칭 양-밀스 이론으로 똑같이 잘 설명된다는 가설을 세웠다.AdS/CFT 대응이라고 불리는 이 가설은 스티븐 굽서, 이고르 클레바노프,[69] 알렉산더 폴랴코프와 에드워드 [70]비튼에 의해 더욱 발전되어 현재는 잘 받아들여지고 있다.홀로그래픽 원리의 구체적인 실현으로 블랙홀, 위치, 물리정보, 중력 상호작용의 [53]성질을 폭넓게 내포하고 있다.이 관계를 통해 끈 이론은 양자 색역학 같은 게이지 이론과 관련이 있다는 것을 보여주었고, 이것은 강입자의 거동에 대한 보다 양적인 이해를 이끌어 내면서 끈 이론을 그 [citation needed]뿌리로 되돌렸다.

★★

수 루루수수

주요 기사:끈 이론 풍경

끈 이론에 기초한 입자 물리학의 모델을 만들기 위해, 물리학자들은 일반적으로 시공간의 추가 차원에 대한 형태를 지정하는 것으로 시작합니다.각각의 다른 모양은 다른 입자 집합과 힘을 가진 다른 가능한 우주, 즉 "진공 상태"에 해당합니다.현재 이해되고 있는 끈 이론은 일반적으로 10개 정도로500 추정되는 엄청난 수의 진공 상태를 가지고 있으며, 이것들은 낮은 [118]에너지에서 관찰될 수 있는 거의 모든 현상을 수용할 수 있을 만큼 충분히 다양할 수 있다.

끈이론에 대한 많은 비평가들은 끈이론에 의해 묘사되는 많은 가능한 우주들에 대해 우려를 표명해왔다.그의 저서 Not Even Wrong에서, 콜롬비아 대학의 수학과 강사 Peter Woit는 많은 다른 물리 시나리오들이 입자 물리학의 모델을 구성하기 위한 프레임워크로서 끈 이론을 공허하게 만든다고 주장해왔다.Woit에 따르면

예를 들어, 슈퍼스트링 이론을 위한 10개의500 일관된 진공 상태의 존재는 아마도 그 이론을 어떤 것을 예측하기 위해 사용할 수 있는 희망을 파괴할 것이다.이 큰 집합 중에서 특성이 현재의 실험 관측과 일치하는 상태만 선택한다면, 여전히 이러한 상태가 너무 많아 새로운 [119]관측 결과에 대해 원하는 값을 얻을 수 있습니다.

일부 물리학자들은 이 많은 양의 해법이 실제로 미덕이라고 믿는다. 왜냐하면 그것은 물리 상수의 관측된 값, 특히 우주 [119]상수의 작은 값에 대한 자연스러운 인간적인 설명을 가능하게 할 수 있기 때문이다.인류학적 원리는 물리 법칙에 나타나는 숫자의 일부는 어떤 기본 원리에 의해서 고정된 것이 아니라 지적 생명체의 진화와 양립할 수 있어야 한다는 것이다.1987년, 스티븐 와인버그는 우주 상수가 너무 크지 않았다면 은하와 지적 생명체가 [120]발달할 수 없었을 것이라고 주장한 기사를 발표했다.와인버그는 각각 다른 우주 상수의 값을 가진, 엄청나게 많은 가능한 일관된 우주가 있을 수 있다고 제안했고, 관측 결과들은 인간이 지적인 생명체와 따라서 관찰자들이 [121]존재할 수 있게 해준 우주에 살게 되었기 때문에 우주 상수의 작은 값을 나타낸다.

끈 이론가 레오나드 서스킨드는 끈 이론이 우주 [122]상수의 작은 가치에 대한 자연스러운 인류학적 설명을 제공한다고 주장했습니다.서스킨드에 따르면 끈 이론의 다른 진공 상태는 더 큰 다중 우주 안에서 다른 우주들로 실현될 수 있다.관측된 우주가 작은 우주 상수를 가지고 있다는 사실은 생명체가 [123]존재하기 위해 작은 값이 필요하다는 사실의 반복적인 결과일 뿐이다.많은 저명한 이론가들과 비평가들은 서스킨드의 [124]결론에 동의하지 않았다.Woit에 따르면, "이 경우 [인류적 추리]는 실패의 변명에 지나지 않는다.추측적 과학 아이디어는 잘못된 예측을 할 뿐만 아니라 공허하고 아무것도 [125]예측할 수 없는 것으로 판명될 때도 실패한다.

에너지와의

끈 이론이 준안정적이고 양의 우주 상수와 양립할 수 있는지는 알려지지 않았다.2003년 [126]카흐루 등이 기술한 모델과 같이 그러한 솔루션의 추정적인 예가 존재한다.2018년, 네 명의 물리학자로 구성된 그룹이 그러한 우주가 존재하지 않는다는 것을 암시하는 논란의 여지가 있는 추측을 내놓았다.이는 양의 진공 에너지를 필요로 하는 δ-CDM과 같은 일부 인기 있는 암흑 에너지 모델과 반대된다.그러나 끈 이론은 암흑 에너지가 이국적인 [127]성질을 가진 새로운 분야에 의해 야기되는 특정 유형의 5진수와 양립할 수 있을 것이다.

주요 기사: 배경 독립성

아인슈타인의 일반 상대성 이론의 기본적인 특성 중 하나는 그것이 배경 독립적이라는 것이고, 이것은 이론의 공식화가 어떤 식으로든 특정한 시공간 기하학에 [128]특권을 부여하지 않는다는 것을 의미합니다.

초기부터 끈이론에 대한 주요 비판 중 하나는 명백하게 배경 독립적이지 않다는 것이다.끈 이론에서는 일반적으로 시공간에서 고정된 기준 기하학을 지정해야 하며, 다른 모든 가능한 기하학은 이 고정된 기하학의 섭동으로 설명됩니다.주변 이론 물리 연구소의 물리학자 리 스몰린은 그의 책 "물리학의 문제"에서, 끈 이론이 일반 상대성 [129]이론으로부터 이 중요한 통찰력을 통합하는데 실패했다고 말하면서, 이것이 양자 중력의 이론으로서 끈 이론의 주요 약점이라고 주장한다.

다른 사람들은 스몰린의 끈 이론의 특징에 동의하지 않는다.스몰린의 책에 대한 리뷰에서 끈 이론가 조셉 폴친스키는 다음과 같이 쓰고 있다.

[Smolin]은(는) 수학 언어의 한 측면을 기술되는 물리학 중 하나로 착각하고 있습니다.새로운 물리 이론은 종종 가장 적합하지 않은 수학적 언어를 사용하여 발견됩니다.끈 이론에서, 사용되는 언어가 아니더라도 물리학은 배경에 의존하지 않는다는 것은 항상 분명했고, 더 적합한 언어를 찾는 것은 계속되고 있다.실제로 Smolin이 뒤늦게 지적한 바와 같이 [AdS/CFT]는 이 문제에 대한 해결책을 제공합니다.이것은 예기치 않은 강력한 [130]해결책입니다.

폴친스키는 양자 중력의 중요한 미해결 문제는 중력장이 점근적으로 반 드 시터(anti-de Sitter)[130]가 될 필요가 없는 중력에 대한 홀로그래픽 기술을 개발하는 것이라고 지적한다.Smolin은 AdS/CFT의 대응이 현재 이해되고 있는 것처럼 배경 [131]독립성에 대한 모든 우려를 해소하기에 충분치 않을 수 있다고 답변했다.

1980년대와 1990년대의 초끈 혁명 이후, 끈 이론은 고에너지 이론 [132]물리학의 지배적인 패러다임 중 하나가 되어왔다.일부 끈 이론가들은 기초 물리학의 깊은 문제를 다루는 동등하게 성공적인 대안 이론이 존재하지 않는다는 견해를 표명했다.1987년의 인터뷰에서 노벨상 수상자인 데이비드 그로스는 끈 이론의 인기에 대한 이유에 대해 다음과 같은 논란을 불러일으키는 발언을 했다.

가장 중요한 것은 다른 좋은 아이디어가 없다는 것이다.그게 대부분의 사람들이 그것에 빠져들게 하는 이유야.사람들이 끈이론에 관심을 갖기 시작했을 때 그들은 끈이론에 대해 아무것도 몰랐다.사실, 대부분의 사람들의 첫 번째 반응은 이 이론이 극도로 추악하고 불쾌하다는 것이다. 적어도 끈이론에 대한 이해가 훨씬 덜 발달했던 몇 년 전만 해도 그랬다.사람들이 그것에 대해 알고 흥분하는 것은 어려웠다.그래서 사람들이 그것에 매력을 느끼는 진짜 이유는 마을에 다른 게임이 없기 때문이라고 생각합니다.대통합이론을 구축하기 위한 다른 모든 접근법은 실패했지만, 처음에는 더 보수적이었지만 점차 급진적으로 변했습니다. 그리고 이 게임은 [133]아직 실패하지 않았습니다.

몇몇 다른 저명한 이론가들과 논평가들도 끈 이론에 대한 [134]실행 가능한 대안이 없다는 것을 암시하며 비슷한 견해를 표명했다.

끈 이론의 많은 비평가들은 이 상황에 대해 논평해 왔다.피터 보이트는 끈이론을 비판하는 그의 책에서 끈이론 연구의 위상을 건강하지 못하고 기초 물리학의 미래에 해롭다고 본다.이론물리학자들 사이에서 끈이론의 극단적인 인기는 부분적으로 학계의 재정 구조와 치열한 자원 [135]경쟁의 결과라고 그는 주장한다.그의 책 로드 리얼리티 위해 수학 물리학자 로저 펜로즈,"종종 제 정신이 아닌 경쟁력은 의사 소통이 일으키의 이것이 과학자들이 그들이에는 참가하지 않나 뒤처지게 우려하고 있bandwagon 효과로 이끕니다."[136]펜로즈는 또한 현대 물리학의 기술적 어려움을 주장하고 있다고 말하는 비슷한 견해를 표현하고 있다.ces젊은 과학자들은 그들만의 [137]새로운 길을 개척하기 보다는 확립된 연구자들의 선호에 의존해야 한다.리 스몰린은 그의 비평에서 약간 다른 입장을 나타내며 끈 이론은 물리학의 기초에 대한 추측을 방해하는 소립자 물리학의 전통에서 비롯되었으며, 그가 선호하는 접근법인 루프 양자 중력은 보다 급진적인 사고를 장려한다고 주장한다.스몰린에 따르면

끈 이론은 강력하고, 좋은 동기 부여가 된 아이디어이며, 그것에 바쳐진 많은 작업을 할 가치가 있다.만약 그것이 지금까지 실패했다면, 주된 이유는 그것의 본질적인 결함이 그것의 강점과 밀접하게 연관되어 있기 때문이다. 그리고 물론, 끈 이론이 진실의 일부가 될 수 있기 때문에 이야기는 끝나지 않았다.진짜 질문은 우리가 왜 끈 이론에 그렇게 많은 에너지를 소비했느냐가 아니라 왜 우리가 대안적인 [138]접근법에 거의 충분히 소비하지 않았느냐는 것이다.

Smolin은 과학자들이 양자 [139]중력 연구에 대한 더 다양한 접근을 어떻게 장려할 수 있는지에 대한 많은 처방전을 계속해서 제공한다.

  1. ^ 예를 들어, 물리학자들은 여전히 쿼크 구속의 현상, 블랙홀의 역설, 그리고 암흑 에너지의 기원을 이해하기 위해 노력하고 있다.
  2. ^ 예를 들어 AdS/CFT 대응의 맥락에서 이론가들은 종종 비물리적 시공간 차원의 중력 이론을 공식화하고 연구한다.
  3. ^ "Top Cited Articles during 2010 in hep-th". Retrieved 25 July 2013.
  4. ^ 더 정확히는 섭동 양자장론의 방법을 적용할 수 없다.
  5. ^ 기벤탈과[97][98] 리안 외 [99][100][101]연구진은 거울 대칭의 두 가지 독립적인 수학적 증거를 제시했다.
  6. ^ 보다 정확하게는 정규 서브그룹만이 단순한 그룹과 그룹 자체일 경우 중요하지 않은 그룹을 단순이라고 부릅니다.요르단-쾰더 정리는 모든 유한 그룹에 대한 구성 요소로서 유한 단순 그룹을 나타낸다.

레퍼런스

  1. ^ a b Becker, Becker 및 Schwarz, 페이지 1
  2. ^ 츠비바흐, 6페이지
  3. ^ a b Becker, Becker 및 Schwarz, 페이지 2-3
  4. ^ Becker, Becker, and Schwarz,
  5. ^ Becker, Becker 및 Schwarz, 페이지 14-15
  6. ^ a b c Klebanov, Igor; Maldacena, Juan (2009). "Solving Quantum Field Theories via Curved Spacetimes" (PDF). Physics Today. 62 (1): 28–33 [28]. Bibcode:2009PhT....62a..28K. doi:10.1063/1.3074260. Archived from the original (PDF) on July 2, 2013. Retrieved 29 December 2016.
  7. ^ a b c d Merali, Zeeya (2011). "Collaborative physics: string theory finds a bench mate". Nature. 478 (7369): 302–304 [303]. Bibcode:2011Natur.478..302M. doi:10.1038/478302a. PMID 22012369.
  8. ^ a b Sachdev, Subir (2013). "Strange and stringy". Scientific American. 308 (44): 44–51 [51]. Bibcode:2012SciAm.308a..44S. doi:10.1038/scientificamerican0113-44. PMID 23342451.
  9. ^ Becker, Becker 및 Schwarz, 페이지 3, 15-16
  10. ^ Becker, Becker 및 Schwarz, 페이지 8
  11. ^ Becker, Becker 및 Schwarz, 13-14페이지
  12. ^ a b 와이트
  13. ^ a b c Zee, Anthony (2010). "Parts V and VI". Quantum Field Theory in a Nutshell (2nd ed.). Princeton University Press. ISBN 978-0-691-14034-6.
  14. ^ Becker, Becker 및 Schwarz, 페이지 2
  15. ^ a b Becker, Becker 및 Schwarz, 페이지 6
  16. ^ 츠비바흐, 12페이지
  17. ^ Becker, Becker 및 Schwarz, 페이지 4
  18. ^ 츠비바흐, 페이지 324
  19. ^ Wald, 페이지 4
  20. ^ 츠비바흐, 9페이지
  21. ^ 츠비바흐, 8페이지
  22. ^ a b 야우와 나디스, 6장
  23. ^ 야우와 나디스, 페이지 ix
  24. ^ Randall, Lisa; Sundrum, Raman (1999). "An alternative to compactification". Physical Review Letters. 83 (23): 4690–4693. arXiv:hep-th/9906064. Bibcode:1999PhRvL..83.4690R. doi:10.1103/PhysRevLett.83.4690. S2CID 18530420.
  25. ^ a b 베커, 베커, 슈바르츠
  26. ^ 츠비바흐, 376페이지
  27. ^ a b c Moore, Gregory (2005). "What is ... a Brane?" (PDF). Notices of the AMS. 52: 214–215. Retrieved 29 December 2016.
  28. ^ a b c Aspinwall, Paul; Bridgeland, Tom; Craw, Alastair; Douglas, Michael; Gross, Mark; Kapustin, Anton; Moore, Gregory; Segal, Graeme; Szendröi, Balázs; Wilson, P.M.H., eds. (2009). Dirichlet Branes and Mirror Symmetry. Clay Mathematics Monographs. Vol. 4. American Mathematical Society. p. 13. ISBN 978-0-8218-3848-8.
  29. ^ a b Kontsevich, Maxim (1995). Homological Algebra of Mirror Symmetry. Proceedings of the International Congress of Mathematicians. pp. 120–139. arXiv:alg-geom/9411018. Bibcode:1994alg.geom.11018K. doi:10.1007/978-3-0348-9078-6_11. ISBN 978-3-0348-9897-3. S2CID 16733945.
  30. ^ Kapustin, Anton; Witten, Edward (2007). "Electric-magnetic duality and the geometric Langlands program". Communications in Number Theory and Physics. 1 (1): 1–236. arXiv:hep-th/0604151. Bibcode:2007CNTP....1....1K. doi:10.4310/cntp.2007.v1.n1.a1. S2CID 30505126.
  31. ^ a b 더프
  32. ^ 더프, 64페이지
  33. ^ Nahm, Walter (1978). "Supersymmetries and their representations" (PDF). Nuclear Physics B. 135 (1): 149–166. Bibcode:1978NuPhB.135..149N. doi:10.1016/0550-3213(78)90218-3. Archived (PDF) from the original on 2018-07-26. Retrieved 2019-08-25.
  34. ^ Cremmer, Eugene; Julia, Bernard; Scherk, Joël (1978). "Supergravity theory in eleven dimensions". Physics Letters B. 76 (4): 409–412. Bibcode:1978PhLB...76..409C. doi:10.1016/0370-2693(78)90894-8.
  35. ^ a b c d e 더프, 65페이지
  36. ^ Sen, Ashoke (1994). "Strong-weak coupling duality in four-dimensional string theory". International Journal of Modern Physics A. 9 (21): 3707–3750. arXiv:hep-th/9402002. Bibcode:1994IJMPA...9.3707S. doi:10.1142/S0217751X94001497. S2CID 16706816.
  37. ^ Sen, Ashoke (1994). "Dyon-monopole bound states, self-dual harmonic forms on the multi-monopole moduli space, and SL(2,Z) invariance in string theory". Physics Letters B. 329 (2): 217–221. arXiv:hep-th/9402032. Bibcode:1994PhLB..329..217S. doi:10.1016/0370-2693(94)90763-3. S2CID 17534677.
  38. ^ Hull, Chris; Townsend, Paul (1995). "Unity of superstring dualities". Nuclear Physics B. 4381 (1): 109–137. arXiv:hep-th/9410167. Bibcode:1995NuPhB.438..109H. doi:10.1016/0550-3213(94)00559-W. S2CID 13889163.
  39. ^ 더프, 67페이지
  40. ^ Bergshoeff, Eric; Sezgin, Ergin; Townsend, Paul (1987). "Supermembranes and eleven-dimensional supergravity" (PDF). Physics Letters B. 189 (1): 75–78. Bibcode:1987PhLB..189...75B. doi:10.1016/0370-2693(87)91272-X. Archived (PDF) from the original on 2020-11-15. Retrieved 2019-08-25.
  41. ^ Duff, Michael; Howe, Paul; Inami, Takeo; Stelle, Kellogg (1987). "Superstrings in D=10 from supermembranes in D=11" (PDF). Nuclear Physics B. 191 (1): 70–74. Bibcode:1987PhLB..191...70D. doi:10.1016/0370-2693(87)91323-2. Archived (PDF) from the original on 2020-11-15. Retrieved 2019-08-25.
  42. ^ 더프, 페이지 66
  43. ^ Witten, Edward (1995). "String theory dynamics in various dimensions". Nuclear Physics B. 443 (1): 85–126. arXiv:hep-th/9503124. Bibcode:1995NuPhB.443...85W. doi:10.1016/0550-3213(95)00158-O. S2CID 16790997.
  44. ^ 더프, 67~68페이지
  45. ^ Becker, Becker 및 Schwarz, 페이지 296
  46. ^ Hořava, Petr; Witten, Edward (1996). "Heterotic and Type I string dynamics from eleven dimensions". Nuclear Physics B. 460 (3): 506–524. arXiv:hep-th/9510209. Bibcode:1996NuPhB.460..506H. doi:10.1016/0550-3213(95)00621-4. S2CID 17028835.
  47. ^ Duff, Michael (1996). "M-theory (the theory formerly known as strings)". International Journal of Modern Physics A. 11 (32): 6523–41 (Sec. 1). arXiv:hep-th/9608117. Bibcode:1996IJMPA..11.5623D. doi:10.1142/S0217751X96002583. S2CID 17432791.
  48. ^ a b c Banks, Tom; Fischler, Willy; Schenker, Stephen; Susskind, Leonard (1997). "M theory as a matrix model: A conjecture". Physical Review D. 55 (8): 5112–5128. arXiv:hep-th/9610043. Bibcode:1997PhRvD..55.5112B. doi:10.1103/physrevd.55.5112. S2CID 13073785.
  49. ^ Connes, Alain (1994). Noncommutative Geometry. Academic Press. ISBN 978-0-12-185860-5.
  50. ^ Connes, Alain; Douglas, Michael; Schwarz, Albert (1998). "Noncommutative geometry and matrix theory". Journal of High Energy Physics. 19981 (2): 003. arXiv:hep-th/9711162. Bibcode:1998JHEP...02..003C. doi:10.1088/1126-6708/1998/02/003. S2CID 7562354.
  51. ^ Nekrasov, Nikita; Schwarz, Albert (1998). "Instantons on noncommutative R4 and (2,0) superconformal six dimensional theory". Communications in Mathematical Physics. 198 (3): 689–703. arXiv:hep-th/9802068. Bibcode:1998CMaPh.198..689N. doi:10.1007/s002200050490. S2CID 14125789.
  52. ^ Seiberg, Nathan; Witten, Edward (1999). "String Theory and Noncommutative Geometry". Journal of High Energy Physics. 1999 (9): 032. arXiv:hep-th/9908142. Bibcode:1999JHEP...09..032S. doi:10.1088/1126-6708/1999/09/032. S2CID 668885.
  53. ^ a b c de Haro, Sebastian; Dieks, Dennis; 't Hooft, Gerard; Verlinde, Erik (2013). "Forty Years of String Theory Reflecting on the Foundations". Foundations of Physics. 43 (1): 1–7 [2]. Bibcode:2013FoPh...43....1D. doi:10.1007/s10701-012-9691-3.
  54. ^ 야우와 나디스, 페이지 187–188
  55. ^ Bekenstein, Jacob (1973). "Black holes and entropy". Physical Review D. 7 (8): 2333–2346. Bibcode:1973PhRvD...7.2333B. doi:10.1103/PhysRevD.7.2333.
  56. ^ a b Hawking, Stephen (1975). "Particle creation by black holes". Communications in Mathematical Physics. 43 (3): 199–220. Bibcode:1975CMaPh..43..199H. doi:10.1007/BF02345020. S2CID 55539246.
  57. ^ Wald, 페이지 417
  58. ^ 야우와 나디스, 189페이지
  59. ^ a b Strominger, Andrew; Vafa, Cumrun (1996). "Microscopic origin of the Bekenstein–Hawking entropy". Physics Letters B. 379 (1): 99–104. arXiv:hep-th/9601029. Bibcode:1996PhLB..379...99S. doi:10.1016/0370-2693(96)00345-0. S2CID 1041890.
  60. ^ 야우와 나디스, 190-192페이지
  61. ^ Maldacena, Juan; Strominger, Andrew; Witten, Edward (1997). "Black hole entropy in M-theory". Journal of High Energy Physics. 1997 (12): 002. arXiv:hep-th/9711053. Bibcode:1997JHEP...12..002M. doi:10.1088/1126-6708/1997/12/002. S2CID 14980680.
  62. ^ Ooguri, Hirosi; Strominger, Andrew; Vafa, Cumrun (2004). "Black hole attractors and the topological string". Physical Review D. 70 (10): 106007. arXiv:hep-th/0405146. Bibcode:2004PhRvD..70j6007O. doi:10.1103/physrevd.70.106007. S2CID 6289773.
  63. ^ 야우와 나디스, 192~193페이지
  64. ^ 야우와 나디스, 194-195페이지
  65. ^ Strominger, Andrew (1998). "Black hole entropy from near-horizon microstates". Journal of High Energy Physics. 1998 (2): 009. arXiv:hep-th/9712251. Bibcode:1998JHEP...02..009S. doi:10.1088/1126-6708/1998/02/009. S2CID 2044281.
  66. ^ Guica, Monica; Hartman, Thomas; Song, Wei; Strominger, Andrew (2009). "The Kerr/CFT Correspondence". Physical Review D. 80 (12): 124008. arXiv:0809.4266. Bibcode:2009PhRvD..80l4008G. doi:10.1103/PhysRevD.80.124008. S2CID 15010088.
  67. ^ Castro, Alejandra; Maloney, Alexander; Strominger, Andrew (2010). "Hidden conformal symmetry of the Kerr black hole". Physical Review D. 82 (2): 024008. arXiv:1004.0996. Bibcode:2010PhRvD..82b4008C. doi:10.1103/PhysRevD.82.024008. S2CID 118600898.
  68. ^ a b Maldacena, Juan (1998). "The Large N limit of superconformal field theories and supergravity". Advances in Theoretical and Mathematical Physics. 2: 231–252. arXiv:hep-th/9711200. Bibcode:1998AdTMP...2..231M. doi:10.4310/ATMP.1998.V2.N2.A1.
  69. ^ a b Gubser, Steven; Klebanov, Igor; Polyakov, Alexander (1998). "Gauge theory correlators from non-critical string theory". Physics Letters B. 428 (1–2): 105–114. arXiv:hep-th/9802109. Bibcode:1998PhLB..428..105G. doi:10.1016/S0370-2693(98)00377-3. S2CID 15693064.
  70. ^ a b Witten, Edward (1998). "Anti-de Sitter space and holography". Advances in Theoretical and Mathematical Physics. 2 (2): 253–291. arXiv:hep-th/9802150. Bibcode:1998AdTMP...2..253W. doi:10.4310/ATMP.1998.v2.n2.a2. S2CID 10882387.
  71. ^ a b c 말라세나 2005, 페이지 60
  72. ^ a b 말라세나 2005, 페이지 61
  73. ^ 츠비바흐, 552페이지
  74. ^ 말라세나 2005, 61~62페이지
  75. ^ Susskind, Leonard (2008). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company. ISBN 978-0-316-01641-4.
  76. ^ 츠비바흐, 554페이지
  77. ^ 말라세나 2005, 페이지 63
  78. ^ Hawking, Stephen (2005). "Information loss in black holes". Physical Review D. 72 (8): 084013. arXiv:hep-th/0507171. Bibcode:2005PhRvD..72h4013H. doi:10.1103/PhysRevD.72.084013. S2CID 118893360.
  79. ^ 츠비바흐, 559페이지
  80. ^ Kovtun, P. K.; Son, Dam T.; Starinets, A. O. (2005). "Viscosity in strongly interacting quantum field theories from black hole physics". Physical Review Letters. 94 (11): 111601. arXiv:hep-th/0405231. Bibcode:2005PhRvL..94k1601K. doi:10.1103/PhysRevLett.94.111601. PMID 15903845. S2CID 119476733.
  81. ^ Luzum, Matthew; Romatschke, Paul (2008). "Conformal relativistic viscous hydrodynamics: Applications to RHIC results at √sNN=200 GeV". Physical Review C. 78 (3): 034915. arXiv:0804.4015. Bibcode:2008PhRvC..78c4915L. doi:10.1103/PhysRevC.78.034915.
  82. ^ Candelas, Philip; Horowitz, Gary; Strominger, Andrew; Witten, Edward (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.
  83. ^ 야우와 나디스, 페이지 147-150
  84. ^ 베커, 베커, 슈바르츠, 530-531페이지
  85. ^ 베커, 베커, 슈바르츠, 페이지 531
  86. ^ Becker, Becker, and Schwarz,
  87. ^ Becker, Becker and Schwarz, 533페이지
  88. ^ 베커, 베커, 슈바르츠, 539–543페이지
  89. ^ Deligne, Pierre; Etingof, Pavel; Freed, Daniel; Jeffery, Lisa; Kazhdan, David; Morgan, John; Morrison, David; Witten, Edward, eds. (1999). Quantum Fields and Strings: A Course for Mathematicians. Vol. 1. American Mathematical Society. p. 1. ISBN 978-0821820124.
  90. ^ 호리, 페이지 17
  91. ^ 호리
  92. ^ 야우와 나디스, 페이지 167
  93. ^ 야우와 나디스, 페이지 166
  94. ^ a b 야우와 나디스, 페이지 169
  95. ^ Candelas, Philip; de la Ossa, Xenia; Green, Paul; Parks, Linda (1991). "A pair of Calabi–Yau manifolds as an exactly soluble superconformal field theory". Nuclear Physics B. 359 (1): 21–74. Bibcode:1991NuPhB.359...21C. doi:10.1016/0550-3213(91)90292-6.
  96. ^ 야우와 나디스, 페이지 171
  97. ^ Givental, Alexander (1996). "Equivariant Gromov-Witten invariants". International Mathematics Research Notices. 1996 (13): 613–663. doi:10.1155/S1073792896000414. S2CID 554844.
  98. ^ Givental, Alexander (1998). A mirror theorem for toric complete intersections. Topological Field Theory, Primitive Forms and Related Topics. pp. 141–175. arXiv:alg-geom/9701016v2. doi:10.1007/978-1-4612-0705-4_5. ISBN 978-1-4612-6874-1. S2CID 2884104.
  99. ^ Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1997). "Mirror principle, I". Asian Journal of Mathematics. 1 (4): 729–763. arXiv:alg-geom/9712011. Bibcode:1997alg.geom.12011L. doi:10.4310/ajm.1997.v1.n4.a5. S2CID 8035522.
  100. ^ Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999a). "Mirror principle, II". Asian Journal of Mathematics. 3: 109–146. arXiv:math/9905006. Bibcode:1999math......5006L. doi:10.4310/ajm.1999.v3.n1.a6. S2CID 17837291.
    Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999b). "Mirror principle, III". Asian Journal of Mathematics. 3 (4): 771–800. arXiv:math/9912038. Bibcode:1999math.....12038L. doi:10.4310/ajm.1999.v3.n4.a4.
  101. ^ Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (2000). "Mirror principle, IV". Surveys in Differential Geometry. 7: 475–496. arXiv:math/0007104. Bibcode:2000math......7104L. doi:10.4310/sdg.2002.v7.n1.a15. S2CID 1099024.
  102. ^ 호리, 페이지 xix
  103. ^ Strominger, Andrew; Yau, Shing-Tung; Zaslow, Eric (1996). "Mirror symmetry is T-duality". Nuclear Physics B. 479 (1): 243–259. arXiv:hep-th/9606040. Bibcode:1996NuPhB.479..243S. doi:10.1016/0550-3213(96)00434-8. S2CID 14586676.
  104. ^ a b Dummit, David; Foote, Richard (2004). Abstract Algebra. Wiley. pp. 102–103. ISBN 978-0-471-43334-7.
  105. ^ a b Klarreich, Erica (12 March 2015). "Mathematicians chase moonshine's shadow". Quanta Magazine. Archived from the original on 15 November 2020. Retrieved 31 May 2015.
  106. ^ 간논, 2페이지
  107. ^ 관음, 페이지 4
  108. ^ Conway, John; Norton, Simon (1979). "Monstrous moonshine". Bull. London Math. Soc. 11 (3): 308–339. doi:10.1112/blms/11.3.308.
  109. ^ 관음, 5페이지
  110. ^ 관음, 8페이지
  111. ^ Borcherds, Richard (1992). "Monstrous moonshine and Lie superalgebras" (PDF). Inventiones Mathematicae. 109 (1): 405–444. Bibcode:1992InMat.109..405B. CiteSeerX 10.1.1.165.2714. doi:10.1007/BF01232032. S2CID 16145482. Archived (PDF) from the original on 2020-11-15. Retrieved 2017-10-25.
  112. ^ Frenkel, Igor; Lepowsky, James; Meurman, Arne (1988). Vertex Operator Algebras and the Monster. Pure and Applied Mathematics. Vol. 134. Academic Press. ISBN 978-0-12-267065-7.
  113. ^ 관음, 11페이지
  114. ^ Eguchi, Tohru; Ooguri, Hirosi; Tachikawa, Yuji (2011). "Notes on the K3 surface and the Mathieu group M24". Experimental Mathematics. 20 (1): 91–96. arXiv:1004.0956. doi:10.1080/10586458.2011.544585. S2CID 26960343.
  115. ^ Cheng, Miranda; Duncan, John; Harvey, Jeffrey (2014). "Umbral Moonshine". Communications in Number Theory and Physics. 8 (2): 101–242. arXiv:1204.2779. Bibcode:2012arXiv1204.2779C. doi:10.4310/CNTP.2014.v8.n2.a1. S2CID 119684549.
  116. ^ Duncan, John; Griffin, Michael; Ono, Ken (2015). "Proof of the Umbral Moonshine Conjecture". Research in the Mathematical Sciences. 2: 26. arXiv:1503.01472. Bibcode:2015arXiv150301472D. doi:10.1186/s40687-015-0044-7. S2CID 43589605.
  117. ^ Witten, Edward (2007). "Three-dimensional gravity revisited". arXiv:0706.3359 [hep-th].
  118. ^ Woit, 페이지 240–242
  119. ^ a b 242페이지
  120. ^ Weinberg, Steven (1987). "Anthropic bound on the cosmological constant". Physical Review Letters. 59 (22): 2607–2610. Bibcode:1987PhRvL..59.2607W. doi:10.1103/PhysRevLett.59.2607. PMID 10035596.
  121. ^ 와이트, 페이지)
  122. ^ Susskind, Leonard (2005). The Cosmic Landscape: String Theory and the Illusion of Intelligent Design. Back Bay Books. ISBN 978-0316013338.
  123. ^ Woit, 페이지 242–243
  124. ^ 와이트, 240페이지
  125. ^ 249페이지
  126. ^ Kachru, Shamit; Kallosh, Renata; Linde, Andrei; Trivedi, Sandip P. (2003). "de Sitter Vacua in String Theory". Phys. Rev. D. 68 (4): 046005. arXiv:hep-th/0301240. Bibcode:2003PhRvD..68d6005K. doi:10.1103/PhysRevD.68.046005. S2CID 119482182.
  127. ^ Wolchover, Natalie (9 August 2018). "Dark Energy May Be Incompatible With String Theory". Quanta Magazine. Simons Foundation. Archived from the original on 15 November 2020. Retrieved 2 April 2020.
  128. ^ 스몰린, 페이지 81
  129. ^ 스몰린, 페이지 184
  130. ^ a b Polchinski, Joseph (2007). "All Strung Out?". American Scientist. 95: 72. doi:10.1511/2007.63.72. Retrieved 29 December 2016.
  131. ^ Smolin, Lee (April 2007). "Response to review of The Trouble with Physics by Joe Polchinski". kitp.ucsb.edu. Archived from the original on November 5, 2015. Retrieved December 31, 2015.
  132. ^ Penrose, p. 1017
  133. ^ Woit, pp. 224–225
  134. ^ Woit, Ch. 16
  135. ^ Woit, p. 239
  136. ^ Penrose, p. 1018
  137. ^ Penrose, pp. 1019–1020
  138. ^ Smolin, p. 349
  139. ^ Smolin, Ch. 20

Bibliography

Further reading

Popular science

Textbooks

  • Becker, K.; Becker, M.; Schwarz, J.H. (2006). String Theory and M-Theory: A Modern Introduction. Cambridge University Press. ISBN 978-0521860697.
  • Blumenhagen, R.; Lüst, D.; Theisen, S. (2012). Basic Concepts of String Theory. Springer. ISBN 978-3642294969.
  • Green, Michael; Schwarz, John; Witten, Edward (2012). Superstring theory. Vol. 1: Introduction. Cambridge University Press. ISBN 978-1107029118.
  • Green, Michael; Schwarz, John; Witten, Edward (2012). Superstring theory. Vol. 2: Loop amplitudes, anomalies and phenomenology. Cambridge University Press. ISBN 978-1107029132.
  • Ibáñez, L.E.; Uranga, A.M. (2012). String Theory and Particle Physics: An Introduction to String Phenomenology. Cambridge University Press. ISBN 978-0521517522.
  • Kiritsis, E. (2019). String Theory in a Nutshell. Princeton University Press. ISBN 978-0691155791.
  • Polchinski, Joseph (1998). String Theory Vol. 1: An Introduction to the Bosonic String. Cambridge University Press. ISBN 978-0-521-63303-1.
  • Polchinski, Joseph (1998). String Theory Vol. 2: Superstring Theory and Beyond. Cambridge University Press. ISBN 978-0-521-63304-8.
  • West, P. (2012). Introduction to Strings and Branes. Cambridge University Press. ISBN 978-0521817479.
  • Zwiebach, Barton (2009). A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.

External links

Look up string theory in Wiktionary, the free dictionary.
Wikimedia Commons has media related to String theory.
Wikiquote has quotations related to String theory.

Websites

Video