초등 대수

초등대수는 수학의 주요 분야 중 하나인 대수의 기본 개념 중 일부를 포함한다.그것은 전형적으로 중등학생에게 가르쳐지고 산수에 대한 이해에 기초한다.산술은 지정된 ^[1]숫자를 다루는 반면, 대수는 ^[2]변수라고 알려진 고정된 값이 없는 양을 도입합니다.변수의 이러한 사용은 대수 표기법의 사용과 산술에 도입된 연산의 일반 규칙에 대한 이해를 수반한다.추상대수학과 달리, 초등대수는 실수와 복소수 영역 밖의 대수 구조와 관련이 없다.

수량을 나타내기 위해 변수를 사용하면 수량 간의 일반적인 관계를 공식적이고 간결하게 표현할 수 있으며, 따라서 더 넓은 범위의 문제를 해결할 수 있다.과학과 수학의 많은 양적 관계는 대수 방정식으로 표현된다.

대수 표기법

대수적 표기법은 표현식의 일부에 대해 말할 때 사용되는 용어뿐만 아니라 수학적 표현식을 쓰는 규칙과 규약을 설명한다.예를 들어 식 $3{\displaystyle \mathrm{}}$ ${\displaystyle {x\mathrm{}}^{}}$2 - ${\displaystyle 2}$ x${\displaystyle y}$ +$$ {\$displaystyle 3x^{2}-2xy+c}$에는 다음 컴포넌트가 있습니다.

계수는 변수를 곱하는 숫자 값 또는 숫자 상수를 나타내는 문자입니다(연산자는 생략됨).항은 더하기 연산자와 빼기 ^[3]연산자에 의해 다른 항과 분리될 수 있는 계수, 변수, 상수 및 지수의 그룹인 덧셈 또는 덧셈입니다.문자는 변수와 상수를 나타냅니다.관례상 알파벳 선두의 문자($예{\displaystyle :}$ ${\displaystyle a,}$ $,$ c\$displaystyle a, b$ c\displaystyle a, c\displaystyle $x,$ y\$displaystyle$ x$$$,$ y$)$ 및 $z{\displaystyle }$)는 일반적으로 ^[4]상수를 나타내는 데 사용됩니다.그것들은 보통 이탤릭체로 ^[5]인쇄된다.

대수 연산은 덧셈, 뺄셈, 곱셈, 나눗셈, 그리고 ^[7]지수와 같은 산술 ^[6]연산과 같은 방식으로 작용한다.대수 변수와 용어에 적용됩니다.곱셈 기호는 일반적으로 생략되며 두 변수 또는 항 사이에 공백이 없거나 계수가 사용되는 경우 암시됩니다.예를 들어${\displaystyle ,}$ ${\displaystyle {}^{}}$ × ${\displaystyle {x\mathrm{}}^{}}$ 2$($ 3$\times$ x$^{2})$는 3 ${\displaystyle {}^{}}$ $($로,${\displaystyle }$2 ×${\displaystyle x}$y($style$ 2$\times xxy$$)$^[8]는 2 ${\displaystyle x}$ y$(\displaystyle$ 2xy)로 쓸 수 있습니다.

일반적으로 최대 전력(exponent)의 용어는 왼쪽에 표시됩니다. 예를 들어 x $({$ x$^{2}})$는 x 왼쪽에 표시됩니다.계수가 1인 경우 보통 생략됩니다($예{\displaystyle \mathrm{}}$: 1 ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ $(\$는 x$$ (\$displaystyle$ x$^{2})$^[9]로 $표기$됩니다).마찬가지로 지수(멱함수)가 1인 경우에도 3 x 1($:$ $3{\displaystyle \mathrm{}}$ x 1 { $displaystyle 3x ^$ {1} )은$$3 x 3(\ $displaystyle$3x )$$^[10]로 표기됩니다.지수가 0인 경우 결과는 항상 1입니다(${\displaystyle {예\mathrm{}}^{}}$: x 0$(\$ x$^{0})$은 항상 ^[11]1로 고쳐씁니다).단, 0 $(\$ 0$^{0$은 정의되어 있지 않으므로 식에 표시할 수 없습니다.또한 변수가 지수로 표시되는 식을 단순화할 때 주의해야 합니다.

대체 표기법

다른 유형의 표기법은 문자 및 기호만 사용할 수 있는 경우와 같이 필요한 서식을 사용할 수 없거나 암시할 수 없는 경우 대수식에서 사용됩니다.예를 들어 $(\$ x$^{2$와 같은 상위 스크립트를 사용하여 인덱스를 포맷하지만, TeX 마크업 언어에서는 캐럿 기호 ^이 지수를 $나타내므로{\displaystyle {}^{}}$ $(\$ x$^{2})$는 "x^2"^[12][13] 및 Lua 등의 일부 프로그래밍 언어로 작성됩니다.Ada,^[14] Fortran,^[15] Perl^[17],^[16] Python 및 ^[18]Ruby와 같은 프로그래밍 언어에서는 이중 아스타리스크가 $사용$되므로 ${\displaystyle {x\mathrm{}}^{}}$ 2$({$ x$^{2}})$는 "x*2"로 표기됩니다.많은 프로그래밍 언어 및 계산기에서는 곱셈 ^[19]기호를 나타내기 위해 하나의 별표를 사용합니다. 예를 들어 3$$(\$displaystyle 3x)$는 "3*x"로 표기됩니다.

개념

변수

초등대수는 일반(불특정) 숫자를 나타내기 위해 변수라고 불리는 문자를 도입함으로써 산술에 기초하고 산술을 확장합니다^[20].이것은 몇 가지 이유로 유용합니다.

1. 변수는 값이 아직 알려지지 않은 숫자를 나타낼 수 있습니다.예를 들어, 현재 온도 C가 전날 온도 P보다 20도 높은 경우, 이 문제는 대수적으로 C ${\displaystyle =P}$ + $({display style$ C$=P+20$^[21]으로 설명할 수 있습니다.
2. 변수를 사용하면 관련된 수량의 값을 지정하지 않고도 일반적인 ^[22]문제를 설명할 수 있습니다.예를 들어, 5분은 60${\displaystyle }$× ${\displaystyle 5}$ ${\displaystyle =}$ ${\displaystyle 300}$（ $displaystyle$ 60 \ $times$ 5 =$300$）초와$$ ${\displaystyle \mathrm{같다고}}$ 구체적으로 말할 수 있습니다.보다 일반적인(더 정확한) 설명은 $s{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 60}$× ${\displaystyle m}$\ $displaystyle$ s =$60$\ $times$ m$（$ m ） 。여기서 m은 분 단위입니다.
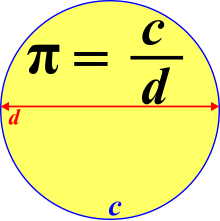
3. 변수를 사용하면 달라질 ^[23]수 있는 양 사이의 수학적 관계를 설명할 수 있습니다.예를 들어 원의 둘레, c 및 직경 d의 관계는 $\pi {\displaystyle }$ ${\displaystyle =c}$ /$$d \ $displaystyle \pi = c/d$로 표현한다.
4. 변수를 사용하면 몇 가지 수학적 특성을 설명할 수 있습니다.예를 들어, 덧셈의 기본 특성은 함께 더하는 숫자의 순서는 중요하지 않다는 것을 나타내는 교환성이다.정류성은 대수적으로 (${\displaystyle a}$+${\displaystyle b}$ ) ${\displaystyle =}$ (${\displaystyle b}$ +${\displaystyle a}$) {$displaystyle (a+b$) $= (b+a$^[24]${\displaystyle }$로 표시됩니다.

표현 단순화

대수식은 산술 연산의 기본 특성(더하기, 빼기, 곱하기, 나눗셈 및 지수화)에 기초하여 평가 및 단순화될 수 있다.예를들면,

• 추가된 항은 계수를 사용하여 단순화됩니다.$예$를 들어${\displaystyle }$x +${\displaystyle x}$ +$$ {\$style$x+$x}는$3 x$$ {\$displaystyle$ 3x$}($$여기$서 3은 숫자 계수)로 단순화할 수 있습니다.
• 곱셈 항은 지수를 사용하여 단순화됩니다.$예$를 들어${\displaystyle }$x ×${\displaystyle x}$x {$style$ x$\times x}$는 ${\displaystyle {x\mathrm{}}^{}}$ 3$($ x$^{3})$으로 $표시$됩니다.
• 정작 x2{\displaystyle x^{2}이 들어 있는}함께 추가됩니다처럼 조건 예를 들어, x2+4b{\displaystyle x^{2}+4ab 2x2+3b− x2+b{2x^{2\displaystyle}+3ab-x^{2}+ab}} 쓰여 있고 together,[25] 더해 지며, 계약 조건에 의해서 b{\displaystyle는}포함하는 toget 추가됩니다.그녀.
• 대괄호는 분산 속성을 사용하여 "승수"할 수 있습니다.${\displaystyle \mathrm{예}}$를 들어${\displaystyle }$x ( 2${\displaystyle x}$ +${\displaystyle 3}$ )$${ $displaystyle$x ( ${\displaystyle 2}$$$${\displaystyle x}$)$$+ (${\displaystyle }$x${\displaystyle }$×${\displaystyle 3}$) { $displaystyle$( x \ $times$ 2 x )${\displaystyle }$+ ( x \ $times$ 3$$) $({\displaystyle }$ 、 2 ${\displaystyle {x\mathrm{}}^{}}$2 + ${\displaystyle 3}$ ( \ $display style$2 x 2 x 2 ) + 3 $x$} 로 쓸 수 있습니다.
• 표현은 인수분해할 수 있습니다.예를 들어, 6 ${\displaystyle {x\mathrm{}}^{}}$5 + ${\displaystyle {}^{}}$ ${\displaystyle {x\mathrm{}}^{}}$2 ({$displaystyle 6x^{5}+3x$$^{2})$는 두 용어를 ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$$$${\displaystyle {2\mathrm{}}^{}}$($2$ ${\displaystyle {x\mathrm{}}^{}}$3 + ${\displaystyle 1}$) $({displaystyle 3x^{2$}+$1)$로$나눌$ 수 있습니다.

방정식

방정식은 등식을 나타내는 기호인 =(등호)^[26]를 사용하여 두 식이 같다는 것을 나타냅니다.가장 잘 알려진 방정식 중 하나는 직각 ^[27]삼각형의 변의 길이에 관한 피타고라스의 법칙을 설명한다.

${\displaystyle c^{2}=a^{2}+b^{2}}}$

이 방정식은 빗변 길이의 제곱을 나타내는 $({$ c$^{2$와 직각 반대쪽의 길이가 a와 b로 표시되는 다른 두 변의 제곱합(더하기)이 같다는 $것$을 나타냅니다.

방정식은 두 식의 값이 같고 동일하다는 주장입니다.일부 방정식은 관련된 변수의 모든 값에 대해 참입니다($예{\displaystyle }$:${\displaystyle }$a + ${\displaystyle b}$ ${\displaystyle =b}$ +$$ {$displaystyle$ a$+b=b+a}).$ 이러한 방정식을 항등식이라고 합니다.조건식은 관련된 변수의 일부 값에만 해당됩니다. 예를 $들어{\displaystyle {}^{}}$ x ${\displaystyle {2\mathrm{}}^{}}$- ${\displaystyle 1}$ ${\displaystyle =}$ ${\displaystyle 8}${$displaystyle$ x$^{2}-1=8}$은 x ${\displaystyle =}$ {$displaystyle$ x$=$$3}$ $및{\displaystyle }$ ${\displaystyle \mathrm{x}}$ ${\displaystyle =}$ -$$3 {$displaystyle$ x=-$3$에 $대해서$만 해당됩니다.방정식을 참되게 만드는 변수의 값은 방정식의 해이며 방정식 해법을 통해 찾을 수 있습니다.

또 다른 형태의 방정식은 불평등이다.부등식은 방정식의 한쪽이 다른 쪽보다 크거나 작다는 것을 보여주기 위해 사용됩니다.에 사용되는 기호는 a> {\$displaystyle a >$ b > 여기서 {\$displaystyle$$>$는 '보다 크다'를 나타내고{\$displaystyle$ a$<b}$는보다 작다'를 나타냅니다.표준 등식처럼 숫자를 더하거나, 빼거나, 곱하거나, 나누거나 할 수 있습니다.유일한 예외는 음수로 곱하거나 나눌 때 부등식 기호를 뒤집어야 한다는 것입니다.

균등성

정의상 등가관계는 (a)반사적 특성($예{\displaystyle }$: b ${\displaystyle =}$ $\$$displaystyle$ $b=b$$)$과 (b)대칭적 특성(${\displaystyle 예}$: a $=$ b ${\displaystyle =}$ b$$}이면 b ${\displaystyle =}=$ transitive($예{\displaystyle }$: a $b$ ${\displaystyle =}$ b 및 $b{\displaystyle }$ $style)$를 갖는 등가 $있다$.$displaystyle$ a$=c}).$^[28]또한 두 개의 기호가 동일한 사물에 사용될 경우 첫 번째 기호에 대한 진실된 진술에서 하나의 기호가 다른 기호로 대체될 수 있고 진술이 참으로 유지된다는 중요한 특성을 충족합니다.여기에는 다음 속성이 포함됩니다.

• a ${\displaystyle =}$ {$displaystyle$ a$=b}$ 및$$ $c{\displaystyle }$ ${\displaystyle =}$ {$displaystyle$ c$=d}$인 $경우{\displaystyle }$${\displaystyle }$a + ${\displaystyle c}$ ${\displaystyle =b}$ +$$ {$displaystyle$a+$c=b+d}$ $및$ c ${\displaystyle =}$ ${\displaystyle b}$d {$displaystyle$ ac=$bd$
• $a{\displaystyle }$ ${\displaystyle =}$ {\$displaystyle$ a$=b}$이면${\displaystyle }$a + ${\displaystyle c}$ ${\displaystyle =b}$ +$$ {$displaystyle$ a$+c=b+c}$ 및$$ ${\displaystyle c}$ ${\displaystyle b}$ {$displaystyle$ ac$=bc$}이다$.$
• 보다 일반적으로 함수 f에 대해 a $=$ f${\displaystyle }$(${\displaystyle a)}$ $=$f ($)$ {$displaystyle$ f$(a$)=$f(b$입니다.

부등식의 성질

$<\displaystyle <\$$displaystyle$ >보다작거나 큰 관계에는 이동성의 특성이 있습니다.^[29]

• a< \ $displaystyle$a <$b$ > 및b < \ $displaystyle$b <$c$ 의 경우 a< \ $displaystyle$a <$c$ ;
• a< \ $displaystyle$a <$b$ >c < \ $displaystyle$c < $d$>의 경우a + < + \ $displaystyle$a +$c$ <$b$ + $d$^[30] ;
• a< \ $displaystyle$a < $b$>및 c>{ $displaystyle$ c $>0}$인 경우 c < \ $displaystyle$ac < $bc$} ;
• a< \ $displaystyle$a < $b$>및c < \ $displaystyle$c < $0$>의 경우 b< \ $displaystyle$bc <ac>입니다.

부등식을 반전시킴으로써 다음과 같이 $<\displaystyle <\$displaystyle >와^[31]$>\displaystyle >$를 스왑할 수 있습니다.

• < b{ $display style$ a$}$는 b> { $display style$ b $}$에 합니다$.$

대체

치환이란 식에서 용어를 대체하여 새 식을 만드는 것입니다.식 a*5에서 a를 3으로 치환하면 15를 의미하는 새로운 식 3*5가 된다.스테이트먼트의 용어를 대체하면 새로운 스테이트먼트가 됩니다.원래 문장이 용어의 값과 독립적으로 참일 경우 대체에 의해 생성된 문장도 참입니다.따라서,${\displaystyle {}^{}2}$ : $=$ ${\displaystyle a}$ ×$$a {\$displaystyle$$$a^{$2}:=a\times$ a$}$가${\displaystyle {}^{}}$a의 정의인 $경우{\displaystyle {}^{}}$$,$ 3을 a의 곱으로 치환하여 $3$을 ${\displaystyle {표시\mathrm{}}^{}}$ 3$^{$$2$$}$이라는 문장의 독자에게 전달할 수 있다.}은 3 × 3 = 9를 의미합니다. 종종 문장이 용어의 값과 독립적으로 참인지 여부를 알 수 없습니다.치환을 통해 가능한 값에 대한 제한을 유도하거나 스테이트먼트가 어떤 조건에 속하는지 알 수 있습니다.예를 들어, x + 1 = 0이라고 하면, x가 1로 치환되면 1 + 1 = 2 = 0을 의미하며, 이는 거짓이며, x + 1 = 0이면 x가 1이 될 수 없다는 것을 의미합니다.

x와 y가 정수, 유리수 또는 실수인 경우 xy = 0은 x = 0 또는 y = 0을 의미합니다. abc = 0을 고려합니다.그런 다음 a를 x로, bc를 y로 대체하면 a = 0 또는 bc = 0을 알 수 있습니다.그런 다음 x = b 및 y = c로 바꿔 bc = 0이면 b = 0 또는 c = 0임을 나타낼 수 있습니다.따라서 abc = 0이면 a = 0 또는 (b = 0 또는 c = 0)이므로 abc = 0은 a = 0 또는 b = 0 또는 c = 0을 의미합니다.

만약 원래의 사실이 "ab = 0이 a = 0 또는 b = 0을 의미함"이라고 언급되었다면, "ab = 0"이라고 말할 때, 우리는 치환할 때 용어 충돌이 있을 것이다.그러나 위의 논리는 abc = 0일 경우 a = a 및 b = bc 대신 a와 b를 bc(및 bc = 0일 경우 b를 a, c를 b로 대체함)에 대입하면 a = 0 또는 b = 0이라는 것을 보여주는 데 여전히 유효하다.이것은 스테이트먼트의 용어를 대체하는 것이 스테이트먼트의 용어를 대체한 용어와 동일하게 하는 것과 항상 같지는 않다는 것을 나타냅니다.이 상황에서 표현식 a를 원래의 방정식의 항으로 치환하면, 치환된 a는 "ab = 0은 a = 0 또는 b = 0을 의미한다"는 문장의 a를 참조하지 않는 것이 분명하다.

대수 방정식을 풀다

다음 절에서는 발생할 수 있는 몇 가지 유형의 대수 방정식의 예를 제시합니다.

변수가 1개인 선형 방정식

선형 방정식은 일명 직선을 나타내기 때문에 일명 선형 방정식이라고 불립니다.가장 간단한 방정식은 변수가 하나만 있는 선형 방정식입니다.이러한 변수에는 지수 없이 상수 및 단일 변수만 포함됩니다.예를 들면, 다음과 같습니다.

말의 문제:아이의 나이를 두 배로 늘리고 4를 더하면 답은 12입니다.아이는 몇 살입니까?

등가 방정식: $2{\displaystyle \mathrm{}x}$ + ${\displaystyle 4}$ ${\displaystyle =}$ ${\displaystyle 12}$（ $displaystyle 2x$ + 4$=$ 12 ）여기서$$ x는 아이의 나이를 나타냅니다.

이런 종류의 방정식을 풀기 위해, 방정식의 한 변에 변수를 분리하기 위해 방정식의 양 변을 같은 수로 덧셈, 뺄셈, 곱셈 또는 나눕니다.변수가 분리되면 방정식의 다른 쪽이 변수의 ^[32]값이 됩니다.이 문제와 해결 방법은 다음과 같습니다.

1. 풀어야 할 방정식:	${\displaystyle 2x+4=12}$
2. 양변에서 4를 뺍니다.	${\displaystyle 2x+4-4=12-4}$
3. 이를 통해 다음과 같은 작업이 간소화됩니다.	${\displaystyle 2x=8}$
4. 양쪽을 2로 나눕니다.	$({displaystyle {2x} {2}} = flac {8} {2} }$
5. 이를 통해 다음과 같은 솔루션이 간소화됩니다.	${\displaystyle x=4}$

한마디로 그 아이는 4살이다.

변수가 1개인 선형 방정식의 일반적인 형식은 ${\displaystyle \mathrm{다음}}$과 $같이{\displaystyle }$ 쓸 수 있습니다. a${\displaystyle }$+ ${\displaystyle b}$ ${\displaystyle =}$ {\$displaystyle$ax + b$= c$ }

동일한 절차(즉, 양쪽에서 b를 뺀 다음 a로 나누기)에 따라 일반 용액은 x ${\displaystyle =\frac{}{}c\frac{}{}}$ - ${\displaystyle \frac{}{}}$a {\$display$ x$=subscfrac {c-b}{a}}$로 지정됩니다.

변수가 두 개인 선형 방정식

변수가 두 개인 선형 방정식에는 많은(^[33]즉, 무한히 많은) 솔루션이 있습니다.예를 들어 다음과 같습니다.

말 그대로의 문제: 아버지는 그의 아들보다 22살이 많다.그들은 몇 살입니까?

등가 방정식: $y{\displaystyle }$ ${\displaystyle =x}$ + ${\displaystyle 22}$ ${displaystyle$ y$=x+22}$ 여기서$$ y는 아버지의 나이, x는 아들의 나이입니다.

그것은 혼자서는 해결할 수 없다.만약 아들의 나이가 알려지면, 더 이상 알려지지 않은 두 개의 변수(변수)가 없을 것이다.이 문제는 위에서 설명한 바와 같이 하나의 변수만으로 선형 방정식이 됩니다.

두 변수(알 수 없음)를 사용하여 선형 방정식을 해결하려면 두 개의 관련 방정식이 필요합니다.예를 들어, 다음과 같은 사실이 밝혀진 경우:

말의 문제

10년 후, 아버지는 아들보다 두 배 더 나이가 많을 것이다.

등가 방정식

$({displaystyle {argent {aligned}y+10&=2\times (x+10)\y&=2\text{양쪽에서 10을 빼다})\y&=2x+20-10&{\text{복수 아웃브래킷}\y&=2x+10&{\text}{\simeligned}}}{\y&{\y&}})$

이제 서로 관련된 두 개의 선형 방정식이 있습니다. 각 방정식은 두 개의 미지수를 가지고 있습니다. 즉, 하나의 변수만으로 다른 변수에서 하나를 빼서 선형 방정식을 생성할 수 있습니다(제거 방법이라고 함).^[34]

${\displaystyle {begin{case}y=x+22&{\text{첫 번째 방정식}}\y=2x+10&{\text{두 번째 방정식}}\end{case}}}$

${\displaystyle {begin{aligned}&{\text{from}\(y-y)&=(2x-x)+10-22&{\text{\text}}y\0&0=x-12&{\text{Simplify}}\12&{\text}}양쪽에 첫 번째 방정식을 추가합니다.$

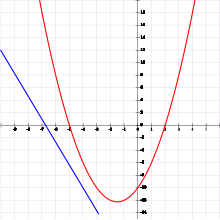
즉, 아들은 12살이고, 아버지는 22살이 더 많으므로 34살이 되어야 한다.10년 후 아들은 22세, 아버지는 44세의 두 배가 될 것이다.이 문제는 방정식의 관련 그림에 설명되어 있습니다.

이러한 방정식을 푸는 다른 방법은 아래의 선형 방정식 시스템을 참조하십시오.

이차 방정식

2차 방정식은 예를 들어 x$$({$displaystyle$ x$^{2$^[35]의 지수를 가진 항을 포함하며, 지수가 높은 항은 포함하지 않습니다.그 이름은 ^[36]사각형이라는 뜻의 라틴어 쿼드러스에서 유래했다.일반적으로 2차 방정식은 ${\displaystyle {}^{}}$ x${\displaystyle {}^{}{2\mathrm{}}^{}}$ + ${\displaystyle b}$x + ${\displaystyle c}$ ${\displaystyle =}$ {\$displaystyle$ ax$^{2$}+$bx+c=0$^[37] $형식$으로 표현될 수 있습니다. 여기서 a는 0이 아닙니다(만약 0이라면, 방정식은 2차식이 아니라 선형입니다).따라서 2차 방정식은 2차 항으로 알려진 ${\displaystyle {}^{}}$ $({$ ax$^{2$를 포함해야 합니다.${\displaystyle \mathrm{따라서}}$ 0$(\displaystyle$ a$\neq$ 0$)$이므로 a로 나누어 방정식을 표준 형식으로 정렬할 수 있습니다.

${\displaystyle x^{2}+px+q=0}$

$여기$서 p ${\displaystyle =}$ ${\displaystyle \frac{b}{}}$ a$${\$displaystyle$ p$=sqfrac {b}{a$$}}$ $및{\displaystyle }$ q ${\displaystyle =}$ ${\displaystyle c\frac{}{}}$ {\$display$ q$=sqfrac {c}{a$ 제곱을 완성하는 과정으로 알려진 과정을 통해 2차 공식으로 이어집니다.

$({displaystyle x=syslogfrac {-b\pm {b^{2}-4ac}}}{2a}},$

여기서 기호 "±"는 다음 사항을 나타냅니다.

${\displaystyle x=bcfrac {-b+{\displayrt {b^{2}-4ac}}}{2a}}\display {text{and}}\display x=bcfrac {-{\displayrt {b^{2}-4ac}}}{2a}}}}$

2차 방정식의 해입니다.

2차 방정식은 인수분해를 사용하여 해결할 수도 있습니다(반대 과정은 팽창이지만 두 선형 항에 대해서는 포일링으로 표시되기도 합니다).팩터링의 예:

${\displaystyle x^{2}+3x-10=0,}$

그것은 같은 것이다

${\displaystyle (x+5)(x-2)=0.}$

0-제품 속성에서 ${\displaystyle \mathrm{x}}$ $=$ 2({$디스플레이$ 스타일 $x$$=$2$$}) $또는{\displaystyle }$ ${\displaystyle \mathrm{x}=}$- 5({$디스플레이$ 스타일 x$=-5$}) 중 $하나$가 해답이라는 것을 알 수 있습니다. 정확히 두 요인 중 하나가 0이어야 합니다.모든 2차 방정식은 복소수 체계에서 두 개의 해를 갖지만, 실수 체계에서는 둘 다 해를 가질 필요가 없습니다.예를들면,

${\displaystyle x^{2}+1=0}$

에는 -1과 같은 실수 제곱이 없기 때문에 실수 해법이 없습니다.때때로 2차 방정식은 다음과 같이 곱셈 2의 근을 갖습니다.

${\displaystyle (x+1)^{2}=0.}$

이 방정식의 경우 -1은 배수 2의 근입니다.이는 방정식이 다음과 같이 인수 형식으로 다시 쓰여질 수 있기 때문에 -1이 두 번 나타난다는 것을 의미합니다.

${\displaystyle [x-(-1)][x-(-1)]= 0 。}$

복소수

모든 2차 방정식은 실수, 허수, 실수의 합과 허수의 합을 포함하는 범주인 복소수에서 정확히 두 개의 해를 가집니다(그러나 서로 같을 수도 있다.복소수는 2차 방정식과 2차 공식의 가르침에서 먼저 발생한다.예를 들어, 2차 방정식은

${\displaystyle x^{2}+x+1=0}$

솔루션을 가지고 있다

${\displaystyle x=syslogfrac {-1+{\syslogrt {-3}}{2}}\syslogs\text{and}}\syslogs x=syslogfrac {-1-{\syslogrt {-3}}}{2}}.}$

- $({$은 실수가 아니기 때문에${\displaystyle \sqrt{}}$x에 대한 이 두 해는 모두 복소수입니다.

지수 방정식 및 로그 방정식

지수방정식은 a$>$ 에 ${\displaystyle x}$ $=$ b(\$displaystyle$ a$^{x$^[38]$b)$의 형태로, 해를 갖는 방정식이다.

${\displaystyle X=\log _{a}b=syslogfrac {\ln a}}$

> { $displaystyle$ b > $0$}。해결에 도달하기 전에 위와 같은 방법으로 주어진 방정식을 다시 쓰기 위해 기초 대수 기법을 사용합니다.예를 들어,

${\displaystyle 3\cdot 2^{x-1}+1=10}$

그리고 방정식의 양변에서 1을 뺀 다음 양변을 3으로 나누면 우리는 얻는다.

${\displaystyle 2^{x-1}=3}$

어디서

${\displaystyle x-1=\log _{2}3}$

또는

$\displaystyle x=\log _{2}3+1.}$

로그 방정식은 a>에 ${\displaystyle l_{}}$ og a ($x$ ) $=$$$b {$displaystyle log$_ { $a$（ x ${\displaystyle ）}$ $= b$ } $형식$의 방정식으로, 해답은 다음과 같습니다.

$(\displaystyle X=a^{b}).}$

예를 들어,

${\displaystyle 4\log _{5}(x-3)-2=6}$

그리고 방정식의 양변에 2를 더하고, 양변을 4로 나누면, 우리는 다음을 얻는다.

$\displaystyle \log _{5}(x-3)=2}$

어디서

${\displaystyle x-3=5^{2}=25}$

우리가 얻을 수 있는 것

$(\displaystyle x=28)$

근방정식

근방정식은 $제곱근{\displaystyle \sqrt{},}$ x$,$ x, ${\displaystyle \text{exception 25:}}$(\displaystyle\sqrt[{3}{x}) 및 $(\$\$displaystyle$$\sqrt[{n}{x$을 포함하는 근방정식입니다$.$ n번째 근방정식은 ${\displaystyle \text{exception 25:}}$과 같이 $지수{\displaystyle \text{exception 25:}}$ 형식으로 고쳐 쓸 수 있습니다.Isplaystyle{\sqrt[{n}]{)}}}x1n{\displaystyle x^{\frac{1}{n}에}}. 정기적으로 되어 멱지수(힘)과 맞물려로 x32{\displaystyle x^{\frac{3}{2}}}는 급진적인 eq의 그래서 공통적인 형태 .[39] 다음 x32{\displaystyle{\sqrt[{2}]{x^{3}}}}(x의 제곱 근 cubed), 다시 쓸 수 있는 동일한 있다.uati${\displaystyle \text{exception 25:}}$은 x ${\displaystyle \sqrt[]{{}^{}}}$ ${\displaystyle \text{exception 25:}}$ \$style$\$displayrt$[ { n$$} { $x$^ { x } ${\displaystyle {=}^{}}$$$${\displaystyle a}$ \ $displaystyle$ x^ { \ $frac${ $m$} { n } =$a$}$$ （ ${\displaystyle {m\frac{}{}}^{}}$ ） 。m과 n은 정수입니다.실제 솔루션은 다음과 같습니다.

n은 홀수입니다.	n은 짝수이다 ${\displaystyle \mathrm{및}}$ ${\displaystyle \S }$ 0$(displaystyle$ a$\geq$ 0$)$	nandm은 짝수이다. 그리고.${\displaystyle a<0}$	n은 짝수, m은 홀수, < { $displaystyle$a <$0$ }
${\displaystyle x=syslogrt[{n}}}{a^{m}}}$ 동등하게 $\displaystyle x=\leftrt[{n}]{a}}\right^{m}}$	${\displaystyle x=\pm {n} {a^{m}}}$ 동등하게 ${\displaystyle x=\pm \left\pmrt[{n}}{a}}\right)^{m}}$	${\displaystyle x=\pm {n} {a^{m}}}$	진정한 해결책이 없다

예를 들어 다음과 같습니다.

${\displaystyle (x+5)^{2/3}=4}$

그리고나서

$({displaystyle {displaystyle}x+5&=({\displayrt {4})^{3},\x+5&=pm 8,\x&=-5\pm 8,\end{aligned})})$

그래서

${\displaystyle x=3\display {or}\display x=-13}$

선형 방정식 체계

두 개의 변수를 사용하여 선형 방정식의 시스템을 푸는 방법은 여러 가지가 있습니다.

소거법

선형 방정식 시스템을 푸는 예로는 다음과 같은 제거 방법을 사용할 수 있습니다.

$(\displaystyle\x+2y&=14\x-y&=1)\end {case}}$

두 번째 방정식의 항에 2를 곱하면:

${\displaystyle 4x+2y=14}$

${\displaystyle 4x-2y=2.}$

두 방정식을 합산하면 다음과 같이 됩니다.

${\displaystyle 8x=16}$

그 결과,

$(\displaystyle x=2)}$

x ${\displaystyle =}$ $({displaystyle x=2})$가 알려져 있기 때문에 원래의 두 공식 중 하나로 y ${\displaystyle =}$ $({displaystyle$ y=$3)$을 $추론$할 수 있습니다(x 대신 2를 사용). 이 문제에 대한 완전한 해결책은 다음과 같습니다.

${\displaystyle}x=2\y=3.\end {case}}$

이것은 이 특정 시스템을 해결하는 유일한 방법이 아닙니다.y는 x보다 먼저 해결되었을 수 있습니다.

대체 방법

선형 방정식의 동일한 체계를 푸는 또 다른 방법은 치환이다.

$(\displaystyle\x+2y&=14\x-y&=1)\end {case}}$

y에 대한 등가는 두 방정식 중 하나를 사용하여 추론할 수 있다.두 번째 방정식 사용:

${\displaystyle 2x-y=1}$

방정식의 각 변에서 $(\displaystyle 2x)$를 뺀 값:

$(\displaystyle {argined} 2x-2x-y&=1-2x&=1-2x\end{aligned})$

곱셈 -1:

$(\displaystyle y=2x-1).}$

원래 시스템의 첫 번째 방정식에서 이 y 값을 사용합니다.

$({displaystyle}{aligned}4x+2(2x-1)&=14\4x+4x-2&=14\end{aligned})$

방정식의 각 변에 2를 더하면:

$(\displaystyle\displaystyle\displaystyle\displaystyle\display\2+2&=14+2\\8x&=16\end{aligned})$

그 결과,

${\displaystyle x=2}$

이 값을 방정식 중 하나로 사용하면 이전 방법과 동일한 해를 얻을 수 있습니다.

${\displaystyle}x=2\y=3.\end {case}}$

이것이 이 특정 시스템을 해결하는 유일한 방법은 아닙니다. 이 경우에도 y는 x보다 먼저 풀릴 수 있습니다.

다른 유형의 선형 방정식

일관성 없는 시스템

위의 예에서는 솔루션이 존재합니다.하지만, 어떤 해법도 없는 방정식 체계도 있다.이러한 시스템을 부정합이라고 합니다.명백한 예는 다음과 같다.

${\displaystyle {\displaystyle}x+y&=1\0x+0y&=2,\end { aligned}\end {case}}$

계의 두 번째 방정식은 022로 해답이 없다.따라서 이 시스템에는 해결책이 없습니다.그러나 모든 일관되지 않은 시스템이 한눈에 인식되는 것은 아닙니다.예를 들어 시스템을 생각해 봅시다.

${\displaystyle}{\displaystyle}4x+2y&=12\-2x-y&=-4,\end { aligned}\end {case}}$

두 번째 방정식의 양변에 2를 곱하고 첫 번째 방정식에 더하면 다음과 같이 됩니다.

$({displaystyle 0x+0y=4,})$

그건 분명히 해결책이 없어요

미정 시스템

또한 고유한 솔루션(x와 y의 고유한 값 쌍)을 가진 시스템과는 대조적으로 솔루션이 무한히 많은 시스템도 있습니다.다음은 예를 제시하겠습니다.

${\displaystyle {case}{\display{aligned}4x+2y&=12\2x-y&=-6\end{aligned}\end{case}}$

두 번째 방정식의 y 분리:

${\displaystyle y=-2x+6}$

시스템의 첫 번째 방정식에서 이 값을 사용합니다.

${\displaystyle {argined} 4x + 2x + 6 = 12 \ 4x + 12 = 12 \ 12 = 12 \ end { aligned } }$

동일성은 사실이지만 x에 대한 값을 제공하지 않습니다. 실제로 x의 일부 값을 입력하는 것만으로 y$=$ -${\displaystyle 2}$ ${\displaystyle \mathrm{x}}$ +$$6({$displaystyle$ y=-$2x+$6$\})$이면 쉽게 솔루션이 있음을 확인할 수 있습니다.이 시스템에는 무한한 솔루션이 있습니다.

과잉 및 과소 결정 시스템

선형 방정식의 수보다 변수가 많은 시스템을 과소 결정 시스템이라고 합니다.그러한 시스템은, 만약 어떤 해결책을 가지고 있다면, 독특한 것이 아니라, 오히려 무한한 것을 가지고 있다.이러한 시스템의 예는 다음과 같습니다.

$(\displaystyle\x+2y&=10\y-z&=2).\end { aligned}\end {case}}$

해결하려고 할 때, 어떤 변수는 다른 변수의 함수로 표현되지만, 어떤 변수는 무한히 많기 때문에 수치로 표현할 수 없다.

변수보다 방정식의 수가 많은 시스템을 과잉 결정이라고 합니다.과도하게 결정된 시스템에 해답이 있는 경우, 필연적으로 일부 방정식은 다른 방정식의 선형 조합입니다.

「 」를 참조해 주세요.

• 초등대수의 역사
• 이진 연산
• 가우스 소거
• 수학 교육
• 번호선
• 다항식
• 소거중
• 타르스키의 고등학교 대수 문제

레퍼런스

• 레온하르트 오일러, 대수학 원소, 1770.영어 번역 Tarquin Press, 2007, ISBN978-1-899618-79-8, 온라인 디지털^[40] 에디션 2006,^[41] 1822.
• 찰스 스미스, 코넬 대학 도서관 수학 역사 논문입니다.
• 레든, 존2016년 6월 10일 웨이백 머신에 Elementary Algebrazy Archived.Flat World Knowledge, 2011

외부 링크

• 위키미디어 커먼스의 초등 대수학 관련 매체