필드(수학)

대수 구조
집단적인 그룹. 세미그룹/모노이드 랙앤쿼들 준군과 고리 아벨 군 마그마 거짓말군 군론
반지같은 울리다 Rng 세미링 니어링 교환환 도메인 적분영역 들판 나눗셈 링 라이링 고리이론
격자 같은 격자 반격자 상보격자 총순서 헤이팅 대수 부울 대수 격자도 격자론
모듈식 모듈 연산자와 그룹화 벡터공간 선형대수
대수적 대수학 연상적인 비연관성 조성대수 리 대수 등급이 매겨진 쌍대하학 호프 대수학
v t

수학에서, 필드는 덧셈, 뺄셈, 곱셈, 나눗셈이 정의되고 유리수와 실수에 대응하는 연산들처럼 행동하는 집합입니다.따라서 장은 대수학, 수론, 그리고 수학의 많은 다른 분야에서 널리 사용되는 기본적인 대수적 구조입니다.

가장 잘 알려진 분야는 유리수 분야, 실수 분야, 복소수 분야입니다.유리함수 분야, 대수함수 분야, 대수수 분야, p-adic 분야와 같은 다른 많은 분야들은 수학, 특히 수론과 대수기하학에서 일반적으로 사용되고 연구됩니다.대부분의 암호화 프로토콜은 유한한 필드, 즉 요소가 유한한 필드에 의존합니다.

두 필드의 관계는 필드 확장 개념으로 표현됩니다.1830년대에 에바리스트 갈루아에 의해 시작된 갈루아 이론은 장 확장의 대칭을 이해하는 데 전념하고 있습니다.다른 결과들 중에서, 이 이론은 각도 분할과 원의 제곱이 나침반과 직선으로 이루어질 수 없다는 것을 보여줍니다.게다가, 그것은 일반적으로 5차 방정식이 대수적으로 해결할 수 없다는 것을 보여줍니다.

필드는 여러 수학 영역에서 기본 개념으로 사용됩니다.여기에는 추가 구조를 가진 필드를 기반으로 하는 다양한 수학적 분석 분야가 포함됩니다.분석의 기본 정리는 실수 분야의 구조적 특성에 달려 있습니다.가장 중요한 것은, 어떤 필드도 선형 대수학의 표준적인 일반적인 맥락인 벡터 공간의 스칼라로 사용될 수 있다는 것입니다.유리수 분야의 형제인 수장은 수론에서 깊이 연구됩니다.함수 필드는 기하학적 객체의 속성을 설명하는 데 도움이 됩니다.

정의.

비공식적으로, 필드는 그 집합에 정의된 두 가지 연산과 함께 집합입니다: a + b로 쓰여진 덧셈 연산과 ⋅ b로 쓰여진 곱셈 연산. 모든 원소 a에 대한 덧셈 역 -a의 존재를 포함하여, 모두 유리수와 실수에 대해 비슷하게 동작합니다.0이 아닌 모든 원소 b에 대한 곱셈 역 b⁻¹.이것은 또한 다음을 정의함으로써 뺄셈인 a - b와 나눗셈인 a / b의 이른바 역연산을 고려할 수 있습니다.

a - b : = a + (-b),

a / b : = a ⋅ b.

고전적 정의

형식적으로, 필드는 덧셈과 곱셈이라고 불리는 F에 대한 두 개의 이진 연산과 함께 집합 F입니다.^[1]F에 대한 이진 연산은 매핑 F × F → F, 즉 F의 고유하게 결정된 원소인 F의 각 순서 쌍의 원소와 연관되는 대응입니다.a와 b의 덧셈의 결과를 a와 b의 합이라고 하고 a + b로 표시합니다. 마찬가지로 a와 b의 곱셈의 결과를 a와 b의 곱이라고 하고 ab 또는 ⋅ b로 표시합니다.필드 공리(field axioms)라고 하는 다음 속성을 만족시키기 위해서는 이러한 연산이 필요합니다(이러한 공리에서 필드 F의 a, b, care 임의 요소).

• 덧셈과 곱셈의 연관성: a + (b + c) = (a + b) + c, ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c.
• 덧셈과 곱셈의 교환성: a + b = b + a, a ⋅ b = b ⋅ a.
• 덧셈 및 곱셈 동일성: F에는 a + 0 = a 및 ⋅ 1 = a와 같은 두 개의 구별되는 원소 0과 1이 존재합니다.
• 덧셈 역수: F의 모든 a에 대해 -a로 표시된 -a라는 원소가 존재하며, a의 덧셈 역수라고 하며, 이는 +(-a) = 0입니다.
• 곱셈 역: F의 모든 ≠ 0에 대해, a 또는 1/a로 표시되는 원소가 F에 존재하며, 이는 a의 곱셈 역이라 불리며 ⋅ a = 1이 됩니다.
• 덧셈에 대한 곱셈의 분포도: a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c).

이와 동등하고 더 간결한 정의는 다음과 같습니다. 필드는 덧셈과 곱셈이라 불리는 두 개의 교환 연산을 갖습니다. 0을 덧셈 항등식으로 하는 덧셈 아래의 그룹입니다. 0이 아닌 요소는 1을 곱셈 항등식으로 하는 곱셈 아래의 그룹입니다. 그리고 곱셈은 덧셈 위에 분포합니다.

더 $간결$한${\displaystyle :}$ 필드는 ${\displaystyle 0}$≠$$1 {\$displaystyle 0\$neq 1}과 0이 아닌 모든 요소가 곱셈 하에서 가역적인 교환 링입니다.

대체정의

필드는 서로 다르지만 동등한 방법으로 정의할 수도 있습니다.또는 4개의 이진 연산( 덧셈, 뺄셈, 곱셈, 나눗셈)과 필요한 속성으로 필드를 정의할 수 있습니다.0으로 나누는 것은 정의상 제외됩니다.^[4]존재 한정자를 피하기 위해 필드는 두 개의 이진 연산( 덧셈 및 곱셈), 두 개의 단항 연산( 덧셈 및 곱셈 역수를 각각 산출) 및 두 개의 null 연산(상수 0 및 1)으로 정의할 수 있습니다.이 작업은 위의 조건에 따라 수행됩니다.실존적 정량자를 피하는 것은 구성 수학과 컴퓨팅에서 중요합니다.^[5]0 = 1 + (-1) 및 -a = (-1)a이므로 동일한 두 개의 이항 연산, 하나의 일항 연산(승수 역) 및 두 개의 (꼭 서로 다른) 상수 1 및 -1로 필드를 동등하게 정의할 수 있습니다.

예

유리수

유리수는 장의 개념이 구체화되기 훨씬 전부터 널리 사용되어 왔습니다.분수 a/b, a와 b는 정수, b는 ≠ 0으로 쓸 수 있는 숫자입니다.이러한 분수의 덧셈 역수는 -a/b이고, 곱셈 역수는 b/a이며, 다음과 같이 볼 수 있습니다.

${\displaystyle {\frac {b}{a}}\cdot {\frac {a}{b}}={\frac {b}}=1.}$

추상적으로 요구되는 필드 공리는 유리수의 표준 속성으로 줄어듭니다.예를 들어, 분배성의 법칙은 다음과 같이 증명될 수 있습니다.^[6]

${\displaystyle {\begin{aligned}&{\frac {a}{b}}\cdot \left ({\frac {c}{d}}+{\frac {e}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left ({\frac {c}{d}}\cdot {\frac {f}}+{\frac {e}{f}}\cdot {\frac {d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left ({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {a}{bdf}}+{\frac {aed}{bdf}}={\frac {a}{bf}}\[6pt]={\frac {a}{b}}\cdot {\frac {d}}+{\frac {a}{b}}\cdot {\frac {e}{f}}.\end{aligned}}$

실수와 복소수

실수 R은 덧셈과 곱셈의 일반적인 연산과 함께 필드를 형성합니다.복소수 C는 수식으로 구성됩니다.

a + bi, a, breal,

여기서 i는 허수 단위, 즉 i = -1을 만족하는 (비실수) 수이다.실수의 덧셈과 곱셈은 이 유형의 표현이 모든 필드 공리를 만족하고 따라서 C를 유지하는 방식으로 정의됩니다.예를 들어, 분배법은

(a + bi)(c + di) = ac + bci + adi + bdi = (ac - bd) + (bc + ad)i.

이는 다시 위 유형의 표현이므로 복소수는 필드를 형성합니다.복소수는 기하학적으로 평면의 점으로 표현할 수 있으며, 직교 좌표는 설명식의 실수로 제공되거나 원점에서 이 점까지 화살표로 표시되며, 길이와 일부 뚜렷한 방향으로 둘러싸인 각도로 지정됩니다.덧셈은 화살표를 직관적인 평행사변형에 결합하는 것에 해당하며(데카르트 좌표 추가), 곱셈은 화살표의 회전 및 스케일링(각도 추가 및 길이 곱하기)을 결합하는 것이 직관적이지 않습니다.실수와 복소수의 분야는 수학, 물리학, 공학, 통계학, 그리고 많은 다른 과학 분야에서 사용됩니다.

구성 가능한 수

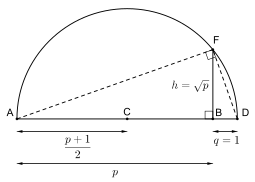
고대에 몇몇 기하학적 문제들은 나침반과 직선으로 특정한 수를 만드는 것의 가능성에 관한 것이었습니다.예를 들어, 그리스인들은 일반적으로 주어진 각도를 이런 식으로 분할하는 것이 불가능하다는 것을 알지 못했습니다.이러한 문제는 구성 가능한 숫자의 장을 사용하여 해결할 수 있습니다.^[7]실수는 정의에 따라 나침반과 직선만을 사용하여 점 0과 1로부터 무한히 많은 단계로 구성할 수 있는 선분의 길이입니다.구성 가능한 숫자로 제한된 실수의 필드 연산이 부여된 이 숫자들은 유리수의 필드 Q를 적절하게 포함하는 필드를 형성합니다.그림은 Q 안에 반드시 포함되지는 않는 구성 가능한 수의 제곱근 구성을 보여줍니다.그림의 레이블을 사용하여 세그먼트 AB, BD 및 BD에서 B를 통과하는 수직선과 점 F의 교차하는 AD(중간점 C의 중심) 위에 BD가 길이 1일 때 B로부터 정확히 $h$ = ${\displaystyle p}$ ${\displaystyle$h={\$sqrt {p}}$의 거리에 반원을 구성합니다.

모든 실수를 구성할 수 있는 것은 아닙니다.2 ${\displaystyle \text{exception 25:}}$ ${\$는 구성 가능한 수가 아님을 알 수 있는데, 이는 고대 그리스인들이 제기한 또 다른 문제점인 나침반으로 구성하고 부피가 2인 정육면체의 변의 길이를 직선화하는 것이 불가능하다는 것을 의미합니다.

원소가 4개인 필드

추가	곱셈
+ O I A B O O I A B I I O B A A A B O I B B A I O	⋅ O I A B O O O O O I O I A B A O A B I B O B I A

유리수와 같은 익숙한 수 체계 외에도, 덜 즉각적인 필드의 예가 있습니다.다음 예는 O, I, A, B라는 네 개의 원소로 구성된 필드입니다.표기법은 O가 덧셈 항등식 요소의 역할을 하고(위 공리에서 0으로 표시), I가 곱셈 항등식(위 공리에서 1로 표시)을 하도록 선택됩니다.필드 공리는 더 많은 필드 이론을 사용하거나 직접 계산을 통해 확인할 수 있습니다.예를들면,

A ⋅ (B + A) = A ⋅ I = A이며, 이는 분포에서 요구하는 A ⋅ B + A ⋅ A = I + B = A와 같습니다.

이 필드는 4개의 원소를 갖는 유한장 또는 갈루아장이라고 불리며, F 또는₄ GF(4)로 표시됩니다.^[8]O와 I로 구성된 부분 집합(오른쪽 표에서 빨간색으로 강조 표시됨)은 또한 이진 필드 F₂ 또는 GF(2)로 알려져 있습니다.컴퓨터 과학과 부울 대수학의 맥락에서, O와 I는 종종 거짓과 참으로 표시되고, 덧셈은 XOR(배타적 또는 )로 표시됩니다.즉, 바이너리 필드의 구조는 비트로 컴퓨팅이 가능한 기본 구조입니다.

기본개념

이 절에서 F는 임의의 필드를 의미하고 a와 b는 F의 임의의 요소입니다.

정의의 결과

하나는 ⋅ 0 = 0이고 -a = (-1) ⋅ a를 갖습니다. 특히 -1을 알면 모든 원소의 덧셈 역을 추론할 수 있습니다.

ab = 0이면 a 또는 b는 0이어야 합니다. ≠ 0이면 b = (aa)b = a(ab) = a ⋅ 0 = 0입니다.이는 모든 필드가 통합 영역임을 의미합니다.

또한 원소 a와 b에 대해서도 다음 속성이 적용됩니다.

−0 = 0

1⁻¹ = 1

(-(-a)) = a

(a) ⋅ b = a ⋅ (-b) = - (a ⋅ b)

(a⁻¹= a if a ≠ 0

필드의 덧셈 및 곱셈 군

필드 F의 공리는 그것이 덧셈 아래의 아벨 군이라는 것을 의미합니다.이 그룹을 필드의 덧셈 그룹이라고 하며, 단순히 F가 혼동할 수 있으므로 나타낼 때는 (F, +)로 표시하기도 합니다.

마찬가지로, F의 0이 아닌 원소들은 곱셈 하에서 아벨 군을 형성하는데, 이는 곱셈 군이라 불리며 (F \ {0}, ⋅) 또는 그냥 F \ {0} 또는 F로 표시됩니다.

따라서 필드는 덧셈과 곱셈으로 표시된 두 가지 연산을 갖춘 집합 F로 정의될 수 있으며, F \ {0}은 곱셈 하에서 아벨 군이며(여기서 0은 덧셈의 항등식 요소임) 곱셈은 덧셈에 대해 분배됩니다.^{[nb 2]}따라서 필드에 대한 몇 가지 기본적인 진술은 그룹의 일반적인 사실을 적용함으로써 얻을 수 있습니다.예를 들어, 덧셈 및 곱셈 역 -a와 a는⁻¹ a에 의해 고유하게 결정됩니다.

1은 0을 포함하지 않는 그룹의 ID 요소이므로 1 ≠ 0 요구 사항이 따릅니다.따라서 단일 요소로 구성된 사소한 링은 필드가 아닙니다.

필드의 곱셈 그룹의 모든 유한 부분군은 순환형입니다(단일치의 루트 § 순환형 그룹 참조).

특성.

F의 두 원소의 곱과 더불어 임의의 원소 a의 곱 n ⋅ a를 양의 정수 n으로 정의하여 n배합으로 하는 것이 가능합니다.

a + a + ⋯ + a (F의 원소임)

다음과 같은 양의 정수가 없는 경우

n ⋅ 1 = 0,

그러면 F는 특징적인 0을 가진다고 합니다.^[11]예를 들어, 유리수 Q의 필드는 양의 정수 n이 0이 아니기 때문에 특성이 0입니다.그렇지 않으면, 만약 이 식을 만족하는 양의 정수 n이 있다면, 그러한 양의 정수 중 가장 작은 정수가 소수임을 알 수 있습니다.일반적으로 p로 표시되며 필드는 특징적인 p를 가지고 있다고 합니다.예를 들어, 필드 F는 (위의 덧셈표 표기법에서) I + I = O이기 때문에 특성 2를 갖습니다.

F가 특성 p를 가지면, F에 있는 모든 a에 대해 p ⋅ a = 0입니다.이것은 다음을 암시합니다.

(a + b) = a + b,

이항식에 나타나는 다른 모든 이항 계수는 p로 나눌 수 있습니다.여기서 a := a ⋅ a ⋅ ⋯ ⋅ a(p인자)는 p번째 거듭제곱, 즉 원소 a의 p절편곱입니다.그러므로 프로베니우스 지도는

Fr: F → F, x ⟼ x

는 F의 덧셈과 (그리고 곱셈과도) 호환되며, 따라서 필드 동형 사상입니다.^[12]이 동형 사상의 존재는 특성 p의 필드를 특성 0의 필드와 상당히 다르게 만듭니다.

서브필드 및 프라임필드

필드 F의 서브 필드 E는 F의 필드 연산에 대한 필드인 F의 서브세트입니다.등가 E는 1을 포함하는 F의 부분 집합이며, 0이 아닌 원소의 덧셈, 곱셈, 덧셈 역수 및 곱셈 역수 하에서 닫힙니다.이는 1 ∊ E, 즉 모든 a에 대해 b ∊ E는 a + b 및 ⋅ b 모두 E에 있고, E의 모든 ≠ 0에 대해 -a 및 1/a 모두 E에 있음을 의미합니다.

필드 동형 사상은 φ(e + e) = φ(e) + φ(e), φ(e) = φ(e) φ(e), φ(e) φ(e) = 1과 같은 두 필드 사이의 지도 φ입니다. 여기서 e와 e는 E의 임의 요소입니다.모든 필드 동형은 주입형입니다.^[13]φ도 사영이면 동형이라고 합니다(또는 필드 E와 F를 동형이라고 합니다).

필드에 적절한 하위 필드가 없는 경우(즉, 매우 작은 경우), 필드를 프라임 필드라고 합니다.임의의 필드 F에는 프라임 필드가 포함됩니다.만약 F의 특성이 p(소수)라면, 프라임 필드는 아래에 소개된 유한 필드 F와_p 동형입니다.그렇지 않으면 프라임 필드는 Q와 동형입니다.^[14]

유한장

유한장(Galois fields라고도 함)은 유한하게 많은 원소를 갖는 장으로, 그 수는 장의 차수라고도 합니다.위의 도입 예 F는₄ 4개의 요소를 갖는 필드입니다.하위 필드 F는 가장 작은 필드입니다. 정의에 따라 필드는 적어도 두 개의 다른 요소 1 ≠ 0을 가지고 있기 때문입니다.

모듈러 산술을 사용하여 가장 단순한 유한장을 가장 직접적으로 접근할 수 있습니다.고정된 양의 정수 n에 대해 산술 "modulon"은 숫자를 사용하는 것을 의미합니다.

Z/nZ = {0, 1, ..., n - 1}입니다.

이 집합의 덧셈과 곱셈은 정수의 집합 Z에서 문제의 연산을 수행하여 n으로 나누고 나머지를 결과로 취함으로써 수행됩니다.이 구조는 n이 소수일 경우 정확하게 필드를 산출합니다.예를 들어, prime n = 2를 취하면 위에서 언급한 필드 F가 됩니다.n = 4 이상 일반적으로 임의의 합성수(즉, 두 개의 엄밀하게 더 작은 자연수의 곱 n = r ⋅로 표현될 수 있는 임의의 수 n)에 대해 Z/nZ는 필드가 아닙니다. Z/nZ에서 r ⋅ = 0이므로 0이 아닌 두 원소의 곱은 0이며, 위에서 설명한 바와 같이 Z/nZ가 필드가 되는 것을 방지합니다.이러한 방식으로 구성된 p 요소(p가 prime)가 있는 필드 Z/pZ는 일반적으로 F로_p 표시됩니다.

모든 유한장 F는 q = p 요소를 가지며, 여기서 p는 소수이고 n은 ≥ 1입니다.이 문장은 F를 그것의 프라임 필드 위의 벡터 공간으로 볼 수 있기 때문에 성립합니다.이 벡터 공간의 차원은 반드시 유한한 n이고, 이는 주장된 문장을 의미합니다.^[15]

q = p 요소가 있는 필드를 다항식의 분할 필드로 구성할 수 있습니다.

f(x) = x - x.

이러한 분할 필드는 다항식 f가 q 0을 가지는_p F의 확장입니다.이것은 f의 정도가 q이기 때문에 f가 가능한 한 많은 0을 가지고 있다는 것을 의미합니다.q = 2 = 4의 경우, F의 네 원소가 모두 식 x = x를 만족하므로, f의 0임을 위의 곱셈표를 이용하여 사례별로 확인할 수 있습니다.반대로, F에서₂ f는 두 개의 0(즉, 0과 1)만 있으므로, f는 이 작은 필드에서 선형 요인으로 분할되지 않습니다.기본 장 이론적 개념을 더 자세히 설명하면, 같은 순서를 가진 두 유한 장이 동형임을 알 수 있습니다.^[16]따라서_q F 또는 GF(q)로 표시되는 q 원소를 갖는 유한장을 말하는 것이 일반적입니다.

역사

역사적으로, 세 가지 대수학 분야가 필드의 개념으로 이어졌습니다: 다항식을 푸는 문제, 대수적 수론,^[17] 그리고 대수적 기하학.장의 개념을 향한 첫 걸음은 1770년에 Joseph-Louis Lagrange에 의해 이루어졌는데, 그는 식에서 입방 다항식의 0 x₁, x₂, x를₃ 순열하는 것을 관찰했습니다.

(x₁ + ωx₂ + ω²x₃)³

(단일화의 세 번째 뿌리인 ω) 두 개의 값만 산출합니다.이러한 방식으로 라그랑주는 미지의 x에 대한 3차 방정식을³ x에 대한 2차 방정식으로 환원함으로써 진행되는 스키피오네 델 페로와 프랑수아 비에테의 고전적인 해법 방법을 개념적으로 설명했습니다.^[18]따라서 라그랑주는 4도 방정식에 대한 유사한 관측과 함께 결국 필드의 개념과 그룹의 개념을 연결시켰습니다.^[19]반데르몽드, 또한 1770년에, 그리고 충분히, Carl Friedrich Gauss는, 그의 산술학(Disquisitiones Armeticae, 1801)에서, 방정식을 연구했습니다.

x = 1

소수의 팬들을 위해, 그리고 다시 현대 언어를 사용하여, 순환 갈루아 그룹.가우스는 p = 2 + 1이면 정규 p-곤을 만들 수 있다고 추론했습니다. 라그랑주의 연구를 바탕으로 파올로 루피니는 (1799) 5차 방정식은 대수적으로 풀 수 없다고 주장했지만 그의 주장은 결함이 있었습니다.이 틈들은 1824년 닐스 헨리크 아벨에 의해 메워졌습니다.^[20]1832년에 에바리스트 갈루아는 다항식이 대수적으로 해결될 수 있는 필요충분조건을 고안하여 오늘날 갈루아 이론으로 알려진 것을 사실상 확립했습니다.아벨과 갈루아 둘 다 오늘날 대수적 수장이라고 불리는 것을 연구했지만, 장의 명시적인 개념도, 군의 개념도 생각하지 못했습니다.

1871년 리처드 데데킨트는 4개의 산술 연산에서 닫힌 실수 또는 복소수의 집합에 대해 "체" 또는 "말뭉치"(유기적으로 닫힌 실체를 암시하는 말)를 의미하는 독일어 단어 쾨르퍼(Körper)를 소개했습니다."필드(field)"라는 영어 용어는 무어(1893)에 의해 소개되었습니다.^[21]

장에 따르면 우리는 실수나 복소수의 무한한 계들이 그 자체로 닫혀 있고 이 두 수 중 하나의 덧셈, 뺄셈, 곱셈, 나눗셈이 다시 계의 수를 산출할 수 있도록 완벽하다는 것을 의미할 것입니다.

— Richard Dedekind, 1871^[22]

1881년 레오폴드 크로네커는 그가 합리성의 영역이라고 부르는 것을 정의했는데, 이것은 현대 용어로 합리적인 분수의 영역입니다.크로네커의 개념은 (데킨트의 의미에서) 모든 대수적 수의 장을 포함하지는 않았지만, 반면에 장의 원소의 본질에 대한 구체적인 가정을 하지 않았다는 점에서 데데킨트의 개념보다 더 추상적이었습니다.크로네커는 Q(π)과 같은 장을 유리함수장 Q(X)로 추상적으로 해석했습니다. 이에 앞서 초월수의 예는 1844년 조셉 리우빌의 연구 이후 샤를 헤르미테(1873)와 페르디난트 폰 린데만(1882)이 각각 e와 π의 초월성을 증명할 때까지 알려져 있었습니다.

추상장의 첫 번째 명확한 정의는 Weber([24]1893)에 기인합니다.특히 하인리히 마르틴 베버의 개념에는 F장이_p 포함되어 있었습니다.Giuseppe Veronese (1891)는 공식적인 멱급수의 분야를 연구했고, 이것은 Hensel (1904)이 p-adic 수의 분야를 소개하도록 이끌었습니다.슈타이니츠(Steinitz, 1910)는 그동안 축적된 추상장이론의 지식을 종합했습니다.그는 필드의 속성을 공리적으로 연구했고 많은 중요한 필드 이론 개념을 정의했습니다.갈루아 이론, 구성 분야 그리고 기초 개념 부분에서 언급된 대부분의 정리들은 스타이리츠의 작품에서 찾을 수 있습니다.Artin & Schreier(1927)는 어떤 분야의 순서의 개념, 즉 분석 영역을 순수한 대수적 성질과 연결시켰습니다.^[25]에밀 아르틴은 1928년부터 1942년까지 갈루아 이론을 재개발하여 원시 원소 정리에 대한 의존성을 없앴습니다.

필드구성중

링에서 필드 구성

가환환은 곱셈 역 a의⁻¹ 존재를 제외한 필드의 모든 공리를 만족시키는 덧셈과 곱셈 연산을 갖춘 집합입니다.^[26]예를 들어 정수 Z는 교환환을 형성하지만 필드는 형성하지 않습니다. 정수 n의 역수는 n = ±1이 아닌 한 정수 자체가 아닙니다.

대수적 구조의 계층에서 필드는 0이 아닌 모든 원소가 단위인 치환환 R로 특징지어질 수 있습니다(즉, 모든 원소가 가역적이라는 것을 의미합니다.마찬가지로, 필드는 정확히 두 개의 서로 다른 이상(0)과 R을 갖는 교환 링입니다.필드는 또한 정확히 (0)이 유일한 주요 이상인 교환환입니다.

가환환 R이 주어지면 R과 관련된 필드를 구성하는 두 가지 방법, 즉 0이 아닌 모든 원소가 가역적이 되도록 R을 수정하는 두 가지 방법, 즉 분수 필드를 형성하는 것과 잔차 필드를 형성하는 것이 있습니다.Z의 분수 필드는 Q, 유리수이며, Z의 잔차 필드는 유한 필드_p F입니다.

분수계

적분 영역 R이 주어졌을 때, 분수 Q(R)은 정수로부터 Q가 구성된 것처럼 정확히 R의 두 원소의 분수로 구성됩니다.더 정확하게 말하면, Q(R)의 원소는 분수 a/b이고, a와 b는 R에 있고, b는 ≠ 0입니다.두 분수 a/b와 c/d는 ad = bc인 경우에만 같습니다.분수에 대한 연산은 유리수에 대한 연산과 정확히 일치합니다.예를들면,

${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}}$

고리가 적분 영역인 경우 분수의 집합이 장을 형성한다는 것을 보여주는 것은 간단합니다.^[27]

필드(또는 적분 도메인) F 위의 유리 분수의 필드 F(x)는 다항식 링 F[x]의 분수 필드입니다.로랑 급수의 F((x)) 장

${\displaystyle \sum _{i=k}^{\infty}a_{i}x^{i}\(k\in \mathbb {Z},a_{i}\in F)}$

필드 F는 (k ≥ 0인) 공식 멱급수의 링 F[[x]의 분수 필드입니다.로랑 급수는 멱급수의 분수를 x의 거듭제곱으로 나눈 값이기 때문에(임의의 거듭제곱 급수와는 반대로), 이러한 상황에서는 분수의 표현은 덜 중요합니다.

잔차 필드

필드에 R을 주입적으로 매립하는 분수 필드 외에도, 필드는 필드 F에 대한 주관적인 맵에 의해 교환 링 R로부터 획득될 수 있습니다.이러한 방법으로 얻은 모든 필드는 R/m의 몫이며, 여기서 m은 R의 최대 이상입니다.만약 R이 오직 하나의 최대 아이디얼만 가진다면, 이 필드는 R의 잔차 필드라고 불립니다.^[28]

다항식 고리 R = E[X]에서 (장 E에 걸쳐) 단일 다항식 f에 의해 생성된 이상은 f가 E에서 감소할 수 없는 경우, 즉 f가 더 작은 차수의 E[X]의 두 다항식의 곱으로 표현될 수 없는 경우에만 최대입니다.필드가 생성됩니다.

F = E[X] / (f(X)).

이 필드 F는 방정식을 만족시키는 원소 x(즉, X의 잔차 클래스)를 포함합니다.

f(x) = 0.

예를 들어, C는 가상의 단위 기호 i에 인접함으로써 R로부터 얻어지는데, 이는 f (i) = 0을 만족하며, 여기서 f (X) = X + 1을 만족합니다. 또한, f는 R에 대해 축소할 수 없으며, 이는 다항식 f (X) ∊ R[X]를 f (i)로 보낸 지도가 동형을 산출함을 의미합니다.

${\displaystyle \mathbf {R} [X]/\left(X^{2}+1\right)\ {\stackrel {\cong}{\longrightarrow}}}\ \mathbf {C} .}$

더 큰 필드 내에 필드 구성

주어진 큰 컨테이너 필드 안에 필드를 작성할 수 있습니다.필드 E와 E를 포함하는 필드 F가 하위 필드로 주어졌다고 가정합니다.F의 임의의 원소 x에 대하여, E와 x를 포함하는 F의 가장 작은 부분 필드가 존재하며, 이는 x에 의해 생성되고 E(x)로 표시되는 F의 부분 필드라고 불립니다.^[29]E에서 E(x)로의 통로는 E에 원소를 인접시킴으로써 지칭됩니다.더 일반적으로, 부분 집합 S ⊂ F의 경우, E(S)로 표시되는 E 및 S를 포함하는 F의 최소 부분 필드가 있습니다.

일부 필드 F의 두 서브 필드 E와 E'의 합성은 E와 E'를 모두 포함하는 F의 가장 작은 서브 필드입니다.합성은 어떤 성질을 만족하는 F의 가장 큰 하위장, 예를 들어, 아래에 소개되는 언어에서 E 위에 대수적인 F의 가장 큰 하위장을 구성하는 데 사용될 수 있습니다.^{[nb 3]}

필드 확장

서브 필드 E ⊂ F의 개념은 반대 관점에서 F가 E의 필드 확장(또는 그냥 확장)이라고 언급함으로써 간주될 수도 있습니다.

F/E,

'Fover E'를 읽습니다.

필드 확장의 기본 데이터는 [F : E]의 정도, 즉 E-벡터 공간으로서의 F의 차원입니다.공식을^[30] 만족합니다.

[G:E] = [G:F] [F:E].

정도가 유한한 확장을 유한 확장이라고 합니다.확장자 C/R과 F₄/F는₂ 차수 2인 반면, R/Q는 무한 확장자입니다.

대수적 확장

필드 확장 F/E 연구의 중심 개념은 대수적 요소입니다.원소 $x$ ∈ ${\displaystyle F}$ ${\displaystyle x\in F}$가 E에 계수가 있는 다항식의 근이면, 즉 다항식을 만족하는 경우, E에 대한 대수적

ex + ex + ex + ⋯ + ex + e = 0,

e, ..., e가 E, e가 ≠ 0인 경우.예를 들어, C의 허수 단위 i는 방정식을 만족시키기 때문에 R 위의 대수적이고, Q 위의 대수적 단위입니다.

i + 1 = 0.

F의 모든 원소가 E 위에 대수적인 필드 확장을 대수적 확장이라고 합니다.위의 곱셈 공식에서 추론할 수 있듯이, 유한 확장은 반드시 대수적입니다.^[31]

위와 같이 원소 x에 의해 생성된 부분장 E(x)는 x가 대수적 원소인 경우에만 E의 대수적 확장입니다.즉, 만약 x가 대수적이라면, E(x)의 다른 모든 원소들도 반드시 대수적입니다.또한 확장 E(x) / E의 정도, 즉 E-벡터 공간으로서의 E(x)의 차원은 위와 같이 x를 포함하는 다항식이 있는 최소의 정도와 같습니다.이 정도가 n이면 E(x)의 원소는 다음과 같은 형태를 갖습니다.

${\displaystyle \sum _{k=0}^{n-1}a_{k}x^{k},\a_{k}\in E.}$

예를 들어, 가우스 유리수의 필드 Q(i)는 a와 b가 모두 유리수인 형태 a + bi의 모든 수로 구성된 C의 하위 필드입니다. a + bi + ci를² a - c + bi로 단순화할 수 있으므로 형식 i의² 합(그리고 더 높은 지수의 경우에도 마찬가지로)을 여기서 고려할 필요가 없습니다.

초월 기저

X가 불확정자인 유리분수 E(X)의 위 필드는 0인 E에 계수를 갖는 다항식이 없기 때문에 E의 대수적 확장이 아닙니다.대수적이지 않은 X와 같은 원소를 초월적이라고 합니다.비공식적으로 말하면, 불확정 X와 그 거듭제곱들은 E의 원소들과 상호작용하지 않습니다.유사한 구조는 단지 하나가 아니라, 일련의 불확정한 구조로 수행될 수 있습니다.

위에서 논의한 필드 확장 E(x) / E가 핵심적인 예이다: 만약 x가 대수적이지 않다면(즉, x는 E에 계수가 있는 다항식의 근이 아님), E(x)는 E(X)와 동형입니다.이 동형은 유리 분수에서 X에 x를 대입함으로써 얻어집니다.

필드 F의 부분 집합 S는 E에 대해 대수적으로 독립적이고(다항 관계를 만족시키지 않음) F가 E(S)의 대수적 확장인 경우 초월 기저입니다.모든 필드 확장 F/E에는 초월 기저가 있습니다.^[32]따라서 필드 확장은 E(S)/E(순수 초월 확장) 형태와 대수 확장 중 하나로 나눌 수 있습니다.

폐쇄작업

만약 어떤 장이 더 큰 대수적 확장을 가지지 않는다면, 또는 임의의 다항식을 가지면, 대수적으로 닫혀있을 것입니다.

f x + fx + ⋯ + fx + f = 0, 계수 f, ..., f ∈ F, n > 0,

해 x ∊ F를 갖습니다.대수학의 기본 정리에 의해 C는 대수적으로 닫혀 있으며, 즉 복잡한 계수를 갖는 임의의 다항식은 복잡한 해를 갖습니다.유리수와 실수는 방정식 이후 대수적으로 닫혀 있지 않습니다.

x + 1 = 0

합리적이거나 실제적인 해결책이 없습니다.F를 포함하는 필드는 F 위의 대수적이고 (대략적으로 말하면, F에 비해 너무 크지 않음) 대수적으로 닫혀 있고 (모든 다항식의 해를 포함할 수 있을 정도로 충분히 큼) F의 대수적 폐쇄라고 불립니다.

위에서 C는 R의 대수적 종결입니다.대수적 폐쇄가 필드 F의 유한 확장이라는 상황은 매우 특별합니다: 아르틴-슈라이어 정리에 의해, 이 확장의 정도는 반드시 2이고, F는 기본적으로 R과 동등합니다.이러한 필드는 실제 닫힌 필드라고도 합니다.

임의의 필드 F는 대수적 폐쇄를 가지며, 또한 (비고유의) 동형까지 유일합니다.흔히 대수적 종결이라고 하며 F로 표시합니다.예를 들어, Q의 대수적 종결 Q를 대수적 수의 장이라고 합니다.F장은 그 구성이 선택 공리보다 약한 집합론적 공리인 초필터 보조자를 필요로 하기 때문에 일반적으로 다소 암시적으로 F장은 선택 공리보다 약한 집합론적 공리를 필요로 합니다.^[34]이 점에서, F의_q 대수적 종결은 예외적으로 간단합니다.이것은 F_q(차수 q의ⁿ 것)를 포함하는 유한장의 결합입니다.특성 0의 임의의 대수적으로 닫힌 필드 F에 대하여, 로랑 급수의 필드 F((t))의 대수적 닫힘은 t의 인접한 근에 의해 얻어진 푸이쇠 급수의 필드입니다.^[35]

구조가 추가된 필드

분야는 수학과 그 이상의 분야에서 어디에나 있기 때문에, 그 개념의 몇 가지 개선은 특정한 수학 영역의 필요에 맞게 조정되었습니다.

순서 필드

두 원소를 비교할 수 있는 경우 필드 F를 순서 필드라고 합니다. 따라서 x + y가 0을 ≥하고 xy가 0을 ≥할 때마다 x + y가 0을 ≥하고 xy가 0을 ≥합니다.예를 들어 실수는 일반적인 순서 ≥와 함께 순서 필드를 구성합니다.아르틴-슈라이어 정리는 어떤 장이 형식적으로 실제인 장일 경우에만 순서가 정해질 수 있다고 말하고, 이것은 어떤 이차방정식을 의미합니다.

${\displaystyle x_{1}^{2}+x_{2}^{2}+\dots +x_{n}^{2}=0}$

솔루션 x = x = ⋯ = x = 0만 있습니다.고정된 필드 F에 대한 모든 가능한 순서의 집합은 F에 대한 2차 형식의 위트 링 W(F)에서 Z까지의 링 동형의 집합과 동형입니다.^[37]

Archimedean 필드는 각 원소에 대해 유한한 식이 존재하도록 정렬된 필드입니다.

1 + 1 + ⋯ + 1

그 값이 그 원소보다 더 크다는 것, 즉 무한한 원소가 없다는 것입니다.이와 동일하게 필드는 무한 소수(모든 유리수보다 작은 원소)를 포함하지 않으며, 필드는 R의 하위 필드와 동형입니다.

순서가 지정된 필드는 모든 상한, 하한(데카인드 컷 참조) 및 한계가 존재하는 경우 데카인드 완성입니다.좀 더 형식적으로, F의 각 경계 부분 집합은 최소 상한을 가져야 합니다.아르키메데스가 아닌 모든 필드에는 최대의 무한소도, 최소의 양의 유리수도 존재하지 않기 때문에,^[38] 모든 원소가 모든 무한소보다 큰 수열 1/2, 1/3, 1/4, ...에 제한이 없기 때문에, 모든 완전한 필드는 반드시 아르키메데스이다.

실수의 모든 적절한 하위 필드도 이러한 공백을 포함하기 때문에, R은 동형까지 유일한 완전 순서 필드입니다.^[39]미적분학의 몇 가지 기초적인 결과는 실제의 이러한 특성화에서 직접적으로 따옵니다.

하이퍼리얼 R은^* Archimedean이 아닌 순서가 있는 필드를 형성합니다.무한소수와 무한소수를 포함하여 얻은 실수의 확장입니다.이것들은 각각 어떤 실수보다도 더 큽니다.하이퍼리얼은 비표준 분석의 기초를 형성합니다.

위상 필드

필드 개념의 또 다른 개선점은 위상 필드인데, 집합 F는 위상 공간이므로 필드의 모든 연산( 덧셈, 곱셈, 지도 a-a 및 ↦ a)은 공간의 위상에 대한 연속적인 지도입니다.아래에서 논의되는 모든 분야의 토폴로지는 메트릭, 즉 함수로부터 유도됩니다.

d : F × F → R,

F의 임의의 두 원소 사이의 거리를 측정합니다.

F의 완성은, 비공식적으로 말하면, 원래 필드 F의 "갭"이 있는 경우, 채워지는 또 다른 필드입니다.예를 들어, x = √2와 같은 임의의 무리수 x는 절대값 x - p/q에 의해 주어진 x와 p/q의 거리가 원하는 만큼 작다는 점에서 유리수 p/q에 의해 임의로 근사될 수 있는 실수라는 점에서 유리수 Q의 "갭"입니다.다음 표에는 이 구성의 몇 가지 예가 나와 있습니다.네 번째 열은 영(zero) 수열, 즉 한계(n → ∞의 경우)가 0인 수열의 예를 보여줍니다.

들판	미터법	완성	순서 0
Q	x - y (usual 절대값)	R	1/n
Q	소수 p에 대해 p-adic 평가를 사용하여 구함.	Qp(p-adic number)	pn
F(t) (모든 필드)	t-adic 평가를 사용하여 얻은	F((t))	tn

Q_p 필드는 수론과 p-adic 분석에서 사용됩니다.대수적 종결 Q는_p Q_p 위에 있는 것을 확장하는 고유한 표준을 가지고 있지만 완전하지는 않습니다.그러나 이 대수적 종결의 완성은 대수적으로 종결되어 있습니다.복소수에 대한 대략적인 비유 때문에 때때로 복소수 p-adic 수의 장으로 불리며 C로_p 표시됩니다.^[41]

로컬 필드

다음 토폴로지 필드를 로컬 필드라고 합니다.^{[42][nb 4]}

• Q의_p 유한 확장(특성 0의 국소 필드)
• F_p((t))의 유한 확장, F_p(특성 p의 국소 장) 위의 로랑 급수의 장.

이 두 가지 유형의 지역 분야는 몇 가지 근본적인 유사점을 공유합니다.이와 관련하여, 요소 p ∈ Q와 t ∈ F(((t))(uniformizer라고 함)는 서로 대응됩니다.이에 대한 첫 번째 표현은 기본 수준입니다. 두 필드의 요소는 F의 계수와_p 함께 균일기에서 멱급수로 표현될 수 있습니다. (그러나 Q의_p 덧셈은 F_p(t))의 경우가 아닌 운반을 사용하여 수행되므로 이 필드들은 동형이 아닙니다.)다음과 같은 사실은 이러한 피상적 유사성이 훨씬 더 심화되었음을 보여줍니다.

• 거의 모든 Q에_p 대해 참인 모든 1차 문장은 거의 모든_p F((t))에도 참입니다.이를 응용한 것이 Q에서_p 동차 다항식의 0을 설명하는 Ax-Kochen 정리입니다.
• 두 분야의 길들여진 확장은 서로 사투를 벌이고 있습니다.
• 각각 t(f_p(t))의 p(q_p))의 임의의 p-파워 루트에 인접하여 퍼펙트로이드 필드로 알려진 필드의 (무한) 확장을 산출합니다.놀랍게도, 이 두 분야의 갈루아 군은 동형이며, 이 두 분야 사이의 놀라운 유사성을 처음으로 엿볼 수 있습니다.^[43]
  $${\displaystyle \operatorname {Gal} \left(\mathbf {Q} _{p}\left(p^{p^{\infty}}}\right)\cong \operatorname {Gal} \left(\mathbf {F} _{p}(t)\left(t^{1/p^{\infty}}\right)\right)}$$

  

차분 필드

미분장은 도함수를 갖춘 장으로, 즉 장에 원소의 도함수를 취할 수 있습니다.^[44]예를 들어, 필드 R(X)은 다항식의 표준 도함수와 함께 미분 필드를 형성합니다.이들 분야는 선형 미분 방정식을 다루는 갈루아 이론의 변형인 미분 갈루아 이론의 중심입니다.

갈루아 이론

갈루아 이론은 덧셈과 곱셈의 산술 연산에서 대칭성을 연구함으로써 장의 대수적 확장을 연구합니다.이 영역에서 중요한 개념은 유한 갈루아 확장 F/E이며, 이는 정의상 분리 가능하고 정상적인 확장입니다.원시 요소 정리는 유한 분리 가능 확장이 반드시 단순하다는 것을 보여줍니다. 즉, 다음과 같은 형태

F = E[X] / f(X),

여기서 f는 (위와 같이) 환원불가능한 다항식입니다.^[45]이러한 확장의 경우, 정상적이고 분리 가능하다는 것은 모든 0의 f가 F에 포함되어 있고 f는 단순한 0만 가지고 있다는 것을 의미합니다.E가 0의 특성을 가지면 후자의 조건은 항상 충족됩니다.

유한 갈루아 확장에 대해, 갈루아 군 Gal(F/E)은 E에서 사소한 F(즉, 덧셈과 곱셈을 보존하고 E의 요소를 자신에게 보내는 바이젝션 σ: F → F)의 필드 오토모피즘의 그룹입니다.이 그룹의 중요성은 Gal(F/E)의 하위 그룹 집합과 확장 F/E의 중간 확장 집합 사이에 명시적인 일대일 대응을 구성하는 Galois 이론의 기본 정리에서 비롯됩니다.^[46]이러한 대응을 통해 그룹 이론적 속성은 필드에 대한 사실로 변환됩니다.예를 들어, 위와 같은 갈루아 확장의 갈루아 군이 해결될 수 없다면(아벨 군으로부터 구축될 수 없음), f 의 0은 덧셈, 곱셈, 라디칼, 즉 ${\displaystyle \text{exception 25:}}$ ${\displaystyle {\sqrt[{n}]{\}}$를 포함하는 표현으로 표현될$$수 없습니다. 예를 들어, 대칭군 S는 n개의 ≥ 5에 대해 해결될 수 없습니다. 결과적으로tly는 다음 다항식의 0을 합, 곱, 라디칼로 표현할 수 없음을 알 수 있습니다.후자의 다항식에서, 이 사실은 아벨-루피니 정리로 알려져 있습니다.

f(X) = X - 4X + 2 (및 E = Q),

f(X) = X + aX + ⋯ + a (여기서 f는 E(a, ..., a)의 다항식으로 간주되며, 일부 불확정된 a, E는 임의의 장, n ≥ 5).

필드의 텐서곱은 일반적으로 필드가 아닙니다.예를 들어, 도 n의 유한 확장 F/E는 F-대수의 동형이 존재하는 경우에만 갈루아 확장입니다.

F ⊗_E F ≅ Fⁿ.

이 사실은 대수기하학 객체에 적용할 수 있는 갈루아 이론의 광범위한 확장인 그로텐디크의 갈루아 이론의 시작입니다.^[48]

필드의 불변량

필드 F의 기본 불변량은 주요 필드에 대한 F의 특성과 초월도를 포함합니다.후자는 소수장에 대해 대수적으로 독립적인 F의 원소의 최대 개수로 정의됩니다.대수적으로 닫힌 두 필드 E와 F는 이 두 데이터가 일치하면 정확하게 동형입니다.^[49]이는 동일한 카디널리티와 동일한 특성의 셀 수 없는 두 개의 대수적으로 닫힌 필드가 동형임을 의미합니다.예를 들어, Q_p, C_p 및 C는 동형입니다(위상 필드로는 동형이 아닙니다).

장 모형론

수학적 논리학의 한 분야인 모델 이론에서, E에 대하여 참인 모든 수학적 문장이 F에 대하여 참이고, 반대로, 두 개의 필드 E와 F는 기본 동치라고 불립니다.해당 수학 문장은 1차 문장(0, 1, 덧셈 및 곱셈 포함)이어야 합니다.대표적인 예로 n > 0, n 정수의 경우 다음과 같습니다.

φ(E) = "E의 임의의 차수의 다항식은 E의 0을 갖습니다."

모든 n에 대한 이러한 공식의 집합은 E가 대수적으로 닫혀 있음을 나타냅니다.레프셰츠 원리는 C가 특성 0의 어떤 대수적으로 닫힌 필드 F와 기본적으로 동등하다고 말합니다.또한, 고정 문 φ는 충분히 높은 특성의 대수적으로 닫힌 필드에서 유지되는 경우에만 C에 유지됩니다.

U가 집합 I의 초필터이고, F가_i I의 모든 i에 대한 필드라면, U에 대한 F의_i 초곱은 필드입니다.^[51]로 표시됩니다.

울림F_i→∞i,

필드 F의 극한으로서 여러 가지 방법으로 작용하기 때문에 F: ło ś의 정리는 유한 개의 F를 제외한 모든 1차 문장이 또한 초곱에 대해 성립한다는 것을 말합니다.위 문장 φ에 적용하면 동형이 있음을 알 수 있습니다.

${\displaystyle \operatorname {ulim} _{p\to \infty} {\overline {\mathbf {F}}}_{p}\cong \mathbf {C} .}$

위에서 언급한 Ax-Kochen 정리는 이 정리와 초곱의 동형화(두 경우 모두 모든 소수 p에 걸쳐)를 따릅니다.

ulim Q ≅ulim F((t)).

또한 모델 이론은 실제 닫힌 필드 또는 지수 필드(지수 함수 exp: F → F)와 같은 다양한 다른 유형의 필드의 논리적 속성도 연구합니다.

절대 갈루아족

대수적으로 닫히지 않은(또는 분리 가능하게 닫히지 않은) 필드의 경우 절대 갈루아 군 Gal(F)이 기본적으로 중요합니다. 위에서 설명한 유한 갈루아 확장의 경우를 확장하면 이 군은 F의 모든 유한 분리 가능 확장을 지배합니다.기본적인 방법으로, 갈(F) 그룹은_q Z의 유익한 완성인 프뤼퍼 그룹임을 보여줄 수 있습니다.이 문장은 Gal(F_q)의 유일한 대수적 확장이 n > 0에 대한 Gal(F_qⁿ) 필드라는 사실과 이 유한 확장의 Galois 그룹이 다음과 같이 주어졌다는 사실을 가정합니다.

Gal(F/F) = Z/nZ.

p-adic number 필드(Q의_p 유한 확장)의 갈루아 그룹에 대해서도 생성기 및 관계에 대한 설명이 알려져 있습니다.^[53]

갈루아 군과 웨일 군과 같은 관련 군의 표현은 랭글런즈 프로그램과 같은 산술의 많은 분야에서 기본적입니다.그러한 표현에 대한 코호몰로지 연구는 갈루아 코호몰로지를 사용하여 수행됩니다.^[54]예를 들어, 중심 단순 F-대수군으로 고전적으로 정의되는 브라우어 군은 갈루아 코호몰로지 군으로 재해석될 수 있습니다.

Br(F) = H(F, G).

케이이론

밀너 K-이론은 다음과 같이 정의됩니다.

${\displaystyle K_{n}^{M}(F)=F^{\times }\otimes \cdotes \otimes F^{\times }/\left\langle x\otimes (1-x)\mid x\in F\setminus \{0,1\}\right\rangle.}$

2000년경 블라디미르 보에보드스키에 의해 증명된 노름잔류 동형 정리는 동형을 통해 갈루아 코호몰로지와 관련이 있습니다.

${\displaystyle K_{n}^{M}(F)/p=H^{n}(F,\mu _{l}^{\otimes n})}$

대수적 K-이론은 주어진 필드의 계수를 갖는 가역 행렬의 그룹과 관련이 있습니다.예를 들어, 가역 행렬의 행렬식을 취하는 과정은 K(F) = F로 이어집니다. 마츠모토의 정리는 K(F)가 K(F)와 일치함을 보여줍니다.더 높은 수준에서 K-이론은 밀너 K-이론에서 발산되며 일반적으로 계산하기 어렵습니다.

적용들

선형대수와 교환대수

만약 ≠가 0이라면, 그 방정식은

도끼 = b

는 필드 F에 고유한 해 x를 갖습니다. 즉 $x$ = a -${\displaystyle 1^{}}$ ${\displaystyle {}^{}}$.${\displaystyle$x = a$^{-1}b.}$$$ 필드 정의의 이러한 즉각적인 결과는 선형 대수학에서 기본적인 것입니다.예를 들어, 이것은 가우스 제거의 필수적인 요소이며, 벡터 공간이 기저를 가지고 있다는 증명입니다.^[55]

모듈 이론(필드 대신 링 위의 벡터 공간의 아날로그)은 위의 방정식에 여러 해가 있을 수도 있고 없을 수도 있기 때문에 훨씬 더 복잡합니다.특히 링 위의 선형 방정식 체계는 정수의 링 Z의 경우에도 필드의 경우보다 훨씬 풀기 어렵습니다.

유한장: 암호학 및 코딩 이론

널리 적용되는 암호화 루틴은 이산 지수화(discrete exponentation), 즉 컴퓨팅을 사용합니다.

a = a ⋅ a ⋅ ⋯ ⋅ a (n 요인, 정수 n ≥ 1의 경우)

(큰) 유한장에서 F는_q 이산 로그보다 훨씬 더 효율적으로 수행될 수 있습니다. 즉, 방정식에 대한 해 n을 결정하는 역연산입니다.

a = b

타원 곡선 암호학에서 유한장의 곱셈은 타원 곡선 위에 점을 추가하는 연산, 즉 형태 방정식의 해로 대체됩니다.

y = x + ax + b.

유한장은 코딩 이론과 조합론에서도 사용됩니다.

지오메트리: 함수 필드

적절한 위상 공간 X 위의 함수를 k 필드에 추가하고 점별로 곱할 수 있습니다. 예를 들어, 두 함수의 곱은 도메인 내의 값의 곱으로 정의됩니다.

(f ⋅ g)(x) = f(x) ⋅ g(x).

이것은 이 함수들을 k-가환 대수로 만듭니다.

함수의 장을 가지려면 적분 영역인 함수의 대수를 고려해야 합니다.이 경우 두 함수의 비율, 즉 형식의 표현

${\displaystyle {\frac {f(x)}{g(x)}},}$

함수의 장(field of functions)이라 불리는 장을 형성합니다.

이는 크게 두 가지 경우에 발생합니다.X가 복소수 다양체 X일 때.이 경우, 동형 함수의 대수, 즉 복잡한 미분 가능 함수를 고려합니다.그들의 비율은 X의 형함수 장을 형성합니다.

대수다양체 X(다항 방정식의 공통 0으로 정의된 기하학적 대상)의 함수 필드는 정규 함수의 비율, 즉 다양체에 대한 다항 함수의 비율로 구성됩니다.k 필드 위의 n차원 공간의 함수 필드는 k(x₁, ..., x_n), 즉 n개의 다항식의 비율로 구성된 필드입니다.X의 함수 필드는 열린 밀도 하위 변수의 함수 필드와 동일합니다.즉, 함수 필드는 X를 (약간) 작은 하위 변수로 대체하는 데 둔감합니다.

함수장은 변종의 동형성과 비이성적 등가성 하에서 불변합니다.그러므로 그것은 추상적인 대수적 품종을 연구하고 대수적 품종을 분류하는 데 중요한 도구입니다.예를 들어, k(X)의 초월도와 같은 차원은 비등가 하에서는 불변합니다.^[56]곡선(즉, 차원이 1)의 경우 함수 필드 k(X)가 X에 매우 가깝습니다. X가 부드럽고 적절할 경우(콤팩트하다는 아날로그) X를 함수 필드에서 동형화까지 재구성할 수 있습니다.^{[nb 6]}높은 차원에서 함수 필드는 X에 대한 덜 기억하지만 여전히 결정적인 정보를 기억합니다.함수 필드와 함수 필드의 기하학적 의미를 더 높은 차원에서 연구하는 것을 birational geometry라고 합니다.최소 모델 프로그램은 지정된 함수 필드로 가장 단순한(특정 정확한 의미에서) 대수적 품종을 식별하려고 시도합니다.

수론 : 전역장

대수적 수론과 산술 기하학에서 글로벌 필드가 각광받고 있습니다.정의에 따라 숫자 필드(Q의 무한 확장) 또는 F_q(F_q(t)) 위의 함수 필드입니다.로컬 필드의 경우, 이 두 유형의 필드는 각각 특성 0과 긍정적 특성임에도 불구하고 몇 가지 유사한 특성을 공유합니다.이 함수 필드 비유는 함수 필드에 대한 질문을 먼저 이해하고 나중에 숫자 필드 사례를 처리함으로써 수학적 기대를 형성하는 데 도움이 될 수 있습니다.후자가 더 어려운 경우가 많습니다.예를 들어, 리만 제타 함수의 0에 관한 리만 가설(2017년 현재 공개)은 웨일 추측(1974년 피에르 들랭에 의해 증명됨)과 평행하다고 간주될 수 있습니다.

사이클로토믹장은 가장 치열하게 연구된 수장 중 하나입니다.그들은 Q(ζ)의 형태이며, 여기서 ζ는 통일성의 원시 n번째 루트, 즉 모든 m < n에 대하여 ζ = 1과 ζ ≠ 1을 만족시키는 복소수입니다.쿰머는 방정식에 0이 아닌 유리해의 존재를 주장하는 페르마의 마지막 정리를 증명하기 위해 사이클로토믹 장을 사용했습니다.

x + y = z.

로컬 필드는 글로벌 필드의 완성입니다.Ostrowski의 정리는 전역장인 Q의 유일한 완성은 국소장 Q와_p R뿐이라고 주장합니다.글로벌 분야의 산술 문제를 공부하는 것은 때때로 현지에서 해당 문제를 보는 것으로 이루어질 수 있습니다.이 기술은 로컬-글로벌 원리라고 불립니다.예를 들어, Hasse-Minkowski 정리는 2차 방정식의 합리적인 해를 찾는 문제를 쉽게 설명할 수 있는_p R과 Q에서 이러한 방정식을 푸는 것으로 감소시킵니다.^[58]

지역 분야와 달리 글로벌 분야의 갈루아 그룹은 알려져 있지 않습니다.역 갈루아 이론은 어떤 유한한 군이 어떤 수장 F에 대한 갈루아 군 Gal(F/Q)인지 여부를 연구합니다.^[59]클래스 필드 이론은 아벨론 확장, 즉 아벨론 갈루아 군을 갖는 확장 또는 이와 동등하게 아벨론화된 글로벌 필드의 갈루아 군을 설명합니다.고전적 진술인 크로네커-베버 정리는 Q의 최대 아벨리안 Q 확장을^ab 설명합니다.

Q(ζ_n, n ≥ 2)

모든 원시 n번째 근들을 서로 인접시킴으로써 얻어집니다.크로네커의 유겐트라움은 일반적인 수 필드 F의 F에^ab 대한 유사한 명확한 설명을 요구합니다.허수 2차장 $F$ = ${\displaystyle Q}$ (${\displaystyle }$-${\displaystyle }$d${\displaystyle }$) ${\displaystyle$F =\$mathbf {Q} ({\sqrt {-d}}),$d > 0, 복소 곱셈 이론은 타원 곡선을 사용하여 F를 설명합니다.일반 숫자 필드의 경우 이러한 명시적인 설명을 알 수 없습니다.

관련개념

필드는 필드가 즐길 수 있는 추가적인 구조 외에도 다양한 관련 개념을 인정합니다.임의의 필드 0 ≠ 1이므로, 임의의 필드에는 적어도 두 개의 요소가 있습니다.그럼에도 불구하고 유한장 F의_p 극한으로 제시되는 원소가 1인 장의 개념이 있습니다.^[60]나눗셈 고리 외에도 준장, 근장 및 준장과 같은 분야와 관련된 다양한 약한 대수 구조가 있습니다.

또한 필드 구조를 가진 적절한 클래스가 있으며, 이 클래스를 F로 하여 Fields라고 부르기도 합니다.초현실수는 실수를 포함하는 필드를 형성하며 집합이 아닌 적절한 클래스라는 사실을 제외하고는 필드가 됩니다.게임 이론에서 나온 개념인 님버도 그러한 필드를 형성합니다.^[61]

나눗셈 링

필드의 정의에서 하나 또는 여러 개의 공리를 떨어뜨리면 다른 대수적 구조로 이어집니다.위에서 언급한 바와 같이, 치환환은 곱셈 역수의 존재를 제외한 모든 장 공리를 만족합니다.대신에 곱셈의 가환성을 떨어뜨리면 분할 고리나 스큐 필드의 개념이 생겨납니다.^{[nb 7]} 때때로 연관성도 약화됩니다.유한 차원 R-벡터 공간인 분할 고리는 R 자체, C(장) 및 4차 이온 H(곱이 비상호적인 경우)뿐입니다.이 결과를 프로베니우스 정리라고 합니다.곱셈이 치환도 연상도 아닌 팔색조 O는 표준화된 대체 나눗셈 대수이지만 나눗셈 고리는 아닙니다.이 사실은 1958년 미셸 케르베어, 라울 바트, 존 밀너에 의해 대수적 위상수학의 방법을 사용하여 증명되었습니다.^[62]홀수 차원 분할 대수의 존재하지 않는 것이 더 고전적입니다.오른쪽에 나와 있는 털이 많은 공 정리에서 추론할 수 있습니다.^{[citation needed]}

메모들

참고문헌

외부 링크