오마르 카이얌

오마르 카이얌(/kaɪˈjɑm, kaɪˈjæm/; 페르시아어: عمرر ر [رم [یم [[oˈmæj xjjˈ 10m; 1048년 5월 18일 – 1131년 12월 4일)은 페르시아의 다산수, 수학자, 천문학자, 철학자, 시인이다. 페르시아 북동부의 네이샤부르에서 태어났으며, 제1차 십자군 원정을 전후하여 셀주크족의 통치와 동시대를 이루었다.

수학자로서 그는 원뿔의 교차점에 의해 기하학적 해답을 제공한 입방정식의 분류와 해법에 관한 연구로 가장 유명하다.^[7] 또한 카이얌은 평행 공리를 이해하는 데 기여했다.^{[8]: 284} 천문학자로서 그는 거의 1천년이 지난 후에도 여전히 사용되고 있는 페르시아 달력의 기초를 제공하는 33년의 매우 정밀한 중간 주기를^{[9][10]: 659} 가진 태양력인 잘랄리 달력을 설계했다.

시를 쿼트라트(rubbaāiyat ععیتیتتتت)의 형태로 쓰여진 오마르 카이얌에게 귀속시키는 전통이 있다. 이 시는 핀 드 시어의 오리엔탈리즘에서 큰 성공을 거둔 에드워드 피츠제럴드(Omar Khayyam, 1859년)의 번역으로 영어 읽기 세계에 널리 알려지게 되었다.

인생

오마르 카이얌은 1048년 셀주크 왕조 시절 11세기 번영의 절정에 이른 중세 코라산의 대표적인 대도시 니샤푸르에서 태어났다.^{[11]: 15 [12][13]} 니샤푸르 역시 조로아스터교의 주요 중심지였으며, 하이야암의 아버지는 이슬람교로 개종한 조로아스터교인이었을 가능성이 높다.^{[14]: 68} 아랍어 출처에 등장하는 그의 정식 이름은 아부엘 파트 오마르 이븐 이브라힘 알 카예암이었다.^[15] 중세 페르시아어 문헌에서 그는 보통 단순히 오마르 카이얌이라고 불린다.^[16] 의심의 여지가 있지만, 카예암이 아랍어로 텐트메이커를 의미하기 때문에 그의 선비들이 텐트 메이킹의 거래를 따랐다고 추측되는 경우가 많다.^{[17]: 30} 오마르와 친분이 있었던 역사학자 바야키는 오마르와 별점을 자세히 소개한다. "그는 제미니였고, 태양과 수성은 상승[...]^{[18]: 471} 했다." 이것은 현대 학자들이 그의 생년월일을 1048년 5월 18일로 정하기 위해 사용했다.^{[10]: 658}

그의 소년 시절은 니샤푸르에서 보냈다.^{[10]: 659} 그의 재능은 초기 스승들이 그를 보내 고라산 지역의 가장 위대한 스승인 이맘 무와파크 니사부리 밑에서 공부하게 한 것으로 인정받았다. 오마르는 오랜 세월 동안 그와 훌륭한 우정을 쌓았다.^{[14]: 20} 하이야암은 조로아스터교의 개종자인 수학자 아부 하산 바흐마마르 빈 마르즈반에게도 가르침을 받았다.^[19] 니샤푸르에서 과학, 철학, 수학, 천문학을 공부한 후, 1068년 경에 부하라 지방을 여행했는데, 그곳에서 그는 방주의 유명한 도서관을 자주 찾았다. 1070년경 그는 사마르칸트로 이주하여, 도시의 주지사 겸 주심인 아부 타히르 압드 알 라흐만 ibn ʿ 알라크의 후원 아래 대수에 관한 그의 유명한 논문을 작곡하기 시작했다.^[20] 오마르 카예암은 카라카니드의 지배자인 샴스 알-물크 나스르로부터 친절하게 맞아들였는데, 그는 "바야흐치에 따르면, 그에게 "오마르"를 그의 왕좌에 앉힐 정도로, 그에게 가장 큰 영광을 안겨줄 것"이라고 말했다.^{[17]: 34 [14]: 47}

1073–4년 카라카니드 영토에 침입한 술탄 말리크-샤 1세와 평화는 종결되었다. 하야마는 1074–5년에 말리크샤의 봉사에 들어갔고, 그란 비지에 니잠 알물크의 초대를 받아 마르브 시에서 말리크샤를 만났다. 그 후 카얌은 이스파한에 천문대를 설치하고, 페르시아 달력 개정을 목표로 한 정확한 천문 관측을 수행하는데 있어서 과학자 집단을 이끄는 임무를 맡았다. 이 사업은 아마도 1076년에 시작되었고 1079년에^{[14]: 28} 오마르 카이얌과 그의 동료들이 놀랄 만큼 정확하게 14명의 중요한 인물들에게 보고하면서 그 해의 길이에 대한 측정을 끝냈을 때 끝났다.

말리크샤와 그의 비지어(살해된 것으로 생각되며, 자객단의 이스마일 명령에 의해)가 죽은 후, 오마르는 법정에서 호감을 잃었고, 그 결과 곧 메카 순례에 나섰다. 알-키프티 기자가 보도한 그의 순례의 숨은 동기는 적대적인 성직자들이 그에게 평준화시킨 비정상적인 (조로아스트리아주의에 대한 동정 가능성 포함) 의혹을 해소하고 이를 반박하기 위한 목적으로 그의 신앙을 공개적으로 입증한 것이었다.^{[21][14]: 29} 그 후 그는 새로운 술탄 산자르의 초청을 받아 마르브에 갔으며, 아마도 궁정 점성술사로 일하게 될 것이다.^[1] 이후 건강이 악화되어 니시푸르로 복귀할 수 있게 되었다. 그가 돌아오자 은둔자 생활을 한 것 같다.^{[22]: 99}

1131년 12월 4일 고향인 니샤푸르에서 83세의 나이로 오마르 카이얌이 사망하였고, 현재 오마르 카이얌의 묘소에 안장되어 있다. 그의 제자 중 한 명인 니자미 아루지는 1112–3년 카예암이 알-이스피자리(잘랄리 달력에 그와 협력했던 과학자 중 한 명)와 함께 발크에 있었다는 이야기를 전하면서 "내 무덤은 북풍이 장미꽃을 흩뿌릴지도 모르는 곳에 있을 것"^{[17]: 36 [12]}이라고 예언했다. 죽은 지 4년 후, 아루지는 그의 무덤을 마르브로 가는 길의 당시 크고 잘 알려진 니샤푸르 사분의 공동묘지에 위치시켰다. 하이야암이 예견한 대로 아루지는 정원 담벼락 기슭에 위치한 무덤을 발견했는데, 그 위에 배나무와 복숭아나무가 머리를 들이밀고 꽃을 떨어뜨려 묘비가 그 밑에 숨겨져 있었다.^[17]

수학

카이얌은 수학자로서 그의 일생 동안 유명했다. 그가 남긴 수학적 저작은 다음과 같다. 유클리드 초등 기하학의 공준에 관한 어려움에 관한 논평, 원(Risālah fīqismah 문제의 al-dā'irah, 날짜가 없는지만 완성되기 전에 그 논문에 algebra[6])의 사분면의 분단과 문제를 대수학에 관련된 증거에서(Risāla fī šarḥmā aškala분muṣādarāt kitāb Uqlīdis, 12월경에 완성되 1077[6]).(Maq1079년에^{[8]: 281} 완성되었을 가능성이 가장 높다. 그는 나아가 이항 정리와 자연수의 n^th 근원을 추출하는 논문을 썼는데, 이 논문은 잃어버린 것이다.^{[14]: 197}

평행 이론

유클리드 원소에 대한 하야마의 논평 중 일부는 평행한 공리를 다루고 있다.^{[8]: 282} 하이야암의 논문은 쁘띠오 공정에 근거한 것이 아니라 보다 직관적인 서술에 근거한 공리학의 첫 번째 취급으로 간주될 수 있다. 하이야암은 그 명제를 증명하기 위한 다른 수학자들의 이전의 시도를 반박하는데, 그 이유는 주로 그들 각자가 제5항체 자체보다 결코 인정하기 쉽지 않은 것을 가정했다는 것이다.^[6] 아리스토텔레스의 관점을 바탕으로 그는 기하학의 움직임의 사용을 거부하고 따라서 알 헤이담의 다른 시도를 일축한다.^[23][24] 수학자들이 유클리드의 진술을 다른 견습관으로부터 증명하지 못한 것에 만족하지 못한 오마르는 모든 직각은 서로 동등하다고 진술한 제4의 견습관과 공리를 연결하려고 했다.^{[8]: 282}

카이얌은 가장 먼저 카이얌-사체리 4각형의 정상 각도에 대해 급, 둔, 직각의 세 가지 뚜렷한 경우를 고려했다.^{[8]: 283} 그에 대한 여러 가지 이론들을 입증한 후, 그는 Postulate V가 직각 가설에서 따온다는 것을 보여주었고, 둔하고 예리한 경우를 자기 모순이라고 반박했다.^[6] 평행 가설임을 입증하려는 그의 정교한 시도는 비유클리드 기하학의 가능성을 분명히 보여주고 있기 때문에 기하학의 추가 발전에 중요한 의미를 지닌다. 급성, 둔탁, 직각의 가설은 현재 가우스-볼라이-로바체프스키의 비유클리드 쌍곡 기하학, 리만 기하학, 유클리드 기하학으로 각각 이어지는 것으로 알려져 있다.^[25]

투시는 하야마의 평행선 치료에 대한 논평이 유럽으로 이어졌다. 옥스퍼드 대학의 기하학 교수인 존 월리스는 투시의 해설을 라틴어로 번역했다. 일반적으로 비유클리드 기하학의 궁극적 발전의 첫걸음으로 여겨지는 예수회 측지계 지롤라모 사케리(Jirolamo Saccheri)는 월리스의 작품에 익숙했다. 미국 수학사학자 데이비드 유진 스미스는 사케리가 "투시와 같은 보조정리법을 사용했으며 심지어 정확하게 같은 방법으로 숫자를 쓰고 같은 목적을 위해 보조정리법을 사용했다"고 언급하고 있다. 그는 또 "투시는 오마르 카이얌 덕분이라고 분명하게 말하고 있으며, 본문만 봐도 후자가 그의 영감을 준 사람임이 분명해 보인다"^{[22]: 104 [26][14]: 195} 고 말한다.

실수개념

이 유클리드 논문은 비율 이론과 비율의 배합을 다루는 또 다른 기여를 포함하고 있다. 카이얌은 비율의 개념과 수의 개념의 관계를 논하고 다양한 이론적 난관을 명시적으로 제기한다. 특히 불합리한 수의 개념에 대한 이론적 연구에 기여하고 있다.^[6] 유클리드(유클리드)의 등비(등비)의 정의에 못마땅한 그는 비율을 표현하는 수단으로서 연속적인 분수를 사용함으로써 숫자의 개념을 재정립했다. 로젠펠트와 유슈케비치(1973)는 "비합리적인 양과 숫자를 같은 작전 규모에 배치함으로써 [케이얌]이 수의 교리에서 진정한 혁명을 시작하게 되었다"고 주장한다. 마찬가지로, D. J. 슈트루익도 오마르가 "실수의 개념으로 이어지는 숫자 개념의 그 연장선에 가고 있다"^{[8]: 284} 는 점에 주목했다.

기하 대수학

Rashed와 Vahabzadeh(2000년)는 대수 방정식에 대한 그의 철저한 기하학적 접근 때문에, Khayyam은 분석 기하학의 발명에 있어서 데카르트의 전조로 간주될 수 있다고 주장해 왔다.^{[27]: 248} 서클 카이얌의 사분면 분할에 관한 논문에서 기하학에 대수학을 적용했다. 그는 이 작품에서 원형의 수직 직경까지 분할점에서 투영된 선분면이 특정 비율을 형성하는 등 원형 사분면을 두 부분으로 나눌 수 있는지 여부를 조사하는 데 주력했다. 그의 해법은 차례로 세제곱과 이차 항을 포함하는 방정식을 만드는 몇 개의 곡선 구조를 채택했다.^{[27]: 248}

입방정식의 해법

카이얌은 최초로 입방정식의^[28] 일반론을 구상하고, 양근에 관한 한 모든 형태의 입방정식을 기하학적으로 푼 것으로 보인다.^[29] 대수학 논문에는 입방정식에 대한 그의 연구가 포함되어 있다.^[30] 나침반과 직선 가장자리로 풀 수 있는 (i)방정식, 원뿔단위로 풀 수 있는 (iii)방정식, 미지의 역이 수반되는 (iii)방정식의 세 부분으로 나뉜다.^[31]

Khayyam은 선, 정사각형, 정육면체를 포함하는 가능한 모든 방정식의 전체 목록을 작성했다.^{[32]: 43} 그는 3개의 이항 방정식, 9개의 삼항 방정식, 7개의 사항 방정식을 고려했다.^{[8]: 281} 1, 2급 다항식에는 기하학적 구조에 의한 수치해결을 제공했다. 그는 14개의 다른 종류의 큐빅이 있다고 결론지었다.^[6] 이것들 때문에 그는 나침반과 직선 가장자리로는 그의 알려지지 않은 부분의 건설을 성취할 수 없었다. 그는 계속해서 원뿔 단면의 특성을 이용하여 모든 유형의 입방정식에 기하학적 해결책을 제시하였다.^{[33]: 157 [8]: 281} 하이야암의 기하학적 증거를 위한 전제 조건 레마는 유클리드 6세, 프로프 13세, 아폴로니우스 2세, 프로프 12세 등이다.^{[33]: 155} 입방정식의 양근은 예를 들어 두 포물선의 교차점, 또는 포물선과 원의 교차점 등 두 원뿔의 교차점 압시사로 결정되었다.^{[34]: 141} 그러나 그는 이들 큐빅들의 산술 문제가 여전히 해결되지 않은 상태임을 인정하면서 "아마도 우리 뒤에 다른 사람이 알게 될 것"이라고 덧붙였다.^{[33]: 158} 이 과제는 16세기까지 열려 있었는데, 르네상스 이탈리아의 카르다노, 델 페로, 타르타글리아에 의해 입방 방정식의 대수적 해법이 그 일반성에서 발견되었다.^{[8]: 282 [6]}

사실상 하야마의 작품은 대수학과 기하학을 통일하려는 노력이다.^{[36]: 241} 입방정식의 이 특정한 기하학적 용액은 M에 의해 추가적으로 조사되었다. 하크트루디와 4급 방정식까지 풀었다.^[37] 메나에흐무스 이후 비슷한 방법들이 산발적으로 나타났고, 10세기 수학자 아부 알 저드에 의해 더욱 발전해 왔으나, 하이얌의 연구는 최초의 체계적인 연구와 최초의 정확한 입방정식 해결방법으로 볼 수 있다.^[38][39][40] 하이야암의 대수학을 프랑스어로 번역해 제시한 수학자 뷔케(1851)는 "일반화의 힘과 엄밀하게 체계적인 절차"를 칭찬했다.^{[41]: 10}

이항정리 및 뿌리채취

그의 대수학 논문에서, Khayyam은 기하학적 형상에 의존하지 않는 법칙을 이용하여 숫자의 $뿌리$인$$n {\$displaystyle n}$의 추출에 대해 쓴 책을 암시한다.^[34] 이 책은 산술의 어려움(모슈켈라트 알-헤사브)^[6]이라는 제목이 유력하며, 현존하지 않다. D. J. 슈트루익과 같은 수학사학자들 사이에서는 오마르가 이항${\displaystyle (+b{}^{}}$)${\displaystyle n^{}}$ ${\$의 팽창 공식을 알고 있었을 것이라고 믿고 있는데, 여기서 n은 양의 정수다.^{[8]: 282} 힘 2의 경우는 유클리드 원소에 명시되어 있으며, 힘 3의 경우는 인도의 수학자들에 의해 성립되었다. 카이얌은 일반적인 이항 정리의 중요성을 알아차린 수학자였다. 카이얌이 일반적인 이항 정리가 있었다는 주장을 뒷받침하는 주장은 그의 뿌리 뽑기 능력에 근거한 것이다.^[43] 카얌의 전임자 중 한 명인 알카라지는 유럽인들이 나중에 파스칼의 삼각형이라고 알게 된 이항 팽창 계수의 삼각형 배열을 이미 발견하였다;^[44] 카얌은 이란에서 이 삼각형 배열을 대중화하여 지금은 오마르 카얌의 삼각형으로 알려져 있다.^[34]

천문학

1074–5년에 오마르 카이얌은 술탄 말리크샤로부터 이스파한에 천문대를 세우고 페르시아 달력을 개혁하라는 의뢰를 받았다. 그곳에는 8명의 학자로 구성된 패널이 카이얌의 지시로 대규모 천문 관측을 하고 천문표를 수정하기 위해 일하고 있었다.^{[34]: 141} 달력을 다시 보정하는 것은 춘분을 가로지르는 태양의 중심이 지나가는 정확한 순간에 그 해의 첫날을 고정시켰다. 이로써 봄이나 노루즈의 시작을 알리게 되는데, 이 날은 태양이 정오 전에 양자리 1도로 들어가는 날이다.^{[45] [46]} 결과 달력은 말리크샤의 영예에 잘랄랄레 달력으로 명명되어 1079년 3월 15일 취임하였다.^[47] 이 전망대 자체는 1092년 말리크샤의 죽음 이후 사용되지 않았다.^{[10]: 659}

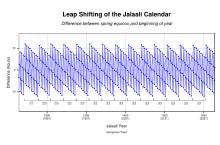
잘랄로 달력은 조디악의 해당 부호를 가로지르는 태양의 통과 시간과 매달의 지속시간이 같은 진정한 태양력이었다. 달력 개혁은 33년 간의 독특한 중간 주기를 도입했다. 카지니의 작품에서 알 수 있듯이, 카이야의 집단은 4년마다, 5년마다의 윤년을 바탕으로 한 분간제를 시행했다. 따라서 달력은 365일을 포함한 25개의 평년과 366일을 포함한 8개의 윤년으로 구성되었다.^[48] 달력은 11세기부터 20세기까지 이란 전역에서 계속 사용되었다. 1911년 잘랄리 달력은 이란의 공식 국가 달력이 되었다. 1925년에 이 달력은 단순화되었고 달들의 이름은 현대화되었고, 그 결과 현대 이란 달력이 탄생했다. 잘랄리 달력은 그레고리력으로 1582년에 비해 정확도가 높으며,^{[10]: 659} 하루의 오차가 5,000년에 걸쳐 누적되는 양력으로는 그레고리력으로 3,330년에 한 번 꼴로 나타나는 것과 비교된다.^{[14]: 200} 모리츠 칸토르는 그것이 지금까지 고안된 달력 중 가장 완벽한 달력이라고 생각했다.^{[22]: 101}

사마칸드의 제자 니자미 아루지는 카예암이 점성술과 점성술에 대한 믿음이 없었던 것으로 보인다고 말했다. 오마르 카이얌)은 점성술적 예언에 대해 대단한 신념을 가지고 있었고, 그런 신념을 가진 위대한 [과학자]들 중 어느 누구도 보거나 들어본 적이 없다."^{[41]: 11} 술탄 산자르에서 점성술사로 일하는 동안 그는 날씨를 예측해 달라는 요청을 받았다. 그는 분명히 잘 하지 못한 직업이었다.^{[14]: 30} 조지 살리바(2002)는 오마르의 삶과 일에 대한 언급이 발견될 수 있는 다양한 출처에서 사용되는 '일름알누주름'이라는 용어가 점성술을 의미하는 것으로 잘못 번역되기도 했다고 설명한다. 그는 덧붙인다: "적어도 10세기 중반부터 파라비의 과학에 대한 열거에 따르면, 이 과학인 'ilm al-nujum'은 이미 점성술과 이론 수학 천문학으로 두 부분으로 나뉘어져 있었다."^{[49]: 224}

'별을 날아가게 하는 돌'을 던지는 태양 광선적 이미지로 첫 줄이 잘못 번역된 에드워드 피츠제럴드의 '하얀 시'를 '헬리오센트리즘'으로 믿었다는 취지의 주장이 대중적 근거다. 사실 피츠제럴드가 가장 많이 번역한 하이야암의 루바이야트 1행 번역본은 "어웨이크! 밤의 그릇 속의 모닝이 별을 날리게 하는 돌을 던져 버렸기 때문이다.'^[50]

기타 작품

그는 아르키메데스의 원칙(전체 타이틀로, 두 권으로 이루어진 화합물에서 금과 은의 두 양을 아는 기만)에 전념하는 짧은 논문을 가지고 있다. 은을 섞은 금의 혼합물에 대해 그는 각 원소의 용량 당 무게를 더 정확하게 측정하는 방법을 설명한다. 무게는 부피보다 정확히 측정하기 쉽기 때문에 공기와 물 모두에서 화합물을 무게를 재는 것이 포함된다. 금과 은 둘 다와 같은 것을 반복함으로써, 사람들은 정확히 물 금, 은, 화합물보다 얼마나 무거운지를 알게 된다. 이 논문은 다른 곳에서도 이 문제를 다룬 카지니나 알 나일리지의 해법보다 하이야암의 해법이 더 정확하고 정교하다고 믿었던 에일하르트 비데만(Eilhard Wiedemann)에 의해 광범위하게 검토되었다.^{[14]: 198}

또 다른 짧은 논문은 음악과 산수의 연관성을 논하는 음악 이론에 관한 것이다. 하야마의 공헌은 음악 음계의 체계적인 분류를 제공하고 음표, 부음, 장음, 사음부, 사음부 사이의 수학적 관계를 논하는 데 있었다.^{[14]: 198}

시

오마르 카얌의 시에 대한 가장 초기의 암시는 역사학자 이마드 앗딘 알 이스파하니(Imad ad-Din al-Isfahani)로부터 나온 것으로, 그는 그를 시인 겸 과학자(Kharidat al-qasr, 1174)라고 명시적으로 밝히고 있다.^{[14]: 49 [52]: 35} 오마르 카이얌의 루비야트의 초기 표본 중 하나는 파흐르 알딘 라지 출신이다. 그의 작품 '알라 바드 아스라르 알-마우'dat fi'l-Qur'an (1160년)에서 그는 그의 시들 중 하나를 인용한다(피츠제랄드 초판의 콰트레인 LXII에 해당한다). 다야는 그의 저술(Mirsad al-'Ibad, ca. 1230)에서 두 개의 쿼트라인을 인용하고 있는데, 그 중 하나는 라지가 이미 보고한 것과 같다. 추가 퀘스트레인(Quatrain)은 역사가 쥬바이니(타리크이 자한구세이, ca. 1226–1283)에 의해 인용된다.^{[52]: 36–37 [14]: 92} 1340년 자하르미는 페르시아의 유명한 시인(Munis al-aharr)의 작품집을 수록한 그의 작품에 13개의 하야람을 포함시켰는데, 그 중 2개는 이전부터 전해져 왔다.^[53] 비교적 늦은 원고는 1460년 시라즈에서 쓰여진 보들리언 MS. 오우슬리 140으로 47폴리아에 158개의 쿼트라인이 들어 있다. 원고는 윌리엄 오슬리(1767–1842)의 소유였으며, 1844년 보들리언 도서관에서 구입하였다.

13, 14세기 작가에게 귀속된 문헌에는 가끔 오마르에게 귀속된 구절이 인용되기도 하지만, 이것들은 진정성이 의심스러워서, 회의적인 학자들은 전체 전통이 유사문자일 수도 있다고 지적한다.^{[52]: 11}

1934년 한스 하인리히 셰더(Hans Heinrich Schaeder)는 자신 있게 그에게 귀속될 수 있는 어떠한 자료도 없기 때문에 오마르 카예암의 이름이 "페르시아 문학사에서 제외될 것"이라고 평했다. 데 블루아(2004)는 샤이더 시대 이후 상황이 크게 변하지 않았다고 비관적으로 결론내리며 원고 전통의 참고 문헌을 제시한다.^[54] 신드바드-나메흐에서 인용된 오마르가 사망한 지 30년이 지난 후 오마르의 침수로 추정되는 5개가 발견된다. 이것이 오마르의 시대에 혹은 곧 후에 이러한 특정 구절이 유통되고 있다는 것을 증명하지만, 이 구절이 그의 구절이 틀림없다는 것을 의미하지는 않는다. 드블루아는 적어도 시를 오마르 카이얌에게 귀속시키는 과정은 이미 13세기에 시작된 것으로 보인다고 결론짓는다.^[55] 에드워드 그랜빌 브라운(1906)은 "하얀이 많은 쿼터를 썼다는 것은 확실하지만, 예외적인 몇 가지 경우, 그가 자신에게 지목된 쿼터를 썼다고 긍정적으로 주장하는 것은 거의 불가능하다"고 말했다.^{[10]: 663}

In addition to the Persian quatrains, there are twenty-five Arabic poems attributed to Khayyam which are attested by historians such as al-Isfahani, Shahrazuri (Nuzhat al-Arwah, ca. 1201–1211), Qifti (Tārikh al-hukamā, 1255), and Hamdallah Mustawfi (Tarikh-i guzida, 1339).^{[14]: 39}

보일레와 프례(1975)는 아비케나, 가잘리, 투시 등 이따금 쿼트라인을 쓴 페르시아 학자들이 다수 있다고 강조한다. 그는 또한 "이 짧은 시는 아마도 제자들의 내면을 교화하거나 즐겁게 하기 위해 휴식의 순간에 그것들을 작곡한 학자들과 과학자들의 작품인 것 같다"고 Khayyam 시에게는 그의 여가 시간의 즐거움이었을 가능성도 있다고 결론짓는다.^{[10]: 662}

오마르 카이얌에게 귀속된 시는 에드워드 피츠제럴드(1859년)가 이러한 구절을 영어로 번역한 것이 극도의 인기를 끈 직접적인 결과로서 근대에 그의 대중적 명성에 크게 기여했다. 오마르 카이얌의 피츠제럴드 루바이야트는 보들레아 필사본에서 나온 쿼트라인을 느슨하게 번역한 내용을 담고 있다. 1929년에 편찬된 서지학은 300개 이상의 개별 판을 나열할 정도로 긴 시어기에 성공을 거두었고,^[56] 그 이후 많은 책이 출판되었다.^[57]

철학

카얌은 지적으로 자신을 아비켄나의 학생으로 여겼다.^[58] 알베이하치에 따르면 그는 죽기 전에 아비케나의 <치유서>에 나오는 형이상학을 읽고 있었다.^{[10]: 661} 하이야암이 쓴 것으로 추정되는 철학 논문은 모두 6편이다. 그 중 하나인 온존(Fi'l-wujud)은 원래 페르시아어로 쓰여진 것으로 존재의 주제와 우주와의 관계를 다루고 있다. '세계의 모순의 필요성, 결정론, 생존론(Darurat al-tadad fi'l-'alam wa'l-jabr wa'l-baqa'라는 제목의 또 다른 논문은 아랍어로 쓰여져 있으며 자유 의지와 결정론을 다루고 있다.^{[58]: 475} The titles of his other works are On being and necessity (Risālah fī’l-kawn wa’l-taklīf), The Treatise on Transcendence in Existence (Al-Risālah al-ulā fi’l-wujūd), On the knowledge of the universal principles of existence (Risālah dar ‘ilm kulliyāt-i wujūd), and Abridgement concerning natural phenomena (Mukhtasar fi’l-Tabi‘iyyāt).

종교관

하야마의 돌격들을 문자 그대로 읽으면 비관주의, 허무주의, 미사여구주의, 숙명주의, 선동주의의 결합으로 삶에 대한 그의 철학적인 태도를 해석하게 된다.^{[14]: 6 [59]} 이 견해는 아서 크리스텐슨, H. 쉐더, 리차드 N과 같은 이란 학자들에 의해 취해진다. 프라이, E. D. 로스,^{[60]: 365} E. H. 와인필드^{[41]: 40} , 조지 새튼.^{[11]: 18} 반대로, 카야민 쿼트라인은 신비로운 수피 시로도 묘사되어 왔다. ^[61] J. C. E. Bowen(1973)은 그의 페르시아의 수구 외에도, Kayyam의 아랍 시들도 "Kayyam이 역사적으로 존재했다고 알려진 깊이 사려 깊은 합리주의 철학의 전망과 전적으로 일치하는 비관적인 관점을 보여준다"^{[62]: 69} 고 언급하고 있다. 에드워드 피츠제럴드는 자신이 하얌에서 발견한 종교적 회의론을 강조했다.^[63] 그 Rubáiyát에 서문에서 그는 그와 부인했다:그의 사키, 플래쉬가 그리고 혈액서 그에게 부어 신의 상징성에 어떤 가식은 포도의 될 그의 와인은 그 참신한 주스:그의 터번,:"다 증오와 무서운에 의해 Sufis"[64]주장했다."[65]:62서덱 헤더 야트는 Khayyam의 philosoph의 가장 두드러진 지지자들의.y는 불가지론적인 회의론자로써, 얀 리프카(1934년)에 따르면, 그는 심지어 카예암을 무신론자로 간주하기도 했다.^[66] 헤다야트(1923년)는 "카이얌은 인체의 투과와 변형을 믿지만 별도의 영혼은 믿지 않는다. 우리가 운이 좋다면 우리의 육체적 입자는 포도주 항아리를 만드는 데 쓰일 것이다"^[67]라고 말한다. 후기 연구(1934–35)에서 그는 더 나아가 "와인"과 같은 수피크 용어를 사용한 것은 문자 그대로이며, "카이얌은 쓴맛을 물리치고 생각의 첨단을 무디게 하기 위해 포도주에 피신했다"^[68]는 존재론적 슬픔의 해독제로서 순간의 쾌락으로 돌아섰다고 주장한다. 이런 전통에서 오마르 카얀의 시는 크리스토퍼 히친스의 <휴대용 무신론자>와 같은 뉴 무신론의 맥락에서 인용되어 왔다.^[69]

알-키프티 (ca. 1172–1248)는 오마르의 철학의 이러한 견해를 확인하기 위해 등장한다.^{[10]: 663} 그의 저서 『학자의 역사』에서 그는 오마르의 시가 겉으로는 수피 양식에 불과했을 뿐, 반종교적인 의제로 쓰여졌다고 보고한다.^{[60]: 365} 그는 또한 그가 어느 순간 불신죄로 기소되었지만, 그가 경건했다는 것을 증명하기 위해 순례길에 올랐다고 언급한다.^{[14]: 29} 보고서는 그가 모국으로 돌아오자마자 깊은 신념을 숨기고 아침저녁으로 예배 장소로 가면서 엄격한 신앙생활을 했다고 밝혔다.^{[60]: 355}

'존재 원리에 대한 지식'이라는 제목의 작품 맥락에서, 카예암은 수피 길을 지지한다.^{[14]: 8} Csillik(1960)은 오마르 카예암이 수피즘에서 정통 종교에 대항하는 동맹으로 볼 수 있는 가능성을 제시한다.^{[70]: 75} 다른 해설가들은 오마르의 시가 반종교적 의제를 갖고 있다는 것을 받아들이지 않고 술과 취미에 대한 그의 언급을 수프리즘에서 흔히 볼 수 있는 전통적인 은유적 의미로 해석한다. 프랑스어 번역가 J. B. 니콜라스는 오마르가 끊임없이 권하는 와인을 문자 그대로 받아 들이지 말고, 오히려 "와인"에 의한 광란의 도취는 바카의 깨달은 상태나 신성한 황홀감에 대한 비유로 이해되어야 하는 수피 사상에 비추어 보아야 한다고 주장했다.^[71] 오마르 카이얌을 수피로 보는 시각은 비에르가르가르드(1915년),^[72] 이드리 샤(1999년),^[73] 더건(1991) 등이 옹호하면서 오마르 시를 '깊은 난해'로 이해해야 한다고 주장하면서 쾌락주의의 평판을 피츠제럴드의 번역 실패 탓으로 돌린다.^[74] 반면 모하마드 알리 포루기, 모하메드 미노비 등 이란 전문가들은 오마르 카예암이 수피족이라는 가설을 일축했다.^{[62]: 72} 포루피는 카얌의 사상이 때때로 수피스의 사상과 일치했을지 모르지만 그가 정식으로 수피족이었다는 증거는 없다고 말했다. 아민라자비(2007)는 "하이야암의 수피 해석은 그의 루바ī야트를 광범위하게 읽고 내용을 고전적인 수피 교리에 맞게 늘려야만 가능하다"^{[14]: 128} 고 말한다. 게다가, Fry(1975)는 같은 세기에 속해 있던 수많은 유명한 수피 신비주의자들로부터 하이야암이 극도의 미움을 받았다고 강조한다. 여기에는 샴스 타브리지(루미의 정신적 안내자),^{[14]: 58} 오마르 카이야를 "불행한 철학자, 무신론자, 물질주의자"^{[62]: 71} 라고 묘사한 나짐 알딘 다야, 그를 동료 신학자가 아닌 자유사상 과학자로 여기며 이후 처벌을 기다리는 아타르가 포함된다.^{[10]: 663}

세이예드 호세인 나스르는 오마르 카얌의 철학을 확립하기 위해 자신의 시구를 문자 그대로 해석하는 것(처음에는 상당수의 진위가 불확실함)을 사용하는 것이 "감소적"이라고 주장한다. 대신 그는 하이야암의 해석적 번역으로 아비켄나의 통일론(Al-Khutbat al-Tawhd)을 인용, 저자와 일치하여 신통합에 대한 정통적 견해를 표현한다.^[75] 오마르의 것으로 추정되는 산문 작품들은 페리파티틱 문체로 쓰여져 있으며 명백히 신과 경계의 존재와 같은 주제를 다루고 있다.^{[14]: 160} 보웬이 지적한 바와 같이 이 작품들은 수피즘의 미묘함보다는 형이상학의 문제에 그가 관여했음을 나타낸다.^{[62]: 71} 카얌의 신앙과/또는 이슬람 관습에 대한 순응의 증거로, 아미라자비는 그의 논문에서 하나님과 무함마드를 찬양하면서 경례와 기도를 드린다고 언급한다. 대부분의 전기적 추출물에서 그는 이맘, 믿음의 수호자(Ghīyáth al-Dnn), 진리의 증거(Hujat al-Haq)와 같은 종교적 존댓말을 인용한다.^[14] 그는 또한 그의 종교성을 찬양하는 전기 작가들은 일반적으로 그의 시를 언급하는 것을 피하는 반면, 그의 시를 언급하는 사람들은 종종 그의 종교적인 성격을 칭찬하지 않는다는 점에 주목한다.^{[14]: 48} 예를 들어, 몇 년 동안 다른 전기적 통지에 의해 언급된 알-베이하치의 계정은 오마르가 그의 마지막 시간까지 정통적인 견해를 공언한 매우 경건한 사람이라고 말한다.^{[76]: 174}

기존의 모든 텍스트와 전기적 증거에 기초하여, 그 질문은 다소 열려 있으며,^{[14]: 11} 그 결과 카얌은 날카롭게 대립되는 감사와 비판을 받았다.^{[60]: 350}

리셉션

오마르 카이얌을 언급하는 다양한 전기적 발췌문은 그가 그의 시대 동안 과학적 지식과 성취에서 타의 추종을 불허하는 것으로 묘사하고 있다.^[77] 많은 사람들은 그를 지혜의 왕(아랍어: ملكككءءء)이라는 비명으로 불렀다. 샤흐라주리(1300년)는 그를 수학자로서 높이 평가하며, 그가 "철학학의 다양한 분야에서 아비케나의 후계자"로 여겨질 수 있다고 주장한다.^{[60]: 352} 알-키프티 (d. 1248년)는 비록 그의 견해에 동의하지 않지만, "자연철학과 천문학에 대한 그의 지식에서 비독점적이었다"는 것을 인정한다.^{[60]: 355} 리차드 N에 따르면, 많은 전기 작가들에 의해 시인으로서 환영을 받았음에도 불구하고, 프례는 "1급 시인으로서의 하야마의 지위는 비교적 늦은 발전이라고 주장할 수 있다"^{[10]: 663} 고 말했다.

토마스 하이드(Thomas Hyde)는 오마르에게 주의를 환기시키고 그의 진부한 말들 중 하나를 라틴어로 번역한 최초의 유럽인이었다(역사 종교는 페르사룸 어룸 마고룸, 1700).^{[78]: 525} 페르시아에 대한 서양의 관심은 19세기 오리엔탈리즘 운동과 함께 커졌다. Joseph von Hammer-Purgstall (1774–1856) translated some of Khayyam's poems into German in 1818, and Gore Ouseley (1770–1844) into English in 1846, but Khayyam remained relatively unknown in the West until after the publication of Edward FitzGerald's Rubaiyat of Omar Khayyam in 1859. 피츠제럴드의 작품은 처음에는 성공하지 못했지만 1861년부터 휘틀리 스톡스에 의해 대중화되었고, 그 작품은 프리 라파엘 사람들의 큰 찬사를 받게 되었다. 1872년에 피츠제럴드는 미국에서 이 작품에 대한 관심을 증가시키는 제3판을 인쇄했다. 1880년대까지 이 책은 수많은 '오마르 카얌 클럽'과 '루바이야트 족의 핀 드 시엘 컬트'가 형성될 정도로 영어권 세계 전역에 매우 잘 알려져 있었다.^[79] Khayyam의 시는 많은 언어로 번역되었다; 최근의 많은 시들은 피츠제럴드의 시보다 더 문자 그대로다.^[80]

피츠제럴드의 번역은 모국인 이란에서도 시인으로서 하이야임에 대한 관심을 다시 불러일으킨 요인이었다.^[81] 사데흐 헤다야트는 그의 '하이야암의 노래'(Taranehha-ye Khayyam, 1934년)에서 오마르의 시적 유산을 현대 이란에 다시 소개했다. 팔라비 왕조 아래, 건축가 하우상 세이훈이 설계한 새 하얀 대리석 기념비가 그의 무덤 위에 세워졌다. 1960년대 테헤란 랄레 파크에 아볼하산 사디기의 동상이 세워졌고, 니사푸르에 있는 하이야암의 묘소 근처에 같은 조각가의 흉상이 세워졌다. 2009년 이란 정부는 비엔나 국제 센터에 문을 연 유엔 사무소에 전시관을 기증했다.^[82] 2016년에는 오클라호마 대학, 니샤푸르, 이탈리아 플로렌스 대학 등 3개 동상이 공개됐다.^[83] 150명 이상의 작곡가들이 루바이야트를 영감의 원천으로 사용해 왔다. 그러한 작곡가의 초창기는 리자 레만이었다.^[6]

피츠제럴드는 오마르의 이름을 '텐트메이커'로 개명했고, 영국식 이름인 '텐트메이커 오마르'는 영어권 대중문화에 한동안 울려 퍼졌다. 그리하여 나단 하스켈 돌은 1898년 텐트메이커 오마르라는 소설을 출판했다. 나이샤푸르 텐트메이커 오마르는 1910년에 출판된 존 스미스 클라크의 역사 소설이다. 텐트메이커 오마르(Omar the Tentmaker)는 1922년 무성영화로 각색된 리처드 월튼 툴리의 1914년 연극 제목이기도 하다. 오마르 브래들리 미국 장군은 제2차 세계대전에서 "천막제조업자 오마르"라는 별명을 얻었다.^[84]

프랑스-레반 작가 아민 마알루프는 그의 역사 소설 사마르칸트의 전반부를 하이야암의 삶과 그의 루바이야트의 창작에 기초했다. 조각가 에두아르도 칠리다(Eduardo Chillida)는 1980년대에 메사 드 오마르 카이얌(Omar Khayyam's Table)이라는 제목의 거대한 철제 4점을 제작했다.^[85][86]

달 분화구 오마르 카이얌은 1970년 그의 영예로 명명되었는데, 1980년 소련의 천문학자 류드밀라 즈후라블료바에 의해 발견된 작은 행성 3095 오마르하얀이 발견되었다.^[87]

구글은 그를 기념하는 구글 두들 2개를 출시했다. 첫 번째는 2012년 5월 18일 그의 964번째 생일이었다. 두 번째는 2019년 5월 18일 그의 971번째 생일이었다.^[88]

• 

  "넝쿨 속의 루비"는 애들레이드 한스콤 리슨 (1905년)이 쓴 오마르 카얌의 피츠제럴드 루바이야트의 삽화다.

• 

  제이 햄비지(1911)의 '오마르 카얌의 무덤에서'

• 

  이란이 기증한 페르시아 학자 정자의 일부로 비엔나 유엔사무소에 있는 하이야암 동상.

참고 항목

• 키퍼: 오마르 카이얌의 전설
• 노자트 알마잘레스
• 오마르 카이얌 (영화)
• 저명한 카이야마학자들:
  • 바디오자만 포우잔파르
  • 압돌호세인 자링쿠브

인용구

일반참조

• Biegstraaten, Jos (2008). "Omar Khayyam (Impact On Literature And Society In The West)". Encyclopaedia Iranica. vol. 15. Encyclopaedia Iranica Foundation. volume= has extra text (help)
• Boyle, J. A., ed. (1968). The Cambridge History of Iran (5): The Saljug and Mongol Periods. Cambridge University Press. ISBN 0-521-06936-X.
• 브라운, E. (1899년) "예트 모어 라이트 '우마르-이-카이야름'" 영국 및 아일랜드 왕립 아시아 협회 저널, 409–420. JSTOR 25208104.
• Katz, Victor (1998). A History of Mathematics: An Introduction (2nd ed.). Addison-Wesley. p. 879. ISBN 0-321-01618-1.
• Knoebel, Art; Laubenbacher, Reinhard; Lodder, Jerry (2007). Mathematical Masterpieces: Further Chronicles by the Explorers. Springer. ISBN 978-0387330617.
• Nasr, S. H. (2006). Islamic Philosophy from Its Origin to the Present: Philosophy in the Land of Prophecy. SUNY Press. ISBN 0-7914-6799-6.
• 로스, E. (1927년) "오마르 카이얌" 런던 대학교 동양학 학회 회보, 4(3), 433–439. JSTOR 606948.
• Rozenfeld, Boris A. (1988). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space. Springer Verlag. pp. 65, 471. ISBN 0-387-96458-4.
• 립카, 1월 (1968년) 이란 문학의 역사. 레이델 출판사. OCLC 460598. ISBN 90-277-0143-1
• Smith, David Eugene (1935). "Euclid, Omar Khayyâm, and Saccheri". Scripta Mathematica. III (1): 5–10. OCLC 14156259.
• Turner, Howard R. (1997). Science in Medieval Islam: An Illustrated Introduction. University of Texas Press. ISBN 0-292-78149-0.

외부 링크

• 표준 전자책의 eBook 형식 Omar Khayyam의 작품
• 프로젝트 구텐베르크의 오마르 카이얌의 작품
• 바랜 페이지의 오마르 카얌 작품 (캐나다)
• 인터넷 아카이브의 오마르 카이얌에 관한 연구
• 리브리복스 오마르 카이얌의 작품 (공영 도메인 오디오북)
• Hashemipour, Behnaz (2007). "Khayyām: Ghiyāth al‐Dīn Abū al‐Fatḥ ʿUmar ibn Ibrāhīm al‐Khayyāmī al‐Nīshāpūrī". In Thomas Hockey; et al. (eds.). The Biographical Encyclopedia of Astronomers. New York: Springer. pp. 627–8. ISBN 978-0-387-31022-0. (PDF 버전)
• 스탠포드 철학 백과사전 우마르 카이암
• 간조르 페르시아 도서관의 페르시아어 원본 작품
• Tarikhema.ir의 Kayyam.
• 인터넷 아카이브의 오마르 하얌의 루바이야트 삽화.
• 에드워드 피츠제럴드가 번역한 오마르 카얌의 루바이야트 1판
• 오마르 카이얌의 루바이야트 – 인터넷 클래식 아카이브
• 애들레이드 한스콤의 루바이야트 삽화
• 바니 리켄백커, 카이야암 웹사이트 탐색. 다른 버전의 잘 알려진 쿼터럴을 노트와 비교했다.