텐서에 작용하는 반대칭 순열 개체
수학 에서, 특히 선형 대수학 , 텐서 해석학 , 미분기하학 에서, 레비-시비타 기호 또는 레비-시비타 엡실론은 어떤 양 의 정수 n에 대한 자연수 1 , 2 ,n의 치환 의 부호로부터 정의되는 수들의 집합을 나타냅니다. 이 이름은 이탈리아의 수학자이자 물리학자인 툴리오 레비-시비타 의 이름을 따서 지어졌습니다. 다른 기호 , 반대칭 기호 또는 교대 기호 가 포함되며 순열에 대한 반대칭 속성 및 정의를 나타냅니다.
레비-시비타 기호를 나타내는 표준 문자는 그리스 소문자 엡실론 ε 또는 ϵ 또는 데카르트 참조 시스템의 e-매트릭스에 대한 라틴 소문자 e입니다. 인덱스 표기법을 사용하면 텐서 분석과 호환되는 방식으로 순열을 표시할 수 있습니다.
ε i 1 i 2 … i n {\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}} 여기 서 각 인덱스 i ,i 1, 2, ..., n n개 있는 기호의 주요 정의 속성은 지수의 전체 반대칭 입니다. 두 지수가 같거나 아니거나 상호 교환되면 기호는 음수가 됩니다. ε … i p … i q … = − ε … i q … i p … . {\displaystyle \varepsilon _{\dots i_{p}\dots i_{q}\dots }=-\varepsilon _{\dots i_{q}\dots i_{p}\dots }
두 지수가 같으면 기호는 0입니다. 모든 지수가 동일하지 않을 때, 우리는 다음을 가집니다.
ε i 1 i 2 … i n = ( − 1 ) p ε 1 2 … n , {\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}=(-1)^{p}\varepsilon _{1\,2\,\dots n},} 여기서 p (순열의 패리티라고 함)는 i 1 ,i , ..., i n 1, 2 2 , ..., n 1)p 를 순열의 부호 또는 서명 이라고 합니다. 값 대부분의 저자는 ε = +1을 선택합니다. 이는 지수가 모두 동일하지 않을 때 레비-시비타 기호는 순열의 부호와 같다는 것을 의미합니다. 이 선택은 이 기사 전반에 걸쳐 사용됩니다.
"n차원 레비-시비타 기호"란 기호 n의 인덱스 수가 유클리드 또는 비유클리드 일 수 있는 문제의 벡터 공간 의 차원 과 일치한다는 사실을 말합니다. 예를 들어 R {\ displaystyle \mathbb {R} ^{3} 민코프스키 공간 . Levi-Civita 기호의 값은 메트릭 텐서 및 좌표계 와 무관합니다. 또한 "기호"라는 특정 용어는 좌표계 간 변환 방식 때문에 텐서 가 아니라는 점을 강조하지만 텐서 밀도 로 해석할 수 있습니다.
레비-시비타 기호는 정방 행렬의 행렬식 과 3차원 유클리드 공간에서 두 벡터의 교차 곱 을 아인슈타인 지수 표기법 으로 표현할 수 있게 합니다.
정의. Levi-Civita 기호는 3차원과 4차원에서 가장 많이 사용되며, 2차원에서 어느 정도 사용되므로 일반적인 경우를 정의하기 전에 여기에 제공됩니다.
이차원 2차원 에서 Levi-Civita 기호는 다음과 같이 정의됩니다.
ε i j = { + 1 한다면 ( i , j ) = ( 1 , 2 ) − 1 한다면 ( i , j ) = ( 2 , 1 ) 0 한다면 i = j {\displaystyle \varepsilon _{ij}={\begin{cases}+1&{\text{if }}(i,j)=(1,2)\\-1&{\text{if }}(i,j)=(2,1)\\\;\;\,0&{\text{if }}i=j\end{cases}}} 값은 2 × 2 반대칭 행렬 로 배열할 수 있습니다. ( ε 11 ε 12 ε 21 ε 22 ) = ( 0 1 − 1 0 ) {\displaystyle {\begin{pmatrix}\varepsilon_{11}&\varepsilon_{12}\\\varepsilon_{21}&\varepsilon_{22}\end{pmatrix}}={\begin{pmatrix}0&1\-1&0\end{pmatrix}}
2차원 기호의 사용은 응축된 물질과 초대칭 [1] 트위스터 이론 과 같은 특정 전문화된 고에너지 주제에서 일반적으로 사용되며,[2] 여기 서 2-스피너의 맥락에서 나타납니다.
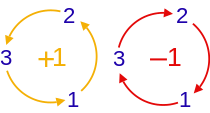
입체감 ε의 지수(i , k ) 의 경우, 1, 2, 3은 순환 순서 (1, 2, 3) 는 ε = +1에 해당하며, 역 순환 순서로 발생하는 경우에는 ε = -1, 그렇지 않은 경우 에는 ε = 0에 해당합니다.3차원 에서 Levi-Civita 기호는 다음과 같이 정의됩니다.[3]
ε i j k = { + 1 한다면 ( i , j , k ) 아. ( 1 , 2 , 3 ) , ( 2 , 3 , 1 ) , 아니면 ( 3 , 1 , 2 ) , − 1 한다면 ( i , j , k ) 아. ( 3 , 2 , 1 ) , ( 1 , 3 , 2 ) , 아니면 ( 2 , 1 , 3 ) , 0 한다면 i = j , 아니면 j = k , 아니면 k = i {\displaystyle \varepsilon _{ijk}={\begin{cases}+1&{\text{if }}(i,j,k){\text{ is }}(1,2,3),(2,3,1),{\text{ or }}(3,1,2),\\-1&{\text{if }}(i,j,k){\text{ is }}(3,2,1),(1,3,2),{\text{ or }}(2,1,3),\\\;\;\,0&{\text{if }}i=j,{\text{ or }}j=k,{\text{ or }}k=i\end{cases}}}
즉 , (i, j, k)가 (1 , 2, 3) 의 짝수 순열 이면 ε이 1 이고, 홀수 순열 이면 -1이고, 어떤 지수라도 반복되면 0입니다. 3차원에서만 (1, 2, 3) 의 순환 순열 은 모두 짝수 순열이고, 마찬가지로 반순환 순열 은 모두 홀수 순열입니다. 이것은 3d에서 (1, 2, 3) 의 순환 또는 반순환 순열을 취하고 모든 짝수 또는 홀수 순열을 쉽게 얻는 것으로 충분하다는 것을 의미합니다.
2차원 행렬과 유사하게, 3차원 Levi-Civita 기호의 값 은 3×3×3 배열로 배열될 수 있습니다.
여기 서 i는 깊이(파란색 1 , 빨간색: i
몇 가지 예:
ε 1 3 2 = − ε 1 2 3 = − 1 ε 3 1 2 = − ε 2 1 3 = − ( − ε 1 2 3 ) = 1 ε 2 3 1 = − ε 1 3 2 = − ( − ε 1 2 3 ) = 1 ε 2 3 2 = − ε 2 3 2 = 0 {\displaystyle {\aligned}\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{2}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}&=-1\\varepsilon _{\color {Violet}{3}\color {BrickRed}{1}\color {Orange}{2}=-\varepsilon _{\color {Orange}{2}\color {BrickRed}{1}\color {Violet}{3}=-(-\varepsilon) _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}}=1\\varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {BrickRed}{1}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}}=-(-\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}}=1\\varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {Violet}\color {3} {오렌지}{2}}=-\varepsilon _{\color{Orange}{2}\color{Violet}{3}\color{Orange}{2}}&=0\end{aligned}}}
사차원 4차원 에서 Levi-Civita 기호는 다음과 같이 정의됩니다.
ε i j k l = { + 1 한다면 ( i , j , k , l ) 의 고른 순열입니다. ( 1 , 2 , 3 , 4 ) − 1 한다면 ( i , j , k , l ) 의 이상한 순열입니다. ( 1 , 2 , 3 , 4 ) 0 그렇지않으면 {\displaystyle \varepsilon _{ijkl}={\begin{case}+1&{\text{if}}(i,j,k,l){\text{는 }(1,2,3,4)\-1&{\text{if}}(i,j,k,l){\text{는 }(1,2,3,4)\;\,0&{\text{case}\end{case}}}
이러한 값은 4차원 이상에서는 그리기가 어렵지만 4×4×4 배열로 배열할 수 있습니다.
몇 가지 예:
ε 1 4 3 2 = − ε 1 2 3 4 = − 1 ε 2 1 3 4 = − ε 1 2 3 4 = − 1 ε 4 3 2 1 = − ε 1 3 2 4 = − ( − ε 1 2 3 4 ) = 1 ε 3 2 4 3 = − ε 3 2 4 3 = 0 {\displaystyle {\begin{aligned}\varepsilon _{\color {BrickRed}{1}\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}\color {RedViolet}{4}}&=-1\\varepsilon _{\color {Orange}{2}\color {BrickRed}{1}\color {Violet}{3}\color{RedViolet}{4}}=-\varepsilon _{\color{BrickRed}{1}\color{Orange}{\color{Orange}{2}\color{Violet}{3}\color{RedViolet}{4}}&=-1\\varepsilon _{\color{RedViolet}{4}\color{3}\color{Orange}{\color{Orange}{2}\color{BrickRed}{1}=-\varepsilon _{Violet}{3}\color{Orange}{\color} {오렌지}{2}}\color {RedViolet}{4}}&=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}\color {RedViolet}{4})=1\\varepsilon _{\color {Violet}{3}\color {Orange}{2}\color {RedViolet}{4}\color {Violet}{3}=-\varepsilon _{\color {Violet}{3}\color {Orange}{2}\color {Orange}} {레드바이올렛}{4}\color{Violet}{3}}&=0\end{aligned}}}
n차원 으로의 일반화일반적으로 n차원 에서 레비-시비타 기호는 다음과 같이 정의됩니다.[4]
ε a 1 a 2 a 3 … a n = { + 1 한다면 ( a 1 , a 2 , a 3 , … , a n ) 의 고른 순열입니다. ( 1 , 2 , 3 , … , n ) − 1 한다면 ( a 1 , a 2 , a 3 , … , a n ) 의 이상한 순열입니다. ( 1 , 2 , 3 , … , n ) 0 그렇지않으면 {\displaystyle \varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}={\begin{case}+1&{\text{if}}(a_{1}, a_{2}, a_{3},\ldots,a_{n}){\text{는 }(1,2,3,\dots,n)\-1&{\text{if}}(a_{1},a_{2},\ldots,a_{n}){\text{는 }(1,2,3,\dots,n)\;\;\,0&{\text{case}}\end{case}}}
따라서 순열의 경우 순열의 부호 이고, 그렇지 않으면 0입니다.
일반적인 숫자의 곱셈에 대문자 pi 표기법 π를 사용하면 기호에 대한 명시적인 표현식은 다음과 같습니다.
ε a 1 a 2 a 3 … a n = ∏ 1 ≤ i < j ≤ n sgn ( a j − a i ) = sgn ( a 2 − a 1 ) sgn ( a 3 − a 1 ) ⋯ sgn ( a n − a 1 ) sgn ( a 3 − a 2 ) sgn ( a 4 − a 2 ) ⋯ sgn ( a n − a 2 ) ⋯ sgn ( a n − a n − 1 ) {\displaystyle {\begin{aligned}\varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}&=\prod _{1\leq i<j\leq n}\operatorname {sgn}(a_{j}-a_{i}) \\&=\operatorname {sgn}(a_{2}-a_{1})\operatorname {sgn}(a_{3}-a_{1})\dotsm \operatorname {sgn}(a_{n}-a_{1})\operatorname {sgn}(a_{3}-a_{2})\operatorname {sgn}(a_{4}-a_{2})\dotsm \operatorname {sgn}(a_{n}-a_{2})\dotsm \operatorname {sgn}(a_{n}-a_{n-1})\end{aligned}}} 여기서 signum 함수 (sgn 으로 표시됨)는 인수의 부호를 반환하고 0이 아닌 경우 절대값 을 폐기합니다. 이 공식은 모든 지수 값과 임의 의 n에 대해 유효 합니다(n = 0 또는 n = 1인 경우, 이것이 빈 곱 입니다). 그러나 위의 공식을 순수하게 계산하는 것 2 O(n)의 시간 복잡성 을 갖는 반면, 부호는 O (n log (n)) 비용으로만 분리된 사이클 의 순열 패리티에서 계산할 수 있습니다.
특성. 정규 기저 에 있는 성분이 Levi-Civita 심볼(공변 랭크 n의 텐서)에 의해 제공되는 텐서를 순열 텐서라고 부르기도 합니다.
텐서에 대한 일반적인 변환 규칙에 따르면 레비-시비타 기호는 순수 회전 하에서는 변하지 않으며, 이는 직교 변환과 관련된 모든 좌표계에서 동일하다는 것과 일치합니다. 그러나 Levi-Civita 심볼은 예를 들어 홀수 차원에서의 반사 와 같은 Jacobian 행렬식 -1의 직교 변환 하에서 텐서일 경우 마이너스 부호를 획득 해야 하기 때문에 의사 텐서입니다. 전혀 변하지 않으므로 레비-시비타 기호는 정의상 의사텐서입니다.
Levi-Civita 기호는 의사텐서이므로 교차 곱을 취한 결과는 벡터가 아닌 의사벡터 입니다.[5]
일반적인 좌표 변화 하에서, 순열 텐서의 성분 은 변환 행렬의 자코비안 에 곱해집니다. 이는 텐서가 정의된 것과 다른 좌표계에서 그 구성요소가 전체적인 요인에 의해 Levi-Civita 심볼의 구성요소와 다를 수 있음을 의미합니다. 프레임이 정상인 경우 프레임의 방향이 동일한지 여부에 따라 인자는 ±1이 됩니다.[5]
인덱스가 없는 텐서 표기에서는 Levi-Civita 기호가 호지 듀얼 의 개념으로 대체됩니다.
합 기호 는 아인슈타인 표기법을 사용하여 제거할 수 있으며, 여기서 두 개 이상의 항 사이에서 반복되는 지수는 해당 지수에 대한 합을 나타냅니다. 예를들면,
i j ε 2 m 다음 예에서는 아인슈타인 표기법을 사용합니다.
이차원 2차원에서, 모든 j , m ,[3]
ε i j ε m n = δ i m δ j n − δ i n δ j m {\displaystyle \varepsilon _{ij}\varepsilon ^{mn}={\delta _{i}}^{m}{\delta _{j}}^{n}-{\delta _{i}}^{\n}{\delta _{j}}^{m} (1 )
ε i j ε i n = δ j n {\displaystyle \varepsilon _{ij}\varepsilon ^{in}={\delta _{j}}^{n}} (2 )
ε i j ε i j = 2. {\displaystyle \varepsilon _{ij}\varepsilon ^{ij}=2.} (3 )
입체감 인덱스 및 기호 값 3차원에서 모든 i ,j ,m ,n [3]
ε i j k ε p q k = δ i p δ j q − δ i q δ j p {\displaystyle \varepsilon _{ijk}\varepsilon ^{pqk}=\ delta _{i}}^{p}\ delta _{j}^{q}-\ delta _{i}^{q}\ delta _{j}^{p}} (4 )
[6]
ε j m n ε i m n = 2 δ j i {\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=2{\delta _{j}}^{i}} (5 )
ε i j k ε i j k = 6. {\displaystyle \varepsilon _{ijk}\varepsilon ^{ijk}=6.} (6 )
제품. 레비-시비타 기호가 반응합니다. ε displaystyle 확장 정리에 의해 크로네커 델타 와 관련 이 있습니다. [4] [7]
δ i j k l m n = ε i j k ε l m n = δ i l δ i m δ i n δ j l δ j m δ j n δ k l δ k m δ k n = δ i l ( δ j m δ k n − δ j n δ k m ) − δ i m ( δ j l δ k n − δ j n δ k l ) + δ i n ( δ j l δ k m − δ j m δ k l ) {\displaystyle {\begin{aligned}\delta {_{ijk}}^{lmn}=\varepsilon _{ijk}\varepsilon ^{lmn}&={\begin{vmatrix}\delta _{il}&\delta _{im}&\delta _{jl}&\delta _{jl}&\delta _{jm}&\delta _{jn}\\delta _{kl}&\delta _{km}\\end{vmatrix}\[6pt]&\\\\delta _{il}\left(\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}\right)-\delta _{im}\left(\delta _{jm}\right) _{jl}\delta _{kn}-\delta _{jn}\delta _{kl}\right)+\delta _{in}\left(\delta _{jl}\delta _{km}-\delta _{jm}\delta _{kl}\right)\end{aligned}} {\displaystyle
이 결과의 특별한 경우는 4차 크로네커 델타와의 그라스만 항등식 입니다.
δ j k m n = ∑ i = 1 3 ε i j k ε i m n = δ j m δ k n − δ j n δ k m , {\displaystyle \delta {_{jk}}{^{mn}}=\sum _{i=1}^{3}\varepsilon _{ijk}\varepsilon ^{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}} 때때로 "수축 된 엡실론 정체성"이라고 불립니다.
더 delta } - ID가 발생합니다.
2 δ k n = ∑ i = 1 3 ∑ j = 1 3 ε i j k ε i j n {\displaystyle 2\;\delta {_{k}}{^{n}}=\sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{ijk}\varepsilon ^{ijn}} 그리고.
2 δ k k = ∑ i = 1 3 ∑ j = 1 3 ∑ k = 1 3 ε i j k ε i j k = 6. {\displaystyle 2\;\delta {_{k}}{^{k}}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}\varepsilon ^{ijk}=6.} 아인슈타인 표기법에서 i , j , k 지수 의 중복은 i resp. j 와 k 의 합을 의미하며, 위의 합 기호는 생략될 수 있습니다.
텐서 변환을 사용하여 the upper δ {\displaystyle \delta } g → β = g i β e → i {\displaystyle \;{\vec {g}}{^{\beta }}=g_{i}{^{\beta }}\;{\vec {e}}{^{i}}} g → γ = g r γ → {\displaystyle \;{\vec {g gamma }} = g gamma 공분산 메트릭 gr }
이 마이스너 ID 로 변환합니다.
in R 3 : {\displaystyle \mathbb {R} ^{3}:\;\;} δ i k = 1 / 2 ∗ e i r p ∗ δ r l ∗ δ p m ∗ ε k l m r e s p . δ i k = 1 / 2 ∗ ε i r p ∗ δ r l ∗ δ p m ∗ ε k l m , {\displaystyle \delta {{_{i}}{^{k}}}=1/2*e{{_{i}}{_{r}}{_{p}}}*\delta {{^{r}}{_{l}}}*\delta {{^{p}}{_{m}}}*\varepsilon {^{k}}{^{l}}{^{m}}\;\;\;\;resp. \;\;\;\;\delta {^{i}{^{k}}}=1/2*\varepsilon {{^{i}}{^{r}}{^{p}}}*\delta {{_{r}}{_{l}}}*\delta {{_{p}}{_{m}}}*\varepsilon {{^{k}}{^{l}}{^{m}}},}
in R 2 : {\displaystyle \mathbb {R} ^{2}:\;\;} δ i k = e i r ∗ δ r l ∗ ε k l r e s p . δ i k = ε i r ∗ δ r l ∗ ε k l , {\displaystyle \delta{_{i}}{^{k}}=e{{_{i}}{_{r}}*\delta{^{r}}{_{l}}}*\varepsilon{^{k}}{_{l}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;resp. \;\;\;\;\delta {{^{i}}{^{k}}}=\varepsilon {{^{i}}{^{r}}}*\delta {_{r}}{_{l}}*\varepsilon {{^{k}}{^{l}}},}
위에서 정의한 Levi-Civita 심볼의 값 ± 1 {\displaystyle e- p 비대칭 참조 시스템의 {\ {\displaystyle {\ \ varepsilon β γ κ = g ∗ e β γ κ {\displaystyle \varepsilon {_{\beta }}{_{\gamma }}{_{\kappa }}={\sqrt {g}}*e{_{\beta }}{_{\gamma }}{_{\kappa }}} ε {\displaystyle \varepsilon } ε β γ κ = 1 / g ∗ e β γ κ . {\displaystyle \varepsilon {^{\beta }}{^{\gamma }}{^{\kappa }}=1/{\sqrt {g}}*e{^{\beta }}{^{\gamma }}{^{\kappa }}. }
따라서 편향된 참조 시스템으로의 적절한 텐서 변환은 여러 인덱스 이름 변경에 의해 다음에 대한 위반 마이스너 기저 변환 으로 이어집니다.
the three-dimensional contravariant basis vectors g i β = 1 / 2 ∗ e i r p ∗ g r γ ∗ g p κ ∗ ε β γ κ {\displaystyle g{_{i}}\;{^{\beta }}=1/2*e{_{i}}{_{r}}{_{p}}*g{^{r}}{_{\gamma }}*g{^{p}}{_{\kappa }}*\varepsilon {^{\beta }}{^{\gamma }}{^{\kappa }}}
and the contravariant metric tensor g α β = 1 / 2 ∗ ε α γ κ ∗ g γ λ ∗ g κ μ ∗ ε β λ μ , {\displaystyle \;\;\;\;\;\;\;\;\;\;\;;\;\;;\;\;;\;;\;;\;;\;;;\;;\;;;\;;;\;;;\;g{{\alpha }=1/2*\varepsilon {^{\alpha gamma }{^{\alpha }}{\gamma }}*g{_{\kappa lambda }}*g{_{\kappa }}}{_{\mu }}*\varepsilon {^{\beta }}{^{\mu }}}
에 대하여 각각
2차원 gi β }}
and the contravariant metric tensor : g α β = ε α γ ∗ g γ λ ∗ ε β λ . {\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g{{^{\alpha }}{^{\beta }}}=\varepsilon {{^{\alpha }}{^{\gamma }}}*g{{_{\gamma }}{_{\lambda }}}*\varepsilon {{^{\beta }}{^{\lambda }}}.}
n차원 인덱스 및 기호 값 n차원 에서, 모든 i 1 ,in 1 ,j,...,j n 1,2,...,n값 을 취할 때:
ε i 1 … i n ε j 1 … j n = δ i 1 … i n j 1 … j n {\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{j_{1}\dots j_{n}}=\delta _{i_{1}\dots i_{n}}^{j_{1}\dots j_{n}}} (7 )
ε i 1 … i k i k + 1 … i n ε i 1 … i k j k + 1 … j n = δ i 1 … i k i k + 1 … i n i 1 … i k j k + 1 … j n = k ! δ i k + 1 … i n j k + 1 … j n {\displaystyle \varepsilon _{i_{1}\dots i_{k}~i_{k+1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{k}~j_{k+1}\dots j_{n}}=\delta _{i_{1}\ldots i_{k}~i_{k+1}\ldots i_{n}}^{i_{1}\dots i_{k}~j_{k+1}\ldots j_{n}}=k! ~\delta _{i_{k+1}\dots i_{n}}^{j_{k+1}\dots j_{n}}} (8 )
ε i 1 … i n ε i 1 … i n = n ! {\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{n}}=n!} (9 )
여기 요인 을 나타내고 δ는 일반화된 크로네커 델타입니다. 여하튼 부동산은
∑ i , j , k , ⋯ = 1 n ε i j k … ε i j k … = n ! {\displaystyle \sum_{i,j,k,\dots =1}^{n}\varepsilon_{ijk\dots }\varepsilon_{ijk\dots }=n!} 라는 사실로 미루어 볼 때
모든 순열은 짝수이거나 홀수입니다. (+1)2 = (−1)2 = 1 , and임의의 n-element 집합의 순열의 수는 정확히 k 8
ε i 1 … i n − 2 j k ε i 1 … i n − 2 l m = ( n − 2 ) ! ( δ j l δ k m − δ j m δ l k ) . {\displaystyle \varepsilon _{i_{1}\dots i_{n-2}jk}\varepsilon ^{i_{1}\dots i_{n-2}lm}=(n-2)!(\delta _{j}^{l}\delta _{k}^{m}-\delta _{j}^{m}\delta _{l}^{k})\,.}
제품. 일반적으로 n차원 에서는 두 개의 레비-시비타 기호의 곱을 다음과 같이 쓸 수 있습니다.
ε i 1 i 2 … i n ε j 1 j 2 … j n = δ i 1 j 1 δ i 1 j 2 … δ i 1 j n δ i 2 j 1 δ i 2 j 2 … δ i 2 j n ⋮ ⋮ ⋱ ⋮ δ i n j 1 δ i n j 2 … δ i n j n . {\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}\varepsilon _{j_{1}j_{2}\dots j_{n}}={\begin{vmatrix}\delta _{i_{1}j_{1}}&\delta _{i_{1}j_{2}}&\dots &\delta _{i_{1}j_{n}}\\\delta _{i_{2}j_{1}}&\delta _{i_{2}j_{2}}&\dots &\delta _{i_{2}j_{n}}\\\vdots &\vdots &\ddots &\vdots \\\delta _{i_{n}j_{1}}&\delta _{i_{n}j_{2}}&\dots &\delta _{i_{n}j_{n}}\\\end{vmatrix}}. } 증명: 양쪽은 두 지수를 바꾸면 부호 1 ≤ ⋯ ≤ in , 1 ⋯ ≤ j n {\displaystyle i_{1 leq \cdots \leq {n {1 leq cdots n i = i {\displaystyle c = i_{c+1}이면 왼쪽이 0입니다. 그리고 오른쪽도 두 행이 같기 때문에 0입니다. j c 마지막 i j 1
증명 (1 ij 와 mn 에 대해 반대칭입니다. 따라서 우리 i j 우리 i m 방정식이 ij 와 mn 에서 반대대칭이므로 이들에 대한 값의 집합은 위의 경우로 축소될 수 있습니다. 따라서 방정식은 ij 와 mn 의 모든 값에 대해 성립합니다.
(1 2
ε i j ε i n = δ i i δ j n − δ i n δ j i = 2 δ j n − δ j n = δ j n . {\displaystyle \varepsilon _{ij}\varepsilon ^{in}=\ delta _{i}^{i}\ delta _{j}^{n}-\ delta _{i}^{n}-\ delta _{j}^{i}=2\ delta _{j}^{n}-\ delta _{j}^{n}=\ delta _{j}^{n}\.} 여기서 우리는 1에서 2로 가는 아인슈타인의 요약 규칙 을 사용했습니다. 다음으로 (3 2
(5 내 j ≠하면 양쪽이 모두 사라짐을 유의하십시오. 실제로 i j ≠하면 왼쪽의 두 치환 기호가 0이 아닌 m과 n을 선택 할 수 없습니다. 그러면 j m 과 n 을 선택하는 방법은 두 가지뿐입니다. 그러한 지수의 경우, 우리는
ε j m n ε i m n = ( ε i m n ) 2 = 1 {\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=\left(\varepsilon ^{imn}\right)^{2}=1} (합계 없음), 결과는 다음과 같습니다.
그러면 (6 3! = 6 이며, 값 1, 2, 3 을 취하는 임의의 구별되는 인덱스 i ,k
ε ijk { 구별 응용프로그램 및 예제 결정요인 선형 대수학에서 3 × 3 제곱 행렬 A a 행렬식 은 다음과 같이 쓸 수 있습니다.
디트 ( A ) = ∑ i = 1 3 ∑ j = 1 3 ∑ k = 1 3 ε i j k a 1 i a 2 j a 3 k {\displaystyle \det(\mathbf {A} )=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}a_{1i}a_{2j}a_{3k}} 마찬가지로 n n A a
디트 ( A ) = ε i 1 … i n a 1 i 1 … a n i n , {\displaystyle \det(\mathbf {A})=\varepsilon _{i_{1}\dots i_{n}}a_{1i_{1}}\dots a_{ni_{n}} 여기서 각각 의r i는 1, ..., n
디트 ( A ) = 1 n ! ε i 1 … i n ε j 1 … j n a i 1 j 1 … a i n j n , {\displaystyle \det(\mathbf {A}) = {\frac {1}{n! }}\varepsilon _{i_{1}\dots i_{n}}\varepsilon _{j_{1}\dots j_{n}}a_{i_{1}j_{1}}\dots a_{i_{n}j_{n}},} 여기 서r 각 i 와r 각 j 는 1, ..., n 이상 [5]
∑ i 1 , i 2 , … ε i 1 … i n a i 1 j 1 … a i n j n = 디트 ( A ) ε j 1 … j n {\displaystyle \sum _{i_{1},i_{2},\dots }\varepsilon _{i_{1}\dots i_{n}}a_{i_{1}\,j_{1}}\dots a_{i_{n}\,j_{n}}=\det(\mathbf {A} )\varepsilon _{j_{1}\dots j_{n}}} 벡터교차곱 교차곱(두 벡터) (e 1 ,e , e ) {\displaystyle (\mathbf {e_{1}},\mathbf {e_{2}},\mathbf {e_{3})} 벡터 공간의 정사규 기저라고 하자 만약 (a1 2 ,, a 3 )와 (b 1 ,b 2 ,b 3 )벡터 a [5]
a × b = e 1 e 2 e 3 a 1 a 2 a 3 b 1 b 2 b 3 = ∑ i = 1 3 ∑ j = 1 3 ∑ k = 1 3 ε i j k e i a j b k {\displaystyle \mathbf {a\times b} ={\begin{vmatrix}\mathbf {e_{1}} &\mathbf {e_{2}} &\mathbf {e_{3}} \\a^{1}&a^{2}&a^{3}\\b^{1}&b^{2}&b^{3}\\\end{vmatrix}}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}\mathbf {e} _{i}a^{j}b^{k}} 따라서 Levi-Civita 기호를 사용하기도 하며, 좀 더 간단히 다음과 같습니다.
( a × b ) i = ∑ j = 1 3 ∑ k = 1 3 ε i j k a j b k . {\displaystyle (\mathbf {a\times b} )^{i}=\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}a^{j}b^{k}.} 아인슈타인 표기법에서, 합 기호들은 생략될 수 있고, 그들의 교차 곱의 i번째 성분은 다음과[4]
( a × b ) i = ε i j k a j b k . {\displaystyle(\mathbf {a\times b})^{i}=\varepsilon _{ijk}a^{j}b^{k}} 첫 번째 구성요소는.
( a × b ) 1 = a 2 b 3 − a 3 b 2 , {\displaystyle (\mathbf {a\times b} )^{1}=a^{2}b^{3}-a^{3}b^{2}\,,} 그리고 1, 2, 3 의 순환 순열에 의해 다른 것들은 위의 공식들로부터 명시적으로 계산하지 않고 바로 유도될 수 있습니다.
( a × b ) 2 = a 3 b 1 − a 1 b 3 , ( a × b ) 3 = a 1 b 2 − a 2 b 1 . {\displaystyle {\begin{aligned}(\mathbf {a\times b} )^{2}&=a^{3}b^{1}-a^{1}b^{3}\,,\\(\mathbf {a\times b} )^{3}&=a^{1}b^{2}-a^{2}b^{1}\,. \end{align}}} 삼중 스칼라 곱(3개의 벡터) 크로스 제품에 대한 위의 식에서 우리는 다음과 같습니다.
a b b s c c c )삼중 스칼라 곱 은 다음과 같습니다.
a ⋅ ( b × c ) = ε i j k a i b j c k . {\displaystyle \mathbf {a} \cdot(\mathbf {b\times c})=\varepsilon _{ijk}a^{i}b^{j}c^{k}} 이 표현식으로부터 어떤 쌍의 인수를 교환할 때 삼중 스칼라 곱이 반대칭임을 알 수 있습니다. 예를들면,
b × c c 컬(한 벡터장) F F ,, F) 가 위치 x = (x, x, x) 의 함수 로 R 3 {\displaystyle \mathbb {R} ^{3}의 일부 열린 집합에 정의된 벡터 필드라면 (직각좌표를 사용하여). 그러면 F 의 컬의 i번째 성분은 다음과[4]
( ∇ × F ) i ( x ) = ε i j k ∂ ∂ x j F k ( x ) , {\displaystyle(\n) bla \times \mathbf {F})^{i}(\mathbf {x})=\varepsilon _{ijk}{\frac {\partial }{\partial x^{j}} F^{k}(\mathbf {x} ),} 위의 교차 곱 식에서 구배 벡터 연산자 (nabla)의 성분을 치환하는 것으로 이어집니다.
텐서 밀도 임의의 곡선 좌표계 및 매니폴드 에 메트릭 이 없는 경우에도 위에서 정의한 바와 같은 Levi-Civita 심볼은 두 가지 다른 방식으로 텐서 밀도 필드로 간주될 수 있습니다. 가중치 +1의 상반 텐서 밀도 또는 가중치 -1의 공변 텐서 밀도로 간주될 수 있습니다. 일반화된 크로네커 델타를 사용한 n차원 에서,[10] [11]
ε μ 1 … μ n = δ 1 … n μ 1 … μ n ε ν 1 … ν n = δ ν 1 … ν n 1 … n . {\displaystyle {\begin{aligned}\varepsilon ^{\mu _{1}\dots \mu _{n}}&=\delta _{\,1\,\dots \,n}^{\mu _{1}\dots \mu _{n}\,\\varepsilon _{\n} u_{1}\dots \n u _{n}}&=\delta _{\n u_{1}\dots \n u_{n}}^{\,1\,\dots \,n}\,\end{aligned}}} 수치적으로 동일하다는 점에 유의하십시오. 특히 간판은 똑같습니다.
레비시비타 텐서 의사 리만 다양체 에서는 좌표 시스템이 어디에 있든지 Levi-Civita 심볼과 좌표 표현이 일치하는 좌표 불변 공변 텐서 필드를 정의하여 접선 공간의 기초가 메트릭에 대해 직교하고 선택된 방향과 일치할 수 있습니다. 이 텐서는 위에서 언급한 텐서 밀도 필드와 혼동되어서는 안 됩니다. 이 섹션의 프레젠테이션은 Carroll 2004 와 밀접하게 관련되어 있습니다.
선택한 방향과 일치하는 모든 좌표계에서 공변 레비-시비타 텐서(리만 볼륨 형태 라고도 함)는
E a 1 … a n = 디트 [ g a b ] ε a 1 … a n , {\displaystyle E_{a_{1}\dots a_{n}}={\sqrt {\left \det[g_{ab}]\right}}\,\varepsilon_{a_{1}\dots a_{n}\,} 여기 서ab g는 해당 좌표계에서의 메트릭의 표현입니다. 마찬가지로 평상시처럼 메트릭으로 지수를 높임으로써 상반된 레비-시비타 텐서를 고려할 수 있습니다.
E a 1 … a n = E b 1 … b n ∏ i = 1 n g a i b i , {\displaystyle E^{a_{1}\dots a_{n}}=E_{b_{1}\dots b_{n}}\prod _{i=1}^{n}g^{a_{i}b_{i}}\,,} 그러나 메트릭 서명 이 홀수 개의 음의 고유값 q
E a 1 … a n = sgn ( 디트 [ g a b ] ) 디트 [ g a b ] ε a 1 … a n , {\displaystyle E^{a_{1}\dots a_{n}}={\frac {\operatorname {sgn} \left(\det[g_{ab}]\right)}{\sqrt {\left \det[g_{ab}]\right}}\,\varepsilon ^{a_{1}\dots a_{n}}} 여기서 sgn(det[g] = (-1) 및 {\displaystyle varepsilon a_{1}\ 보다 n det gab E01 . n sgn (det [ gab ] ) det [ gab ] {\displaystyle E^{01\dots n} }{\sqrt {\left \det[g_{ab}]\right
이것으로 정체를 추론할 수 있습니다.
E μ 1 … μ p α 1 … α n − p E μ 1 … μ p β 1 … β n − p = ( − 1 ) q p ! δ β 1 … β n − p α 1 … α n − p , {\displaystyle E^{\mu_{1}\dots \mu_{p}\alpha_{1}\dots \alpha_{n-p}E_{\mu_{1}\beta \mu_{p}\beta _{1}\dots \(- _{n-p}}=delta1)^{q}p!\dots _{\beta _{1}\beta \dots _{n-p}^{\alpha_{1}\dots \alpha _{n-p}\,} 어디에
δ β 1 … β n − p α 1 … α n − p = ( n − p ) ! δ β 1 [ α 1 … δ β n − p α n − p ] {\displaystyle \delta _{\beta _{1}\dots \beta _{n-p}}^{\alpha _{1}\dots \alpha _{n-p}}=(n-p)! \delta _{\beta _{1}}^{\lbrack \alpha _{1}}\dots \delta _{\beta _{n-p}}^{\alpha _{n-p}\rbrack }} 일반화된 크로네커 삼각주입니다.
예제: 민코프스키 공간 민코프스키 공간(특수 상대성 이론의 4차원 시공간 )에서 공변 레비-시비타 텐서는
E α β γ δ = ± 디트 [ g μ ν ] ε α β γ δ , {\displaystyle E_{\alpha \beta \gamma}=\pm {\sqrt {\left \det[g_{\mu \n u}]\right}}\,\varepsilon_{\alpha \beta \gamma}\,} 기호는 기초의 방향에 따라 달라집니다. 상반된 레비-시비타 텐서는
E α β γ δ = g α ζ g β η g γ θ g δ ι E ζ η θ ι . {\displaystyle E^{\alpha \beta \gamma}=g^{\alpha \zeta }g^{\beta \theta }g^{\gamma \theta }g^{\delta \iota }E_{\zeta \theta \iota }\,} 다음은 민코프스키 공간에 특화된 위의 일반적인 아이덴티티의 예입니다(두 기호 규칙에서 메트릭 텐서의 서명에서 홀수의 음수로 인해 발생하는 음의 부호).
E α β γ δ E ρ σ μ ν = − g α ζ g β η g γ θ g δ ι δ ρ σ μ ν ζ η θ ι E α β γ δ E ρ σ μ ν = − g α ζ g β η g γ θ g δ ι δ ζ η θ ι ρ σ μ ν E α β γ δ E α β γ δ = − 24 E α β γ δ E ρ β γ δ = − 6 δ ρ α E α β γ δ E ρ σ γ δ = − 2 δ ρ σ α β E α β γ δ E ρ σ θ δ = − δ ρ σ θ α β γ . {\displaystyle {\begin{aligned} E_{\alpha \beta \gamma \delta }E_{\rho \sigma \mu \n u}&=-g_{\alpha \zeta }g_{\beta \eta }g_{\gamma \theta }g_{\delta \iota }\delta _{\rho \sigma \mu \n u }^{\zeta \eta \theta \iota }\\E^{\alpha \beta \gamma \delta }E^{\rho \sigma \mu \n u}&=-g^{\alpha \zeta }g^{\beta \eta }g^{\gamma \theta }g^{\delta \iota }\delta _{\zeta \theta \iota }^{\rho \sigma \mu \n u }\\\E^{\alpha \beta \gamma}E_{\alpha \beta \gamma \delta }&=-24\ E^{\alpha \beta \gamma}E_{\rho \beta \delta \gamma}E_{\rho \delta}&=-6\beta _{\rho }^{\alpha }\\\E^{\alpha \gamma \delta beta}E_{\rho \sigma }^{\delta }&=-2\delta _{\rho \sigma }^{\alpha \beta }\\E^{\rho \gamma }E_{\rho \sigma }\delta \delta =-\rho \sigma \theta }&_{\rho \delta \theta }^{\alpha \gamma \delta gamma \beta}\, \end{align}}} 참고 항목 메모들 ^ Labelle, P. (2010). Supersymmetry . Demystified. McGraw-Hill. pp. 57–58. ISBN 978-0-07-163641-4 ^ Hadrovich, F. "Twistor Primer" . Retrieved 2013-09-03 . ^ a b c Tyldesley, J. R. (1973). An introduction to Tensor Analysis: For Engineers and Applied Scientists . Longman. ISBN 0-582-44355-5 ^ a b c d Kay, D. C. (1988). Tensor Calculus . Schaum's Outlines. McGraw Hill. ISBN 0-07-033484-6 ^ a b c d e Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). Mathematical Methods for Physics and Engineering ISBN 978-0-521-86153-3 ^ Weisstein, Eric W. "Permutation Symbol" . mathworld.wolfram.com . Retrieved 2022-10-17 . ^ a b c Meissner, Udo F. (2022). Tensorkalkül mit objektorientierten Matrizen für numerische Methoden in Mechanik und Ingenieurwesen . SpringerVieweg. doi :10.1007/978-3-658-39881-1 . ISBN 978-3-658-39880-4 ^ Herman. "The Levi-Civita Symbol" (PDF) . ^ Lipcshutz, S.; Lipson, M. (2009). Linear Algebra . Schaum's Outlines (4th ed.). McGraw Hill. ISBN 978-0-07-154352-1 ^ Murnaghan, F. D. (1925), "The generalized Kronecker symbol and its application to the theory of determinants", Amer. Math. Monthly , 32 (5): 233–241, doi :10.2307/2299191 , JSTOR 2299191 ^ Lovelock, David; Rund, Hanno (1989). Tensors, Differential Forms, and Variational Principles . Courier Dover Publications. p. 113. ISBN 0-486-65840-6 참고문헌 Misner, C.; Thorne, K. S.; Wheeler, J. A. (1973). Gravitation ISBN 0-7167-0344-0 Neuenschwander, D. E. (2015). Tensor Calculus for Physics . Johns Hopkins University Press. pp. 11, 29, 95. ISBN 978-1-4214-1565-9 Carroll, Sean M. (2004), Spacetime and Geometry ISBN 0-8053-8732-3 외부 링크 이 기사는 PlanetMath 의 Levi-Civita 치환 심볼 의 자료를 통합한 것으로, 이는 Creative Commons Attribution/Share-Alike License 에 따라 라이선스가 부여되어 있습니다.



















![{\displaystyle {\begin{aligned}\delta {_{ijk}}^{lmn}=\varepsilon _{ijk}\varepsilon ^{lmn}&={\begin{vmatrix}\delta _{il}&\delta _{im}&\delta _{in}\\\delta _{jl}&\delta _{jm}&\delta _{jn}\\\delta _{kl}&\delta _{km}&\delta _{kn}\\\end{vmatrix}}\\[6pt]&=\delta _{il}\left(\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}\right)-\delta _{im}\left(\delta _{jl}\delta _{kn}-\delta _{jn}\delta _{kl}\right)+\delta _{in}\left(\delta _{jl}\delta _{km}-\delta _{jm}\delta _{kl}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdf17e18a018e10eb89a4ac409bb146bc9a1349e)




































![{\displaystyle E_{a_{1}\dots a_{n}}={\sqrt {\left|\det[g_{ab}]\right|}}\,\varepsilon _{a_{1}\dots a_{n}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37e9a92e440539e0513ae569542bc390a4f154c1)

![{\displaystyle E^{a_{1}\dots a_{n}}={\frac {\operatorname {sgn} \left(\det[g_{ab}]\right)}{\sqrt {\left|\det[g_{ab}]\right|}}}\,\varepsilon ^{a_{1}\dots a_{n}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a560604067e888ef1a335e34f9e405519a8d818)
![{\displaystyle E^{01\dots n}={\frac {\operatorname {sgn}(\det[g_{ab}])}{\sqrt {\left|\det[g_{ab}]\right|}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b580c03f614708b26f6c3723071527fd82f130)


![{\displaystyle E_{\alpha \beta \gamma \delta }=\pm {\sqrt {\left|\det[g_{\mu \nu }]\right|}}\,\varepsilon _{\alpha \beta \gamma \delta }\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69cea2c0f47be8b11eed0db78ca4d4cb4cf5230d)