미적분학의 역사

초기 역사에서 미적분으로 알려진 미적분은 한계, 연속성, 파생성, 통합성, 무한 계열에 초점을 맞춘 수학 학문이다. 아이작 뉴턴과 고트프리드 빌헬름 라이프니즈는 17세기 후반에 미적분학 이론을 독자적으로 발전시켰다. 17세기 말까지 라이프니츠와 뉴턴은 모두 다른 사람이 자신의 작품을 훔쳤다고 주장했고 라이프니즈--뉴턴 미적분 논란은 1716년 라이프니즈가 사망할 때까지 계속되었다.

미적분학의 선구자

고대

고대 시대는 적분 미적분학을 초래한 사상의 일부를 도입했지만, 엄격하고 체계적인 방법으로 이러한 사상을 전개한 것 같지는 않다. 적분 미적분의 한 목표인 부피와 면적의 계산은 이집트 모스크바 파피루스(기원전 1820년)에서 찾을 수 있지만, 그 공식은 구체적인 숫자에 대해서만 주어지며, 일부는 근사적으로만 사실이며 연역적 추론에 의해 도출되지 않는다.^[1] 바빌로니아인들은 목성의 천문 관측을 하면서 사다리꼴의 법칙을 발견했을지도 모른다.^[2][3]

그리스 수학의 시대부터 에우독서스(기원전 408–355년)는 한계 개념을 예시하는 탈진법을 이용하여 면적과 부피를 계산하였고, 아르키메데스(기원전 287–212년)는 적분법의 방법과 유사한 휴리스틱스를 발명하면서 이 생각을 더욱 발전시켰다.^[4] 그리스 수학자들 역시 인피니티멀을 상당히 많이 사용한 것으로 인정받고 있다. 데모크리토스는 사물을 무한히 많은 횡단면으로 분할하는 것을 진지하게 고려한 최초의 인물이지만, 원뿔의 매끄러운 경사로 이산 횡단면을 합리화하지 못한 것이 그 사상을 수용하지 못하게 했다. 거의 동시에, 엘레아의 제노는 그들이 만들어 내는 역설들에 대한 그의 표현에 의해 더 많은 불신자들을 깎아내렸다.

아르키메데스는 그의 <파라볼라의 사분법>, <방법>, <구체와 원통위에>에서 현대적 개념과 다소 유사한 휴리스틱적인 방법을 발명하면서 이 방법을 더욱 발전시켰다.^[5] 그러나 이 시기 동안 인피니티멘탈이 엄중한 입장에 놓였다고 생각하면 안 된다. 적절한 기하학적 증거로 보완되어야만 그리스 수학자들이 명제를 참으로 받아들일 수 있을 것이다. 17세기에 이르러서야 그 방법이 인디비시블의 방법으로 카발리에리에리에 의해 공식화되었고 결국 뉴턴에 의해 적분학의 일반적인 틀에 편입되었다. 아르키메데스는 미분적분과 유사한 방법으로 원 이외의 곡선에 접하는 것을 처음으로 발견했다. 나선형을 연구하는 동안 그는 한 점의 운동을 하나의 방사형 운동 구성 요소와 하나의 원형 운동 구성 요소인 두 개의 구성 요소로 분리시킨 다음, 계속해서 두 구성 요소 운동을 함께 추가함으로써 곡선에 대한 접선을 찾았다.^[6] 아이작 바로와 요한 베르누이와 같은 미적분학의 선구자들은 아르키메데스의 부지런한 학생이었다. 예를 들어 C. S. 로로(1983)를 보라.

탈진 방법은 서기 4세기 중국에서 원형의 면적을 찾기 위해 류휘에 의해 재창조되었다.^[7] 5세기에 주총지는 구의 부피를 찾는 카발리에리의 원리라고 불릴 수 있는 방법을 세웠다.^[8]

중세

이슬람 중동에서는 11세기 아랍 수학자 이븐 알 하이트암(알하젠)이 4강 합계의 공식을 도출했다. 그는 그 결과를 통합이라고 불릴 만한 것을 수행하는데 사용했는데, 여기서 적분 제곱과 제 4의 힘의 합계에 대한 공식은 파라볼로이드의 부피를 계산할 수 있게 했다.^[9] 12세기에 페르시아의 수학자 샤라프 알 딘 알 투스는 입방 다항식의 파생물을 발견했다.^[10] 그의 방정식에 관한 논문은 양의 해답이 없을 수 있는 입방정식을 해결하기 위해 파생 함수, 곡선의 최대치 및 최소치 등 미분적분과 관련된 개념을 개발했다.^[11]

미적분학에 대한 몇몇 아이디어들은 후에 인도의 수학, 케랄라 천문학과 수학에서 나타났다.^[9] 14세기 상암아극의 마드하바와 이후 케랄라 학파의 수학자들은 테일러 시리즈와 무한 시리즈 근사치와 같은 미적분학의 구성요소를 기술했다.^[12] 그러나, 그들은 파생상품과 적분이라는 두 통일된 주제 아래 많은 다른 생각들을 결합시킬 수 없었고, 둘 사이의 연관성을 보여주었으며, 미적분을 오늘날 우리가 가진 강력한 문제 해결 도구로 바꿀 수 없었다.^[9]

연속성에 대한 수학적인 연구는 14세기에 옥스퍼드 계산기와 니콜 오레스메와 같은 프랑스 협력자들에 의해 부활되었다. 그들은 "머튼 평균 속도 정리"를 증명했다: 균일하게 가속된 신체는 가속된 신체의 최종 속도의 절반인 동일한 속도로 신체와 같은 거리를 이동한다.^[13]

얼리 모던

17세기에 유럽의 수학자 아이작 바로우, 르네 데카르트, 피에르 드 페르마, 블라이즈 파스칼, 존 월리스 등이 파생상품에 대한 아이디어를 토론하였다. 특히 메소더스 ad disqui렌담 maximam et minima와 De tangentibus linearum curvearum에서 페르마트는 분화와 밀접한 관련이 있는 다양한 곡선으로 최대값, 최소값, 접선을 결정하는 적절한 방법을 개발했다.^[14] 아이작 뉴턴은 나중에 미적분학에 대한 자신의 초기 생각은 "페르마의 접선 그리는 방식"^[15]에서 직접 나왔다고 쓰곤 했다.

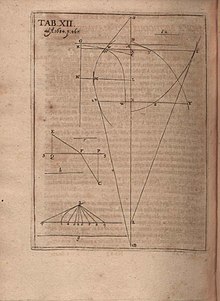
적분 쪽을 보면, 카발리에리는 1630년대와 1640년대의 가장 고대 그리스 법의 좀 더 현대적 형태를 제공하는 indivisibles 방법을 개발하고, 카발리에리의 횡축 공식, 더 높은 정도, 이전에는 단지 포물선 반사경이, 아르키메데스에 의해 계산된 곡선 xn, 밑의 구역 컴퓨팅 exhaustion,[논쟁 – 토론했다.].. 토리첼리는 이 작품을 사이클로이드와 같은 다른 곡선으로 확장시켰고, 그 후 1656년 왈리스에 의해 이 공식이 분절력과 음력으로 일반화되었다. 1659년 논문에서 페르마트는 동력 기능의 적분을 직접 평가하기 위한 기발한 속임수로 인정받고 있다.^[16] 페르마트는 또한 다양한 평면과 고체 형상의 무게중심을 찾는 기법을 얻었고, 이는 사분법에서의 후속 작업에 영향을 주었다. 제임스 그레고리는 페르마트가 접선성과 사분면에 기여한 것에 영향을 받아 17세기 중반 미적분학의 두 번째 기본 정리의 제한된 버전을 증명할 수 있었다.^[17][18] 미적분학의 근본적인 정리에 대한 최초의 완전한 증거는 아이작 바로우가 주었다.^{[19]: p.61 when arc ME ~ arc NH at point of tangency F fig.26 [20]}

실제 변수의 함수 미적분학을 확립하기 위한 한 가지 전제조건은 합리적인 $함수{\displaystyle }$ f${\displaystyle (}$ ${\displaystyle x}$) = ${\displaystyle \frac{1}{}}$x . ${\displaystyle f(x)\\\\\\frac {1}{x}}$에 대한 해독제를 찾는 것이었다.$}}$ 이 문제는$$ 직사각형 하이퍼볼라 xy = 1의 4각으로 표현할 수 있다. 1647년 Greggoire de Saint-Vincent는 필수 함수 $F$가 F${\displaystyle }$( ${\displaystyle s}$)${\displaystyle }$= ${\displaystyle F}$(${\displaystyle }$)${\displaystyle }$+ ${\displaystyle F}$( )${\displaystyle }$,${\displaystyle$ F$(st)=F(s)+F(t)}$를 만족하여$$ F 아래에서 기하학적 시퀀스가 산술 시퀀스가 되었다고 지적했다. A. A. de Sarasa는 이 특징과 현대 알고리즘을 연결했는데, 이 알고리즘은 덧셈에 곱을 표시하여 산술을 절약했다. 그래서 F는 처음에는 쌍곡선 로그로 알려져 있었다. 오일러가 e = 2.71828...을 착취하고 F가 지수함수의 역함수로 식별된 후 d d ${\displaystyle \frac{}{}}$ x${\displaystyle \frac{}{}}$= ${\displaystyle \frac{1}{}}$ ${\displaystyle \frac{x}{}}$. ${\$dfrac {$dF}{dx}}\\\\\\frac {1}{x}}}$을 만족하는 자연 로그가 되었다.$}$

롤의 정리에 대한 첫 번째 증거는 1691년 미셸 롤에 의해 네덜란드의 수학자 요한 반 웨이브렌 허드가 개발한 방법을 사용하여 제시되었다.^[21] 현대적 형태의 평균값 정리는 현대 미적분학의 창시 후인 베르나르 볼자노와 아우구스틴루이 카우치(1789–1857)에 의해서도 명기되었다. 중요한 공헌은 바로우, 후이겐스, 그리고 다른 많은 사람들에 의해서도 이루어졌다.

뉴턴과 라이프니즈

뉴턴과 라이프니즈 이전에는 '미적분'이라는 단어는 수학의 어떤 본체를 지칭했지만, 그 다음 해에는 그들의 통찰력을 바탕으로 한 수학 분야의 통용되는 용어가 되었다.^[22] 이 작품을 바탕으로 한 뉴턴과 라이프니즈는 17세기 후반에 주변 미적분학 이론을 독자적으로 발전시켰다. 또한 라이프니츠는 일관되고 유용한 표기법과 개념을 개발하는 데 많은 노력을 기울였다. 뉴턴은 물리학, 특히 적분 미적분학에 가장 중요한 응용의 일부를 제공했다. 이 절의 목적은 뉴턴과 라이프니츠의 미적분학의 발전 분야에 대한 조사를 조사하는 것이다. 그들이 미적분을 스스로 생각해낸 것처럼 이해하려고 시도하면서 사용한 명분과 서술 용어에 구체적인 중요성이 부여될 것이다.

17세기 중반에 이르러 유럽 수학은 지식의 일차적 저장소를 바꾸게 되었다. 헬레니즘 수학을 연구의 출발점으로 유지했던 지난 세기에 비해 뉴턴, 라이프니즈, 그리고 그 동시대인들은 점점 더 현대적인 사상가들의 작품을 지향했다.^[23] 유럽은 급성장하는 수학 공동체의 본거지가 되었고 향상된 제도적, 조직적 기반이 등장하면서 새로운 수준의 조직과 학문적 통합이 이루어지고 있었다. 그러나 중요한 것은, 지역사회는 형식주의가 부족했다; 대신에 그것은 다양한 방법, 기술, 명언, 이론, 그리고 역설의 질서 없는 집단으로 구성되었다.

뉴턴은 물리학과 기하학에 대한 연구의 일환으로 미적분학을 하게 되었다. 그는 미적분을 운동과 크기의 생성에 대한 과학적 설명으로 보았다. 이에 비해 라이프니츠는 접선 문제에 초점을 맞추고 미적분학이 변화에 대한 형이상학적 설명이라고 믿게 되었다. 중요한 것은, 그들의 통찰력의 핵심은 함수의 적분과 미분 사이의 역 성질의 공식화였다. 이러한 통찰은 전임자들이 예상한 것이지만, 그들은 미적분을 새로운 미사여구와 서술어가 만들어지는 체계로 가장 먼저 착안했다.^[24] 이들의 독특한 발견은 상상력뿐만 아니라 주변의 통찰력을 보편적인 알고리즘 과정으로 합성해 새로운 수학 체계를 형성하는 능력에도 놓여 있었다.

뉴턴

뉴턴은 그의 유동적인 미적분을 공식화하는 결정적인 출판물을 완성하지 못했다; 오히려 그의 많은 수학적인 발견들은 통신, 작은 논문을 통해 전달되거나 프린세스와 옵틱스와 같은 그의 다른 결정적인 컴필레이션에 내재된 측면으로 전달되었다. 뉴턴은 캠브리지에서 아이작 바로우의 후계자로 선정된 수학 훈련을 시작할 것이다. 그의 적성은 일찍부터 인정받았고 그는 현재의 학설을 빨리 배웠다. 1664년까지 뉴턴은 분수 및 음수 지수를 포함하도록 확장한 이항 정리를 진전시킴으로써 그의 첫 번째 중요한 공헌을 했다. 뉴턴은 무한 계열의 분석에 유한 수량의 대수학을 적용함으로써 이항 정리의 적용성을 확대하는 데 성공했다. 그는 무한 시리즈를 근사적인 장치뿐만 아니라 용어를 표현하는 대안적인 형태로 보겠다는 의지를 보였다.^[25]

뉴턴의 많은 비판적 통찰은 1665–1666년의^[26] 역병 기간 동안 발생했는데, 후에 그는 "이후 어느 때보다도 발명과 마인드 수학과 [자연] 철학의 전성기"라고 묘사했다. 유속 미적분의 첫 번째 서면 착상이 아에퀴네스 누메로 터미네로 인피니타스에 의해 미발표 디 애널리시에 기록된 것은 그의 페스트 유도 고립 기간이었다. 이 논문에서 뉴턴은 먼저 순간적인 변화율을 계산한 다음 전체 영역을 추론함으로써 곡선 아래 영역을 결정했다. 그는 면적이 x와 y의 함수인 무한정 작은 삼각형에 대해 추론하는 것으로 시작했다. 그는 이어 압시사의 극소수 증가가 x = x + o(중요하게는 o가 숫자 0이 아니라 글자임)라는 새로운 공식을 만들어 낼 것이라고 추론했다. 그런 다음 그는 이항 정리의 도움을 받아 그 지역을 다시 계산하고, o자를 포함한 모든 양을 제거하고 그 영역에 대한 대수적 식을 다시 만들었다. 의미심장하게, 뉴턴은 o가 포함된 수량을 "깜짝" 쏟아낼 것이다. 왜냐하면 용어는 "그것들에 의해 곱해진 것은 나머지에 관해서는 아무것도 아닐 것"이기 때문이다.

이때 뉴턴은 역전의 중심적 속성을 깨닫기 시작했다. 그는 순간적인 증가를 한 지점에서 고려함으로써 곡선 아래 지역에 대한 표현을 만들어냈었다. 사실상 미적분의 근본적인 정리가 그의 계산 속에 쌓였다. 그의 새로운 공식화가 믿을 수 없는 잠재력을 제공했지만, 뉴턴은 그 당시 그것의 논리적 한계를 잘 알고 있었다. 그는 "수학에서는 아무리 작아도 오류를 무시해서는 안 된다"고 인정하고, 자신이 이룬 것이 "정확하게 입증하기보다는 짧게 설명되었다"고 인정한다.

미적분학을 보다 엄격한 탐색과 틀을 주기 위한 노력의 일환으로 뉴턴은 1671년 Methodus Fluxionum et Serierum Infinitarum을 편찬했다. 이 책에서는 뉴턴의 엄격한 경험주의가 그의 유동적 미적분을 형성하고 규정했다. 그는 순간적인 움직임과 반감을 비공식적으로 이용했다. 그는 물리적 세계를 설명하기 위해 수학을 방법론적 도구로 이용했다. 뉴턴이 개정한 미적분학의 기초는 연속성이 되었다. 그렇게 그는 계속 흐르는 움직임의 관점에서 그의 계산을 다시 정의했다. 뉴턴에게 있어서 가변 크기는 극소수 원소의 집합체가 아니라, 논란의 여지가 없는 움직임의 사실에 의해 생성된다. 그의 많은 작품들과 마찬가지로 뉴턴은 출판을 연기했다. Methodus Fluxionum은 1736년에야 출판되었다.^[27]

뉴턴은 변화의 비율에 근거한 계산을 구성함으로써 극소수의 사용을 피하려고 시도했다. 그는 Methodus Fluxionum에서 발생된 변화의 속도를 점문자로 나타낸 플럭션으로 정의했으며, 발생된 양은 유창하다고 정의했다. 예를 들어, $x{\displaystyle }$ ${\$와 y$${\$dot{$$x}}$가 형광펜인 경우$$, $x{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{\dot{}}}$ ${\$와 y ${\displaystyle \stackrel{}{\dot{}}}$ ${\dottyle$ {$y}$은(는) 각각 플럭션이다$$. 이 수정된 비율의 미적분은 계속 개발되어 1676년 본문 De Quadratura Crevarum에서 성숙하게 서술되었는데, 여기서 뉴턴은 현재의 파생상품을 문제의 순간에 순수하게 발생되는 증분(유속 비율) 사이의 비율로 정의했다. 본질적으로 궁극적인 비율은 증분이 무로 사라짐에 따른 비율이다. 중요한 것은 뉴턴이 운동에 호소함으로써 궁극적인 비율의 존재를 설명했다는 것이다.

"최대의 속도에 의해 신체가 움직이는 것을 의미하기 때문에, 신체가 마지막 장소에 도착하기 전, 움직임이 멈추는 순간, 그 직후가 아니라, 그것이 도착하는 순간... 발생 수량의 궁극적인 비율을 파악해야 한다. 수량이 사라지기 전이나 후에 없어지는 것이 아니라 사라지게 되는 것이다.^[28]

뉴턴은 자신의 계산에서 불분명한 것을 비공식적으로 사용하지 않으려는 시도로 그의 유동 미적분을 개발했다.

라이프니츠

뉴턴이 1665–1666년에 그의 유동 미적분학의 개발을 시작한 동안, 그의 발견은 나중에야 널리 퍼졌다. 그 사이에 라이프니즈도 미적분을 만들기 위해 노력했다. 어린 나이에 수학에 온 뉴턴에 비해 라이프니츠는 성숙한 지성으로 엄격한 수학 공부를 시작했다. 그는 다산수학이었고, 그의 지적 흥미와 업적에는 형이상학, 법률, 경제, 정치, 논리, 수학 등이 포함되어 있었다. 라이프니츠의 미적분학 추리를 이해하기 위해서는 그의 배경을 염두에 두어야 한다. 특히 우주를 모나드학이라고 묘사한 그의 형이상학, 그리고 "이성의 모든 진리가 일종의 계산으로 전락하는 일반적인 방법"^[29]이라는 정밀한 형식논리를 창조하려는 그의 계획 등이 그것이다.

1672년 라이프니즈는 라이프니즈를 설득하여 수학 연구에 상당한 시간을 할애하도록 한 수학자 휴겐스를 만났다. 1673년까지 그는 파스칼의 <특징> des Sincy du Quarte Cercle>을 읽게 되었고, 라이프니즈가 "불이 켜졌다"고 말한 것은 그의 대부분 자기역학 연구 중에 있었다. 뉴턴처럼 라이프니츠는 접선을 비율로 보면서도 단순히 서수와 아비사이의 비율로 선언했다. 그는 이 추론을 계속하여 그 적분은 사실 압시사 내 극소수의 간격에 대한 서수의 합, 사실상 무한히 많은 직사각형의 합이라고 주장했다. 이러한 정의로부터 역관계나 차이는 분명해졌고 라이프니즈는 수학의 전혀 새로운 체계를 형성할 수 있는 가능성을 재빨리 깨달았다. 라이프니츠는 뉴턴이 자신의 경력에 걸쳐 여러 가지 접근법을 사용했던 곳과 더불어 인피니티멀을 이용한 접근법을 사용했던 곳에서는 이것을 그의 표기법과 미적분학의 초석으로 삼았다.^[30][31]

1675년 10월 25일부터 11월 11일까지의 원고에서 라이프니즈는 다양한 형태의 표기법으로 그의 발견과 실험을 기록했다. 그는 사용된 명목적인 용어들을 예리하게 알고 있었고 정확한 논리적 상징성을 형성하려는 그의 초기 계획이 명백해졌다. 결국 라이프니즈는 아바시사의 극소수 증분을 나타내며 dx와 dy를 서열하고, 무한히 많은 무한히 얇은 직사각형을 긴 s로 합한 것이 현재의 일체형 기호 $\int {\displaystyle }$ ${\$이(가) 되었다$.$^[32]

라이프니츠의 표기법은 현대 수학에서 쓰는 것이지만 그의 논리적인 근거는 지금의 우리 것과 달랐다. 라이프니츠는 "파스칼이 그랬던 것처럼 무한히 작은 것을 미스터리로 만들지 않기 위해서"라고 극구 글을 썼다.^[33] 길레스 델레우제(Gilles Delleuze)에 따르면, 라이프니츠의 영은 "없지만, 그것들은 절대적으로 없는 것이 아니라 각각" "각각"이다.(라이브니츠의 텍스트 "일반대수의 미적분에 의한 불분수의 정당화"^[34]를 인용한다.) 또는, 그는 그것들을 "어떤 주어진 수량보다 적다"라고 정의한다. 라이프니즈에게 있어 세계는 극히 미미한 점들의 집합체였고 그들의 존재에 대한 과학적 증거의 부족은 그를 괴롭히지 않았다. 라이프니츠에 대한 인피니티시멀은 주목할 만한 숫자와 다른 유형의 이상적인 양이었다. 연속성의 진실은 존재 자체로 증명되었다. 라이프니츠에게는 연속성의 원칙과 따라서 그의 미적분의 타당성이 보장되었다. 라이프니츠가 일한 지 300년이 지난 후, 아브라함 로빈슨은 미적분학에서 극미량의 양을 사용하는 것이 견고한 기초를 제공할 수 있다는 것을 보여주었다.^[35]

레거시

미적분의 상승은 수학에서 독특한 순간으로 두드러진다. 미적분학은 움직임과 변화의 수학이며, 이와 같이 미적분학의 발명은 새로운 수학적 시스템의 창조를 필요로 했다. 중요한 것은 뉴턴과 라이프니즈는 같은 미적분을 만들지 않았고 현대 미적분을 상상하지도 않았다는 것이다. 두 사람 모두 가변적인 수량을 다루기 위한 수학적 시스템을 만드는 과정에 관여하고 있었지만, 그들의 기본적인 기반은 달랐다. 뉴턴에게 변화는 시간의 경과에 따른 가변적 수량이었고 라이프니츠의 경우 무한히 가까운 값의 순서에 걸친 차이였다. 특히 각 시스템이 변화를 설명하기 위해 만든 서술 용어는 달랐다.

역사적으로, 미적분을 처음 '발견'한 사람이 뉴턴인지 라이프니즈인지에 대해 많은 논쟁이 있었다. 독일인인 라이프니츠와 영국인 뉴턴이 관련된 이 논쟁, 라이프니츠와 뉴턴 미적분 논쟁은 한 세기 넘게 지속되는 유럽 수학계의 균열을 초래했다. 라이프니츠는 그의 조사를 처음으로 발표한 사람이었지만, 뉴턴이 라이프니즈보다 몇 년 전부터 연구를 시작했으며 라이프니즈가 이 문제에 관심을 갖게 될 무렵에는 이미 접선 이론을 발전시켰다는 것은 잘 알려진 사실이다. 이것이 라이프니즈에게 얼마나 큰 영향을 미쳤는지는 알려지지 않았다. 초기 고발은 세기가 바뀔 무렵 두 명의 위대한 과학자의 학생들과 지지자들에 의해 이루어졌으나, 1711년 이후 두 사람 모두 서로 표절 행위를 고발하며 개인적으로 연루되었다.

우선권 분쟁은 수년간 유럽 대륙에서 영어를 사용하는 수학자들과 분리하는 효과를 가져왔다. 1820년대에 들어서야 영국에서는 분석학회의 노력으로 라이프니지안 분석 미적분이 받아들여졌다. 오늘날 뉴턴과 라이프니즈 둘 다 미적분학의 기초를 독자적으로 개발한 공로를 인정받고 있다. 그러나 새로운 규율에게 오늘날까지 알려진 이름인 "미적분"을 준 사람은 라이프니즈다. 그것에 대한 뉴턴의 이름은 "유행과 유동성의 과학"이었다.

뉴턴과 라이프니즈 모두의 작업은 오늘날 사용되는 표기법에 반영되어 있다. 뉴턴은 함수 f의 파생형에 대해$$ $f{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{\dot{}}}$ ${\$라는 표기법을 도입했다.^[36] 라이프니츠는 적분 기호$$$$integral{\$displaystyle \int }$을(를) 도입하고 변수 x의 함수 y의 $파생상품$을 d ${\displaystyle \frac{y}{}}$ d ${\displaystyle \frac{}{}}${\$displaystyle {\\frac$ {$dy}{dx}}}$로 작성했는데$,$ 둘 다 아직 사용되고 있다.

라이프니츠와 뉴턴 시대부터 많은 수학자들이 미적분학의 지속적인 발전에 기여했다. 미적분과 적분 둘 다에 대한 첫 번째 그리고 가장 완전한 작품들 중 하나는 1748년에 마리아 가에타나 아그네시에 의해 쓰여졌다.^[37][38]

운영 방법

앙투안 아르보가스트(1800)는 미분방정식에서 처음으로 작동의 상징과 양의 상징을 분리했다. 프랑수아 요제프 세르보아(1814년)는 가장 먼저 이 문제에 대한 올바른 규칙을 제시한 것으로 보인다. 찰스 제임스 하그리브(1848)는 미분방정식에 관한 회고록에서 이런 방법을 적용했고, 조지 볼은 이를 자유자재로 채용했다. 헤르만 그라스만과 헤르만 행클은 그의 복잡한 숫자 이론에서 전자는 방정식을 연구하는 데, 후자는 그의 이론을 크게 활용했다.

변이 미적분학

변동의 미적분은 요한 베르누이(1696)의 문제에서 시작된다고 할 수 있다. 그것은 즉시 야콥 베르누이의 주의를 끌었지만 레온하르트 오일러는 먼저 그 주제를 상세히 설명했다. 그의 공헌은 1733년에 시작되었고, 그의 원소 칼쿨리 변주곡은 과학에 그 이름을 붙였다. 조셉 루이 라그랑주(Joseph Louis Lagrange)가 이 이론에 크게 공헌하였고, 아드리아-마리 레전드르(Arien-Marie Legendre, 1786)는 맥시마와 미니마(Minima)의 차별에 대해 전적으로 만족스럽지는 않은 방법을 내놓았다. 이러한 차별에 브루나치(1810), 칼 프리드리히 가우스(1829), 시메온 데니스 포아송(1831), 미하일 바실리예비치 오스트로그라스키(1834), 칼 구스타프 야콥 야코비(1837) 등이 기여자로 이름을 올렸다. 중요한 일반 저작은 오거스틴 루이 코치(1844년)가 응축·개선한 사루스(1842)의 작품이다. 그 밖에 스트라우치(1849년), 젤렛트(1850년), 오토 헤세(1857년), 알프레드 클레브슈(1858년), 칼(1885년)에 의해 귀중한 서간과 회고록이 저술되었지만 아마도 세기의 가장 중요한 작품은 카를 바이어스트라스의 작품일 것이다. 그 이론에 대한 그의 진로는 미적분을 확고하고 엄격한 기초 위에 놓는 첫 번째 방법이라고 주장될 수 있다.

통합

닐스 헨리크 아벨은 일반적인 기능의 도움에 의해 유한한 형태로 통합될 수 있는 미분방정식이 무엇인지에 대해 일반적인 방법으로 가장 먼저 고려한 것으로 보이며, 이는 리우빌에 의해 확대된 조사인 것으로 보인다. 코치는 일찍이 확실한 통합을 결정하는 일반 이론을 맡았으며, 이 주제는 19세기 동안 두드러져 왔다. Frullani integrals, David Bierens de Haan's work on the theory and his elaborate tables, Lejeune Dirichlet's lectures embodied in Meyer's treatise, and numerous memoirs of Legendre, Poisson, Plana, Raabe, Sohncke, Schlömilch, Elliott, Leudesdorf and Kronecker are among the noteworthy contributions.

오일러 통합은 처음에 오일러에 의해 연구되었고, 이후 레전드레에 의해 조사되었으며, 이들에 의해 다음과 같이 1종과 2종의 오일러 통합으로 분류되었다.

${\displaystyle \int _{0}^{1}x^{n-1}(1-x)^{n-1}\,dx}$

${\displaystyle \int_{0}^{0}^{\\infit }e^{-x}x^{n-1}\,dx}$

비록 이것들이 오일러의 연구의 정확한 형태는 아니었지만.

n이 양의 정수인 경우:

${\displaystyle \int _{0}^{\infit }e^{-x^{n-1}dx=(n-1)!,}$

그러나 모든 양의 실제 $n{\displaystyle }$ ${\displaystyle n}$에 대한 통합이 이루어지며$$ 0의 극과 음의 정수를 제외한 모든 복잡한 평면에 대한 요인 함수의 분석적 연속성을 정의한다. 그것에 레전드르에는 기호 $\gamma {\displaystyle \mathrm{}}${\$displaystyle \Gamma }$이$($가) 할당되었으며, 현재는 감마함수라고 불린다. ℝ⁺+reals over에 대해 분석적인 것 외에도, ${\displaystyle \mathrm{\gamma }}$ ${\displaystyle \Gamma}$은(는) ${\displaystyle }$ ⁡ ${\displaystyle \log \Gamma}$을(를) 볼록스(colfx)로$$ 기록하는 고유한 정의 속성을 즐기며, 이는 다른 분석적 지속에 대해 요인 함수의 분석적 지속을 미학적으로 정당화한다. 주제에는 르주네 디리클레트가 중요한 정리(Liouville, 1839년)를 기고했는데, 이 정리에는 리우빌, 카탈란, 레슬리 엘리스 등이 상세히 기술되어 있다. 라베(1843~44), 바우어(1859), 구더만(1845) 등은 $\gamma {\displaystyle \mathrm{}(x}$) ${\디스플레이$ 스타일 $\$$감마(x$$)}$와 ${\displaystyle \mathrm{로그}}$ $⁡$ ${\displaystyle \mathrm{x}(x)}$x($x)}$에 대한 평가에 대해 저술했다$.$ 1816년 레전드레의 훌륭한 테이블이 등장했다.

적용들

물리학과 천문학의 문제에 극소수의 미적분학을 적용한 것은 과학의 기원과 동시대적인 것이었다. 18세기 내내 이러한 적용은 증배되었고, 라플레이스와 라그랑쥬는 그 가까운 곳에서 힘의 연구 전 범위를 분석의 영역으로 가져왔었다. 라그랑주(1773년)에게 우리는 잠재력 이론을 역학적으로 도입해야 하는데, 비록 "잠재함수"라는 명칭과 그 주제의 근본적 회고록은 그린(1827년, 1828년 인쇄)에 기인한다. "잠재력"이라는 이름은 가우스(1840년)에 기인하며, 클라우시우스에게 잠재능력과 잠재능력의 구분이 있기 때문이다. 그 발전과 함께 르주네 디리클레, 리만, 폰 노이만, 하이네, 크로네커, 립슈치츠, 크리스토펠, 키르호프, 벨트라미, 그리고 세기의 대표적인 물리학자들의 이름이 연결되어 있다.

이 곳에서는 물리적 문제에 대한 분석의 아주 다양한 적용에 들어가는 것은 불가능하다. Among them are the investigations of Euler on vibrating chords; Sophie Germain on elastic membranes; Poisson, Lamé, Saint-Venant, and Clebsch on the elasticity of three-dimensional bodies; Fourier on heat diffusion; Fresnel on light; Maxwell, Helmholtz, and Hertz on electricity; Hansen, Hill, and Gyldén on astronomy; Maxwell on spherical harmonics; 음향에 관한 레일리 경; 그리고 레전 디리클레트, 베버, 키르흐호프, F. 노이만, 켈빈 경, 클로스우스, 비에르크네스, 맥컬라흐, 푸어만 등이 물리학계에 종사한다. 헬름홀츠의 노동력은 특히 언급되어야 하는데, 그는 역학, 전기 등의 이론에 기여했고, 그의 위대한 분석력을 순수 수학의 공리뿐만 아니라 역학의 근본적인 공리에도 견줄 수 있게 했기 때문이다.

나아가 신고전주의 경제학을 시작으로 사회과학에 미적분학이 도입되었다. 오늘날, 그것은 주류 경제학의 귀중한 도구다.

참고 항목

• 해석 기하학
• 로그의 역사
• 수학의 역사
• 비표준 미적분학

메모들

추가 읽기

• Roero, C.S. (2005). "Gottfried Wilhelm Leibniz, first three papers on the calculus (1684, 1686, 1693)". In Grattan-Guinness, I. (ed.). Landmark writings in Western mathematics 1640–1940. Elsevier. pp. 46–58. ISBN 978-0-444-50871-3.
• Roero, C.S. (1983). "Jakob Bernoulli, attentive student of the work of Archimedes: marginal notes to the edition of Barrow". Boll. Storia Sci. Mat. 3 (1): 77–125.
• Boyer, Carl (1959). The History of the Calculus and its Conceptual Development. New York: Dover Publications. 제목이 다른 1939년 책 공화국(1949년 2차 인쇄)
• Calinger, Ronald (1999). A Contextual History of Mathematics. Toronto: Prentice-Hall. ISBN 978-0-02-318285-3.
• Reyes, Mitchell (2004). "The Rhetoric in Mathematics: Newton, Leibniz, the Calculus, and the Rhetorical Force of the Infinitesimal". Quarterly Journal of Speech. 90 (2): 159–184. doi:10.1080/0033563042000227427. S2CID 145802382.
• 그랜튼가인니스, 아이보르 수학의 무지개: 수학 과학의 역사 5, 6장 W. W. Norton & Company, 2000.
• 호프만, 루스 아이린, "뉴턴과 라이프니즈 이전의 미적분학의 개발과 사용에 대하여,"논문 (M.A.), 콜로라도 대학교, 1937년

외부 링크

• 맥튜터 수학사 아카이브의 미적분학 역사, 1996.
• 수학의 일부 단어의 초기 알려진 사용: 미적분 & 분석
• 케임브리지 대학교 디지털 도서관 뉴턴 페이퍼스
• (영어 및 아랍어) 1772년 미적분학 소풍