지역

지역
공통 기호	A
SI 단위	평방미터[m2]
SI 기준 단위	1미터2
치수	$(\displaystyle\mathsf {L}}^{2})$

면적은 평면 또는 곡면상의 영역의 범위를 나타내는 양입니다.평면 영역 또는 평면 영역의 영역은 형상 또는 평면 적층 영역을 나타내며, 표면 영역은 열린 표면의 영역 또는 3차원 물체의 경계를 나타냅니다.면적이란 특정 두께의 재료의 양으로 형상 모형을 제작하는 데 필요한 양 또는 표면을 단일 ^[1]코팅으로 덮는 데 필요한 페인트 양으로 이해할 수 있습니다.곡선의 길이(1차원 개념) 또는 고체의 부피(3차원 개념)의 2차원 아날로그입니다.

도형의 면적은 도형을 고정된 ^[2]크기의 정사각형과 비교하여 측정할 수 있습니다.국제 단위계(SI)에서 면적의 표준 단위는 평방미터(m으로 표기²)이며, 이는 변의 길이가 ^[3]1미터인 정사각형의 면적이다.면적이 3평방미터인 모양은 그러한 세 개의 정사각형과 같은 면적을 가진다.수학에서 단위 제곱은 면적 1을 가지도록 정의되며, 다른 형상 또는 표면의 면적은 차원 없는 실수입니다.

삼각형, 직사각형, 원과 같은 단순한 형태의 영역에 대해 잘 알려진 몇 가지 공식들이 있습니다.이러한 공식을 사용하여 폴리곤을 ^[4]삼각형으로 분할하여 폴리곤의 영역을 찾을 수 있습니다.곡선 경계가 있는 도형의 경우 일반적으로 면적을 계산하기 위해 미적분이 필요합니다.사실, 평면 도형의 면적을 결정하는 문제는 ^[5]미적분학의 역사적 발전의 주요 동기였다.

구체, 원뿔 또는 실린더와 같은 입체 형상의 경우 경계 표면의 영역을 ^[6][7][8]표면적이라고 합니다.단순한 형상의 표면적에 대한 공식은 고대 그리스에 의해 계산되었지만, 더 복잡한 형상의 표면적을 계산하는 것은 보통 다변수 미적분을 필요로 한다.

영역은 현대 수학에서 중요한 역할을 한다.기하학 및 미적분학에서의 명백한 중요성 외에도, 영역은 선형 대수학에서의 결정 인자의 정의와 관련이 있으며, 미분 ^[9]기하학에서 표면의 기본 특성입니다.해석에서, 모든 부분 집합이 ^[11]측정 가능한 것은 아니지만, 평면의 부분 집합의 면적은 르베그 ^[10]측정을 사용하여 정의된다.일반적으로 고등 수학에서 영역은 2차원 영역에 ^[6]대한 부피의 특별한 경우로 간주됩니다.

영역은 공리를 사용하여 정의할 수 있으며, 실수의 집합에 대한 특정 평면 도형의 집합 함수로서 정의할 수 있습니다.그러한 기능이 존재함을 증명할 수 있다.

형식적 정의

"지역"이 의미하는 바를 정의하는 방법은 공리를 통해 이루어집니다."면적"은 특별한 종류의 평면 도형(측정 가능한 집합)의 집합 M에서 다음 ^[12]특성을 충족하는 실수 집합까지의 함수로 정의할 수 있다.

• M의 모든 S에 대해 a(S)는 0입니다.
• S와 T가 M이면 S t T와 S t T도 마찬가지이며, a(S) = a(S) + a(T) - a(StT)도 마찬가지이다.
• S와 T가 S t T일 때 M이면 T - S는 M이고 a(T-S) = a(T) - a(S)이다.
• 집합 S가 M에 있고 S가 T와 동일하다면, T도 M에 있고 a(S) = a(T)이다.
• 모든 직사각형 R은 M이다.직사각형의 길이가 h이고 폭이 k이면 a(R) = hk이다.
• Q는 2개의 스텝 영역 S와 T 사이에 둘러싸인 세트라고 합니다.단차영역은 공통기저에 놓여 있는 인접한 직사각형의 유한합체, 즉 S t Q t T에서 형성된다.단차영역 S 및 T에 대해 a(S) c c ( a(T)가 되는 고유수 c가 있으면 a(Q) = c이다.

이러한 면적 함수가 실제로 ^[13]존재함을 증명할 수 있다.

단위

길이의 각 단위는 대응하는 면적의 단위, 즉 주어진 변의 길이를 가진 정사각형의 면적을 가진다.따라서 면적은 평방미터(m²), 평방센티미터(cm²), 평방밀리미터(mm²), 평방킬로미터(km²), 평방피트(ft²), 평방야드(yd²), 평방마일(mi²)^[14] 등으로 측정할 수 있습니다.대수적으로 이들 단위는 대응하는 길이 단위의 제곱으로 생각할 수 있다.

면적의 SI 단위는 SI 파생 ^[3]단위로 간주되는 평방미터이다.

변환

길이와 폭이 1m인 정사각형 면적의 계산은 다음과 같다.

1m x 1m = 1m²

따라서 서로 다른 변을 가진 직사각형(길이 3m, 폭 2m 등)은 다음과 같이 제곱 단위로 계산될 수 있다.

3m × 2m = 6m²이것은 600만 평방 밀리미터에 해당합니다.기타 유용한 변환은 다음과 같습니다.

• 1평방킬로미터 = 1,000,000평방미터
• 1평방미터 = 10,000평방센티미터 = 1,000,000평방밀리미터
• 1평방센티미터 = 100평방밀리미터.

비미터 단위

비메트릭 단위에서 두 개의 제곱 단위 간의 변환은 대응하는 길이 단위 간의 변환의 제곱입니다.

1피트 = 12인치,

평방피트와 평방인치 사이의 관계는

1평방피트 = 144평방인치,

여기서 144 = 12² = 12 × 12 입니다.마찬가지로:

• 1 평방 야드 = 9 평방 피트
• 1평방마일 = 3,097,600평방야드 = 2,787,400평방피트

또한 변환 요인에는 다음이 포함됩니다.

• 1평방인치 = 6.4516평방센티미터
• 1평방피트 = 0.09290304평방미터
• 1평방야드 = 0.83612736평방미터
• 1평방마일 = 2.589988110336평방킬로미터

이력 등 기타 유닛

면적에는 몇 가지 공통 단위가 있습니다.are는 미터법에서 원래 면적의 단위이며, 다음과 같습니다.

• 1은 = 100평방미터

비록 헥타르는 사용되지 않게 되었지만,^[14] 여전히 토지를 측정하는 데 일반적으로 사용됩니다.

• 1헥타르 = 100 ares = 10,000 평방 미터 = 0.01 평방 킬로미터

다른 흔치 않은 측정 단위로는 테트라드, 헥타드, 무수한 측정 단위가 있습니다.

에이커는 또한 일반적으로 육지 면적을 측정하는데 사용된다.

• 1에이커 = 4,840평방야드 = 43,160평방피트.

1에이커는 헥타르의 약 40%이다.

원자 규모에서 면적은 다음과 같이 ^[14]축사 단위로 측정된다.

• 1 축사 = 10⁻²⁸ 평방미터.

헛간은 ^[14]핵물리학에서 상호작용의 단면적을 설명하는 데 일반적으로 사용된다.

인도에서는

• 20 dhurki = 1 dhur
• 20 dhur = 1 khatha
• 20 khata = 1 bigha
• 32 khata = 1에이커

역사

원 영역

기원전 5세기에, 히포크라테스의 히포크라테스는 ^[15]히포크라테스의 룬의 직경의 정사각형의 일부로서 디스크의 면적(원으로 둘러싸인 영역)이 비례한다는 것을 처음으로 보여주었지만, 비례의 상수를 식별하지는 못했다.역시 기원전 5세기 크니두스의 에우독소스는 원반 면적이 반지름 ^[16]제곱에 비례한다는 것을 발견했다.

그 후, 유클리드의 원소의 1권은 2차원 도형 사이의 영역 평등을 다루었다.수학자 아르키메데스는 그의 책 원의 측정에서 원 안에 있는 영역이 원의 둘레의 길이를 가지고 있고 원의 반지름과 높이가 같은 직각 삼각형과 같다는 것을 보여주기 위해 유클리드 기하학의 도구를 사용했다.(둘레는 2µr, 삼각형의 면적은 높이의 절반으로 디스크의 면적 µr이² 됩니다.)아르키메데스는 원에 규칙적인 삼각형을 새기고 그 면적을 주목한 다음, 규칙적인 육각형을 주기 위해 변의 수를 두 배로 늘리고, 다각형 면적이 원형의 면적에 점점 가까워짐에 따라 변의 수를 두 배로 하는 그의 두 배법으로 θ의 값(그리고 따라서 단위 반지름 원의 면적)을 근사했다.cle(및 제한된 폴리곤에서도 마찬가지)

1761년 스위스 과학자 요한 하인리히 램버트는 원의 면적과 반지름의 제곱의 비율인 θ가 불합리하다는 것을 증명했는데, 이는 두 개의 정수의 ^[17]몫과 같지 않다는 것을 의미한다.1794년, 프랑스의 수학자 Adrien-Marie Legendre는 θ가^{2 [18]}비이성적이라는 것을 증명했다.1882년, 독일의 수학자 페르디난트 폰 린데만은 θ가 초월적이라는 것을 증명했고, 레전드르와 ^{[17]: p. 196} 오일러에 의해 만들어진 추측을 확인했습니다.

삼각형 영역

알렉산드리아의 헤론(또는 영웅)은 삼각형의 면적에 대한 헤론의 공식으로 알려진 것을 발견했고, 증거는 서기 60년경에 쓰여진 그의 책, 메트릭타에서 찾을 수 있다.아르키메데스가 2세기 전에 ^[19]그 공식을 알고 있었다는 주장이 제기되었고, 메트릭타가 고대 세계에서 사용 가능한 수학적 지식의 집합이기 때문에, 그 공식은 ^[20]그 연구에서 주어진 참조보다 앞서 있을 가능성이 있다.

499년 인도 수학과 인도 천문학의 고전 시대의 위대한 수학자이자 천문학자 아리아바타는 삼각형의 면적을 아리아바티야에서 밑변의 1/2 곱하기 높이의 1/2로 표현했다.

헤론과 동등한 공식은 그리스인과는 독립적으로 중국인에 의해 발견되었다.그것은 1247년 진주샤오에 의해 쓰여진 수서주장에 출판되었다.

사각형 면적

서기 7세기에, 브라흐마굽타는 현재 브라흐마굽타의 공식으로 알려진 공식을 그 변의 관점에서 순환 사각형(원 안에 새겨진 사각형)의 면적에 대해 개발했습니다.1842년, 독일의 수학자 칼 안톤 브레츠나이더와 칼 게오르크 크리스티안 폰 슈타우트는 독립적으로 브레츠나이더의 공식으로 알려진 사각형 면적을 구했다.

일반 폴리곤 영역

17세기에 르네 데카르트에 의한 데카르트 좌표의 개발은 19세기에 가우스에 의해 알려진 정점 위치를 가진 모든 다각형 영역에 대한 측량자의 공식을 개발할 수 있게 했다.

미적분을 사용하여 결정된 영역

17세기 후반의 적분학의 발달은 타원의 면적과 다양한 곡선의 3차원 물체의 표면적과 같은 더 복잡한 영역을 계산하는데 사용될 수 있는 도구를 제공하였다.

면적식

폴리곤 공식

n개의 정점이 알려진 데카르트 좌표${\displaystyle }$(${\displaystyle x_{}}$ i${\displaystyle {}_{}}$ ${\displaystyle y_{}}$i$$) {style $(x_{i$}, $y_{i})}$ (i=0, 1, ..., n-1)의 경우, 면적은 평가관의 ^[21]공식에 의해 지정됩니다.

${\displaystyle A=biggl \vert } {\sum _{i=0}^{n-1}(x_{i+1}-x_{i+1}y_{i}}{\Biggr \vert}}$

여기서 i=n-1일 때, i+1은 계수 n으로 표현되며, 따라서 0을 참조한다.

직사각형

가장 기본적인 면적 공식은 직사각형의 면적 공식입니다.길이가 l이고 폭이 w인 직사각형이 주어지면 면적의 공식은 다음과 같습니다.^[2][22]

A = lw(표준).

즉, 직사각형의 면적은 길이에 너비를 곱한 것입니다.특별한 경우로, 정사각형의 경우 l = w와 같이, 변 길이가 s인 정사각형의 면적은 다음 ^[6][2][23]공식으로 주어진다.

A = s²(사각형)

직사각형의 영역에 대한 공식은 영역의 기본 속성에서 직접 따르며 정의 또는 공리로 간주되기도 합니다.한편, 기하학이 산술보다 먼저 개발되면, 이 공식을 사용하여 실수의 곱셈을 정의할 수 있습니다.

단면, 평행사변형 및 삼각형

대부분의 다른 간단한 면적 공식은 해부 방법을 따릅니다.이것은 모양을 조각으로 자르는 것을 포함하며, 그 면적이 원래 모양의 면적과 합해야 합니다.

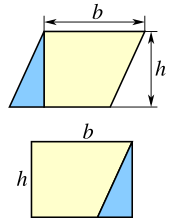
예를 들어 왼쪽 그림과 같이 평행사변형을 사다리꼴과 직각삼각형으로 세분할 수 있다.삼각형을 사다리꼴의 반대쪽으로 이동하면 그림이 직사각형입니다.따라서 평행사변형의 면적은 ^[2]직사각형의 면적과 동일합니다.

A = bh(심전도).

그러나 오른쪽 그림과 같이 대각선을 따라 동일한 평행사변형을 2개의 합동삼각형으로 절단할 수도 있습니다.따라서 각 삼각형의 면적은 평행사변형의 ^[2]절반입니다.

${\displaystyle A}$ ${\displaystyle =}$ ${\displaystyle \frac{12}{}}$ $(표시$ A =$scapfrac {1}{2}})$ ($표준$).$$

사다리꼴과^[24] 더 복잡한 ^[25]다각형에 대한 면적 공식을 찾기 위해 유사한 인수를 사용할 수 있습니다.

곡선 형태의 면적

서클

원의 면적 공식(원 또는 디스크 영역으로 둘러싸인 영역이라고 더 적절하게 불림)은 유사한 방법을 기반으로 합니다.반지름 r의 원이 지정되면 오른쪽 그림과 같이 원을 섹터로 분할할 수 있습니다.각 섹터는 대략 삼각형 모양이며, 섹터를 재배치하여 대략적인 평행사변형을 형성할 수 있다.이 평행사변형의 높이는 r이고 폭은 원의 절반인 µr입니다.따라서 원의 총 면적은 µr²:^[2]

A = "r²" (표준).

이 공식에 사용된 절개는 근사치이지만 원이 점점 더 많은 섹터로 분할됨에 따라 오차는 점점 더 작아집니다.대략적인 평행사변형 영역의 한계는 ^[26]원의 면적인 정확히 θr입니다².

이 주장은 사실 미적분학의 개념을 단순하게 적용한 것이다.고대에는 원의 면적을 구하는 것과 유사한 방법으로 탈진법을 사용하였고, 이 방법은 현재 적분학의 전조로 인식되고 있다.최신 방법을 사용하여 원의 면적을 일정한 적분을 사용하여 계산할 수 있습니다.

${\displaystyle A\;=\;2\int _{-r}^{r}{\displayrt {r^2}-x^{2}},syslog\;=\;\pi r^{2}.}$

줄임표

타원으로 둘러싸인 영역의 공식은 원의 공식과 관련이 있습니다. 반장축 및 반단축 x 및 y가 있는 타원의 공식은 다음과 같습니다.^[2]

${\displaystyle A=\pi xy}$

비평면 표면적

표면적에 대한 대부분의 기본 공식은 표면을 자르고 평평하게 하는 방법으로 얻을 수 있습니다(개발 가능한 표면 참조).예를 들어 실린더(또는 프리즘)의 측면을 세로로 자르면 표면이 직사각형으로 평평해질 수 있습니다.마찬가지로 원뿔의 측면을 따라 절단하면 측면은 원형의 섹터로 평탄화해 그 면적을 산출할 수 있다.

구의 표면적에 대한 공식은 도출하기가 더 어렵습니다. 구는 0이 아닌 가우스 곡률을 가지기 때문에 평탄화할 수 없습니다.구체의 표면적에 대한 공식은 아르키메데스가 구와 원통에 관한 그의 작품에서 처음으로 얻었다.공식은 다음과 같습니다.^[7]

A = 4µr²(구면),

여기서 r은 구의 반지름입니다.원의 면적 공식과 마찬가지로, 이 공식의 파생은 본질적으로 미적분과 유사한 방법을 사용한다.

일반식

2차원 도형의 영역

• $A{\displaystyle \frac{\mathrm{}}{}}$ 삼각형: $(\style\tfrac {1}{2}}Bh)($여기서 B는 임의의 변이고 h는 B가 놓여 있는 선에서 삼각형의 다른 꼭지점까지의 거리입니다).이 공식은 높이 h를 알고 있는 경우에 사용할 수 있습니다.세 변의 길이를 알 수 있는 경우 헤론의 공식을 사용할 수 있습니다${\displaystyle \sqrt{.}}$ s (${\displaystyle \sqrt{}}$s -${\displaystyle \sqrt{a}}$) (${\displaystyle \sqrt{s}}$ -${\displaystyle \sqrt{b}}$) ($-$c ) \ displaystyle { $display$ style $}$（ a 、 c 、${\displaystyle \frac{\mathrm{c}}{}}$ ） $=$( ${\displaystyle a}$ +$$b + c ) $sac$ style {$frt$$$}각도와 그 2개의 포함 변이 주어지면 면적은 ${\displaystyle \frac{1}{}}$ ${\displaystyle 2}$ ${\displaystyle a}$ ${\displaystyle b}$ sin${\displaystyle }$θ (${\displaystyle C}$) { $displaystyle${ $tfrac {1}$ {$2}ab\sin (C$$)$ } 이며, 여기서 C는 주어진 각도, a와 b는 그 포함 ^[2]변이다.삼각형을 좌표평면에 그래프로 그릴 경우 행렬을 ${\displaystyle \frac{\mathrm{사용}}{}}$하여 절대값 1 2${\displaystyle ({x\mathrm{}}_{}}$ 1 ${\displaystyle {y\mathrm{}}_{}}$2 + ${\displaystyle {x\mathrm{}}_{}}$ 2 ${\displaystyle {y\mathrm{}}_{}}$3 + ${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {}_{}{}_{}{}_{}}$1 - ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {y\mathrm{}}_{}}$ 1 - ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ y${\displaystyle {}_{}}$3$$) { $display$style \ $tfrac${ $1$ { 1 - ${\displaystyle {x\mathrm{}}_{}}$ 1 ${\displaystyle {y\mathrm{}}_{}}$ 2$$（ $x _$ { 1 }$y _ 2$} + x$$2 _ 3 y { 3 } ) { 3 .이 공식은 신발끈 공식이라고도 하며 3개의 점(x₁,y₁), (x₂,y₂), (x₃,y₃)을 대입하여 좌표 삼각형의 면적을 쉽게 푸는 방법입니다.신발끈 공식은 정점이 알려진 다른 폴리곤의 영역을 찾는 데도 사용할 수 있습니다.좌표 삼각형의 또 다른 접근법은 면적을 구하기 위해 미적분을 사용하는 것이다.
• 폴리곤의 모든 정점이 그리드 포인트${\displaystyle (}$i +${\displaystyle \frac{\mathrm{b}}{}}$ -$$ {$displaystyle$ i$+{\frac {b}{2}}-1$가 되도록 등거리 점(즉, 정수 좌표가 있는 점)의 그리드에 구성된 단순한 폴리곤입니다. 여기서 i는 폴리곤 내부의 그리드 포인트 수이고 b는 경계 포인트 수입니다.이 결과는 픽의 ^[27]정리라고 알려져 있다.

미적분의 면적

• 수평축의 두 값 a와 b 사이에서 측정된 양수 값 곡선과 수평축 사이의 면적(b는 두 값 중 큰 값으로 정의됨)은 ^[6]곡선을 나타내는 함수의 a에서 b까지의 적분에 의해 주어진다.

${\displaystyle A=\int _{a}^{b}f(x),149}$

• 두 함수의 그래프 사이의 면적은 한 함수의 적분인 f(x)에서 다른 함수의 적분인 g(x)를 뺀 것과 같다.

${\displaystyle A}$ ${\displaystyle =}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle a_{}^{}}$ ${\displaystyle {}_{}^{}}$( ${\displaystyle f}$(${\displaystyle x}$) -${\displaystyle g}$ (${\displaystyle x}$) ${\displaystyle dx}$, {\$displaystyle$ A = \$int _$ {a$}^{b}(f(x)-g($x) , $f$$,$ $displaystyle$ f$(x)}$는 y 값이 큰 곡선입니다.

• 극좌표로 표현되는 $함수{\displaystyle }$ r ${\displaystyle =r}$ ( $))$ {$displaystyle$ r$=r(\theta)}$에 의해 경계되는 영역은 다음과 같다.^[6]

${\displaystyle A={1 \over 2)\int r^{2},d\theta .}$

• $파라메트릭{\displaystyle \stackrel{}{}}$ $곡선$으로 둘러싸인 영역 u ${\displaystyle \to }$ (${\displaystyle t}$ ) ${\displaystyle =}$ (${\displaystyle x}$ (${\displaystyle t}$ ) ,${\displaystyle y}$ (${\displaystyle t}$)$$} ${\displaystyle \to }$ ( x ($t$ )$= u$ =${\displaystyle }$( ${\displaystyle {t\mathrm{}}_{}{1\mathrm{}}_{}}$) { $display$ style {$vec${ $u$$} =$ ( t _ $0$) ${\displaystyle \stackrel{}{\to }}$ $u$ ( t ) （ t ） } { display cve {$t$} { t } { t } } 。

${\displaystyle \point _{t_{0}}{t_{1}}xdot {y},dt=-\point _{t_{0}^{t_{1},dt={1 \over2}\point _{t_{1}}{t}{t}{t}{{x}}},dot {x}},$

또는 의 z 성분

${\displaystyle {1\over2}\point _{t_{1}}{vec {u}}\times {\dot {vec {u}},dt.}$

(자세한 내용은 그린의 정리 ② 면적 계산 참조)이것이 평면계 기계 장치의 원리입니다.

두 2차 함수 사이의 경계 영역

두 2차 함수 사이의 경계 영역을 찾기 위해, 우리는 차이를 다음과 같이 쓰기 위해 다른 함수에서 하나를 뺀다.

$({displaystyle f(x)-g(x)=ax^{2}+bx+c=a(x-\alpha)(x-\alpha)}$

여기서 f(x)는 2차 상한이고 g(x)는 2차 하한입니다.f(x)-g(x)의 판별식을 다음과 같이 정의합니다.

$\displaystyle \Delta = b^{2}-4ac.}$

두 함수의 그래프 사이의 적분 공식을 단순화하고(위 절에서 주어진 바와 같이) 비에타의 공식을 사용함으로써 우리는 얻을 수 있다^[28][29].

${{displaystyle A}={delta}{6a^{2}}={6}{6}}({display-\alpha}^{3},\qquad a\neq 0})$

위의 내용은 경계 함수 중 하나가 2차 함수 대신 선형인 경우에도 유효합니다.

3차원 도형의 표면적

• 원뿔:^[30] ${\displaystyle \delta r}$( r +${\displaystyle \sqrt{{}^{}{r\mathrm{}}^{}}}$ 2 + ${\displaystyle \sqrt{{h\mathrm{}}^{}}}$ 2$){ displaystyle$ \$pi$r $\left$ (r$+{\sqrt$ {$r^{2$}+$h^{2}}}\right$ (r은 원형 밑면의 반지름, h는 높이)${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle r}$r r ${\displaystyle r}$ ( $displaystyle \pi$ r^ {2$}$ + \$pi$ rl$$} 또는$$^[30] r${\displaystyle }$(${\displaystyle r}$ +${\displaystyle l}$) ${\displaystyle r}$ ( r ) （ $displaystyle \pi$r ($r$ + l ) , \ !$$} 。r은 반지름, l은 원뿔의 경사 높이입니다.${\displaystyle {r\mathrm{}}^{}}$ r$2$ \$displaystyle$ \$pi r^{$2$$}는 베이스 ${\displaystyle \mathrm{영역}}$이고$${\ $r$l \ $displaystyle \$pi$$ rl은 ^[30]콘의 측면 영역이다.
• $큐브{\displaystyle \mathrm{}}$: $(\$ 여기서 s는 엣지의 ^[7]길이입니다.
• 실린더: $2{\displaystyle \mathrm{}}$ ${\displaystyle \mu }$r (${\displaystyle r}$ +${\displaystyle h}$ $){$ $displaystyle$2 \$pi$ r ( $r$+ $h$)$$。여기서 r은 베이스의 반지름, h는 높이입니다.$2{\displaystyle \mathrm{}}$ ${\displaystyle r}$r \ $displaystyle$ 2 \ $pi$ r$$${\displaystyle \mathrm{d<img\; alt="2\backslash pi\; r"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/71e811131a9c6c5f45e6657e0fc506e7e2a37f06"\; style="vertical-align:\; -0.338ex;\; width:3.543ex;\; height:2.176ex;">}}$、 $displaystyle$\ $pi$ d 로 $고쳐$ 쓸 수도 있습니다$.$여기서 d는 직경입니다.
• 프리즘 : ${\displaystyle \mathrm{2B}}$+ ${\displaystyle \mathrm{Ph}}$(B는 베이스의 면적, $P는 베이스$의 둘레$,$ h는 프리즘의 높이$)$
• 피라미드:${\displaystyle B}$+ ${\displaystyle P\frac{}{}}$ ${\displaystyle \frac{L}{}}$ (\$style$ B$+{\frac {PL}{2$ (B는 베이스 면적, P는 베이스 둘레, L은 경사 길이)
• 직사각형 프리즘: $2{\displaystyle \mathrm{}}$( ${\displaystyle w}$w + ${\displaystyle h}$h + ${\displaystyle w}$ h $){$ $displaystyle$ 2 $(\ell$ w$+\ell$ h$+wh )$。$여기$서 ${\$ \ $displaystyle \ell$은 길이, w는 폭, h는 높이입니다.

표면적의 일반 공식

연속 미분 가능한 $함수{\displaystyle }$ z ${\displaystyle =f}$ (${\displaystyle x}$ ,${\displaystyle y}$)$$, {\$display$ z = f (${\displaystyle x}$$$,${\displaystyle }$y )${\displaystyle \mathrm{d<img\; alt="z=f(x,y),"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/1269bfd7a8dbf5a109363ce2a7992efdf8e406a9"\; style="vertical-align:\; -0.838ex;\; width:11.44ex;\; height:2.843ex;">}}$ D ${\displaystyle \subset }$ ${\displaystyle {\mathbb{}}^{}}$ 2$$( ${\displaystyle {\mathrm{}}^{}}$ $y$)\$in$ D$\subset \mathbb {R} ^{2}}$ 및$$$D{\displaystyle }$ {\$displaystyle$ D$}$의 그래프 표면적의 일반 공식은 다음과 같습니다$.$

${\displaystyle A=\iint _{D}{\sqrt {\sqrt {\frac f}{\frak x}}+\frac {\frac y}{2}+1}, dy.}$

보다 일반적인 벡터 ${\displaystyle 형식\mathbf{}}$ $=$ ($$u${\displaystyle }$, v ${\displaystyle )}$ , ${\displaystyle \mathbf$ {r} $=\mathbf$ {$r}$ (u$$ $,$${\displaystyle v}$) 에서의${\displaystyle }$파라메트릭 표면 그래프 영역의 공식은$$r \$displaystyle$\$mathbf {r}$ $2이다.$$}^{2$$}}:$^[9]

$\displaystyle A=\iint_{D}\left\frac {\frac u}\times\frac {\frac\mathbf {r}{\frac v}\right \,du,dv.}$

공식 목록

영역에 대한 기타 일반적인 공식:

모양.	공식	변수
직사각형	${\displaystyle A=ab}$
삼각형	${\displaystyle A=syslogfrac {1}{2}}개,\!}$
삼각형	${\displaystyle A=black {1}{2}}ab\sin(\displaystyle ),\!}$
삼각형 (왜가리의 공식)	${{displaystyle A=sqrt {s(s-a)(s-b)(s-c)}},\!}$	$({displaystyle s=squaltfrac {1}{2}}(a+b+c)}$
이등변 삼각형	$({displaystyle A=sqfrac {b}{4}}{\sqrt {4a^{2}-c^{2}}}})$
정삼각형 (등각 삼각형)	$({displaystyle A=black {3}} {4}}a^{2},\!}$
마름모꼴/Kite	${\displaystyle A=black {1}{2}}de}$
평행사변형	$(\displaystyle A=ah_{a},\!)$
사다리꼴	${\displaystyle A=syslogfrac {(a+c)h}{2}},\!}$
정육각형	${\displaystyle A=black {3}{2}}{\displayrt {3}}a^{2},\!}$
정팔각형	${\displaystyle A=2(1+{\sqrt {2}})a^{2},\!}$
정다각형 (${\displaystyle }$ $\$ $display style$n )측면$$	${\displaystyle A=n{\frac {ar}{2}}=parfrac {pr}{2}}$ $({displaystyle\displaystyle} = tfrac {1}{4}}na^{2}\cotfrac\tfrac {n}})$ $({displaystyle\displaystyle=display^{2}\tanfrac {pi }{n}})$ $({displaystyle \displaystyle = ptfrac {1}{4n}}p^{2}\cotfrac\tfrac {pi }{n}})$ ${\displaystyle \tfrac {1}{2}}nR^{2}\sin({\tfrac {2\pi }{n}}),\!}$	${\displaystyle p}$ ${\displaystyle =}$ ${\displaystyle n}$ a$${\$displaystyle p=$na$\}$ (표준) ${\displaystyle r=block tfrac {a}{2}}\cot\tfrac {\pi }{n}},}$ $({displaystyle {tfrac {a}{2}}=r\tanfrac\tfrac{n})=R\sin({\tfrac {pi }{n}})}}$ ${\displaystyle r}$ ${\displaystyle :}${\$displaystyle$ r$:}$원$$ 반지름 ${\displaystyle R}$ {\$displaystyle$ R$:}$원반경$$
원형	$({displaystyle A=\pi r^{2}=\pi d^{2}}{4})$ (${\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 2r}$: {\$displaystyle$ d$=2r:}$ 직경$$)
원형 섹터	${\displaystyle A=black {\theta }{2}}r^{2}=black {L\cdot r}{2}},\!}$
타원	$(\displaystyle A=\pi ab,\!)$
일체형	${\displaystyle A=\int _{a}^{b(x)\mathrm {d} x,\f(x)\geq 0}$
	표면적
구	${\displaystyle A=4\pi r^{2}=\pi d^{2}}$
입방체	${\displaystyle A=2(ab+ac+bc)}$
실린더 (하단 및 상단 포함)	${\displaystyle A=2\pi r(r+h)}$
원뿔 (하단 포함)	$({displaystyle A=\pi r(r+{\displayrt {r^{2}+h^{2}})})}$
토러스	${\displaystyle A=4\pi ^{2}\cdot R\cdot r}$
회전면	${\displaystyle A=2\pi \int _{a}^{b}\!f(x){\secrt {1+\left[f'(x)\right]^{2}}\mathrm {d}x}$ (x축을 중심으로 이동)

위의 계산은 많은 일반적인 모양의 영역을 찾는 방법을 보여줍니다.

불규칙(따라서 임의) 폴리곤의 면적은 "조사자 공식"(슈엘레스 공식)^[26]을 사용하여 계산할 수 있습니다.

면적과 둘레의 관계

등각 부등식은 길이 L의 닫힌 곡선(따라서 둘레 L을 갖는 영역)과 둘레 A에 대해 다음과 같이 기술한다.

$(\displaystyle 4\pi A\leq L^{2})$

그리고 곡선이 원일 때만 평등이 유지된다.따라서 원은 주어진 둘레를 가진 닫힌 도형 중에서 가장 큰 면적을 가집니다.

다른 극단에서, 주어진 둘레 L을 가진 그림은 임의로 작은 면적을 가질 수 있다.마름모꼴이 임의로 "넘겨져" 있어 두 개의 각도가 임의로 0°에 가깝고 다른 두 개의 각도가 임의로 180°에 가깝다.

원의 경우 둘레에 대한 면적 비율(원 둘레에 대한 용어)은 반지름 r의 절반과 같습니다.이는 면적식 θr과² 원주식 2µr에서 알 수 있다.

일반 폴리곤의 면적은 둘레의 절반에 원점을 곱한 값입니다(여기서 원점은 중심에서 변의 가장 가까운 점까지의 거리입니다).

프랙탈

폴리곤의 가장자리 길이를 두 배로 하면 폴리곤의 면적이 네 배로 증가합니다. 즉, 2의 거듭제곱(폴리곤이 위치한 공간의 치수)에 대한 2(새 변 길이 대 이전 변 길이의 비율)입니다.그러나 2차원으로 그려진 프랙탈의 1차원 길이가 모두 2배라면 프랙탈의 공간적 내용은 반드시 정수가 아닌 2의 거듭제곱으로 확장됩니다.이 힘을 프랙탈의 프랙탈 차원이라고 합니다.^[31]

면적 이등분선

삼각형의 면적을 양분하는 선은 무한하다.이들 중 3개는 삼각형의 중앙점(변의 중간점과 반대쪽 꼭지점을 연결하는 것)이며, 이들은 삼각형의 중심에서 동시에 나타나며, 실제로 중심을 통과하는 유일한 면적 이등분선입니다.삼각형의 면적과 둘레를 둘로 나누는 삼각형을 통과하는 선은 삼각형의 인센티브(첨두의 중심)를 통과합니다.어느 삼각형이든 1개, 2개 또는 3개가 있습니다.

평행 사변형의 중간점을 통과하는 선은 영역을 이등분합니다.

원이나 다른 타원의 모든 영역 이등분선은 중심을 통과하고 모든 화음은 중심을 이등분합니다.원의 경우, 그것들은 원의 지름이다.

최적화

와이어 윤곽선, 최소 면적 스패닝("채움")의 표면은 최소 표면입니다.친숙한 예로는 비누 거품이 있습니다.

리만 원의 채우기 영역에 대한 문제는 여전히 ^[32]해결되지 않은 채로 있다.

원은 같은 둘레를 가진 모든 2차원 물체 중 가장 큰 면적을 가지고 있습니다.

순환 폴리곤(원 안에 새겨진 것)은 길이가 동일한 특정 변의 수를 가진 폴리곤 중 가장 큰 면적을 가집니다.

삼각형의 등각 부등식의 버전은 주어진 둘레를 가진 모든 삼각형의 면적이 가장 큰 삼각형이 ^[33]등변이라고 말한다.

주어진 원 안에 새겨진 모든 면적의 가장 큰 삼각형은 등변형이고, 주어진 원 주위에 있는 모든 면적의 가장 작은 삼각형은 ^[34]등변형이다.

정삼각형 면적에 대한 첨탑 면적의 ${\displaystyle \frac{비율}{}}$인 § ${\displaystyle \frac{3\sqrt{\mathrm{}}}{}}$($표시$ 스타일$){3{\sqrt {3$은 어떤 비정삼각형 ^[35]면적의 비율보다 크다.

정삼각형 둘레의 제곱에 $대한{\displaystyle \frac{\mathrm{}}{}}$ 면적 대비 1 ${\displaystyle \frac{12}{}}$3 ,$${\$displaystyle {1}{12{\sqrt {3}}}}$은(는) 다른 ^[33]삼각형보다 큽니다.

「 」를 참조해 주세요.

• 브라마굽타 사변형, 정수 변, 정수 대각선 및 정수 면적을 가진 순환 사변형.
• 등면적 지도
• 헤로니아 삼각형, 정수 변과 정수 면적을 가진 삼각형.
• 삼각 부등식 목록
• 기준 삼각형의 7분의 1 면적을 가진 내부 삼각형인 7분의 1 영역 삼각형입니다.

• 루스의 정리, 7분의 1 면적 삼각형의 일반화.

• [Orders of magnitude] : 크기별 영역 목록.
• 오각형 공식의 도출
• 평면계, 예를 들어 지도에서 작은 면적을 측정하기 위한 도구입니다.
• 볼록 사각형 면적
• 로빈스 오각형은 변의 길이와 면적이 모두 유리수인 순환 오각형입니다.

레퍼런스

외부 링크