대수기하학

이 토글리아티 표면은 5도의 대수 표면이다.그 그림은 실제 궤적의 일부를 나타내고 있다.

대수기하학은 다변량 다항식의 0을 고전적으로 연구하는 수학의 한 분야이다.현대의 대수기하학은 주로 교환대수의 추상 대수기법의 사용에 기초하고 있으며, 이러한 0의 집합에 대한 기하학적 문제를 해결하기 위해 사용된다.

대수기하학의 기본 연구 대상은 다항식 시스템의 해법의 기하학적 표현인 대수적 다양성이다.가장 많이 연구된 대수적 다양성의 등급의 예로는 선, 원, 포물선, 타원곡선, 타원곡선, 타원곡선 같은 입방곡선, 그리고 렘니스케이트와 카시니 타원곡선과 같은 사분곡선을 포함하는 평면 대수적 곡선이 있다.평면의 점은 좌표가 주어진 다항식 방정식을 만족할 경우 대수 곡선에 속합니다.기본 질문은 특이점, 변곡점, 무한대의 점 등 특별한 관심점의 연구를 포함한다.보다 고도의 질문에는 곡선의 위상과 다른 방정식에 의해 주어진 곡선 사이의 관계가 포함됩니다.

대수기하학은 현대 수학에서 중심적인 위치를 차지하고 있으며 복잡한 해석, 위상, 수 이론과 같은 다양한 분야와 여러 개념적 연관성을 가지고 있다.처음에 몇몇 변수에서 다항식 방정식의 시스템에 대한 연구는 방정식 해법이 중단되는 곳에서 시작되고, 특정한 해법을 찾는 것보다 방정식 시스템의 해법의 전체성의 본질적인 속성을 이해하는 것이 훨씬 더 중요하다; 이것은 가장 깊은 것 중 몇 가지로 이어진다.개념적으로나 기술적으로나 모든 수학의 영역.

20세기에 대수기하학은 여러 하위 영역으로 나뉘었다.

대수기하학의 주류는 대수적 다양성의 복잡한 점들을 연구하는 데 전념하며, 보다 일반적으로는 대수적으로 닫힌 장에서 좌표를 갖는 점들에 전념한다.
실제 대수기하학은 대수다양성의 실점을 연구하는 학문이다.
디오판틴 기하학, 그리고 보다 일반적으로, 산술 기하학은 대수적으로 닫히지 않고 유리수, 숫자장, 유한장, 함수장, 그리고 p-adic장과 같은 대수적 수 이론에서 발생하는 장에서 좌표를 갖는 대수적 다양성의 점들에 대한 연구이다.
특이점 이론의 많은 부분이 대수적 다양성의 특이점에 할애되어 있다.
계산 대수기하학은 컴퓨터의 발전과 함께 대수기하학과 컴퓨터 대수학의 교차점에 나타난 영역이다.그것은 주로 명시적으로 주어진 대수적 다양성의 특성을 연구하기 위한 알고리즘 설계와 소프트웨어 개발로 구성된다.

20세기 대수기하학의 주류의 발전의 대부분은 추상적인 대수적 틀 안에서 일어났으며, 주변 좌표 공간에 다양성을 포함시키는 어떤 특정한 방법에 의존하지 않는 대수적 다양성의 "내적" 특성에 대한 강조가 증가하고 있다; 이것은 토폴로에서의 발전과 평행하다.GY, 미분 및 복잡한 기하학입니다.이 추상 대수기하학의 한 가지 중요한 업적은 그로텐디크의 체계 이론으로, 미분 및 해석 다양체의 연구에서 사용되는 것과 매우 유사한 방식으로 대수적 다양성을 연구할 수 있게 해준다.이것은 점의 개념을 확장함으로써 얻을 수 있다.고전 대수기하학에서, 대응하는 아핀 스킴의 점들은 모두 이 고리의 주요 이상인 반면, 힐베르트의 늘스텔렌사츠를 통해 좌표환의 최대 이상을 통해 식별될 수 있다.즉, 이러한 구성의 점이 일반 점일 수도 있고 하위 변수일 수도 있습니다.이 접근법은 또한 주로 복잡한 점들과 관련된 고전 대수 기하학의 언어와 도구의 통합을 가능하게 한다.페르마의 마지막 정리라고 불리는 오랜 추측에 대한 와일즈의 증거는 이 접근법의 힘을 보여주는 한 예이다.

의 0

와

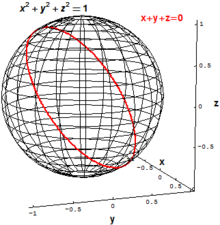
고전 대수기하학에서, 관심의 주 객체는 하나 이상의 다항식 방정식을 동시에 만족시키는 모든 점들의 집합을 의미한다.예를 들어, 3차원 유클리드 공간³ R에서 반지름 1의 2차원 구는 다음과 같은 모든 점의 집합(x,y,z)으로 정의될 수 있다.

xdisplaystyle x^{2}+y^{2}+z^{2}-1=0.,}

R의³ "기울어진" 원은 두 다항식 방정식을 만족시키는 모든 점(x,y,z)의 집합으로 정의할 수 있다.

xdisplaystyle x^{2}+y^{2}+z^{2}-1=0,})

{\displaystyle x+y+z=0.

먼저 필드 k부터 시작합니다.고전 대수기하학에서, 이 장은 항상 복소수 C였지만, 만약 우리가 k만이 대수적으로 닫힌다고 가정한다면, 많은 같은 결과들이 사실이다.우리는 A(k)로 표기된ⁿ k에 대한 차원 n의 아핀 공간을 고려한다(또는 k가 문맥에서 명확할 경우 더 간단히ⁿ A).좌표계를 수정할 때 A(k)를ⁿ k로 식별할ⁿ 수 있다.k를 사용하지ⁿ 않는 목적은 k가 운반하는ⁿ 벡터 공간 구조를 "포기"하는 것을 강조하기 위함이다.

함수 f : Aⁿ → A는¹ 다항식으로 쓸 수 있다면 다항식(또는 규칙)이라고 한다. 즉, 좌표(t₁,…t_n_n)가 A에 있는ⁿ 모든 점 M에 대해 f(M) = p(t₁,…)가 되는 k[x₁,x_n]의 다항식 p가 있다면 말이다.다항식(또는 정규) 함수의 속성은 A의ⁿ 좌표계 선택에 따라 달라지지 않습니다.

좌표계가 선택되면, 아핀 n-공간의 정규 함수는 k 이상의 n개의 변수에 있는 다항식 함수의 링으로 식별될 수 있다.따라서 A의 정규ⁿ 함수 세트는 k[Aⁿ]라고 하는 링입니다.

우리는 다항식이 그 지점에서 평가하면 그 지점에서 사라진다고 말한다.S를 k[Aⁿ]의 다항식 집합이라고 하자.S의 소실 집합(또는 소실 궤적 또는 영점 집합)은 S의 모든 다항식이 소실되는 A의ⁿ 모든 점의 집합 V(S)이다.상징적으로

=\{{n}\{n})=displaystyle V(S1},\dots,t_{n})

A의 부분ⁿ 집합인 V(S)는 일부 S에 대해 대수 집합이라고 불린다.V는 다양성(아래에서 정의될 특정 유형의 대수 집합)을 나타냅니다.

A의ⁿ 부분집합 U가 주어지면, 그것을 생성하는 다항식 집합을 복구할 수 있는가?U가 A의 하위ⁿ 집합이라면, 소실 집합이 U를 포함하는 모든 다항식의 집합으로 I(U)를 정의합니다.I는 이상을 의미합니다. 두 다항식 f와 g가 U에서 모두 사라지면 U에서 f+g가 사라지며, h가 다항식이면 U에서 hf가 사라집니다. 따라서 I(U)는 항상 다항식 고리 k[Aⁿ]의 이상입니다.

다음 두 가지 자연스러운 질문이 있습니다.

A의 부분ⁿ 집합 U가 주어졌을 때, U = V(I(U)는 언제입니까?
다항식 집합 S가 주어졌을 때, S = I(V(S)는 언제인가?

첫 번째 질문에 대한 답은 닫힌 집합이 대수 집합이고 k[Aⁿ]의 대수 구조를 직접적으로 반영하는 A의 위상인ⁿ Zariski 토폴로지를 소개함으로써 제공된다.그러면 U = V(I(U)는 U가 대수 집합이거나 자리스키 닫힌 집합인 경우에만 해당된다.두 번째 질문에 대한 답은 힐버트의 Nullstellensatz에 의해 주어집니다.그 형태 중 하나는 I(V(S)가 S에 의해 생성된 이상기라고 말한다.좀 더 추상적인 언어에서는 두 개의 폐쇄 연산자를 발생시키는 갈로아 연결이 있다. 그들은 식별될 수 있고 이론에서 자연스럽게 기본적인 역할을 한다. 예는 갈로아 연결에서 상세하게 설명된다.

여러 가지 이유로 우리는 대수적 집합 U에 대응하는 전체 이상을 항상 가지고 작업하기를 원하지 않을 수 있다. 힐버트의 기본 정리는 k[Aⁿ]의 이상은 항상 최종적으로 생성된다는 것을 암시한다.

대수집합은 두 개의 작은 대수집합들의 합집합으로 쓸 수 없다면 환원불능이라고 불린다.모든 대수 집합은 환원 불가능한 대수 집합의 유한 결합이며 이 분해는 독특하다.그래서 그 요소들은 대수 집합의 환원 불가능한 성분이라고 불린다.축소할 수 없는 대수 집합은 품종이라고도 불린다.대수 집합은 다항식 고리의 소실 이상 집합으로 정의될 수 있는 경우에만 다양하다는 것이 밝혀졌다.

일부 저자는 대수 집합과 변종을 명확히 구분하지 않고 필요할 때 이를 구분하기 위해 축소할 수 없는 다양성을 사용한다.

★★★★

연속함수가 위상공간상의 자연지도이고 평활함수가 미분가능한 다양체상의 자연지도인 것처럼, 대수집합에는 규칙함수 또는 다항함수라고 불리는 자연함수의 종류가 있다.A에 포함되는ⁿ 대수 집합 V의 정규 함수는 A에ⁿ 대한 정규 함수의 V에 대한 제한이다.복소수 필드에 정의된 대수 집합의 경우, 정규 함수는 매끄럽고 심지어 해석적이다.

정규 함수가 항상 주변 공간까지 확장되도록 요구하는 것은 부자연스럽게 제한적으로 보일 수 있지만, 이는 일반 위상 공간의 상황과 매우 유사합니다. 여기서 Tietze 확장 정리는 닫힌 부분 집합의 연속 함수가 항상 주변 위상 공간까지 확장되도록 보장합니다.

아핀 공간의 정규 함수와 마찬가지로 V의 정규 함수는 k[V]로 나타내는 링을 형성합니다.이 고리는 V의 좌표 고리라고 불립니다.

V의 정규 함수는 A의 정규ⁿ 함수에서 나오기 때문에 좌표 링 사이에 관계가 있습니다.특히, V 위의 정규 함수가 k[Aⁿ]의 두 함수 f와 g의 제한이라면, f - g는 V 위의 null이므로 I(V)에 속한다.따라서 k[V]는 k[Aⁿ]/I(V)로 식별될 수 있다.

아핀 바리에이션에서 A까지의¹ 정규 함수를 사용하여 아핀 바리에이션에서 다른 아핀 바리에이션으로의 정규 맵을 정의할 수 있습니다.먼저 다양한 공간에서 아핀 공간으로 일반 맵을 정의합니다.V를 A에 포함된ⁿ 다양한 것으로 합니다.V에서 m개의 정규 함수를 선택하고 f₁, ..., f라고_m 합니다. 우리는 f = (f_m, ..., f)로₁ 하여 V에서 A로의^m 정규 맵 f를 정의합니다.즉, 각 f는_i f 범위의 1개의 좌표를 결정한다.

V'가 A에 포함되는^m 품종인 경우 f의 범위가 V'에 포함되는 경우 f는 V에서 V'로의 정규 맵이라고 합니다.

규칙 지도의 정의는 대수 집합에도 적용된다.모든 아핀 대수 집합의 컬렉션을 범주로 만들기 때문에 규칙 맵은 또한 형태소라고도 불립니다. 여기서 개체는 아핀 대수 집합이고 형태소는 규칙 맵입니다.아핀 다양성은 대수 집합의 범주의 하위 범주이다.

V에서 V'로의 정규 맵 g와 k[V]의 정규 함수 f가 주어지면 f µg µk[V]가 됩니다.지도 f → f δg는 k[Vδ]에서 k[V]까지의 고리 동형사이다.반대로 k[V]에서 k[V]까지의 모든 링 동형사상에 의해 V에서V'로의 정규 맵이 정의됩니다.이것은 대수 집합의 범주와 최종 생성된 환원 k-대수의 반대 범주 사이의 범주의 동등성을 정의한다.이 동등성은 체계 이론의 출발점 중 하나이다.

와

앞의 절과 대조적으로, 이 절에서는 다양성만을 다루고 대수적 집합은 다루지 않는다.한편, 아핀 품종과 그 투영 완료는 기능 분야가 같기 때문에 정의는 자연스럽게 투영 품종(다음 절)까지 확장된다.

만약 V가 아핀 품종이라면, 그 좌표 고리는 적분 영역이며, 따라서 K(V)로 표기되고 V 위의 유리 함수의 장 또는 짧게는 V의 함수장이라 불리는 분수장을 가진다.이 요소는 V를 포함하는 아핀 공간에 대한 합리적인 함수 V에 대한 제한입니다.유리함수 f의 영역은 V가 아니라 f의 분모가 사라지는 부분변수(초면)의 보완이다.

일반 지도와 마찬가지로 다양한 V'에서 다양한 V'까지의 합리적인 지도를 정의할 수 있다.정규맵과 마찬가지로 V'에서 V'로의 유리맵은 k(V')에서 k(V)까지의 필드 동형사상에 대해 식별될 수 있다.

두 아핀 변종은 둘 다 정의된 영역에서 서로 반대되는 두 개의 유리 함수가 있는 경우 선천적으로 동등하다.마찬가지로 함수 필드가 동형인 경우 이들은 선천적으로 동등합니다.

아핀 품종은 아핀 공간과 선천적으로 동등한 경우 합리적인 품종이다.이는 다양성이 합리적인 매개 변수화, 즉 합리적인 함수를 가진 매개 변수화를 허용한다는 것을 의미합니다.예를 들어, $x^{2}+y^{2}-1=0$ x $x^{2}+y^{2}-1=0$ + y 2 $x^{2}+y^{2}-1=0$ - $x^{2}+y^{2}-1=0$ $x^{2}+y^{2}-1=0$ {\ $displaystyle$ x $^{2}+y^{2}-1=0}$ 의 $x^{2}+y^{2}-1=0$ 원은 파라메트릭 방정식을 가지므로 유리 곡선이다.

x=검은색 {2,t}{1+t^{2

y=블랙 {1-t^{2}}{1+t^{2

선에서 원까지의 합리적인 지도로도 볼 수 있다.

특이점 분해의 문제는 모든 대수적 다양성이 비사영적 완성도를 갖는 다양성과 선천적으로 동등한지를 아는 것이다(원활한 완성도 참조).1964년 히로나카 헤이스케에 의해 특성 0의 긍정으로 해결되어 아직 유한성이 풀리지 않았다.

투영 공간의 포물선(y = x², 빨간색) 및 입방형(y = x³, 파란색)

2차, 3차, 4차 다항식의 근에 대한 공식들이 복소수의 보다 완전한 설정으로 실수를 확장하는 것을 암시하듯이, 대수적 다양성의 많은 특성들은 아핀 공간을 보다 기하학적으로 완전한 투영 공간으로 확장하는 것을 제안한다.복소수는 다항식² x + 1의 근인 숫자 i를 더하는 반면, 투영 공간은 평행선이 만날 수 있는 점인 "무한대"에서 적절한 점을 더함으로써 구한다.

어떻게 되는지 알아보려면 V(y - x²) 품종을 고려해 보십시오.포물선을 그리면 포물선이 나와요.x가 양의 무한대로 이동하면 원점에서 점(x, x²)까지 선의 기울기도 양의 무한대로 이동합니다.x가 음의 무한대로 가면, 같은 선의 기울기는 음의 무한대로 갑니다.

이것을 다양한 V(y³ - x)와 비교해 보십시오.이것은 입방체 곡선입니다.x가 양의 무한대로 이동함에 따라 원점에서 점(x³, x)까지 선의 기울기는 전과 같이 양의 무한대로 이동한다.하지만 이전과 달리 x가 음의 무한대로 가면 같은 선의 기울기도 양의 무한대로 갑니다. 포물선과는 정반대입니다.따라서 V(y - x³)의 "무한에서" 동작은 V(y² - x)의 "무한에서" 동작과 다릅니다.

투영 평면에서의 두 곡선의 투영 완료에 대한 고려는 이 차이를 정량화할 수 있습니다. 포물선의 무한대점은 접선이 무한대인 정규점인 반면 입방곡선의 무한대점은 첨두부입니다.또한, 두 곡선은 모두 x에 의해 매개 변수화되기 때문에 합리적이며, 리만-로흐 정리는 아핀 공간 내의 모든 점이 규칙적이기 때문에 입방곡선은 무한대에 있어야 하는 특이점을 가져야 한다는 것을 암시한다.

따라서, 선천적 등가성과 모든 위상적 특성을 포함한 대수적 변종의 많은 속성은 "무한에서의" 행동에 의존하며, 따라서 투영 공간에서의 변형을 연구하는 것은 자연스러운 일입니다.게다가 투영 기술의 도입으로 대수기하학의 많은 이론들이 보다 단순하고 명료하게 되었다.예를 들어, 두 변종 사이의 교차점 수에 대한 베주 정리는 투영 공간에서만 가장 명확한 형태로 언급될 수 있다.이러한 이유로, 사영 공간은 대수기하학에서 기본적인 역할을 한다.

현재 차원 n의 투영 공간ⁿ P는 보통 차원 n+1의 아핀 공간 내에서 원점으로 간주되는 점을 통과하는 선들의 집합 또는 차원 n+1의 벡터 공간에서의 벡터 선들의 집합과 동등하게 정의된다.차원 n + 1의 공간에서 좌표계를 선택한 경우, 선의 모든 점은 k 요소의 곱셈까지 동일한 좌표 집합을 가집니다.이것은 p점의ⁿ 균질 좌표를 기준 필드 k의 n + 1 요소의 시퀀스로 정의하며, k의 0이 아닌 요소에 의한 곱까지 정의한다(전체 시퀀스에 대해 동일).

n + 1 변수의 다항식은 원점을 통과하는 선의 모든 점에서 균일한 경우에만 사라집니다.이 경우, P의 대응점에서ⁿ 다항식이 사라진다고 말할 수 있다.이를 통해 P의 투영ⁿ 대수 집합을 집합 V(f₁, ..., f_k)로 정의할 수 있으며, 여기에서 유한 집합의 균질 다항식 {f₁, ..., f_k}이 사라집니다.아핀 대수 집합과 마찬가지로, 사영 대수 집합과 그것들을 정의하는 축소된 동질적 이상 사이에는 분사가 있다.사영변수는 정의적 이상이 소수인 사영 대수 집합이다.즉, 투영 다양성은 균질한 좌표 링이 적분 영역인 투영적 대수 집합이며, 투영 좌표 링은 균질한(감소된) 이상에 의해 등급화된 링의 몫으로 정의되거나 n+1 변수에서 다항식으로 정의된다.모든 사영 대수 집합은 사영 다양성의 유한 결합으로 고유하게 분해될 수 있다.

투영적 다양성에 적절하게 정의될 수 있는 유일한 정규 함수는 상수 함수이다.따라서 이 개념은 투영 상황에서는 사용되지 않습니다.한편 유리함수 또는 함수장의 장은 아핀의 경우와 마찬가지로 균질좌표환에서 같은 정도의 두 균질원소의 몫집합으로 정의되는 유용한 개념이다.

대수

실제 대수기하학은 대수적 다양성의 실제 포인트를 연구하는 학문이다.

이러한 연구에서는 실수장이 순서장이라는 사실을 무시할 수 없다.예를 들어 x $x^{2}+y^{2}-a=0$ + $x^{2}+y^{2}-a=0$ - $x^{2}+y^{2}-a=0$ $x^{2}+y^{2}-a=0$ $x^{2}+y^{2}-a=0$ ${\displaystyle$ x $^{2}+y^{2}-a=0$ $}$ 의 $x^{2}+y^{2}-a=0$ 곡선은 a $a<0$ $a>0$ 이면 $원$ 이지만 a < $a<0$ 0 ${displaystyle$ a $>$ 0이면 $실점$ 이 $a<0$ .따라서, 실제 대수기하학은 실제 대수적 다양성에 대한 연구일 뿐만 아니라 다항식 및 다항식 부등식의 시스템의 해인 반 대수 집합의 연구로 일반화되었다. $xy-1=0$ 를 들어 $xy-1=0$ x $xy-1=0$ - $xy-1=0$ $=$ 0(\ $displaystyle$ $xy-1=0)$ 의 $xy-1=0$ $xy-1=0$ $xy-1=0$ 쌍곡선의 분기는 대수적 종류가 아니라 $xy-1=0$ y - $xy-1=0$ $xy-1=0$ $(\$ $displaystyle$ $xy-1=0)$ 및 $x>0$ x $x>0$ > $x>0$ $($ $xy-1=0$ $xy-1=0$ $xy-1=0$ $xy-1=0$ 0) $xy-1=0$ $x+y>0$ + $style$ x $x+y>0$ $x+y>0$ 으로 정의된 반수 $집합$ 입니다.

실제 대수기하학의 어려운 문제 중 하나는 해결되지 않은 힐베르트의 16번째 문제입니다.각도 8의 비음각 평면 곡선의 난수에 대해 가능한 각 위치를 결정합니다.

대수

계산 대수기하학의 기원은 1979년 6월 프랑스 마르세유에서 열린 EUROSAM'79(상징과 대수조작에 관한 국제 심포지엄)를 만난 것으로 추정할 수 있다.이번 미팅에서

데니스 S.Arnon은 George E. Collins의 원통형 대수분해(CAD)가 반대수 집합의 위상을 연산할 수 있음을 보여주었다.
브루노 부크버거는 그뢰브너 베이스와 알고리즘을 제시했고
다니엘 라자드는 예상해 수에서 본질적으로 다항식이고 따라서 미지의 수에서 간단히 지수적인 계산 복잡도로 동종 다항식 방정식의 시스템을 풀기 위한 새로운 알고리즘을 제시했다.이 알고리즘은 Macaulay의 다변량 결과와 밀접한 관련이 있습니다.

그 이후 이 영역의 대부분의 결과는 이들 알고리즘 중 하나를 사용하거나 개선하거나 변수 수가 단순히 지수화된 알고리즘을 찾는 것에 의해 이들 항목 중 하나 또는 여러 개와 관련된다.

수치 대수 기하학이라고 불리는 상징적 방법을 보완하는 수학 이론의 집합체가 지난 수십 년 동안 개발되었습니다.주된 계산 방법은 호모토피 연속이다.이것은 예를 들어 대수기하학 문제를 해결하기 위한 부동소수점 계산 모델을 지원한다.

그뢰브너 베이스는 이상에 의해 정의된 아핀 대수적 다양성의 많은 특성을 추론할 수 있는 연산을 허용하는 다항식 이상 생성기 시스템이다.

대수 집합 V를 정의하는 이상 I가 주어지면:

단항 순서에 대한 Gröbner 기준이 {1}(으)로 감소하는 경우에만 V는 비어 있습니다(기본 필드의 대수적으로 닫힌 확장).
힐베르트 급수를 통해 전체 정도를 정제하는 단항식 순서에 대해 I의 그뢰브너 기준에서 V의 치수와 정도를 계산할 수 있다.
V의 치수가 0인 경우, I의 그뢰브너 기준에서 V의 점(확정 수)을 계산할 수 있다(다항식 시스템 참조).
그뢰브너 기준 연산을 통해 주어진 하이퍼서페이스에 포함된 환원 불가능한 모든 성분을 V에서 제거할 수 있다.
그뢰브너 베이스 연산을 통해 k개의 제1좌표에 투영하여 V의 화상의 자리스키 클로저를 계산할 수 있으며, 이 투영법이 적절하지 않은 화상의 서브셋을 계산할 수 있다.
보다 일반적으로 Gröbner 기준 계산을 통해 이미지의 Zariski 폐쇄와 V의 합리적 함수의 임계점을 다른 아핀 품종으로 계산할 수 있다.

그뢰브너 기준 계산은 I의 1차 분해나 V의 환원 불가능한 성분을 정의하는 주요 이상을 직접 계산할 수 없지만, 이를 위한 대부분의 알고리즘은 그뢰브너 기준 계산을 포함한다.그뢰브너 베이스에 기초하지 않은 알고리즘은 정규 체인을 사용하지만 일부 예외적인 상황에서는 그뢰브너 베이스가 필요할 수 있다.

그뢰브너 염기는 계산하기 어려운 것으로 간주된다.사실 최악의 경우 변수 수가 두 배로 기하급수적인 다항식과 두 배로 기하급수적인 다항식을 포함할 수 있습니다.그러나 이것은 단지 최악의 경우 복잡성일 뿐이며 1979년 라자드 알고리즘의 복잡성 경계가 자주 적용될 수 있다.Faugere F5 알고리즘은 1979년 Lazard 알고리즘의 개선으로 간주될 수 있기 때문에 이 복잡성을 인식합니다.따라서 최상의 구현에서는 100보다 큰 대수 집합을 사용하여 거의 일상적으로 계산할 수 있습니다.이는 현재 그로브너 기초 계산의 난이도가 문제의 본질적 난이도와 강하게 관련되어 있음을 의미한다.

CAD는 1973년 G. Collins에 의해 도입된 알고리즘으로, 실수에 대한 양자화 제거에 대한 타르스키-세이덴버그 정리를 허용 가능한 복잡성으로 구현하기 위해 도입되었다.

이 정리는 원자식이 실제 계수를 가진 다항식 사이의 다항식 등식 또는 부등식인 1차 논리의 공식과 관련이 있다.따라서 이들 공식은 논리연산자에 의해 원자식으로 구성될 수 있는 공식이며, 모든 (),)에 대해 (),)가 아닌 (),) 또는 (∨)로 구성될 수 있으며, 존재하는 (∃)이다.타르스키의 정리는 이러한 공식으로부터 정량자(,, ∃) 없이 동등한 공식을 계산할 수 있다고 주장한다.

CAD의 복잡성은 변수 수에서 두 배로 기하급수적입니다.이것은 CAD가 이론적으로 그러한 공식으로 표현될 수 있는 실제 대수기하학의 모든 문제를 풀 수 있게 한다는 것을 의미합니다. 이는 명시적으로 주어진 다양성과 반 대수기하 집합에 관한 거의 모든 문제입니다.

Gröbner 기본 계산은 드문 경우에만 두 배의 기하급수적 복잡성을 가지지만 CAD는 거의 항상 이렇게 복잡합니다.이는 입력에 나타나는 대부분의 다항식이 선형식이 아닌 한, 4개 이상의 변수가 있는 문제를 해결하지 못할 수 있음을 의미합니다.

이 에 대한 은 CAD의 하고 있습니다.1973년, CAD는 CAD에 관한 것입니다.

최첨단 예로서 반대칭 집합의 연결된 모든 구성요소에서 적어도 점을 찾아 반대칭 집합이 비어 있는지 테스트하는 효율적인 알고리즘이 있다.한편, CAD는 아직 실제로 접속되어 있는 컴포넌트의 수를 세는 데 최적의 알고리즘입니다.

vs.

계산기하학의 기본 일반 알고리즘은 이중 지수적 최악의 경우 복잡성을 가진다.보다 정확하게 말하면, d가 입력 다항식의 최대 정도이고 변수 수 n이면, 그 복잡도는 어떤 상수 c에 $d^{2^{cn}}$ $d^{2^{cn}}$ (\ $displaystyle d^{2$ $^{$ cn $d^{2^{cn}}$ $d^{2^{c'n}}$ })이고, 어떤 입력에 대해 어떤 상수 c에 대해 $d^{2^{c'n}}$ $d^{2^{c'n}}$ (\ $displaystyle$ d $^{2^{cn$ }}}}})이다.

20세기의 지난 20년 동안 특정 하위 문제를 더 복잡하게 해결하기 위해 다양한 알고리즘이 도입되었습니다.이러한 알고리즘의 대부분은 $d^{O(n^{2})}$ d O $d^{O(n^{2})}$ ( $d^{O(n^{2})}$ 2 $){$ $displaystyle$ d $^{O(n^{2$ ^[1] 입니다.

그뢰브너 베이스에 의해 해결된 문제의 하위 문제를 해결하는 알고리즘 중에서, 아핀 종류가 비어 있는지 테스트하고 유한한 수의 해답을 갖는 비균질 다항식 시스템을 해결하는 것을 인용할 수 있다.대부분의 항목에서 Faugere의 F4 및 F5 알고리즘이 더 나은 실용적 효율성과 아마도 비슷하거나 더 나은 복잡성을 가지고 있기 때문에 그러한 알고리즘은 거의 구현되지 않는다(아마도 특정 항목 클래스에 대한 Gröbner 기반 알고리즘의 복잡성 평가는 몇 가지 특별한 c에서만 수행되었던 어려운 작업이기 때문이다).as)

CAD에 의해 해결된 문제를 해결하는 실제 대수기하학의 주요 알고리즘은 반 대수 집합의 위상과 관련이 있다.연결된 구성요소의 수를 세거나, 두 점이 동일한 구성요소에 있는지 테스트하거나, 실제 대수 집합의 휘트니 계층화를 계산하는 것을 예로 들 수 있다. $d^{O(n^{2})}$ 는 d $d^{O(n^{2})}$ ( $d^{O(n^{2})}$ 2 $d^{O(n^{2})}$ ) \ $displaystyle$ d $^{O(n^{2$ 입니다.그러나 O 표기법에 의한 상수는 매우 높아 CAD에 의해 효과적으로 해결되는 중요한 문제를 해결하기 위해 그것들을 사용하는 것은 전 세계의 모든 컴퓨팅 파워를 사용할 수 있다고 해도 불가능합니다.따라서 이러한 알고리즘은 구현된 적이 없으며 점근 복잡성이 우수하고 실질적인 효율성이 뛰어난 알고리즘을 찾는 활발한 연구 영역이다.

추상적 근대관

대수기하학에 대한 현대적 접근법은 일반성의 다양한 수준에서 기본 객체의 범위를 체계, 형식적 체계, 인드스켐, 대수공간, 대수적 스택 등으로 재정의하고 효과적으로 확장한다.이것의 필요성은 이미 다양성 이론 내의 유용한 아이디어에서 발생한다. 예를 들어 Zariski의 공식 기능은 구조 고리에 0의 잠재 요소를 도입함으로써 수용될 수 있다. 루프와 호 공간을 고려하고, 그룹 작용에 의한 지수를 구성하며, 자연 교차 이론과 변형을 위한 공식 근거를 개발한다. 이론은 몇 가지 추가 확장을 이끈다.

가장 주목할 만한 것은 1950년대 후반에 대수적 다양성이 알렉산더 그로텐디크의 체계 개념에 포함되었다는 것이다.이들의 국소 객체는 아핀 체계 또는 일차 스펙트럼으로, 국소 링 공간은 교환 단수 링의 범주에 반등가이며, 필드 k에 걸쳐 아핀 대수 변종의 범주와 최종적으로 생성된 감소 k-대수의 범주 사이의 이중성을 확장한다.접착은 Zariski 토폴로지를 따릅니다.국소 링형 공간 범주 내에서 접착할 수 있을 뿐만 아니라 Yoneda 매립을 사용하여 아핀 체계 범주에서 더 추상적인 세트의 범주 내에서 접착할 수 있습니다.그 후 Zariski topology는 이론적인 의미에서 Grothendieck topology로 대체됩니다.그로텐디크는 조잡한 자리스키 토폴로지, 즉 에테일 토폴로지, fppf와 fpqc 두 개의 플랫 그로텐디크 토폴로지보다 더 이국적이지만 기하학적으로 더 세밀하고 민감한 예를 가진 그로텐디크 토폴로지를 도입했다.오늘날에는 니스네비치 토폴로지를 포함한 몇 가지 다른 예가 두드러졌다.시브는 그로텐디크의 의미에서 스택으로 더욱 일반화될 수 있으며, 일반적으로 Artin 스택과 더 미세하게는 Deligne-Mumford 스택으로 이어지는 몇 가지 추가 표현성 조건이 있습니다. 둘 다 대수적 스택이라고 불립니다.

때때로 다른 대수적 사이트들이 아핀 체계 범주를 대체한다.예를 들어, 니콜라이 뒤로프는 일반화 대수 기하학에서 국소 물체의 일반화로서 교환 대수 모나드를 도입했다.열대기하학, 한 요소의 장에 걸친 절대기하학 및 아라켈로프 기하학의 대수적 유사체 버전이 이 설정에서 실현되었다.

모든 종류의 대수학이 독자적인 대수기하학을 갖는 보편 대수기하학으로 또 다른 형식적인 일반화가 가능하다.대수의 다양성이라는 용어는 대수 다양성과 혼동해서는 안 된다.

체계, 스택 및 일반화의 언어는 기하학적 개념을 다루는 귀중한 방법임이 증명되었고 현대 대수기하학의 주춧돌이 되었다.

대수적 스택은 더욱 일반화 될 수 있으며 변형 이론과 교차 이론과 같은 많은 실용적인 질문에서 이것은 종종 가장 자연스러운 접근법이다.아핀 체계의 그로텐디크 부위는 미분 등급의 교환 대수의 무한 범주, 또는 그로텐디크 토폴로지의 적절한 변종으로 단순 교환 고리 또는 유사한 범주로 대체함으로써 파생 아핀 체계의 더 높은 범주 부위로 확장할 수 있다.또한 집합의 프리히브를 단순한 집합의 프리히브(또는 무한대 그룹체의 프리히브)로 대체할 수 있다.그런 다음, 적절한 동질성 기계가 존재하는 경우, 파생된 아핀 스킴의 무한 범주에서 파생된 스택의 개념을 개발할 수 있으며, 이는 시프 공리의 특정 무한 범주 버전(및 대수학적으로는 일련의 대표성 조건을 유도적으로 충족한다)을 충족한다.퀴렌 모델 범주, 세갈 범주 및 준 범주들은 Andre Hirschowitz, Bertrand Toén, Gabriel Vezosi, Michel Vaquié 등을 포함한 Carlos Simpson 학파에 의해 도입된 이러한 파생 대수 기하학을 공식화하기 위해 가장 자주 사용되는 도구들 중 일부이며, 그리고 루리, Bertierand에 의해 개발되었다.가브리엘 베조시.A-무한 범주를 사용하여 파생 대수기하학의 또 다른 (비교환형) 버전은 막심 콘체비치와 추종자들에 의해 1990년대 초부터 개발되었다.

역사

16세기 이전

대수기하학의 뿌리는 기원전 5세기 헬레니즘 그리스인들의 작업으로 거슬러 올라간다.예를 들어 델리안 문제는 x의 입방체가 a와 b의 직사각형 상자² ab과 같은 부피를 가지도록 길이 x를 구성하는 것이었습니다.메네크무스(c.기원전 350년)는 평면 원뿔 ay = x와² xy = ^[2]ab의 쌍을 교차시켜 문제를 기하학적으로 고려했다.기원전 3세기에, 아르키메데스와 아폴로니우스는 ^[2]^[3]좌표계를 이용하여 원뿔 단면의 추가적인 문제들을 체계적으로 연구했다.서기 ^[4]10세기 이븐 알-헤이담을 포함한 중세 이슬람 수학자들은 순수하게 대수적인 방법으로 입방정식을 풀고 그 결과를 기하학적으로 해석했다.페르시아의 수학자 오마르 카이얌(1048년생)은 포물선과 원을^[5] 교차시켜 입방정식을 푸는 방법을 발견했고, 입방정식의 ^[6]일반 이론을 최초로 고안한 것으로 보인다.오마르 카이야름 이후 몇 년 후, 샤라프 알-딘 알-투시의 방정식은 로쉬디 라쉬드에 의해 "대수기하학의 시작을 알렸다"^[7]고 묘사되었다.이것은 방정식에 의한 곡선의 연구가 17세기에 ^[8]데카르트에서 시작되었다고 주장하는 제프리 오크스에 의해 비판되었다.

르네상스

대수적 문제에 기하학적 구조를 적용하는 그러한 기술은 또한 제롤라모 카르다노와 니콜로 폰타나 "타르타글리아"와 같은 르네상스 수학자들에 의해 입방정식의 연구에 채택되었다.구조 문제에 대한 기하학적 접근법은 대수적 접근법보다는 대부분의 16세기와 17세기 수학자들, 특히 ^[9]기하학에서 대수적, 해석적 방법의 사용에 반대했던 블레즈 파스칼에 의해 선호되었다.프랑스의 수학자 프란시스쿠스 비에타와 후에 르네 데카르트와 피에르 드 페르마는 좌표 기하학의 도입을 통해 구조 문제에 대한 전통적인 사고방식을 혁신했다.그들은 주로 디오판토스 방정식에 의해 정의된 것과 같은 대수 곡선의 특성과 원뿔과 입체파(데카르트의 경우)에 대한 고전 그리스 작품의 대수적 재구성에 관심이 있었다.

같은 시기에 블레즈 파스칼과 제라르 드사르게는 투영 기하학의 합성 개념을 발전시키면서 다른 관점에서 기하학에 접근했다.파스칼과 데사르게스도 곡선을 연구했지만 순수하게 기하학적 관점에서: 그리스 지배자와 나침반 구조의 유사점.결국, 데카르트와 페르마의 해석 기하학은 18세기 수학자들에게 뉴턴과 라이프니츠의 새로운 미적분을 사용하여 물리적인 문제를 연구하는데 필요한 구체적인 정량적 도구를 제공했기 때문에 승리했다.하지만, 18세기 말까지, 좌표 기하학의 대수적 특징의 대부분은 라그랑주와 오일러의 무한소수의 미적분에 포함되었습니다.

19세기에서 20세기 초반

19세기에는 비유클리드 기하학과 아벨 적분이 동시에 발달하여 옛 대수적 사상을 기하학적 접힘으로 되돌렸다.이러한 새로운 개발 중 첫 번째는 에드몬드 라게어와 아서 케일리가 차지했는데, 그는 투영 공간의 일반화된 미터법 특성을 확인하려고 시도했다.케일리는 투영 공간에 균질 다항식 형식, 특히 2차 형식의 개념을 도입했다.그 후, 펠릭스 클라인은 공간의 기하학이 공간의 특정 변환 클래스로 인코딩된다는 관점에서 (다른 유형의 기하학과 함께)19세기 말까지, 투영 기하학자들은 투영 공간의 도형에 대한 더 일반적인 종류의 변환을 연구했습니다.통상 사영공간에 기본적인 클라이니아 기하학을 주는 것으로 여겨졌던 사영 선형 변환보다는 높은 수준의 이성 변환에 관심을 기울였다.이 더 약한 합성의 개념은 나중에 20세기 이탈리아의 대수 기하학 학파 멤버들로 하여금 대수 표면을 2차 동형사상으로 분류하도록 이끌 것이다.

아벨 적분인 19세기 초의 두 번째 발전은 베른하르트 리만을 리만 표면으로 이끌었다.

같은 시기에 교환대수를 통한 대수기하학의 대수화가 시작되었다.이 방향에서 두드러진 결과는 대수기하학과 교환대수 사이의 연결의 기초가 되는 힐베르트 기저정리와 힐베르트 늘스텔렌사츠, 그리고 소거 이론의 기초가 되는 맥컬리의 다변량 결과물이다.아마도 다변량 결과물이 암시하는 계산의 크기 때문에, 제거 이론은 특이점 이론과 계산 대수 ^[a]기하학에 의해 갱신될 때까지 20세기 중반 동안 잊혀졌다.

B . L. van der Waerden, Oscar Zariski, André Weil은 평가 이론과 이상 이론을 포함한 현대 가환 대수에 기초한 대수 기하학의 기초를 개발했습니다.목표 중 하나는 이탈리아 대수기하학파의 결과를 증명하기 위한 엄격한 틀을 제공하는 것이었다.특히 이 학파는 1930년대 이들 저자가 처음 제시한 '정확한 정의' 없이 '일반점'이라는 개념을 체계적으로 사용했다.

1950년대와 1960년대에 장-피에르 세르와 알렉산더 그로텐디크는 시프 이론을 이용하여 기초를 다시 다졌다.이후 1960년경부터, 주로 그로텐디크에 의해 주도되어, 매우 정교한 호몰로지 기법의 기구와 함께 계획의 아이디어가 고안되었다.10년간의 급속한 발전 후 1970년대에 이 분야는 안정화되었고, 대수적 다양성, 특이점, 모듈리 및 형식적 모듈리에 대한 수 이론과 보다 고전적인 기하학적 질문 모두에 새로운 응용이 이루어졌다.

정의 방정식으로부터 직접 이해되지 않는 중요한 변종들은 아벨 군을 이루는 점들을 가진 사영 변종들이다.원형의 예는 풍부한 이론을 가진 타원 곡선입니다.그것들은 페르마의 마지막 정리를 증명하는 데 중요한 역할을 했고 타원곡선 암호학에도 사용된다.

다양성에 대한 일반적인 서술과 관련된 대수기하학의 추상적 경향과 병행하여, 구체적으로 주어진 다양성으로 효과적인 계산을 위한 방법 또한 개발되었고, 이는 계산 대수기하학의 새로운 영역으로 이어졌다.이 영역의 기초 방법 중 하나는 1965년 브루노 부크버거에 의해 소개된 그뢰브너 기저 이론이다.실제 대수기하학에 더 전념하는 또 다른 기초 방법은 1973년 조지 E. 콜린스에 의해 도입된 원통형 대수분해이다.

참고 항목: 파생 대수 기하학.

분석 다양성은 분석 함수를 포함하는 여러 방정식의 공통해 집합으로 국소적으로 정의된다.그것은 실수 또는 복소수 다양성의 포함된 개념과 유사하다.모든 복잡한 다양체는 분석적 다양성이다.분석 변종이 특이점을 가질 수 있기 때문에, 모든 분석 변종이 다양체는 아니다.

현대 해석기하학은 장 피에르 세르가 그의 논문 GAGA에서 증명한 바와 같이 실질적이고 복잡한 대수기하학과 동등하다.그 이름은 프랑스어로 대수기하학과 해석기하학을 뜻한다.그럼에도 불구하고, 증명 방법은 상당히 다르고 대수 기하학 또한 유한 특성에서 기하학을 포함하기 때문에 두 개의 분야는 구별된다.

프로그램

대수기하학은 이제 통계학,^[10] 제어 이론,^[11]^[12] 로봇 공학,^[13] 오류 정정 코드,^[14] 계통학^[15] 및 기하학적 ^[16]모델링에서 응용 분야를 찾아낸다.스트링 이론,^[17] ^[18]게임 이론, 그래프 ^[19]매칭, 솔리톤 [20], ^[21]정수 프로그래밍과도 관련이 있습니다.

「」도 .

^ 이러한 망각의 증인은 반 데 바덴이 ^{[citation needed]}그의 논문 Moderne 대수의 제3판(그리고 그 이후의 모든 것)에서 제거 이론에 대한 장을 삭제했다는 사실이다.

^ "Complexity of Algorithms". www.cs.sfu.ca. Retrieved 2022-07-12.
^ ^a ^b Dieudonné, Jean (October 1972). "The Historical Development of Algebraic Geometry". The American Mathematical Monthly. 79 (8): 827–866. doi:10.2307/2317664. ISSN 0002-9890. JSTOR 2317664. Wikidata Q55886951.
^ 클라인 1972, 페이지 108, 90
^ 클라인 1972, 193페이지
^ Kline 1972, 193-195페이지
^ O'Connor, J. J.; Robertson, E. F. "Omar Khayyam". School of Mathematics and Statistics, University of St Andrews. Archived from the original on November 12, 2017. Khayyam himself seems to have been the first to conceive a general theory of cubic equations.
^ Rashed, Roshdi (1994). The Development Of Arabic Mathematics Between Arithmetic And Algebra. Springer. pp. 102–103.
^ Oaks, Jeffrey (January 2016). "Excavating the errors in the "Mathematics" chapter of 1001 Inventions". Pp. 151-171 in: Sonja Brentjes, Taner Edis, Lutz Richter-Bernburd Edd., 1001 Distortions: How (Not) to Narrate History of Science, Medicine, and Technology in Non-Western Cultures. Archived from the original on 2021-02-27.
^ 클라인 1972, 페이지 279
^ Drton, Mathias; Sturmfels, Bernd; Sullivant, Seth (2009). Lectures on Algebraic Statistics. Springer. ISBN 978-3-7643-8904-8.
^ Falb, Peter (1990). Methods of Algebraic Geometry in Control Theory Part II Multivariable Linear Systems and Projective Algebraic Geometry. Springer. ISBN 978-0-8176-4113-9.
^ Tannenbaum, Allen (1982). Invariance and Systems Theory: Algebraic and Geometric Aspects. Lecture Notes in Mathematics. Vol. 845. Springer-Verlag. ISBN 9783540105657.
^ Selig, J. M. (2005). Geometric Fundamentals of Robotics. Springer. ISBN 978-0-387-20874-9.
^ Tsfasman, Michael A.; Vlăduț, Serge G.; Nogin, Dmitry (1990). Algebraic Geometric Codes Basic Notions. American Mathematical Soc. ISBN 978-0-8218-7520-9.
^ Cipra, Barry Arthur (2007). "Algebraic Geometers See Ideal Approach to Biology" (PDF). SIAM News. 40 (6). Archived from the original (PDF) on 3 March 2016.
^ Jüttler, Bert; Piene, Ragni (2007). Geometric Modeling and Algebraic Geometry. Springer. ISBN 978-3-540-72185-7.
^ Cox, David A.; Katz, Sheldon (1999). Mirror Symmetry and Algebraic Geometry. American Mathematical Soc. ISBN 978-0-8218-2127-5.
^ Blume, L. E.; Zame, W. R. (1994). "The algebraic geometry of perfect and sequential equilibrium". Econometrica. 62 (4): 783–794. doi:10.2307/2951732. JSTOR 2951732.
^ Kenyon, Richard; Okounkov, Andrei; Sheffield, Scott (2003). "Dimers and Amoebae". arXiv:math-ph/0311005.
^ Fordy, Allan P. (1990). Soliton Theory A Survey of Results. Manchester University Press. ISBN 978-0-7190-1491-8.
^ Cox, David A.; Sturmfels, Bernd. Manocha, Dinesh N. (ed.). Applications of Computational Algebraic Geometry. American Mathematical Soc. ISBN 978-0-8218-6758-7.

★★★

Kline, M. (1972). Mathematical Thought from Ancient to Modern Times. Vol. 1. Oxford University Press. ISBN 0195061357.

읽기 ★★★★★★★★★★★★★★」

보다 앞선 고전

van der Waerden, B. L. (1945). Einfuehrung in die algebraische Geometrie. Dover.
Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 1. Cambridge University Press. ISBN 978-0-521-46900-5. Zbl 0796.14001.
Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 2. Cambridge University Press. ISBN 978-0-521-46901-2. Zbl 0796.14002.
Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 3. Cambridge University Press. ISBN 978-0-521-46775-9. Zbl 0796.14003.

의 하지 않는

Garrity, Thomas; et al. (2013). Algebraic Geometry A Problem Solving Approach. American Mathematical Society. ISBN 978-0-821-89396-8.
Griffiths, Phillip; Harris, Joe (1994). Principles of Algebraic Geometry. Wiley-Interscience. ISBN 978-0-471-05059-9. Zbl 0836.14001.
Harris, Joe (1995). Algebraic Geometry A First Course. Springer-Verlag. ISBN 978-0-387-97716-4. Zbl 0779.14001.
Mumford, David (1995). Algebraic Geometry I Complex Projective Varieties (2nd ed.). Springer-Verlag. ISBN 978-3-540-58657-9. Zbl 0821.14001.
Reid, Miles (1988). Undergraduate Algebraic Geometry. Cambridge University Press. ISBN 978-0-521-35662-6. Zbl 0701.14001.
Shafarevich, Igor (1995). Basic Algebraic Geometry I Varieties in Projective Space (2nd ed.). Springer-Verlag. ISBN 978-0-387-54812-8. Zbl 0797.14001.

Cox, David A.; Little, John; O'Shea, Donal (1997). Ideals, Varieties, and Algorithms (2nd ed.). Springer-Verlag. ISBN 978-0-387-94680-1. Zbl 0861.13012.
Schenck, Hal (2003). Computational Algebraic Geometry. Cambridge University Press.
Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006). Algorithms in real algebraic geometry. Springer-Verlag.
González-Vega, Laureano; Recio, Tómas (1996). Algorithms in algebraic geometry and applications. Birkhaüser.
Elkadi, Mohamed; Mourrain, Bernard; Piene, Ragni, eds. (2006). Algebraic geometry and geometric modeling. Springer-Verlag.
Dickenstein, Alicia; Schreyer, Frank-Olaf; Sommese, Andrew J., eds. (2008). Algorithms in Algebraic Geometry. The IMA Volumes in Mathematics and its Applications. Vol. 146. Springer. ISBN 9780387751559. LCCN 2007938208.
Cox, David A.; Little, John B.; O'Shea, Donal (1998). Using algebraic geometry. Springer-Verlag.
Caviness, Bob F.; Johnson, Jeremy R. (1998). Quantifier elimination and cylindrical algebraic decomposition. Springer-Verlag.

의 및 자료

Eisenbud, David; Harris, Joe (1998). The Geometry of Schemes. Springer-Verlag. ISBN 978-0-387-98637-1. Zbl 0960.14002.
Grothendieck, Alexander (1960). Éléments de géométrie algébrique. Publications Mathématiques de l'IHÉS. Zbl 0118.36206.
Grothendieck, Alexander; Dieudonné, Jean Alexandre (1971). Éléments de géométrie algébrique. Vol. 1 (2nd ed.). Springer-Verlag. ISBN 978-3-540-05113-8. Zbl 0203.23301.
Hartshorne, Robin (1977). Algebraic Geometry. Springer-Verlag. ISBN 978-0-387-90244-9. Zbl 0367.14001.
Mumford, David (1999). The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (2nd ed.). Springer-Verlag. ISBN 978-3-540-63293-1. Zbl 0945.14001.
Shafarevich, Igor (1995). Basic Algebraic Geometry II Schemes and complex manifolds (2nd ed.). Springer-Verlag. ISBN 978-3-540-57554-2. Zbl 0797.14002.

( )

라비 바킬의 대수기하학의 기초, 808쪽.
PlanetMath의 대수기하학 엔트리
데르 영어
Dieudonné, Jean (March 3, 1972). "The History of Algebraic Geometry". Talk at the Department of Mathematics of the University of Wisconsin–Milwaukee. Archived from the original on 2021-11-22 – via YouTube.
스택스프로젝트, 오픈소스 교과서 및 대수스택과 대수기하학에 관한 레퍼런스 작업

[10] 이러한 망각의 증인은 반 데 바덴이 ^{[citation needed]}그의 논문 Moderne 대수의 제3판(그리고 그 이후의 모든 것)에서 제거 이론에 대한 장을 삭제했다는 사실이다.

[1] "Complexity of Algorithms". www.cs.sfu.ca. Retrieved 2022-07-12.

[Dieudonné-2] Dieudonné, Jean (October 1972). "The Historical Development of Algebraic Geometry". The American Mathematical Monthly. 79 (8): 827–866. doi:10.2307/2317664. ISSN 0002-9890. JSTOR 2317664. Wikidata Q55886951.

[FOOTNOTEKline1972108,_90-3] 클라인 1972, 페이지 108, 90

[FOOTNOTEKline1972193-4] 클라인 1972, 193페이지

[FOOTNOTEKline1972193–195-5] Kline 1972, 193-195페이지

[6] O'Connor, J. J.; Robertson, E. F. "Omar Khayyam". School of Mathematics and Statistics, University of St Andrews. Archived from the original on November 12, 2017. Khayyam himself seems to have been the first to conceive a general theory of cubic equations.

[7] Rashed, Roshdi (1994). The Development Of Arabic Mathematics Between Arithmetic And Algebra. Springer. pp. 102–103.

[8] Oaks, Jeffrey (January 2016). "Excavating the errors in the "Mathematics" chapter of 1001 Inventions". Pp. 151-171 in: Sonja Brentjes, Taner Edis, Lutz Richter-Bernburd Edd., 1001 Distortions: How (Not) to Narrate History of Science, Medicine, and Technology in Non-Western Cultures. Archived from the original on 2021-02-27.

[FOOTNOTEKline1972279-9] 클라인 1972, 페이지 279

[11] Drton, Mathias; Sturmfels, Bernd; Sullivant, Seth (2009). Lectures on Algebraic Statistics. Springer. ISBN 978-3-7643-8904-8.

[12] Falb, Peter (1990). Methods of Algebraic Geometry in Control Theory Part II Multivariable Linear Systems and Projective Algebraic Geometry. Springer. ISBN 978-0-8176-4113-9.

[13] Tannenbaum, Allen (1982). Invariance and Systems Theory: Algebraic and Geometric Aspects. Lecture Notes in Mathematics. Vol. 845. Springer-Verlag. ISBN 9783540105657.

[14] Selig, J. M. (2005). Geometric Fundamentals of Robotics. Springer. ISBN 978-0-387-20874-9.

[15] Tsfasman, Michael A.; Vlăduț, Serge G.; Nogin, Dmitry (1990). Algebraic Geometric Codes Basic Notions. American Mathematical Soc. ISBN 978-0-8218-7520-9.

[16] Cipra, Barry Arthur (2007). "Algebraic Geometers See Ideal Approach to Biology" (PDF). SIAM News. 40 (6). Archived from the original (PDF) on 3 March 2016.

[17] Jüttler, Bert; Piene, Ragni (2007). Geometric Modeling and Algebraic Geometry. Springer. ISBN 978-3-540-72185-7.

[18] Cox, David A.; Katz, Sheldon (1999). Mirror Symmetry and Algebraic Geometry. American Mathematical Soc. ISBN 978-0-8218-2127-5.

[19] Blume, L. E.; Zame, W. R. (1994). "The algebraic geometry of perfect and sequential equilibrium". Econometrica. 62 (4): 783–794. doi:10.2307/2951732. JSTOR 2951732.

[20] Kenyon, Richard; Okounkov, Andrei; Sheffield, Scott (2003). "Dimers and Amoebae". arXiv:math-ph/0311005.

[21] Fordy, Allan P. (1990). Soliton Theory A Survey of Results. Manchester University Press. ISBN 978-0-7190-1491-8.

[22] Cox, David A.; Sturmfels, Bernd. Manocha, Dinesh N. (ed.). Applications of Computational Algebraic Geometry. American Mathematical Soc. ISBN 978-0-8218-6758-7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[a]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[21]

v t ★★★
★★★ ★★★★★★★★★★★★ ★★
기초
	★★★ ★★★
.	★★★★★★ 분석 한 분석
	★★★
	★★★ 술술 ★★★
	술술
	★★★★ ★★★
	★★★ 정보 리서치
★★★	★★★★
★★★	수학
★★★★★★ ★★★ Project

Search