입방정식

대수학에서, 한 변수에서의 입방정식은 다음과 같은 형태의 방정식이다.

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

여기서 a는 0이 아닙니다.

이 방정식의 해는 방정식의 왼쪽에 의해 정의된 입방정 함수의 근이라고 불립니다.입방정식의 모든 계수 a, b, c 및 d가 실수이면 최소 1개의 실근(이는 모든 홀수 다항식 함수에 해당)이 있는 것입니다.입방정식의 모든 근은 다음 방법으로 구할 수 있습니다.

• 대수적으로, 즉, 그것들은 네 개의 계수와 네 개의 기본 산술 연산과 n번째 루트(n번째 루트)를 포함하는 입방식으로 표현될 수 있다.(이것은 아벨-루피니 정리에 의한 2차 방정식과 4차 방정식에도 해당되지만, 고차 방정식에는 해당되지 않습니다.)
• 삼각법으로
• 근의 수치적 근사치는 뉴턴의 방법과 같은 근원 찾기 알고리즘을 사용하여 찾을 수 있다.

계수가 실수일 필요는 없습니다.아래에서 다루는 내용의 대부분은 특성이 2와 3이 아닌 모든 분야의 계수에 유효합니다.입방정식의 해는 반드시 계수와 같은 필드에 속하지는 않습니다.예를 들어, 유리 계수를 갖는 일부 입방정식에는 비이성(비실수) 복소수인 근이 있습니다.

역사

입방정식은 고대 바빌로니아인, 그리스인, 중국인, 인도인,^[1][2][3] 이집트인들에게 알려져 있었다.바빌로니아(기원전 20세기~16세기) 설형판에는 큐브와 큐브 ^[4][5]루트를 계산하는 표가 있다.바빌로니아인들은 입방정식을 풀기 위해 표를 사용할 수 있었지만,^[6] 그들이 풀었다는 것을 확인할 증거는 없다.입방체를 두 배로 하는 문제는 가장 간단하고 오래 연구된 입방정식을 포함하며, 고대 이집트인들은 해답이 ^[7]존재한다고 믿지 않았다.기원전 5세기에 히포크라테스는 이 문제를 한 선과 두 배의 길이의 다른 선 사이에 있는 두 개의 평균 비례수를 찾는 것으로 줄였지만, 나침반과 직선 ^[8]구조로는 이것을 해결할 수 없었고, 이것은 현재 불가능하다고 알려져 있다.입방정식을 푸는 방법은 기원전 2세기경에 편찬되고 3세기에 ^[2]류후이가 논평한 중국의 수학 교과서인 수학예술 9장에 나온다.서기 3세기에, 그리스 수학자 디오판토스는 몇 가지 이변량 ^[3][9]입방정식에 대한 정수 또는 합리적인 해답을 발견했습니다.히포크라테스, 메네크무스, 아르키메데스는 교차하는 원뿔 ^[8]단면을 사용하여 입방체를 두 배로 하는 문제를 해결하는 데 근접했다고 믿어지지만, 레비엘 네츠와 같은 역사가들은 그리스인들이 입방정식을 생각했는지 아니면 입방정식을 이끌 수 있는 문제만을 생각했는지에 대해 논쟁을 벌인다.아르키메데스의 모든 작품을 번역한 T. L. 히스와 같은 몇몇 사람들은 동의하지 않고 아르키메데스가 두 원뿔의 교차점을 사용하여 입방정식을 풀었다는 증거를 제시하지만, 근이 0, 1 또는 ^[10]2인 조건도 논의했다.

7세기에 당나라의 천문학자 왕샤오통은 지구 쑤안징이라는 수학 논문에서 x + px² + qx = N 형태의 25개의³ 입방정식을 체계적으로 정립하고 풀었는데, 그 중 23개는 p, q 0 0이고, 2개는 q = ^[11]0이다.

11세기에 페르시아의 시인이자 수학자인 오마르 카이얌 (1048–1131)은 입방정식 이론에서 중요한 진전을 이뤘다.초기 논문에서, 그는 입방정식이 하나 이상의 해답을 가질 수 있다는 것을 발견했고 나침반과 직선 구조로는 풀 수 없다고 말했다.그는 또한 기하학적 ^[12][13]해법을 발견했다.그의 후기 작품인 '대수의 문제 증명에 관한 논문'에서, 그는 교차하는 원뿔 ^[14][15]단면을 통해 발견된 일반적인 기하학적 해법으로 입방정식의 완전한 분류를 썼다.

12세기에 인도의 수학자 바스카라 2세는 일반적인 성공 없이 입방정식을 풀려고 시도했다.하지만, 그는 입방정식의 한 예를 들었다: x³ + 12x = 6x² + 35.^[16]12세기에, 또 다른 페르시아의 수학자 샤라프 알-돈 알-투수 (1135–1213)는 양의 해를 가진 8가지 입방정식과 양의 해를 가지지 않을 수 있는 5가지 입방정식을 다룬 알-무샤달랏 (방정식 조문)을 썼다.그는 나중에 "루피니-호너 방법"으로 알려진 것을 사용하여 입방정식의 근을 수치적으로 근사했다.그는 또한 양의 ^[17]해를 가지지 않을 수 있는 입방정식을 풀기 위해 곡선의 최대와 최소의 개념을 사용했다.그는 특정 유형의 ^[18]입방정식에 대한 대수적 해법을 찾기 위해 입방정식의 판별식의 중요성을 이해했다.

그의 책 플로스에서, 피보나찌로도 알려진 레오나르도 드 피사는 x + 2x² + 10x = 20의 입방정식에³ 대한 양의 해와 밀접하게 근접할 수 있었다.바빌로니아 숫자로 쓴 결과 1,22,7,42,33,4,40(1 +22/60 +7/60² +42/60³ +33/60 +33/60⁴ +4/60⁵ +40/60⁶)로 나타나며 상대 오차는 약 ^[19]10이다⁻⁹.

16세기 초, 이탈리아 수학자 스키피오네 델 페로(1465–1526)는 입방정식의 종류, 즉 x + mx = n 형태의³ 방정식을 푸는 방법을 발견했습니다.사실, m과 n이 음수라면 모든 입방정식을 이 형태로 줄일 수 있지만, 그 당시에는 음수가 알려지지 않았다.델 페로는 죽기 직전까지 자신의 업적을 비밀로 유지하다가 그의 제자 안토니오 피오르에게 이 사실을 알렸다.

1535년 니콜로 타르타글리아 (1500–1557)는 주안느 다 코이로부터 입방정식의 두 가지 문제를 받았고 그가 그것들을 풀 수 있다고 발표했다.그는 곧 피오르의 도전을 받았고, 이것은 둘 사이의 유명한 경연대회로 이어졌다.각 참가자는 일정 금액을 지불하고 경쟁자가 해결해야 할 많은 문제를 제안해야 했다.30일 안에 더 많은 문제를 푼 사람이 돈을 다 받을 것이다.타르타글리아는 일반적인 방법을 고안한 x + mx = n 형식의³ 질문을 받았다.피어는 x + mx² = n 형식으로 질문을 받았는데³, 이는 그가 해결하기에는 너무 어려운 것으로 판명되었고, 타르타글리아는 대회에서 우승했습니다.

나중에, 타르타글리아는 제롤라모 카르다노 (1501–1576)에 의해 설득되어 입방정식을 푸는 그의 비밀을 밝혔다.1539년, 타르타글리아는 카르다노가 그것을 절대 밝히지 않는다는 조건과 만약 그가 큐빅에 관한 책을 쓴다면 타르타글리아가 출판할 시간을 주겠다는 조건만을 가지고 그렇게 했다.몇 년 후, 카르다노는 델 페로의 이전 연구에 대해 알게 되었고 1545년 그의 책 아르스 마그나에서 델 페로의 방법을 발표했는데, 이는 카르다노가 타르타글리아에게 그의 결과를 발표하도록 6년을 주었다는 것을 의미한다.타르타글리아에 대한 카르다노의 약속은 타르타글리아의 작품을 출판하지 않겠다고 말했고, 카르다노는 그 약속을 피하기 위해 델 페로의 작품을 출판하고 있다고 느꼈다.그럼에도 불구하고, 이것은 타르타글리아 출신의 카르다노에게 도전으로 이어졌고, 카르다노는 이를 부인했다.이 도전은 결국 카다노의 학생인 로도비코 페라리 (1522–1565)에 의해 받아들여졌다.페라리는 대회에서 타르타글리아보다 더 잘했고 타르타글리아는 그의 위신과 수입을 ^[20]모두 잃었다.

카르다노는 타르타글리아의 방법이 때때로 음수의 제곱근을 추출해야 한다는 것을 알아챘다.그는 아르스 마그나에 이 복소수들의 계산까지 포함시켰지만, 그는 그것을 제대로 이해하지 못했다.라파엘 봄벨리는 이 문제를 자세히^[21] 연구했고, 따라서 종종 복소수의 발견자로 여겨진다.

프랑수아 비에트 (1540–1603)는 독립적으로 3개의 실근을 가진 입방정체의 삼각해법을 도출했고 르네 데카르트 (1596–1650)는 비에트의 ^[22]연구를 확장했다.

인수분해

만약 입방정식의 계수가 유리수라면, 모든 계수에 분모의 공통 배수를 곱함으로써 정수 계수를 갖는 등가 방정식을 얻을 수 있다.그런 방정식

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

정수 계수의 경우 왼쪽 다항식이 낮은 차수의 다항식의 곱이라면 환원 가능하다고 합니다.Gauss의 법칙에 따르면 방정식이 환원 가능한 경우 요인에 정수 계수가 있다고 가정할 수 있습니다.

환원 입방정식의 근을 찾는 것은 일반적인 경우를 푸는 것보다 쉽습니다.사실, 방정식이 환원가능하다면, 요인들 중 하나는 반드시 1도를 가져야 하고, 따라서 다음과 같은 형태를 가져야 한다.

${\displaystyle qx-p}$

q와 p는 공칭 정수입니다.합리적인 근검정에서는 한정된 수의 경우를 조사함으로써 q와 p를 찾을 수 있습니다(q는 a의 제수이고 p는 d의 제수여야 하기 때문입니다).

따라서, 한 근은 ${\displaystyle {x\mathrm{}}_{}}$ 1 $=$ ${\displaystyle \frac{p}{}}$q$$, ${\displaystyle$ \$textstyle x_{$1}=$sqfrac {$p}{q$}}$이고, 다른 근은 다항식 긴 나눗셈으로 구할 수 있는 다른 인자의 근입니다.또 다른 요인은

${\displaystyle {frac {a} {q} {\frac {bq+ap} {q^{2}} x+{\frac {cq^{2}+bpq+ap^{2}}}{q^{3}}}}}:$

(계수는 정수가 아닌 것처럼 보이지만 p/q가 루트인 경우에는 정수여야 합니다.)

그런 다음, 다른 근은 이 2차 다항식의 근이며 2차 공식을 사용하여 찾을 수 있습니다.

움푹 패인 입방체

형태의 입체파

${\displaystyle t^{3}+pt+q}$

우울하다고 합니다.그것들은 일반적인 입방체보다 훨씬 단순하지만 기초적이다. 왜냐하면 모든 입방체의 연구는 변수의 단순한 변화에 의해 침체된 입방체의 것으로 축소될 수 있기 때문이다.

허락하다

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

입방정식이다변수의 변경

${\displaystyle x=t-{\frac {b}{3a}}$

는 t항이² 없는 세제곱(t)을 나타냅니다.

1로 나눈 후, 움푹 들어간 입방정식을 구한다

${\displaystyle t^{3}+pt+q=0,}$

와 함께

$({displaystyle {displaystyle {b}&x+{\frac {b}{3a}}&{\frac {3ac-b^{2}}{3a^{2}}\q={}&{\frac {2b^{3}-9b+27a^{2}d}{27a}}}}}}}}).\end { aligned}}$

원래 방정식의 $루트{\displaystyle {}_{}}$ x ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}{}_{}{2\mathrm{}}_{}}$, ${\displaystyle {x\mathrm{}}_{}}$ 3$({$$displaystyle$ $x_{1}, x_{2}, x_{3})$은 압축 방정식의 $루트{\displaystyle {}_{}}$ ${\displaystyle {t1\mathrm{}}_{}}$ ${\displaystyle {t2\mathrm{}}_{}}$ $({$}, $t_{3$})에$$ 관계되어 있습니다.

${\displaystyle x_{i}=t_{i}-{\frac {b}{3a}},$

$i{\displaystyle }$ ${\displaystyle =1}$,${\displaystyle 2}$, $({style i=1$, 2,$$3$\}$ $표시$).

뿌리의 구별과 성질

세제곱근의 성질(실제든 아니든 구별하든 아니든)은 판별식을 사용하여 명시적으로 계산하지 않고 결정할 수 있다.

식별자

다항식의 판별식은 다항식이 다중 근을 가지거나 다항식의 제곱으로 나눌 수 있는 경우에만 0인 계수의 함수입니다.즉, 다항식이 제곱 자유인 경우에만 판별식이 0이 아닙니다.

r, r₂, r이₃ $세제곱{\displaystyle }$ a ${\displaystyle {}^{}{3\mathrm{}}^{}}$ + ${\displaystyle {}^{}}$ x${\displaystyle {}^{}{2\mathrm{}}^{}}$ + ${\displaystyle c}$x +${\displaystyle d}$의 3개의 루트(반드시 구별되거나 실수는 아님)인 경우₁({$display style$ ax$^{3}+bx^{2}+cx+d$$,})$ 판별식은 다음과 같습니다.

${{displaystyle a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}}$

움푹 들어간 $입방체{\displaystyle {}^{}}$ ${\displaystyle {t3\mathrm{}}^{}}$+ ${\displaystyle p}$t +$$q { $displaystyle$ t$^{3}$ +$pt$ +$$q }의$$ 판별은 다음과 같습니다.

$(\displaystyle -\left(4,p^{3}+27,q^{2}\오른쪽).}$

일반 $세제곱{\displaystyle }$ a ${\displaystyle {}^{}{3\mathrm{}}^{}}$ + ${\displaystyle b}$ ${\displaystyle {x\mathrm{}}^{}}$2 + ${\displaystyle cx}$ + ${\displaystyle d}${\$displaystyle$ax$^{3$} +$bx^{$2} + $cx+d}$의 판별식은 다음과 같습니다.

${\displaystyle 18,abcd-4,b^{3}d+b^{2}c^{2}-4,ac^{3}-27,a^{2}d^{2}{2}.}$

이는 4$(\$ a$^{4$})의 곱으로, 해당하는 움푹 들어간 입방체 판별기입니다.일반 입방체 및 관련된 움푹 들어간 입방체 관련 공식을 사용하여, 이것은 일반 입방체의 판별식이 다음과 같이 기록될 수 있음을 암시한다.

${{displaystyle {4(b^{2}-3ac)^{3}-(2b^{3}-9b+27a^{2}d)^{2}}{27a^{2}}}.}$

따라서 이 두 판별식 중 하나는 다른 판별식도 0인 경우에만 0이고 계수가 실재하는 경우에는 두 판별식 중 하나의 판별식 부호는 같다.요약하면, 동일한 정보는 이 두 가지 차별 요소 중 하나에서 추론할 수 있다.

위의 공식을 증명하기 위해, 모든 것을 다항식으로 r, r₂, r₃, a로₁ 표현하기 위해 비에타의 공식을 사용할 수 있다.증명은 두 다항식의 동일성을 검증하는 결과를 낳는다.

뿌리의 성질

다항식의 계수가 실수이고 판별식$\delta {\displaystyle \mathrm{}}$(\$displaystyle\Delta)$가 0이 아닌 경우 두 가지 경우가 있습니다.

• > 0、 {$display$ \ $Delta$> 0 ,}인 경우, 큐빅에는 3개의 다른 실제 루트가 있습니다.
• , \$display$ \ $Delta$< 0 ,}인 경우, 입방체에는 1개의 실근과 2개의 비실복소공역근이 있습니다.

이것은 다음과 같이 증명될 수 있다.첫째, 만약 r이 실계수를 갖는 다항식의 근이라면, 그 복소공역도 근이다.그래서 만약 존재한다면, 비실제 뿌리는 복잡한 켤레 뿌리의 쌍으로 발생합니다.대수의 기본 정리에 의해 입방 다항식이 3개의 근을 가지기 때문에, 적어도 1개의 근은 실재해야 한다.

위에서 설명한 바와 같이 r, r₂, r이₃ $세제곱{\displaystyle }$ a ${\displaystyle {x\mathrm{}}^{}}$3 + ${\displaystyle b}$ ${\displaystyle {}^{}{2\mathrm{}}^{}}$ + ${\displaystyle c}$x + ${\displaystyle d}$\ $displaystyle$ $^{3}+bx^{2}+cx+d$의 세 가지 루트인 경우₁ 판별식은 다음과 같습니다.

${\displaystyle \Delta = a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^2}(r_{2}-r_{3})^{2}}$

3개의 루트가 실재하고 구별되는 경우 판별자는 양의 실수의 곱, 즉 $.\displaystyle \Delta >$$0$입니다.$}$

만약 하나의₁ 루트, 예를 들어 r만 실재한다면, r과₂₃ r은 복소 공역이며, 이는 r – r이₃ 순수하게 허수이고, 따라서 (r₂ – ²r₃)이 실재하고 음수라는 것을 의미한다₂.반면₁, r – r과₂₁ r – r – r은₃ 복소공역체이며, 이들의 곱은 실수이고 ^[23]양수이다.따라서 판별식은 하나의 음수와 여러 양의 곱이다.이것은 < 0$.\displaystyle \Delta$ <0 입니다.$}$

다중 루트

입방체의 판별식이 0이면 입방체는 배수근을 갖는다.또한 계수가 실재하는 경우에는 모든 근이 실재하는 것입니다.

$4{\displaystyle \mathrm{}}$ ${\displaystyle {p\mathrm{}}^{}}$3 + ${\displaystyle {}^{}}$ ${\displaystyle {q\mathrm{}}^{}}$ 2 ${\displaystyle {}^{}0}$. { \ $displaystyle$ 4p$^{$$3}$ +$pt+$q\ ; } 의$$ ${\displaystyle 압축입방체{}^{}}$ t${\displaystyle {}^{}{3\mathrm{}}^{}}$ + ${\displaystyle pt}$ +$$q + q \ ; 의 $판별$은 0 입니다. (\ displaystyle$$$4p^{3$} + $27q^{2$} =$0$\ ; ) ;} p도$$ 0이면 p = q = 0이고, 0은 입방체의 3배근이다$.$${\displaystyle {}^{}}$ ${\displaystyle {p\mathrm{}}^{}}$3 + ${\displaystyle {}^{}}$ ${\displaystyle {q\mathrm{}}^{}}$ 2 $=$ $,$ {\$displaystyle$\;$4p^{3$}+27q$^{2$}=$0\;,}$ 및 p , 0일 ${\displaystyle 경우\mathrm{}}$, 입방체는 단순 루트를 가집니다.

${\displaystyle t_{1}=black {,3q,}{p}}$

그리고 이중근

${\displaystyle t_{2}=t_{3}=-{\frac {,3q,}{2p}}~.}$

바꿔 말하면

$\displaystyle t^{3}+pt+q=\left(t-{\frac {3q}{p}\right)\left(t+{\frac {,3q,}{2p}\right)^2}\;}$

이 결과는 후자의 곱을 확장함으로써 증명되거나 비에타의 공식에서 비롯된 다소 단순한 방정식 시스템을 풀어서 얻을 수 있다.

움푹 들어간 입방체의 환원을 이용함으로써 이러한 결과를 일반 입방체까지 확장할 수 있다.그 결과, 다음과 같이 됩니다.${\displaystyle {}^{}}$ x${\displaystyle {}^{}{3\mathrm{}}^{}}$ + ${\displaystyle {}^{}}$ ${\displaystyle {x\mathrm{}}^{}}$2 + ${\displaystyle c}$x + ${\displaystyle d}$ \$displaystyle$\ ;$ax^{3}$ + $bx^{2$} +$cx$+ d \ ; $}$ 세제곱의$$ 판별식이 0일 경우,

• ${\displaystyle {b\mathrm{}}^{}}$ 2 $=$ ${\displaystyle 3}$ ${\displaystyle a}$ $,$ {\$displaystyle$ b$^{2$}=$3ac\;}$인 $경우{\displaystyle {}^{}}$ 입방체는 3중 루트를 가진다.

${\displaystyle x_{1}=x_{2}=x_{3}=-{\frac {b}{,3a,}}~,}$

그리고.

${\displaystyle ax^{3}+bx^{2}+cx+d=a\left(x+{\frac {b}{,3a,}}\right)^{3}}$

• ${\displaystyle {또는\mathrm{}}^{}}$ b 2${\displaystyle {}^{}3}$ ${\displaystyle 3}$ ${\displaystyle a}$ c$,$ {\$displaystyle \;b^{2$}\$neq$ 3ac$\;}$인 ${\displaystyle 경우{}^{}}$ 입방체는 이중 루트를 가집니다.

$({displaystyle x_{2}=x_{3}=blac {9ad-bc}{,2(b^{2}-3ac)},}~,}$

그리고 단순한 뿌리,

${\displaystyle x_{1}=subscfrac {,440-9a^{2}d-b^{3},}{a(b^{2}-3ac)}}~}$

그래서

${\displaystyle ax^{3}+bx^{2}+cx+d=a,\left(x-x_{1}\right)\left(x-x_{2}\right)^{2}~}$

특성 2 및 3

위의 결과는 계수가 2 또는 3 이외의 특성 필드에 속할 때 유효하지만, 특성 2 또는 3은 나눗셈 2와 3으로 나누기 때문에 특성 2 또는 3에 대해 수정해야 한다.

움푹 들어간 입방체로의 감소는 특성 2에는 효과가 있지만 특성 3에는 효과가 없습니다.그러나 두 경우 모두 일반 입방체 결과를 설정하고 설명하는 것이 더 쉽습니다.이를 위한 주요 도구는 다항식의 공통 근과 그 형식 도함수라는 사실이다.이러한 특성에서 도함수가 상수가 아닐 경우 특성 3에서는 선형 다항식이 되고 특성 2에서는 선형 다항식의 제곱이 된다.따라서 특성 2 또는 특성 3에 대해 도함수는 하나의 루트만 갖는다.이를 통해 다중 루트를 계산할 수 있으며, 세 번째 루트는 루트의 합에서 추론할 수 있습니다. 이 합계는 비에타의 공식에 의해 제공됩니다.

다른 특징과의 차이점은 특성 2에서 이중근 공식은 제곱근을 포함하고 특성 3에서 삼중근 공식은 세제곱근을 포함한다.

카르다노의 공식

Gerolamo Cardano는 Scipione del Ferro와 Nicolo Fontana Tartaglia에 기인하여 입방정식을 푸는 첫 번째 공식을 발표한 것으로 알려져 있습니다.이 공식은 움푹 패인 입방정식에 적용되지만, ① 움푹 패인 입방정식과 같이 모든 입방정식을 풀 수 있다.

카르다노의 결과는 만약

${\displaystyle t^{3}+pt+q=0}$

p와 q가 4 3 + 2>, {\$displaystyle 4p^{3}+27q^{2}> 0,$ 실수인 입방정식.

${{displaystyle {\frac {q} {2}} + {\frac {\frac {q} {4}} + {\frac {p^{3} {27}}}} + {\frac {q} {-} - {\frac {q} {4}}}} {\frac rt {{\frac {q}}}} {\frac {4}}}}} {\frac {\frac}}}}}} {\frac {\frcrcrc}}}}}}}}}}}}} {{{{{}$

이 결과를 얻기 위한 몇 가지 방법은 § 아래의 루트의 도출을 참조하십시오.

②근의 성질에서 보듯이, 다른 두 근은 비실재 복소 공역수이다.나중에 (Cardano는 복소수를 알지 못함) 두 개의 다른 루트에${\displaystyle \frac{1}{}}$+ ${\displaystyle \frac{i2}{\mathrm{}},}$(\$displaystyle${-$1+i{\sqrt {3}}{$2})의 $원시$큐브 루트에${\displaystyle \frac{}{}}$1${\displaystyle \frac{}{}}$- ${\displaystyle \frac{i3}{\mathrm{}}}${$displaystyle {frac {1-q3-rt}{$2}을$$ 곱하여 얻어진다는 것이 밝혀졌다$.$$}}$

4 3 + 2< , ${\displaystyle 4p^{3}+27q^{2}<0,}$이면 3개의 실수근이 존재하지만, 갈로아 이론은 유리근이 없으면 실수만을 포함한 대수식으로 근을 표현할 수 없다는 것을 증명한다.따라서 이 경우 카르다노의 시대에 대한 지식으로는 방정식을 풀 수 없다.그래서 이 경우는 casus irreducibilis라고 불리는데, 라틴어로 환원 불가능한 경우를 의미합니다.

Casus irreducibilis에서는 Cardano의 조제식을 사용할 수 있지만, 입방근의 사용에 있어 약간의 주의가 필요합니다.첫 번째 방법은 루트 함수(실제 부분이 가장 큰 루트)의 주요 값을 나타내는 $기호$로서${\style {{~}^~}}$과(와)$$3 {{$displaystyle${\$sqrt[{3}}{~}}}}$을 정의하는 것입니다.이 규칙에서 3개의 근에 대한 카르다노의 공식은 유효하지만, 주요 부분의 정의는 실제 부분을 비교하는 부등식을 포함하기 때문에 순수하게 대수적인 것이 아니기 때문에 순수하게 대수적인 것은 아니다.또한 계수가 실수 복소수가 아닌 경우 주 세제곱근을 사용하면 잘못된 결과가 나올 수 있습니다.또한 계수가 다른 필드에 속하는 경우 일반적으로 주 세제곱근은 정의되지 않습니다.

Cardano의 공식을 항상 옳게 만드는 두 번째 방법은 두 입방근의 곱이 -p/3이어야 한다는 것이다.그 결과 방정식의 근원은

${\displaystyle C-{\frac {p}{3C}}\quad {text{with}\quad C=sqrt[{3}}{-{\frac {q}{2}}+{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}}}.}$

이 공식에서 기호$displaystyle {{~}^{~}})$와 기호$(\${\$sqrt[{3}{~}^~}})$는 제곱근과 세제곱근을 나타냅니다.방정식의 다른 루트는 세제곱근을 변경하거나 마찬가지로 세제곱근에 ${\displaystyle \frac{-1\sqrt{}}{}}$± - ${\displaystyle \frac{3}{\mathrm{}}}$2의 원시 세제곱근을 곱하여 얻을 수 있습니다$.\$ $displaystyle$\$frac {$ - 1 \$pm$ \ $sqrt${ - 3$$} { 2} $。$$}$

이 근 공식은 p = q = 0일 때를 제외하고 항상 옳다. 단, p = 0일 경우 C 0 0이 되도록 제곱근을 선택한다. 그러나, 이러한 경우에는 입방근 없이 근을 표현할 수 있기 때문에 이 공식은 쓸모가 없다.${\displaystyle {}^{}}$로 입방근${\displaystyle {}^{}4}$ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ + 27 ${\displaystyle \mathrm{q}}$ 2$=$ 0 {\$displaystyle 4p^{3}+27q$^{2}=$0}$인 경우와 입방 다항식이 환원 불가능한 경우에도 이 공식은 무용하다.

이 공식은 p와 q가 2 또는 3 이외의 특성 필드에 속해 있는 경우에도 정확합니다.

일반입방식

일반 입방정식의 근에 대한 입방정식(θ 0)

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

Cardano 공식의 모든 변형에서 압축된 입방정식으로 추론할 수 있습니다.여기에 제시된 변형은 실제 계수뿐만 아니라 2와 3의 다른 특성 필드에 속하는 계수 a, b, c, d에도 유효하다.

그 공식은 다소 복잡하기 때문에 더 작은 공식으로 나눌 가치가 있다.

허락하다

${\displaystyle {begin{aligned}\Delta _{0}&=b^{2}-3ac,\\Delta _{1}&=2b^{3}-9b+27a^{2}d.\end { aligned}}$

( ${\displaystyle {\delta \mathrm{}}_{}}$ 0$$\ $display$style \ $Delta$_ { $0$} 및$$ ${\displaystyle {\delta \mathrm{}}_{}}$1 \ $displaystyle$\$Delta$_ {1$}$은 모두 세제곱과 그 파생물의 결과로 나타낼 수 있습니다). ${\displaystyle {1\mathrm{}}_{}}$ 1$$\ $displaystyle$\$Delta$ _ {$}은$-1/8a의 세제곱과 그 2차 도함수, ${\displaystyle {\delta \mathrm{}}_{}}$0$(\displaystyle$ \$Delta _{$0$$})은 세제곱 다항식의 1차 도함수 및 2차 도함수의 -1/12a의 합이다.)

그리고나서

${\displaystyle C=sqrt[{3}}{\frac {Delta _ {1}\pm {\delta _ {1}^{2}-4\Delta _ {0}{3}}}{2}}}$

여기서 기호$displaystyle {{~}^{~}})$와 기호$(\${\displaystyle {{$3}{~}^~}})$는 각각 제곱근과 세제곱근으로 해석됩니다.제곱근 앞의 기호 "±"는 "+" 또는 "–"이며, 선택은 거의 임의이며, 이를 변경하는 것은 다른 제곱근을 선택하는 것과 같다.단, C = 0이 되는 경우, 즉 ${\displaystyle {\delta \mathrm{}}_{}}$ 0 $=$ 0${\displaystyle \mathrm{이}}$되는 경우(\$displaystyle \Delta$ _${0$}=$0,}),$ 대신$$ 다른 기호를 선택해야 합니다.두 가지 선택 항목 모두 C = 0인 경우, 즉 ${\displaystyle {\delta \mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle \mathrm{\delta }}$ 1 $=$0인 경우$,$ (\$displaystyle \Delta$ _${0$}=\$Delta$ _{1}=$0,})$ 다음 공식에서 분수 0/0이 발생하므로 0으로 해석해야 합니다(이 섹션의 끝 참조).그러면 뿌리 중 하나는

${\displaystyle x=-{\frac {1}{3a}}\left(b+C+{\frac {Delta _{0}}{C}}\right}{\text{\text}}.}}}$

다른 두 개의 루트는 C의 정의에서 세제곱근의 선택을 바꾸거나 C에 –1 ± µ–3/2의 원시 세제곱근을 곱함으로써 얻을 수 있다.즉, 3개의 뿌리는

${\displaystyle x_{k}=-{\frac {1}{3a}\left(b+\xi ^{k}C+{\frac {0}}{\xi ^{k}C}}}\right},\qquad k\in \{0,1,2\text,}}}}$

여기서 θ = –1 + θ – 3/2 입니다.

움푹 들어간 입방체의 특수한 경우, 이 공식은 적용되지만 입방근 없이 근을 표현할 수 있는 경우에는 쓸모가 없다.특히, ${\displaystyle {\delta \mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle {\delta \mathrm{}}_{}}$ ${\displaystyle 1}$ $=$ 0$$, \$displaystyle \Delta _{$0}=\$Delta$_{1$}=0, 공식$은 3개의$$ 루트가${\displaystyle \frac{b}{}}$ ${\displaystyle \frac{}{}\frac{a}{}}$ ,$$\$displaystyle \frac${-$b}{3a},$ 즉$$, 입방체 다항식을 ($x3$로 인수분해할 수 있음을 나타냅니다$.$간단한 계산을 통해 이 인수분해가 ${\displaystyle {\delta \mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle {\delta \mathrm{}}_{}}$ 1 $=$ $.\displaystyle \Delta$ _${0$}=\$Delta$ _${1$}=$0과$동일한지 확인할 수 있습니다.$}$

3개의 실근에 대한 삼각해

실수 계수를 갖는 입방정식이 3개의 실근을 갖는 경우, 이러한 근을 라디칼로 표현하는 공식은 복소수를 포함한다.갈로아 이론은 세 개의 뿌리가 진짜이고 어느 것도 합리적이지 않을 때, 그 뿌리는 진짜 라디칼로 표현할 수 없다는 것을 증명하게 한다.그럼에도 불구하고, 삼각함수, 특히 코사인 및 아크코신 ^[24]측면에서 순수하게 실제 해식을 얻을 수 있다.더 정확히 말하자면, 움푹 패인 입방체의 뿌리는

${\displaystyle t^{3}+pt+q=0}$

하고^[25] 있다

${\displaystyle t_{k}=2,{\cosrt {-{\frac {p}{3}}},\cos \left[, {\frac {3}{2p}}{\cosrt {frac {-3}},\frac {pi}},\right}k}, {\cos\frac {\frac {\},},\frac {\frac {3}, {\}}, {\}, {\}, {\frac {\},\frac {3}}, {\}, {\}, {$

이 공식은 프랑수아 비에트 ^[22]덕분이다.방정식이 3개의 실근(4 3 + 2 < \ $displaystyle 4p^{3}$ + $27q^{2}<0})$을 가지고 있는 경우, 이는 순전히 실수입니다.그렇지 않으면, 이는 여전히 맞지만, 실제 근이 하나일 때는 복잡한 코사인 및 아크코사인(arccosine)을 포함하며, p = 0일 때는 무의미하다.

이 공식은 θ Driped cubic에서 설명된 역치환을 사용하여 일반 입방정식의 근에 대한 공식으로 쉽게 변환할 수 있다.

이 공식은 다음과 같이 증명할 수 있다.방정식³ t + pt + q = 0에서 t = u cos θ로 설정합니다.방정식을 항등식과 일치시키기 위해 u를 선택하는 것이 목적이다.

$(\displaystyle 4\cos^{3}\theta-3\cos -\cos(3\theta)=0).}$

이 경우 ${\displaystyle \mathrm{u}}$ ${\displaystyle =\sqrt{2\frac{}{}}}$ - p${\displaystyle \sqrt{}\sqrt{\frac{3}{}}}$, {\$displaystyle u=$ 2,${\frac {p}}}}}},$ , , , , , , 를$$ $선택$하고 방정식을 ${\displaystyle \frac{{u\mathrm{}}^{}}{}\frac{{}^{}}{}}$으로 나눕니다$.$ {\$displaystyle {u^{3}}$ {$4}$ .}이것에$$ 의해$,$

${\displaystyle 4\cos ^{3}\theta-3\cos \theta -{\frac {3q}{2p}},{\displayrt {-3}{p}}= 0.}$

위의 정체성과 결합하면

${\displaystyle \cos(3\theta)=black {3q}{2p}{\displayrt {-3}{p}},}$

뿌리는 이렇게 되어 있습니다.

${\displaystyle t_{k}=2,{\cosrt {-{\frac {p}{3}}},\cos \left[{\frac {1}{3q}}{\arccos \left\frac {3q}{2p}}}{\p}}{\fracright-{\frac2\piq}}{\}}}{\csq}}}}{right}}}}{right}}}}}}}}{right}}}}}}}}}}}}}}}$

1개의 실근에 대한 쌍곡선 해

실근(및 p p 0)이 하나뿐인 경우, 이 근은 다음과 같이^[26][27] 쌍곡 함수를 사용하여 비슷하게 표현될 수 있습니다.

${\displaystyle{\begin{정렬}t_{0}&, =-2{\frac{q}{q}}{\sqrt{-{\frac{p}{3}}}}\cosh \left[{\frac{1}{3}}{}arcosh\operatorname \left({\frac{-3q}{파운드당 2펜스}}{\sqrt{\frac{-3}{p}}}\right)\right]\qquad{\text{만약}}~4p^{3}+27q^{2}>, 0~{\text{과}}~p<, 0,\\t_{0}&, =-2{\sqrt{\frac{p}{3}}}\sinh\left[{\frac{1}{3}}\operatorname{arsinh}\left(.{\frac{3q}{파운드당 2펜스}}{\frac {3}{p}}\right}\qquad {text{if}}~p>0.\end { aligned}}$

p 0 0과 오른쪽의 부등식이 만족되지 않는 경우(실근 3개의 경우), 공식은 유효하지만 복잡한 수량을 수반한다.

p = ±3일 때 위의 t 값을₀ 체비셰프 ^[28]입방근이라고 부르기도 합니다.보다 정확하게는 코사인 및 쌍곡 코사인 값을 사용하여 p = -3일 때 C(q)로_1/3 표시된 동일한 분석 함수가 정의되며, 이는 적절한 체비셰프 입방근이다.쌍곡선이 포함된 값은 p = 3일 때 비슷하게 S(q)로 표시됩니다_1/3.

기하학적 해법

오마르 카이얌의 솔루션

n > 0인³ 입방정식² x + mx = n을 풀기 위해, Omar Khayyam은 포물선 y = x²/m, 양의 x축에 선분 [0, n/m²]을 직경으로 갖는 원 및 원과 포물선이 X축 위에서 교차하는 지점을 통과하는 수직선을 구성했다.솔루션은 원점에서 수직선과 x축의 교차점까지의 수평선 세그먼트의 길이로 제공됩니다(그림 참조).

간단한 현대적 증거는 다음과 같다.방정식에 x/m을² 곱하고 항을 다시 정리하면 다음과 같이 됩니다.

$({displaystyle {x^{4}}{m^{2}}=x\left\frac {n}{m^{2}}-x\right).}$

왼쪽은 포물선의 y 값입니다².원의 방정식은² y + x(x - n/m²) = 0이며, 오른쪽은 원의 y² 값입니다.

각도 삼등분기가 있는 용액

실수계수를 갖는 입방정식은 ^{[29]: Thm. 1} 3개의 실수근을 갖는 경우에만 나침반, 직선 및 각도 삼등분기를 사용하여 기하학적으로 풀 수 있습니다.

입방정식은 합리적인 근이 있는 경우에만 나침반과 직선 구조(트리섹터 없음)로 풀 수 있습니다.이것은 고대 그리스 수학자들이 설정한 각도 삼분할과 입방체 배가라는 오래된 문제들이 나침반과 직선 구조로는 해결될 수 없다는 것을 암시한다.

근의 기하학적 해석

삼근

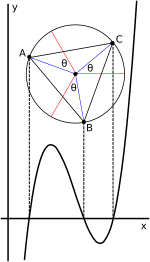
비에트의 삼근법적 표현은 ^[22][30]원의 관점에서 기하학적 해석에 도움이 된다.위에서와 같이 입방체를 움푹 패인 형태(2), t³ + pt + q = 0으로 쓸 때, 용액은 다음과 같이 표현할 수 있다.

$({displaystyle t_{k}=2grt {-{\frac {p}{3}}}\cos \left\frac {1}{3}}}\arccos \left\frac {3q}{2p}}{\frac {p}}}{\fright}{3}}\cos\text}}\cos\frapsyp}{-kfrac {-frac}{\frac{{\f}}}{\fr}}{\t {-fr}}}}}{\t}}$

여기서 ${\displaystyle \arccos }$θ ( ${\displaystyle \frac{3}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}\sqrt{\frac{}{}}}$p - ${\displaystyle \sqrt{\frac{}{}}}$p$$) { $displaystyle$\$arccos \$ left \ $frac${$3q$} { $2p$} { \ $frac$rt { - $3 }$ { p $}$ \ right }는$$ 단위 원 내의 각도이다.그 각도의 1/3을 취하면 복소수의 세제곱근을 구하는 것과 같으며, -k2/3를 더하면, k3를 더하면, k3를 더하면 1 = 1이다.각도가${\displaystyle \sqrt{\frac{2}{}}}$ - p$$3({$displaystyle 2sqrt {-{\frac {p}{3}}})$이면 척도가 보정됩니다$$.

비반복 케이스 (1)(첨부 그래프 참조)에 대해서는 x = t - b/3a가 t = x + b/3a가 되도록 t를 정의함으로써 전술과 같이 움푹 패인 케이스를 구한다.그래프적으로 이것은 변수 t와 x 사이를 변경할 때 각도 관계를 변경하지 않고 단순히 그래프를 수평으로 이동하는 것에 해당합니다.이 이동은 변곡점과 원의 중심을 Y축으로 이동합니다.그 결과, 방정식의 근은 0이 된다.

1개의 실제 루트

데카르트 평면에서

세제곱 함수의 그래프가 데카르트 평면에 플롯될 때, 실제 루트가 하나뿐인 경우, 그것은 곡선의 수평 절편의 가로축(그림의 R점)의 가로축(x좌표)입니다.또,^[31][32][33] 복소공역근을 g±hi라고 하면, 실수부 g는, 입방체의 x절편 RM을 통과하는 입방체에 대한 탄젠트선의 접점 H의 외측치(즉, 부호길이 RM, 그림상의 음)가 된다.가상의 부분 ±h는 이 접선과 수평 ^{[clarification needed]}축 사이의 각도의 접선의 제곱근입니다.

복소평면

1개의 실근과 2개의 복소근으로, 3개의 근은 입방체의 도함수의 두 근과 같이 복소평면에서 점으로 표현될 수 있다.이 모든 뿌리들 사이에는 흥미로운 기하학적 관계가 있다.

3개의 루트를 나타내는 복소평면의 점은 이등변 삼각형의 꼭지점 역할을 합니다.(삼각형이 이등변하는 이유는 한 뿌리는 수평(실제) 축에 있고 다른 두 뿌리는 복잡한 공역체이므로 실제 축의 위와 아래에 대칭적으로 나타나기 때문입니다.)마르덴의 정리는 입방체의 도함수의 근을 나타내는 점들은 삼각형의 스타이너 타원 즉, 변의 중간점에서 삼각형에 접하는 독특한 타원이라고 말한다.실축상의 정점의 각도가 θ/3보다 작을 경우, 타원의 장축은 실축에 놓여 있으며, 그 포치 및 이에 따른 도함수의 근원에도 해당된다.이 각도가 θ/3보다 크면 장축은 수직이고 그 도함수의 근원인 foci는 복소공역이다.그리고 만약 그 각도가 θ/3이면, 삼각형이 등변이고, 스타이너 타원형은 단순히 삼각형의 절치이고, 그 포치는 실제 축에 있는 유인기에서 서로 일치하므로, 따라서 도함수는 두 개의 실제 근을 가집니다.

갈루아군

2와 3과는 다른 특성의 장 K에 걸쳐서 입방정식의 경우, K 위의 갈로아 그룹은 K의 가장 작은 확장 K(분할장)를 고정하는 장 자기동형군이다.이러한 자기동형은 다항식의 근을 순열해야 하므로, 이 그룹은 3개의 근의 6개의 순열 중 S군₃ 또는 3개의 원형 순열 중 A군이다₃.

세제곱의 판별 δ는 다음의 제곱이다.

$({displaystyle {delta }}=a^{2}(r_{1}-r_{2})(r_{1}-r_{3})(r_{2}-r_{3}),}$

여기서 a는 입방체의 선행 계수이고 r₁, r₂, r은₃ 입방체의 세 가지 루트입니다.2개의 루트가 교환되면 $($ 스타일$)$이 바뀌므로 $(표시$ 스타일$)$은 갈로아 그룹이 A일₃ 경우에만 갈로아 그룹이 고정합니다$.$즉, 판별자가 k 원소의 제곱인 경우에만 갈로아 그룹은 A이다₃.

대부분의 정수는 제곱이 아니기 때문에, 유리수의 필드 Q에 대해 작업할 때, 대부분의 환원 불가능한 입방 다항식의 갈로아 그룹은 6개의 원소를 가진 군 S이다₃.세 가지 원소를 가진 갈로아 군 A의₃ 예는 p(x) = x³ - 3x - 1로, 판별식은 81 = 9이다².

뿌리의 파생

이 섹션에서는 카다노의 공식을 도출하기 위한 몇 가지 방법을 다시 정리합니다.

카르다노법

이 방법은 Scipione del Ferro와 Tartaglia에 의한 것이지만, 그의 책 Ars Magna (1545)에 그것을 처음 발표한 Gerolamo Cardano의 이름을 따서 명명되었다.

이 방법은 움푹 들어간 세제곱³ t + pt + q = 0에 적용됩니다.아이디어는 u + v = t가 되도록 두 개의 변수 u와 v를 도입하고 이것을 압축된 입방체 안에 대입하는 것이다.

${\displaystyle u^{3}+(3uv+p)(u+v)+q=0.}$

이때 Cardano는 3uv + p = 0이라는 조건을 부과했다.이것은 이전의 등식에서 세 번째 항을 제거하여 방정식의 시스템으로 이어집니다.

${\displaystyle {\frac {p}{3}+v^{3}&=-q\uv&=-{\frac {p}{3}}.\end { aligned}}$

u와³ v의³ 합과 곱을 알면 2차 방정식의 두 가지 해라고 추론할 수 있다.

${{displaystyle (x-u^{3})(x-v^{3})=x^{2}-(u^{3}+v^{3}=x^{2}-(u^{3}+v^{3})x+(uv)=0,}$

그렇게

${\displaystyle x^{2}+qx-{\frac {p^{3}}{27}}=0,}$

이 방정식의 판별식은 ${\displaystyle {}^{}}$ ${\displaystyle =}$ ${\displaystyle {q\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle \frac{{}^{}}{}}$ p ${\displaystyle \frac{{3\mathrm{}}^{}}{}}$ ${\displaystyle \frac{27}{{}^{}}}${\$displaystyle \Delta =q^{2}+{\frac {4p^{3}}{27$이며, 양수라고 가정하면, 이 방정식에 대한 실제 해는 다음과 같다(제곱근에서 4로 접은 후).

${\displaystyle - {\frac {q} {{\frac {q^{2}} {4}} + {\frac {p^{3}} {27}}}}}.}$

따라서 (u 또는 v를 선택할 때 일반성을 잃지 않음)

${{displaystyle u=paramrt[{3}}{-{\frac {q}{2}}+{4}}+{\frac {p^{3}}{27}}}}}}}}.}$

${{displaystyle v=paramrt[{3}}{-{\frac {q}{2}}-{\frac {q^{2}}}{4}}+{\frac {p^{3}}{27}}}}}}}}}}.}$

u + v = t로서, 이러한 용액의 세제곱근의 합은 방정식의 근이다.그것은

${{displaystyle t=blashrt[{3} \over2}+{\blashrt {q^{2} \over 4}+{p^{3} \over 27}}}+{\blashrt [{3} \over 27}}}}}+{\blashrt[{q \over 2}-{q \over 4}}}}}}}}+{-{-{-{-{-{p^{p^{p^{{{{{{{{{{{}}}}}}}}}}}}}}}}}}}$

방정식의 근이고, 이것이 카르다노의 공식입니다.

이것은 4 3+ 2> ,{\$displaystyle 4p^{3$} + $27q^{2}$ > $0$, 그러나 4 3 + 2<, \ $display$ style $4p^{3}$ + $27q^{2}$ <$0$ , 0 , } 의 으로 동작합니다.복소수는 3개의 세제곱근을 가지므로, 카다노의 공식을 함부로 사용하면 9개의 근을 얻을 수 있지만, 1개의 세제곱식은 3개 이상의 근을 가질 수 없다.이것은 라파엘 봄벨리에 의해 그의 책 L'Algebra (1572년)에서 처음으로 명확해졌다.해결책은 uv = –p/3, 즉 v = –p/3u라는 사실을 사용하는 것입니다.즉, 1개의 입방근만 계산하면 되고, § Cardano 공식에 제시된 두 번째 공식으로 이어집니다.

방정식의 다른 근은 세제곱근을 바꾸거나, 입방근에 ${\displaystyle \frac{-1\sqrt{}\pm }{}}$ - ${\displaystyle \frac{\sqrt{3}}{}\frac{2}{}}$의$$각 기본 입방근(\$displaystyle\frac${-1$\pm {-3}}{2})$을 곱하여 얻을 수 있습니다.$}$

비에타 치환

비에타의 치환은 프랑수아 비에트가 1615년에 사후에 발표한 텍스트에서 도입한 방법으로, 카르다노법의 두 번째 공식을 직접 제공해, 두 개의 다른 ^[34]입방근을 계산하는 문제를 회피한다.

움푹 패인 세제곱³ t + pt + q = 0에서 비에타의 치환은 t = w – p/3w이다.^[35]

치환 t = w – p/3w는 압축된 입방체를 다음과 같이 변환합니다.

${\displaystyle w^{3}+q-{\frac {p^{3}}{27w^{3}}=0.}$

w를³ 곱하면 w의³ 2차 방정식을 얻을 수 있습니다.

${{displaystyle (w^{3})^{2}+q(w^{3})-{\frac {p^{3}}:{27}}=0.}$

허락하다

${\displaystyle W=-{\frac {q}{p^{3}}{27}+{\frac {q^{2}}{4}}}}\pm$

이 2차 방정식의 0이 아닌 루트입니다.w, w₂, w가₃ W의 3입방근이면 원래의₁ 움푹 들어간 입방근은 w₁ - p/3w₁, w₂ - p/3w₂, w₃ - p/3w이다₃.2차 방정식의 다른 근은 - ${\displaystyle \frac{{p\mathrm{}}^{}}{}}$ 3 ${\displaystyle \frac{\mathrm{27}}{}}$W입니다$.\${\$frac {p^{3}}$ {$27$$W}}.}$ 이는$$ 제곱근 부호를 변경해도 i = 1, 2, 3에 대해 w와 -p/3w가_i 교환되므로_i 루트가 변경되지 않음을 의미합니다.이 방법은 2차 방정식의 두 근이 모두 0일 때, 즉 p = q = 0일 때에만 실패합니다. 이 경우, 움푹 들어간 입방체의 유일한 근은 0입니다.

라그랑주법

그의 논문 "Réflexions sur la résolution algébrique des questions"("^[36]방정식의 대수적 해법에 관한 생각")에서, 조셉 루이 라그랑주는 낮은 차수의 방정식을 더 높은 차수로 일반화할 수 있다는 희망과 함께 균일한 방식으로 푸는 새로운 방법을 도입했다.이 방법은 입방정식과 사분방정식에 잘 적용되지만, 라그랑주는 최소 ^[37][38][39]6도의 분해능 다항식을 풀어야 하기 때문에 5차 방정식에 적용하는데 성공하지 못했다.이전에는 아무도 문제를 푸는 데 성공하지 못했다는 것을 제외하고, 이것은 5차 이상의 대수 공식의 부존재를 나타내는 첫 번째 표시였다; 이것은 나중에 아벨-루피니 정리로서 증명되었다.그럼에도 불구하고, 해결 가능한 5차 방정식을 푸는 현대적인 방법은 주로 라그랑주의 방법에 ^[39]기초한다.

입방정식의 경우, 라그랑쥬의 방법은 카르다노와 같은 해답을 제공한다.라그랑주 방법은 일반 입방정식³ ax + bx² + cx + d = 0에 직접 적용할 수 있지만, t + pt + q = 0으로³ 계산하면 더 간단하다.

라그랑쥬의 주요 아이디어는 루트 자체 대신 루트의 이산 푸리에 변환으로 작업하는 것이었습니다.좀 더 정밀하게 통합의 ξ은 원시적인 3뿌리, 그것은 번호가 ξ3)1과 ξ2+ξ+1=0때 복잡한 숫자의 우주에서의 작업(, 팔짱 ξ다 − 1±자 나는 32)e2나는 π/3,{\displaystyle\textstyle \xi){\frac{-1\pm 나는{\sqrt{3}}}{2}}=e^{2i\pi /3},}지만 이런 복잡한 해석은 사용된다.)풀어야 할₁ 입방정식의₂ 세 근을 x, x, x로 나타내면₀,

${\displaystyle {signed}s_{0}&=x_{1}+x_{2}&=x_{0}+xi x_{1}+\xi x_{2}&=x_{2}&=x_{0}x_{1}+xi x_{2},\s_{1}xi_{1}+xi}x_{1}x_{1}x_{1}x_{2}x_{1}x_x_x_x_x_x_x_x_x_x_x_x_x_x_x_x_x_x_x_$

루트의 이산 푸리에 변환입니다.s, s₁ 및₂ s가 알려진 경우₀, 루트는 이 선형 변환을 반전하는 것으로 구성된 역 푸리에 변환으로 그것들로부터 회복될 수 있다. 즉,

${{displaystyle {displaystyle}x_{0}&=tfrac {1}+s_{2},\x_{1}+s_{3},\xi ^{2}s_{1}+xi ^{1}+xi_{2},\xi},\x},\x_{2},\x},\x,\x,\x,\x,\x,\x,\x,\end { aligned}}$

비에타의 공식에 따르면₀, s는 움푹 들어간 입방체의 경우 0, 일반 입방체의 경우 -b/a로 알려져 있다.따라서₁ 와만₂ 계산하면 됩니다.이들은 루트의 대칭함수가 아니지만(x와₂ x 교환도₁ s와₁₂ s) s와₂ s의 간단한₁ 대칭함수도 풀어야 할 입방정식의 루트에서 대칭함수이다.따라서 이러한 대칭 함수는 원래 입방체의 (알려진) 계수로 표현될 수 있으며, 이를 통해 s를 알려진_i 계수로 다항식의 근으로 표현할 수 있습니다.이것은 모든 차수에 대해 잘 작동하지만, 4도보다 높은 차수에서는 s를_i 루트로 하는 결과 다항식이 초기 다항식의 차수보다 높기 때문에 해결에 도움이 되지 않습니다.이것이 라그랑주 방법이 5단계 이상에서 실패하는 이유입니다.

입방정식의 경우, $P{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle {s\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ s${\displaystyle {}_{}}$2, ${\displaystyle$ P=$s_{1}$ $s\_{\displaystyle }$${2}$ 및 S$$ ${\displaystyle =}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$3 + ${\displaystyle {\mathrm{}}_{}^{}}$2 {\$displaystyle$ S=$s_{1}^{3}+s_{2$$}^{$3$$}}은 대칭 다항식이다(아래 참조).${\displaystyle {따라서\mathrm{}}_{}^{}}$, s 1$$ ({$displaystyle s_{1}^{$3$$})과 ${\displaystyle {\mathrm{}}_{}^{}}$2 ({$displaystyle s_{2}^{$3$$})는 $2차{\displaystyle {}^{}}$ ${\displaystyle {방정식\mathrm{}}^{}}$z ${\displaystyle 2}$ -${\displaystyle S}$ ${\displaystyle {}^{}}$ + ${\displaystyle {P\mathrm{}}^{}}$ 3 $=$ 0$.$ ({$displaystyle z^{2}-Sz+P$^{$3}=$0$$})의 2차 방정식 2차 방정식의 2차 근이 된다.${1}$ 및$$ ${\displaystyle {s\mathrm{}}_{}}$ 2$${{$displaystyle s_{2}}$는 u 및 v 대신 사용합니다.

움푹 패인 입방체의 경우 ${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle 0\frac{\mathrm{}}{}}$ ${\displaystyle {}_{}\frac{1}{}}$ ${\displaystyle {}_{}}$ (${\displaystyle {}_{}{s\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ + s$$2 ) { $display$x _ { 0 }$$= s $tfrac {1}$ {3} （$s$_${1$} +$s$ _$${2} } } $s$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {s\mathrm{}}_{}}$ ${\displaystyle 2{}_{}}$ -${\displaystyle }$3 $,$ \ $display$s $_${1}$s$_ {2} =$3$p, card$$ ' ' 、 ${\displaystyle {0\mathrm{}}_{}}$ ' '' 。$=bsqtfrac {1}{3}}$$p.}$$$ 따라서 u와 v의 교환까지는 ${\displaystyle {s\mathrm{}}_{}}$ 1 $=$ $u$ (\${\displaystyle \mathrm{displaystyle}}$ $s_{1$}=$3u)$와 ${\displaystyle {s\mathrm{}}_{}}$ 2 $=$ ${\displaystyle 3}$ v$.$ (\$displaystyle s_{2$}=$3v.)$ 즉$$, Cardano의 방법과 Lagrange의 방법은 보조 변수인 3가지까지 정확히 동일하게 계산한다.d에서는 이러한 보조 변수가 문제에 표시되는 이유를 설명합니다.

S와 P의 계산

ξ³² = 1 및 + + + + 1 = 0의 관계를 사용한 간단한 계산은 다음과 같다.

$디스플레이 스타일P&=s_{1}s_{2}=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-(x_{0}x_{1}+x_{1)}x_{2}+x_{2}x_{0}),\\S&=s_{1}^{3}+s_{2}^{3}=2(x_{0}^{3}+x_{1)}^{3}+x_{2}^{3}-3(x_{0}^{2}x_{1}+x_{1)}^{2}x_{2}+x_{2}}^{2}x_{0}+x_{0}}x_{1}^{2}+x_{1}x_{2}^{2}+x_{2}x_{0}^{2}+12x_{0}x_{1}x_{2}.\end { aligned}}$

이것은 P와 S가 루트의 대칭 함수임을 보여준다.뉴턴의 항등식을 사용하여, 뿌리의 기본 대칭 함수의 관점에서 그것들을 표현하는 것은 간단하다.

$디스플레이 스타일P&=e_{1}^{2}-3e_{2},\S&=2e_{1}^{3}-9e_{1}e_{2}+27e_{3},\end{aligned}}}$

e₁ = 0, e₂ = p 및₃ e = -q일 경우, 그리고₁ e = -b/a, e₂ = c/a₃, e = -d/a일 경우이다.

적용들

입방정식은 다양한 다른 맥락에서 발생합니다.

수학에서

• 각도 3분할과 입방체 이중화는 직선과 나침반 구조로는 해결할 수 없는 것으로 증명된 기하학의 두 가지 오래된 문제인데, 이는 입방정식을 푸는 것과 같기 때문입니다.
• 마르덴의 정리는 삼각형의 세 꼭지점들의 복소 평면에서의 좌표가 근원인 입방함수를 사용함으로써 모든 삼각형의 스타이너 타원형의 포치를 찾을 수 있다고 말한다.이 입방체의 첫 번째 도함수의 근은 그러한 포치의 복소 좌표이다.
• 정육각형의 면적은 입방체의 근으로 표현될 수 있다.또한 장대각선변, 단대각선변, 단대각선변과 장대각선의 음의 비율이 모두 특정 입방정식을 만족한다.또한 7각형 삼각형의 원반경에 대한 인반경의 비는 입방정식의 해 중 하나이다.${\displaystyle \mathrm{2\mu }}$/ $({디스플레이 스타일$ 2$\pi$/ 7$})$과 $관련$된 각도의 삼각함수 값은 입방정식을 만족합니다.
• 임의의 각도의 코사인(또는 다른 삼각함수)이 주어졌을 때, 그 각도의 1/3 코사인(cosine)은 입방체의 루트 중 하나입니다.
• 일반 4차 방정식의 해는 분해능 입방정식의 해법에 의존한다.
• 3×3 행렬의 고유값은 행렬의 특성 다항식인 입방 다항식의 근이다.
• 3차 상수 계수 또는 코시-울러(등차원 변수 계수) 선형 미분 방정식 또는 차분 방정식의 특성 방정식은 입방정식이다.
• 베지어 곡선을 나타내는 직입방정식을 사용하여 입방 베지어 곡선과 직선의 교차점을 계산할 수 있다.
• 4차 함수의 임계점은 입방정식(도함수 집합은 0)을 풀어서 구한다.
• 5차 함수의 변곡점은 입방정식의 해이다(두 번째 도함수 집합은 0과 같다.

기타 과학 분야

• 분석화학에서 완충용액의 pH를 구하는 데 사용할 수 있는 샬롯 방정식은 입방정식을 사용하여 풀 수 있다.
• 열역학에서 (물질의 압력, 부피 및 온도와 관련된) 상태 방정식은 부피에서 입방정식입니다.
• 선형 가속도 속도를 포함하는 운동 방정식은 입방체이다.
• 지진 레일리파의 속도는 레일리파 입방정식의 해법이다.
• 일정한 입력 파워에 대한 공기 마찰로 경사면을 주행하는 차량의 정상 상태 속도를 압축 입방정식으로 푼다.

메모들

레퍼런스

• Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter, 5 (4): 8–12, doi:10.2307/3027812, JSTOR 3027812

추가 정보

• Anglin, W. S.; Lambek, Joachim (1995), "Mathematics in the Renaissance", The Heritage of Thales, Springers, pp. 125–131, ISBN 978-0-387-94544-6 24장
• Dence, T. (November 1997), "Cubics, chaos and Newton's method", Mathematical Gazette, Mathematical Association, 81 (492): 403–408, doi:10.2307/3619617, ISSN 0025-5572, JSTOR 3619617
• Dunnett, R. (November 1994), "Newton–Raphson and the cubic", Mathematical Gazette, Mathematical Association, 78 (483): 347–348, doi:10.2307/3620218, ISSN 0025-5572, JSTOR 3620218
• Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
• Mitchell, D. W. (November 2007), "Solving cubics by solving triangles", Mathematical Gazette, Mathematical Association, 91: 514–516, doi:10.1017/S0025557200182178, ISSN 0025-5572, S2CID 124710259
• Mitchell, D. W. (November 2009), "Powers of φ as roots of cubics", Mathematical Gazette, Mathematical Association, 93, doi:10.1017/S0025557200185237, ISSN 0025-5572, S2CID 126286653
• Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007), "Section 5.6 Quadratic and Cubic Equations", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Rechtschaffen, Edgar (July 2008), "Real roots of cubics: Explicit formula for quasi-solutions", Mathematical Gazette, Mathematical Association, 92: 268–276, doi:10.1017/S0025557200183147, ISSN 0025-5572, S2CID 125870578
• Zucker, I. J. (July 2008), "The cubic equation – a new look at the irreducible case", Mathematical Gazette, Mathematical Association, 92: 264–268, doi:10.1017/S0025557200183135, ISSN 0025-5572, S2CID 125986006

외부 링크

• "Cardano formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• MacTutor 아카이브에 대한 2차, 3차 및 4차 방정식의 이력.
• 500년 동안 큐빅 공식을 가르치지 않았으니 네가 감당할 수 없다고 생각하는 게 뭐야?– Mathologer의 YouTube 비디오에서 입방정식의 역사와 Cardano의 해법 및 Ferrari의 4차 방정식 해법에 대한 설명