컬(수학)

에 관한 일련의 기사의 일부
미적분학.
기본 정리 라이프니츠 적분 규칙 기능의 제한 연속성 평균값 정리 롤의 정리
차동 정의들 도함수(일반화) 차동 극소수의 함수의 총 개념 미분 표기법 이차 도함수 암묵적 미분 로그 미분 관련 요금 테일러의 정리 규칙과 아이덴티티 합 제품. 체인 힘 몫 로피탈의 법칙 역 라이프니츠 장군 파디 브루노의 공식 레이놀즈.
일체형 적분 목록 적분 변환 정의들 반파생적 내장(부적합) 리만 적분 르베그 적분 등고선 통합 역함수의 적분 통합: 부품. 디스크 원통형 셸 치환(트리거메트릭, 탄젠트 반각, 오일러) 오일러 공식 부분 분수 순서 변경 환원 공식 적분 기호로 구분 라이시 알고리즘
시리즈 기하학(산술-기하학) 고조파 교대로 힘 이항 테일러 컨버전스 테스트 Summand limit(항 검정) 비율 뿌리 일체형 직접 비교 한계 비교 교대 급수 코시 응축 디리클레 아벨
벡터 그라데이션 발산 컬 라플라시안 방향 도함수 아이덴티티 정리 그라데이션 녹색의 스토크스 발산 일반화 스토크스
다변수 형식주의 매트릭스 텐서 외부 기하학 정의들 편도함수 다중 적분 라인 적분 표면적분 볼륨 적분 야코비안 헤시안
고급. 유클리드 공간의 미적분 분배의 한계
특화된 프랙셔널 말리아빈 확률적 바리에이션
여러가지 종류의 계산 전 역사 용어집 토픽 리스트 인테그레이션 분석.
v t

벡터 미적분학에서 컬은 3차원 유클리드 공간에서 벡터장의 극소 순환을 설명하는 벡터 연산자이다.필드의 한 지점에서 컬은 길이와 방향이 최대 ^[1]순환의 크기와 축을 나타내는 벡터로 표현됩니다.필드의 컬은 필드의 각 지점에서 순환 밀도로 정식으로 정의됩니다.

컬이 0인 벡터장을 비회전이라고 합니다.컬은 벡터 필드의 미분 형식입니다.미적분학의 기본정리의 대응형태는 스토크스의 정리이며, 이것은 벡터장의 컬 표면적분과 경계곡선 주위의 벡터장의 선적분과의 관련을 짓는다.

대체 용어 회전 또는 회전 및 대체 표기법 썩음 F 또는 del (nabla) 연산자 δ × F와의 교차 곱이 컬 ^[2]F에 사용되는 경우가 있습니다.

구배와 발산과는 달리, 벡터 미적분학에서 공식화된 컬은 단순히 다른 차원으로 일반화되지 않습니다; 일부 일반화는 가능하지만, 3차원에서만 벡터 필드의 기하학적으로 정의된 컬입니다.이 결손은 벡터 미적분의 한계로 인한 직접적인 결과이다; 기하학 미적분의 쐐기 연산자를 통해 표현될 때, 컬은 모든 차원으로 일반화된다.아쉽게도 3차원 크로스 곱에 있는 것과 비슷하며, 컬의 경우 δ× 표기로도 연결이 반영되어 있습니다.

"컬"이라는 이름은 1871년 제임스^[3] 클러크 맥스웰에 의해 처음 제안되었지만 분명히 1839년 ^[4][5]제임스 맥컬라에 의해 광학장 이론의 구축에 처음 사용되었다.

정의.

벡터장 F의 컬(curl F, θ × F 또는 rot F)은 점을 통과하는 다양한 라인에 투영되는 관점에서 정의된다.n$^$ {\$displaystyle \mathbf {n}}$이(가) 단위 벡터일 $경우{\displaystyle \stackrel{}{\mathbf{}}}$, n$^$ {\$displaystyle \mathbf {n$$}}$에 대한$$ F의 컬 투영을 n$^$ {$displaystyle \mathbf {n}}}$에 $대한{\displaystyle \stackrel{}{\mathbf{}}}$ 폐선 적분의 한계치로 정의한다.통합의 h는 그 점을 중심으로 축소된다.

curl 연산자는 연속 미분 가능 함수 f : R³ → R을³ 연속 함수 g : R³ → R에³ 매핑하고, 특히 R의³ C 함수를 R의³ C 함수에^k−1 매핑한다^k.

암묵적으로, 컬은 p 지점에서^[6][7] 다음과 같이 정의된다.

$(\displaystyle (\times \mathbf {F})(p)\cdot \mathbf {n}\{underset {mathrm {def} {}}{}}\lim _{A\to 0}{\frac {1}}{C}\mathbf}\cdot {F}\cd}\cdot \mathbf {F}\f}\F}\f}\F}\cd}\mathbf}\f}\f}\cd}\cdisit {F}\$

여기서 선 적분은 해당 영역 A의 경계 C를 따라 계산되며, A는 해당 영역의 크기이다.이 방정식은 F의 컬을${\displaystyle \stackrel{}{\mathbf{}}}$n$^(\$에 투영하는 것을 정의합니다. C로 둘러싸인 극소 표면은 n$^\$을$($를$)$ 법선으로 합니다.C는 오른손 법칙을 통해 배향됩니다.

위의 공식은 벡터 필드의 컬이 해당 필드 순환의 극소 면적 밀도로 정의된다는 것을 의미합니다.이 정의에 자연스럽게 들어맞다

• 정의에 대응하는 전역 공식으로서의 켈빈-스토크스 정리, 그리고
• 곡선 직교 좌표의 컬에 대한 다음과 같은 "기억하기 쉬운" 정의(예: 데카르트 좌표, 구형, 원통형 또는 타원 또는 포물선 좌표)
  $${\displaystyle{\begin{정렬}&,(\operatorname{컬}\mathbf{F})_{1}={\frac{1}{h_{2}h_{3}}}\left({\frac{\partial(h_{3}F_{3})}{\partial u_{2}}}-{\frac{\partial(h_{2}F_{2})}{\partial u_{3}}}\right),\\[5pt]&,(\operatorname{컬}\mathbf{F})_{2}={\frac{1}{h_{3}h_{1}}}\left({\frac{\partial(h_{1}F_{1})}{\partial u_{3}}}-{\frac{\part.ial(h_{3)F_{3}}}{\partial u_{1}\right},\[5pt]&(operatorname {f}\mathbf {F})_{3}=partial frac {1}{h_{2}\partial\frac(h_2}F_1}{1}\partial\partial u1}\partial\end { aligned}}$$

  

각 성분(예: F)_k에 대한 방정식은 첨자 1, 2, 3의 각 발생을 순환 순열로 교환하여 얻을 수 있습니다. 1 → 2, 2 → 3, 3 → 1(첨자가 관련 지수를 나타냄)입니다.

만약₁ (x₂, x₃, x)가 데카르트 좌표이고₁ (u₂, u₃, u)가 직교 좌표라면,

u에 대응하는_i 좌표 벡터의 길이입니다.컬의 나머지 두 가지 구성 요소는 3,1,2 → 1,2,3 → 2,3,1 지수의 주기적 순열에서 비롯된다.

직관적인 해석

벡터장이 유체 흐름의 속도장(액체 또는 가스의 큰 탱크 등)을 기술하고 작은 공이 유체 또는 가스(볼의 중심이 특정 지점에 고정됨) 안에 있다고 가정합니다.볼의 표면이 거칠면 볼을 통과하는 오일이 볼을 회전시킵니다.회전축(오른쪽 규칙에 따라 방향)은 볼의 중심에 있는 필드의 컬 방향을 가리키며, 회전의 각 속도는 이 지점에서 ^[8]컬 크기의 절반이다.

임의의 지점에서 벡터의 컬은 xy 평면(컬의 z축 구성요소의 경우), zx 평면(컬의 y축 구성요소의 경우) 및 yz 평면(컬 벡터의 x축 구성요소의 경우)의 극소 영역의 회전에 의해 제공됩니다.이것은, 다음의 예에서 명확하게 확인할 수 있습니다.

사용.

실제로 위의 정의는 거의 사용되지 않습니다. 왜냐하면 사실상 모든 경우에, 컬 연산자는 보다 단순한 표현이 도출된 곡선 좌표 세트를 사용하여 적용될 수 있기 때문입니다.

θ × F 표기법은 3차원 교차곱과의 유사성에서 유래하며, θ를 벡터 미분 연산자 del로 취할 경우 데카르트 좌표의 니모닉으로 유용하다.연산자를 포함하는 이러한 표기법은 물리학과 대수학에서 흔히 볼 수 있다.

3차원 데카르트 좌표로 확장됨(구면 및 원통 좌표 표현에 대한 원통 및 구면 좌표의 델 참조) δ × F는 [F_x, F_y, F_z]로 구성된 F에 대해 다음과 같다(첨자가 부분 도함수가 아닌 벡터의 성분을 나타낸다).

$\displaystyle \times \mathbf {F} = {\boldsymbol {hat } {\boldsymbol {jmath}} & {\boldsymbol {k} \ [ 5 \ dfrac } {\ dfrac }F_{x}&F_{y}&F_{z}\end{vmatrix}}$

여기서 i, j 및 k는 각각 x-, y- 및 z-의 단위 벡터입니다.다음과 ^{[9]: 43} 같이 확장됩니다.

$\displaystyle \times \mathbf {F} = \leftfrac {\flac F_{z} {\partial y}-{\frac {\flac} {\partial z} {\boldsymbol {\imath} +\frac {\f} {\frac} - {\flac}l y}}\오른쪽) {\boldsymbol {hat {k}=bmatrix} {\frac {\partial y} - {\frac {\frac F_{y} {\partial z} \ {\frac {\frac F_{x} {\partial z} - {\frac F}$

좌표의 관점에서 표현되지만 좌표축의 적절한 회전에서는 결과는 변하지 않지만 반사에서는 반전된다.

일반 좌표계에서 컬은 다음과 같이 주어진다^[1].

${\displaystyle (\displayla \times \mathbf {F})^{k}=varepsilon ^{k\ell m}\displayla _{\ell}F_{m}}$

여기서 θ는 Levi-Civita 텐서, θ 공변 도함수 $\$는 야코비안이고 아인슈타인 합계 규칙은 반복 지수가 합산됨을 의미한다.공변 도함수에 참여하는 크리스토펠 기호의 대칭성 때문에 이 식은 부분 도함수로 감소합니다.

${\displaystyle(\displayla \times \mathbf {F})=blac {1}{\displayrt {g}}\mathbf {R}_{k}\varepsilon ^{k\ell m}\displaystyl}F_{m}$

여기서_k R은 로컬 베이스 벡터입니다.마찬가지로 외부 도함수를 사용하면 다음과 같이 컬을 표현할 수 있습니다.

$\displaystyle \times \mathbf {F} = \left(\star {\mathrm {d}\mathbf {F} ^{\flat}{\big}}\right)^{\filename}}:$

여기서 ♭와 are는 음악적 동형사상이고, ★는 호지 별 연산자이다.이 공식은 좌표계에서 F의 컬을 계산하는 방법과 방향성이 있는 3차원 리만 다양체로 컬을 확장하는 방법을 보여줍니다.이것은 방향 선택에 따라 달라지기 때문에 컬은 키랄 수술입니다.즉, 방향이 반전되면 컬의 방향도 반전됩니다.

예

예 1

벡터 필드

${\displaystyle \mathbf {F}(x,y,z)=y'boldsymbolhat(\imath}}-x'boldsymbolhat(\jmath}}}}$

로 분해할 수 있다

${\displaystyle F_{x}=y,F_{y}=-x,F_{z}=0.}$

육안으로 검사하면 필드가 "회전 중"이라고 설명할 수 있습니다.필드의 벡터가 그 지점에 존재하는 물체에 작용하는 선형 힘을 나타내며 물체가 필드 안에 배치되면 물체는 그 자체에서 시계방향으로 회전하기 시작합니다.이는 객체의 배치 위치에 관계없이 적용됩니다.

컬 계산:

$(\displaystyle \times \mathbf {F} = 0 bold symbol {hat} + 0 bold symbol hat {jmath } + 0 bold symbol hat {\frac } {\frac x} - {-x} - {\frac } {\bold sy} = {\baldmbalf}$

컬을 설명하는 벡터 필드는 모든 점에서 음의 z 방향을 가리킵니다.이 방정식의 결과는 오른손 좌표계를 사용하여 오른손 법칙을 사용하여 예측할 수 있었던 것과 일치합니다.균일한 벡터장이기 때문에 앞에서 설명한 물체는 배치 위치에 관계없이 동일한 회전 강도를 가집니다.

예 2

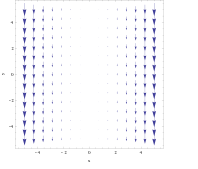
벡터 필드의 경우

${\displaystyle \mathbf {F}(x,y,z)=-x^{2}{\boldsymbol {\hat {\jmath}}}}$

그래프에서 볼 때 컬이 뚜렷하지 않습니다.그러나 앞의 예에서 물체를 가져다가 x = 3 선의 아무 곳에나 놓으면 오른쪽에 가해지는 힘이 왼쪽에 가해지는 힘보다 약간 더 커 시계 방향으로 회전하게 된다.오른손 법칙을 사용하면 결과 컬이 음의 z 방향으로 직선임을 예측할 수 있습니다.반대로 x = -3에 놓이면 물체는 시계 반대 방향으로 회전하고 오른쪽 규칙은 양의 z 방향을 가져옵니다.

컬 계산:

$\displaystyle \times \mathbf {F} = 0 bold symbol {hat} + 0 bold symbol {jmath} + {\frac } {\flac } {\flac } {\leftx^{2} } = 2 bold symbold symbolmbol {hat}}$

x가 양수일 때 컬은 음의 z 방향을 가리키고 그 반대도 마찬가지입니다.이 필드에서 회전 강도는 물체가 평면 x = 0에서 멀어질수록 커진다.

설명 예

• 회전 원반의 각 부분의 선형 속도를 기술하는 벡터 필드에서 컬은 모든 점에서 동일한 값을 가진다.
• 맥스웰 방정식 4개 중에서 패러데이의 법칙과 암페르의 법칙 2개는 컬을 사용하여 콤팩트하게 표현될 수 있다.패러데이의 법칙은 전기장의 컬이 자기장의 시간 변화 속도와 반대라고 말하는 반면, Ampér의 법칙은 자기장의 컬을 전기장의 전류와 변화 속도에 관련짓습니다.

아이덴티티

(데카르트 좌표뿐만 아니라) 일반적인 곡선 좌표에서, 벡터장 v와 F의 교차곱의 컬은 다음과 같이 보일 수 있다.

$\displaystyle \times \left(\mathbf {v\times F} \right)=\left(\mathbf \cdot F} +\mathbf {F\cdot \cdla } \mathbf {v} - {\big(\mathbot F} \right)$

벡터장 v와 θ 연산자를 교환하면 벡터장의 컬과 벡터장의 교차곱에 도달한다.

$\displaystyle \mathbf {v\times F} \left(\mathbf {v\cdot F} \right)\mathbf {v\cdot F} \left(\mathbf {v\cdot \times F} \right)\mathbf {\right} \mathbf} {\f},$

여기서 _Fθ는 Feynman 첨자 표기법이며, 벡터 필드 F에 의한 변동만을 고려한다(즉, 이 경우 v는 공간 내에서 일정하게 처리된다).

다른 예로는 벡터 필드의 컬이 있습니다.일반적인 좌표로 볼 수 있다.

$\displaystyle \times \left(\mathbf \times F)=\mathbf(\mathbf\cdot F)-\mathbf {F}$

그리고 이 항등식은 F의 벡터 라플라시안을 정의하며,² F는 F로 나타낸다.

스칼라 필드 θ의 그라데이션의 컬은 항상 제로 벡터 필드이다.

$\displaystyle \times (\displayla \varphi )=\displaybold 심볼 {0}}$

이는 컬의 정의와 2차 도함수의 대칭성의 반대칭성에서 비롯된다.

θ가 스칼라 값 함수이고 F가 벡터 필드일 경우

$\displaystyle \times (\varphi \mathbf {F})=\displayla \varphi \times \mathbf {F} +\varphi \times \mathbf {F}$

일반화

그라데이션, 컬 및 div의 벡터 미적분 연산은 여러 단계를 포함하는 미분 형식의 맥락에서 가장 쉽게 일반화됩니다.즉, 각각 0-형식, 1-형식, 2-형식의 도함수에 해당합니다.회전으로서의 컬의 기하학적 해석은 벡터에 의한 회전을 식별하기 위해 벡터에 의한 회전을 나타내는 한편, 무한소 회전의 특수 직교 리 $대수{\displaystyle \mathfrak{}}$ ${\displaystyle \mathfrak{s}}$o {\$displaystyle${\$mathfrak${so$\}\}\}($3)로 3차원의 바이벡터(2-벡터)를 식별하는 데 대응한다.1차원 공간(지속적으로 2차원 공간) $및{\displaystyle \mathfrak{}}$($디스플레이$ 스타일 ${mathfrak {so$3)입니다.

미분 형식

3차원에서 미분 0-형식은 단순히 함수 f(x, y, z)이고 미분 1-형식은 다음과 같은 식입니다. 여기서 계수는 함수입니다.

${\displaystyle a_{1}, display+a_{2}, dy+a_{3}, dz;}$

미분 2-양식은 함수 계수를 갖는 공식 합입니다.

$({displaystyle a_{12}, display dy+a_{13}, display dz+a_{23}, dy\display dz;}$

미분 3-형태는 하나의 함수를 계수로 하는 단일 항에 의해 정의된다.

$displaystyle a_{123}, display dy.}$

(여기서 a-계수는 3가지 변수의 실함수입니다. 예를 들어 dx ) dy 등 "dx ) dy"는 일종의 지향성 영역 요소인 dx ) dy = -dy dx dx 등으로 해석할 수 있습니다.)

R에서³ k-양식의 외부 파생물은 위에서 (k + 1)-양식으로 정의되며, 예를 들어 다음과 같은 경우 R에서ⁿ 정의된다.

$\displaystyle \oscriptstyle {i_{1} <\cdots <i_{k}} \forall \scriptstyle {i_{nu} \in 1,\ldots,\ldots,i_k} =\sum _ i_{1} \sum \cdotsuall \cdots {i_{k} \cdots {i}$

그 후 외부 도함수 d는 로 이어진다.

${\displaystyle d\opha ^{(k)}=\sum _{\scriptstyle {j=1} \sum \scriptstyle {i_{k}}{n}{\frac {{i_{1},\ldots,i_{k}}}{\frac {\frac x_{{j}},\criptstyl}{i}}}{i}{i}}{i}}}}{i}}{i}}}}}{\sum {\criptsum {i}}}$

따라서 1-폼의 외부 파생상품은 2-폼이고 2-폼은 3-폼이다.한편, 혼합 파생상품의 교환 가능성 때문에, 예를 들어 다음과 같은 이유로

${\displaystyle {\frac ^{2}}{\frac x,\frac y}=frac {\frac y,\frac x}}$

외부 파생 제품을 이중으로 적용하면 0이 됩니다.

따라서, k-형식의 공간을^k δ³(R)로, 외부 도함수를 d로 나타내면 시퀀스를 얻을 수 있다.

${\displaystyle 0,{\longrightarrow}}\;\Omega ^{0}\left(\mathbb {R}^{3}\right),{\overset {d}{\longrightarrow}}\;\;\Omega ^{1}\left(\longright(\mathbbbbb {R}\right}\right}) {d}\light}\right}\light}, {d}\light}\light},w}, 0.}$

여기서 δ^k(Rⁿ)는 R 위의ⁿ 외부 대수 δ^k(Rⁿ) 벡터 다발의 단면의 공간이며, 그 차원은 이항 계수()ⁿ
_k이다. k > 3 또는 k < 0에 대해^k δ³(R) = 0이라는 점에 유의한다. 차원만을 쓰면 파스칼 삼각형의 열을 얻는다:

0 → 1 → 3 → 3 → 1 → 0;

1차원 파이버는 스칼라 필드에 대응하고 3차원 파이버는 벡터 필드에 대응합니다.모듈로 적절한 식별, 외부 도함수의 세 가지 중요하지 않은 발생은 그라데이션, 컬 및 div에 해당합니다.

미분 형식과 미분 형식은 리만 메트릭의 개념 없이 모든 유클리드 공간, 또는 실제로 모든 다양체에 정의될 수 있습니다.리만 다양체 또는 보다 일반적으로 의사 리만 다양체에서 k-형식은 k-벡터 필드(k-형식은 k-벡터 필드, 의사 리만 메트릭은 벡터와 코벡터 사이의 등형성을 제공함)와 비이형 형태(벡터와 코벡터 사이의 동형성)를 가진 배향 벡터 공간에서 식별될 수 있다.k-벡터와 (n - k)-벡터 사이의 동형사상, 특히 지향성 의사-리만 다양체의 (접선 공간)에서.따라서 지향성 의사 리만 다양체에서 k-형식, k-벡터장, (n - k)-형식 및 (n - k)-벡터장을 교환할 수 있다. 이를 호지 이중성이라고 한다.구체적으로는 R에 대해³ 다음과 같이 구한다.

• 1-형식 및 1-형식 필드: 1-형식_x a dx + a_y dy_z + dz는 벡터 필드(a_x, a_y, a_z)에 해당합니다.
• 1형식 및 2형식: dx를 이중량 dy z dz(즉, dx 생략)로 대체하고, 마찬가지로 방향을 고려하여 dy는 dz ∧ dx = -dx ∧ dz에 대응하며, dz는 dx ∧ dy에 대응합니다.따라서_x dx + a_y dy + az_z 형식은 "이중 형식" a_z dx_y dy dy + dz a_x dx + a dy d dz에 해당합니다.

따라서 스칼라 필드가 있는 0 형식과 3 형식, 벡터 필드가 있는 1 형식과 2 형식을 식별합니다.

• 그라드는 스칼라 필드(0-형식)를 벡터 필드(1-형식)로 가져간다.
• 컬은 벡터 필드(1-폼)를 의사 벡터 필드(2-폼)로 변환한다.
• div는 의사벡터 필드(2-폼)를 의사벡터 필드(3-폼)로 가져옵니다.

한편, d = 0이라는 사실은² 동일성에 해당한다.

$\displaystyle \times (\displayla f)=0}$

모든 스칼라 필드 f에 대해

$\displaystyle \cdot (\displayla \times \mathbf {v})=0}$

모든 벡터 필드 v에 대해.

각 점에서의 0-형식과 n-형식의 공간은 항상 1차원이고 스칼라 필드로 식별될 수 있는 반면, 1-형식과 (n - 1)-형식의 공간은 항상 섬유적으로 n차원이고 벡터 fie로 식별될 수 있기 때문에, 동일한 기하학적 해석으로 모든 지향성 의사 리만 다양체에 일반화된다.lds.

컬은 이러한 방식으로 4차원 이상(또는 2차원 이하)으로 일반화되지 않습니다. 4차원에서 치수는 다음과 같습니다.

0 → 1 → 4 → 6 → 4 → 1 → 0;

그래서 1차원 필드의 컬은 각 점에서 6차원 벡터 공간에 속하는 2차원 필드입니다. 그래서 한 사람은

${\displaystyle \obega ^{(2)}=\sum _{i=1,2,3,4}a_{i,k},sub_{i}\displaydx_{k}}$

이 값은 6개의 독립된 항의 합계를 나타내며, 1자리 필드에서는 식별할 수 없습니다.또한 미분 값을 두 번 구하면 0(d² = 0)이 되기 때문에 1-소수자 필드에서 2-소수자 필드로 의미 있게 이동할 수 없습니다(4 → 6 → 4).따라서 이러한 방식으로 발생하는 다른 차원의 벡터 필드에서 벡터 필드까지 컬 함수는 없습니다.

그러나 벡터 필드의 컬은 일반적으로 다음과 같이 2-벡터 필드로 정의할 수 있습니다.

기하학적으로 구부러지다

2-벡터는 외부 검정력 δV에² 해당하며, 내부곱이 존재할 경우 좌표상 스큐-대칭 행렬은 기하학적으로 무한소 회전의 특수 직교 $리{\displaystyle \mathfrak{}}$ 대수 s$$ {\$displaystyle {\mathfrak {so$V)로 간주됩니다.이(n2)).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px soli다.D}.mw-parser-output .sr-onlyᆪ1(n− 1)치수고 또 하나는 아주 작은 회전으로1-vector 필드의 미분을 해석할 수 있다.3차원(0차원)에서만 n = 1/2n(n - 1)이 됩니다. 이는 가장 우아하고 일반적인 경우입니다.2차원에서 벡터장의 컬은 벡터장이 아니라 함수입니다. 2차원 회전은 각도(스칼라 - 시계방향 또는 시계반대방향 회전 중 하나를 정의로 카운트하기 위해 방향이 필요함)에 의해 주어지기 때문입니다.이것은 나눗셈이 아니라 오히려 수직입니다.3차원에서는 벡터 필드의 컬이 익숙한 벡터 필드인 반면(1 및 0차원에서는 벡터 필드의 컬이 0이다. 왜냐하면 비사소한 2-벡터가 없기 때문이다) 4차원에서는 벡터 필드의 컬이 기하학적으로 6차원 리 $대수{\displaystyle \mathfrak{}}$ ${\displaystyle \mathfrak{s}}$o (4$)의$각 점에서 벡터 필드의 $요소$이다.${so}}(4$

2개의 좌표(예를 들어 x와 y)에만 의존하는 3차원 벡터 필드의 컬은 이 페이지의 예시와 같이 2차원 벡터 필드의 컬인 수직 벡터 필드(z 방향)입니다.

컬을 2-벡터 필드(반대칭 2-텐서)로 간주하여 벡터 미적분과 관련 물리학을 더 높은 ^[10]차원으로 일반화했습니다.

역

벡터장 V의 발산량이 0인 경우에는 V=컬(W)^{[citation needed]}이 되도록 벡터장 W가 존재한다.이것이 바로 제로 발산이 특징인 자기장이 자기 벡터 전위의 컬로 표현될 수 있는 이유입니다.

만약 W가 컬(W) = V인 벡터장이라면, W에 경사 벡터장 그라데이션(f)을 더하면 컬(W + 그라데이션(f)) = V와 같은 또 다른 벡터장 W + 그라데이션(f)이 된다.이것은 3차원 벡터장의 역컬을 비오트-사바트의 법칙으로 알려지지 않은 비회전장까지 얻을 수 있다고 말하는 것으로 요약할 수 있다.

「 」를 참조해 주세요.

• 헬름홀츠 분해
• 원통 및 구면 좌표의 Del
• 소용돌이

레퍼런스

추가 정보

• Korn, Granino Arthur and Theresa M. Korn (January 2000). Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York: Dover Publications. pp. 157–160. ISBN 0-486-41147-8.
• Schey, H. M. (1997). Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. New York: Norton. ISBN 0-393-96997-5.

외부 링크

• "Curl", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Multivariable calculus". mathinsight.org. Retrieved February 12, 2022.
• "Divergence and Curl: The Language of Maxwell's Equations, Fluid Flow, and More". June 21, 2018. Archived from the original on 2021-11-24 – via YouTube.