명제 미적분학

명제 미적분학은^[a] 논리학의 한 분야입니다.^[1] 명제 논리,^[2] 진술 논리,^[1] 문장 논리, 문장 미적분학,^[3] 문장 논리 ^[1]또는 때로는 0차 논리라고도 합니다.^[4][5] 명제^[1](참일 수도 거짓일 수도 있는)^[6]와 이를 기반으로 한 논증 구성을 ^[7]포함한 명제 간의 관계를 다룹니다.^[8] 복합 명제는 결합, 분리, 암시, 등가 및 부정의 진리 함수를 나타내는 논리적 연결에 의해 명제를 연결함으로써 형성됩니다.^{[9][10][11][12]} 일부 소스에는 아래 표와 같이 다른 연결 장치가 포함됩니다.

명제 논리는 1차 논리와 달리 논리적이지 않은 대상, 그 대상에 대한 술어, 수량자를 다루지 않습니다. 그러나 명제 논리의 모든 기계는 1차 논리와 고차 논리에 포함됩니다. 이런 의미에서 명제 논리는 1차 논리와 고차 논리의 토대입니다.

명제 논리는 일반적으로 명제가 문자로 표현되는 형식적인 언어로 연구되며, 이를 명제 변수라고 합니다. 그런 다음 연결 기호와 함께 복합 명제를 만드는 데 사용됩니다. 이 때문에 명제 변수를 형식적인 0차 언어의 원자 공식이라고 합니다.^[10][2] 원자 명제는 일반적으로 알파벳 문자로 표시되지만 ^[10]논리적 연결을 나타내는 다양한 표기법이 있습니다. 다음 표는 명제 논리의 각 연결에 대한 주요 표기법 변형을 보여줍니다.

커넥터의^[13][14] 표기법 변형

커넥티브	기호.
그리고.	${\displaystyle A\land B}$, ${\displaystyle A\cdot B}$, ${\displaystyle AB}$, ${\displaystyle A\&B}$, ${\displaystyle A\&\&B}$
동치의	$A ≡$ B ${\display style$ A$\backslash$$}$${\displaystyle ,}$ A ⇔ $B${\$display$ style A$left$$arrow$ B}${\displaystyle ,}$ A ⇋ B {\display$style$ A\left harrowps B}
암시하는	$A ⇒$ B ${\displaystyle$ A$\$$}$${\displaystyle ,}$ $A$⊃ $B${\$displaystyle$ A\supset $}$${\displaystyle ,}$ A → $B${\$displaystyle$ A\rightarrow B}
낸드	${\displaystyle A}$∧ ¯ B {\display$style$ A ${\overline$${\displaystyle \}\}}$${\displaystyle ,}$ $A$$∣$ B ${\$$displaystyle{\displaystyle \stackrel{}{}}$A\${\displaystyle \stackrel{}{\mathrm{mid}}}$B}${\displaystyle ,}$ $A$${\displaystyle \cdot }$$$B ¯ {\$displaystyle$ {\cdot B}}
비당량의	$A ≢$$ot$$\equiv$ B$},$A $⇎$$B$ {\$displaystyle$ A\n$ot$\오른쪽 $화살표 B},$$A$ $↮$ $B$ {\$display style$ A\n$왼쪽 오른쪽 화살표 B}$
도 아니다	${\displaystyle }$∨ ¯$$$B$ {\$display style$ A${\overline {\lor$ $A$ $↓$ ${\displaystyle B}$ {\$displaystyle$ A$\downarrow$$B{\displaystyle \stackrel{}{\},}}$ ${\displaystyle \stackrel{}{A}}$${\displaystyle +}$ B$¯ {\displaystyle {\overline {$A+B}}
것은 아니다.	${\display$${\displaystyle 예}$ $A$$$- A ${\displaystyle -A$ $A$$¯$ {\$displaystyle {\overline$$$$\{$$},$ ~ A${\displaystyle$\sim A}
OR	$A ∨$ B ${\displaystyle$A$\backslash$$},$ A + B${\displaystyle$A$}$${\displaystyle ,}$ $A$$∣$ $B$$displaystyle$ $\mid$ B}${\displaystyle ,}$ $A$∥ B {\$displaystyle$ A\parallel B}
XNOR	${\displaystyle A}$ ${\displaystyle$ A$}$ XNOR$$ $B{\displaystyle }$ ${\displaystyle$ B$}$
XOR	${\displaystyle A}$ $∨$ _ B {\$displaystyle A{\$$lor$$$$}$${\displaystyle ,}$ A ⊕ $B {\displaystyle$ A\oplus B}

역사

명제 논리(명제적 미적분학과 상호 교환 가능)는 초기 철학자들에 의해 암시되었지만, 기원전^[15] 3세기에 크리시푸스에 의해 형식적 논리(스토이적 논리)로 발전되었고, 그의 후계자인 스토이학에 의해 확장되었습니다. 논리는 명제에 초점이 맞춰졌습니다. 이것은 용어에 초점을 맞춘 전통적인 삼단논법 논리와는 달랐습니다. 그러나 대부분의 원래 글은 소실되었고^[16], 서기 3세기와 6세기 사이 어느 시점에서 스토아학파의 논리는 망각으로 사라졌고, 명제 논리의 (재)발견을 계기로 20세기에 와서야 부활했습니다.^[17]

명제 논리를 다듬는 데 중요하게 사용될 기호 논리는 17세기/18세기 수학자 고트프리트 라이프니츠에 의해 처음 개발되었지만, 그의 미적분 비율 계산기는 더 큰 논리학계에 알려지지 않았습니다. 따라서 라이프니츠가 이룬 많은 발전은 라이프니츠와 완전히 독립한 조지 부울과 아우구스투스 드 모르간과 같은 논리학자들에 의해 재현되었습니다.^[18]

고틀롭 프레게의 술어 논리는 명제 논리를 기반으로 하며, "삼단논법 논리와 명제 논리의 독특한 특징"을 결합한 것으로 묘사되었습니다.^[19] 그 결과 술어 논리학은 논리학의 역사에 새로운 시대를 열었지만 프레게 이후에도 자연적 추론, 진리나무, 진리표 등 명제 논리학의 발전은 계속되었습니다. 자연적 추론은 게르하르트 겐첸과 스타니스와프 자 ś코프스키에 의해 발명되었습니다. 진실의 나무는 에버트 윌렘 베스에 의해 발명되었습니다.^[20] 그러나 진실표의 발명은 불확실한 속성을 가지고 있습니다.

프레지와^[21] 버트런드 러셀의 작품 ^[22]속에는 진리표의 발명에 영향을 미치는 아이디어들이 있습니다. 실제 표 형식의 구조(표 형식화)는 일반적으로 루트비히 비트겐슈타인 또는 에밀 포스트(또는 둘 다 독립적으로)에 기인합니다.^[21] 프레지와 러셀 외에도 필로, 부울, 찰스 샌더스 피어스,^[23] 에른스트 슈뢰더 등이 진실표에 선행하는 아이디어를 가지고 있는 것으로 알려져 있습니다. 표 구조로 인정받은 다른 사람들로는 얀 우카시에비치, 알프레드 노스 화이트헤드, 윌리엄 스탠리 제본스, 존 벤, 클래런스 어빙 루이스가 있습니다.^[22] 궁극적으로, 존 쇼스키처럼 "어떤 사람에게도 진실표의 '발명가'라는 칭호가 주어져야 한다는 것은 분명하지 않습니다."라고 결론을 내린 사람들도 있습니다.^[22]

특성.

명제 논리는 현재 대학에서 연구되고 있는 것처럼 문장의 진리 조건을 평가할 때 명제적 연결어의 의미만을 고려한 논리적 결과의 표준을 명시한 것입니다. 또는 문장이 다른 문장이나 문장 그룹에서 논리적으로 따라오는지 여부.^[2]

간단한 문장

명제 논리는 진리값을 갖는 선언문으로 정의되는 진술을 다룹니다.^[24][25] 다음과 같은 문장의 예를 들 수 있습니다.

• 위키피디아는 누구나 편집할 수 있는 무료 온라인 백과사전입니다.
• 런던은 영국의 수도입니다.
• 모든 위키백과 편집자들은 최소 3개 국어를 구사합니다.

선언문은 "위키피디아란 무엇인가?"와 같은 질문과 "이 글의 주장을 뒷받침할 인용문을 추가해 주세요."와 같은 명령문과 대조됩니다.^[26][27] 그러한 선언적이지 않은 문장은 진리값이 없으며,^[28] 난해하고 명령적인 논리라고 불리는 비고전적인 논리에서만 다루어집니다.

복합문

때로는 문장에 하나 이상의 다른 문장이 부분으로 포함될 수 있습니다.^[1] 복합문은 보다 단순한 문장으로 형성되며 구성문간의 관계를 표현합니다.^[29] 복합문의 주요 유형은 부정, 접속사, 접속사, 접속사, 시사점, 쌍조건이며,^[29] 이것들은 명제를 대응하는 논리 접속사와 결합하여 형성됩니다.^[30][31] 영어에서 이러한 연결은 "and"(접합), "or"(접합), "not"(부정) 및 "if"(물질적 조건), "if and only if"(이중 조건)라는 단어로 표현됩니다.^[1][9]

명제 논리의 범위 내에서 추론한 예는 다음과 같습니다.

전제 1: 비가 오면 흐립니다.

전제 2: 비가 오고 있습니다.

결론: 날이 흐리네요.

전제와 결론 모두 명제입니다. 전제는 당연한 것으로 간주되며, 모드포넨스(추론 규칙)를 적용하면 ^[32]결론은 다음과 같습니다.

명제변수

명제 논리는 더 이상 논리적 연결에 의해 분해될 수 없는 지점을 넘어 명제의 구조와 관련이 없기 때문에,^[1] 일반적으로 그러한 원자(분할 수 없는) 진술을 진술(명제 변수)을 나타내는 변수로 해석되는 알파벳의 문자로 대체하여 연구됩니다.^[1] 명제 변수를 사용하면 위의 주장은 다음과 같이 기호화됩니다.

전제 1: ${\displaystyle P\to Q}$

전제 2: ${\displaystyle P}$

결론: ${\displaystyle Q}$

P를 "비가 온다"로, Q를 "흐리다"로 해석하면 이러한 상징적 표현은 자연어의 원래 표현과 정확히 일치합니다. 뿐만 아니라, 그들은 동일한 논리적 형태를 가진 다른 추론과도 일치할 것입니다.

젠젠 표기법

모두스포넨스의 유효성이 공리로 받아들여졌다고 가정하면, 같은 주장을 다음과 같이 나타낼 수도 있습니다.

${\displaystyle {\frac {P\to Q,P}{Q}}$

이를 표시하는 방법은 자연 연역과 후행 미적분에 대한 젠젠의 표기법입니다.^[33] 전제는 쉼표로 구분하여 추론 행이라고 하는 선 위에 표시되며,^[11] 이는 전제의 조합을 나타냅니다.^[34] 결론은 추론 라인 아래에 작성됩니다.^[11] 추론 줄은 구문적 결과를 나타내며, 때로는 연역적 결과라고 하며, 이는 ⊢로 상징되기도 합니다. 따라서 위의 내용을 $P$ → ${\displaystyle Q,}$ $P$⊢ Q ${\displaystyle$P\$to$ Q,$P$vdash Q}로 한 줄로 쓸 수도 있습니다.

통사적 결과는 ⊨으로 상징되는 의미론적 결과와 대비됩니다. 이 경우 모듈포넨스의 자연 추론 규칙을 가정했기 때문에 구문론적으로 결론이 뒤따릅니다. 추론 규칙에 대한 자세한 내용은 아래 증명 시스템 섹션을 참조하십시오.

형식화

명제 논리는 공식 언어의 공식이 명제를 나타내기 위해 해석될 수 있는 공식 시스템을 통해 연구될 수 있습니다. 증명 시스템을 사용하면 특정 공식을 도출할 수 있습니다. 이렇게 도출된 공식을 정리라고 하며, 참 명제라고 해석할 수도 있습니다. 이러한 공식의 구성된 수열을 유도 또는 증명이라고 하며 수열의 마지막 공식이 정리입니다. 유도는 정리로 표현되는 명제의 증명으로 해석될 수 있습니다.

형식 논리를 나타내기 위해 형식 시스템을 사용하는 경우 문 문자(일반적으로 $P{\displaystyle }$ ${\displaystyle$ $P$$\},$ Q ${\displaystyle$ Q$}$ $및$ R ${\displaystyle R}$과 같은 대문자$)$만 직접 표시됩니다. 해석할 때 발생하는 자연어 명제는 체계의 범위 밖에 있고, 형식 체계와 그 해석의 관계 역시 형식 체계 자체의 범위 밖에 있습니다.

명제 논리의 가장 철저하게 연구된 분야는 고전적 진리-함수 명제 논리이며,^[1] 공식은 정확히 두 가지 가능한 진리 값, 즉 참의 진리 값 또는 거짓의 진리 값 중 하나를 갖는 것으로 해석됩니다.^[38] 쌍가성의 원칙과 배제중간의 법칙이 지켜집니다. 진리함수 명제 논리는 1차 논리와 비교하여 0차 논리로 간주됩니다.^[4][5]

언어

에 관한 시리즈의 일부
형식 언어
주요 개념 알파벳 구문 의미론 (컴퓨터 과학) 의미론(논리) 형식문법 오토마타 이론 지면표현식 정규식 잘 형성된 공식 잘 정의된 표현
적용들 형식적 방법 명제 미적분학 술어 논리 수학적 표기법 자연어 처리 프로그래밍 언어 이론 전산언어학 구문분석 형식검증
v t

명제 미적분학의 언어($일반적$으로 L ${\$이라고 함$)$^[39][40]는 다음과 같이 정의됩니다.^[2][10]

1. 원자 공식, 자리 표시자, 명제 문자, 원자,^[41] 소수 공식 ^[41]또는 변수라고 불리는 원시 기호의 집합.
2. 논리 연산자 또는 논리적 연결 또는 명제적 연결이라고 하는 연산자 기호의 집합.

잘 형성된 공식은 모든 원자 공식, 또는 문법의 규칙에 따라 연산자 기호를 사용하여 원자 공식으로부터 구축할 수 있는 모든 공식입니다. 언어 $L{\displaystyle \mathcal{}}$ ${\$은$($는) 잘 형성된 공식 집합으로 정의됩니다.

수식의 구성

More specifically, given a set of atomic propositional variables ${\displaystyle p_{1}}$, ${\displaystyle p_{2}}$, ${\displaystyle p_{3}}$, ..., and a set of propositional connectives ${\displaystyle c_{1}^{1}}$, ${\displaystyle c_{2}^{1}}$, ${\displaystyle c_{3}^{1}}$, ..., ${\displaystyle c_{1}^{2}}$, ${\displaystyle c_{2}^{2}}$, ${\displaystyle c_{3}^{2}}$, ..., ${\displaystyle c_{1}^{3}}$, ${\displaystyle c_{2}^{3}}$, ${\displaystyle c_{3}^{3}}$, ..., 명제 논리의 공식은 재귀적으로 다음과 같은 정의에 의해 정의됩니다.^[2][10][42]

정의 1: 원자 명제 변수는 공식입니다.

정의 2: 만약 ${\displaystyle {}_{}^{}}$ ${\displaystyle c_{n}^{m}$가 명제 접속이고, ⟨ ${\displaystyle$\$langle$} A,$$B,$C$, … ⟩$${\$displaystyle$ \langle}은 m의 수열이며, 원자적일 수도 있지만 반드시 구별될 수는 없습니다. 그런 다음 ${\$$displaystyle$ $c_{n}^{m}$을(를) ⟨ ${\displaystyle$\$langle$} A,$$B,$C$, … ⟩${\displaystyle$ \rangle}에 적용한 결과가 공식입니다.

정의 3: 다른 것은 공식이 아닙니다.

${\displaystyle {}_{}^{}}$ ${\$$displaystyle$ $c_{n}^{m}$을(를) ⟨ ${\displaystyle$\$langle$} A,$$B,$C$, … ⟩${\displaystyle$ \langle}을(를$)$ $함수 표기법$으로 작성하여 잘 구성된 공식의 예로 다음을 사용합니다.

• ${\displaystyle p_{5}}$
• ${\displaystyle c_{3}^{2}(p_{2},p_{9})}$
• ${\displaystyle c_{3}^{2}(p_{1},c_{2}^{1}(p_{3}))}$
• ${\displaystyle c_{1}^{3}(p_{4},p_{6},c_{2}^{2}(p_{1},p_{2}))}$
• ${\displaystyle c_{4}^{2}(c_{1}^{1}(p_{7}),c_{3}^{1}(p_{8}))}$
• ${\displaystyle c_{2}^{3}(c_{1}^{2}(p_{3},p_{4}),c_{2}^{1}(p_{5}),c_{3}^{2}(p_{6},p_{7}))}$
• ${\displaystyle c_{3}^{1}(c_{1}^{3}(p_{2},p_{3},c_{2}^{2}(p_{4},p_{5})))}$

$L{\displaystyle \mathcal{}}$ ${\$ 언어의 모든 공식은 궁극적인 구성 요소로서 원자로부터 구축되기$$ 때문에 명제 변수에 대한 "원자"의 사용을 정당화하는 일종의 재귀적 정의입니다.^[2] 합성 공식(원자를 제외한 모든 공식)을 분자라고 합니다.^[41] (화학 분자는 단원자 기체처럼 원자 하나만 가지고 있는 경우도 있기 때문에 이것은 화학과 불완전한 비유입니다.)^[41]

상수 및 도식

수학자들은 명제 상수, 명제 변수, 도식을 구분하기도 합니다. 명제 상수는 일부 특정 명제를 나타내며,^[43] 명제 변수는 모든 원자 명제 집합에 걸쳐 있습니다.^[43] 그러나 도식 문자 또는 도식 문자는 모든 공식에 걸쳐 있습니다.^[44] 명제 상수는 A, B, C로, 명제 변수는 P, Q, R로 나타내는 것이 일반적이며, 도식 문자는 그리스 문자인 경우가 많으며, φ, ψ, χ가 가장 많습니다.

그러나 일부 저자는 공식 시스템에서 항상 True로 평가하는 $특수$ 기호 ⊤ ${\displaystyle$top}과 항상 False로 평가하는 특수 $기호$⊥$displaystyle$ \bot} 두 가지만 인식합니다.

의미론

명제적 연결 의미론

의미론적으로 고전 명제 논리에서 모든 명제는 정확히 두 개의 진리값 중 하나로 평가됩니다. 참 또는 거짓.^[1][48] 예를 들어, "위키피디아는 누구나 편집할 수 있는 무료 온라인 백과사전입니다"는 True,^[49] "위키피디아는 종이 백과사전입니다"는 False로 평가합니다.^[50]

논리적 연결
그리고. ${\displaystyle A\land B}$, ${\displaystyle A\cdot B}$, ${\displaystyle AB}$, ${\displaystyle A\&B}$, ${\displaystyle A\&\&B}$ 동치의 $A ≡$ B ${\display style A$$}$${\displaystyle ,}$ A ⇔ $B${\$display$ style A$left$$arrow$ B}${\displaystyle ,}$ A ⇋ B {\display$style$ A\left harrowps B} 암시하는 $A ⇒$ B ${\displaystyle$ A$\$$}$${\displaystyle ,}$ $A$⊃ $B${\$displaystyle$ A\supset $}$${\displaystyle ,}$ A → $B${\$displaystyle$ A\rightarrow B} 낸드 ${\displaystyle A}$∧ ¯ B {\display$style$ A ${\overline$${\displaystyle \}\}}$${\displaystyle ,}$ $A$$∣$ B ${\$$displaystyle{\displaystyle \stackrel{}{}}$A\${\displaystyle \stackrel{}{\mathrm{mid}}}$B}${\displaystyle ,}$ $A$${\displaystyle \cdot }$$$B ¯ {\$displaystyle$ {\cdot B}} 비당량의 $A ≢$$ot$$\equiv$ B$},$A $⇎$$B$ {\$displaystyle$ A\n$ot$\오른쪽 $화살표 B},$$A$ $↮$ $B$ {\$display style$ A\n$왼쪽 오른쪽 화살표 B}$ 도 아니다 ${\displaystyle }$∨ ¯$$$B$ {\$display style$ A${\overline {\lor$ $A$ $↓$ ${\displaystyle B}$ {\$displaystyle$ A$\downarrow$$B{\displaystyle \stackrel{}{\},}}$ ${\displaystyle \stackrel{}{A}}$${\displaystyle +}$ B$¯ {\displaystyle {\overline {$A+B}} 것은 아니다. ${\display$${\displaystyle 예}$ $A$$$- A ${\displaystyle -A$ $A$$¯$ {\$displaystyle {\overline$$$$\{$$},$ ~ A${\displaystyle$\sim A} OR $A ∨$ B ${\displaystyle$A$\backslash$$},$ A + B${\displaystyle$A$}$${\displaystyle ,}$ $A$$∣$ $B$$displaystyle$ $\mid$ B}${\displaystyle ,}$ $A$∥ B {\$displaystyle$ A\parallel B} XNOR ${\displaystyle A}$ ${\displaystyle$ A$}$ XNOR$$ $B{\displaystyle }$ ${\displaystyle$ B$}$ XOR ${\displaystyle A}$ $∨$ _ B {\$displaystyle A{\$$lor$$$$}$${\displaystyle ,}$ A ⊕ $B {\displaystyle$ A\oplus B} 말을 걸다 $A ⇐$ B ${\display style$ A$\backslash$$}$${\displaystyle ,}$ $A$⊂ $B${\$displaystyle$ A\subset $}$${\displaystyle ,}$ A ← $B${\$displaystyle$ A\leftarrow B}
관련개념
명제 미적분학 술어 논리 부울 대수 진리표 진리함수
적용들
디지털 로직 프로그래밍 언어 수학논리학 논리철학
카테고리
v t

그런 다음 논리적 연결은 두 가지 가능한 진리값 중 하나를 얻기 위해 적용되는 명제 변수를 취할 때 취하는 진리값의 관점에서 의미론적으로 정의됩니다.^[1] 이것은 일반적으로 아래에서 ^[1]볼 수 있듯이 각 연결에 대한 진리표로 표시됩니다.

p	q	p ∧ q	p ∨ q	p → q	p ⇔ q	¬p	¬q
T	T	T	T	T	T	F	F
T	F	F	T	F	F	F	T
F	T	F	T	T	F	T	F
F	F	F	F	T	T	T	T

이 표에서는 주요 다섯 가지 논리적 연결(연결음 p ∧ q), 분리(p ∨ q), 암시(p → q), 동등성(p ⇔ q) 및 부정(¬ p 또는 ¬ q)을 다룹니다. 이러한 연산자 각각의 의미론을 결정하는 데 충분합니다.^[1][51] 5개의 각 항목에 대한 자세한 내용은 각 항목에 대한 기사와 "논리적 연결" 및 "진실 기능" 항목을 참조하십시오. 더 다양한 종류의 연결에 대한 더 많은 진리표는 기사 "진실표"를 참조하십시오.

이러한 연결 중 일부는 다른 연결의 관점에서 정의될 수 있습니다. 예를 들어, 암시 p → q는 불일치와 부정의 관점에서 ¬ p ∨ q로 정의될 수 있습니다. 사실, 모든 고전적인 명제의 동형어들만이 정리라는 의미에서, 진리-함수적으로 완전한 체계는, (Russell, Whitehead, Hilbert가 그랬던 것처럼)^[2] 불연속과 부정만을 사용하거나 (Frege가 그랬던 것처럼)^[2] 암시와 부정만을 사용하거나 (또는) 결합과 부정만을 사용하거나 (^[2]Sheffer stroke)^[3][2] 장 니코드가 그랬던 것처럼 (not and) 단일 연결만을 사용하여 유도할 수 있습니다.^[2]

두 개 이상의 진리값을 가진 비고전적 논리가 존재하며, 이들의 의미론은 물론 다릅니다. 이에 대해 알아보려면 "다중값 논리", "삼중값 논리", "무한값 논리" 및 "무한값 논리" 항목을 참조하십시오.

기호의 해석

진리함수 명제 $미적분학{\displaystyle \mathcal{}}$ P ${\$에 대한 해석은 진리값 T와 거짓값 F 중 하나 또는 다른 $하나$의 P ${\$에 대한 각 명제 기호에 대한 할당입니다$$.^[53][54] $그리고{\displaystyle \mathcal{}}$ P ${\$의 연결 기호에 대한 일반적인 진리-함수적 의미를 할당합니다.^[55][56] 진리함수 명제 미적분학에 대한 해석은 진리표로 표현될 수도 있습니다.^[56]

$n개$의 ${\displaystyle$ n$}$개의$$ 고유한 명제 기호에 대해 ${\displaystyle {2개}^{}}$의 ${\$ 2$^{n}$개의 고유한$$ 해석이 있습니다. 예를 들어$,$ 특정 기호 $a$ ${\displaystyle$ a$}$에 대해 ${\displaystyle {21}^{}}$ = ${\displaystyle 2}$ ${\displaystyle 2^{1$}=$2}$의 가능한 해석이 있습니다. ${\displaystyle$ a$}$에는 T가 할당되거나 ${\displaystyle a}$에는 F가 할당됩니다. $그리고{\displaystyle }$ ${\display style$ a$}$ 쌍의 경우$,$ ${\displaystyle b}$ there are ${\displaystyle 2^{2}=4}$ possible interpretations: either both are assigned T, or both are assigned F, or ${\displaystyle a}$ is assigned T and ${\displaystyle b}$ is assigned F, or ${\displaystyle a}$ is assigned F and ${\displaystyle b}$ is assigned T.^[56] $P$ ${\displaystyle {\mathcal {P}}$은(는)$$ℵ 0 ${\displaystyle \alep$_${$0}}, 즉 명제 기호가 수 없이 많기 ${\displaystyle {{때문}_{}}^{}}$에$$ℵ$$0$$=$$c${\displaystyle$2^{\alep _{$0$=$\{\backslash$mathfrak {c}}, $따라서{\displaystyle \mathcal{}}$ P ${\$ 전체에$$ 대해 셀 수 없이 많은 가능한 해석이 가능합니다.^[56]

수식의 해석

φ 및 ψ가 P ${\displaystyle$ $\{\backslash$mathcal ${$}}의 $공식이고$ ${\displaystyle {\$mathcal {I}}이 P ${\displaystyle$ $\{\backslash$mathcal {P}}의 $해석$인 경우 다음 정의가 적용됩니다.

• 명제 논리의 문장은 ${\$이(가) 진리 값 T를 해당 문장에 할당하면$$$$ ${\$ {I$}}}$ $해석$에서 참입니다.^[54][56] 해석상 문장이 사실이라면 그 해석을 그 문장의 모델이라고 합니다.^[56]
• $I$$${\$displaystyle${\$mathcal$ {I}}에서$$φ가 $참$이 아니면 $I {\displaystyle$ {I}} 해석에서 φ가 거짓입니다.
• 명제 논리의 문장은 모든 해석에서 참이면 논리적으로 유효합니다.^[54][56]

  ${\displaysty$}${\displaystyle }\phi$은 φ이 논리적으로 유효하다는 것을 의미합니다.

• 명제 논리의 문장 ψ은 문장이 참이고 ψ이 거짓인 해석이 없는 경우 φ φ의 의미론적 결과입니다.
• 명제 논리의 문장은 적어도 하나의 해석 아래에서 사실이면 일관됩니다. 일관성이 없으면 일관성이 없습니다.^[54][56]

이러한 정의의 몇 가지 결과:

• 주어진 해석에 대해 주어진 공식은 참이거나 거짓입니다.^[56][57]
• 동일한 해석 하에서 참이면서 거짓인 공식은 없습니다.^[56][57]
• 지정된${\displaystyle \mathrm{해석}}$에 대해${\displaystyle$ \$n$φ가 거짓입니다.$eg \phi }$은(는) 해당 해석에 참이고,$$$φ$는${\displaystyle$ \n$\}$의 해석에 참입니다.$eg \phi }$는 해당 해석에 따라 거짓입니다$$.^[56][57]
• 주어진 해석 하에서$$φ 및 (ϕ →ψ)${\displaystyle$(\phi \to \psi)}이(가) 모두 참이면 해당 해석 하에서 ψ은 참입니다.
• ⊨$$$P$ϕ${\displaystyle \$models _${\$mathrm$${${\displaystyle P{\}\}\backslash }_{}}$phi }을(를) ⊨$하고$ P(ϕ →ψ$)$ {\$displaystyle$\models$$_${\$mathrm {P} }(\phi \$to$ \psi )을$($를) ⊨하면 P$$ψ {\displaystyle \models _{\mathrm {P}}\psi }을(를) .합니다.
• $ϕ {\displaystyle$$eg \phi }$은(는) $I$ ${\displaystyle {\mathcal$${I$$}}$에서 f $φ$가 $참$이 아니면 I {\mathcal $\{$I}}에서 참입니다.
• ${\displaystyle (\phi \to \psi )}$ is true under ${\displaystyle {\mathcal {I}}}$ iff either φ is not true under ${\displaystyle {\mathcal {I}}}$ or ψ is true under ${\displaystyle {\mathcal {I}}}$.^[56]
• A sentence ψ of propositional logic is a semantic consequence of a sentence φ iff ${\displaystyle (\phi \to \psi )}$ is logically valid, that is, ${\displaystyle \phi \models _{\mathrm {P} }\psi }$ iff ${\displaystyle \models _{\mathrm {P} }(\phi \to \psi )}$.^[56][57]

증명 시스템

명제 논리의 증명 시스템은 논리적 결과의 종류에 따라 의미 증명 시스템과 통사 증명 시스템으로 크게 분류될 수 있습니다: 의미 증명 시스템은 의미적 결과에 의존합니다(φ ⊨ ψ {\$displaystyle \varphi \models$\psi}), 구문 증명 시스템은 구문 결과에 의존합니다(φ ⊢ ψ {\$displaystyle \varphi \vdash$\psi }). 의미론적 결과는 모든 가능한 해석에서 명제의 진리 값을 다루는 반면, 통사론적 결과는 공식 시스템 내의 규칙과 공리에 기반한 전제에서 결론을 도출하는 것에 관한 것입니다.^[63]

의미 증명 시스템

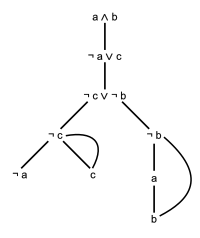
의미 증명 시스템은$$φ ⊨ ψ {\$displaystyle \varphi \models \$psi$$}로 상징되는 의미론적 결과의 개념에 의존하며, 이는$$φ ${\displaystyle$ $\$varphi }가$참$이면 가능한 모든 해석에서 ψ$${\displaystyle \psi }도 참이어야 함을 나타냅니다.

진리표

진리표는 가능한 모든 시나리오에서 명제 논리식의 진리값을 결정하는 데 사용되는 의미론적 증명 방법입니다.^[64] 진리표는 어떤 명제가 참인지, 거짓인지, 동형인지, 모순인지를 구성 원자들의 진리값을 철저히 나열함으로써 나타낼 수 있습니다.^[65]

시맨틱 테이블 aux

명제의 진실을 체계적으로 탐구하는 또 다른 의미론적 증명 기법은 시맨틱 테이블au입니다.^[66] 각 분기가 관련된 명제에 대한 가능한 해석을 나타내는 트리를 구성합니다.^[67] 모든 가지가 모순에 이르게 되면 원래의 명제는 모순으로 간주되고, 그 부정은 동음이의어로 간주됩니다.^[68]

통사 증명 체계

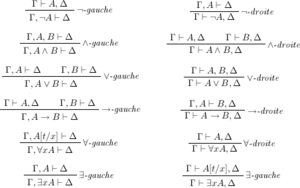
이와 대조적으로 구문 증명 시스템은 특정 규칙에 따라 기호를 형식적으로 조작하는 데 중점을 둡니다. 구문 결과의 개념인$$φ ⊢ ψ {\$displaystyle \varphi \vdash$\psi$\}$는 형식 시스템의 규칙을 사용하여$$φ${\$$displaystyle$ \varphi}에서$파생$될 수 $있음$을 의미합니다.

공리계

공리계는 다른 진술(정리)이 논리적으로 도출되는 일련의 공리 또는 가정입니다.^[69] 명제 논리에서 공리 체계는 자명하게 참인 것으로 간주되는 명제의 기본 집합을 정의하며, 이러한 공리에 추론 규칙을 적용하여 정리를 증명합니다.^[70]

자연공제

자연적 추론은 일반적인 추론을 반영한 직관적인 규칙을 사용하여 전제로부터 결론을 도출하는 것을 강조하는 통사적 증명 방법입니다.^[71] 각 규칙은 특정 논리적 연결을 반영하며, 이를 도입하거나 제거하는 방법을 보여줍니다.^[71]

순차 미적분학

순차 미적분학은 논리적 추론을 수식의 시퀀스 또는 "시퀀트"로 나타내는 형식적 시스템입니다.^[72] 게르하르트 젠첸(Gerhard Gentzen)이 개발한 이 접근 방식은 논리적 추론의 구조적 속성에 초점을 맞추고 명제 논리 내에서 진술을 증명할 수 있는 강력한 프레임워크를 제공합니다.^[72][73]

자연공제

변환 규칙
명제 미적분학
추론 규칙
시사점 도입/제거(모두스포넨스) 이중조건 도입/제거 접속 도입/제거 분리 도입/제거 가정적 삼단 논법 건설적/파괴적 딜레마 흡수/모드 톨렌/모드 포넨도 톨렌 부정소개
교체 규정
연상성 교환성 유통성 이중부호 드 모건의 법칙 전치 중요한의미 수출 튜톨로지
술어 논리
추론 규칙
보편적 일반화/인스턴스화 실존적 일반화/인스턴스화

이 섹션은 어떤 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 섹션을 개선하는 데 도움을 주시기 바랍니다. 출처가 없는 자료에 이의를 제기하여 제거할 수 있습니다. (2024년 3월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

명제 미적분학에 대한 자연적 연역 증명 체계에서 논증은 명제의 목록으로 정의됩니다. 유효한 인수는 명제의 목록이며, 마지막 인수는 나머지 인수에서 뒤따르거나 그에 의해 암시됩니다. 다른 인수는 모두 유효하지 않습니다. 가장 단순하게 유효한 인수는 modusonens이며, 그 중 하나가 다음 명제 목록입니다.

${\displaystyle {\begin {array}{rl}1.&P\에서 Q\2.&P\\\hline \따라서 &Q\end{array}}$

이것은 세 가지 명제의 목록이며, 각 행은 명제이며, 마지막은 나머지에서 따릅니다. 앞의 두 줄을 전제라고 하고, 마지막 줄을 결론이라고 합니다. 집합 $({\displaystyle {P\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle ...,}$ P ${\displaystyle n_{}}$ ${\displaystyle(P_{1},$ $..., P_{$$n}}$의 모든 구성원이 참일$$ 때마다 C가 참이어야 하는 경우$,$ 임의의 명제 C는 임의의 명제 집합${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle ...,}$ $P_{$n$})$에서 나온다고 합니다. 위의 논법에서 임의의 P와 Q에 대하여 P → Q와 P가 참일 때마다 Q는 반드시 참입니다. P가 참일 때, 우리는 (진실표로부터) 경우 3과 4를 고려할 수 없습니다. P → Q가 참인 경우에는 사례 2를 고려할 수 없습니다. 이것은 Q도 참인 경우인 경우 1만 남습니다. 따라서 Q는 전제에 의해 암시됩니다.

이것은 도식적으로 일반화됩니다. 따라서, φ과 ψ이 어떠한 명제라도 될 수 있는 경우에는,

${\displaystyle {\begin {array}{rl}1.&\varphi \to \psi \\2.&\varphi \\hline \therefore &\psi \end{array}}$

다른 인수 양식은 편리하지만 반드시 필요한 것은 아닙니다. 완전한 공리들의 집합이 주어지면(이러한 집합 중 하나에 대해서는 아래 참조), 모더스포넨스는 명제 논리에서 다른 모든 논증 형식을 증명하기에 충분하므로, 이들은 도함수로 간주될 수 있습니다. 참고로 명제 논리를 1차 논리와 같은 다른 논리로 확장하는 것은 그렇지 않습니다. 1차 논리는 완전성을 얻기 위해 적어도 하나의 추론 규칙을 추가로 요구합니다.

형식 논리학에서 논증의 중요성은 확립된 진리로부터 새로운 진리를 얻을 수 있다는 것입니다. 위의 첫 번째 예에서 두 가지 전제를 감안할 때 Q의 진실은 아직 알 수 없거나 진술되지 않습니다. 논증이 이루어진 후에 Q가 추론됩니다. 이러한 방식으로 우리는 공제 시스템을 다른 명제 집합에서 추론할 수 있는 모든 명제의 집합으로 정의합니다. 예를 들어, 명제 $A$ =${\displaystyle }${ ${\displaystyle P}$ ∨${\displaystyle Q}$, ¬${\displaystyle }$Q ∧ ${\displaystyle R,}$(P ∨ Q ) →$R$} ${\displaystyle$ A =\{P\lor Q,\n$예$를 들어, Q$\land R,$ ($P\lor$ Q$)\to R$ A로부터 이어지는 모든 명제의 집합인 $γ$를 정의할 수 있습니다. 반복은 항상 가정되므로 ${\displaystyle P}$ ∨${\displaystyle Q}$, ¬${\displaystyle Q}$ ∧ R${\displaystyle ,}$ ($P$∨ Q ) → R ∈ γ {\displaystyle P\lor Q,\n$예$를 들어, $Q\land$ R, ($P\lor Q)\to$ R$\in \Gamma }$입니다$.$ 또한, 모듈러스 포넨 뿐만 아니라 마지막 원소인 A의 첫 번째 원소로부터, R은 결과이고, $따라서$ R$$$∈$$$$γ$${\displaystyle$R\in \Gamma }입니다. 우리는 충분히 완전한 공리를 포함하지 않았기 때문에, 하지만, 다른 것은 추론할 수 없습니다. $따라서$ 명제 논리에서 연구된 대부분의 추론 ${\displaystyle \mathrm{시스템}}$이$$(${\displaystyle P}$ ∨ Q) ↔ (¬ $P$→ Q)${\displaystyle$ (P\$lor$ Q$)\left$ arrow (\n)$예$를 들어 $P\to Q$ 이 명제는 너무 약해서 그러한 명제를 증명할 수 없습니다.

자연 공제 인수 양식의 표

이러한 추론 규칙은 자연 추론에 사용됩니다. 기본적인 것(다른 것에서 파생되지 않은 것)은 자연 공제 증명 시스템의 예에서 다시 제공됩니다. 이 절에서는 기호를 이해하지 못하는 독자를 위해 기호 공식 옆에 기호를 번역하여 표로 규칙을 제공합니다.

이름.	시퀀트[74]	묘사
모두스 포넨스	${\displaystyle((p\to q)\land p)\vdash q}$	만약 p이면 q; p; 따라서 q
모두스 톨렌스	${\displaystyle ((p\to q)\land \neg q)\vdash \negp}$	p이면 q; not q; 따라서 p가 아닙니다.
가설 삼단논법	${\displaystyle((p\to q)\land(q\tor)\vdash(p\tor)}$	p이면 q, q이면 r, 따라서 p이면 r
삼단논법	${\displaystyle((p\lor q)\land \neg p)\vdash q}$	p가 아닌 p 또는 q 또는 둘 다. 따라서 q
건설적 딜레마	${\displaystyle((p\to q)\land(r\to s)\land(p\lor r)\vdash(q\lor s)}$	p이면 q; 그리고 r이면 s; 그러나 p 또는 r이므로 q 또는 s
파괴적 딜레마	${\displaystyle ((p\to q)\land (r\to s)\land (\n)egq\lor \neg s))\vdash (\negp\lor\nerg)}$	p이면 q이고, r이면 q이고, 그렇지 않으면 q 또는 not이면 p 또는 not r입니다.
쌍방향 딜레마	${\displaystyle((p\to q)\land(r\to s)\land(p\lor\n)eg s))\vdash (q\lor \nerg)}$	p이면 q이고, r이면 s이고, p 아니면 s이고, 따라서 q 또는 not r입니다.
단순화	${\displaystyle(p\land q)\vdash p}$	p와 q는 참이므로 p는 참입니다.
접속사	${\displaystyle p,q\vdash(p\land q)}$	p와 q는 따로따로 참입니다. 따라서 그들은 합집합적으로 참입니다.
추가	${\displaystyle p\vdash (p\lor q)}$	p는 참이고, 따라서 불일치(p 또는 q)는 참입니다.
구성.	${\displaystyle ((p\to q)\land (p\to (q\land r))}$	p이면 q이고, p이면 r이고, 따라서 p가 참이면 q와 r이 참입니다.
드 모건의 정리 (1)	${\displaystyle \neg (p\land q)\dashv \vdash (\negp\lor\nq)}$	(p와 q)의 음수는 (p 또는 q가 아님)와 같습니다.
De Morgan의 정리 (2)	${\displaystyle \neg (p\lor q)\dashv \vdash (\negp\land \nq)}$	(p 또는 q)의 음수는 (p 및 q가 아님)와 같습니다.
감차(1)	${\displaystyle(p\lor q)\dash v \vdash(q\lor p)}$	(p 또는 q)는 (q 또는 p)와 같습니다.
감차 (2)	${\displaystyle(p\land q)\dash v \vdash(q\land p)}$	(p와 q)는 (q와 p)와 같습니다.
감차(3)	${\displaystyle(p\left right arrow q)\dash v \vdash(q\left right arrow p)}$	(p iff q) is equiv. to (q iff p)
협회 (1)	${\displaystyle (p\lor (q\lor r))\dash v \vdash ((p\lor q)\lor r)}$	p 또는 (q 또는 r)는 (p 또는 q) 또는 r과 같습니다.
협회 (2)	${\displaystyle(p\land(q\land r))\dash v \vdash((p\land q)\land r)}$	p와 (q와 r)은 (p와 q)와 r과 같습니다.
분포(1)	${\displaystyle(p\land(q\lor r))\dash v \vdash((p\land q)\lor(p\land r))}$	p 및 (q 또는 r)은 (p 및 q) 또는 (p 및 r)과 같습니다.
유통 (2)	${\displaystyle(p\lor(q\land r))\dash v \vdash(((p\lor q)\land(p\lor r))}$	p 또는 (q와 r)은 (p 또는 q)와 (p 또는 r)과 같습니다.
이중 네거티브	${\displaystyle p\dash v \vdash \neg \negp}$	p는 not p의 부정에 해당합니다.
전치	${\displaystyle (p\to q)\dash v \vdash (\n)eg q\n에서 \n까지egg)}$	p이면 q는 동등하고, 그렇지 않으면 q는 동등하지 않습니다.
중요한 의미	${\displaystyle (p\to q)\dash v \vdash (\n)egp\lorq)}$	p가 같으면 q는 p 또는 q가 아닌 것과 같습니다.
재료 등가성 (1)	${\displaystyle(p\left right arrow q)\dash v \vdash((p\to q)\land(q\top))}$	(piff q)는 다음과 같습니다. (p가 참이면 q가 참입니다.) 그리고 (q가 참이면 p가 참입니다.)
재료등가성 (2)	${\displaystyle (p\left right arrow q)\dash v \vdash ((p\land q)\lor (\n)egp\land \nq)}$	(piff q)는 (p와 q는 참) 또는 (p와 q는 모두 거짓)과 같습니다.
재료등가성(3)	${\displaystyle(p\left right arrow q)\dash v \vdash((p\lor \n)egq)\land(\negp\ 또는 q)}$	(piff q)는 (p 또는 q가 참이 아님) 및 (p 또는 q가 참이 아님) 둘 다와 같습니다.
수출[75]	${\displaystyle((p\land q)\tor)\vdash(p\to(q\tor))}$	에서 (p와 q가 참이면 r이 참이면 증명할 수 있습니다). (q가 참이면 r이 참이면 p가 참이면)
수입	${\displaystyle (p\to (q\tor)\dash v \vdash ((p\land q)\tor)}$	만약 p이면 (만약 q이면 r)은 if p와 q이면 r과 같음
자반증 (1)	${\displaystyle p\dash v \vdash (p\lor p)}$	p는 true이고 p는 true입니다. top는 true이고 p는 true입니다.
자반증 (2)	${\displaystyle p\dash v \vdash (p\land p)}$	p는 참이고 p는 참입니다. top는 참이고 p는 참입니다.
Tertium non datur (제외된 중간의 법칙)	${\displaystyle \vdash (p\lor \n)egg)}$	p가 참인지 아닌지
비모순의 법칙	${\displaystyle \vdash \neg (p\land \negg)}$	p와 p가 거짓이 아니고 참문입니다.

규칙의 건전성 및 완전성

이 규칙 세트의 중요한 특성은 건전하고 완전하다는 것입니다. 비공식적으로 이것은 규칙이 정확하고 다른 규칙이 필요하지 않다는 것을 의미합니다. 이러한 주장은 다음과 같이 좀 더 공식화할 수 있습니다. 명제 논리의 건전성과 완전성에 대한 증명은 명제 논리 자체의 증명이 아닙니다. 이는 명제 논리의 특성을 증명하기 위한 메타 이론으로 사용되는 ZFC의 정리입니다.

우리는 진리 할당을 명제 변수를 참 또는 거짓으로 매핑하는 함수로 정의합니다. 비공식적으로 그러한 진실 할당은 특정 진술이 사실이고 다른 진술이 사실이 아닌 가능한 상황(또는 가능한 세계)에 대한 설명으로 이해될 수 있습니다. 그런 다음 공식의 의미론은 다음 정의에 의해 수행되는 어떤 "정세"에 대해 참인 것으로 간주되는지 정의함으로써 공식화될 수 있습니다.

우리는 그러한 진리 할당 A가 다음과 같은 규칙으로 잘 형성된 특정 공식을 만족할 때를 정의합니다.

• A(P) = true인 경우에만 명제 변수 P를 만족합니다.
• A가 φ을 만족하지 않는 경우에만 A가 ¬φ을 만족합니다.
• A가 φ과 ψ을 모두 만족하는 경우에만 (φ ∧ ψ)를 만족합니다.
• A가 φ 또는 ψ 중 하나 이상을 만족하는 경우에만 (φ ∨ ψ)를 만족합니다.
• A가 φ을 만족하지만 ψ을 만족하지 않는 경우에만 A가 (φ → ψ)를 만족합니다.
• A가 φ과 ψ을 모두 만족하거나 둘 중 하나를 모두 만족하는 경우에만 (φ ↔ ψ)를 만족합니다.

이 정의를 통해 우리는 이제 공식 φ가 특정한 공식 집합 S에 의해 암시되는 것이 무엇을 의미하는지 공식화할 수 있습니다. 공식적으로 이것은 공식 S의 집합이 주어졌을 때 가능한 모든 세계에서 φ 공식도 성립하는 경우에 해당됩니다. 이는 다음과 같은 공식적인 정의로 이어집니다. 우리는 S의 모든 공식을 만족하는 모든 진리 할당이 φ을 만족한다면 잘 형성된 공식의 집합 S가 의미론적으로 어떤 잘 형성된 공식 φ을 수반(또는 암시)한다고 말합니다.

마지막으로 우리는 φ가 S에 의해 구문적으로 수반되도록 구문적 수반성을 정의합니다. 이는 위에 제시된 추론 규칙으로 도출할 수 있는 경우에만 가능합니다. 이를 통해 추론 규칙 집합이 건전하고 완전하다는 것이 무엇을 의미하는지 정확히 공식화할 수 있습니다.

건전성: 잘 형성된 공식 집합 S가 구문론적으로 잘 형성된 공식 φ를 수반하면 S는 의미론적으로 φ를 수반합니다.

완성도: 만약 잘 형성된 공식 집합 S가 의미론적으로 잘 형성된 공식 φ를 수반한다면, S는 구문론적으로 φ를 수반합니다.

위의 일련의 규칙에 대해서는 실제로 그렇습니다.

건전성 증명 스케치

(대부분의 논리적 시스템의 경우 비교적 "단순한" 증명 방향입니다.)

국가 규약: 문장 집합에 걸쳐 G를 변수로 설정합니다. A, B, C가 문장에 걸쳐 범위를 정하도록 합니다. "G는 구문론적으로 A를 수반한다"에 대해 "G는 A를 증명한다"고 적습니다. "G는 의미론적으로 A를 수반한다"에 대해 "G는 A를 내포한다"고 적습니다.

우리는 (A)(G)(G가 A를 증명한다면 G는 A를 의미합니다)를 보여주고 싶습니다.

우리는 "G가 A를 증명한다"는 귀납적 정의를 가지며, 이는 "G가 A를 증명한다면..."라는 형식의 주장을 증명할 수 있는 즉각적인 자료를 제공한다는 것에 주목합니다. 따라서 우리의 증명은 귀납적 방법으로 진행됩니다.

자연 공제 시스템의 경우 공리가 없기 때문에 Basis Step II를 생략할 수 있습니다. 사용될 때, 단계 II는 각각의 공리가 (의미론적) 논리적 진리라는 것을 보여주는 것을 포함합니다.

기초 단계는 G에서 가장 간단하게 증명할 수 있는 문장이 G에 의해서도 암시된다는 것을 보여줍니다. (집합이 그 구성원들 중 어느 하나를 암시한다는 의미론적 사실도 사소하기 때문에 증명은 간단합니다.) 귀납적 단계는 추론 규칙을 사용하여 논리적 결론에 도달할 수 있는 각 경우를 고려하여 증명 가능한 모든 추가 문장을 체계적으로 다루며, 새로운 문장이 증명 가능하다면 논리적으로도 암시된다는 것을 보여줍니다. (예를 들어, "A"에서 "A 또는 B"를 도출할 수 있다는 규칙이 있을 수 있습니다. III.a에서 우리는 A가 증명 가능하다면 그것은 암시된다고 가정합니다. 우리는 또한 A가 증명 가능하다면 "A 또는 B"가 증명 가능하다는 것을 알고 있습니다. 그러면 "A 또는 B"도 암시된다는 것을 보여주어야 합니다. 우리는 의미론적 정의와 방금 한 가정에 호소하여 그렇게 합니다. A는 G로부터 증명할 수 있다고 가정합니다. 따라서 G에 의해서도 암시됩니다. 따라서 G를 모두 참으로 만드는 의미론적 가치 평가는 A를 참으로 만듭니다. 그러나 A를 참으로 만드는 모든 가치 평가는 "또는"에 대한 정의된 의미론에 의해 "A 또는 B"를 참으로 만듭니다. 따라서 G를 모두 참으로 만드는 모든 가치 평가는 "A 또는 B"를 참으로 만듭니다. 따라서 "A 또는 B"는 암시됩니다.) 일반적으로 귀납적 단계는 모든 추론 규칙에 대한 장황하지만 간단한 사례별 분석으로 구성되어 각 추론 규칙이 의미론적 의미를 "보존"한다는 것을 보여줍니다.

증명 가능성의 정의에 따라 G의 구성원이거나 공리이거나 규칙을 따르는 것 외에는 증명할 수 있는 문장이 없으므로 그 모든 것이 의미론적으로 내포되어 있다면 추론 연산은 건전합니다.

완전성 증명 스케치

(이는 일반적으로 훨씬 더 어려운 증명 방향입니다.)

우리는 위와 동일한 표기 규칙을 채택합니다.

우리는 보여주고 싶습니다: 만약 G가 A를 암시한다면, G는 A를 증명합니다. 우리는 다음과 같이 대위법으로 진행합니다. 대신 G가 A를 증명하지 않으면 G가 A를 의미하지 않는다는 것을 보여줍니다. G가 참임에도 불구하고 A가 성립하지 않는 모형이 있다는 것을 보여준다면, 분명히 G는 A를 의미하지 않습니다. 이 아이디어는 G가 A를 증명하지 않는다는 우리의 가정에서 그러한 모델을 구축하는 것입니다.

따라서 추론 규칙으로 모듈러스를 가지며, 다음 정리(이 정리의 대체 포함)가 완전하다는 것을 증명하는 모든 시스템은 다음과 같습니다.

• ${\displaystyle p\to (\n)egp\toq)}$
• ${\displaystyle (p\to q)\to ((\n)eg p\to q)\to q)}$
• ${\displaystyle p\to (q\to (p\to q))}$
• ${\displaystyle p\to (\n)eg q\n에서 \n까지eg (p\to q)}$
• ${\displaystyle \neg p\to (p\to q)}$
• ${\displaystyle p\top}$
• ${\displaystyle p\to (q\top)}$
• ${\displaystyle (p\to (q\tor))\to (p\to q)\to (p\tor)}$

앞의 5개는 위의 3단계에서 5개 조건을 만족시키는 데 사용되고, 뒤의 3개는 연역 정리를 증명하는 데 사용됩니다.

예

예를 들어, 앞에서 설명한 고전적 명제 미적분학 체계의 세 가지 공리는 위를 만족하는, 즉 추론 규칙으로 모더스포넨스를 갖는 어떤 체계에서도 증명될 수 있으며, 위의 여덟 가지 정리(그 치환 포함)를 증명한다는 것을 알 수 있습니다. 8개의 정리 중 마지막 2개는 3개의 공리 중 2개이며, 세 번째 ${\displaystyle \mathrm{공리}}$인${\displaystyle (}$¬ ${\displaystyle q}$ → ¬ ${\displaystyle p}$) →${\displaystyle }$($p$→ q) {\$displaystyle$ (\n)$eg q\n에서 \n까지$$egg)\to(p\to q$ 또한 지금 보여주는 것처럼 증명할 수 있습니다.

증명을 위해 우리는 가상 삼단논법 정리(이 공리계와 관련된 형태)를 사용할 수 있습니다. 왜냐하면 그것은 위의 8개의 정리 집합에 이미 있는 두 개의 공리에만 의존하기 때문입니다. 그 증거는 다음과 같습니다.

1. ${\displaystyle q}$ ${\displaystyle \to }$(p${\displaystyle }$→ ${\displaystyle q}$)${\displaystyle q\$to ($p\to q)}$ (7번째 ${\displaystyle \mathrm{정리의\; inst}}$ance)
2. $q →$$eg q\n에서 \n까지$$egg)\to(q\to(p\to(q))}($7번째 정리의 $instance$)
3. $→$$eg q\n에서 \n까지$$egg)\to(q\to(p\to(q))}($모두소넨스에 의해 (1) 및 (2)부터)
4. $→$$eg p\to (p\to q))\to ((\n$$eg q\n에서 \n까지$$egg)\to(\n$$)$$egg q\to (p\to q))}$ (가정적 삼단논법 정리의 $instance$)
5. $→$$egp\to (p\to q)}$ (5번째 정리의 $instance$)
6. $→$$eg q\n에서 \n까지$$egg)\to(\n$$)$$egg q\to (p\to q)}($모두소넨스 기준으로 (5) 및 (4)부터)
7. $→$$egg q\to (p\to q)\to (p\to q)}$ (2차 정리의 $instance$)
8. ${\displaystyle ((q\to (p\to q))\to ((\n$$eg q\to (p\to q))\to (p\to q)))\to ((\n$$eg q\n에서 \n까지$$eg p)\to ((q\to (p\to q))\to ((\n$$egg q\to (p\to q)\to (p\to q)}$ (7번째 정리의 $instance$)
9. $→$$eg q\n에서 \n까지$$eg p)\to ((q\to (p\to q))\to ((\n$$egg q\to (p\to q)\to (p\to q)}($모두소넨스에 의해 (7) 및 (8)부터)
10. ${\displaystyle((\n))eg q\n에서 \n까지eg p)\to ((q\to (p\to q))\to ((\neg q\to (p\to q))\to (p\to q))))\to }$

    $p q))$$eg q\n에서 \n까지$$eg p)\to (q\to (p\to q)))\to ((\n$$eg q\n에서 \n까지$$egg)\to((\n$$)$$egg q\to (p\to q)\to (p\to q)}$ (8번째 정리의 $instance$)

11. ${\displaystyle ((\n$$eg q\n에서 \n까지$$eg p)\to (q\to (p\to q)))\to ((\n$$eg q\n에서 \n까지$$egg)\to((\n$$)$$egg q\to (p\to q)\to (p\to q)}($모두소넨스에 의해 (9) 및 (10)부터)
12. $q$$eg q\n에서 \n까지$$egg)\to((\n$$)$$egg q\to (p\to q)\to (p\to q)}$ $$(3) 및 (11)에서 모듈로 변환)
13. ${\displaystyle ((\n$$eg q\n에서 \n까지$$egg)\to((\n$$)$$eg q\to (p\to q))\to (p\to q)))\to (((\n$$eg q\n에서 \n까지$$egg)\to(\n$$)$$eg q\to (p\to q)))\to ((\n$$eg q\n에서 \n까지$$egg)\to(p\to q)}($제8정리의 $instance$)
14. ${\displaystyle ((\n$$eg q\n에서 \n까지$$egg)\to(\n$$)$$eg q\to (p\to q)))\to ((\n$$eg q\n에서 \n까지$$egg)\to(p\to q)}($모두소넨스에 의해 (12) 및 (13)부터)
15. $p$$eg q\n에서 \n까지$$egg)\to(p\to q)}($모두소넨스에 의해 (6) 및 (14)부터)

고전적 명제 미적분 체계에 대한 완전성 검증

우리는 이제 앞에서 설명한 고전적인 명제 미적분 체계가 위에서 언급한 필요한 8개의 정리를 실제로 증명할 수 있는지 확인합니다. 우리는 여기서 입증된 몇 가지 렘을 사용합니다.

(${\displaystyle \mathrm{DN1}}$)${\displaystyle \mathrm{}}$¬ ¬ ${\displaystyle p}$ → p {\$displaystyle$\n$eg \n$$egp\top}$ $$- 이중 네거티브(한 방향)

(DN2) ${\displaystyle p}$ →$$¬ ¬ p {\$displaystyle p$\to \n$eg \n$$egp}$ $$- 이중 네거티브(다른 방향)

(HS1)$$(${\displaystyle q}$ → ${\displaystyle r)}$ →${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q)}$ →${\displaystyle }$(${\displaystyle p}$ → r${\displaystyle (q\to$ r$)\to (p\to q)\to$ (p\to (p$\to q))}$ - 가상 삼단논법의 한 형태

(HS2)$$(${\displaystyle p}$ → ${\displaystyle q)}$ →${\displaystyle ((q}$ → ${\displaystyle r}$) →${\displaystyle }$(${\displaystyle p}$ → r${\displaystyle }$)${\displaystyle (p\to q)\to ((q\to$ q$)\to (p\to))}$ - 가정적 삼단논법의 또 다른 형태

(TR1)$$(${\displaystyle p}$ → ${\displaystyle q)}$ →${\displaystyle \mathrm{(}}$¬ $q$ → ¬ p$) {\displaystyle$ (p\to q)\to (\n)$eg q\n에서 \n까지$$eggp)}$ $$- 전치

(${\displaystyle \mathrm{TR2}}$)${\displaystyle (}$¬ ${\displaystyle p}$ → ${\displaystyle q}$) → (¬$q$ → p) {\$displaystyle$(\n$eg p\to q)\to (\n$$egg q\top)}$ $$- 다른 형태의 전치.

($L1$) p →${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$) → ${\displaystyle q}$) ${\displaystyle p\to ((p\to q)\to q)}$

(${\displaystyle \mathrm{L3}}$)${\displaystyle \mathrm{(}}$¬ ${\displaystyle p}$ → p ) → p${\displaystyle$ (\n$eg p\to p)\to p}$

우리는 또한 여러 증명 단계의 축약어로 가상 삼단논법 메타이론의 방법을 사용합니다.

• $→$$egp\to q)}$ $$- 증명:
  1. $→$$eg q\top)}(($A1)의 인스턴스)
  2. $→$$eg q\to p)\to (\n$$egp\n에서 \n까지$$eg \n$$egq)}(($TR1의 인스턴스)
  3. $($$egp\n에서 \n까지$$eg \n$$egq)}$ $$(가정적 삼단논법 메타이론을 이용한 (1), (2)부터)
  4. $q {\displaystyle$$eg \n$$egg q\to q}(($DN1)의 인스턴스)
  5. $q$$eg \n$$eg q\to q)\to ((\n$$egp\n에서 \n까지$$eg \n$$q)\to(\n$$)$$egp\to q)}(($HS1의 인스턴스)
  6. $($$egp\n에서 \n까지$$eg \n$$q)\to(\n$$)$$egp\to q)}($모두스포넨을 사용하여 (4) 및 (5)부터)
  7. $→$$egp\to q)}$ $$(가정적 삼단논법 메타 정리를 사용하여 (3)과 (6)에서)
• $→$$egp\to q)\to q)}$ $$- 증명:
  1. $→$$eg q\to p)\to (\n$$egg q\to q)}(($HS1)의 인스턴스)
  2. $→$$egg\to q)\to q}(($L3)의 인스턴스)
  3. $q →$$eg q\to q)\to q)\to (((\n$$eg q\to p)\to (\n$$eg q\to q))\to ((\n$$egg q\top)\to q)}(($HS1의 인스턴스)
  4. $→$$eg q\to p)\to (\n$$eg q\to q))\to ((\n$$egg q\top)\to q)}($모두소넨스 기준으로 (2) 및 (3)부터)
  5. $→$$egg q\top)\to q)}$ $$(가정적 삼단논법 메타 정리를 사용하여 (1)과 (4)부터)
  6. $q$$eg p\to q)\to (\n$$eg q\top)}(($TR2)의 인스턴스)
  7. $p → q$$eg p\to q)\to (\n$$eg q\to p))\to (((\n$$eg q\to p)\to q)\to ((\n$$egp\to q)\to q)}(($HS2)의 인스턴스)
  8. $q)$$eg q\to p)\to q)\to ((\n$$egp\to q)\to q)}($모두소넨을 사용하여 (6) 및 (7)부터)
  9. $→$$egp\to q)\to q)}($가정적 삼단논법 메타 정리를 사용하여 (5)와 (8)부터)
• ${\displaystyle p}$ ${\displaystyle \to }$(${\displaystyle q}$ ${\displaystyle \to (p}$ → ${\displaystyle q}$)${\displaystyle p\to (q\to (p\to q))}$ - 증명:
  1. ${\displaystyle q}$ ${\displaystyle \to }$(${\displaystyle p}$→ ${\displaystyle q}$)${\displaystyle q\to$ (p$\to q)}(($A${\displaystyle \mathrm{1)의\; inst}}$ance)
  2. ${\displaystyle (}$ ${\displaystyle q}$ ${\displaystyle \to }$(${\displaystyle p}$ ${\displaystyle \to }$ ${\displaystyle q}$)${\displaystyle }$→${\displaystyle }$(${\displaystyle p\to }$ ${\displaystyle (p}$ ${\displaystyle (q\to (p\to q))\to (p\to (p\to q))}$ ((${\displaystyle A1의\; inst}$ance)
  3. ${\displaystyle p}$ ${\displaystyle \to }$(${\displaystyle q}$ ${\displaystyle \to }$(${\displaystyle p}$ → ${\displaystyle p\to (q\to (p\to q))}($모두스포넨을 사용하여 (1) 및 (2)부터)
• $p$$eg q\n에서 \n까지$$eg (p\to q)}$ $$- 증명:
  1. ${\displaystyle p}$ ${\displaystyle \to }$(${\displaystyle (p}$ ${\displaystyle \to }$ ${\displaystyle q}$) → ${\displaystyle q)}$ ${\displaystyle$ p$\to ((p\to q)\to q)}$ ((L${\displaystyle \mathrm{1)의\; inst}}$ance)
  2. $→$$eg q\n에서 \n까지$$eg (p\to q)}(($TR1)의 인스턴스)
  3. $p$$eg q\n에서 \n까지$$eg (p\to q)}$ $$(가정적 삼단논법 메타 정리를 사용하여 (1)과 (2)에서)
• ${\displaystyle \n$$egp\to (p\to q)}$ $$- 증명:
  1. $p$$egp\to(\n$$)$$eg q\n에서 \n까지$$egg)}(($A1의 인스턴스)
  2. $p$$eg q\n에서 \n까지$$egg)\to(p\to q)}(($A3)의 인스턴스)
  3. ${\displaystyle \n$$egp\to (p\to q)}$ $$(가정적 삼단논법 메타 정리를 사용하여 (1)과 (2)에서)
• ${\displaystyle p}$ ${\displaystyle \to }$ ${\displaystyle p}$ ${\displaystyle p\top}$ - 위의 증명 예제에서 제공된 증명
• ${\displaystyle p}$ ${\displaystyle \to }$(${\displaystyle q}$ → ${\displaystyle p)}$ ${\displaystyle$ p$\to (q\top))}$ - axiom (A1)
• ${\displaystyle (}$ ${\displaystyle p}$ ${\displaystyle \to }$(${\displaystyle q}$ ${\displaystyle \to }$ ${\displaystyle r}$)${\displaystyle \to }$(${\displaystyle p\to }$ ${\displaystyle q}$) →${\displaystyle }$(${\displaystyle p}$ → r${\displaystyle }$)${\displaystyle (p\to (q\tor))\to (p\to q)\to (p\tor)}$ - axiom (A2)

완전성 증명을 위한 또 다른 개요

공식이 동명사인 경우 각 값이 공식에 대한 참값을 산출한다는 것을 보여주는 진리표가 있습니다. 그러한 가치 평가를 고려하십시오. 하위 공식의 길이에 대한 수학적 귀납법을 통해 하위 공식의 참 또는 거짓이 하위 공식의 각 명제 변수의 참 또는 거짓(가치 평가에 적합함)에서 나온다는 것을 보여줍니다. 그런 다음 "(P is true는 S를 의미하고 (P is false는 S를 의미한다)"를 사용하여 진리표의 행을 한 번에 두 개씩 결합합니다. 명제 변수에 대한 종속성이 모두 제거될 때까지 이를 계속 반복합니다. 그 결과 우리는 주어진 긴장감을 증명했습니다. 모든 교수법이 증명 가능하기 때문에 논리는 완전합니다.

기타 구문 증명 시스템 예제

명제 미적분학의 주요 용도 중 하나는 논리적 응용을 위해 해석될 때 명제 공식 간의 논리적 동등성 관계를 결정하는 것입니다. 이러한 관계는 사용 가능한 변환 규칙을 통해 결정되며, 그 시퀀스를 파생 또는 증명이라고 합니다.

명제 미적분에 대한 증명 체계의 다음 예는 형식 체계 $L$ = L${\displaystyle (A,}$ω${\displaystyle ,}$ Z$,$ I) ${\displaystyle {\mathcal$ {L$}}$=${\mathcal${$L}}\left(\mathrm {A$}),\$\omega,\mathrm {Z},\mathrm {I$ \right)}로 정의되는 미적분을 가정합니다.

• $알파{\displaystyle \mathrm{}}$ 집합 A ${\$는 명제 기호 또는 명제 변수라고 하는 셀 수 없을 정도로 무한한 원소 집합입니다. 구문론적으로 말하면, 이들은 공식 $언어{\displaystyle \mathcal{}}$ L ${\$의 가장 기본적인 요소이며$,$ 그렇지 않으면 원자 공식 또는 터미널 요소라고 합니다. $다음{\displaystyle \mathrm{}}$ 예제에서 A ${\$의 요소는 일반적으로 문자 p, q, r 등입니다$$.
• 오메가 집합 ω은 연산자 기호 또는 논리적 연결이라고 하는 요소의 유한 집합입니다. 집합 ω는 다음과 같이 서로 분리된 하위 집합으로 분할됩니다.
• ${\displaystyle \Omega =\Omega _{0}\cup \Omega _{1}\cup \cdots \cup \Omega _{j}\cup \cdots \cup \Omega _{m}}$

이 파티션에서$$ω j ${\displaystyle \Omega$_{j}는 연산자 j의 집합입니다.

더 익숙한 명제 계산에서 ω는 일반적으로 다음과 같이 분할됩니다.

• ${\displaystyle \Omega _{1}=\{\lnot \}$
• ${\displaystyle \Omega _{2}\subseteq \{\land,\lor,\to,\\왼쪽 화살표 \}$

자주 채택되는 규칙은 일정한 논리 값을 연산자 0으로 취급하므로 다음과 같습니다.

• ${\displaystyle \Omega _{0}=\{\bot,\top \}$

일부 작성자는 ¬ 대신 tilde(~) 또는 N을 사용하고, $일부$ 작성자는 ∨${\displaystyle$ \vee}$$대신 v를 사용하고 앰프샌드(&),$$접두사 K $또는$∧ {\displaystyle \wedge}$대신$ ⋅ {\displaystyle $\cdot$}을(를) 사용합니다. 논리 값 집합에 대해 표기법은 {false, true}, {F, T} 또는 {0}과 같은 기호로 더 다양합니다. $1$}이$($가${\displaystyle )}$ 모두 ${$⊥$,$ ⊤ } ${\displaystyle$bot,\top \}이(가) 아닌 다양한 컨텍스트에서 표시됩니다.

• 제타 $집합{\displaystyle \mathrm{}}$ Z ${\$는 논리적 응용 프로그램을 획득할 때 추론 규칙이라고 하는 유한한 변환 규칙 집합입니다.
• iota $집합{\displaystyle \mathrm{}}$ I ${\$은 논리적 해석을 받을 때 공리라고 하는 셀 수 있는 초기 점 집합입니다.

$L{\displaystyle \mathcal{}}$ ${\$의 언어는 공식 집합이라고도 하며$,$ 잘 형성된 공식은 다음 규칙에 의해 귀납적으로 정의됩니다.

1. 밑: 알파 $집합{\displaystyle \mathrm{}}$ A ${\$의 임의의 요소는$$ L ${\$의 공식입니다$.$
2. If ${\displaystyle p_{1},p_{2},\ldots ,p_{j}}$ are formulas and ${\displaystyle f}$ is in ${\displaystyle \Omega _{j}}$, then ${\displaystyle fp_{1}p_{2}\ldots p_{j}}$ is a formula.
3. 마감: 다른 것은 $L{\displaystyle \mathcal{}}$ ${\$의 공식이 아닙니다$.$

이러한 규칙을 반복적으로 적용하면 복잡한 수식을 만들 수 있습니다. 예:

• 규칙 1에 의해 p는 공식입니다.
• 규칙 2에 ${\displaystyle \mathrm{의해}}$ ¬ p${\displaystyle$ \n$egp}$는 공식입니다.
• 규칙 1에 의해, q는 공식입니다.
• 규칙 2에 따라 p$$∨ $q${\displaystyle \${\displaystyle n}$을 ¬합니다.$egp\lor q}$는 공식입니다.^[c]

다음 논의에서는 증명 시스템이 정의된 후 증명을 번호가 매겨진 선의 시퀀스로 제시하고 각 선은 단일 공식으로 구성되며 그 공식을 도입하는 이유 또는 정당성이 뒤따릅니다. 논변의 각 전제, 즉 논변의 가설로 도입된 가정은 순서의 맨 앞에 나열되어 있고, 다른 정당화 대신에 '전제'로 표시되어 있습니다. 결론은 마지막 줄에 나열되어 있습니다. 변환 규칙을 올바르게 적용하여 모든 행이 이전 행을 따라가면 증명이 완료됩니다(대조적인 접근 방법은 증명-트리 참조).

단순 공리계

Let ${\displaystyle {\mathcal {L}}_{1}={\mathcal {L}}(\mathrm {A} ,\Omega ,\mathrm {Z} ,\mathrm {I} )}$, where ${\displaystyle \mathrm {A} }$, ${\displaystyle \Omega }$, ${\displaystyle \mathrm {Z} }$, ${\displaystyle \mathrm {I} }$ are defined as follows:

• $집합{\displaystyle \mathrm{}}$ A ${\$ $\},$ 논리적 명제를 나타내는 역할을 하는 셀 수 없이 무한한 기호 집합:

  ${\displaystyle \mathrm {A} =\{p,q,r,s,t,u,p_{2},\ldots \}.}$

• 논리 연산자(논리 연결 및 네거티브)의 기능적으로 완전한 집합$$ω${\displaystyle$\Omega}은 다음과 같습니다. 결합, $분리$, 암시의 세 가지 연결(∧, ∨${\displaystyle$wedge,\lor }, →) 중 하나는 원시적인 것으로 간주하고 나머지 두 가지는 그것과 부정(¬)의 관점에서 정의할 수 있습니다. 또는 모든 논리 연산자를 셰퍼 스트로크(nand)와 같이 단독으로 충분한 연산자로 정의할 수도 있습니다. 물론 쌍조건(${\displaystyle a}$ ↔ b ${\displaystyle$ a\left $arrow$ b$\})$은 $({\displaystyle a}$ → b${\displaystyle )}$∧(${\displaystyle b}$ → a) ${\displaystyle$(a\$to b)\land ($b$\backslash$to a)}와 같이 결합 및 함의 측면에서 정의될 수 있습니다.
  명제 미적분학의 두 원시 연산으로 부정과 암시를 채택하는 것은 오메가 집합 ω$$=$$ω 1 ∪ ω 2 ${\displaystyle \Omega$=\Omega _{1}\cup \Omega _{2}} 파티션을 다음과 같이 설정하는 것과 같습니다.

  ${\displaystyle \Omega _{1}=\{\lnot \}$

  ${\displaystyle \Omega _{2}=\{\to \}}$

$그러면$ ∨ b ${\displaystyle$a\lor b}가 ¬ a → $b${\displaystyle \n로${\displaystyle \mathrm{정의}}$됩니다.$예$를 들어 a$\to b}$이고$∧$ b${\displaystyle$a\land b}는 $¬$($a$$→$ $¬$ b) {\displaystyle \n)로${\displaystyle }$정의됩니다.$예(a\n~\n$$)$$egb$

• 집합 $I{\displaystyle \mathrm{}}$ ${\$논리적 추론의 초기 점들의 집합, 즉 논리적 공리)은 얀 우카시에비치가 제안한 공리 시스템으로, 힐베르트 시스템의 명제-계산 부분으로 사용됩니다. 공리는 다음의 모든 치환 인스턴스입니다.
  • ${\displaystyle p\to (q\top)}$
  • ${\displaystyle (p\to (q\tor))\to (p\to q)\to (p\tor)}$
  • ${\displaystyle(\n)egp\n에서 \n까지eg q)\to (q\to p)}$
• 변환 규칙(추론의 rules)의 $집합$ Z ${\displaystyle \mathrm {Z} }$은(는) 유일한 규칙 모두스 포넨입니다(즉$,$ $양식$φ ${\displaystyle$\${\displaystyle \mathrm{varphi}}$} 및 (φ $$→$$ψ$) {\displaystyle$ $\backslash$$to$ \psi$}$의 공식에서, 추론 ψ ${\$displaystyle \psi }입니다).

이 시스템은 Metamath set.mm 공식 증명 데이터베이스에서 사용됩니다.

공리 명제 미적분학 체계에서의 증명 예

우리는 이제 위에서 설명한 얀 우카시에비치에 의해 공리계에서 동일한 $정리$ ${\displaystyle A}$ → ${\displaystyle$ A$\to A}$를 증명하는데, 이는 고전 명제 미적분학에 대한 힐베르트 스타일 연역 체계의 예입니다.

공리는 다음과 같습니다.

(A1)$$(${\displaystyle p}$ →${\displaystyle }$(${\displaystyle q}$ → p${\displaystyle }$)${\displaystyle (p\to (q\top))}$

(A2)${\displaystyle ((p}$ →${\displaystyle }$(${\displaystyle q}$ → r${\displaystyle }$)${\displaystyle }$→${\displaystyle }$(${\displaystyle p}$→ ${\displaystyle q}$) →${\displaystyle }$(${\displaystyle p}$ → ${\displaystyle r}$)${\displaystyle }$)${\displaystyle ((p\to (q\to$ (q\$to))\to (p\to$ (p$\to q))}$

(${\displaystyle \mathrm{A3}}$)${\displaystyle ((}$¬ ${\displaystyle p}$ → ¬ ${\displaystyle q}$ ) →${\displaystyle }$($q$→ p ) ${\displaystyle$((\n))$egp\n에서 \n까지$$eg q)\to (q\to p))}$

그리고 그 증명은 다음과 같습니다.

1. ${\displaystyle A}$ ${\displaystyle \to }$(${\displaystyle (B}$ ${\displaystyle \to }$ ${\displaystyle A}$) → ${\displaystyle A}$) ${\display$ style $A\to ((B\to A)\to$ A$)}$ ((${\displaystyle \mathrm{A1의\; inst}}$ance)
2. ${\displaystyle (}$ A ${\displaystyle \to }$(${\displaystyle }$(${\displaystyle B}$ ${\displaystyle \to }$ ${\displaystyle A}$)${\displaystyle \to }$(${\displaystyle A\to }$(${\displaystyle B}$ → ${\displaystyle A))}$ →${\displaystyle (A}$ → ${\displaystyle A}$)${\displaystyle (A\to (B\to$ (A\to ($A))\to$ (B\to A$))\to (A\to (B\to$ ($A))}$ (${\displaystyle A2의\; inst}$ance)
3. ${\displaystyle (}$ A ${\displaystyle \to (B}$ → ${\displaystyle A}$)${\displaystyle \to }$(${\displaystyle A}$ → A${\displaystyle )}$ ${\displaystyle (A\to (B\to$ A$))\to (A\to$ A$)}$ ((1) 및 (2) 모드 포넨스 기준)
4. ${\displaystyle A}$ ${\displaystyle \to }$(${\displaystyle B}$ → A${\displaystyle )}$ ${\display style$ A$\to (B\to$ A$)}$ (${\displaystyle \mathrm{A1의\; inst}}$ance)
5. ${\displaystyle A}$ ${\displaystyle \to }$ ${\displaystyle A}$ ${\display$ style $A\to$ A$}($모드포넨 기준)

자연공제제도

Let ${\displaystyle {\mathcal {L}}_{2}={\mathcal {L}}(\mathrm {A} ,\Omega ,\mathrm {Z} ,\mathrm {I} )}$, where ${\displaystyle \mathrm {A} }$, ${\displaystyle \Omega }$, ${\displaystyle \mathrm {Z} }$, ${\displaystyle \mathrm {I} }$ are defined as follows:

• 알파 집합 $A{\displaystyle \mathrm{}}$ ${\$은$($는) 셀 수 없을 정도로 무한한 기호 집합입니다. 예를 들어 다음과 같습니다.

  ${\displaystyle \mathrm {A} =\{p,q,r,s,t,u,p_{2},\ldots \}.}$

• 오메가 세트 ω$$=$$ω 1 ∪ ω 2 ${\displaystyle \Omega$=\Omega _{1}\cup \Omega _{2}}는 다음과 같이 분할됩니다.

  ${\displaystyle \Omega _{1}=\{\lnot \}$

  ${\displaystyle \Omega _{2}=\{\land,\lor,\to,\\left arrow \}}$

다음의 명제적 미적분학의 예에서, 변환 규칙은 소위 자연적 추론 시스템의 추론 규칙으로 해석하고자 합니다. 여기에 제시된 특정 시스템에는 초기 점이 없으므로 논리적 응용에 대한 해석은 빈 공리 집합에서 정리를 도출한다는 것을 의미합니다.

• 초기 점 집합이 비어 있습니다. 즉, $I$ =$$∅ {\$displaystyle \mathrm$ {I} =\varnothing$\}$입니다.
• 변환 규칙 $집합$인 Z ${\$은$($는) 다음과 같이 설명됩니다.

우리의 명제 미적분학에는 11개의 추론 규칙이 있습니다. 이러한 규칙을 통해 참인 것으로 가정되는 공식 집합이 주어지면 다른 참인 공식을 도출할 수 있습니다. 처음 10개는 단순히 우리가 다른 잘 형성된 공식들로부터 어떤 잘 형성된 공식들을 추론할 수 있다고 말합니다. 그러나 마지막 규칙은 규칙의 전제에서 특정 다른 공식을 추론할 수 있는지 확인하기 위해 추론된 공식 집합의 일부가 되는 (검증되지 않은) 가설을 일시적으로 가정한다는 의미에서 가상 추론을 사용합니다. 처음 10개의 규칙은 이를 수행하지 않기 때문에 일반적으로 가상이 아닌 규칙으로 설명되고 마지막 규칙은 가상의 규칙으로 설명됩니다.

변환 규칙을 설명할 때, 우리는 $금속$ 언어 기호 ⊢ ${\displaystyle$vdash}를 소개할 수 있습니다. 이것은 기본적으로 "그것을 추론하라"는 말의 편리한 속기입니다. 형식은$$γ$$⊢ ψ ${\displaystyle \Gamma$vdash \psi}이며, 여기서 γ는 전제라는 (가능하면 빈) 공식 집합이고, ψ는 결론이라는 공식입니다. 변환 규칙$$γ$$⊢ ψ ${\displaystyle \Gamma \$vdash \psi}는 γ의 모든 명제가 정리(또는 공리와 동일한 진리값을 갖는) 경우 ψ도 정리임을 의미합니다. 다음 규칙 접속 도입부를 고려하면, γ이 두 개 이상의 공식을 가질 때, 접속을 사용하여 항상 안전하게 하나의 공식으로 줄일 수 있음을 알 수 있습니다. 그래서 간단히 말해서, 그때부터 우리는 γ을 집합이 아닌 하나의 공식으로 나타낼 수 있습니다. 편의상 생략된 또 다른 경우는 γ이 빈 집합일 때 γ이 나타나지 않을 수 있습니다.

부정소개

$({\displaystyle p}$ → ${\displaystyle q)}$ ${\displaystyle (p\to q)}$ 및$$(${\displaystyle p}$ → ¬ q) ${\displaystyle (p$\to \n)부터$egq$ ${\displaystyle \mathrm{추론}}$ $¬$ p${\displaystyle$ \n$egp$

$즉$ { ${\displaystyle (p}$ → ${\displaystyle q),}$(${\displaystyle p}$ → ¬${\displaystyle \mathrm{}q}$ ) $}$ ⊢ ¬ p ${\displaystyle$\{(p$\to$ q), (p\to \n)$eg q)\}\vdash \n$$egp$

네거티브 제거

¬$p$ {\$displaystyle$ \n에서$eggp$ 추론$({\displaystyle p}$ $→$ r${\displaystyle )}$ ${\displaystyle(p\tor$

${\displaystyle 즉},$ ${\displaystyle \{}$¬ p} ⊢$p$→ r) ${\displaystyle$ \{\n$eg p\}\vdash (p\to r)}$.

이중 네거티브 제거

¬ ¬$$p {\$displaystyle$\n에서$eg \n$$egp$ app을 추론합니다.

${\displaystyle 즉}$,${\displaystyle }$¬ ¬ $p$⊢ p ${\displaystyle$ \n$eg \n$$eg p\vdash p}$.

접속사 소개

p와 q에서 추론$({\displaystyle p}$ ∧ q) ${\displaystyle(p$land q)}.

${\displaystyle 즉},$ {${\displaystyle p,}$ ${\displaystyle q\}}$⊢$p$∧ q)${\displaystyle$\{p$,q\}\$vdash$($p\land q)}입니다.

접속 제거

$({\displaystyle p}$ ∧ q) ${\displaystyle(p$land q)}에서 p를 추론합니다.

$({\displaystyle p}$ ∧ q) ${\displaystyle(p$land q)}에서 q를 추론합니다.

$즉$ (${\displaystyle p}$ ∧$$q) ⊢ $p {\displaystyle (p\$land$$q${\displaystyle )\backslash \mathrm{vdash}}$p${\displaystyle \}}$ $및$(p ∧$q)$⊢ q${\$displaystyle (p\land q)\vdash q}입니다.

단절소개

p에서 추론$({\displaystyle p}$ ∨ q) ${\displaystyle(p$lor q)}.

${\displaystyle q}$에서 (${\displaystyle p}$∨$q$) {\$displaystyle(p\$lor$$q)}을(를) 추론합니다.

즉, ${\displaystyle p}$⊢$p$∨ q)${\displaystyle p\$vdash($p{\displaystyle \backslash \mathrm{lor}}$q)}$q$ ⊢($p$∨ q$)$displaystyle q\vdash(p\lor q)}입니다.

단차제거

$({\displaystyle p}$ ∨ q) ${\displaystyle(p$\lor$$q)} ${\displaystyle 및}$ (${\displaystyle p}$ → r) ${\displaystyle($p\tor$)\}$ ${\displaystyle 및}$ (${\displaystyle q}$ → r) ${\displaystyle($q$\backslash$tor)}에서 추론합니다.

즉$,$ {${\displaystyle p}$ ∨ ${\displaystyle q}$, p → r, ${\displaystyle q}$ → $r}$ ⊢ r${\displaystyle$\{$p\lor$q,p\tor,$q$tor\}\vdashr}입니다.

쌍조건 도입

$({\displaystyle p}$ → ${\displaystyle q)}$ ${\displaystyle(p\to q)}$ 및$$(${\displaystyle q}$ → p${\displaystyle )}$ ${\displaystyle(q\top)}$에서 추론$({\displaystyle p}$ ↔ ${\displaystyle q})$ ${\displaystyle(p\left$ arrow $q)}.$

${\displaystyle 즉},$ {${\displaystyle p}$ → ${\displaystyle q,}$ ${\displaystyle q}$ → p${\displaystyle \}}$⊢(${\displaystyle p}$ ↔ q) ${\displaystyle$\{$p\to q,$q\$top\}\vdash($p$\left$arrow q)}입니다.

이중조건 탈락

$({\displaystyle p}$ ↔ ${\displaystyle q)}$ ${\displaystyle(p\left$ right arrow $q)}$에서 추론$({\displaystyle p}$ → ${\displaystyle q)}$ ${\displaystyle(p\to q$

$({\displaystyle p}$ ↔ ${\displaystyle q)}$ ${\displaystyle(p\left$ right arrow $q)}$에서 추론$({\displaystyle q}$ → ${\displaystyle p)}$ ${\displaystyle(q\top$

${\displaystyle 즉},$ (${\displaystyle p}$ ↔ ${\displaystyle q)}$ ⊢ (${\displaystyle p}$ → q) ${\displaystyle (p\left$arrow $q)\vdash$(p\to$$q)} ${\displaystyle 및}$ (${\displaystyle p}$ ↔ ${\displaystyle q}$) ⊢ $q$→ p)${\displaystyle$ (p\$left arrow q$vdash (q\to q)}입니다.

모드스포넨(조건부 탈락)

p와 $({\displaystyle p}$ → ${\displaystyle q)}$ ${\displaystyle(p\to q)}$에서$$q를 추론합니다.

${\displaystyle 즉},$ {${\displaystyle p,}$ ${\displaystyle p}$ → ${\displaystyle q\}}$ ⊢ q${\displaystyle$\{$p,$p\$to q\}\$vdash$$q}입니다.

조건부 증명(조건부 도입)

[accepting p는 q의 증명을 허용함$]$에서 추론$({\displaystyle p}$ → ${\displaystyle q)}$ ${\displaystyle(p\to q)}.$

${\displaystyle 즉},$ (${\displaystyle p}$ ⊢ ${\displaystyle q}$) ⊢${\displaystyle }$($p$→ q)${\displaystyle(p\vdash q)\$vdash$($p\to q)}입니다.

자연공제제도의 증명예

• A → A라는 것을 보여주는 것.
• 이에 대한 한 가지 가능한 증명(유효하긴 하지만 필요 이상의 단계가 포함되어 있음)은 다음과 같이 정리될 수 있습니다.

증명의 예

번호	공식	이유
1	${\display style A}$	전제의
2	${\displaystyle A\lor A}$	(1)부터 분리도입에 의한
3	${\displaystyle(A\lor A)\land A}$	(1)과 (2)의 접속 도입에 의한
4	${\display style A}$	결합 제거에 의한 (3)부터
5	${\displaystyle A\vdash A}$	(1)부터 (4)까지의 요약
6	${\displaystyle \vdash A\to A}$	조건부 증명에 의한 (5)부터

$A$⊢ A ${\displaystyle A\$vdash A}를 "A로 가정하고 A를 추론하십시오"로 해석합니다. ⊢${\displaystyle A}$ → $A {\displaystyle$ \$vdash A$\to A}를 "아무것도 가정하지 말고 A가 A를 암시하는 것을 추론하라"거나 "A가 A를 암시하는 것은 동어이다"거나 "A가 A를 암시하는 것은 항상 사실이다"로 읽습니다.

더 복잡한 공리계

논리 연산자의 구문 대부분을 공리를 통해 정의하고 하나의 추론 규칙만 사용하는 또 다른 버전의 명제 미적분학을 정의할 수 있습니다.

공리

φ, χ 및 ψ는 잘 형성된 공식을 의미합니다. (잘 형성된 공식 자체에는 그리스 문자가 포함되지 않고 대문자 로마자, 연결 연산자 및 괄호만 포함됩니다.) 그렇다면 공리는 다음과 같습니다.

공리

이름.	Axiom 스키마	묘사
THN-1	${\displaystyle \phi \to (\chi \to \phi )}$	가설 χ 추가, 시사점 소개
N-2	${\displaystyle (\phi \to (\chi \to \psi )\to (\phi \to \chi )\to (\phi \to \to \psi )}$	함의에 대해 가설$$ϕ${\displaystyle \$phi} 배포
AND-1	${\displaystyle \phi \land \chi \to \phi }$	결합 제거
AND-2	${\displaystyle \phi \land \chi \to \chi }$
AND-3	${\displaystyle \phi \to (\chi \to (\phi \land \chi )}$	접속사를 소개합니다.
OR-1	${\displaystyle \phi \to \phi \ 또는 \chi }$	단차를 도입합니다.
OR-2	${\displaystyle \chi \to \phi \ 또는 \chi }$
OR-3	${\displaystyle(\phi \to \psi)\to((\chi \to \psi)\to(\phi \lor \chi \to \psi)}$	단절 제거
NO-1	${\displaystyle (\phi \to \chi )\to ((\phi \to \n)eg \chi )\n에서 \n까지eg \phi )}$	부정을 도입합니다.
NOT-2	${\displaystyle \phi \to (\n)eg \phi \to \chi )}$	부정 제거
NOT-3	${\displaystyle \phi \ 또는 \neg \phi }$	제외된 중간, 고전 논리
IFF-1	${\displaystyle (\phi \left right arrow \chi )\to (\phi \to \chi )}$	등가성 제거
IFF-2	${\displaystyle (\phi \left right arrow \chi )\to (\chi \to \phi )}$
IFF-3	${\displaystyle(\phi \to \chi )\to((\chi \to \phi )\to(\phi \우측 화살표 \chi )}$	등가성을 도입합니다.

• Axiom THN-2는 "임의에 관한 암시의 분산 속성"으로 간주될 수 있습니다.
• 공리 AND-1 및 AND-2는 "접합 제거"에 해당합니다. AND-1과 AND-2 사이의 관계는 결합 연산자의 가환성을 반영합니다.
• Axiom AND-3은 "접합 도입"에 해당합니다.
• 공리 OR-1 및 OR-2는 "분리 도입"에 해당합니다. OR-1과 OR-2 사이의 관계는 분리 연산자의 교환성을 반영합니다.
• 공리 NOT-1은 "부조리한 축약"에 해당합니다.
• 공리 NOT-2는 "모순으로부터 무엇이든 추론할 수 있다"고 말합니다.
• Axiom NOT-3는 "tertium non-datur"(라틴어: "3분의 1은 주어지지 않는다")라고 불리며 명제 공식의 의미론적 가치를 반영합니다. 공식은 참 또는 거짓 중 하나의 진리 값을 가질 수 있습니다. 적어도 고전 논리에는 제3의 진리값이 없습니다. 직관주의 논리학자들은 공리 NOT-3을 받아들이지 않습니다.

추론 규칙

추론 규칙은 모드포넨스(modusonens)입니다.

${\displaystyle \frac{}{}}$ → χ χ${\displaystyle {\frac${\$phi,\\phi \$to $\backslash$chi}{\chi }}.

메타 추론 규칙

개찰구 왼쪽에 가설이 있고 개찰구 오른쪽에 결론이 있는 수열로 데모를 표현합니다. 그러면 연역 정리는 다음과 같이 나타낼 수 있습니다.

순서대로라면

${\displaystyle \phi _{1},\ \phi _{2},\...,\ \phi _{n},\chi \vdash \psi }$

입증되었습니다. 그러면 시퀀스를 입증하는 것도 가능합니다.

${\displaystyle {}_{}}$1$2$ ${\displaystyle {.}_{}}$..,${\displaystyle {\mathrm{\varphi \; n}}_{}}$ ${\displaystyle {⊢}_{}}$ $→$ ψ ${\displaystyle$ \$phi _{1},\$ \$phi _{2$ \phi _{n}\vdash \chi ${\displaystyle {\mathrm{\backslash to}}_{}}$\psi $}.$

이 추론 정리(DT)는 그 자체가 명제 미적분학으로 공식화된 것이 아닙니다. 명제 미적분학의 정리가 아니라 명제 미적분학에 대한 정리입니다. 이런 의미에서 명제적 미적분학의 건전성이나 완전성에 관한 정리에 버금가는 메타이론입니다.

반면에 DT는 구문 증명 과정을 단순화하는 데 매우 유용하여 모듈스포넨을 수반하는 또 다른 추론 규칙으로 고려하고 사용할 수 있습니다. 이러한 의미에서 DT는 이 글에서 소개한 명제 미적분학의 첫 번째 버전의 일부인 자연 조건부 증명 추론 규칙에 해당합니다.

DT의 반대도 유효합니다.

순서대로라면

${\displaystyle \phi _{1},\ \phi _{2},\...,\\phi _{n}\vdash \chi \to \psi }$

입증되었습니다. 그러면 시퀀스를 입증하는 것도 가능합니다.

${\displaystyle \phi _{1},\ \phi _{2},\...,\ \phi _{n},\chi \vdash \psi }$

사실, DT의 역방향의 유효성은 DT의 역방향에 비해 거의 사소한 것입니다.

한다면

${\displaystyle \phi _{1},\...,\\phi _{n}\vdash \chi \to \psi }$

그리고나서

1:${\displaystyle }$ϕ${\displaystyle }$1${\displaystyle ,}$ ${\displaystyle {}_{}}$ϕ n,$$χ ⊢ χ →$$ψ ${\displaystyle$\phi$_{1}, ...,\ \phi$ _${n},\$chi \vdash \chi \to \psi }

2:${\displaystyle }$ϕ${\displaystyle }$1${\displaystyle ,}$ ${\displaystyle {}_{}}$ϕ n,$$χ ⊢ χ ${\displaystyle \phi _{1}, ...,\$ \$phi$_{$n},\$chi \vdash \chi}

그리고 (1)과 (2)로부터 추론할 수 있습니다.

3:${\displaystyle }$ϕ${\displaystyle }$1${\displaystyle ,}$ ${\displaystyle {}_{}}$ϕ n,$$χ ⊢ ψ ${\displaystyle \phi _{1}, ...,\$ \$phi$_{$n},\$chi \vdash \psi }

모드포넨스, Q.E.D.를 이용해서요.

DT의 반대는 공리를 추론 규칙으로 변환하는 데 사용할 수 있다는 강력한 의미를 가지고 있습니다. 예를 들어, 우리가 가진 공리 AND-1에 의해,

${\displaystyle \vdash \phi \wedge \chi \to \phi,}$

연역 정리의 역수에 의해 변환될 수 있는

${\displaystyle \phi \wedge \chi \vdash \phi,}$

추론 규칙이

${\displaystyle {\fac {\phi \wedge \chi}{\phi }}$

허용됩니다. 이 추론 규칙은 명제 미적분학의 첫 번째 버전(이 글)에서 사용된 10개의 추론 규칙 중 하나인 결합 제거입니다.

보다 복잡한 공리계에서의 증명 예

다음은 공리 THN-1 및 THN-2만 포함하는 (통사적) 시연의 예입니다.

증명: $A$ → ${\displaystyle A}$ { {\$displaystyle A\to A}($의미의 반영성).

증명:

1. ${\displaystyle (A\to ((B\to A)\to A))\to ((A\to (B\to A))\to (A\to A))}$

   ϕ =$A$, χ $$=$B$→ A, ψ = A {\$displaystyle$\phi =$A,\chi$ = B\$to$A,\psi = A}

2. ${\display style A\to ((B\to A)\to A)}$

   ϕ = ${\displaystyle A}$, χ = B$$→ A ${\displaystyle$ \$phi$=$A$,\$chi$= B\to A}인 Axiom N-1

3. ${\display style(A\to(B\to(A))\to(A\to(A))}$

   (1)과 (2)부터 모듈포넨스에 의해.

4. ${\display style A\to (B\to A)}$

   ϕ $$= $A$, χ = B ${\displaystyle$ \$phi$= A,\$chi$= B}인 Axiom N-1

5. ${\display style A\to A}$

   (3) 및 (4)부터 모듈포넨스.

솔버

명제 미적분학과 술어 미적분학의 한 가지 주목할 만한 차이점은 명제 공식의 만족도가 결정적이라는 것입니다.^[77] 명제 논리 공식의 만족도를 결정하는 것은 NP-완전 문제입니다. 그러나 많은 유용한 경우에 매우 빠른 실용적인 방법(예: DPLL 알고리즘, 1962; Chaff 알고리즘, 2001)이 존재합니다. 최근 연구에서는 SAT 솔버 알고리즘을 산술식을 포함하는 명제와 함께 작동하도록 확장했습니다. SMT 솔버입니다.

참고 항목

높은 논리적 수준

• 1차 논리
• 2차 명제 논리
• 2차 논리
• 고차 논리

관련항목

메모들

참고문헌

추가읽기

• 브라운, 프랭크 마컴(2003), 부울 추론: 부울 방정식의 논리, 제1판, 클루어 학술 출판사, 노웰, MA. 제2판, 도버 출판사, 미네올라, 뉴욕.
• Chang, C.C. and Keisler, H.J. (1973), 모델 이론, 노스홀랜드, 네덜란드 암스테르담.
• Kohavi, Zvi (1978), 스위칭과 유한 오토마타 이론, 제1판, McGraw–Hill, 1970. 제2판, McGraw–Hill, 1978.
• Korfage, Robert R. (1974), 이산 계산 구조, 학술 출판부, 뉴욕.
• Lambek, J. and Scott, P.J. (1986), 고차 범주 논리학 소개, Cambridge University Press, Cambridge, UK.
• 멘델슨, 엘리엇 (1964), 수학 논리학 개론, D. 반 노스트랜드 컴퍼니.

관련 작품

• Hofstadter, Douglas (1979). Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books. ISBN 978-0-465-02656-2.

외부 링크

• Klement, Kevin C. (2006), "명제 논리", James Fieser and Bradley Dowden (eds.), 인터넷 철학 백과사전, Eprint.
• 형식 술어 미적분학은 대체 미적분학의 선을 따라 체계적인 형식적 발전을 포함합니다.
• 모든 x에 대해: 공식 논리학에 대한 소개, P.D. Magnus는 문장 논리에 대한 형식적 의미론과 증명 이론을 다룹니다.
• 2장 / 논리의 명제 논리 행동
• 프로젝트 나유키에 대한 명제적 순차 미적분 증명. (주: 함축은 양식에 입력할 수 있습니다. !X Y, 그리고 sequent는 접두사가 붙은 단일 공식일 수 있습니다. > 쉼표가 없는 경우)
• 명제논리 - 생성문법
• 간단한 표현을 이해하는 데 도움이 되는 명제 계산기