구면 삼각법

구면 삼각법은 구면에서 교차하는 다수의 대원에 의해 정의된 구면 다각형(특히 구면 삼각형)의 변과 각도의 삼각함수 사이의 관계를 다루는 구면 기하학의 한 분야이다.구면 삼각법은 천문학, 측지학, 항법에서의 계산에 매우 중요하다.

그리스 수학에서의 구면 삼각법의 기원과 이슬람 수학의 주요 발전은 중세 이슬람의 삼각법과 수학의 역사에서 충분히 논의된다.이 주제는 존 네이피어, 델람브레 등의 중요한 개발과 함께 근대 초기에 결실을 맺었고, 19세기 말까지 대학과 학교의 사용을 위한 ^[1]토드헌터의 교과서 구면 삼각법의 출판으로 근본적으로 완전한 형태를 갖추게 되었다.그 이후 벡터법의 적용과 수치법의 사용이 중요한 발전이었다.

예단

구면 폴리곤

구면 폴리곤은 다수의 대원호로 정의되는 구면의 표면에 있는 폴리곤으로, 구면의 중심을 통과하는 평면과 표면의 교차점입니다.이러한 폴리곤에는 임의의 수의 변이 있을 수 있습니다.두 개의 평면은 삼각형의 양면 유사체인 "디곤" 또는 바이앵글이라고도 불리는 루네를 정의합니다. 친숙한 예는 오렌지 부분의 곡면입니다.세 개의 평면이 이 기사의 주요 주제인 구면 삼각형을 정의한다.4개의 평면이 구면 사변형을 정의합니다. 이러한 도형과 높은 변의 폴리곤은 항상 구면 삼각형의 수로 취급할 수 있습니다.

흥미로운 성질을 가진 구형 다각형 중 하나는 모든 직각을 가진 구형 5면성 다각형인 펜타그램마 미리피쿰이다.

이 시점부터 기사는 단순히 삼각형으로 표시된 구면 삼각형으로 제한될 것입니다.

표기법

• 정점의 정점과 각도는 모두 동일한 대문자 A, B 및 C로 표시됩니다.
• 삼각형의 각도 A, B, C는 구의 표면을 교차하는 평면 사이의 각도 또는 정점에서 만나는 대원호의 접선 벡터 사이의 각도입니다.각도는 라디안 단위입니다.적절한 구면 삼각형의 각도는 θ < A + B + C < 3µ가 되도록 (관례상) θ보다 작다. (Todhunter,^[1] Art.22,32)
• 각 변은 소문자 a, b 및 c로 표시됩니다.단위 구에서 대원호가 중심에서 서브텐드하는 각도의 라디안 측정값과 같은 길이입니다.적절한 구면 삼각형의 변은 (관례상) 0 < a + b + c < 2µ보다 작다.(토드헌터,^[1] Art.22,32)
• 구의 반지름은 통일체로 간주됩니다.반지름 R의 구에 대한 특정 실제 문제의 경우, 아래에 제시된 식별 정보를 사용하기 전에 측면의 측정된 길이를 R로 나누어야 한다.마찬가지로, 단위 구에 대한 계산 후, 변 a, b, c에 R을 곱해야 한다.

극삼각형

삼각형 ABC와 관련된 극삼각형은 다음과 같이 정의된다.BC 변을 포함하는 큰 원을 생각해 보십시오.이 큰 원은 지름 평면과 지표면의 교점에 의해 정의됩니다.중심에 있는 평면에 법선을 그린다. 법선이 두 지점에서 지표면과 교차하고 A와 같은 평면의 면에 있는 점을 (통례적으로) A의 극이라고 하며 A'로 나타낸다.포인트 B'와 C'는 동일하게 정의되어 있습니다.

삼각형 AbBcC is는 삼각형 ABC에 대응하는 극삼각형이다.매우 중요한 정리(Todhunter,^[1] Art.27)는 극 삼각형의 각도와 변이 다음과 같이 주어진다는 것을 증명한다.

${\displaystyle\alignat}{3}A'=\pi -a,\qquad B'=\pi -b,\qquad C'=\pi -c,\a'=\pi -A,&b'&=\pi -B,&c'=\pi -C.\end {alignedat}}$

따라서, 만약 삼각형 ABC에 대한 어떤 항등식이 증명된다면, 우리는 위의 치환을 함으로써 극삼각형에 첫 항등식을 적용함으로써 즉시 두 번째 항등식을 도출할 수 있다.이것이 보충 코사인 방정식이 코사인 방정식에서 도출되는 방법입니다.마찬가지로, 사분면 삼각형의 동일성은 직각 삼각형의 동일성에서 파생될 수 있습니다.극삼각형의 극삼각형이 원래 삼각형이다.

코사인 규칙과 사인 규칙

코사인 규칙

코사인 규칙은 구면 삼각법의 기본 동일성입니다. 사인 규칙을 포함한 다른 모든 동일성은 코사인 규칙에서 파생될 수 있습니다.

$(\displaystyle \cos a=\cos b+\sin b\sin cos A,\!)$

$(\displaystyle\cos b=\cos c+\sin a\cos B,\!)$

$(\displaystyle\cos c=\cos a\cos b+\sin a\sin b\cos C,\!)$

이러한 동일성은 평면 삼각법의 코사인 법칙을 일반화하며, 작은 내부각의 한계에서 점근적으로 동등하다.(단위구상에서 a${\displaystyle ,}$ ${\displaystyle b,}$ ${\displaystyle c}$ ${\displaystyle \to }$$$ {$display a, b, c\rightarrow$ 0$}$이 sin ${\displaystyle }$ a ${\displaystyle \mathrm{display}}$a display a \ $display$style \$sin$a\ $about$ a$$${\displaystyle \}}$ ${\displaystyle {및}^{}}$ ($cosisplay$ a${\displaystyle }$- ${\displaystyle \mathrm{costeryle}}$0${\displaystyle {}^{}}$$a-\cos$ b$)^{2}\약$0$$ 등; 코사인 구체의 법칙 참조).

사인 규칙

사인 구형의 법칙은 다음 공식에 의해 주어진다.

$(\displaystyle\frac{\sin a}=frac{\sin b}=frac{\sin C}{\sin c}).}$

이러한 식별은 변이 구의 반지름보다 훨씬 작을 때 평면 삼각법의 사인 법칙에 가깝습니다.

코사인 규칙 도출

구형 코사인 공식은 원래 초등 기하학과 평면 코사인 규칙에 의해 증명되었다(Todhunter,^[1] Art.37).그는 또한 단순 좌표 기하학과 평면 코사인 규칙을 사용하여 도출을 제공한다(Art.60).여기서 개략적으로 설명하는 접근방식은 보다 단순한 벡터 방법을 사용한다.(이 방법들은 코사인 구면 법칙에서도 논의된다.)

원점에서 삼각형의 꼭지점(단위 구면)까지 그려진 세 개의 단위 벡터 OA, OB 및 OC를 고려합니다.아아크 BC는 중심에서 a 등급의 각을 세팅하므로 OB·.OC = cos a.z축을 따라 OA를 사용하고 xz 평면에서 OB를 사용하여 z축과 각도 c를 만드는 데카르트 베이스를 도입합니다.벡터 OC는 xy 평면에서 ON으로 투영되며 ON과 x축 사이의 각도는 A입니다.따라서 3개의 벡터에는 다음 컴포넌트가 있습니다.

OA${\displaystyle }$(${\displaystyle 0}$ ,$0$ , ${\displaystyle 1\mathrm{}}$) { $displaystyle$( $0$, $0$, 1$$)${\displaystyle }$OB$$ ( ${\displaystyle \sin c\mathrm{}}$ c ,${\displaystyle 0}$ , $cos$ c ) \ $displaystyle$ ( \$sin$ c , 0 , ,$$\ cos$$ c )${\displaystyle }$、 ${\displaystyle \mathrm{OC}}$ (${\displaystyle \sin }$ 、 b ${\displaystyle \cos \sin }$ ${\displaystyle A}$ , ${\displaystyle \sin 、}$ A ) 、 $sin$ ${\displaystyle 、}$ cos$$、 cos \ $sin$、$cos$ ） $。$

구성 요소 측면에서 스칼라 제품 OB·OC는

OB · ${\displaystyle \mathrm{OC}}$ ${\displaystyle =}$ sin${\displaystyle \sin }$ c ${\displaystyle \sin }$ ${\displaystyle }$ b cos${\displaystyle a}$A + cos${\displaystyle \cos }$ c c ${\displaystyle \cos }$ ${\displaystyle \{\backslash }$ b$$\ $display$ style { } = \ $sin$ c\$sin$b \ $cos$ A + \ $cos$ c\$cos$b $\}$ 。

스칼라 제품에 대한 두 식을 같게 하면

$(\displaystyle\cos a=\cos b+\sin b\sin c\cos A)$

이 방정식은 변의 관점에서 각도에 대한 명시적인 표현을 제공하도록 다시 배열할 수 있습니다.

$(\displaystyle\cos A=cosfrac\cos b\cos c}{\sin b\sin c}).}$

다른 코사인 규칙은 순환 순열을 통해 얻습니다.

사인 법칙의 파생

이 파생은 Todhunter,^[1] (Art.40)에 제시되어 있다.${\displaystyle {\mathrm{항등식}}^{}}$ ${\displaystyle {sin\mathrm{}}^{}}$ 2${\displaystyle {}^{}a}$ A ${\displaystyle =1}$ - ${\displaystyle {cos\mathrm{}}^{}}$ 2${\displaystyle {}^{}a}$A { \$displaystyle$ \ $sin ^$ {2} A$= 1$ - \ $cos ^$ ${$2$}$A$$the$$${\displaystyle }$the the the ${\displaystyle \mathrm{the}}$ A \ $displaystyle$\$cos$ A$$ 。

${\displaystyle {\cos ^{2}A&=1-\left({\frac {cos a-\cos b\sin c}}\right)^{2}\[5pt]&=sfrac {(1-\cos ^{2}b)\cos cos 2\cos cos ^2\cos ^2\c\cos }\end { aligned}}$

${\displaystyle 오른쪽}$은${\displaystyle }$a${\displaystyle ,}$ b, $(\displaystyle$ a$,\;b,\;c)$의 순환 순열에서는 불변하므로 구면 사인 규칙이 즉시 뒤따릅니다.

대체 파생상품

기본 코사인 규칙과 사인 규칙 및 다음 섹션에서 설명하는 기타 규칙을 도출하는 방법은 여러 가지가 있습니다.예를 들어, Todhunter는^[1] 코사인 규칙(제37조 및 제60조)의 두 가지 교정과 사인 규칙(제40조 및 제42조)의 교정 두 가지를 제공한다.구면 코사인 법칙의 페이지는 코사인 규칙에 대한 네 가지 다른 증거를 제공한다.측지학(Clarke 등^[2])과 구면 천문학(Smart^[3] 등)에 관한 교과서는 서로 다른 증거를 제공하며, MathWorld의 온라인 리소스는 더 ^[4]많은 것을 제공한다.투영행렬의 선형대수를 사용하여 공식을 도출하고 미분기하학 및 회전군 이론을 인용하는 배너지의^[5] 공식과 같은 더 이국적인 파생도 있다.

위에 제시된 코사인 규칙의 도출은 단순성과 직접성의 장점이 있으며 사인 규칙의 도출은 코사인 규칙 외에 별도의 증거가 필요하지 않다는 사실을 강조한다.그러나 위의 형상을 사용하여 사인 법칙의 독립적인 증거를 제공할 수 있습니다.스칼라 삼중곱 OA·(OB × OC)는 다음과 같은 기준으로 sin${\displaystyle \sin }$b ${\displaystyle \sin \sin }$c ${\$ A {\$displaystyle \sin$b$\sin$c\sin A$$}로 평가된다.마찬가지로, OB를 따라 z축을 기준으로 하는 삼중곱 OB·(OC × OA)는 sin ${\displaystyle }$ ${\displaystyle \sin }$ ${\displaystyle a}$ sin${\displaystyle }$b sin ${\displaystyle b}$B(\$displaystyle \sin$ c$\sin$ a$\sin$ B$)$로 평가되므로, 주기적 순열 하에서의 삼중곱의 불변성은 ${\displaystyle \sin \sin }$ sin ${\displaystyle }$ ${\displaystyle A=}$ sin B(\$displaystyle$ B$)$이다${\displaystyle .}$사인 법칙의 irst.이 파생에 대한 자세한 내용은 사인의 법칙의 곡선 변형을 참조하십시오.

아이덴티티

보충 코사인 규칙

극삼각형에 코사인 규칙을 적용하면 (Todhunter,^[1] Art.47), 즉 A를 θ – a로 대체한다.

$cos A+=-cos B, cos C+, sin C, cos B&=-cos C, cos A+, sin C, sin A, cos C+, sin A, cos B, \cos C=-\cos B, \cos B+, sin B, sin B, cos C, cos C, \c Cos Cos C, cos Cos Cos C.\end { aligned}}$

코탄젠트 4부 공식

삼각형의 6개 부분은 순환 순서로 (aCbAcB)로 쓸 수 있습니다.코탄젠트 또는 4부분 공식은 삼각형 주위에 연속된 4부분을 형성하는 두 변과 두 각도를 관련짓습니다(예: (aCbA) 또는 (BaCb).이러한 세트에는 내측과 외측부가 있습니다.예를 들어 세트(BaCb)에서는 내측각이 C, 내측면이 a, 외측각이 B, 외측면이 b입니다.코탄젠트 규칙은 (Todhunter,^[1] 제4조)로 표기할 수 있다.

$\displaystyle \cosf {side}\cosmathsf {side}=\cot\mathsf {side}\sinmathsf {side}\cot\mathsf {side}\cot\mathsf {side}\cotsf {sf}\mathsf {sf}{sf}}\cothf {sf}\contangle}\mathsf {sf}\craple}$

6개의 가능한 방정식은 다음과 같습니다(오른쪽에 표시된 관련 집합).

${\displaystyle {begin{array}{(CT1)}}\cos b,\cos C=\cot a,\sin b-\cot A,\sin C,\qquad &(aCbA)\\[0ex]{\text{(CT2)}}&\cos b,\cos A=\cot c,\sin b-\cot C,\sin A,\(CbAc)\[0ex]{(CT3)}&\cos c,\cos A=\cot b,\cot B,\cos A.\\[0ex]{\text{(CT4)}}&\cos c,\cos B=\cot a,\sin c-\cot A,\sin B,&(AcBa)\\[0ex]{\text{(CT5)}}\cos a,\cos B=\cot c,\sin a-\cot C,\sin B,&(cBaC)\\[0ex]{\text{(CT6)}}&\cos a,\cos C=\cot b,\sin a-\cot B,\sin C,&(BaCb)\end {array}}$

첫 번째 공식은 첫 번째 코사인 규칙에서 시작하여 오른쪽에서 세 번째 코사인 규칙에서 cos${\displaystyle }$"$c\$style \$cos$ c$"$를 대체함을 증명하려면 다음 절차를 수행합니다.

$(\displaystyle\cos a\cos b+\cos b\sin c\cos b+\sin a\sin b\cos C)+\cos b\sin A\cos a\cos a\cos a\cos b+\cos C\cos C\cos B\cos C\cos B\c sin A\cos B\cos B\cos C\cos C\cos A\cos A\cos C\cos C\cos C\cos C\cos A\cos A\csin A\\end { aligned}}$

결과는 sin${\displaystyle a}$ ${\displaystyle a}$ sin${\displaystyle b}$b \$displaystyle \sin$ a$\sin$로$$나누면 나타난다.다른 2개의 코사인 규칙과 유사한 기법으로 CT3과 CT5를 얻을 수 있다.나머지 세 개의 방정식은 극삼각형에 규칙 1, 3, 5를 적용함으로써 뒤따른다.

반각 및 반측 공식

${\displaystyle \mathrm{2초}}$ ${\displaystyle =}$ (${\displaystyle a}$ +${\displaystyle b}$ +$c$) {{ $displaystyle 2s$= ( $a$ + b + $c$) } $및$ 2 ${\displaystyle S}$ ${\displaystyle =}$ (${\displaystyle A}$+ B + ${\displaystyle C}$) $、$ { $displaystyle 2S$= ($A$+$B$ + C ) 、$$}

또 다른 12개의 정체성은 주기적 순열로 이어집니다.

첫 번째 공식의 증명(Todhunter,^[1] Art.49)은 항등식 2sin²(A/2) = 1 – cosA에서 시작하며, 변의 관점에서 A를 표현하기 위해 코사인 규칙을 사용하고 두 코사인 합을 곱으로 대체한다(합계-제품 동일성 참조).두 번째 공식은 항등식² 2cos(A/2) = 1 + cosA에서 시작하고, 세 번째 공식은 몫이며, 나머지는 결과를 극삼각형에 적용하여 시작합니다.

델람브르의 유사점

델람브레 유추법(가우스 유추법이라고도 함)은 델람브레, 가우스, 몰와이드에 의해 1807–1809년에 ^[6]독립적으로 출판되었다.

또 다른 8개의 정체성은 주기적 치환으로 이어진다.

분자를 확장하고 반각 공식을 사용하여 증명되었습니다.(토드헌터,^[1] 제54조 및 델람브레^[7])

네이피어의 비유

또 다른 8개의 정체성은 주기적 치환으로 이어진다.

이러한 정체성은 델람브레 공식의 분할에 따른다.(토드헌터,^[1] 제52조)

이들의 지수를 취하면 페르시아 수학자 나시르 알-딘 알-투시 (1201–1274)에 의해 처음 언급된 접선의 법칙이 산출된다.

직구 삼각형에 대한 네이피어의 법칙

구면 삼각형의 각도, 예를 들어 C가 θ/2일 때 위에 주어진 다양한 동일성은 상당히 단순화된다.집합 a, b, c, A, B에서 선택된 세 가지 요소에 관련된 10개의 ID가 있습니다.

Napier는^[8] 10개의 독립적인 방정식에 우아한 니모닉을 제공했습니다: 니모닉은 Napier의 원 또는 Napier의 오각형이라고 불립니다.

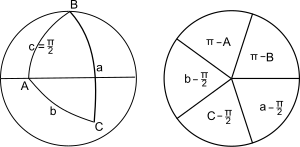
먼저 삼각형의 6개 부분(3개의 정점 각도, 변의 3개의 호 각도)을 삼각형의 어느 회로 주위에서나 발생하는 순서대로 적습니다.왼쪽 삼각형에 대해서는 a부터 시계 방향으로 가면 aCbAcB가 됩니다.다음으로 C에 인접하지 않은 부품(A, c, B)을 보완 부품으로 교체한 후 목록에서 각도 C를 삭제합니다.나머지 부품은 위 그림(오른쪽)과 같이 5개의 순서가 매겨진 동일한 펜타그램 슬라이스 또는 원으로 그릴 수 있습니다.3개의 연속된 부품을 선택할 경우, 1개(가운데 부분)는 2개의 부품에 인접하고 나머지 2개의 부품에는 반대입니다.Napier의 10가지 규칙은 다음과 같습니다.

• 중간 부분의 사인 = 인접한 부분의 접선 곱
• 중간 부분의 사인 = 반대 부분의 코사인 곱

예를 들어$,$ \$displaystyle$a를$$ $포함$하는 섹터부터 시작합니다.

$\displaystyle \sin a=\tan(\pi /2-B),\tan b=\cos(\pi /2-c),\cos(\pi /2-A)=\cot B,\tan b=\sin c,\sin A}$

오른쪽 구면 삼각형의 전체 규칙 집합은 다음과 같다(토드헌터,^[1] 제6조).

사분면 삼각형에 대한 네이피어의 법칙

사분면 구면삼각형은 구체의 중심에서 변의 한쪽이 θ/2 라디안의 각도로 섬세하게 되는 구면삼각형으로 정의된다.단위구에서는 변의 길이가 θ/2이다.변 c가 단위구상의 길이 θ/2인 경우, 나머지 변과 각도를 지배하는 방정식은 변 a', b', c'를 갖는 극삼각형 A'B'C'에 대해 A'=θ - a, a'=θ - A' 등으로 적용하면 된다.결과는 다음과 같습니다.

5부 규칙

두 번째 코사인 규칙을 첫 번째 코사인 규칙으로 대체하고 단순화하면 다음과 같이 됩니다.

$\cos a=(\cos a,\cos c+\sin a,\sin c,\cos B)\cos c+\sin b,\sin c,\cos A)$

$\displaystyle \cos a,\sin ^{2}c=\sin a,\cos c,\sin c,\cos B+,\sin b,\sin c,\cos A}$

sin${\displaystyle \mathrm{계수}}$를 ${\displaystyle \mathrm{소거}}$하면$$c$\displaystyle\sin$c는$$

$\displaystyle \cos a\sin c=\sin a,\cos c,\cos B+\sin b,\cos A}$

다른 코사인 공식과 보충 코사인 공식에서 유사한 치환은 다양한 5부 규칙을 제공합니다.그것들은 거의 사용되지 않는다.

카그놀리의 방정식

첫 번째 코사인 ${\displaystyle \mathrm{규칙}}$에 ${\displaystyle \cos }$를${\displaystyle }$곱하면 A$(\displaystyle \cos$ A$)$는 다음과 같습니다.

$\displaystyle \cos a=\cos b,\cos c,\cos A+\sin b,\sin c,\sin ^{2}A.}$

마찬가지로 첫 번째 보충 코사인 ${\displaystyle \mathrm{규칙}}$에 ${\displaystyle \cos }$를${\displaystyle }$곱하면$$\$displaystyle \cos$a가$$ 생성됩니다.

$(\displaystyle \cos a=-\cos B, cos a+\sin B, sin C, sin ^{2}a).}$

이 둘을 빼고 사인 규칙에서 sin${\displaystyle 2}$ b${\displaystyle {\sin }^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ c sin 2${\displaystyle {}^{}a}$ ${\displaystyle A}$ ${\displaystyle =}$ ${\displaystyle \sin b}$ B sin${\displaystyle c}$ C ${\displaystyle {sin\mathrm{}}^{}}$ 2${\displaystyle {}^{}a}$ $a$\ displaystyle \$sin$ b , \$sin$c$$, \$sin ^{$2}$$로 이어지는 것을 ${\displaystyle \mathrm{주목}}$한다.$A=\sin$ B$,\sin$ C$,\sin ^{2}a}$는 Cagnoli의 방정식을 생성합니다.

$(\displaystyle\sin b,\sin c,\cos A=\sin B,\cos C,\cos a)$

구면 ^[9]삼각형의 여섯 부분 사이의 관계입니다.

삼각형의 해

사삼각형

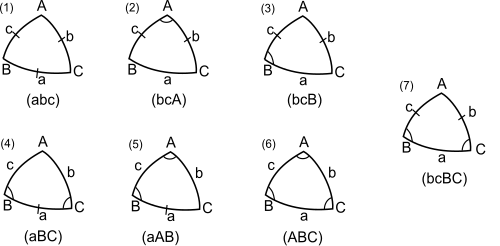
삼각형의 해는 구면 삼각법의 주요 목적이다: 삼각형의 세 가지, 네 가지 또는 다섯 가지 요소가 주어지면, 다른 요소를 결정한다.주어진 5개의 요소가 있는 경우는 단순하며 사인규칙을 한 번만 적용하면 됩니다.4개의 요소에 대해 아래에 설명되어 있는 하나의 중요하지 않은 경우가 있습니다.3개의 요소에 대해 6개의 케이스가 있습니다. 3개의 사이드, 2개의 사이드, 2개의 각도, 포함 또는 반대되는 사이드, 3개의 각도입니다.(마지막 사례는 평면 삼각법에서 유사점이 없습니다.)한 가지 방법으로 모든 문제를 해결할 수는 없습니다.아래 그림은 7가지 중요하지 않은 경우를 보여줍니다.각각의 경우, 지정된 변은 십자 막대로 표시되고 지정된 각도는 호로 표시됩니다(지정된 요소도 삼각형 아래에 나열됩니다).ASA와 같은 요약 표기법에서 A는 주어진 각도를 가리키고 S는 주어진 변을 가리키며 표기법 A와 S의 시퀀스는 삼각형 내의 대응하는 시퀀스를 가리킵니다.

• 케이스 1: 3면 지정(SSS).코사인 규칙을 사용하여 각도 A, B 및 C를 지정할 수 있지만 모호성을 피하기 위해 반각 공식을 사용하는 것이 좋습니다.
• 케이스 2: 두 변과 포함된 각도(SAS).코사인 규칙에 의해가 주어지고 케이스1로 돌아갑니다
• 케이스 3: 2변과 반대각(SSA).사인법칙은 C를 나타내며, 다음으로 케이스 7을 나타냅니다.한두 가지 해결책이 있습니다.
• 케이스 4: 2개의 각도와 포함된 변(ASA)세트(cBaC) 및 (BaCb)의 4분할 코탄젠트 공식은 c와 b를 나타내며 A는 사인 규칙에서 나옵니다.
• 케이스 5: 2개의 각도와 반대쪽(AAS)이 주어집니다.사인규칙은 b를 나타내며 케이스 7(회전)이 있습니다.한두 가지 해결책이 있습니다.
• 사례 6: 주어진 3개의 각도(AAA).보조 코사인 규칙을 사용하여 변 a, b 및 c를 지정할 수 있지만 모호함을 피하기 위해 반쪽 공식이 선호됩니다.
• 케이스 7: 2개의 각도와 2개의 반대쪽(SSAA)이 주어진다.A와 A에 Napier의 유추를 사용하거나 Case 3(SSA) 또는 Case 5(AAS)를 사용합니다.

여기에 기재되어 있는 솔루션 방법만이 가능한 것은 아닙니다.다른 많은 방법이 가능합니다.일반적으로 각도와 그 보충 사이에 모호성이 있을 수 있으므로 역사인식을 사용하지 않는 방법을 선택하는 것이 좋습니다.반각 공식을 사용하는 것이 권장되는 경우가 많다. 왜냐하면 반각 공식이 θ/2보다 작기 때문에 모호성이 없기 때문이다.토드헌터에서는 충분한 논의가 있다.삼각형의 해법 #구면 삼각형의 해법 기사에서는 이러한 방법에 대한 변형을 약간 다른 표기법으로 제시한다.

토드헌터에서는 ^{[1]: Chap. VI} 사삼각형의 해법에 대한 완전한 논의가 있다.Ross의 ^[10]토론도 참조해 주세요.

직각 삼각형에 의한 해결

또 다른 방법은 삼각형을 두 개의 직각 삼각형으로 나누는 것입니다.예를 들어 케이스 3의 예를 들어 b, c, B가 주어집니다.점 D에 수직인 A부터 변 BC까지 대원을 생성한다.삼각형 ABD를 풀기 위해 Napier의 규칙을 사용합니다. AD, BD 및 각 BAD를 구하려면 c와 B를 사용합니다.그런 다음 Napier의 규칙을 사용하여 삼각형 ACD를 해결합니다. 즉, AD와 b를 사용하여 변 DC와 각도 C와 DAC를 찾습니다.각도 A와 변은 덧셈으로 이어집니다.

수치에 관한 고려사항

예를 들어 각도가 0이나 θ에 가까워지는 경우 등 극단적인 예에서 얻어진 모든 규칙이 수치적으로 견고한 것은 아닙니다.문제와 해결책은 특히 임의의 삼각형을 해결하기 위해 코드를 작성할 때 주의 깊게 검토해야 할 수 있습니다.

면적 및 구면 초과

N면 구면 폴리곤을 고려하여 A가 n번째 내부 각도를 나타내도록 합니다_n.이러한 폴리곤의 면적은 (Todhunter,^[1] Art.99)에 의해 주어진다.

${\displaystyle {\text{{N}}\equiv E_{N}=\left(\sum_{n=1}^{N}A_{n}\right)-(N-2)\pi.}$

삼각형의 경우, 이것은 지라드의 정리로 줄어든다.

${\displaystyle {{text}}\equiv E=E_{3}=A+B+C-\pi}$

여기서 E는 각도의 합계가 θ 라디안을 초과하는 양입니다.양 E를 삼각형의 구면 초과라고 한다.이 정리는 작가인 Albert ^[11]Girard의 이름을 따서 붙여졌다.이전의 증거는 영국의 수학자 토마스 해리엇에 의해 도출되었지만 발표되지는 않았다.반지름 R의 구상에서 위의 두 영역식에 R을² 곱한다.과잉의 정의는 구체의 반지름과는 무관하다.

반대의 결과는 다음과 같이 쓸 수 있다.

$({displaystyle A+B+C=\pi +{\frac {4\pi \times {text {triangle의 영역}}) {\text {구체의 영역}}}).}$

삼각형의 면적은 음수일 수 없기 때문에 구면 초과는 항상 양수이다.각도의 합계가 5µ(적절한 각도의 경우 3µ)에 달할 수 있기 때문에 반드시 작을 필요는 없습니다.예를 들어 구체의 옥탄트는 직각이 3개인 구면 삼각형이므로 초과분은 θ/2이다.실제 적용에서 그것은 종종 작다. 예를 들어 측지학 조사의 삼각형은 일반적으로 1'보다 훨씬 작은 호를 가진다. (랩^[12] 클라크,^[13] 구면 삼각형에 대한 레전드르의 정리)지구에서 변이 21.3km(및 면적 393km²)인 정삼각형의 초과는 약 1초이다.

과잉에 대한 많은 공식들이 있다.예를 들어, Todhunter,^[1] (Art.101~103)는 L'Huilier의 예를 포함하여 10가지 예를 제시합니다.

${\displaystyle\tfrac{1}{4}E=tfrcrt{tfrac{1}{2}s,\tan{tfrac{1}{2},(s-a),\tan{tfrac{1}{2},(s-b)},\tfrac{1}{2},(c)$

$여기$서 s $=$ (${\displaystyle a}$ +${\displaystyle b}$ +${\displaystyle c}$) /$$ {\$displaystyle$ s=($a+b+c)/2$ 일부 삼각형의 모서리 특성이 좋지 않기 때문에($예$: a $=$ $b1\frac{\mathrm{}}{}$ 1 $\frac{2}{}$ { $textstyle$ a=$b\approx$ {$frac {1$}{$2}c}),$ 종종 두 모서리의 초과에 대한 공식을 사용하는 것이 좋다.

${\displaystyle\tan\frac{E}{2}=bfrac{1}{2}a\tan{1+\tan{1}{2}a\tan{frac{1}{2}}b\cos C}{1+\tan{frac{1}{2}}a\cos C}.}$

각도 결손은 쌍곡선 지오메트리에 대해서도 마찬가지로 정의됩니다.

위도와 경도에서

적도로 둘러싸인 구면 사각형의 구면 초과, 1$(\$ _${1$$})$과 $(\displaystyle \lambda$ _${2}),$ 2(\displaystyle \$lambda _{2$}) 및$$ 2$displaystyle$lambda $_1})$ 사이의$$ 대원호${\displaystyle }$( ${\displaystyle {2\mathrm{}}_{}}$ 2,${\displaystyle {}_{}{2\mathrm{}}_{}}$2 $){$ $display$ ( \ $display da$_ {$2$ , \ $varphi$_ { 2$$} )는${\displaystyle ,}$

이 결과는 네이피어의 유추 중 하나에서 얻어진 것이다.${\displaystyle {1\mathrm{}}_{}}$ 1,${\displaystyle {}_{}{text\mathrm{}}_{}}$ 2,${\displaystyle {}_{}{text\mathrm{}}_{}}$2 - ${\displaystyle {text\mathrm{}}_{}}$1 ( \$$$displaystyle$ \ $varphi _$ ${$ 1} , \ $lambda _${2} - \ $lambda _$ {1} $)$이 모두 작기 때문에 익숙한 사다리꼴 영역 E ${4\mathrm{}}_{}1\frac{1}{}$ ( ${text\mathrm{}}_{}$ 2 +${}_{}$ 1 $)$이 $.$$_{1}}$ 입니다$.$

폴리곤의 면적은 위 유형의 개별 사각형, 폴리곤의 세그먼트와 두 개의 ^[14]자오선으로 둘러싸인 개별 삼각형, 그린의 ^[15]정리와 통합된 선 또는 GIS에서 일반적으로 수행되는 등면적 투영을 통해 계산할 수 있습니다.다른 알고리즘은 여전히 대원 거리 공식을 사용하여 계산된 변 길이를 사용할 수 있습니다.

「 」를 참조해 주세요.

• 항공 항법
• 천체 항법
• 타원 삼각법
• 대원거리 또는 구면거리
• 레나트 구
• 슈바르츠 삼각형
• 구면 기하학
• 구면 다면체

레퍼런스

외부 링크

• Weisstein, Eric W. "Spherical Trigonometry". MathWorld. 몇 가지 파생된 더 철저한 신원 목록
• Weisstein, Eric W. "Spherical Triangle". MathWorld. 몇 가지 파생된 더 철저한 신원 목록
• TriSph 구면 삼각형을 해결하기 위한 무료 소프트웨어로, 다양한 실용적인 응용 프로그램에 맞게 구성되며 gnomonic용으로 구성됩니다.
• Sudipto Banerjee의 "직교 투영기를 사용한 구면 삼각법 재방문"이 논문은 기본 선형 대수와 투영 행렬을 사용하여 코사인 구와 사인 법칙을 도출한다.
• "A Visual Proof of Girard's Theorem". Wolfram Demonstrations Project. OK Arik의
• 1740년으로 거슬러 올라가는 아랍어로 된 구면 삼각법에 대해 도표와 함께 말하는 "이탈평면과 단순평면에 대한 책"
• 구면 Robert G의 폴리곤에 대한 일부 알고리즘.체임벌린, 제트추진연구소 윌리엄 H 듀켓입니다이 논문은 많은 유용한 공식을 개발하고 설명하는데, 아마도 내비게이션과 지도 제작에 초점을 맞추고 있을 것이다.
• 구면 삼각형의 온라인 계산