3D 투영

일부 3D 투영 분류

3D 투영(또는 그래픽 투영)은 3차원(3D) 객체를 2차원(2D) 표면에 표시하는 데 사용되는 설계 기법입니다.이러한 투영법은 시각적 원근법 및 종횡 분석에 의존하여 보다 단순한 평면에서 보기 위한 복잡한 객체를 투영합니다.

3D 투영은 객체의 기본 형상의 주요 특성을 사용하여 점 지도를 만든 다음, 점 지도를 서로 연결하여 시각적 요소를 만듭니다.그 결과, 그림이나 이미지가 실제로는 평면(2D)이 아니라, 2D 디스플레이로 표시되는 솔리드 객체(3D)로 해석하는 개념적 속성이 포함된 그래픽이 생성됩니다.

3D 물체는 주로 2차원 매체(예: 종이와 컴퓨터 모니터)에 표시됩니다.따라서 그래픽 투영법은 일반적으로 사용되는 설계 요소이며, 특히 엔지니어링 도면, 제도 및 컴퓨터 그래픽에서 사용됩니다.투영도는 수학적 분석과 공식의 적용 또는 다양한 기하학적 및 광학 기술을 사용하여 계산할 수 있습니다.

개요

여러 유형의 그래픽 투영 비교

다양한 예상과 그 제작 방법

투영은 상상 속의 "프로젝터"를 사용하여 이루어집니다.투사된 정신적 이미지는 정비사가 원하는 완성된 ^{[further explanation needed]}그림에 대한 비전이 됩니다.방법은 기술 그래픽스(기계 도면, 컴퓨터 지원 설계 등) 훈련을 받은 사람 간에 동일한 이미징 절차를 제공합니다.방법을 따르는 것으로, 기술자는, 그리기 용지등의 평면면에 구상 화상을 작성할 수 있다.

두 가지 그래픽 투영 범주가 있으며 각각 고유한 방법을 사용합니다.

평행 투영

평행투영은 가상의 시점을 가진 투시투영에 해당합니다.즉, 카메라가 물체로부터 무한히 떨어져 있고 무한 초점거리 또는 "줌"을 갖는 투시투영입니다.

평행 투영에서는 물체에서 투영 평면까지의 시선이 서로 평행합니다.따라서 3차원 공간에서 평행한 선은 2차원 투영 영상에서 평행하게 유지됩니다.평행 투영은 초점 거리(카메라 렌즈 및 초점으로부터의 거리)가 무한히 넓은 투시 투영 또는 "줌"에도 해당합니다.

평행투영으로 그려진 이미지는 폴케의 정리에 설명된 대로 축을 따라 측정하기 위해 축측정에 의존합니다.일반적으로 결과 영상은 비스듬하지만(레이가 영상 평면에 수직이 아님), 특수한 경우 결과는 직교입니다(레이가 영상 평면에 수직).축삭측정법은 축삭측정법 투영법과 혼동해서는 안 된다. 영문학에서는 축삭측정법은 보통 특정 종류의 화보만을 지칭한다(아래 참조).

맞춤법 투영법

맞춤법 투영법은 기술 기하학의 원리에서 파생되며 3차원 물체의 2차원 표현입니다.평행 투영입니다(실제 및 투영 평면 모두에서 투영 선이 평행합니다).작업 도면의 투영 유형입니다.

보기 평면(카메라 방향)의 법선이 기본 축(x, y 또는 z 축) 중 하나에 평행한 경우 수학적 변환은 다음과 같습니다.3D $b_{x}$ $a_{x}$ x $a_{x}$ x {\ $displaystyle a_{x$ $a_{y}$ {\ $displaystyle a_{y$ $a_{z}$ $b_{y}$ {\ $displaystyle$ $a_{z}},$ y {\displaystyle $b_{x$ $b_{y}$ {\ $displaystyle b_{y$ }}를 $a_{z}$ $b_{y}$ y축에 평행한 직각 투영(양수 y는 전방 프로파일 v)로 투영합니다.iw)는 다음과 같은 방정식을 사용할 수 있다.

\displaystyle b_{x}=s_{x}a_{x}+c_{x}

b_{y}=s_{z}a_{z}+c_{z}

여기서 벡터 s는 임의 스케일 계수이고 c는 임의 오프셋입니다.이러한 상수는 옵션이며 뷰포트를 올바르게 정렬하는 데 사용할 수 있습니다.행렬 곱셈을 사용하면 방정식은 다음과 같이 됩니다.

{bmatrix}b_{x}\\b_{y}\end{bmatrix}=param {bmatrix}s_{x}&0\end {bmatrix}a_{x}\a_y}\a_{bmatrix}\end{bmatrix}}}=param {bmatrix}

정자로 투영된 이미지는 투영된 물체의 3차원 특성을 나타내지만, 관찰자가 직접 관찰한 물체는 사진에 기록되거나 인식되기 때문에 물체를 나타내지 않습니다.특히, 맞춤법 투사 화상의 모든 점에서의 평행길이는 가상 뷰어와의 거리가 먼지, 가까운지에 관계없이 같은 척도로 한다.그 결과 투시 투영과 같이 길이가 단축되지 않습니다.

다중 뷰 투영

다중 뷰 투영이 세 번째 각도(오른쪽) 또는 첫 번째 각도(왼쪽)인지 정의하는 데 사용되는 기호입니다.

멀티뷰 투영을 사용하면 각 투영 평면이 객체의 좌표 축 중 하나에 평행한 최대 6개의 객체 사진(기본 뷰라고 함)이 생성됩니다.뷰는 첫 번째 각도 투영 또는 세 번째 각도 투영이라는 두 가지 방식 중 하나에 따라 서로 상대적으로 배치됩니다.각각의 경우 뷰의 외관은 객체 주위에 6면 상자를 형성하는 평면에 투영된 것으로 간주할 수 있습니다.6개의 다른 면을 그릴 수 있지만 일반적으로 3D 객체를 만드는 데 필요한 정보를 3개의 도면 뷰에서 얻을 수 있습니다.이러한 뷰를 전면 뷰, 상단 뷰 및 끝 뷰라고 합니다.표고, 평면 및 단면이라는 용어도 사용됩니다.

경사 투영

45° 각도, 2/3 비율의 캐비닛 투영으로 그려진 화분 벤치

군사적 관점에서 그려진 석조 아치

경사 투영에서 평행 투영 광선은 직각 투영과 같이 보기 평면에 수직이 아니라 90도 이외의 각도로 투영 평면을 타격합니다.직교 투영과 경사 투영 모두에서 공간의 평행선이 투영된 영상에 평행하게 나타납니다.사선 투영은 단순하기 때문에 형식적인 작업 도면이 아닌 그림 용도로만 사용됩니다.사선도면에서는 축간의 표시각도와 전단률(척도)이 임의이다.이것에 의해 생성되는 왜곡은, 통상, 투영 평면에 평행하도록 이미징 오브젝트의 1개의 평면을 정렬하는 것에 의해서 감쇠해, 선택한 평면의 실제 형상의 풀 사이즈 이미지를 작성합니다.사선 투영의 특수 유형은 다음과 같습니다.

캐벌리어 투영(45°)

카발리어 투영(카발리어 투시 또는 하이 뷰 포인트)에서 객체의 점은 x, y 및 z의 세 가지 좌표로 표시됩니다.도면에 x and와 y″ 두 개의 좌표만으로 표시됩니다.평면도에서는 그림상의 2개의 축 x와 z가 수직이며, 이들 축의 길이는 1:1 축척으로 그려집니다.따라서 세 번째 축 y는 대각선으로 그려지며, 보통 30° 또는 45°의 X축과 임의의 각도를 형성하기 때문에 축척 투영과 유사합니다.세 번째 축의 길이는 축척되지 않습니다.

캐비닛 투영

캐비닛 투영(캐비닛 투사)이라는 용어는 ^{[citation needed]}가구업계의 일러스트레이션에서 사용되었기 때문에 유래합니다.투사된 물체의 한쪽 면이 시야 평면에 평행하고 세 번째 축이 각도(일반적으로 30° 또는 45° 또는 arctan(2) = 63.4°)로 투영됩니다.세 번째 축이 길이를 유지하는 캐벌리어 투영과 달리 캐비닛 투영에서는 후퇴하는 선의 길이가 반으로 잘립니다.

군사 계획

사선 투영의 변형은 군사 투사라고 불립니다.이 경우 평면도가 왜곡되지 않도록 수평 단면을 등각도로 그린다.밀리터리 투영법은 xy 평면에서 회전하고 수직 변환은 양 ^[1]z로 제공됩니다.

축각 투영법

3개의 축삭 측정 뷰

축도 투영법은 한 ^[2]사진에서 공간의 세 방향(축)을 모두 나타내기 위해 기울어진 방향에서 바라본 물체의 이미지를 보여줍니다.축색 투영법은 직교 투영법 또는 경사 투영법일 수 있습니다.축색계 계측기 도면은 종종 그래픽 투시 투영에 사용되지만 근사치에 보조 왜곡이 있습니다.그림 투영에는 본질적으로 이러한 왜곡이 포함되어 있기 때문에, 그림 도면에서 노력과 최선의 ^{[clarification needed]}효과를 위해 많은 자유를 취할 수 있다.

축도 투영법은 뷰가 ^[3]^[4]직교에서 벗어나는 정확한 각도에 따라 등각 투영, 치수 투영 및 삼각 투영이라는 세 가지 범주로 세분됩니다.정형 화보의 전형적인 특징은 보통 한 축의 공간이 수직으로 표시된다는 것입니다.

축도 투영법은 멀티뷰 투영법의 기본 뷰와는 반대로 보조 뷰라고도 합니다.

등각 투영법

등각도 화보(방법에 대해서는 등각도 투영 참조)에서 시야의 방향은 공간의 세 축이 동일하게 단축된 것으로 나타나며, 이들 사이에 120°의 공통 각도가 있다.전축에 의한 왜곡은 균일하기 때문에 모든 변과 길이의 비례성이 유지되고 축이 공통의 축척을 공유합니다.이를 통해 도면에서 직접 측정치를 읽거나 가져올 수 있습니다.

치수 투영

치수화상(방법에 대해서는 치수투영 참조)에서 시야방향은 공간의 3축 중 2축이 동일하게 단축되어 보이도록 하고, 그 중 어텐던트 스케일 및 프레젠테이션 각도는 시야각에 따라 결정되며, 제3방향(수직)의 스케일은 별도로 결정된다.근사치는 치수 도면에서 흔히 볼 수 있습니다.

삼각 투영법

트리메트릭 화보(방법에 대해서는 트리메트릭 투영 참조)에서 보기 방향은 공간의 모든 축이 균일하게 단축된 것처럼 보입니다.3개의 축을 따른 축척과 축 사이의 각도는 보는 각도에 따라 별도로 결정됩니다.트리메트릭 도면의 근사치는 일반적입니다.

평행 투영 한계

등각 투영 제한의 예제입니다.빨간색 공과 파란색 공 사이의 높이 차이는 국지적으로 결정할 수 없다.

펜로즈 계단은 시계방향으로 오르거나 내리거나(시계방향으로) 연속적인 고리를 형성하는 계단을 묘사합니다.

평행 투영으로 그려진 개체는 뷰어에 더 가깝거나 뷰어에서 멀어질 때 더 크거나 더 작게 나타나지 않습니다.이미지에서 직접 측정해야 하는 건축 도면에는 유리하지만, 투시 투영과 달리 이것은 보통 우리의 눈이나 사진이 작동하는 방식이 아니기 때문에 그 결과는 지각된 왜곡입니다.또한 오른쪽 그림과 같이 깊이와 고도를 측정하기 어려운 상황에서도 쉽게 발생할 수 있습니다.

이 등각도에서는 파란색 구체가 빨간색 구면보다 두 단위 높습니다.그러나 오른쪽 반을 덮으면 높이를 나타내는 단서가 되는 상자가 가려지기 때문에 이러한 표고 차이는 분명하지 않다.

이러한 시각적 모호성은 "불가능한 객체" 도면뿐만 아니라 opart에서도 이용되었습니다.M. C. 에셔 폭포(1961년)는 엄밀하게 평행투영을 이용하지는 않지만, 물의 통로가 도움을 받지 않고 아래쪽으로 이동하는 것처럼 보이지만, 그 근원으로 돌아오면 역설적으로 다시 떨어지는 잘 알려진 사례이다.따라서 물은 에너지 보존의 법칙에 위배되는 것으로 보인다.영화 Inception에서 극단적인 예가 묘사되어 있는데, 여기서 움직이지 않는 계단이 강제로 원근법을 통해 연결성을 변화시킵니다.비디오 게임 Fez는 원근법을 사용하여 플레이어가 퍼즐처럼 움직일 수 있는 위치와 그렇지 않은 위치를 결정합니다.

투시 투영

두 개의 소실점을 사용한 기하학적 실체의 원근법.이 경우, 그라운드 평면을 구부리는 것처럼 솔리드(직교 투영)의 맵이 원근법 아래에 그려집니다.

수직 화상 평면 투시의 관련 요소를 표시하는 스킴의 축각 투영.스탠딩 포인트(P.S.)는 지상 평면 θ에 위치하고 시점(P.V.)은 그 바로 위에 있으며, P.P.는 그림 평면 α에 투영되어 있다. L.O.와 L.T.는 수평선 및 그라운드 라인(linea d'izzonte and linea di terra)이다.굵은 선 s와 q는 θ 위에 있고, Ts와 Tq에서는 각각 α를 가로채고 있습니다.P.V.를 통과하는 평행선(빨간색)은 소실점 Fs와 Fq에서 L.O.를 가로채기 때문에 R에 투영 sθ와 qθ를 그릴 수 있으며, 그 교차점 Rθ도 그릴 수 있다.

투시 투영 또는 투시 변환은 3차원 물체가 그림 평면에 투영되는 선형 투영입니다.이것은 멀리 있는 물체가 가까운 물체보다 작아 보이는 효과가 있다.

이것은 또한 자연에서 평행한 선들이 투영된 이미지에서 교차하는 것처럼 보인다는 것을 의미합니다. 예를 들어, 철도가 투시 투영으로 촬영된 경우, 소실점이라 불리는 단일 점으로 수렴되는 것처럼 보입니다.사진 렌즈와 사람의 눈은 같은 방식으로 작동하기 때문에 투시 투영법이 가장 ^[5]사실적으로 보입니다.투시투영은 일반적으로 묘사된 객체의 ^[6]축을 향한 투영 평면의 방향에 따라 1점, 2점 및 3점 투시로 분류됩니다.

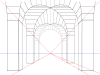
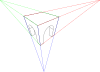
그래픽 투영 방법은 선과 점 사이의 이중성에 의존합니다. 즉, 두 개의 직선이 점을 결정하는 반면 두 개의 점이 직선을 결정합니다.그림 평면에 대한 시점의 직교 투영을 주 소실점이라고 합니다. (르네상스 ^[7]시대에 만들어진 이탈리아어 punto principale에서 왼쪽에 있는 스킴의 P.P.)

라인에 관련된 두 가지 점은 다음과 같습니다.

그림 평면과의 교차점, 그리고
시점과 그림 평면 사이의 교차점에서 발견된 소실점.

주요 소실점은 화면 평면에 수직인 모든 수평선의 소실점입니다.모든 수평선의 소실점은 수평선에 있습니다.흔히 그렇듯이 화상평면이 수직이고 모든 수직선이 수직으로 그려지며 화상평면에 유한 소실점이 없는 경우.기하학적 장면을 투영하기 위해 다양한 그래픽 방법을 쉽게 상상할 수 있습니다.예를 들어 45°의 시점에서 그림 평면으로 추적된 선은 반경 45° 선의 모든 소실점을 구성하는 데 도움이 되는 원을 따라 후자와 교차한다. 특히 이 원과 수평선의 교차점은 두 개의 원류로 구성된다.ance 포인트체스판 바닥을 그리는 데 유용하며, 체스판 바닥은 씬(scene)에서 객체의 밑면을 찾는 데 사용됩니다.오른쪽의 기하학적 실체의 관점에서는 수평선을 결정하는 주요 소실점을 선택한 후 도면 왼쪽에 있는 45° 소실점을 선택하면 (등거리) 시점의 특성화가 완료됩니다.각 정점의 직교 투영에서 두 개의 선이 그려집니다. 하나는 45°이고 다른 하나는 화면 평면에 대해 90°입니다.접지선과 교차한 후 이러한 선은 거리점을 향해 갑니다(45°의 경우).또는 주점(90°의 경우)을 선택합니다.그들의 새로운 교차로는 지도의 투영 위치를 찾아낸다.자연 높이는 그라운드 라인 위에서 측정된 후 지도에서 수직과 만날 때까지 동일한 방식으로 투영됩니다.

정확한 측정을 위해 원근법을 무시한 반면 원근법 투영법은 원근법을 더 작은 크기로 표시하여 사실감을 더합니다.

수학 공식

투시 투영에는 맞춤법 투영에 비해 더 복잡한 정의가 필요합니다.이 투영의 구조를 이해하는 데 개념적으로 도움이 되는 것은 마치 카메라 뷰파인더를 통해 물체를 보는 것처럼 2D 투사를 상상하는 것입니다.카메라의 위치, 방향 및 시야는 투영 변환의 동작을 제어합니다.이 변환을 설명하기 위해 정의된 변수는 다음과 같습니다.

$\mathbf {a} _{x,y,z}$ x $\mathbf {a} _{x,y,z}$ $\mathbf {a} _{x,y,z}$ \ $displaystyle \mathbf {a} _{x,y,z}$ – 투영되는 점 A의 3D 위치.
$\mathbf {c} _{x,y,z}$ x , $\mathbf {c} _{x,y,z}$ , $\mathbf {c} _{x,y,z}$ \ $displaystyle \mathbf {c} _{x,y,z}$ – 카메라를 나타내는 점 C의 3D 위치.
$\mathbf {\theta } _{x,y,z}$ $\mathbf {\theta } _{x,y,z}$ $,$ $z$ \displaystyle \ $mathbf \theta$ } $_{x,y$ ,z} – 카메라의 방향 (Tait-Bryan 각도로 표시됨).
$\mathbf {e} _{x,y,z}$ x $\mathbf {e} _{x,y,z}$ $\mathbf {e} _{x,y,z}$ \ $displaystyle \mathbf {e} _{x,y,z}$ – 카메라 핀홀 ^[8]C에 대한 디스플레이 표면의 위치.

대부분의 규칙은 양의 z 값(평면이 핀홀 앞에 있음)을 사용하지만, 음의 z 값이 물리적으로 더 정확하지만 이미지가 수평과 수직으로 모두 반전됩니다.그 결과:

$\mathbf {b} _{x,y}$ x , $\mathbf {b} _{x,y}$ \ $displaystyle \mathbf {b} _{x,y}$ – $\mathbf {a} .$ 의 $\mathbf {a} .$ 투영 $.\displaystyle \mathbf {a}$

$\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ x , $\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ , $\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ $\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ 0 , $\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ , 0 $\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ , { $displaystyle \mathbf$ { $c$ $}$ $_$ { $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ $x$ , $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ $y$ , z $=$ \ $scaple$ 0 $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ , $0$ , $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ , $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ . $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ $rangle$ , $\mathbf {c} _{x,y,z}=\langle 0,0,0\rangle ,$ } $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,$ xdisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay $、$ \ $displaystyle$ \ $mathbf$ { $0$ , 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . 0 . $aystyle \sysle$ 1 $,2\rangle$ } $\langle 1,2\rangle$ 。

$\mathbf {b} _{x,y}$ 않으면 b x $\mathbf {b} _{x,y}$ \ $display \mathbf {b} _{x,y}$ 를 ${\mathbf {b}}_{{x,y}}$ $\mathbf {b} _{x,y}$ 하기 위해 먼저 $\mathbf {d} _{x,y,z}$ d $,$ z\ $displaystyle \mathbf {d} _{x,y,z}$ 를 ${\mathbf {d}}_{{x,y,z}}$ 카메라에서 정의하여 C에서 원점을 C로 하고 $\display$ \ $mathbf {ta}$ 에 $\mathbf {\theta }$ 의해 회전하는 점 A의 위치로 정의합니다.e 초기 좌표계.이를 $위해서$ 는 \displaystyle $\mathbf {a}$ 에서 $\mathbf {a}$ c $\$ 를 $\mathbf {c}$ $\mathbf {c}$ 뺀 다음 $-\mathbf {\theta }$ 에 - $-\mathbf {\theta }$ {\(\ $displaystyle$ -\ $mathbf {c})$ 회전을 $-\mathbf {\theta }$ 적용합니다.이 변환은 카메라 변환이라고 불리며 x, y 및 z 축에 대한 회전으로 다음과 같이 나타낼 수 있습니다(이 계산에서는 축이 왼쪽 축 시스템으로 정렬된다고 가정합니다).^[9] ^[10]

{\displaystyle{\begin{bmatrix}\mathbf{d}_{)}\\\mathbf{d}_{y}\\\mathbf{d}_{z}\end{bmatrix}}={\begin{bmatrix}1&, 0&, 0\\0&, \cos(\mathbf{\theta}_{x})&, \sin(\mathbf{\theta}_{x})\\0&, \sin(\mathbf{\theta}_{x})&, \cos(\mathbf{\theta}_{x})\end{bmatrix}}{\begin{bmatrix}(\mathbf{\theta}_{y})&, 0&, -\sin(\mathbf{년.theta}_{y})\\0&, 1&, 0\\\sin(\mathBf{\theta}_{y})&0&, +\cos(\mathbf{\theta}_{y})\end{bmatrix}}{\begin{bmatrix}(\mathbf{\theta}_{z})&, \sin(\mathbf{\theta}_{z})&, 0\\-\sin(\mathbf{\theta}_{z})&, \cos(\mathbf{\theta}_{z})&, 0\\0&, 0&, 1\end{bmatrix}}\left({{\begin{bmatrix}\mathbf{를}_{)}\\\mathbf{를}_{y}\\\mathbf{를}_{z}\\\end{bmatrix}}-{\b.egin{bmatrix}\mathbf{c}_{)}\\\mathbf {c}_{y}\\mathbf {c}_{z}\\end {bmatrix}}\right}}

이 표현은 xyz 규칙을 사용하여 3개의 오일러 각도(더 적절하게 타이-브라이언 각도)로 회전하는 것에 해당하며, 이는 "z, y, y, y, y의 순서로 카메라의 내적 축(축)을 중심으로 회전한다" 또는 "x, y의 순서로 카메라의 고유 축(축)을 중심으로 회전한다"로 해석될 수 있다.eft-to-right).카메라가 회전하지 않은 경우( $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ , $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ , y , $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ , 0 , $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ , 0 ${\$ { $display style$ \ $mathbf } _ { x$ , $y$ , z } = \ $scaple$ 0 , $0$ , 0 \ $rangle$ } $\mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle$ ) 매트릭스는 드롭되고 이는 $\mathbf {d} =\mathbf {a} -\mathbf {c} .$ 시프트: $\mathbf {d} =\mathbf {a} -\mathbf {c} .$ $\mathbf {d} =\mathbf {a} -\mathbf {c} .$ $\mathbf {d} =\mathbf {a} -\mathbf {c} .$ - $display$ . $\mathbf {d} =\mathbf {a} -\mathbf {c} .$ display { $df$ = \ $mathb$ style $=$

또는 행렬을 사용하지 않고 ( $a_{x}-c_{x}$ $a_{x}-c_{x}$ $a_{x}-c_{x}$ x $a_{x}-c_{x}$ x { $displaystyle$ a $_$ { x $a_{x}-c_{x}$ } - $c$ _ { $x$ } 를 $a_{x}-c_{x}$ x $\mathbf {x}$ \ $displaystyle$ \ $mathbf { x }$ $\mathbf {x}$ 으로 $\mathbf {x}$ $a_{x}-c_{x}$ 하고 cos $\cos \left(\theta _{\alpha }\right)$ ( $α$ ) \ $displaystyle$ \ $\cos \left(\theta _{\alpha }\right)$ $cos$ \ left $\cos \left(\theta _{\alpha }\right)$ ( \ $thta$ _ { \ { \ $alpha$ } \ $\cos \left(\theta _{\alpha }\right)$ right } \ $\sin \left(\theta _{\alpha }\right)$ )를 $c_{\alpha }$ $\cos \left(\theta _{\alpha }\right)$ $c_{\alpha }$ $\sin \left(\theta _{\alpha }\right)$ $sin$ sin )로 단축합니다. $e \sin \left(\theta$ _ ${\alpha$ }\ $right)$ 에서 $\sin \left(\theta _{\alpha }\right)$ $(\$ }): $s_{\alpha }$

{\displaystyle{\begin{정렬}\mathbf{d}_{)}&, =c_ᆯ(s_{z}\mathbf{y}+c_{z}\mathbf{x})-s_{y}\mathbf{z}\\\mathbf{d}_{y}&, =s_ᆴ(c_{y}\mathbf{z}+s_{y}(s_{z}\mathbf{y}+c_{z}\mathbf{x}))+c_ᆵ(c_{z}\mathbf{y}-s_{z}\mathbf{x})\\\mathbf{d}_{z}&, =c_ᆸ(c_{y}\mathbf{z}+s_{y}(s_{z}\mathbf{y}+c_{z}\mathbf{x}))-s_{)}(c_{z}.\mathbf{y}-s_{z}\mathbf {x}\end {aligned}}

변환된 이 점은 다음 공식을 사용하여 2D 평면에 투영할 수 있습니다(여기서 x/y는 투영 평면으로 사용되며, 문헌에서도 x/z를 사용할 수 있습니다).^[11]

{\displaystyle\mathbf {b}_{x}&=mathbf {e}_{z}}{\mathbf {d}_{x}+\mathbf {e}_{x}\[5pt]\mathbf {b}_y={z}\end { aligned}}

또는, 동종 좌표를 사용하는 행렬 형식에서,

{\displaystyle{\begin{bmatrix}\mathbf{f}_{)}\\\mathbf{f}_{y}\\\mathbf{f}_{w}\end{bmatrix}}={\begin{bmatrix}1&, 0&,{\frac{\mathbf{e}_{)}}{\mathbf{e}_{z}}}\\0&, 1&,{\frac{\mathbf{e}_{y}}{\mathbf{e}_{z}}}\\0&, 0&,{\frac{1}{\mathbf{e}_{z}}}\end{bmatrix}}_{y}\\\mathbf{d}{d}즉{d}_{)}\\\mathbf{\begin{bmatrix}\mathbf.{z}\end{bmatrix}}}

유사한 삼각형을 사용하는 논쟁과 함께, 균질한 좌표에 의해 나눗셈을 유도, 주어

{displaystyle} \mathbf {b} _{x} /\mathbf {f} _{w} \\\mathbf {b} _{y} &=\mathbf {f} / \mathbf {f} _{w

표시 표면으로부터의 뷰어 거리 $\mathbf {e} _{z}$ z $(\$ 는 시야와 직접 관련되며, $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ 서 α $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ ( $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ / $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ z $\alpha =2\cdot \arctan(1/\mathbf {e} _{z})$ ) { $displaystyle \alpha = 2$ \ $cdot \arctan$ ( $1$ / \ $mathbf {e$ } _ ${z}$ ) } } } } 。(주의: (-1,-1)과 (1,1)을 표시면의 모서리에 매핑하는 것을 전제로 합니다.)

위의 방정식은 다음과 같이 다시 작성할 수도 있습니다.

{signed}\mathbf {b}_{x}&=(\mathbf {d}_{x})/(\mathbf {d}_{z}\mathbf {r}_{x})\mathbf {r}_mathbf {b}_y={x}\end { aligned}

$\mathbf {s} _{x,y}$ 서 s x $\mathbf {s} _{x,y}$ 는 ${\mathbf {s}}_{{x,y}}$ 디스플레이 크기, $\mathbf {r} _{x,y}$ $\mathbf {r} _{x,y}$ $\$ 는 ${\mathbf {r}}_{{x,y}}$ 기록 표면 크기(CCD 또는 필름), $\$ _ ${z}$ 는 ${\mathbf {r}}_{z}$ 기록 표면에서 동공까지의 거리(카메라 $\mathbf {d} _{z}$ $센터$ )입니다. $ystyle \mathbf {d} _{z}$ 는 ${\mathbf {d}}_{z}$ 투영되는 3D 점에서 입구 동공까지의 거리입니다.

2D 평면을 특정 디스플레이 미디어에 매핑하려면 후속 클리핑 및 스케일링 작업이 필요할 수 있습니다.

약한 투시법

"약한" 투시 투영에서는 같은 원리의 맞춤법 투영을 사용하지만 축척 계수를 지정해야 하므로 투영에서 더 가까운 객체가 더 크게 나타나도록 하고 그 반대도 마찬가지입니다.이는 맞춤법과 투시법 사이의 혼성 투영으로 볼 수 있으며, $Z_{i}$ $Z_{i}$ 깊이 Zi $(\$ i $Z_{i}$ })가 $Z_{\text{ave}}$ 고정 $Z_{\text{ave}}$ Z $ave$ (\ $displaystyle Z_{\text{$ ave $Z_{\text{ave}}$ ^[12]로 대체된 투시 투영 또는 단순히 맞춤법 투영 + ^[13]스케일링으로 설명할 수 있습니다.

따라서 약한 관점 모델은 순수한(스케일링되지 않은) 맞춤법 원근법 원근법과 유사한 단순한 모델을 사용하면서 원근법 투영에 근접한다.카메라와의 거리에 비해 시야를 따라 있는 물체의 깊이가 작고 시야가 작을 때 적당한 근사치입니다.이러한 조건에서는, 3D 물체의 모든 점이 투영에 큰 오류 없이 카메라로부터 Z $(\$ Z_ ${\text{ave}})$ $Z_{\text{ave}}$ 에 $Z_{\text{ave}}$ 있다고 가정할 수 있습니다(전체 투시 모델에 비해).

방정식

{\displaystyle\begin{aligned}&P_{x}=param frac {X}{Z_{\text{ave}}}\[5pt]&P_{y}=param frac {Y}{Z_{\text{ave}}}}}\end{aligned}}}

초점 $f=1$ f $f=1$ $f=1$ f $=$ 로 가정합니다.

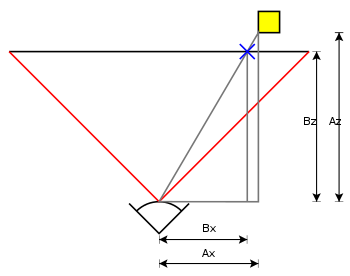
도표

A x의 $A_{x},A_{z}$ 에 해당하는 $A_{x},A_{z}$ x 좌표를 확인하려면 A $A_{x},A_{z}$ {\ $displaystyle A_{x},A_{z}}$ 에 $A_{x},A_{z}$ 점 좌표를 곱합니다.

\displaystyle B_{x}=A_{x}{\frac {B_{z}}{A_{z}}}}

어디에

B_{x}

x {\

displaystyle B_{x}}

는

B_x

화면 x 좌표입니다.

(\

는

A_x

모델 x 좌표입니다.

B_{z}

z(\

displaystyle B_{z})

는

B_z

초점 거리입니다. 카메라 중심에서 이미지 평면까지의 축 방향 거리입니다.

z(\

A_

{z})

는

A_z

피사체 거리입니다.

카메라는 3D이기 때문에 위의 도표와 식에서 x 대신 y를 사용하여 화면 y 좌표도 동일하게 동작합니다.

이를 사용하여 잘라내기 기술을 수행할 수 있습니다. 변수를 FOV 각도를 벗어난 점 및 카메라 매트릭스 내부의 점 값으로 대체할 수 있습니다.

"역방향 카메라"라고도 하는 이 기술은 필요한 변환이 모두 완료된 후 보이지 않는 지점에서 투영되는 가시 각도의 마지막 점을 계산하기 위해 알려진 값을 가진 투시 투영 미적분입니다.

「」를 참조해 주세요.

레퍼런스

^ "Axonometric projections - a technical overview". Retrieved 24 April 2015.
^ Mitchell, William; Malcolm McCullough (1994). Digital design media. John Wiley and Sons. p. 169. ISBN 978-0-471-28666-0.
^ Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell University Press. p. 22. ISBN 978-0-8014-7280-0.
^ McReynolds, Tom; David Blythe (2005). Advanced graphics programming using openGL. Elsevier. p. 502. ISBN 978-1-55860-659-3.
^ D. Hearn, M. Baker(1997).컴퓨터 그래픽스, C 버전엥글우드 절벽: 프렌티스 홀, 9장
^ 제임스 폴리(1997).컴퓨터 그래픽스보스턴:애디슨 웨슬리.ISBN 0-201-84840-6], 6장
^ Kirsti Andersen (2007), The geometry of an art, Springer, p. xxix, ISBN 9780387259611
^ Ingrid Carlbom, Joseph Paciorek (1978). "Planar Geometric Projections and Viewing Transformations" (PDF). ACM Computing Surveys. 10 (4): 465–502. CiteSeerX 10.1.1.532.4774. doi:10.1145/356744.356750. S2CID 708008.
^ Riley, K F (2006). Mathematical Methods for Physics and Engineering. Cambridge University Press. pp. 931, 942. ISBN 978-0-521-67971-8.
^ Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). Reading, Mass.: Addison-Wesley Pub. Co. pp. 146–148. ISBN 978-0-201-02918-5.
^ Sonka, M; Hlavac, V; Boyle, R (1995). Image Processing, Analysis & Machine Vision (2nd ed.). Chapman and Hall. p. 14. ISBN 978-0-412-45570-4.
^ Subhashis Banerjee (2002-02-18). "The Weak-Perspective Camera".
^ Alter, T. D. (July 1992). 3D Pose from 3 Corresponding Points under Weak-Perspective Projection (PDF) (Technical report). MIT AI Lab.

추가 정보

Kenneth C. Finney (2004). 3D Game Programming All in One. Thomson Course. p. 93. ISBN 978-1-59200-136-1. 3D projection.
Koehler; Dr. Ralph (December 2000). 2D/3D Graphics and Splines with Source Code. ISBN 978-0759611870.

외부 링크

디지털 사진으로 3D 환경 조성

[1] "Axonometric projections - a technical overview". Retrieved 24 April 2015.

[2] Mitchell, William; Malcolm McCullough (1994). Digital design media. John Wiley and Sons. p. 169. ISBN 978-0-471-28666-0.

[maynard-3] Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell University Press. p. 22. ISBN 978-0-8014-7280-0.

[mcreynolds-4] McReynolds, Tom; David Blythe (2005). Advanced graphics programming using openGL. Elsevier. p. 502. ISBN 978-1-55860-659-3.

[5] D. Hearn, M. Baker(1997).컴퓨터 그래픽스, C 버전엥글우드 절벽: 프렌티스 홀, 9장

[6] 제임스 폴리(1997).컴퓨터 그래픽스보스턴:애디슨 웨슬리.ISBN 0-201-84840-6], 6장

[7] Kirsti Andersen (2007), The geometry of an art, Springer, p. xxix, ISBN 9780387259611

[8] Ingrid Carlbom, Joseph Paciorek (1978). "Planar Geometric Projections and Viewing Transformations" (PDF). ACM Computing Surveys. 10 (4): 465–502. CiteSeerX 10.1.1.532.4774. doi:10.1145/356744.356750. S2CID 708008.

[9] Riley, K F (2006). Mathematical Methods for Physics and Engineering. Cambridge University Press. pp. 931, 942. ISBN 978-0-521-67971-8.

[10] Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). Reading, Mass.: Addison-Wesley Pub. Co. pp. 146–148. ISBN 978-0-201-02918-5.

[11] Sonka, M; Hlavac, V; Boyle, R (1995). Image Processing, Analysis & Machine Vision (2nd ed.). Chapman and Hall. p. 14. ISBN 978-0-412-45570-4.

[12] Subhashis Banerjee (2002-02-18). "The Weak-Perspective Camera".

[13] Alter, T. D. (July 1992). 3D Pose from 3 Corresponding Points under Weak-Perspective Projection (PDF) (Technical report). MIT AI Lab.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Search

3D 투영

네임스페이스

더

목차

개요