게임 이론

복잡한 시스템
토픽
자기 조직화 출현
집단 행동 사회 역학 집단 인텔리전스 단체 행동 자기 조직화된 중요도 군중심리 상전이 에이전트 기반 모델링 동기 개미 군락 최적화 입자 군집 최적화 군집 행동 집단 의식
네트워크 확장성이 없는 네트워크 소셜 네트워크 분석 소규모 네트워크 중앙집중성 모티브 그래프 이론 스케일링 견고성 시스템 생물학 동적 네트워크 적응형 네트워크
진화 및 적응 인공신경망 진화 계산 유전 알고리즘 유전자 프로그래밍 인공 생명 기계 학습 진화발달생물학 인공지능 진화형 로봇 공학 진화 가능성
패턴 형성 프랙탈 반응 확산계 편미분 방정식 산란 구조 퍼콜레이션 셀룰러 오토마타 공간생태학 셀프 리플리케이션 지형학
시스템 이론과 사이버네틱스 자동 인식 정보 이론 엔트로피 피드백 목표 지향적 항상성 운용화 2차 사이버네틱스 자기 참조 시스템 다이내믹스 시스템 사이언스 시스템 사고 센스 메이킹 다양성 계산 이론
비선형 역학 시계열 분석 상미분 방정식 위상 공간 어트랙터 모집단 역학 카오스 다기능 분기 결합된 지도 격자
게임 이론 죄수의 딜레마 합리적 선택 이론 한정적 합리성 진화 게임 이론
v t

시리즈의 일부
경제학
역사 개요 색인
지점 및 분류 경제학부 주류 경제 JEL 류 j j j
,, ★★★★ 리서치 ★★★
★★★ ★★★ 인 ★★★★★★★★★★★ ★ ★★ ★★ ★★★★★ ★★★★★★ ★★★ 페미니스트 페미니스트 ★★★★★★ ★★★ ★★★ ★★★ » ★★★ 연연자자 natural natural ★★★★ ★★★ ★★★ 퍼블릭/소셜 선택 ★★★★★ ★★★★★★★ ★★
저명한 경제학자 리카르도 로버트 밀 스탠리 마셜 피셔 케인스 세실 많은 정보를 얻을 수
저명한 경제학 비평가 마르크스 많은 정보를 얻을 수
출판물(여행)
및
v t

게임 이론은 합리적인 ^[1]대리인 간의 전략적 상호작용에 대한 수학적 모델의 연구입니다.논리학, 시스템 과학 및 컴퓨터 과학뿐만 아니라 사회과학의 모든 분야에서 응용되고 있습니다.원래는 각 참가자의 득실이 다른 참가자의 득실에 의해 정확히 균형을 이루는 2인 제로섬 게임을 다루었다.21세기에 게임 이론은 광범위한 행동 관계에 적용된다; 그것은 이제 인간, 동물, 그리고 컴퓨터에서의 논리적 의사결정에 대한 과학의 포괄적인 용어이다.

현대 게임 이론은 2인용 제로섬 게임에서의 혼합 전략 균형 아이디어와 존 폰 노이만의 증명에서 시작되었다.폰 노이만의 원래 증명은 콤팩트 볼록 집합으로의 연속 매핑에 대한 브루어 고정점 정리를 사용했는데, 이것은 게임 이론과 수리 경제학에서 표준적인 방법이 되었다.그의 논문은 1944년 오스카 모겐스턴과 공동 집필한 게임 이론과 경제 행동이라는 책이 뒤따랐는데, 이 책은 여러 선수들의 협력적인 게임을 고려했다.이 책의 제2판은 수학 통계학자와 경제학자가 불확실한 상황에서 의사결정을 다룰 수 있도록 하는 기대 효용에 대한 자명한 이론을 제공했다.

게임 이론은 1950년대에 많은 학자들에 의해 광범위하게 개발되었다.그것은 1970년대에 진화에 분명히 적용되었지만, 비슷한 발전은 적어도 1930년대까지 거슬러 올라간다.게임 이론은 많은 분야에서 중요한 도구로 널리 인식되어 왔다.2020년 현재^[update], 노벨 경제학상은 게임 이론가 폴 밀그롬과 로버트 B에게 돌아간다. 윌슨, 15명의 게임 이론가가 노벨 경제학상을 수상했습니다.존 메이나드 스미스는 진화 게임 이론을 응용한 공로로 크레이포드 상을 받았다.

★★★

게임의 수학에 대한 논의는 현대 수학 게임 이론이 등장하기 훨씬 전에 시작되었다.1564년경에 쓰여졌지만 1663년에 사후에 출판된 Liber de Ludo Aleae (운명의 게임에 관한 책)의 우연의 게임에 대한 카르다노의 연구는 이 분야의 기본적인 생각의 일부를 형성했다.1650년대에 파스칼과 호이겐스는 우연의 게임의 구조에 대한 추론에 대한 기대 개념을 발전시켰고, 호이겐스는 1657년에 그의 도박 미적분을 루도 알레의 데 라티오키니스에서 출판했다.

1713년, 찰스 월드그레이브에게 전해진 편지는 "르 허"라고 불리는 게임을 분석했다.그는 활동적인 자코바이트였고 영국 ^[2][3]외교관 제임스 월드그레이브의 삼촌이었다.이 편지에서 Waldegrave는 2인용 카드 게임 Le Her에 미니맥스 혼합 전략 솔루션을 제공했으며, 현재 이 문제는 Waldegrave 문제로 알려져 있습니다.앙투안 오귀스틴 쿠르는 1838년 '부(富) 이론의 수학적 원리로의 연구'에서 이중성을 고려하지 않고 게임의 내시 균형이라는 해법을 제시했다.

1913년, 에른스트 체르멜로는 최적의 체스 전략이 엄격히 결정된다는 것을 증명한 "Theorie des Schachspiels"를 출판했다.이것은 보다 일반적인 ^[4]이론의 기반을 닦았다.

1938년 덴마크 수학 경제학자 프레데릭 주텐은 브루어의 고정점 ^[5]정리를 사용하여 수학 모델이 승리 전략을 가지고 있다는 것을 증명했다.1938년 저서 Applications Juux de Hassard와 그 이전의 노트에서 에밀 보렐은 보상 행렬이 대칭일 때만 2인용 제로섬 매트릭스 게임에 대한 미니맥스 정리를 증명하고 사소한 무한 게임(Blotto game)에 대한 해답을 제공했다.보렐은 유한한 2인용 제로섬 게임에서 혼합 전략 평형의 부존재를 추측했는데, 이는 폰 노이만에 의해 거짓으로 판명되었다.

과

게임이론은 ^[6][7]1928년 존 폰 노이만이 전략 게임에 관한 논문을 발표하기 전까지 독특한 분야로 존재하지 않았다.폰 노이만의 원래 증명은 콤팩트 볼록 집합으로의 연속 매핑에 대한 브루어의 고정점 정리를 사용했는데, 이것은 게임 이론과 수리 경제학에서 표준적인 방법이 되었다.그의 논문은 1944년 오스카 모겐스턴과 ^[8]공동 집필한 게임 이론과 경제 행동이라는 책으로 이어졌다.이 책의 제2판은 다니엘 베르누이의 오래된 효용 이론을 독립적인 학문으로 환생시킨 자명한 효용 이론을 제공했다.폰 노이만의 게임 이론 연구는 1944년 이 책에서 정점을 찍었습니다.이 기초 작업은 2인용 제로섬 게임의 상호 일관된 해결책을 찾는 방법을 포함하고 있다.후속 연구는 주로 개인 그룹을 위한 최적의 전략을 분석하는 협동 게임 이론에 초점을 맞췄고, 적절한 전략에 대해 ^[9]그들 사이의 합의를 시행할 수 있다고 가정했다.

1950년, 죄수의 딜레마에 대한 첫 번째 수학적인 논의가 나타났고, 유명한 수학자 메릴 M.에 의해 실험이 수행되었다. Flood와 Melvin Dresher, RAND Corporation의 게임 이론 조사에 참여했습니다.RAND는 글로벌 핵 ^[10]전략에 적용할 수 있는 가능성 때문에 연구를 추구했다.비슷한 시기에, 존 내쉬는 내쉬 균형으로 알려진 플레이어 전략의 상호 일관성을 위한 기준을 개발하였고, 폰 노이만과 모르겐슈테른이 제안한 기준보다 더 다양한 게임에 적용할 수 있다.Nash는 모든 유한한 n플레이어, 넌제로섬(2플레이어 제로섬이 아닌) 비협력 게임이 혼합 전략에서 현재 내쉬 균형이라고 알려진 것을 가지고 있다는 것을 증명했다.

게임 이론은 1950년대에 핵심 개념, 광범위한 형태 게임, 가상 플레이, 반복 게임, 그리고 섀플리 가치의 개념이 개발되는 동안 많은 활동을 경험했다.1950년대 또한 게임 이론이 철학과 정치학에 처음으로 적용되었다.

경력 ★★★★★★

1965년 라인하르트 셀텐은 서브게임 완전균형의 솔루션 개념을 도입하여 내시균형을 더욱 개선하였다.나중에 그는 떨리는 손의 완벽함도 소개했다.1994년 내쉬, 셀텐, 하샤니는 경제 게임 이론에 대한 공헌으로 노벨 경제학상 수상자가 되었다.

1970년대에 게임 이론은 생물학에 광범위하게 적용되었는데, 주로 존 메이나드 스미스의 연구와 그의 진화적으로 안정된 전략의 결과였다.또한 상관평형, 떨리는 손의 완성도, 상식의^[a] 개념을 소개하고 분석하였다.

2005년, 게임 이론가 토마스 셸링과 로버트 아우만이 노벨상 수상자로 내시, 셀튼, 그리고 하샤니를 따랐다.셸링은 진화 게임 이론의 초기 사례인 동적 모델을 연구했습니다.아우만은 평형학파에 더 많은 기여를 했고, 평형협화 및 상관균형을 도입했으며, 상식의 가정과 그 결과에 대한 광범위한 공식 분석을 개발했습니다.

2007년 레오니드 후르비츠, 에릭 마스킨, 로저 마이어슨은 "메커니즘 설계 이론의 기초를 닦은" 공로로 노벨 경제학상을 수상했다.마이어슨의 공헌은 적절한 균형에 대한 개념과 중요한 졸업 교재: 게임 이론, ^[1]갈등의 분석을 포함합니다.Hurwicz는 인센티브 호환성의 개념을 도입하고 공식화했습니다.

2012년, 앨빈 E. 로스와 로이드 S. 섀플리는 "안정적 배분 이론과 시장 디자인 실천"으로 노벨 경제학상을 받았다.2014년에 노벨상은 게임 이론가 장 티롤에게 돌아갔다.

★★★★★★

플레이어가 (예를 들어 계약법을 통해) 외부에서 강제된 구속력 있는 약속을 형성할 수 있다면 게임은 협조적이다.플레이어가 동맹을 맺을 수 없거나 모든 합의가 자기강제가 필요한 경우(예: 신뢰할 수 있는 ^[11]위협을 통해) 게임은 비협조적입니다.

협동 게임은 종종 협동 게임 이론의 틀을 통해 분석됩니다. 협동 게임 이론은 어떤 연합이 형성될지, 그룹이 취하는 공동 행동과 그에 따른 집단 보상을 예측하는 데 초점을 맞춥니다.이것은 각각의 플레이어의 행동과 보상을 예측하고 내쉬 ^[12][13]평형을 분석하는 것에 초점을 맞춘 전통적인 비협력 게임 이론과 반대된다.개인의 이익에 초점을 맞추면 자원이 집단적으로 비효율적인 수준으로 사용되는 '공통의 비극'으로 알려진 현상이 발생할 수 있습니다.공식적인 협상의 부재는 과도한 ^[14]사용과 민간 인센티브에 의한 공급 부족에 의한 공공재의 악화를 초래한다.

협동 게임 이론은 단지 동맹의 구조, 전략, 보상만을 기술하기 때문에 높은 수준의 접근을 제공하는 반면, 비협조 게임 이론은 협상 절차가 각 연합 내의 보상 분배에 어떻게 영향을 미칠지 또한 살펴본다.비협조 게임 이론이 보다 일반적이기 때문에, 비협조 게임 이론의 접근방식을 통해 협력 게임을 분석할 수 있다(반대가 성립하지 않음). 단, 외부의 협력 집행 가능성으로 인해 플레이어가 이용할 수 있는 모든 가능한 전략을 포괄할 수 있는 충분한 가정을 할 수 있다.단일 이론을 사용하는 것이 바람직할 수 있지만, 많은 경우 전략적 협상 과정 동안 이용 가능한 공식 절차를 정확하게 모델링할 수 있는 정보가 부족하거나, 결과 모델이 너무 복잡하여 실제 세계에서 실용적인 도구를 제공할 수 없을 것이다.이러한 경우, 협동 게임 이론은 협상력에 대한 어떠한 가정도 하지 않고 게임을 전반적으로 분석할 수 있는 단순화된 접근법을 제공한다.

대칭/비대칭

	E	F
E	1, 2	0, 0
F	0, 0	1, 2
비대칭 게임

대칭 게임은 특정 전략을 수행하는 것에 대한 보상이 누가 실행하는 것이 아니라 사용된 다른 전략에 의해서만 좌우되는 게임이다.즉, 전략을 바꾸지 않고 플레이어의 신분을 변경할 수 있다면 게임은 대칭이 됩니다.일반적으로 연구되는 많은 2×2 게임들은 대칭이다.닭고기, 죄수의 딜레마, 사슴사냥의 일반적인 표현은 모두 대칭적인 게임이다.일부^[who?] 학자들은 또한 특정 비대칭 게임을 이러한 게임의 예로 생각할 것이다.그러나 이러한 각 게임의 가장 일반적인 보상은 대칭입니다.

가장 일반적으로 연구되는 비대칭 게임은 두 플레이어에게 동일한 전략 세트가 없는 게임이다.예를 들어 최후통첩 게임과 마찬가지로 독재자 게임은 각 플레이어마다 다른 전략을 가지고 있다.그러나 두 선수의 전략은 동일하지만 비대칭일 수도 있다.예를 들어, 이 섹션의 그래픽에 표시된 게임은 양쪽 플레이어의 전략 세트가 동일함에도 불구하고 비대칭적입니다.

제로섬/논제로섬

	A	B
A	–1, 1	3, –3
B	0, 0	–2, 2
제로섬 게임

제로섬 게임(좀 더 일반적으로, 연속섬 게임)은 플레이어의 선택이 사용 가능한 자원을 증가시키거나 감소시킬 수 없는 게임이다.제로섬 게임에서, 모든 전략의 조합에 대해, 게임의 모든 플레이어에게 총 이득이 돌아가며, 항상 0이 추가됩니다(더 비공식적으로 말하면,^[15] 플레이어는 다른 플레이어와 동일한 비용으로 이익을 얻습니다).포커는 제로섬 게임(하우스 컷 가능성을 무시한 것)의 전형이다. 왜냐하면 상대방이 지는 만큼 정확히 승리하기 때문이다.다른 제로섬 게임에는 동전 맞추기 게임과 바둑과 체스를 포함한 대부분의 클래식 보드 게임이 포함된다.

게임 이론가들이 연구한 많은 게임들은 논제로섬 게임인데, 그 이유는 그 결과가 0보다 크거나 작기 때문이다.비공식적으로 논제로섬 게임에서 한 플레이어의 이득이 다른 플레이어의 손실과 반드시 일치하는 것은 아니다.

컨스턴스섬게임은 절도나 도박과 같은 활동에 해당하지만 무역으로 잠재적인 이득을 얻는 근본적인 경제상황에는 해당되지 않는다.플레이어의 순이익을 보상하는 더미 플레이어(종종 "보드"라고 불림)를 추가함으로써 어떤 연속 합 게임도 (비대칭일 수 있음) 제로 합 게임으로 바꿀 수 있다.

/시퀀셜

동시 게임은 두 플레이어가 동시에 이동하거나, 그 대신 더 늦은 플레이어는 더 이른 플레이어의 행동을 알지 못하는 게임입니다.순차 게임(또는 동적 게임)은 이후 플레이어가 이전 액션에 대해 어느 정도 알고 있는 게임입니다.이것은 초기 참가자들의 모든 행동에 대한 완벽한 정보가 될 필요는 없습니다. 매우 적은 지식일 수도 있습니다.예를 들어, 플레이어는 이전 플레이어가 특정 액션을 수행하지 않은 것을 알 수 있지만, 첫 번째 플레이어가 실제로 실행한 다른 사용 가능한 액션은 알 수 없습니다.

동시 게임과 순차 게임의 차이는 위에서 설명한 다양한 표현에서 확인할 수 있습니다.보통 일반 형식은 동시 게임을 나타내는 데 사용되는 반면 확장 형식은 순차 게임을 나타내는 데 사용됩니다.확장형식을 일반형으로 변환하는 것도 한 가지 방법입니다. 즉, 여러 확장형식 게임이 동일한 일반형에 해당합니다.따라서 동시 게임에 대한 균형 개념은 순차적 게임에 대한 추론에는 불충분합니다. 서브게임의 완벽성을 참조하십시오.

	★★★★★★	★★
보통 다음과 같이 표시됩니다.	(Decision Tree)	매트릭스
지식 ★★★★ 대편의? ??	.	.
★★★★★★★★★★★★★★★★★?	.	.
'	한 게임	게임 ★★★★★★★

Cournot 쟁쟁 cour cour cour

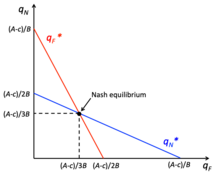
Cournot 경쟁 모델에서는 참가자들이 동종 제품의 수량을 선택하여 독립적으로 동시에 생산할 수 있습니다.여기서 한계비용은 기업마다 다를 수 있고 기업의 이익은 이익입니다.생산 원가는 공공 정보이며, 기업은 다른 회사가 독점처럼 생산하고 행동할 것이라고 믿는 것을 바탕으로 이윤 극대화 수량을 찾는 것을 목표로 한다.이 게임사는 독점 수량으로 제작하기를 원하지만, 이탈하여 더 많이 제작하려는 동기가 높기 때문에 시장 정리 ^[16]가격이 낮아진다.예를 들어,^[16] 기업은 이익을 극대화하기 위해 생산을 늘리기 위해 독점 수량이 낮고 가격이 높은 경우에 독점 수량에서 벗어나려는 유혹을 받을 수 있다.그러나 이윤을 극대화할 수 있는 기업의 능력은 시장점유율과 ^[17]시장수요의 탄력성에 따라 다르기 때문에 이 선택권은 가장 높은 보상을 제공하지 않는다.Cournot 균형은 각 기업이 다른 기업의 ^[16]산출물을 바탕으로 최선의 반응을 보이므로 이탈 동기가 없이 반응 기능에 따라 작동할 때 도달한다.게임 내에서 기업은 Cournot 평형이 달성되면 Nash 평형에 도달합니다.

Competition

베르트랑 경쟁은 균질한 제품과 일정한 한계 비용을 가정하고 참가자들은 ^[16]가격을 선택합니다.가격 경쟁의 균형은 경쟁업체의 비용에 대한 완전한 정보를 가정할 때 가격이 한계 비용과 동일한 것이다.따라서, 기업들은 더 낮은 가격을 가진 균질 제품이 비용 우위로 ^[18]알려진 모든 시장 점유율을 얻을 것이기 때문에 균형에서 벗어나도록 동기를 부여한다.

한 와 불완전한

시퀀셜 게임의 중요한 서브셋은 완벽한 정보의 게임으로 구성됩니다.게임은 게임의 모든 동작에 대해 모든 플레이어가 이전에 다른 모든 플레이어가 했던 동작을 알고 있다면 완벽한 정보 중 하나입니다.실제로,^[19] 이것은 시장에서 이용 가능한 모든 상품의 가격과 품질에 대한 정보를 가진 기업과 소비자에게 적용될 수 있다.동시이동 게임 등 ^[16]상대방이 이미 하고 있는 모든 움직임을 유기자가 모르는 경우에는 불완전한 정보게임을 한다.게임 이론에서 연구되는 대부분의 게임은 불완전한 정보 게임이다.^{[citation needed]}완벽한 정보 게임의 예로는 틱택토, 체커, 체스, ^{[20][21][22][23]}바둑 등이 있다.

많은 카드 게임들은 포커나 ^[24]브리지와 같은 불완전한 정보의 게임들이다.완벽한 정보는 종종 완전한 정보와 혼동되는데, 이는 유사한 ^{[citation needed]}개념이다.완전한 정보는 모든 플레이어가 다른 플레이어가 이용할 수 있는 전략과 보상을 알고 있어야 하지만 반드시 취해야 할 행동은 아닌 반면, 완벽한 정보는 게임과 ^[25]플레이어의 모든 측면에 대한 지식입니다.그러나, 「본연의 움직임」^[26]을 도입하는 것으로, 불완전한 정보의 게임으로 전락할 수 있다.

베이즈 game베이지안 게임

내쉬 균형의 가정 중 하나는 모든 참가자들이 다른 선수들의 행동에 대해 올바른 믿음을 가지고 있다는 것이다.그러나 게임 이론에는 참가자들이 상대의 특성을 완전히 이해하지 못하는 상황이 많이 있다.협상자는 협상 대상에 대한 상대방의 평가를 모를 수 있고, 기업은 상대방의 비용 함수를 모를 수 있으며, 전투원은 상대의 강점을 모를 수 있으며, 배심원은 재판 중인 증거에 대한 동료의 해석을 모를 수 있다.경우에 따라서는, 참가자는 상대의 성격을 잘 알 수 있지만, 상대가 자신의 ^[27]성격을 얼마나 잘 알고 있는지 모를 수도 있다.

베이지안 게임은 정보가 불완전한 전략 게임을 의미합니다.전략 게임의 경우 의사결정자는 플레이어이며 모든 플레이어는 액션 그룹을 가지고 있습니다.불완전한 정보 사양의 핵심 부분은 상태 집합이다.모든 상태는 플레이어의 선호도 및 플레이어에 대한 세부사항과 같은 플레이어와 관련된 특성 집합을 완전히 설명합니다.플레이어에 따라서는 ^[28]존재한다고 생각되는 모든 기능 세트에는 상태가 있어야 합니다.

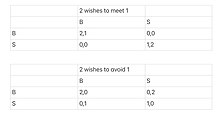
예를 들어, 플레이어 1은 플레이어 2가 자신과 사귀는 것이 좋을지 아니면 그녀와 떨어져 있는 것이 좋을지 확실하지 않은 반면, 플레이어 2는 이전과 같이 플레이어 1의 기본 설정을 이해합니다.구체적으로 말하면, 플레이어 1이 플레이어 2가 1/2의 확률로 그녀와 사귀고 싶어하고, 플레이어 2가 1/2의 확률로 그녀에게서 벗어나고 싶어한다고 믿는다고 가정하면, 이 평가는 플레이어 1의 경험에서 나온 것으로, 그녀는 그러한 경우에서 자신의 절반의 시간을 사귀고 싶어하는 선수들과 마주하고 싶어 하는 선수들과 마주하고 있다.관관 、 록록 、 록록 、 이이 、 이이황 、 이황의의의의분있있있 。

최적의 전략을 찾는 데 어려움이 가능한 움직임의 다양성에서 비롯되는 게임을 조합 게임이라고 합니다.예를 들면 체스와 바둑이 있다.불완전한 정보를 포함하는 게임에는 백개먼과 같은 강력한 조합 특성이 있을 수 있습니다.게임에서 조합적 요소를 다루는 통일된 이론은 없습니다.하지만, 특정한 문제를 풀고 일반적인 ^[29]질문에 대답할 수 있는 수학적 도구들이 있다.

완벽한 정보의 게임은 조합 게임 이론에서 연구되어 왔는데, 조합 게임 이론에서는 예를 들어 초현실적인 숫자와 같은 새로운 표현을 개발했으며, 무한히 긴 일련의 움직임을 야기할 수 있는 "루피한" 게임을 포함하여 특정 유형의 게임을 해결하기 위한 조합 및 대수적(때로는 비건설적) 증명 방법을 개발했습니다.이러한 방법들은 전통적인 (또는 "경제적인") 게임 ^[30][31]이론에서 일반적으로 고려되는 것보다 더 높은 조합 복잡성을 가진 게임을 다룬다.이렇게 해결된 대표적인 게임이 헥스입니다.계산 복잡도 이론에서 파생된 관련 연구 분야는 최적의 전략을 찾는 계산 난이도의 ^[32]추정에 관련된 게임 복잡도입니다.

인공지능 연구는 입증 가능한 최적의 전략이 발견되지 않은 매우 복잡한 조합 구조(체스, 바둑, 백개먼 등)를 가진 완벽하고 불완전한 정보 게임을 다루었다.실제 솔루션은 알파 베타 가지치기 또는 강화 학습에 의해 훈련된 인공 신경망의 사용과 같은 계산 휴리스틱스를 포함하며, 이는 게임을 컴퓨팅 ^[29][33]실습에서 더 다루기 쉽게 만든다.

의 게임

경제학자들과 실제 게임 플레이어들이 연구한 바와 같이, 게임은 일반적으로 최종적으로는 많은 동작으로 완성된다.순수 수학자들은 그렇게 제약받지 않고, 특히 무한히 많은 움직임을 지속하는 연구 게임에서 이론가를 설정하며, 승자(또는 다른 성과)는 그 모든 움직임이 완료된 후에야 알 수 있다.

관심의 초점은 보통 그러한 게임을 하는 최선의 방법이 아니라 한 선수가 승리 전략을 가지고 있는지에 있다.(선택의 공리를 사용하여 완벽한 정보를 가지고도 게임이 있다는 것을 증명할 수 있으며, 이 게임에는 "승부" 또는 "패부"라는 결과가 있을 뿐이며, 어느 쪽도 승리 전략을 가지고 있지 않습니다.영리하게 설계된 게임을 위한 그러한 전략의 존재는 기술 집합 이론에서 중요한 결과를 가져온다.

과 연속 게임

게임 이론의 대부분은 한정된 수의 플레이어, 움직임, 이벤트, 결과 등을 가진 유한하고 이산적인 게임과 관련이 있다.그러나 많은 개념을 확장할 수 있습니다.연속 게임을 통해 플레이어는 연속 전략 집합에서 전략을 선택할 수 있습니다.예를 들어, Cournot 경쟁은 일반적으로 참가자의 전략이 부분 수량을 포함하여 음수가 아닌 수량으로 모델링됩니다.

연속 추격 게임과 회피 게임과 같은 미분 게임은 플레이어의 상태 변수의 진화가 미분 방정식에 의해 지배되는 연속 게임입니다.미분 게임에서 최적의 전략을 찾는 문제는 최적 제어 이론과 밀접한 관련이 있다.특히, 두 가지 유형의 전략이 있습니다. 즉, 개방 루프 전략은 폰트랴긴 최대 원리를 사용하여 찾는 반면 폐쇄 루프 전략은 벨만의 동적 프로그래밍 방법을 사용하여 찾는 것입니다.

차분 게임의 특별한 예는 랜덤한 시간 ^[34]범위를 가진 게임입니다.이러한 게임에서 단말시간은 주어진 확률분포함수를 갖는 랜덤 변수이다.따라서, 참가자들은 비용 함수의 수학적 기대치를 극대화합니다.수정된 최적화 문제는 무한 시간 간격에 걸쳐 할인된 차등 게임으로 재구성할 수 있는 것으로 나타났다.

게임

진화 게임이론은 반드시 합리적이거나 선견지명이 ^[35]없는 규칙에 따라 시간이 지남에 따라 전략을 조정하는 플레이어를 연구합니다.일반적으로 이러한 규칙에 따른 전략의 시간 경과에 따른 진화는 현재의 전략 프로파일이나 최근 게임이 어떻게 진행되었는지 등의 상태 변수를 가진 마르코프 체인으로 모델링된다.그러한 규칙들은 적자생존의 모방, 최적화, 또는 생존을 특징으로 할 수 있다.

생물학에서, 그러한 모델은 진화를 나타낼 수 있는데, 이 진화에서는 후손이 부모의 전략을 채택하고 더 성공적인 전략을 수행하는 부모(즉, 더 높은 보상에 해당하는)가 더 많은 수의 자손을 가질 수 있다.사회과학에서 이러한 모델은 일반적으로 평생 동안 여러 번 게임을 하고 의식적이든 무의식적이든 간에 때때로 ^[36]전략을 조정하는 플레이어에 의한 전략적 조정을 나타냅니다.

확률적 결과(및 다른 분야와의 관계)

확률적 결과에 대한 개별 의사결정 문제는 때때로 "1인용 게임"으로 간주된다.의사결정 이론, 운영 연구, 인공지능 분야, 특히 AI 계획(불확실성 있음) 및 다중 에이전트 시스템 등의 관련 분야 내에서 유사한 도구를 사용하여 모델링할 수 있다.이러한 분야는 다른 동기를 가질 수 있지만, 관련된 수학은 실질적으로 동일하다. 예를 들어 마르코프 의사결정 과정(MDP)^[37]을 사용한다.

확률적 결과는 "천성적으로 움직이는"^[38] 무작위로 행동하는 플레이어를 추가함으로써 게임 이론의 관점에서 모델링될 수도 있습니다.이 플레이어는 일반적으로 2인용 게임에서 세 번째 플레이어로 간주되지 않고 게임에서 필요한 경우 주사위를 굴리는 역할을 합니다.

일부 문제의 경우, 확률적 결과 모델링에 대한 다른 접근방식은 다른 해결책으로 이어질 수 있다.예를 들어, 민주당과 미니맥스 솔루션 간의 접근법의 차이는 후자가 고정된 확률 분포에서 이러한 움직임에 대한 예상에서 추론하기 보다는 일련의 적대적 움직임에 대해 최악의 경우를 고려한다는 것이다.미니맥스 접근방식은 불확실성의 확률적 모델을 이용할 수 없는 경우에 유리할 수 있지만, 또한 매우 가능성이 낮은(그러나 비용이 많이 드는) 사건을 과대평가하여 상대가 그러한 사건을 강제로 ^[39]발생시킬 수 있다고 가정할 경우 그러한 시나리오에서 전략을 크게 흔들 수 있다.(특히 투자 뱅킹의 손실 예측 및 제한과 관련된 이러한 모델링 문제에 대한 자세한 내용은 Black swan 이론을 참조하십시오.)

확률적 결과, 적대자, 부분적 또는 잡음적 관찰 가능성(다른 참가자의 움직임)의 모든 요소를 포함하는 일반 모델도 연구되었다."골드 스탠더드"는 부분적으로 관측 가능한 확률 게임(POSG)으로 간주되지만, POSG ^[39]표현에서 계산적으로 실현 가능한 현실적인 문제는 거의 없다.

이 게임들은 다른 게임, 타깃 게임 또는 대상 게임에 대한 규칙을 개발하는 게임입니다.메타게임은 개발된 규칙 집합의 효용 값을 최대화하려고 합니다.메타게임의 이론은 메커니즘 설계 이론과 관련이 있다.

메타게임 분석이라는 용어는 Nigel ^[40]Howard가 개발한 실용적인 접근법을 지칭하는 데 사용되기도 하는데, 여기서 상황은 이해 당사자들이 이용 가능한 옵션을 통해 자신의 목표를 실현하려는 전략 게임으로 형성된다.이후의 발전은 대립 분석의 공식으로 이어졌다.

풀링 ★★★★★★

이것들은 모든 형태의 사회에 널리 퍼져 있는 게임들이다.풀링 게임은 경험된 경로에 걸쳐 일반적으로 변화하는 보수표와 함께 반복되는 게임이며, 이들의 균형 전략은 대개 진화적인 사회적 관습과 경제적 관습의 형태를 취한다.풀링 게임 이론은 하나의 플레이에서 최적의 선택과 다가오는 보상 테이블 업데이트 경로의 출현 사이의 상호작용을 공식적으로 인식하고, 불변의 존재와 견고성을 식별하고, 시간에 따른 변화를 예측하기 위해 등장합니다.이 이론은 분산과 불변성을 예측하기 위해 시간 경과에 따른 보수표 업데이트의 위상 변환 분류에 기초하고 있으며, 또한 질서 ^[41]있는 시스템에 대한 도달 가능한 최적성의 계산 법칙의 관할권 내에 있다.

게임

평균 필드 게임 이론은 매우 많은 수의 상호작용하는 에이전트의 전략적 의사결정에 대한 연구입니다.보얀 조바노비치와 로버트 W. 로젠탈의 경제학 문헌, 피터 E. 케인의 공학 문헌, 그리고 수학자 피에르 루이 라이온스와 장 미셸 라스트리에 의해 이러한 종류의 문제들이 고려되었습니다.

의

게임 이론에서 연구되는 게임들은 잘 정의된 수학적 객체들이다.완전히 정의될려면(에릭 Rasmusen의 약어"PAPI"에 의해 이 4"필수 원소"을 말한다.)[42][43][44][45] 게임 이론가는 일반적으로 더불어 구성 요소를 사용한 게임이다. 다음의 요소:게임의 선수들의 영향이 큰 정보와 조치 각 결정 시점에서 각 선수들에게 이용할 수 있으며 각 결과를 보는 일이 줄게를 지정해야 합니다.한solutio과n 선택 개념, 각 참가자에 대한 균형 전략 집합을 추론하여, 이러한 전략이 사용될 때, 어느 참가자도 그들의 전략에서 일방적으로 벗어나 이익을 얻을 수 없다.이러한 평형 전략은 게임에 대한 균형, 즉 하나의 결과 또는 일련의 결과가 알려진 확률로 발생하는 안정적인 상태를 결정합니다.

대부분의 협동 게임은 특징적인 함수 형태로 제시되며, 광범한 형태와 일반 형태는 비협조 게임을 정의하기 위해 사용된다.

【장 extensive】

확장 형식을 사용하여 이동의 시간 시퀀스를 사용하여 게임을 공식화할 수 있습니다.여기서 하는 게임은 나무 위에서 한다(사진과 같이).여기서 각 정점(또는 노드)은 플레이어의 선택 포인트를 나타냅니다.플레이어는 정점으로 나열된 번호로 지정됩니다.정점에서 나오는 선은 해당 플레이어가 수행할 수 있는 작업을 나타냅니다.보상은 트리 하단에 명시되어 있습니다.광범위한 형태는 의사결정 ^[46]트리의 멀티플레이어 일반화로 볼 수 있습니다.광범위한 폼 게임을 해결하려면 역유도를 사용해야 합니다.이는 합리적인 플레이어가 트리의 마지막 정점에서 무엇을 할 것인지, 마지막 수를 가진 플레이어가 합리적이라면 이전 수를 가진 플레이어가 무엇을 할 것인지를 결정하기 위해 게임 트리의 첫 번째 정점에 ^[47]도달할 때까지 게임 트리를 역방향으로 작업하는 것을 포함한다.

사진 속의 게임은 두 명의 선수로 구성되어 있다.이 특정 게임의 구조화 방식(순차적인 의사결정과 완벽한 정보)은 플레이어 1이 먼저 다음 중 하나를 선택하여 '움직인다'는 것입니다.F ★★★★★★★★★★★★★★★★★」U(공정 또는 불공정)다음 순서에서 플레이어 1의 움직임을 본 플레이어 2는 다음 중 하나를 선택합니다.A ★★★★★★★★★★★★★★★★★」R플레이어 2가 선택을 하면 게임은 종료된 것으로 간주되며 각 플레이어는 각자의 보상을 받게 됩니다.플레이어 1이 다음을 선택했다고 가정합니다.U그리고 플레이어 2는A: 플레이어 1은 "8"의 보상을 받습니다(실제로는 여러 가지로 해석할 수 있지만 가장 간단한 것은 돈으로 해석할 수 있지만 8일간의 휴가, 8개국의 정복, 또는 다른 플레이어와 같은 게임을 할 수 있는 8개의 기회 등). 플레이어 2는 "2"의 보상을 받습니다.

또한 이 광범위한 형태는 불완전한 정보를 가진 동시 이동 게임과 게임을 캡처할 수 있습니다.이를 나타내기 위해 점선은 서로 다른 정점을 연결하여 동일한 정보 세트의 일부로 나타내거나(즉, 플레이어는 자신이 어느 지점에 있는지 알지 못함), 또는 이들 주위에 닫힌 선을 그린다.(불완전한 정보 섹션의 예를 참조하십시오.)

(상상形)

	2 왼쪽 선택	2 오른쪽 선택
1 선택	4, 3	–1, –1
1 아래를 선택합니다.	0, 0	3, 4
인 형태 2인2 normal normal of2 normal normal normal of of2 normal normal of of normal of of of of of of2 normal normal of normal of of normal normal normal normal 。

통상적인 (또는 전략적인 형태)게임은 보통 플레이어, 전략 및 보상을 보여주는 매트릭스로 표현된다(오른쪽 예 참조).보다 일반적으로, 각 참가자에 대한 보상을 가능한 모든 동작의 조합과 연관짓는 함수로 나타낼 수 있다.첨부된 예에서는 두 명의 플레이어가 있습니다.한 명은 행을 선택하고 다른 하나는 열을 선택합니다.각 플레이어는 행 수와 열 수로 지정되는 두 가지 전략을 가지고 있습니다.보상은 인테리어에서 제공됩니다.첫 번째 숫자는 열 플레이어(이 예에서는 플레이어 1)가 받은 보수입니다.두 번째 숫자는 컬럼 플레이어(이 예에서는 플레이어 2)의 보수입니다.플레이어 1이 Up을 재생하고 플레이어 2가 Left를 재생한다고 가정합니다.그러면 플레이어 1은 4의 보상을 받고, 플레이어 2는 3의 보상을 받습니다.

게임이 정상적인 형태로 제시될 때, 각 플레이어는 동시에 또는 적어도 상대방의 행동을 알지 못하고 행동하는 것으로 추정됩니다.만약 플레이어들이 다른 플레이어의 선택에 대한 정보를 가지고 있다면, 게임은 대개 광범위한 형태로 제공됩니다.

모든 확장형 게임은 동등한 정규형 게임을 가지고 있지만, 정규형 게임으로의 변환은 표현의 크기를 기하급수적으로 증가시켜 계산상 ^[48]실용적이지 않을 수 있다.

함수

분리 가능한 유틸리티가 있는 게임에서는 별도의 보상이 주어지지 않습니다.대신 특성 함수에 따라 각 통합의 보상이 결정됩니다.그 생각은 말하자면 공허한 단결은 전혀 보상을 받지 못한다는 것이다.

이 형식의 기원은 John von Neumann과 Oskar Morgenstern의 책에서 찾을 수 있습니다.이러한 예들을 보면 $유니언{\displaystyle \mathbf{}}$C(\$displaystyle \mathbf {$$C})$가 나타나면 분수$displaystyle \left({\frac${\$mathbf}${C$})$에 반하는 것으로 추측됩니다.e는 평범한 게임을 한다.C의 균형 보상은 기본 함수이다.일반 게임과 연합 금액을 결정하는 데 도움이 되는 예는 다르지만, 모든 것이 기능 형태에서 그러한 것에서 파생될 수 있는 것은 아닌 것으로 보인다.

형식적으로 특성 함수는 다음과 같이 보인다. (N,v) 여기서 N은 사람 집단을 $나타내고{\displaystyle }$v : ${\displaystyle 2^{}}$ ${\displaystyle N\mathbf{}}$ $→$ R {\$displaystyle v:2^{N}\$to \$mathbf${R$}}$은 정규 효용이다.

이러한 특징적인 기능은 탈부착 가능한 유틸리티가 없는 게임을 묘사하는 데까지 확대되었다.

게임

대체 게임 표현 양식은 게임의 일부 하위 클래스에 사용되거나 학제 ^[49]간 연구의 필요에 따라 조정됩니다.고전적인 게임 표현 외에, 일부 대체 표현은 시간 관련 측면도 인코딩합니다.

름 name 。	★★★	: ★★	의 종류	★★★★★
[50]	1973	" " "	, 동시 이동 n-person 게임, 동시 이동	.
시퀀셜[51] 폼	1994	'''」	불완전한	.
시간[52][53] 제한 게임	1994	" " "	게임 2인용 게임	네, □□입니다.
갈라[54]	1997	으로 해석하다	불완전한	.
로컬 이펙트[55] 게임	2003	" " "	, 동시 이동 n-person 게임, 동시 이동	.
GDL [56]	2005	으로 해석하다	게임, 이동, n-person 게임, n-person 게임	.
게임 페트리넷[57]	2006		게임, 이동, n-person 게임, n-person 게임	.
연속[58] 게임	2007	" " "		네, □□입니다.
PNSI[59][60]	2008		불완전한	네, □□입니다.
액션 그래프[61] 게임	2012	, 함수	게임,, n인용 게임	.
[62]	2015	, 함수	게임,, n인용 게임	.

및

응용 수학의 방법으로서, 게임 이론은 인간과 동물의 다양한 행동을 연구하는데 사용되어 왔다.처음에는 기업, 시장 및 소비자의 행동을 포함한 많은 경제 행동을 이해하기 위해 경제학에서 개발되었습니다.게임 이론 분석의 첫 번째 사용은 1838년 앙투안 오귀스틴 쿠르노가 쿠르노 이중 독점에 대한 그의 해결책과 함께 사용한 것이다.사회과학에서의 게임 이론의 활용은 확대되었고, 게임이론은 정치, 사회학, 심리학적 행동에도 ^[63]적용되었다.

비록 찰스 다윈과 같은 20세기 이전의 자연학자들은 게임이론적인 종류의 진술을 했지만, 생물학에서 게임이론 분석의 사용은 1930년대 동물 행동에 대한 로널드 피셔의 연구에서 시작되었다.이 작품은 '게임 이론'이라는 이름보다 앞서지만, 이 분야와 많은 중요한 특징을 공유하고 있다.경제학에서의 발전은 1982년 존 메이나드 스미스의 저서 '진화와 게임 ^[64]이론'에서 생물학에 주로 적용되었다.

행동을 기술, 예측, 설명하는 데 사용될 뿐만 아니라, 게임 이론은 윤리적 또는 규범적 행동에 대한 이론을 개발하고 그러한 ^[65]행동을 규정하는 데에도 사용되어 왔다.경제학 및 철학에서 학자들은 게임 이론을 적용하여 선하거나 올바른 행동을 이해하는 데 도움을 주었다.이런 유형의 게임이론적인 주장은 ^[66]플라톤까지 거슬러 올라갈 수 있다.화학 게임 이론이라고 불리는 게임 이론의 다른 버전은 "knowlecules"^[67]라고 불리는 은유적인 화학 반응 물질 분자로 플레이어의 선택을 나타냅니다.화학 게임 이론은 그 결과를 화학 반응 시스템에 대한 평형 해법으로 계산한다.

및

게임 이론의 주된 용도는 인간의 행동을 ^{[citation needed]}묘사하고 모델링하는 것이다.어떤^[who?] 학자들은 게임의 균형을 찾음으로써 연구되고 있는 게임과 유사한 상황에 직면했을 때 실제 인구가 어떻게 행동할지를 예측할 수 있다고 믿는다.게임 이론에 대한 이러한 특정한 관점은 비판을 받아왔다.게임 이론가들의 가정은 실제 상황에 적용될 때 종종 위반된다는 주장이 있다.게임 이론가들은 보통 플레이어들이 이성적으로 행동한다고 가정하지만, 실제로 인간의 행동은 종종 이 모델에서 벗어난다.게임 이론가들은 그들의 가정을 물리학에서 사용되는 것과 비교함으로써 반응한다.따라서 그들의 가정이 항상 성립하는 것은 아니지만, 그들은 게임 이론을 물리학자들이 사용하는 모델과 유사한 합리적인 과학적 이상으로 취급할 수 있다.그러나 지네 게임, 평균 게임의 2/3를 맞히는 게임, 독재자 게임과 같은 일부 고전 게임에서는 사람들이 정기적으로 내쉬 이퀄리어를 하지 않는다는 것이 실증적인 연구로 밝혀졌다.이러한 실험의 중요성과 실험 분석이 관련 ^[b]상황의 모든 측면을 완전히 포착할 수 있는지 여부에 대한 논쟁이 계속되고 있다.

존 메이너드 스미스와 조지 R의 활동 이후 일부 게임 이론가들,이들 현안을 해결하는 가격, 진화 게임 이론으로 방향을 돌렸다.이 모델들 선수들의 부분에 어떤 합리성 또는 경계 합리성이라고 생각하다.그 이름에도 불구하고, 진화 게임 이론이 반드시 가장 생물학적인 점의 자연 도태한다.진화 게임 이론에서 둘 다 문화적 생물학적 진화와 개개인의 학습(예를 들어, 거짓 연극 역학에 대해)도 모델을 포함한다.

규범적 또는 규범적 분석

	을	결함
을	-1, -1	-10, 0
결함	0, -10	-5, -5
죄수의 딜레마

일부 학자들 인간의 행동에 대해 예방의 수단이 아니라 사람들이 어떻게 처신해야 하기 위한 제안처럼 게임 이론을 볼 수 있다.전략부터 게임의 내쉬 균형에 해당하는 다른 선수들의 행동에 대한 자신의 최상의 구성하 – 정하는 바에( 같은)내시 균형 –를 전략 일부인의 내쉬 균형 같다게임 이론의 이 규범적인 사용도 비난에 처했다.[표창 필요한]

경제 및 비즈니스

게임 이론은 주요 법 수학적 경제 및 비즈니스로 상호 작용하는 요원들의 경쟁 행동 모델링에 사용된다.[c][69][70][71]응용 프로그램은 경제 현상, 경매, 협상, 합병과 인수 pricing,[72]균등한 분배, duopolies, 과점이며, 사회적 네트워크 형성,agent-based 계산 economics,[73][74]일반 균형, 메커니즘 design,[75][76][77][78][79]과 투표 시스템과 같은 접근법의 광범위한 배열이고,[80] 같은 b을 포함한다실험 경제로 도로 지역.S,[81][82][83][84][85]행동 economics,[86][87][88][89][90][91]정보 economics,[42][43][44][45]산업 organization,[92][93][94][95]과 정치 경제.[96][97][98][99]

이 연구는 보통 전략"해결책 개념"또는"평형"로 알려진 특정 세트에 초점을 맞춘다.일반적인 가정은 선수들이 이성적으로 행동한다는 것이다.비협력 게임에서 가장 유명한 것은 내쉬 균형이다.각 전략이 다른 전략에 대한 최상의 반응을 나타낸다면 일련의 전략은 내쉬 균형이다.만약 모든 참가자들이 내쉬 균형에서 전략을 구사하고 있다면, 그들의 전략은 다른 사람들이 ^[100][101]하고 있는 것을 감안할 때 그들이 할 수 있는 최선의 것이기 때문에, 그들은 이탈할 일방적인 동기가 없다.

게임의 보상은 일반적으로 개인 플레이어들의 효용을 나타내는 것으로 받아들여진다.

경제학에서 게임이론에 대한 시제품 논문은 특정 경제 상황을 추상화한 게임을 제시하는 것으로 시작한다.하나 이상의 솔루션 개념을 선택하고, 저자는 제시된 게임에서 어떤 전략 세트가 적절한 유형의 평형인지 설명한다.경제학자 및 비즈니스 교수들은 (위에서 언급한) 두 가지 주요 용도, 즉 서술적 용도와 규범적 ^[65]용도를 제안합니다.

Chartered Institute of Procures & Supply(CIPS)는 비즈니스 ^[102]조달의 맥락에서 게임 이론의 지식과 사용을 촉진합니다.CIPS와 TWS 파트너는 조달 프로페셔널 간의 게임 이론의 이해, 인식 및 적용을 검토하기 위해 일련의 조사를 실시했습니다.세 번째 연례 조사(2019년)의 주요 조사 결과에는 다음이 포함된다.

• 조달 에 대한 중 였습니다.19퍼센트
• 의 65.
• 70%는 ' 그 에 대한 이해.
• 참가자의 20%가 게임 이론의 현장 훈련을 받았다.
• 50%가 새로운 솔루션 또는 했습니다.
• 응답자의 90%는 ^[103]업무에 필요한 소프트웨어가 없다고 답했다.

현명한 의사결정은 프로젝트의 성공에 매우 중요합니다.프로젝트 관리에서 게임 이론은 투자자, 프로젝트 매니저, 계약자, 하청업자, 정부 및 고객과 같은 참가자의 의사결정 과정을 모델링하기 위해 사용됩니다.이러한 플레이어는 종종 서로 경쟁하는 이해관계를 가지고 있으며, 때때로 그들의 이해관계가 다른 플레이어에 직접적으로 해가 되므로 프로젝트 관리 시나리오는 게임 이론에 따라 모델화하기에 적합합니다.

Piravenan(2019)^[104]은 리뷰에서 게임 이론을 사용하여 프로젝트 관리 시나리오를 모델링하는 몇 가지 예를 제시합니다.예를 들어 투자자는 일반적으로 여러 투자옵션을 가지고 있으며, 각 옵션은 다른 프로젝트를 초래할 가능성이 높기 때문에 프로젝트 헌장을 작성하기 전에 투자옵션을 선택해야 한다.마찬가지로 건설 프로젝트 등 하청업체가 관여하는 대형 프로젝트도 주청업자(프로젝트 매니저)와 하청업자 또는 하청업자 간에 복잡한 상호작용이 있어 일반적으로 여러 의사결정 지점이 있다.예를 들어, 계약자와 하도급자 간의 계약에 모호성이 있는 경우, 프로젝트 전체를 위태롭게 하지 않고 각자의 사례를 얼마나 강하게 추진할 것인지, 그리고 이에 대한 자신의 지분을 결정해야 한다.마찬가지로 경쟁사로부터 프로젝트를 시작할 때 마케팅 담당자는 프로젝트 또는 그 결과물 또는 서비스를 마케팅하기 위한 최적의 타이밍과 전략을 결정해야 합니다.이것에 의해, 경쟁에 직면했을 때에 최대한의 관심을 얻을 수 있습니다.이러한 시나리오 각각에서 필요한 결정은 의사결정자의 이익과 어떤 방식으로든 경쟁하는 이해관계를 가진 다른 참가자의 결정에 따라 결정되며, 따라서 게임 이론을 사용하여 이상적으로 모델링될 수 있다.

Piravenan은^[104] 2인용 게임이 주로 프로젝트 관리 시나리오를 모델링하는 데 사용되며, 이러한 플레이어의 아이덴티티에 따라 프로젝트 관리에는 5가지 유형의 게임이 사용된다고 요약합니다.

• 관민 게임(관민 파트너십을 모델로 한 게임)
• Contractor–contractor games청부업자-청부업자 게임
• Contractor–subcontractor games청부업자-청부업자 게임
• Subcontractor–subcontractor games하청업체-하청업체 게임
• 게임 다른 players다른과 관련된 플레이어가 참여하는 게임

게임의 유형 조합뿐만 아니라, normal-form 비협조적인 뿐만 아니라 extensive-form, 그리고 제로 섬뿐만 아니라 넌 제로 섬 다양한 프로젝트 관리 시나리오 모델에 사용된다의 면에서요.게임의 종류에 관해서는, 다양한 프로젝트 관리 시나리오의 모델화에 비협조형, 일반형, 확장형, 제로섬,넌제로섬이 사용되고 있습니다.

정치학에 대한 게임 이론의 적용은 공정 분열, 정치 경제, 공공 선택, 전쟁 협상, 긍정 정치 이론, 그리고 사회 선택 이론의 중복된 영역에 집중되어 있다.이러한 각 영역에서 연구자들은 플레이어가 종종 유권자, 주, 특수 이익 단체 및 정치인이 되는 게임 이론 모델을 개발했다.

정치학에 적용된 게임 이론의 초기 예는 앤서니 다운스에 의해 제공되었습니다.1957년 저서 민주주의 경제이론(An Economic Theory of Democracy)^[105]에서 그는 Hoteling 회사의 입지 모델을 정치적 과정에 적용했다.다운스식 모델에서 정치 후보들은 1차원적인 정책 공간에서 이데올로기에 전념한다.다운스는 우선 유권자들에게 충분한 정보를 제공한다면 정치 후보들이 중앙 유권자들이 선호하는 이념에 어떻게 수렴할 것인지를 보여주지만, 그 다음에는 유권자들이 이성적으로 무지한 채로 남아서 후보들의 분열을 초래한다고 주장한다.게임 이론은 존 F 대통령 재임 시절인 1962년 쿠바 미사일 위기에 적용됐다.케네디.^[106]

게임 이론이 어떤 형태의 정치 정치든 안정성에 대해 설명한다는 주장도 제기되어 왔다.예를 들어, 가장 단순한 왕정 사례를 들자면, 왕은 한 사람일 뿐이며, 개인적으로 그의 신하들 전부 또는 심지어 상당한 수의 신하들에 대한 물리적 통제권을 행사함으로써 그의 권위를 유지하지도 못하고 유지할 수도 없다.대신 주권 통제는 다른 모든 시민들이 서로 왕(또는 다른 기성 정부)을 명령에 따를 사람으로 볼 것을 기대한다는 각 시민들의 인식으로 설명된다.군주를 교체하려는 음모는 일반적으로 범죄로 처벌받을 수 있기 때문에 군주를 교체하기 위해 시민들 간의 의사소통을 조정하는 것은 사실상 금지된다.그러므로, 죄수의 딜레마의 변형에 의해 모델화될 수 있는 과정에서, 비록 모든 시민들이 ^[107]집단으로 행동한다면 더 나아질 것이라는 것을 알더라도, 안정기에 군주를 교체하는 것이 합리적이라는 것을 발견할 수 없을 것이다.

민주주의 평화에 대한 게임 이론적인 설명은 민주주의에서 공공적이고 공개적인 토론이 그들의 의도에 관한 명확하고 신뢰할 수 있는 정보를 다른 나라에 보낸다는 것이다.반면 비민주적 지도자들의 의도와 양보는 어떤 영향을 미칠지, 약속은 지켜질지 알기는 어렵다.따라서 분쟁 당사자 중 적어도 한 명이 ^[108]비민주주의 국가라면 불신과 양보를 꺼리게 될 것이다.

그러나 게임 이론은 비록 두 나라의 지도자들이 싸움의 대가를 알고 있더라도 여전히 전쟁을 할 수 있다고 예측한다.전쟁은 비대칭적인 정보에서 비롯될 수 있다; 두 나라는 그들이 가지고 있는 군사 자원의 양을 잘못 표현하도록 동기를 부여하여, 싸움에 의존하지 않고 분쟁을 합의 없이 해결할 수 없게 만들 수 있다.게다가, 전쟁은 약속 문제 때문에 일어날 수 있다: 만약 두 나라가 분쟁을 평화적인 방법으로 해결하기를 원하지만, 각각 그 해결 조건을 되돌리기를 원한다면, 그들은 전쟁에 의존할 수밖에 없을 것이다.마지막으로, 전쟁은 이슈의 ^[109]불가분성에서 비롯될 수 있다.

게임 이론은 또한 그 나라에 적용될 새로운 규칙이나 법이 있을 때 그 나라의 반응을 예측하는데 도움을 줄 수 있다.한 가지 예는 기후 변화를 줄이기 위해 국가들이 무엇을 할 수 있는지를 연구하는 피터 존 우드(2013)의 연구이다.우드는 온실 가스 배출을 줄이기 위해 다른 나라들과 조약을 맺음으로써 이것이 달성될 수 있다고 생각했다.하지만,^[110] 그는 이 생각이 국가들을 위해 죄수의 딜레마를 일으킬 것이기 때문에 효과가 없을 것이라고 결론지었다.

★★★★★★

	★★★
★★★	, 20	80, 40
	40, 80	, 60
매사냥

경제학과는 달리, 생물학에서 게임의 보상은 종종 적합성에 해당하는 것으로 해석됩니다.또한, 합리성의 개념에 해당하는 균형보다는 진화적인 힘에 의해 유지될 균형에 초점을 맞추고 있다.생물학에서 가장 잘 알려진 균형은 (메이나드 스미스 & 프라이스 1973)에서 처음 도입된 진화적으로 안정된 전략(ESS)으로 알려져 있다.초기 동기는 내쉬 평형의 정신적 요구 사항을 포함하지 않았지만, 모든 ESS는 내쉬 평형이다.

생물학에서, 게임 이론은 많은 다른 현상들을 이해하기 위한 모델로 사용되어 왔다.그것은 처음에 약 1:1 성비의 진화(및 안정성)를 설명하기 위해 사용되었다.(Fisher 1930) harv 오류: 목표 없음: CITEREFFisher1930 (도움말)은 1:1 성비는 그들의 손자 수를 최대화하려는 것으로 보여질 수 있는 개인에게 작용하는 진화적 힘의 결과라고 제안했다.

추가적으로, 생물학자들은 동물의 ^[111]의사소통의 출현을 설명하기 위해 진화 게임 이론과 ESS를 사용해 왔다.시그널링 게임과 다른 커뮤니케이션 게임들의 분석은 동물들 사이의 의사소통의 진화에 대한 통찰력을 제공해 왔다.예를 들어, 많은 수의 먹잇감이 더 큰 포식자를 공격하는 많은 종들의 집단 행동은 자발적인 신생 조직의 한 예로 보인다.개미는 또한 패션과 유사한 피드포워드(feed-forward) 행동을 보이는 것으로 나타났다(Paul Ormerod의 Butterfly Economics를 참조하십시오.

생물학자들은 싸움 행동과 영역성을 ^[112]분석하기 위해 닭고기 게임을 사용해 왔다.

메이나드 스미스는 진화와 게임이론의 서문에서 "기타적으로, 게임이론은 원래 설계된 경제 행동 분야보다 생물학에 더 쉽게 적용되는 것으로 밝혀졌다"고 말했다.진화적 게임 이론은 자연에서 ^[113]겉으로 보기에 맞지 않는 많은 현상을 설명하기 위해 사용되어 왔다.

그러한 현상 중 하나는 생물학적 이타주의로 알려져 있다.이것은 유기체가 다른 유기체에 이롭고 자신에게 해로운 방식으로 행동하는 것처럼 보이는 상황입니다.이것은 전통적인 이타주의 개념과는 다르다. 왜냐하면 그러한 행동은 의식적이지 않지만, 전반적인 체력을 증가시키기 위한 진화적 적응으로 보이기 때문이다.하룻밤 사냥으로 얻은 피를 역류시켜 먹이지 못한 집단 구성원에게 주는 뱀파이어 박쥐부터 여왕벌을 평생 돌보고 짝짓기를 하지 않는 일벌, 포식자의 접근을 경고하는 버벳 원숭이까지 다양한 종에서 볼 수 있다.그 개인의 ^[114]생존 가능성입니다.이러한 모든 행동은 그룹의 전체적인 적합성을 증가시키지만, 개인에게는 대가를 치르게 됩니다.

진화적 게임 이론은 이러한 이타주의를 친족 선택이라는 개념으로 설명한다.이타주의자들은 그들이 돕고 친척들을 우대하는 사람들을 차별한다.해밀턴의 법칙은 c < b × r 등식을 사용하여 이 선택 뒤에 있는 진화적 근거를 설명한다. 여기서 비용은 다음과 같다.c이타주의자에게는 이익보다 적어야 한다b수신자에게 관련 계수를 곱한 값r더 밀접하게 연관된 두 유기체는 많은 동일한 대립 유전자를 공유하기 때문에 이타주의의 발생을 증가시킨다.이것은 이타적인 개인이, 가까운 친척의 대립 유전자가 자손의 생존을 통해 전달되도록 함으로써, 같은 수의 대립 유전자가 전달되기 때문에 자손을 갖는 선택 자체를 포기할 수 있다는 것을 의미한다.예를 들어, 형제자매(이배체 동물)를 돕는 것은 계수가(평균적으로) 한 개인이 형제자매의 자손에서 대립 유전자의 절반을 공유하기 때문이다.형제자매의 자손들이 성인이 될 때까지 생존하도록 보장하는 것은 이타적인 개인이 ^[114]자손을 낳을 필요성을 배제한다.계수 값은 경기 영역의 범위에 따라 크게 좌우된다. 예를 들어, 어떤 사람을 선호할지 선택하는 것이 단지 모든 친척이 아닌 모든 유전 생물을 포함한다면, 우리는 모든 인간 사이의 불일치가 경기 영역의 다양성의 약 1%를 차지한다고 가정한다. 더 작은 영역에서 1⁄2였던 계수는 더 작아진다.s 0.995.마찬가지로 유전적 특성(예: 후생유전학, 종교, 과학 등) 이외의 정보가 시간이 지남에 따라 여전히 경쟁의 장이 커지고 불일치는 작아진다고 간주되는 경우.

컴퓨터 과학과 논리

게임 이론은 논리학과 컴퓨터 과학에서 점점 더 중요한 역할을 하게 되었다.게임 의미론에는 몇 가지 논리 이론이 근거를 가지고 있다.게다가, 컴퓨터 과학자들은 게임을 쌍방향 계산을 모델링하기 위해 사용해 왔다.또한, 게임 이론은 다중 에이전트 ^[115]시스템 분야에 이론적 근거를 제공합니다.

이와는 별도로, 온라인 알고리즘에서는 게임 이론이 중요한 역할을 하고 있으며, 특히 과거에는 이동 비용이 드는 게임과 요청 응답 ^[116]게임이라고 불렸던 서버 문제가 그 역할을 하고 있습니다.Yao의 원리는 랜덤화 알고리즘, 특히 온라인 알고리즘의 계산 복잡성에 대한 하한을 증명하기 위한 게임 이론 기술이다.

인터넷의 출현은 게임, 시장, 컴퓨터 경매, 피어 투 피어 시스템, 보안 및 정보 시장에서 균형을 찾기 위한 알고리즘의 개발에 동기를 부여했다.알고리즘 게임^[117] 이론과 알고리즘 메커니즘^[118] 설계는 복잡한 시스템의 계산 알고리즘 설계와 분석을 경제 ^{[119][120][121]}이론과 결합합니다.

철학

	숫사슴	토끼
숫사슴	3, 3	0, 2
토끼	2, 0	2, 2
사슴 사냥

게임 이론은 철학에서 여러 가지 용도로 사용되어 왔다.W.V.O. Quine(1960, 1967)의 두 논문에 대해 루이스(1969)는 게임 이론을 사용하여 관습에 대한 철학적 설명을 개발했습니다.그렇게 함으로써, 그는 상식에 대한 첫 번째 분석을 제공하고 그것을 코디네이션 게임의 플레이 분석에 활용했다.또 시그널링 게임의 의미도 이해할 수 있다고 제안했다.이 이후의 제안은 루이스 ^[122][123]이후 몇몇 철학자들에 의해 추구되어 왔다.루이스(1969년)의 게임 이론적인 관습 설명에 이어 에드나 울만-마르갈리트(1977년)와 비치에리(2006년)는 혼합 자동차 게임을 코디네이션 ^[124][125]게임으로 변형시킨 결과 발생하는 내쉬 평형이라고 정의하는 사회 규범 이론을 개발했다.

게임 이론은 또한 철학자들에게 상호작용적 인식론의 관점에서 생각하도록 도전했습니다: 집합체가 공통의 믿음이나 지식을 갖는 것이 무엇을 의미하는지, 그리고 에이전트의 상호작용으로 인한 사회적 결과에 대한 이 지식의 결과는 무엇인지.이 분야에서 일한 철학자들로는 비치에리(1989, 1993),^[126][127] 스카이럼스(1990),^[128] 스탈나커(1999)^[129] 등이 있다.

윤리학에서, 몇몇 작가들(특히 데이비드 고티에, 그레고리 카브카, 그리고 진 햄튼)^[who?]은 이기심으로부터 도덕성을 이끌어내는 토마스 홉스의 프로젝트를 추구하려고 시도했다.죄수의 딜레마 같은 게임은 도덕성과 사리사이의 명백한 상충을 일으키기 때문에, 왜 사리사욕에 의해 협력이 요구되는지를 설명하는 것은 이 프로젝트의 중요한 구성요소이다.이 일반적인 전략은 정치 철학에서 일반적인 사회 계약 관점의 구성요소이다(예를 들어, Gauthier(1986)와 Kavka(1986) harvts 오류: no target: CITREFKavka1986 (도움말)^[d] 참조).

다른 작가들은 도덕성과 그에 상응하는 동물 행동에 대한 인간의 태도의 출현을 설명하기 위해 진화적 게임 이론을 사용하려고 시도했다.이 저자들은 죄수의 딜레마, 스태그 헌트, 내쉬 협상 게임을 포함한 몇몇 게임을 도덕성에 대한 태도의 출현에 대한 설명으로 본다.

소매 및 소비자 제품 가격 설정

게임 이론 애플리케이션은 소매 및 소비자 시장의 가격 전략, 특히 비탄력적인 상품의 판매를 위해 종종 사용됩니다.소매업자들이 소비자 시장 점유율을 놓고 끊임없이 경쟁하고 있는 가운데, 소매업자들이 벽돌과 모르타르 로케이션의 풋트래픽(전자상거래 소매업자의 웹 사이트 방문)을 늘리거나 보조 제품 또는 무료 제품의 판매를 늘리기 위해 특정 상품을 간헐적으로 할인하는 것은 꽤 흔한 일이 되고 있다.를 ^[130]참조해 주세요.

미국의 인기 쇼핑 휴일인 블랙 프라이데이는 많은 소매상들이 휴일 쇼핑 시장을 잡기 위해 최적의 가격 전략에 초점을 맞추는 날이다.블랙 프라이데이 시나리오에서 게임 이론 애플리케이션을 사용하는 소매업체는 일반적으로 "저에 대한 주요 경쟁업체의 반응은 어떻습니까?"라고 묻습니다.^[131]이러한 시나리오에서 게임은 소매업자와 소비자라는 두 명의 플레이어로 구성됩니다.소매업체는 최적의 가격 전략에 초점을 맞추고 소비자는 최상의 거래에 초점을 맞추고 있습니다.이 폐쇄적인 시스템에서는 두 선수 모두 대안을 가지고 있기 때문에 지배적인 전략이 없는 경우가 많다.즉, 소매점은 다른 고객을 찾을 수 있고, 소비자는 다른 ^[131]소매점에서 쇼핑할 수 있습니다.그러나 그날의 시장 경쟁을 감안할 때 유통업체들의 지배적인 전략은 경쟁업체들을 능가하는 데 있다.오픈 시스템은, 복수의 소매업자가 유사한 상품을 판매해, 한정된 수의 소비자가 최적 가격으로 상품을 요구하는 것을 전제로 하고 있다.코넬 대학 교수의 블로그는 이러한 전략의 예를 제시했는데, 아마존은 삼성 TV의 가격을 소매 가격보다 100달러 낮게 책정하여 경쟁업체보다 효과적으로 가격을 낮췄습니다.아마존은 HDMI 케이블의 가격을 인상해 일부분을 메워 2차 ^[131]품목 판매에 있어 소비자가 가격 차별을 덜 받는 것으로 나타났다.

소매 시장은 소비재 가격 책정에 관한 전략과 게임 이론의 적용을 계속 발전시키고 있다.통제된 환경에서의 시뮬레이션과 실제 소매 경험 사이에서 발견된 주요 통찰력은 각 소매업체가 가격, 공급업체 관계, 브랜드 이미지 및 보다 수익성이 ^[132]높은 품목의 판매를 저해할 수 있는 가능성 사이에서 최적의 균형을 찾아야 하기 때문에 이러한 전략의 적용이 더 복잡하다는 것을 보여줍니다.

역학

특정 질병에 대한 백신을 접종하는 결정은 종종 개인에 의해 이루어지기 때문에, 이러한 결정을 내릴 때 다양한 요인과 매개변수를 고려할 수 있다(예: 질병의 발병률과 유병률, 질병 수축과 관련된 인식 및 실제 위험, 사망률, 인식 및 공허와 관련된 실제 위험).국가, 그리고 예방접종의 재정적 비용) 게임 이론은 사회에서 ^[133][134]예방접종 흡수를 모델링하고 예측하기 위해 사용되어 왔다.

대중문화에서

• 실비아 ^[135]나사의 1998년 저서를 바탕으로 게임 이론가이자 수학자인 존 내쉬의 인생 스토리가 러셀 크로가 ^[136]내쉬로 출연한 2001년 전기 영화 '뷰티풀 마인드'로 바뀌었다.
• 1959년 로버트 A가 쓴 군용 공상과학 소설 스타십 트루퍼스. 하인라인은 "게임 이론"과 "게임 이론"^[137]을 언급했다.1997년 동명의 영화에서 칼 젠킨스는 자신의 군사 정보 임무를 "게임과 이론"에 배정되었다고 언급했다.
• 1964년 영화 스트란젤로브 박사는 억지 이론에 대한 게임의 이론적인 생각을 풍자한다.예를 들어 핵 억지력은 핵 공격이 탐지될 경우 치명적으로 보복할 위협에 달려 있다.게임 이론가는 그러한 위협은 서브게임의 불완전한 균형으로 이어질 수 있다는 점에서 신뢰할 수 없다고 주장할 수 있다.이 영화는 이 아이디어를 한 걸음 더 나아가 소련이 위협을 ^[138]공개하지 않고 핵으로 인한 대재앙에 대해 돌이킬 수 없는 대응을 약속하고 있다.
• 1980년대 파워 팝 밴드 게임 이론은 가수이자 작곡가인 스콧 밀러에 의해 설립되었는데, 그는 밴드의 이름이 "적에게 주어진 가장 적절한 행동을 계산하여 자신에게 최소한의 실패를 ^[139]주는 연구"를 암시한다고 설명했다.
• 2005년 일본 만화와 2007년 텔레비전 시리즈인 라이어 게임은 ^{[citation needed]}주인공들이 적용한 전략으로 입증되었듯이, 매회 주인공들에게 게임 이론에서 전형적으로 도출된 게임이나 문제를 제시한다.
• 1974년 Len Deighton의 소설 Spy Story는 냉전시대 군대 훈련에 관한 게임 이론의 요소를 탐구한다.
• 류시신의 2008년 소설 다크 포레스트는 외계 생명체, 인간성, 게임 이론 사이의 관계를 탐구한다.
• 영화 다크나이트의 주요 적대자 조커는 게임 이론 개념을 제시하는데, 특히 두 개의 다른 페리를 타고 있는 승객들에게 자신의 페리를 구하기 위해 다른 페리를 폭파하도록 요청하는 장면에서 죄수의 딜레마를 보여준다.

「 」를 참조해 주세요.

리스트

• 인지편향 목록
• 새로운 테크놀로지 목록
• 게임 이론의 게임 목록

메모들

레퍼런스

Further reading

Textbooks and general literature

• Aumann, Robert J (1987), "game theory", The New Palgrave: A Dictionary of Economics, vol. 2, pp. 460–82.
• Camerer, Colin (2003), "Introduction", Behavioral Game Theory: Experiments in Strategic Interaction, Russell Sage Foundation, pp. 1–25, ISBN 978-0-691-09039-9, archived from the original on 14 May 2011, retrieved 9 February 2011, Description.
• Dutta, Prajit K. (1999), Strategies and games: theory and practice, MIT Press, ISBN 978-0-262-04169-0. Suitable for undergraduate and business students. https://b-ok.org/book/2640653/e56341.
• Fernandez, L F.; Bierman, H S. (1998), Game theory with economic applications, Addison-Wesley, ISBN 978-0-201-84758-1. Suitable for upper-level undergraduates.
• Gibbons, Robert D. (1992), Game theory for applied economists, Princeton University Press, ISBN 978-0-691-00395-5. Suitable for advanced undergraduates.
  • Published in Europe as Gibbons, Robert (2001), A Primer in Game Theory, London: Harvester Wheatsheaf, ISBN 978-0-7450-1159-2.
• Gintis, Herbert (2000), Game theory evolving: a problem-centered introduction to modeling strategic behavior, Princeton University Press, ISBN 978-0-691-00943-8
• Green, Jerry R.; Mas-Colell, Andreu; Whinston, Michael D. (1995), Microeconomic theory, Oxford University Press, ISBN 978-0-19-507340-9. Presents game theory in formal way suitable for graduate level.
• Joseph E. Harrington (2008) Games, strategies, and decision making, Worth, ISBN 0-7167-6630-2. Textbook suitable for undergraduates in applied fields; numerous examples, fewer formalisms in concept presentation.
• Howard, Nigel (1971), Paradoxes of Rationality: Games, Metagames, and Political Behavior, Cambridge, MA: The MIT Press, ISBN 978-0-262-58237-7
• Isaacs, Rufus (1999), Differential Games: A Mathematical Theory With Applications to Warfare and Pursuit, Control and Optimization, New York: Dover Publications, ISBN 978-0-486-40682-4
• Maschler, Michael; Solan, Eilon; Zamir, Shmuel (2013), Game Theory, Cambridge University Press, ISBN 978-1-108-49345-1. Undergraduate textbook.
• Miller, James H. (2003), Game theory at work: how to use game theory to outthink and outmaneuver your competition, New York: McGraw-Hill, ISBN 978-0-07-140020-6. Suitable for a general audience.
• Osborne, Martin J. (2004), An introduction to game theory, Oxford University Press, ISBN 978-0-19-512895-6. Undergraduate textbook.
• Osborne, Martin J.; Rubinstein, Ariel (1994), A course in game theory, MIT Press, ISBN 978-0-262-65040-3. A modern introduction at the graduate level.
• Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations, New York: Cambridge University Press, ISBN 978-0-521-89943-7, retrieved 8 March 2016
• Watson, Joel (2013), Strategy: An Introduction to Game Theory (3rd edition), New York: W.W. Norton and Co., ISBN 978-0-393-91838-0. A leading textbook at the advanced undergraduate level.
• McCain, Roger A. (2010), Roger McCain's Game Theory: A Nontechnical Introduction to the Analysis of Strategy (Revised ed.), ISBN 978-981-4289-65-8
• Webb, James N. (2007), Game theory: decisions, interaction and evolution, Undergraduate mathematics, Springer, ISBN 978-1-84628-423-6 Consistent treatment of game types usually claimed by different applied fields, e.g. Markov decision processes.

Historically important texts

• Aumann, R. J.; Shapley, L. S. (1974), Values of Non-Atomic Games, Princeton University Press
• Cournot, A. Augustin (1838), "Recherches sur les principles mathematiques de la théorie des richesses", Libraire des Sciences Politiques et Sociales
• Edgeworth, Francis Y. (1881), Mathematical Psychics, London: Kegan Paul
• Farquharson, Robin (1969), Theory of Voting, Blackwell (Yale U.P. in the U.S.), ISBN 978-0-631-12460-3
• Luce, R. Duncan; Raiffa, Howard (1957), Games and decisions: introduction and critical survey, New York: Wiley

• reprinted edition: R. Duncan Luce; Howard Raiffa (1989), Games and decisions: introduction and critical survey, New York: Dover Publications, ISBN 978-0-486-65943-5{{citation}}: CS1 maint: multiple names: authors list (link)

• Maynard Smith, John (1982), Evolution and the theory of games, Cambridge University Press, ISBN 978-0-521-28884-2
• Maynard Smith, John; Price, George R. (1973), "The logic of animal conflict", Nature, 246 (5427): 15–18, Bibcode:1973Natur.246...15S, doi:10.1038/246015a0, S2CID 4224989
• Nash, John (1950), "Equilibrium points in n-person games", Proceedings of the National Academy of Sciences of the United States of America, 36 (1): 48–49, Bibcode:1950PNAS...36...48N, doi:10.1073/pnas.36.1.48, PMC 1063129, PMID 16588946
• Shapley, L.S. (1953), A Value for n-person Games, In: Contributions to the Theory of Games volume II, H. W. Kuhn and A. W. Tucker (eds.)
• Shapley, L.S. (1953), Stochastic Games, Proceedings of National Academy of Science Vol. 39, pp. 1095–1100.
• von Neumann, John (1928), "Zur Theorie der Gesellschaftsspiele", Mathematische Annalen, 100 (1): 295–320, doi:10.1007/bf01448847, S2CID 122961988 English translation: "On the Theory of Games of Strategy," in A. W. Tucker and R. D. Luce, ed. (1959), Contributions to the Theory of Games, v. 4, p. 42. Princeton University Press.
• von Neumann, John; Morgenstern, Oskar (1944), "Theory of games and economic behavior", Nature, Princeton University Press, 157 (3981): 172, Bibcode:1946Natur.157..172R, doi:10.1038/157172a0, S2CID 29754824
• Zermelo, Ernst (1913), "Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels", Proceedings of the Fifth International Congress of Mathematicians, 2: 501–4

Other material

• Ben David, S.; Borodin, Allan; Karp, Richard; Tardos, G.; Wigderson, A. (1994), "On the Power of Randomization in On-line Algorithms" (PDF), Algorithmica, 11 (1): 2–14, doi:10.1007/BF01294260, S2CID 26771869
• Downs, Anthony (1957), An Economic theory of Democracy, New York: Harper
• Gauthier, David (1986), Morals by agreement, Oxford University Press, ISBN 978-0-19-824992-4
• Allan Gibbard, "Manipulation of voting schemes: a general result", Econometrica, Vol. 41, No. 4 (1973), pp. 587–601.
• Grim, Patrick; Kokalis, Trina; Alai-Tafti, Ali; Kilb, Nicholas; St Denis, Paul (2004), "Making meaning happen", Journal of Experimental & Theoretical Artificial Intelligence, 16 (4): 209–243, doi:10.1080/09528130412331294715, S2CID 5737352
• Harper, David; Maynard Smith, John (2003), Animal signals, Oxford University Press, ISBN 978-0-19-852685-8
• Lewis, David (1969), Convention: A Philosophical Study, ISBN 978-0-631-23257-5 (2002 edition)
• McDonald, John (1950–1996), Strategy in Poker, Business & War, W. W. Norton, ISBN 978-0-393-31457-1. A layman's introduction.
• Papayoanou, Paul (2010), Game Theory for Business: A Primer in Strategic Gaming, Probabilistic, ISBN 978-0-9647938-7-3.
• Quine, W.v.O (1967), "Truth by Convention", Philosophica Essays for A.N. Whitehead, Russel and Russel Publishers, ISBN 978-0-8462-0970-6
• Quine, W.v.O (1960), "Carnap and Logical Truth", Synthese, 12 (4): 350–374, doi:10.1007/BF00485423, S2CID 46979744
• Satterthwaite, Mark A. (April 1975), "Strategy-proofness and Arrow's Conditions: Existence and Correspondence Theorems for Voting Procedures and Social Welfare Functions" (PDF), Journal of Economic Theory, 10 (2): 187–217, doi:10.1016/0022-0531(75)90050-2
• Siegfried, Tom (2006), A Beautiful Math, Joseph Henry Press, ISBN 978-0-309-10192-9
• Skyrms, Brian (1990), The Dynamics of Rational Deliberation, Harvard University Press, ISBN 978-0-674-21885-7
• Skyrms, Brian (1996), Evolution of the social contract, Cambridge University Press, ISBN 978-0-521-55583-8
• Skyrms, Brian (2004), The stag hunt and the evolution of social structure, Cambridge University Press, ISBN 978-0-521-53392-8
• Sober, Elliott; Wilson, David Sloan (1998), Unto others: the evolution and psychology of unselfish behavior, Harvard University Press, ISBN 978-0-674-93047-6
• Thrall, Robert M.; Lucas, William F. (1963), "${\displaystyle n}$-person games in partition function form", Naval Research Logistics Quarterly, 10 (4): 281–298, doi:10.1002/nav.3800100126
• Dolev, Shlomi; Panagopoulou, Panagiota; Rabie, Mikael; Schiller, Elad Michael; Spirakis, Paul (2011), "Rationality authority for provable rational behavior", Proceedings of the 30th annual ACM SIGACT-SIGOPS symposium on Principles of distributed computing, pp. 289–290, doi:10.1145/1993806.1993858, ISBN 978-1-4503-0719-2, S2CID 8974307
• Chastain, Erick; Livnat, Adi; Papadimitriou, Christos; Vazirani, Umesh (June 2014), "Algorithms, games, and evolution", Proceedings of the National Academy of Sciences of the United States of America, 111 (29): 10620–10623, Bibcode:2014PNAS..11110620C, doi:10.1073/pnas.1406556111, PMC 4115542, PMID 24979793

External links

• James Miller (2015): Introductory Game Theory Videos.
• "Games, theory of", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Paul Walker: History of Game Theory Page.
• David Levine: Game Theory. Papers, Lecture Notes and much more stuff.
• Alvin Roth:"Game Theory and Experimental Economics page". Archived from the original on 15 August 2000. Retrieved 13 September 2003. — Comprehensive list of links to game theory information on the Web
• Adam Kalai: Game Theory and Computer Science — Lecture notes on Game Theory and Computer Science
• Mike Shor: GameTheory.net — Lecture notes, interactive illustrations and other information.
• Jim Ratliff's Graduate Course in Game Theory (lecture notes).
• Don Ross: Review Of Game Theory in the Stanford Encyclopedia of Philosophy.
• Bruno Verbeek and Christopher Morris: Game Theory and Ethics
• Elmer G. Wiens: Game Theory — Introduction, worked examples, play online two-person zero-sum games.
• Marek M. Kaminski: Game Theory and Politics — Syllabuses and lecture notes for game theory and political science.
• Websites on game theory and social interactions
• Kesten Green's Conflict Forecasting at the Wayback Machine (archived 11 April 2011) — See Papers for evidence on the accuracy of forecasts from game theory and other methods.
• McKelvey, Richard D., McLennan, Andrew M., and Turocy, Theodore L. (2007) Gambit: Software Tools for Game Theory.
• Benjamin Polak: Open Course on Game Theory at Yale videos of the course
• Benjamin Moritz, Bernhard Könsgen, Danny Bures, Ronni Wiersch, (2007) Spieltheorie-Software.de: An application for Game Theory implemented in JAVA.
• Antonin Kucera: Stochastic Two-Player Games.
• Yu-Chi Ho: What is Mathematical Game Theory; What is Mathematical Game Theory (#2); What is Mathematical Game Theory (#3); What is Mathematical Game Theory (#4)-Many person game theory; What is Mathematical Game Theory ?( #5) – Finale, summing up, and my own view