호몰로지 대수

뱀 보조개념에서 사용되는 다이어그램으로, 동종 대수의 기본 결과입니다.

호몰로지 대수는 일반적인 대수적 환경에서 호몰로지를 연구하는 수학의 한 분야이다.이것은 비교적 젊은 학문으로, 그 기원은 주로 앙리 푸앵카레와 다비드 힐베르에 의해 19세기 말에 조합 위상과 추상 대수학의 연구로 추적할 수 있다.

호몰로지 대수의 발달은 범주론의 출현과 밀접하게 연관되어 있었다.대체로, 호몰로지 대수는 호몰로지 함수와 그것들이 수반하는 복잡한 대수 구조에 대한 연구이다.수학에서 매우 유용하고 유비쿼터스한 개념은 연쇄 복합체의 개념으로, 이들의 호몰로지와 코호몰로지 모두를 통해 연구될 수 있다.호몰로지 대수는 이러한 복합체에 포함된 정보를 추출하여 고리, 모듈, 위상 공간 및 기타 '유형' 수학적 객체의 호몰로지 불변성의 형태로 제시할 수 있는 수단을 제공한다.이를 위한 강력한 도구는 스펙트럼 시퀀스에 의해 제공됩니다.

바로 그 기원으로부터, 호몰로지 대수학은 대수적 위상학에서 엄청난 역할을 해왔다.그 영향은 점차 확대되어 현재는 교환 대수학, 대수 기하학, 대수적 수 이론, 표현 이론, 수리 물리학, 연산자 대수학, 복소수 분석, 편미분 방정식 이론을 포함한다.K이론은 Alain Connes의 비가환 기하학처럼 호몰로지 대수학의 방법을 이용하는 독립적인 학문이다.

상동대수의 역사

호몰로지 대수학은 1800년대에 위상학의 한 분야로서 가장 기본적인 형태로 연구되기 시작했지만,^[1] 1940년대에 이르러서야 엑스트 펑터와 토르 펑터와 같은 사물에 대한 연구와 함께 독립적인 과목이 되었다.

연쇄 복합체와 호몰로지

연쇄 복합체의 개념은 호몰로지 대수학의 중심이다.추상 사슬 복합체는 연속된 두 맵의 구성이 0이라는 특성을 가진 아벨 군과 군 동형사상의 시퀀스 $(C_{\bullet },d_{\bullet })$ $(C_{\bullet },d_{\bullet })$ $(C_{\bullet },d_{\bullet })$ $)(C_{\bullet$ }, $d_{\bullet$ })입니다 $(C_{\bullet },d_{\bullet })$ .

C_{\bullet}:\cdots\longrightarrow C_{n+1}{\stackrel {d_{n+1}}{\longrightarrow}{d_{n}}{\longrightarrow}}{\cdots\longrightarrow}{n}}{n}{n}{n}}}}}}{\cdots\longrightarrow}{\cdots}{\cdots\rightrightarrow}

C의_n 원소를 n체인이라고 하고 동형사상_n d를 경계 맵 또는 미분이라고 합니다.체인 그룹_n C에는 추가 구조가 부여될 수 있습니다.예를 들어 고정 링 R 위의 벡터 공간 또는 모듈일 수 있습니다.미분은 추가 구조가 존재하는 경우 추가 구조를 보존해야 합니다. 예를 들어, 선형 맵 또는 R-모듈의 동형이어야 합니다.인지적 편의를 위해 주의를 아벨 군(더 정확하게는 아벨 군 Ab 범주로 제한)으로 제한한다. Barry Mitchell에 의한 유명한 정리는 결과가 모든 아벨 군 범주로 일반화됨을 의미한다.모든 연쇄 복합체는 두 개의 추가적인 아벨 그룹의 시퀀스를 정의한다. 즉, 사이클_n Z = Ker_n d와_n 경계 B = Im_n+1 d이다. 여기서 Ker d와 Im d는 d의 커널과 이미지를 나타낸다.2개의 연속된 경계 맵의 구성은 제로이기 때문에 이들 그룹은 서로 다음과 같이 포함됩니다.

\displaystyle B_{n}\subseteq Z_{n}\subseteq C_{n}.}

아벨 그룹의 하위 그룹은 자동으로 정규적이므로 n번째 호몰로지 그룹_n H(C)를 n-cycle의 인자 그룹으로 n-cycle에 의해 정의할 수 있다.

{\displaystyle H_{n}(C)=Z_{n}/B_{n}=\operatorname {Ker},d_{n}/\operatorname {Im},d_{n+1}.

연쇄 복합체는 모든 호몰로지 그룹이 0일 경우 비순환 또는 정확한 배열이라고 불립니다.

연쇄 복합체는 대수학과 대수 위상에서 풍부하게 발생한다.예를 들어, X는 위상 공간 그때는 단수 체인 Cn(X)은 정상 선형 조합의 지속적인 지도에서 표준 n-simplex에 X;만약 K는 단체의. 단지는 단체의. 체인 Cn(K)은 정상 선형 조합이라는 n-simplices의 K;만약 A=F/R 있는 프리젠테이션의abelian 그룹 A에 의해 발생 relat.ions, 여기서 F는 생성자에 의해 확장된 자유 아벨 군이고 R은 관계의 부분군이다. 여기서, 다른 모든 n에 대해_n C(A) = R₀, C(A) = F, C(A) = 0을 허용하면₁ 일련의 아벨 군을 정의할 수 있다.이 모든 경우에, C를 사슬 복합체로 만드는_n 자연 미분_n d가 존재하며, 그 호몰로지는 위상 공간 X, 단순 복합체 K 또는 아벨 군 A의 구조를 반영한다.위상 공간의 경우, 우리는 단수 호몰로지의 개념에 도달한다. 단수 호몰로지는 그러한 공간의 특성, 예를 들어 다양체의 특성을 조사하는데 있어 기본적인 역할을 한다.

철학적인 차원에서, 호몰로지 대수는 우리에게 대수적 또는 기하학적 객체와 연관된 특정한 사슬 복합체(위상 공간, 단순 복합체, R-모듈)가 호몰로지가 가장 쉽게 이용할 수 있는 부분인 그것들에 대한 많은 귀중한 대수적 정보를 포함하고 있다는 것을 가르쳐준다.기술적 차원에서, 호몰로지 대수는 복합체를 조작하고 이 정보를 추출하기 위한 도구를 제공한다.여기 두 가지 일반적인 예가 있습니다.

2개의 오브젝트 X, Y가 맵 f로 접속되어 있다.호몰로지 대수학은 지도 f에 의해 유도된 X와 Y와 관련된 연쇄 복합체와 이들의 호몰로지 사이의 관계를 연구한다.이는 여러 객체와 맵이 이들을 연결하는 경우로 일반화되어 있습니다.범주 이론의 언어로 표현되는, 호몰로지 대수학은 사슬 복합체의 다양한 구조와 이러한 복합체의 호몰로지의 함수적 특성을 연구합니다.
오브젝트 X는 복수의 기술(예를 들어 위상공간 및 단순복합체로서)을 허용하거나 복합체 $C_{\bullet }(X)$ ( $X)$ (\ $displaystyle C_$ {\bullet $}(X$ ))는 비표준적 선택을 수반하는 X의 '제시'를 사용하여 구축된다.X와 관련된 연쇄 복합체에 대한 X 설명의 변화 효과를 아는 것이 중요합니다.일반적으로 콤플렉스와 그 호몰로지 H $H_{\bullet }(C)$ ( $H_{\bullet }(C)$ C )(\ $displaystyle H_{\bullet }(C))$ 는 $H_\bullet(C)$ 프레젠테이션에 관해 기능적이다.호몰로지(복합체 자체는 아니지만)는 실제로 선택된 프레젠테이션과 독립적이므로 X의 불변이다.

표준 도구

정확한 시퀀스

집단 이론의 맥락에서, 수열은

G_{0}\;{\xright 화살표 {f_{1}}\;G_{1}\;{\xright 화살표 {f_{2}}\;G_{2}\;{\xrightarrow {f_{3}}\;\cdots\;{\xrightarrow {f_{n}}\;G_{n}

각 동형의 이미지가 다음 동형의 커널과 동일할 경우, 그룹 및 그룹 동형성을 정확하게 호출한다.

\displaystyle \mathrm {im}(f_{k})=\mathrm {ker}(f_{k+1}).\!}

그룹 및 동형사상의 순서는 유한하거나 무한할 수 있습니다.

다른 어떤 대수적 구조에도 비슷한 정의를 내릴 수 있다.예를 들어, 벡터 공간과 선형 맵의 정확한 시퀀스를 가질 수 있고, 모듈 및 모듈 동형성을 가질 수 있습니다.보다 일반적으로, 정확한 시퀀스의 개념은 커널과 코커넬이 있는 범주에서 의미가 있습니다.

짧은 정확한 시퀀스

정확한 시퀀스의 가장 일반적인 유형은 짧은 정확한 시퀀스입니다.이 폼의 정확한 순서입니다.

A\;{\overset {f}{\hookright 화살표}}\;B\;{\overset {g}{\twohead right arrowoheadrightarrow}\;C

여기서 θ는 단형사상이고 g는 에피모르피즘이다.이 경우, A는 B의 서브 오브젝트이며, 대응하는 몫은 C와 동형이다.

\displaystyle C\cong B/f(A)}

(여기서 f(A) = im(f)).

아벨 그룹의 짧은 정확한 시퀀스는 5개의 항을 가진 정확한 시퀀스로도 쓸 수 있다.

0\;{\xright 화살표 {}}\;A\;{\xrightarrow {f}}\;B\;{\xrightarrow {g}}\;C\;{\xright 화살표 {}\;0

여기서 0은 사소한 그룹이나 0차원 벡터 공간과 같은 0개체를 나타냅니다.0의 힘 θ는 단형사상, g는 에피모르피즘이 된다(아래 참조).

길고 정확한 시퀀스

길고 정확한 수열은 자연수에 의해 색인화된 정확한 수열이다.

다섯 가지 보조군

임의의 아벨 범주(예: 주어진 필드의 아벨 군 범주 또는 벡터 공간의 범주) 또는 그룹의 범주에서 다음의 교환 도표를 고려하십시오.

5개의 법칙은 행이 정확하다면 m과 p가 동형사상이고, l이 에피모르피즘이고, q가 단형사상이고, n도 동형사상이라고 기술한다.

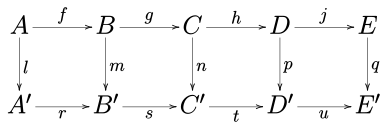
뱀 보조군

아벨 범주(예: 아벨 그룹의 범주 또는 주어진 필드의 벡터 공간의 범주)에서, 교환 도표를 고려합니다.

여기서 행은 정확한 시퀀스이고 0은 제로 객체입니다.다음으로 a, b 및 c의 커널과 코커넬에 관한 정확한 시퀀스가 있습니다.

{\displaystyle\ker a\to\ker b\to\ker coverset {d}{\to }}\operatorname {coker}a\to\operatorname {coker}b\to\operatorname {coker}c}에 \operatorname {coker}coker}cer

또한 형태소 f가 단형이면 형태소 ker a → ker b이고, g'가 에피모르피즘이면 코커 b → 코커 c도 마찬가지이다.

아벨 범주

수학에서, 아벨 범주(Abelian category)는 형태론과 객체가 추가될 수 있고, 커널과 코커넬이 존재하고 바람직한 특성을 갖는 범주이다.아벨 범주의 동기부여 원형 예는 아벨 군, Ab이다.그 이론은 알렉산더 그로텐디크의 몇 가지 코호몰로지 이론을 통합하려는 잠정적인 시도에서 비롯되었다.아벨의 범주는 매우 안정적인 범주로, 예를 들어 규칙적이고 뱀 보조군을 만족시킵니다.아벨 범주의 클래스는 몇 가지 범주 구조 하에서 닫힙니다. 예를 들어, 아벨 범주의 사슬 복합체의 카테고리 또는 작은 범주에서 아벨 범주의 펑터의 카테고리도 아벨리안입니다.이러한 안정성 특성은 호몰로지 대수학 및 그 이상에서 그것들을 불가피하게 만듭니다; 이 이론은 대수 기하학, 코호몰로지 및 순수 범주 이론에서 주요 응용 분야를 가지고 있습니다.아벨의 범주는 닐스 헨리크 아벨의 이름을 따왔다.

좀 더 구체적으로, 범주는 아벨리안이다.

물체는 0이지만
모든 바이너리 제품과 바이너리 공동 제작물을 갖추고 있습니다.
그것은 모든 알맹이와 코커넬을 가지고 있다.
모든 단형 및 에피모픽스는 정상입니다.

Ext 펑터

R을 링으로 하고 Mod를 R 위의 모듈 카테고리로 합니다_R.B를 Mod로_R 하고 고정 A를 Mod로_R T(B) = Home_R(A,B)로 설정한다.이 함수는 왼쪽 정밀 함수이므로 오른쪽 파생 함수ⁿ RT가 있습니다.Ext 펑터는 다음과 같이 정의됩니다.

\operatorname {Ext} _{R}^{n}(A,B)=(R^{n}T)(B)

이는 어떤 주입 분해능을 취하여 계산할 수 있습니다.

({displaystyle 0\right 화살표 B\right 화살표 I^{0}\right 화살표 I^{1}\cdots,})

및 컴퓨팅

0\rightarrow \operatorname {Hom}_{R}(A,I^{0})\rightarrow \operatorname {Hom}_{R}(A,I^{1})\rightarrow \cdots

그리고 (RTⁿ)(B)가 이 복합체의 상동성이다.Hom(A, B)은 복합체에서 제외됩니다_R.

펑터 G(A)=Hom_R(A,B)를 사용하여 대체 정의를 제공한다.고정 모듈 B의 경우, 이것은 반변수 좌완전함수이며, 따라서 우측 유도함수ⁿ RG도 있으며, 이를 정의할 수 있습니다.

\operatorname {Ext}_{R}^{n}(A,B)=(R^{n}G)(A)

이는 임의의 투영 해상도를 선택하여 계산할 수 있습니다.

\displaystyle \dots \right 화살표 P^{1}\right 화살표 P^{0}\right 화살표 A\right 화살표 0,}

그리고 컴퓨팅을 통해 더디게 진행됩니다.

0\rightarrow \operatorname {Hom}_{R}(P^{0},B)\rightarrow \operatorname {Hom}_{R}(P^{1},B)\rightarrow \cdots

다음으로 (RGⁿ)(A)가 이 복합체의 상동성이다.Hom(A, B)은 제외됩니다_R.

이 두 구성에서는 동형 결과를 얻을 수 있으므로 Ext 함수를 계산하는 데 둘 다 사용할 수 있습니다.

Tor 펑터

R이 고리이고 R-Mod가 왼쪽 R-모듈의 범주를 나타내고 Mod-R이 오른쪽 R-모듈의 범주를 나타냅니다(R이 가환이면 두 범주가 일치합니다).모듈 B를 R-Mod로 수정합니다.Mod-R의 A에 대해서는 T(A) = _RAµB로 설정한다.다음으로 T는 Mod-R에서 아벨 군 Ab의 범주(R이 가환인 경우 Mod-R에서 Mod-R로 가는 오른쪽 정밀 함수)로, 왼쪽 유도 함수_n LT가 정의됩니다.설정했습니다.

\mathrm {Tor} _{n}^R}(A,B)=(L_{n}T)(A)

즉, 투사적인 해결책을 취한다.

\displaystyle \cdots \rightarrow P_{2}\rightarrow P_{1}\rightarrow P_{0}\rightarrow A\rightarrow 0}

그런 다음 A항을 제거하고 B로 투사 분해능을 텐서하여 복합체를 구한다.

\displaystyle \cdots \rightarrow P_{2}\otimes _{R}B\rightarrow P_{1}\otimes _{R}B\rightarrow 0}

(A'_RB는 표시되지 않고 마지막 화살표는 제로 맵일 뿐이라는 점에 주의해 주십시오).이 복합체의 호몰로지를 취합니다.

스펙트럼 배열

링 위의 모듈 범주 등의 아벨 범주를 수정합니다.스펙트럼 시퀀스는 음이 아닌 정수₀ r과 세 가지 시퀀스의 집합이다.

모든 정수 r r₀ r에 대해, (종이에서와 같이) 시트라고 불리는 객체_r E, 또는 때로는 페이지 또는 항에 대해,
내형사상_r d : 경계_r 맵 또는_r 미분이라고 불리는 d o_r d = 0을_r 만족하는 E → E,
E와 H(E_r)의_r+1 동형사상, d에_r 대한 E의_r 동형사상.

코호몰로지₂ 스펙트럼 시퀀스의 E 시트

이중 등급의 스펙트럼 시퀀스는 추적해야 할 엄청난 양의 데이터를 가지고 있지만 스펙트럼 시퀀스의 구조를 명확하게 하는 공통 시각화 기술이 있다.r, p, q의 세 가지 인덱스가 있습니다.각 r에 대해 그래프 용지가 한 장 있다고 가정합니다.이 시트에서는 p를 수평방향으로, q를 수직방향으로 합니다.각 격자점에는 $E_{r}^{p,q}$ $E_{r}^{p,q}$ p $E_{r}^{p,q}$ q(\ $displaystyle E_{r}^{p,$ q $E_{r}^{p,q}$ 가 있습니다.

n = p + q가 스펙트럼 시퀀스의 또 다른 자연 지표가 되는 것은 매우 일반적이다.n은 각 시트에 걸쳐 대각선으로 북서쪽에서 남동쪽으로 뻗어 있습니다.호몰로지의 경우 미분에는 쌍방향(-r, r - 1)이 있으므로 n개씩 감소합니다.코호몰로지 케이스에서는 n이 1씩 증가한다.r이 0일 경우 차분은 객체를 한 칸 아래로 또는 위로 이동합니다.이것은 체인 콤플렉스의 디퍼렌셜과 유사합니다.r이 1일 경우 차분은 객체를 왼쪽 또는 오른쪽으로 한 칸 이동합니다.r이 2일 때, 차분은 체스 기사의 움직임과 같이 오브젝트를 이동합니다.r이 높을 경우 미분 값은 일반화된 기사 이동과 같습니다.

파생함수

두 아벨 범주 A와 B 사이에 공변 왼쪽 정확한 함수 F : A → B가 주어졌다고 가정합니다.0 → A → B → C → 0인 경우 F를 적용하면 정확한 시퀀스 0 → F(A) → F(B) → F(C)가 생성되며, 이 시퀀스를 오른쪽으로 계속하여 긴 정밀 시퀀스를 형성하는 방법을 물어볼 수 있습니다.엄밀히 말하면, 이 질문은 잘못된 것이다.왜냐하면, 주어진 정확한 순서를 오른쪽으로 이어가는 방법은 항상 수없이 많기 때문이다.그러나 (A가 충분히 "나이스"인 경우) F의 올바른 파생 함수에 의해 주어진 하나의 표준적인 방법이 있는 것으로 판명되었습니다.모든 iµ1에는 기능자 RFⁱ: A → B가 있으며, 위의 시퀀스는 0 → F(A) → F(B) → F¹(A) → RF(A) → RF¹¹(B) → RF(A) → RF(B) → .RF(B)와²²¹ 같이 계속됩니다.

기능성

위상 공간의 연속된 지도는 모든 n에 대해 n번째 호몰로지 그룹 간에 동형성을 발생시킨다.대수위상의 이 기본적인 사실은 사슬 복합체의 특정 특성을 통해 자연스러운 설명을 찾는다.여러 위상 공간을 동시에 연구하는 것은 매우 일반적이기 때문에, 호몰로지 대수에서 하나는 다중 사슬 복합체의 동시 고려로 이어진다.

두 개의 체인 $F:C_{\bullet }\to D_{\bullet },$ 사이의 형태, $F:C_{\bullet }\to D_{\bullet },$ F : $F:C_{\bullet }\to D_{\bullet },$ $F:C_{\bullet }\to D_{\bullet },$ $F:C_{\bullet }\to D_{\bullet },$ $F:C_{\bullet }\to D_{\bullet },$ $F:C_{\bullet }\to D_{\bullet },$ 、 \ $displaystyle$ F : $C_{\bullet }\to$ D_ ${\bullet }}$ 는 $F:C_{\bullet }\to D_{\bullet },$ 아벨 $F_{n}:C_{n}\to D_{n}$ $F_{n}:C_{n}\to D_{n}$ n : $F_{n}:C_{n}\to D_{n}$ n $F_{n}:C_{n}\to D_{n}$ $F_{n}:C_{n}\to D_{n}$ n \ $displaystyle F_{n :$ 미분과 함께 이동하는 $C_{n}\to$ D_ ${n$ 즉, 모든 $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ 에 $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ 대해 F n - $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ d n $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ D ${\$ $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ n \ $displaystyle$ F _ { n - { n - 1 } \ $circ d$ _ { $n$ } = d _ { $n$ $}^{ D$ } \ $circ$ F $_$ { n $F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}$ } 。연쇄 복합체의 형태론은 $H_{n}(F):H_{n}(C)\to H_{n}(D)$ n ( F ) $H_{n}(F):H_{n}(C)\to H_{n}(D)$ : $H_{n}(F):H_{n}(C)\to H_{n}(D)$ n $H_{n}(F):H_{n}(C)\to H_{n}(D)$ ( $H_{n}(F):H_{n}(C)\to H_{n}(D)$ ) $H_{n}(F):H_{n}(C)\to H_{n}(D)$ $H_{n}(F):H_{n}(C)\to H_{n}(D)$ n ( $H_{n}(F):H_{n}(C)\to H_{n}(D)$ ) \ $display style$ H_ ${\$ $bullet$ } ( $F$ $H_{n}(F):H_{n}(C)\to H_{n}(D)$ 로 $H_\bullet(F)$ 구성된 호몰로지 $H_{n}(F):H_{n}(C)\to H_{n}(D)$ 의 $H_{\bullet }(F)$ H $H_{\bullet }(F)$ δ ( $F)$ (\ $H_{n}(F):H_{n}(C)\to H_{n}(D)$ $H_{n}(F):H_{n}(C)\to H_{n}(D)$ { $n}$ ( $F):$ 모든 n에 $대해 H_{n$ }( $C)\to$ H_ ${n}(D$ )}.형태소 F는 n번째 호몰로지 상에서 모든 n에 대해 동형성을 유도하면 준동형성이라고 한다.

단수 호몰로지를 포함한 대수학 및 기하학에서 발생하는 사슬 복합체의 많은 구조는 다음과 같은 함수 특성을 가지고 있다. 두 물체 X와 Y가 지도 f로 연결되면 연관된 사슬 복합체는 $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ F $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ ( f $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ ) : C $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ ( $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ ) $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ C $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ ( Y ) $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ , \ $display$ F $=$ C ( $F$ ) :C_ ${\bullet$ }( $X)\to$ C_ ${\bullet$ }( $Y)$ 및 $F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),$ g: $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ → Z 맵의 $g\circ f$ g $g\circ f$ f {\ $displaystyle$ g $\$ $display$ f $}$ 는 $g\circ f$ $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ C $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ f $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ ) $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ C $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ style $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ Z $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ X ) $C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)$ 。 $C(g)\circ C(f).$ ${\bullet }(X)\to$ C_ ${\bullet$ }( $Z$ $)}.\displaystyle$ C $(g$ )\ $circ$ C $(f).$ } $H_{\bullet }(C)$ $H_{\bullet }(C)$ 그룹 H $H_{\bullet }(C)$ ( $C$ ) { $displaystyle$ H_ ${\bullet$ } ( $C$ }도 함수적이어서 대수적 또는 위상적 객체 간의 형태론이 호몰로지 간에 호환 가능한 맵을 생성한다 $.$

다음 정의는 대수학과 위상학의 전형적인 상황에서 나타난다.3개의 사슬 $L_{\bullet },M_{\bullet },N_{\bullet }$ Lδ $L_{\bullet },M_{\bullet },N_{\bullet }$ $L_{\bullet },M_{\bullet },N_{\bullet }$ $({$ }, $M_{\$ bullet }})와 그 사이의 2개의 $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ f $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ M $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ δ $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ → M $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ : $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ N $f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },$ δ $、$ {\ $bullet$ }, {\bullet $L_{\bullet },M_{\bullet },N_{\bullet }$ }로 $L_\bullet, M_\bullet, N_\bullet$ 이루어진 3중합체 f $:$ n （ $displaystyle$ ） $L_{\bullet}\to M_{\bullet},g:$ $M_{\bullet }\to$ N_ ${\bullet }}$ 은 $f:L_\bullet\to M_\bullet, g: M_\bullet\to N_\bullet,$ (는) 정확히 3중 또는 짧은 정확한 복합수열이라고 불리며 다음과 같이 쓰여진다.

0\longrightarrow L_{\bullet}{\overset {f}{\longrightarrow}{\bullet}{\overset {g}{\longrightarrow}}}N_{\bullet}\longrightarrow 0,

임의의 n에 대해서, 그 순서는

0\longrightarrow L_{n}{\overset {f_{n}}{\longrightarrow}{\longrightarrow}}{\longrightarrow 0}}{\longrightarrow 0}{n

아벨 그룹의 짧고 정확한 순서입니다.정의에 따르면, 이는 f가 주입_n, g가 돌출, Im_n f = Ker_n g를_n 의미한다.호몰로지 대수학의 가장 기본적인 이론들 중 하나는, 때때로 지그재그 보조 보조 이론으로 알려져 있는데, 이 경우, 호몰로지에는 길고 정확한 순서가 있다고 말한다.

\displaystyle \longrightarrow H_{n}(L){\overset {H_{n}(f)}{\longrightarrow}(G){\overset {H_{n}(N)}{\overset {H_{n}{n}{\longrightarrow}{n}{n}(N}{\delta}{\set}{n}{\delta}

여기서 L, M, N의 호몰로지 그룹은 서로 순환적으로 따르며, θ는_n 연결 호몰로지라고 불리는 f와 g에 의해 결정되는 특정 호몰로지이다.이 정리의 위상학적 표현은 메이어-베트남 수열과 상대 호몰로지에 대한 길고 정확한 수열을 포함한다.

기본적 측면

코호몰로지 이론은 위상 공간, 단층, 그룹, 고리, 리 대수, C*-대수와 같은 많은 다른 물체에 대해 정의되어 왔다.현대 대수기하학의 연구는 층 코호몰로지 없이는 거의 생각할 수 없을 것이다.

호몰로지 대수의 중심은 정확한 수열의 개념이다; 이것들은 실제 계산을 수행하는데 사용될 수 있다.호몰로지 대수의 고전적인 도구는 파생 함수의 도구이다; 가장 기본적인 예는 Ext와 Tor이다.

다양한 응용 프로그램을 염두에 두고 전체 주제를 통일적으로 설정하려고 하는 것은 자연스러운 일이었다.그 문제가 진정되기 전에 몇 번의 시도가 있었다.대략적인 이력은 다음과 같습니다.

카르탄 에일렌버그:1956년 저서 "호몰로지 대수"에서, 이 저자들은 투영적 및 주입적 모듈 해상도를 사용했다.
'동호쿠':1957년 도호쿠 수학 저널의 제2시리즈에 등장한 알렉산더 그로텐디크의 유명한 논문에서 아벨 범주 개념(아벨 군 단을 포함)을 사용한 접근법.
그로텐디크와 베르디에에서 파생된 범주입니다.파생된 범주는 Verdier의 1967년 논문으로 거슬러 올라간다.그것들은 많은 현대 이론에서 사용되는 삼각 범주의 예입니다.

계산 가능성에서 일반성으로 이동합니다.

계산적 해머 파 우수성은 스펙트럼 시퀀스이다. 예를 들어 두 함수의 구성 요소에서 파생된 함수를 계산하기 위해 필요한 카탄-에일렌버그 및 도호쿠 접근법에 필수적이다.스펙트럼 시퀀스는 파생 범주 접근법에서 덜 중요하지만, 여전히 구체적인 계산이 필요할 때마다 역할을 한다.

최초의 코호몰로지를 비틀림으로써 확장시키는 '비교환적' 이론에 대한 시도가 있었다(갈로아 코호몰로지에서 중요하다.

「」를 참조해 주세요.

추상적 난센스, 호몰로지 대수학 및 범주 이론의 용어
파생상품
동질 대수
호몰로지 대수 주제 목록

레퍼런스

^ Weibel, Charles A. (1999). "History of Homological Algebra". History of Topology. pp. 797–836. doi:10.1016/b978-044482375-5/50029-8. ISBN 9780444823755.

앙리 카르탕, 사무엘 아일렌버그 호몰로지 대수학입니다데이비드 A의 부록과 함께.벅스바움.1956년 원본의 전재.프린스턴의 수학 랜드마크.Princeton University Press, 프린스턴, NJ, 1999.16+390pp.ISBN 0-691-04991-2
Grothendieck, Alexander (1957). "Sur quelques points d'algèbre homologique, I". Tohoku Mathematical Journal. 9 (2): 119–221. doi:10.2748/tmj/1178244839.
손더스 맥 레인, 호몰로지1975년판 전재.수학의 고전.Springer-Verlag, 베를린, 1995년 x+422pp.ISBN 3-540-5862-8
피터 힐튼; 미국, 스탬바흐. 호몰로지 대수학 강좌.제2판수학 대학원 교재, 4. 뉴욕, 스프링거-벨락, 1997.xi+364pp.ISBN 0-387-94823-6
겔판드, 세르게이 1세;유리 마닌, 호몰로지 대수법1988년 러시아어판 번역.제2판수학의 스프링거 모노그래프.스프링거-벨라그, 베를린, 2003년xx+372 페이지.ISBN 3-540-43583-2
겔판드, 세르게이 1세;유리 마닌, 호몰로지 대수학 교수야1989년 저자에 의해 러시아어 원문에서 번역되었다.수리과학 백과사전 시리즈(Algebra, V, Encyclopedia Math)의 영어판 원판을 전재.Sci., 38, Springer, Berlin, 1994).1999년 베를린 스프링거-벨라그iv+222pp.ISBN 3-540-65378-3
Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.

[Weber-1] Weibel, Charles A. (1999). "History of Homological Algebra". History of Topology. pp. 797–836. doi:10.1016/b978-044482375-5/50029-8. ISBN 9780444823755.

[1]

v t 토폴로지
필드	일반(포인트 세트) 대수적 조합 연속체 차동 기하학 저차원의 호몰로지 코호몰로지 집합 이론 디지털.
주요 개념	오픈 세트 / 클로즈드 세트 내부 연속성 공간 작은 연결된 하우스도르프 미터법 균일한 호모토피 호모토피군 기본군 단순 복합체 CW 콤플렉스 다면체 복합체 다지관 번들(수학) 두 번째 셀 수 있는 공간 코보디즘
메트릭 및 속성	오일러 특성 베티수 권선번호 체른 번호 방향성
주요 결과	바나흐 고정점 정리 드 람의 정리 영역의 불변성 푸앵카레 추측 티코노프의 정리 유리손의 보조군
카테고리 수학 포털 위키북 위키 다양성 토픽 일반적인 대수적 기하학적 출판물

Search

호몰로지 대수

네임스페이스

더

목차

상동대수의 역사

연쇄 복합체와 호몰로지