반응-확산계

반응-확산 시스템은 여러 물리적 현상에 해당하는 수학적 모델입니다. 가장 일반적인 것은 하나 이상의 화학 물질의 농도의 공간과 시간의 변화입니다: 물질들이 서로 변환되는 국소적인 화학 반응, 그리고 물질들이 공간의 표면 위에 퍼지게 하는 확산입니다.

반응-확산 시스템은 자연스럽게 화학에 적용됩니다. 그러나 시스템은 비화학적 특성의 동적 프로세스도 설명할 수 있습니다. 생물학, 지질학 및 물리학(중성자 확산 이론)과 생태학에서 그 예를 찾을 수 있습니다. 수학적으로 반응-확산 시스템은 반선형 포물선 편미분 방정식의 형태를 취합니다. 일반적인 형태로 표현할 수 있습니다.

${\displaystyle \partial _{t}{\boldsymbol {q}}={\boldsymbol {D}}\,\nabla ^{2}{\boldsymbol {q}}+{\boldsymbol {R}}({\boldsymbol {q}}),}$

여기서 q(x, t)는 미지수 벡터 함수를 나타내고, D는 확산 계수의 대각선 행렬이며, R은 모든 국소 반응을 설명합니다. 반응-확산 방정식의 해법은 이동하는 파동과 파동과 같은 현상의 형성뿐만 아니라 줄무늬, 육각형 또는 소산 솔리톤과 같은 더 복잡한 구조와 같은 다른 자기 조직화된 패턴을 포함한 광범위한 행동을 보여줍니다. 그러한 패턴은 "튜링 패턴(Turing patterns)"이라고 불립니다.^[1] 반응 확산 미분 방정식이 성립하는 각 함수는 사실상 농도 변수를 나타냅니다.

일성분 반응-확산 방정식

가장 간단한 반응-확산 방정식은 평면 기하학에서 하나의 공간 차원에 있습니다.

${\displaystyle \partial _{t}u=D\partial _{x}^{2}u+R(u),}$

콜모고로프-페트로프스키-피스쿠노프 방정식이라고도 합니다.^[2] 반응항이 사라지면 방정식은 순수한 확산 과정을 나타냅니다. 그에 해당하는 방정식이 픽의 제2법칙입니다. R(u) = u(1 - u) 선택은 원래 생물학적 개체군의 확산을 설명하는 데 사용된 피셔 방정식인 뉴웰-을 산출합니다.레일리-베나드 대류를 설명하기 위해 R(u) = u(1 - u)가 있는 화이트헤드-세겔 방정식, 연소 이론에서 발생하는 R(u) = u(1 - u)e 및 0 < β < ∞(젤도비치 번호)가 있는 젤도비치-프랑크-카메네츠키 방정식, 때때로 젤도비치 방정식이라고도 하는 R(u) = u - u가 있는 특정 축퇴 경우.

진화 방정식도 변형 형태로 작성될 수 있기 때문에 일 구성 요소 시스템의 역학은 특정 제한을 받습니다.

${\displaystyle \partial _{t}u=-{\frac {\delta {\mathfrak {L}}}{\deltau}}$

따라서 함수에 의해 주어진$$ "자유 에너지" $L{\displaystyle \mathfrak{}}$ ${\$의 영구적인 감소를 설명합니다.

${\displaystyle {\mathfrak {L}}=\int _{-\infty}^{\infty}\left[{\tfrak {D}{2}}\left(\partial _{x}u\right)^{2}-V(u)\right]\,{\text{d}}x}$

R(u) = dV(u)/du와 같은 전위 V(u)를 사용합니다.

하나 이상의 고정된 균질해가 있는 시스템에서는 균질한 상태를 연결하는 전선을 이동하여 일반적인 해를 제공합니다. 이 솔루션은 모양이 변하지 않고 일정한 속도로 움직이며 ξ = x - ct인 u(x, t) = û(ξ) 형식입니다. 여기서 c는 진행파의 속도입니다. 이동하는 파동은 일반적으로 안정적인 구조이지만 모든 비단조적인 정지해 있는 솔루션(예: 전면-반전 쌍으로 구성된 국부 도메인)은 불안정하다는 점에 유의하십시오. c = 0인 경우, 이 문장에 대한 간단한 증명이 있습니다: 만약 u(x)가 정지해 있고 u = u(x) + ũ(x, t)가 무한히 교란된 해라면, 선형 안정성 분석은 방정식을 산출합니다.

${\displaystyle \partial _{t}{\tilde {u}}=D\partial _{x}^{2}{\tilde {u}}-U(x){\tilde {u}},\qquad U(x)=-R^{\prime }(u){\Big }_{u=u_{0}(x)}.}$

ansatz ũ = ψ(x)exp (-λt)를 사용하면 고유값 문제에 도달합니다.

${\displaystyle {\hat {H}}\psi =\lambda \psi,\qquad {\hat {H}}=-D\partial _{x}^{2}+U(x),}$

슈뢰딩거 유형의 경우, 음의 고유값으로 인해 해가 불안정해집니다. 번역 불변성으로 인해 ψ = ∂ u(x)는 고유값 λ = 0을 갖는 중성 고유함수이며, 다른 모든 고유함수는 노드 수가 증가함에 따라 정렬될 수 있으며, 해당 실제 고유값의 크기는 0의 수에 따라 단조적으로 증가합니다. 고유함수 ψ = ∂ u(x)는 적어도 하나의 0을 가져야 하며, monot이 아닌 정지해의 경우 해당 고유값 λ = 0이 가장 낮을 수 없으므로 불안정성을 의미합니다.

움직이는 전선의 속도 c를 결정하기 위해서는 움직이는 좌표계로 가서 정지해 있는 해를 볼 수 있습니다.

${\displaystyle D\partial _{\xi }^{\hat {u}}(\xi )+c\partial _{\xi }{\hat {u}}(\xi )+R({\hat {u}}(\xi ))=0.}$

이 방정식은 감쇠 계수 c가 있는 힘 R 아래의 "시간" ξ 과정에서 위치 û을 갖는 질량 D의 운동으로 좋은 기계적 아날로그를 가지고 있습니다. 이는 다양한 유형의 솔루션 구성 및 c의 결정에 대한 다소 실례가 되는 접근을 가능하게 합니다.

하나의 공간 차원에서 더 많은 공간 차원으로 이동할 때에도 1차원 시스템의 여러 문을 적용할 수 있습니다. 평면파면 또는 곡선파면은 전형적인 구조이며, 곡선파면의 국소 속도가 국소 곡률 반경에 의존하게 됨에 따라 새로운 효과가 발생합니다(극점 좌표로 이동하면 이를 알 수 있습니다). 이러한 현상은 이른바 곡률 중심의 불안정성으로 이어집니다.^[9]

2성분 반응-확산 방정식

2성분 시스템은 1성분 시스템보다 훨씬 더 큰 범위의 가능한 현상을 허용합니다. 앨런 튜링이 처음 제안한 중요한 아이디어는 로컬 시스템에서 안정적인 상태가 확산이 있을 때 불안정해질 수 있다는 것입니다.^[10]

그러나 선형 안정성 분석 결과 일반적인 2성분 시스템을 선형화할 때

${\displaystyle {\begin{pmatrix}\partial _{t}u\\\\partial _{t}v\end{pmatrix}}={\begin{pmatrix}D_{u}&0\0&D_{v}\end{pmatrix}}{\begin{pmatrix}\partial _{xx}u\\\partial _{xx}v\end{pmatrix}}+{\begin{pmatrix}F(u,v)\\G(u,v)\end{pmatrix}}}$

평면파 섭동

${\displaystyle {\tilde {\boldsymbol {q}}_{\boldsymbol {k}}({\boldsymbol {x}},t)={\begin{pmatrix}{\tilde {u}}(t)\{\tilde {v}}(t)\end{pmatrix}}e^{i\boldsymbol {k}\cdot {\boldsymbol {x}}}$

고정 동차 해의 다음을 만족시킬 것입니다.

${\displaystyle {\begin{pmatrix}\partial _{tilde{u}}_{\boldsymbol {k}}(t)\\\partial _{t}{\tilde{v}}_{\boldsymbol{k}}(t)\end{pmatrix}}=-k^{2}{\begin{pmatrix}D_{u}{\tilde{u}}_{\boldsymbol{k}}(t)\\D_{v}{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}}+{\boldsymbol {R}}^{\prime }{\begin{pmatrix}{\tilde {u}}_{\boldsymbol {k}}(t)\\{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}}.}$

튜링의 아이디어는 반응 함수의 자코비안 R'의 부호로 특징지어지는 4개의 동등한 등급의 계에서만 실현될 수 있습니다. 특히 유한한 파동벡터 k가 가장 불안정하다고 가정할 경우, 야코비안은 부호를 가지고 있어야 합니다.

${\displaystyle {\begin{pmatrix}+&-\++-\end{pmatrix}},\quad {\begin{pmatrix}+&+\-&-\end{pmatrix},\quad {\begin{pmatrix}-&+\-+\-+\end{pmatrix}},\quad {\begin{pmatrix}-&-\+++\end{pmatrix}}.$

이 종류의 시스템은 첫 번째 대표자의 이름을 따서 활성화제-억제제 시스템으로 명명됩니다: 바닥 상태에 가까운 한 구성 요소는 두 구성 요소의 생성을 자극하고 다른 구성 요소는 성장을 억제합니다. 가장 두드러진 대표적인 것은 피츠휴-나구모 방정식입니다.

${\displaystyle {\begin{aligned}\partial _{t}u&=d_{u}^{2}\,\nabla ^{2}u+f(u)-\sigma v,\\\tau \partial _{t}v&=d_{v}^{2}\,\nabla ^{2}v+u-v\end{aligned}}}$

f(u) = λu - u - κ로 활동전위가 신경을 통해 이동하는 방법을 설명합니다. 여기서 d, d, τ, σ 및 λ는 양의 상수입니다.

활성화제-억제제 시스템이 매개변수의 변화를 겪을 때, 균질한 접지 상태가 안정적인 조건에서 선형적으로 불안정한 조건으로 전달될 수 있습니다. 해당 분기는 지배적인 파동 수 k = 0을 가진 전역적으로 진동하는 균질한 상태로의 홉프 분기 또는 지배적인 유한 파동 수를 가진 전역적으로 패턴화된 상태로의 튜링 분기일 수 있습니다. 두 공간 차원의 후자는 일반적으로 줄무늬 또는 육각형 패턴으로 이어집니다.

• 아임계 튜링 분기: Fitzhuh-Nagumo 타입의 상기 2성분 반응-확산 시스템에서 잡음이 많은 초기 조건으로부터 육각형 패턴의 형성.
• 
  t = 0에서 노이즈가 많은 초기 조건.
• 
  t = 10에서 시스템의 상태.
• 
  t = 100에서 거의 수렴된 상태입니다.

Fitzhuh–Nagumo 예제의 경우, 튜링과 호프 분기에 대한 선형 안정 영역의 경계를 표시하는 중립 안정 곡선은 다음과 같이 주어집니다.

${\displaystyle {\begin{aligned}q_{\text{n}}^{H}(k):&{}\quad {\frac {1}{\tau }}+\left(d_{u}^{2}+{\frac {1}{\tau }}d_{v}^{2}\right)k^{2}&=f^{\prime }(u_{h}),\\[6pt]q_{\text{n}}^{T}(k):&{}\quad {\frac {\kappa }{1+d_{v}^{2}k^{2}}}+d_{u}^{2}k^{2}&=f^{\prime }(u_{h}).\end{align}}}$

분기가 아임계인 경우 패턴이 기저 상태와 공존하는 이력 영역에서 종종 국부적인 구조(분산 솔리톤)가 관찰될 수 있습니다. 자주 접하는 다른 구조에는 펄스 열(주기적인 이동 파동이라고도 함), 나선파 및 표적 패턴이 있습니다. 이 세 가지 솔루션 유형은 또한 로컬 동역학이 안정적인 한계 사이클을^[13] 갖는 2(또는 그 이상) 성분 반응-확산 방정식의 일반적인 특징입니다.

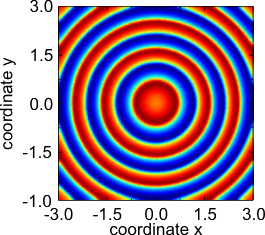
• Fitzhuh-Nagumo type의 상기 2성분 반응-확산 시스템에서 발견되는 다른 패턴.
• 
  회전 나선.
• 
  목표 패턴.
• 
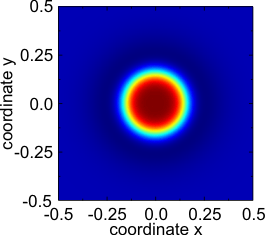
  정지된 국소 펄스(분극 솔리톤).

삼성분 반응-확산 방정식

혈액 응고,^[14][15] 핵분열파^[16] 또는 평면 가스 배출 시스템에 대해 벨루소프-자보틴스키 반응과 같이 두 가지 이상의 성분을 갖는 반응-확산 방정식이 다양한 시스템에 대해 제안되었습니다.^[17]

더 많은 구성요소를 갖는 시스템은 하나 또는 두 개의 구성요소를 갖는 시스템(예: 전역 피드백 없이 하나 이상의 공간 차원에서 안정적으로 실행되는 펄스)에서 가능하지 않은 다양한 현상을 허용하는 것으로 알려져 있습니다.^[18] 기본 시스템의 속성에 따라 발생 가능한 현상에 대한 소개와 체계적인 개요가 제공됩니다.^[19]

응용프로그램 및 보편성

최근에 반응-확산 시스템은 패턴 형성의 프로토타입 모델로 많은 관심을 끌고 있습니다.^[20] 위에서 언급한 패턴(전면, 나선, 표적, 육각형, 줄무늬 및 소산 솔리톤)은 예를 들어 국소 반응 용어의 큰 불일치에도 불구하고 다양한 유형의 반응-확산 시스템에서 발견할 수 있습니다. 또한 반응-확산 과정이^[21][22] 생물학의 형태 형성과 관련된 과정의 필수적인 기초이며 동물의 외투 및 피부 색소 침착과 관련이 있을 수 있다고 주장되었습니다.^[23][24] 반응-확산 방정식의 다른 응용에는 생태학적 침입,^[25] 전염병 확산,^[26] 종양 성장,^[27][28][29] 핵분열 파동의 역학,^[30] 상처 치유^[31] 및 시각적 환각이 포함됩니다.^[32] 반응-확산 시스템에 관심을 갖는 또 다른 이유는 비선형 편미분 방정식이지만 종종 분석 처리의 가능성이 있기 때문입니다.^{[8][9][33][34][35][20]}

실험

화학 반응-확산 시스템에서 잘 제어 가능한 실험은 지금까지 세 가지 방법으로 실현되었습니다. 먼저 젤 반응기^[36] 또는 충전된 모세관을^[37] 사용할 수 있습니다. 둘째, 촉매 표면의 온도 펄스가 조사되었습니다.^[38][39] 셋째, 작동 중인 신경 펄스의 전파는 반응-확산 시스템을 사용하여 모델링됩니다.^[11][40]

이러한 일반적인 예를 제외하고, 플라즈마^[41] 또는 반도체와^[42] 같은 전기 수송 시스템은 적절한 상황에서 반응-확산 접근 방식으로 설명될 수 있는 것으로 밝혀졌습니다. 이러한 시스템에 대해 패턴 형성에 대한 다양한 실험이 수행되었습니다.

수치처리

반응-확산 시스템은 수치 수학의 방법을 사용하여 해결할 수 있습니다. 연구 문헌에는 기존의 몇 가지 수치 처리가 있습니다.^[43][20][44] 또한 복잡한 기하학적 구조에 대해서도 수치 솔루션 방법이 제안됩니다.^[45][46] SRSim 또는 ReaDDy와^[47] 같은 입자 기반 시뮬레이션 도구를 사용하여 반응 확산 시스템이 가장 상세하게 설명됩니다. 이는 예를 들어 가역적 상호 작용 입자 반응 역학을 사용합니다.^[48]

참고 항목

• 오토웨이브
• 확산 제어 반응
• 화학동역학
• 위상공간법
• 자기 촉매 반응 및 순서 생성
• 패턴형성
• 자연의 패턴
• 주기적 주행파
• 확률기하학
• MC론
• 형태형성의 화학적 기초
• 튜링 패턴
• 생체분자의 다중상태 모델링

예

• 피셔 방정식
• 젤도비치-프랑크-카메네츠키 방정식
• 피츠휴-나구모 모형
• 주름페인트

참고문헌

외부 링크

• 반응-회색-스콧 모형에 의한 확산: 피어슨의 매개변수화는 회색-스콧 반응 확산의 매개변수 공간에 대한 시각적 지도입니다.
• 현장개요를 통한 반응-확산패턴에 관한 논문
• RD Tool : 반응 확산 시뮬레이션을 위한 대화형 웹 응용 프로그램