입자군 최적화

Particle swarm optimization
함수의 전역 최소값을 찾는 입자 무리
시리즈의 일부
진화 알고리즘
유전 알고리즘
유전자 프로그래밍

입자 군집 최적화(,[1] PSO)는 컴퓨터 과학에서 주어진 품질 측정과 관련하여 후보 솔루션을 개선하기 위해 반복적으로 시도함으로써 문제를 최적화하는 컴퓨터 방법입니다.입자라고 불리는 후보해군을 가지고 이 입자들을 입자의 위치와 속도 위에서 간단한 수학 공식에 따라 탐색공간에서 이동시킴으로써 문제를 해결합니다.각 입자의 움직임은 국소적으로 가장 잘 알려진 위치에 의해 영향을 받지만, 다른 입자에 의해 더 나은 위치가 발견됨에 따라 업데이트되는 검색 공간에서 가장 잘 알려진 위치로 안내됩니다.이것은 그 무리를 최상의 해결책으로 이끌 것으로 예상됩니다.

PSO는 원래 케네디, 에버하트, 시의[2][3] 것으로 간주되며 처음에는 새 떼나 물고기 무리에서 생물체의 움직임을 양식화한 표현으로 사회적 행동을 시뮬레이션하기 위해 고안되었습니다.[4]알고리즘은 단순화되었고 최적화를 수행하는 것으로 관찰되었습니다.케네디와 에버하트의[5] 책은 PSO와 군집 지능의 많은 철학적 측면을 묘사하고 있습니다.Poli는 PSO 애플리케이션에 대한 광범위한 조사를 실시합니다.[6][7]최근 PSO에 대한 이론적, 실험적 작업에 대한 종합적인 리뷰가 Bonyadi and Michaelwicz에 의해 발표되었습니다.[1]

PSO는 최적화된 문제에 대한 가정을 거의 하지 않고 매우 넓은 공간의 후보 솔루션을 검색할 수 있기 때문에 메타휴리스틱(metaheuristic)입니다.또한 PSO는 최적화되는 문제의 기울기를 사용하지 않으며, 이는 PSO가 기울기 하강 및 준뉴턴 방법과 같은 고전적인 최적화 방법에서 요구하는 것처럼 최적화 문제를 구별할 필요가 없다는 것을 의미합니다.그러나 PSO와 같은 메타 휴리스틱은 최적의 솔루션을 찾는 것을 보장하지 않습니다.

알고리즘.

PSO 알고리즘의 기본 변형은 후보 솔루션(입자라고 함)의 집단(집단)을 가짐으로써 작동합니다.이 입자들은 몇 가지 간단한 공식에 따라 탐색 공간에서 이동합니다.[8]입자의 움직임은 전체 무리의 가장 잘 알려진 위치뿐만 아니라 탐색 공간에서의 가장 잘 알려진 위치에 의해 유도됩니다.개선된 위치가 발견되면 이러한 위치는 무리의 움직임을 안내합니다.이 과정은 반복되며, 그렇게 함으로써 결국 만족스러운 해결책을 찾을 수 있기를 바라지만 보장할 수는 없습니다.

공식적으로 f: ℝ → ℝ은 최소화되어야 하는 비용 함수입니다.함수는 실수 벡터 형태의 인수로 후보해를 취하고 주어진 후보해의 객관적인 함수 값을 나타내는 실수를 출력으로 생성합니다.기울기 off는 알 수 없습니다.목표는 검색 공간에서 모든 b에 대한 f(a) ≤ f(b)인 해 a를 찾는 것이며, 이는 a가 전역 최소값임을 의미합니다.

S를 탐색 공간에서 각각의 위치 x ∈ ℝ와 속도 v ∈ ℝ를 갖는 군집 내 입자의 수라 하자. p를 입자 i의 가장 잘 알려진 위치라고 하고 g를 전체 군집의 가장 잘 알려진 위치라고 하자.비용 함수를 최소화하기 위한 기본 PSO 알고리즘은 다음과 같습니다.[9]

각 입자 i = 1, ..., S도 균일 분포 랜덤 벡터로 입자의 위치 초기화: x ~ U(b, b) 입자의 가장 잘 알려진 위치를 초기 위치로 초기화: p ← x if f(p) < f(g) 이후 스웜의 가장 잘 알려진 위치를 업데이트: g ← p 종료 크리트 동안 입자의 속도 초기화: v ~ U(- b-b, b-b)rion이 충족되지 않음: 각 입자 i = 1, ..., 각 차원 D = 1, ..., ndo 난수 선택: r, r ~ U(0,1)             입자의 속도 갱신: v ← w v + φ r (p-x) + φ r (g-x) 입자의 위치 갱신: x ← x + v if f(x) < f(p) 다음 입자의 가장 잘 알려진 위치 갱신: p ← x if f(p) < f(g) 다음 스웜의 가장 잘 알려진 위치 갱신: g ← p

값 b와lo b는up 각각 검색 공간의 하한과 상한을 나타냅니다.w 파라미터는 관성 가중치입니다.φ와 φ라는 매개변수는 종종 인지 계수와 사회 계수라고 불립니다.

종료 기준은 수행된 반복 횟수일 수도 있고, 적절한 목적 함수 값이 발견된 해일 수도 있습니다.[10]parameter w, φ, φ은 실무자가 선택하여 PSO method(아래)의 동작과 효능을 제어합니다.

파라미터선택

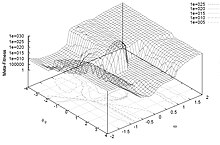
두 개의 PSO 매개 변수를 변화시킬 때 단순한 PSO 변형이 여러 벤치마크 문제에서 종합적으로 어떻게 수행되는지 보여주는 성능 환경입니다.

PSO 파라미터의 선택은 최적화 성능에 큰 영향을 미칠 수 있습니다.따라서 우수한 성능을 제공하는 PSO 파라미터를 선택하는 것은 많은 연구의 대상이 되었습니다.[11][12][13][14][15][16][17][18][19]

발산("폭발")을 방지하려면 관성 가중치가 1보다 작아야 합니다.다른 두 개의 매개변수는 제한 접근법 덕분에 [16]도출되거나 자유롭게 선택될 수 있지만, 분석은 이를 제한하기 위한 수렴 영역을 제안합니다.일반적인은 [3 {\ [ 3에 있습니다

PSO 파라미터는 메타 최적화로 알려진 개념인 다른 오버레이 최적화기를 사용하여 조정하거나 퍼지 논리 등을 [20][21][22][23]통해 최적화 중에 미세 조정할 수도 있습니다.[24][25]

또한 다양한 최적화 시나리오를 위해 매개변수가 조정되었습니다.[26][27]

인접 영역 및 토폴로지

군집의 위상은 각 입자가 정보를 교환할 수 있는 입자의 부분 집합을 정의합니다.[28]알고리즘의 기본 버전은 전역 토폴로지를 스웜 통신 구조로 사용합니다.[10]이 위상은 모든 입자들이 다른 모든 입자들과 소통할 수 있도록 하여, 전체 무리는 하나의 입자로부터 같은 최상의 위치 g를 공유합니다.그러나 이 접근법은 무리를 국소적인 최소값에 갇히게 할 수 있으므로 입자 [29]사이의 정보 흐름을 제어하기 위해 다양한 위상이 사용되어 왔습니다.예를 들어, 로컬 토폴로지에서 입자는 입자의 부분 집합과만 정보를 공유합니다.[10]이 부분 집합은 기하학적인 것[30], 예를 들어 "가장 가까운 입자"일 수도 있고, 더 자주 사회적인 것, 즉 거리에 의존하지 않는 입자의 집합일 수도 있습니다.이러한 경우 PSO 변형은 로컬 베스트(기본 PSO의 경우 글로벌 베스트)라고 합니다.

일반적으로 사용되는 군집 위상은 고리인데, 고리는 각 입자가 단지 두 개의 이웃을 가지고 있지만, 다른 많은 입자들도 있습니다.[10]토폴로지가 반드시 정적인 것은 아닙니다.실제로, 토폴로지는 입자의 통신의 다양성과 관련이 있기 때문에 [31]적응 토폴로지(SPSO,[32] APSO,[33] 확률적 별,[34] TRIBS,[35] Cyber Swarm,[36] C-PSO[37])를 만들기 위한 노력이 어느 정도 진행되었습니다.

내공

PSO 알고리즘이 최적화를 수행할 수 있는 이유와 방법에 대한 여러 생각이 있습니다.

연구자들 사이의 공통적인 믿음은 군집 행동이 탐색 공간의 더 넓은 영역을 탐색하는 것과 (아마도 지역적인) 최적화에 더 가까이 접근하기 위한 지역 지향적인 탐색 사이에서 달라진다는 것입니다.이 사상학파는 PSO가 시작된 이래로 널리 퍼져 있었습니다.[3][4][12][16]이 사상학파는 PSO 알고리즘과 매개 변수가 탐색과 활용 사이의 적절한 균형을 유지하여 로컬 최적으로 조기 수렴하는 것을 피하면서도 최적으로 수렴하는 좋은 비율을 보장할 수 있도록 선택되어야 한다고 주장합니다.이 믿음은 많은 PSO 변형의 전조이며, 아래를 참조하십시오.

또 다른 생각은 PSO 군집의 행동이 실제 최적화 성능에 영향을 미치는 방식, 특히 불연속적이고 소음이 심하며 시간이 변화할 수 있는 고차원 검색 공간 및 최적화 문제에 대해 잘 이해되지 않는다는 것입니다.이 학파는 단지 탐색 및 착취와 관련하여 군집 행동이 어떻게 해석될 수 있는지에 관계없이 우수한 성능을 유발하는 PSO 알고리즘 및 매개 변수를 찾으려고 노력할 뿐입니다.이러한 연구는 PSO 알고리즘의 단순화를 이끌어냈습니다. 아래를 참조하십시오.

컨버전스

PSO와 관련하여 컨버전스라는 단어는 일반적으로 두 가지 다른 정의를 나타냅니다.

  • 최적일 수도 있고 그렇지 않을 수도 있는 탐색공간의 한 지점에 모든 입자가 수렴된 솔루션(일명, 안정성 분석, 수렴)의 시퀀스의 수렴,
  • 모든 개인적인 베스트 또는 스웜의 가장 잘 알려진 위치 g가 스웜의 행동 방식에 관계없이 문제의 로컬 최적에 접근하는 로컬 최적으로의 수렴.

PSO에 대해 솔루션 시퀀스의 수렴이 조사되었습니다.[15][16][17]이러한 분석을 통해 한 점으로 수렴을 유발하고 군집 입자의 발산을 방지하는 것으로 추정되는 PSO 매개 변수를 선택하는 지침이 도출되었습니다(입자는 무한히 이동하지 않고 어딘가로 수렴할 것입니다).그러나 페데르센은[22] 무리가 단 하나의 입자만을 가지고 있다고 가정하고 확률변수를 사용하지 않으며, 최적화 과정 내내 인력점, 즉 입자의 가장 잘 알려진 위치 p와 무리의 가장 잘 알려진 위치 g가 일정하다고 가정하여 분석이 지나치게 단순화되었다는 비판을 받았습니다.그러나 이러한 단순화는 군집이 수렴하는 매개변수에 대해 이러한 연구에서 발견한 경계에 영향을 미치지 않는 것으로 나타났습니다[38].최근 PSO의 안정성 분석 시 사용되는 모델링 가정을 약화시키기 위해 상당한 노력을 기울이고 있으며, 가장 최근의 일반화된 결과는 다양한 PSO 변형에 적용되고 필요한 최소한의 모델링 가정을 사용했습니다.[39][40]

그리고[41] PSO에 대한 국소 최적화로의 수렴이 분석되었습니다.[42]PSO는 로컬 최적화를 보장하기 위해 약간의 수정이 필요한 것으로 입증되었습니다.

이는 다양한 PSO 알고리즘과 매개 변수의 수렴 능력을 결정하는 것이 여전히 경험적 결과에 의존한다는 것을 의미합니다.이 문제를 해결하기 위한 한 가지 시도는 p와 g 사이의 관계에 이미 존재하는 정보의 개선된 사용을 위한 "직교 학습" 전략을 개발하여 선도적인 수렴 예시를 형성하고 임의의 PSO 토폴로지로 효과적으로 사용하는 것입니다.글로벌 컨버전스 속도 향상,[43] 솔루션 품질 향상, 견고성 강화 등 전반적인 PSO 성능 향상을 목표로 하고 있습니다.그러나 그러한 연구들은 그들의 주장을 실제로 증명할 수 있는 이론적인 증거를 제공하지 못합니다.

적응 메커니즘

수렴('익스플로티지')과 발산('익스플로티지') 사이의 트레이드-오프(trade-off) 없이 적응적 메커니즘을 도입할 수 있습니다.APSO(adaptive particle swarm optimization)는 기존 PSO보다 우수한 검색 효율성을 특징으로 하며, APSO는 보다 빠른 수렴 속도로 전체 검색 공간에 대한 전역 검색을 수행할 수 있습니다.실행 시간에 관성 가중치, 가속도 계수 등의 알고리즘 파라미터를 자동으로 제어할 수 있어 검색의 효율성과 효율성을 동시에 높일 수 있습니다.또한 APSO는 가능성 있는 로컬 최적화에서 벗어나 글로벌 최고의 입자에 작용할 수 있습니다.그러나 APSO는 새로운 알고리즘 매개변수를 도입할 것이지만, 추가적인 설계나 구현의 복잡성은 도입하지 않습니다.

변형

기본적인 PSO 알고리즘도 여러 가지 변형이 가능합니다.예를 들어 입자와 속도를 초기화하는 여러 가지 방법(예: 대신 0 속도로 시작), 속도를 감소시키는 방법, 전체 군집이 업데이트된 후 p와 g만i 업데이트하는 방법 등이 있습니다.이러한 선택의 일부와 그에 따른 성능 영향에 대해서는 문헌에서 논의되어 왔습니다.[14]

일련의 표준 구현은 "기술 개선의 성능 테스트를 위한 기준이자 PSO를 보다 광범위한 최적화 커뮤니티에 표현하기 위한 기준으로 사용하기 위한 것입니다.잘 알려져 있고 엄격하게 정의된 표준 알고리즘을 사용하면 연구 분야 전반에서 새로운 발전을 더 잘 테스트하는 데 사용할 수 있는 귀중한 비교 지점을 제공할 수 있습니다."[10]가장 최근의 것은 Standard PSO 2011(SPSO-2011)입니다.[45]

혼성화

최적화 성능을 향상시키기 위해 새롭고 더 정교한 PSO 변형도 지속적으로 도입되고 있습니다.그 연구에는 특정한 경향이 있습니다. 하나는 다른 최적화기와 결합된 PSO를 사용하여 하이브리드 최적화 방법을 만드는 것입니다.[46][47][48] 예를 들어 생물지리학 기반 최적화와 결합된 PSO, 그리고 효과적인 학습 방법의 통합입니다.[49][43]

조기 수렴 완화

또 다른 연구 동향은 PSO 입자의 움직임을 반전시키거나 교란시킴으로써 조기 수렴(즉, 최적화 정체)을 완화하려고 시도하는 것이며,[19][50][51][52] 조기 수렴을 처리하기 위한 또 다른 접근법은 다중 군집[53](다중 군집 최적화)의 사용입니다.다중 스웜(multi-swarm) 접근 방식은 다중 목적 최적화를 구현하는 데에도 사용될 수 있습니다.[54]마지막으로, 최적화하는 동안 PSO의 동작 파라미터를 적용하는 데 발전이 있습니다.[44][24]

단순화

또 다른 사고방식은 PSO의 성능을 손상시키지 않으면서 PSO를 최대한 단순화해야 한다는 것입니다. 오캄의 면도기라고 불리는 일반적인 개념입니다.PSO를 단순화하는 것은 원래 Kennedy에[4] 의해 제안되었으며 보다 광범위하게 연구되어 왔으며,[18][21][22][55] 여기서 최적화 성능이 향상된 것으로 나타났으며, 매개 변수는 조정하기가 더 쉬웠으며 다양한 최적화 문제에서 보다 일관성 있게 수행되었습니다.

PSO를 단순화하는 데 찬성하는 또 다른 주장은 메타 휴리스틱이 유한한 수의 최적화 문제에 대해 계산 실험을 수행함으로써 그 효과를 경험적으로 입증할 수 있다는 것입니다.이는 PSO와 같은 메타휴리스틱은 정확한 것으로 입증될 수 없으며, 이로 인해 설명 및 구현에 오류가 발생할 위험이 증가한다는 것을 의미합니다.이것의[56] 좋은 예는 유전 알고리즘의 유망한 변형(또 다른 인기 있는 메타 휴리스틱)을 제시했지만 나중에 검색 공간의 다른 차원에 대한 유사한 값에 대한 최적화 검색에 강하게 편향되어 결함이 있는 것으로 밝혀졌습니다. 이는 고려된 벤치마크 문제의 최적화였습니다.이러한 편향은 프로그래밍 오류 때문에 발생한 것이며, 현재는 수정되었습니다.[57]

속도를 초기화하려면 추가 입력이 필요할 수 있습니다.Bare Bones PSO 변종은[58] James Kennedy에 의해 2003년에 제안되었으며 속도를 전혀 사용할 필요가 없습니다.

또 다른 간단한 변형은 가속 입자 군집 최적화(APSO)인데,[59] 이는 속도를 사용할 필요가 없고 많은 응용 분야에서 수렴 속도를 높일 수 있습니다.APSO의 간단한 데모 코드를 사용할 수 있습니다.[60]

다목적 최적화

PSO는 다중 목적 문제에도 적용되었는데,[61][62][63] 목적 함수 비교는 PSO 입자를 이동할 때 파레토 지배를 고려하고 파레토 전선에 근접하도록 비지배적 솔루션이 저장됩니다.

이진법, 이산법, 조합법

위에서 주어진 PSO 방정식이 실수에 대해 작동하기 때문에 이산 문제를 해결하기 위해 일반적으로 사용되는 방법은 이산 검색 공간을 연속 도메인에 매핑하고 고전적인 PSO를 적용한 다음 결과를 디매핑하는 것입니다.이러한 매핑은 매우 단순하거나(예: 반올림된 값을 사용하는 것으로) 더 정교할 수 있습니다.[64]

그러나 이동 방정식은 다음과 같은 네 가지 동작을 수행하는 연산자를 사용한다는 점에 유의할 수 있습니다.

  • 두 위치의 차이를 계산하는 것입니다.결과는 속도(정확히는 변위)입니다.
  • 속도에 수치 계수를 곱하기
  • 두 개의 속도를 더하기
  • 위치에 속도를 적용하기

일반적으로 위치와 속도는 n개의 실수로 표시되며, 이 연산자는 단순히 -, *, +, 그리고 다시 +입니다.그러나 이 모든 수학적 대상은 이진 문제(또는 더 일반적으로 이산적인 문제) 또는 조합 문제에 대처하기 위해 완전히 다른 방식으로 정의될 수 있습니다.[65][66][67][68]한 가지 접근 방식은 집합을 기반으로 연산자를 재정의하는 것입니다.[69]

참고 항목

참고문헌

  1. ^ a b Bonyadi, M. R.; Michalewicz, Z. (2017). "Particle swarm optimization for single objective continuous space problems: a review". Evolutionary Computation. 25 (1): 1–54. doi:10.1162/EVCO_r_00180. PMID 26953883. S2CID 8783143.
  2. ^ Kennedy, J.; Eberhart, R. (1995). "Particle Swarm Optimization". Proceedings of IEEE International Conference on Neural Networks. Vol. IV. pp. 1942–1948. doi:10.1109/ICNN.1995.488968.
  3. ^ a b Shi, Y.; Eberhart, R.C. (1998). "A modified particle swarm optimizer". Proceedings of IEEE International Conference on Evolutionary Computation. pp. 69–73. doi:10.1109/ICEC.1998.699146.
  4. ^ a b c Kennedy, J. (1997). "The particle swarm: social adaptation of knowledge". Proceedings of IEEE International Conference on Evolutionary Computation. pp. 303–308. doi:10.1109/ICEC.1997.592326.
  5. ^ Kennedy, J.; Eberhart, R.C. (2001). Swarm Intelligence. Morgan Kaufmann. ISBN 978-1-55860-595-4.
  6. ^ Poli, R. (2007). "An analysis of publications on particle swarm optimisation applications" (PDF). Technical Report CSM-469. Archived from the original (PDF) on 2011-07-16. Retrieved 2010-05-03.
  7. ^ Poli, R. (2008). "Analysis of the publications on the applications of particle swarm optimisation" (PDF). Journal of Artificial Evolution and Applications. 2008: 1–10. doi:10.1155/2008/685175.
  8. ^ Zhang, Y. (2015). "A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications". Mathematical Problems in Engineering. 2015: 931256.
  9. ^ Clerc, M. (2012). "Standard Particle Swarm Optimisation" (PDF). HAL Open Access Archive.
  10. ^ a b c d e Bratton, Daniel; Kennedy, James (2007). "Defining a Standard for Particle Swarm Optimization". 2007 IEEE Swarm Intelligence Symposium (PDF). pp. 120–127. doi:10.1109/SIS.2007.368035. ISBN 978-1-4244-0708-8. S2CID 6217309.
  11. ^ Taherkhani, M.; Safabakhsh, R. (2016). "A novel stability-based adaptive inertia weight for particle swarm optimization". Applied Soft Computing. 38: 281–295. doi:10.1016/j.asoc.2015.10.004.
  12. ^ a b Shi, Y.; Eberhart, R.C. (1998). "Parameter selection in particle swarm optimization". Proceedings of Evolutionary Programming VII (EP98). pp. 591–600.
  13. ^ Eberhart, R.C.; Shi, Y. (2000). "Comparing inertia weights and constriction factors in particle swarm optimization". Proceedings of the Congress on Evolutionary Computation. Vol. 1. pp. 84–88.
  14. ^ a b Carlisle, A.; Dozier, G. (2001). "An Off-The-Shelf PSO" (PDF). Proceedings of the Particle Swarm Optimization Workshop. pp. 1–6. Archived from the original (PDF) on 2003-05-03.
  15. ^ a b van den Bergh, F. (2001). An Analysis of Particle Swarm Optimizers (PDF) (PhD thesis). University of Pretoria, Faculty of Natural and Agricultural Science.
  16. ^ a b c d Clerc, M.; Kennedy, J. (2002). "The particle swarm - explosion, stability, and convergence in a multidimensional complex space". IEEE Transactions on Evolutionary Computation. 6 (1): 58–73. CiteSeerX 10.1.1.460.6608. doi:10.1109/4235.985692.
  17. ^ a b Trelea, I.C. (2003). "The Particle Swarm Optimization Algorithm: convergence analysis and parameter selection". Information Processing Letters. 85 (6): 317–325. doi:10.1016/S0020-0190(02)00447-7.
  18. ^ a b Bratton, D.; Blackwell, T. (2008). "A Simplified Recombinant PSO" (PDF). Journal of Artificial Evolution and Applications. 2008: 1–10. doi:10.1155/2008/654184.
  19. ^ a b Evers, G. (2009). An Automatic Regrouping Mechanism to Deal with Stagnation in Particle Swarm Optimization (Master's thesis). The University of Texas - Pan American, Department of Electrical Engineering.
  20. ^ Meissner, M.; Schmuker, M.; Schneider, G. (2006). "Optimized Particle Swarm Optimization (OPSO) and its application to artificial neural network training". BMC Bioinformatics. 7 (1): 125. doi:10.1186/1471-2105-7-125. PMC 1464136. PMID 16529661.
  21. ^ a b Pedersen, M.E.H. (2010). Tuning & Simplifying Heuristical Optimization (PDF). University of Southampton, School of Engineering Sciences, Computational Engineering and Design Group. S2CID 107805461. Archived from the original (PhD thesis) on 2020-02-13.
  22. ^ a b c Pedersen, M.E.H.; Chipperfield, A.J. (2010). "Simplifying particle swarm optimization". Applied Soft Computing. 10 (2): 618–628. CiteSeerX 10.1.1.149.8300. doi:10.1016/j.asoc.2009.08.029.
  23. ^ Mason, Karl; Duggan, Jim; Howley, Enda (2018). "A Meta Optimisation Analysis of Particle Swarm Optimisation Velocity Update Equations for Watershed Management Learning". Applied Soft Computing. 62: 148–161. doi:10.1016/j.asoc.2017.10.018.
  24. ^ a b Nobile, M.S; Cazzaniga, P.; Besozzi, D.; Colombo, R.; Mauri, G.; Pasi, G. (2018). "Fuzzy Self-Tuning PSO: a settings-free algorithm for global optimization". Swarm and Evolutionary Computation. 39: 70–85. doi:10.1016/j.swevo.2017.09.001. hdl:10446/106467.
  25. ^ Nobile, M.S; Pasi, G.; Cazzaniga, P.; Besozzi, D.; Colombo, R.; Mauri, G. (2015). "Proactive particles in swarm optimization: a self-tuning algorithm based on fuzzy logic". Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2015), Istanbul (Turkey). pp. 1–8. doi:10.1109/FUZZ-IEEE.2015.7337957.
  26. ^ Cazzaniga, P.; Nobile, M.S.; Besozzi, D. (2015). "The impact of particles initialization in PSO: parameter estimation as a case in point, (Canada)". Proceedings of IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology. doi:10.1109/CIBCB.2015.7300288.
  27. ^ Pedersen, M.E.H. (2010). "Good parameters for particle swarm optimization". Technical Report HL1001. CiteSeerX 10.1.1.298.4359.
  28. ^ Kennedy, J.; Mendes, R. (2002). "Population structure and particle swarm performance". Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No.02TH8600). Vol. 2. pp. 1671–1676 vol.2. CiteSeerX 10.1.1.114.7988. doi:10.1109/CEC.2002.1004493. ISBN 978-0-7803-7282-5. S2CID 14364974.{{cite book}}: CS1 메인 : 일자 및 연도 (링크)
  29. ^ 멘데스, R. (2004)인구토폴로지와 입자군 성능에 미치는 영향(PhD 논문)대학생 민호가. 민호.
  30. ^ Suganthan, Ponnuturai N. "이웃 운영자와 입자 무리 최적화자."진화적 계산, 1999.CEC 99.1999년 의회의 의사진행.제3권 IEEE, 1999
  31. ^ Oliveira, M.; Pinheiro, D.; Andrade, B.; Bastos-Filho, C.; Menezes, R. (2016). "Communication Diversity in Particle Swarm Optimizers". Swarm Intelligence. Lecture Notes in Computer Science. Vol. 9882. pp. 77–88. doi:10.1007/978-3-319-44427-7_7. ISBN 978-3-319-44426-0. S2CID 37588745.
  32. ^ SPSO 입자 무리 중심부
  33. ^ 알마시, O.N. 그리고 쿠반, M.H. (2017)적응형 모집단 기반 알고리즘을 통한 실제 데이터 세트 분류를 위한 인색한 SVM 모델 선택 기준.뉴럴 컴퓨팅 및 응용, 1-9. https://doi.org/10.1007/s00521-017-2930-y
  34. ^ 미란다, V., Keko, H. and Duque, AA.J. (2008).진화입자군에서의 확률적 항성통신 토폴로지(EPSO)국제컴퓨터지능연구학회지(IJCIR), 제4권, 제2호, pp. 105-116
  35. ^ Clerc, M. (2006).입자 군집 최적화.ISTE (국제과학기술대백과사전), 2006
  36. ^ Yin, P., Glover, F., Laguna, M., & Zhu, J. (2011).상호 보완적인 사이버 스웜 알고리즘.국제 스웜 인텔리전스 리서치 저널(IJSIR), 2(2), 22-41
  37. ^ Elshamy, W.; Rashad, H.; Bahgat, A. (2007). "Clubs-based Particle Swarm Optimization" (PDF). IEEE Swarm Intelligence Symposium 2007 (SIS2007). Honolulu, HI. pp. 289–296. Archived from the original (PDF) on 2013-10-23. Retrieved 2012-04-27.
  38. ^ Cleghorn, Christopher W (2014). "Particle Swarm Convergence: Standardized Analysis and Topological Influence". Swarm Intelligence. Lecture Notes in Computer Science. Vol. 8667. pp. 134–145. doi:10.1007/978-3-319-09952-1_12. ISBN 978-3-319-09951-4.
  39. ^ Liu, Q (2015). "Order-2 stability analysis of particle swarm optimization". Evolutionary Computation. 23 (2): 187–216. doi:10.1162/EVCO_a_00129. PMID 24738856. S2CID 25471827.
  40. ^ Cleghorn, Christopher W.; Engelbrecht, Andries. (2018). "Particle Swarm Stability: A Theoretical Extension using the Non-Stagnate Distribution Assumption". Swarm Intelligence. 12 (1): 1–22. doi:10.1007/s11721-017-0141-x. hdl:2263/62934. S2CID 9778346.
  41. ^ Van den Bergh, F. "A convergence proof for the particle swarm optimiser" (PDF). Fundamenta Informaticae.
  42. ^ Bonyadi, Mohammad reza.; Michalewicz, Z. (2014). "A locally convergent rotationally invariant particle swarm optimization algorithm" (PDF). Swarm Intelligence. 8 (3): 159–198. doi:10.1007/s11721-014-0095-1. S2CID 2261683.
  43. ^ a b Zhan, Z-H.; Zhang, J.; Li, Y; Shi, Y-H. (2011). "Orthogonal Learning Particle Swarm Optimization" (PDF). IEEE Transactions on Evolutionary Computation. 15 (6): 832–847. doi:10.1109/TEVC.2010.2052054.
  44. ^ a b Zhan, Z-H.; Zhang, J.; Li, Y; Chung, H.S-H. (2009). "Adaptive Particle Swarm Optimization" (PDF). IEEE Transactions on Systems, Man, and Cybernetics. 39 (6): 1362–1381. doi:10.1109/TSMCB.2009.2015956. PMID 19362911. S2CID 11191625.
  45. ^ Zambrano-Bigiarini, M.; Clerc, M.; Rojas, R. (2013). "Standard Particle Swarm Optimisation 2011 at CEC-2013: A baseline for future PSO improvements". 2013 IEEE Congress on Evolutionary Computation. Evolutionary Computation (CEC), 2013 IEEE Congress on. pp. 2337–2344. doi:10.1109/CEC.2013.6557848. ISBN 978-1-4799-0454-9. S2CID 206553432.
  46. ^ Lovbjerg, M.; Krink, T. (2002). "The LifeCycle Model: combining particle swarm optimisation, genetic algorithms and hillclimbers" (PDF). Proceedings of Parallel Problem Solving from Nature VII (PPSN). pp. 621–630.
  47. ^ Niknam, T.; Amiri, B. (2010). "An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis". Applied Soft Computing. 10 (1): 183–197. doi:10.1016/j.asoc.2009.07.001.
  48. ^ 장, 웬준; 셰, 샤오펑 (2003).DEPSO: 차동 진화 연산자를 가진 하이브리드 입자 무리.시스템, 인간 및 사이버네틱스(SMCC)에 관한 IEEE 국제 회의, 워싱턴 DC, 미국: 3816-3821
  49. ^ Zhang, Y.; Wang, S. (2015). "Pathological Brain Detection in Magnetic Resonance Imaging Scanning by Wavelet Entropy and Hybridization of Biogeography-based Optimization and Particle Swarm Optimization". Progress in Electromagnetics Research. 152: 41–58. doi:10.2528/pier15040602.
  50. ^ Lovbjerg, M.; Krink, T. (2002). "Extending Particle Swarm Optimisers with Self-Organized Criticality" (PDF). Proceedings of the Fourth Congress on Evolutionary Computation (CEC). Vol. 2. pp. 1588–1593.
  51. ^ Xinchao, Z. (2010). "A perturbed particle swarm algorithm for numerical optimization". Applied Soft Computing. 10 (1): 119–124. doi:10.1016/j.asoc.2009.06.010.
  52. ^ 셰, 샤오펑; 장, 원준; 양, 지롄 (2002).소산 입자 무리 최적화입니다.진화적 계산에 관한 의회, HI, 미국 호놀룰루: 1456-1461
  53. ^ Cheung, N. J.; Ding, X.-M.; Shen, H.-B. (2013). "OptiFel: A Convergent Heterogeneous Particle Sarm Optimization Algorithm for Takagi-Sugeno Fuzzy Modeling". IEEE Transactions on Fuzzy Systems. 22 (4): 919–933. doi:10.1109/TFUZZ.2013.2278972. S2CID 27974467.
  54. ^ Nobile, M.; Besozzi, D.; Cazzaniga, P.; Mauri, G.; Pescini, D. (2012). "A GPU-Based Multi-Swarm PSO Method for Parameter Estimation in Stochastic Biological Systems Exploiting Discrete-Time Target Series". Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Lecture Notes in Computer Science. Vol. 7264. pp. 74–85. doi:10.1007/978-3-642-29066-4_7.
  55. ^ Yang, X.S. (2008). Nature-Inspired Metaheuristic Algorithms. Luniver Press. ISBN 978-1-905986-10-1.
  56. ^ Tu, Z.; Lu, Y. (2004). "A robust stochastic genetic algorithm (StGA) for global numerical optimization". IEEE Transactions on Evolutionary Computation. 8 (5): 456–470. doi:10.1109/TEVC.2004.831258. S2CID 22382958.
  57. ^ Tu, Z.; Lu, Y. (2008). "Corrections to "A Robust Stochastic Genetic Algorithm (StGA) for Global Numerical Optimization". IEEE Transactions on Evolutionary Computation. 12 (6): 781. doi:10.1109/TEVC.2008.926734. S2CID 2864886.
  58. ^ Kennedy, James (2003). "Bare bones particle swarms". Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS'03 (Cat. No.03EX706). pp. 80–87. doi:10.1109/SIS.2003.1202251. ISBN 0-7803-7914-4. S2CID 37185749.
  59. ^ X. S. 양, S. 데브 그리고 S.Fong, 비즈니스 최적화 및 응용을 위한 가속 입자 군집 최적화 및 지원 벡터 머신, NDT 2011, Springer CCIS 136, pp. 53-66 (2011).
  60. ^ "Search Results: APSO - File Exchange - MATLAB Central".
  61. ^ Parsopoulos, K.; Vrahatis, M. (2002). "Particle swarm optimization method in multiobjective problems". Proceedings of the ACM Symposium on Applied Computing (SAC). pp. 603–607. doi:10.1145/508791.508907.
  62. ^ Coello Coello, C.; Salazar Lechuga, M. (2002). "MOPSO: A Proposal for Multiple Objective Particle Swarm Optimization". Congress on Evolutionary Computation (CEC'2002). pp. 1051–1056.
  63. ^ Mason, Karl; Duggan, Jim; Howley, Enda (2017). "Multi-objective dynamic economic emission dispatch using particle swarm optimisation variants". Neurocomputing. 270: 188–197. doi:10.1016/j.neucom.2017.03.086.
  64. ^ Roy, R., Dehuri, S., & Cho, S. B. (2012).다목적 조합 최적화 문제를 위한 새로운 입자군 최적화 알고리즘'국제 응용 메타휴리스틱 컴퓨팅 저널(IJAMC)', 2(4), 41-57
  65. ^ 케네디, J. & 에버하트, R.C. (1997)입자 스웜 알고리즘의 이산 바이너리 버전, 시스템, 인간 및 사이버네틱스에 관한 컨퍼런스, Piscataway, 뉴저지: IEEE 서비스 센터, pp. 4104-4109
  66. ^ Clerc, M. (2004).이산 입자 군집 최적화, 출장 판매원 문제, 공학의 새로운 최적화 기법, Springer, pp. 219-239
  67. ^ Clerc, M. (2005).이진 입자 군집 옵티마이저: 도구 상자, 유도 및 수학적 통찰력, 오픈 아카이브 HAL
  68. ^ Jarboui, B.; Damak, N.; Siarry, P.; Rebai, A. (2008). "A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems". Applied Mathematics and Computation. 195: 299–308. doi:10.1016/j.amc.2007.04.096.
  69. ^ Chen, Wei-neng; Zhang, Jun (2010). "A novel set-based particle swarm optimization method for discrete optimization problem". IEEE Transactions on Evolutionary Computation. 14 (2): 278–300. CiteSeerX 10.1.1.224.5378. doi:10.1109/tevc.2009.2030331. S2CID 17984726.

외부 링크

위키미디어 커먼즈는 입자 군집 최적화와 관련된 미디어를 보유하고 있습니다.