포브스폼 게임

광범위한 형식 게임은 게임 이론에서 게임의 사양으로, 플레이어들의 가능한 움직임의 순서, 모든 결정 지점에서의 그들의 선택, 각 플레이어가 다른 플레이어의 움직임에 대해 가지고 있는 (완전하지 않을 가능성이 있는) 정보 등 여러 가지 주요 측면의 명시적 표현을 허용하는 것이다.cision, 그리고 가능한 모든 게임 결과에 대한 그들의 보상. 광범위한 형태의 게임은 또한 "자연에 의한 운동"으로 모델링된 우연한 사건의 형태로 불완전한 정보를 표현할 수 있게 한다.

유한양식 게임

일부 저자들, 특히 입문 교과서에서 초창기에는 광범한 형태의 게임을 성과(불완전하거나 불완전한 정보는 없음)가 있는 게임 나무로만 정의하고 후속 장에 있는 다른 요소들을 세분화하여 덧붙인다. 이 글의 나머지 부분은 동기를 부여하는 예와 함께 이 온화한 접근법을 따르는 반면에, 우리는 여기서 만들어진 (궁극적으로) 유한한 광범위한 형태의 게임을 앞에 제시한다. 이 일반적인 정의는 해롤드 쿤에 의해 1953년에 도입되었는데, 그는 1928년부터 폰 노이만의 초기 정의를 확장했다. 하트(1992)의 프레젠테이션에 따라 n-플레이어 광폭 폼 게임은 다음과 같이 구성된다.

• 유한한 n(합리적) 플레이어 세트
• 게임 트리라고 불리는 뿌리깊은 나무
• 게임 트리의 각 터미널(리프) 노드는 보상의 n-tuple을 가지고 있는데, 이는 가능한 모든 플레이가 끝날 때마다 각 플레이어에 대한 보상이 하나씩 있다는 것을 의미한다.
• 게임 트리의 비단말 노드의 파티션(n+1 하위 집합)으로, 각 (합리적) 플레이어마다 하나씩, 그리고 Chance(또는 Nature)라는 가상 플레이어를 위한 특별한 하위 집합이 있다. 각 플레이어의 노드 서브셋을 "플레이어의 노드"라고 한다. (완전한 정보의 게임은 따라서 빈 찬스 노드 세트를 가진다.)
• 찬스 플레이어의 각 노드는 나가는 가장자리에 대해 확률 분포를 가진다.
• 합리적인 플레이어의 각 노드 세트는 정보 세트로 더욱 분할되어, 다음과 같은 의미에서 플레이어가 이동할 때 특정 선택을 구별할 수 없게 한다.
  • 동일한 정보 집합의 두 노드의 발신 에지 사이에는 일대일 일치성이 있다. 즉, 정보 집합의 모든 발신 에지 세트가 동등성 등급으로 분할되고, 각 클래스는 어느 시점에서 플레이어의 이동에 대한 가능한 선택을 나타낸다.
  • 루트부터 터미널 노드까지의 트리의 모든 (방향) 경로는 최대 한 번에 각 정보 세트를 가로지를 수 있다.
• 위의 파라미터로 특정된 게임에 대한 완전한 설명은 선수들 사이의 상식이다.

따라서 연극은 루트부터 터미널 노드까지의 트리를 통과하는 길이다. 찬스에 속하는 주어진 비터미널 노드에서는 확률 분포에 따라 나가는 분기를 선택한다. 어떤 합리적인 플레이어의 노드에서든 플레이어는 가장자리에 대한 동등성 클래스 중 하나를 선택해야 하는데, 이 클래스는 (일반적으로) 플레이어가 어떤 것을 따르고 있는지 모르는 것을 제외하고 정확히 하나의 외향적 우위를 결정한다.(외부 관찰자는 그 시점까지 다른 플레이어의 모든 선택과 자연의 움직임의 실현을 알 수 있다)e 가장자리 정확히) 따라서 플레이어를 위한 순수한 전략은 선택으로 구성된다. 즉, 모든 정보 집합에 대해 하나의 클래스의 발신 에지를 정확하게 선택하는 것이다. 완벽한 정보의 게임에서 정보 세트는 단골격이다. 찬스 노드가 있는 게임에서 보상이 어떻게 해석되어야 하는지는 명확하지 않다. 각 플레이어는 모든 게임 결과에 대해 정의된 폰 노이만-모겐스터른 유틸리티 함수를 가지고 있다고 가정한다. 이러한 가정은 모든 합리적인 플레이어가 예상 효용에 의해 선험적인 무작위 결과를 평가한다는 것을 수반한다.

그러나 위의 프레젠테이션은 게임이 실행되는 수학 구조를 정확하게 정의하면서 "플레이어가 결정을 내릴 때 동일한 정보에서 노드를 구분할 수 없다"와 같이 게임이 어떻게 실행되는지에 대한 진술을 공식화하는 기술적인 논의는 생략한다. 이는 인식론적 모달 논리를 사용하여 정밀하게 만들 수 있다. 자세한 내용은 Shoham & Leyton-Brown(2009, 13장)을 참조한다.

게임 트리를 통한 완벽한 정보 2인용 게임(합성 게임 이론과 인공지능에서 정의한 것)은 결과가 있는 광범위한 형태 게임(예: 승패 또는 무승부)으로 표현될 수 있다. 그러한 게임의 예로는 틱택토, 체스, 무한 체스 등이 있다.^[1][2] 백개몬처럼 기대 미니맥스 나무 위의 게임은 불완전한 정보가 없지만(모든 정보 세트는 단골격이다) 운명의 움직임을 가지고 있다. 예를 들어 포커는 우연한 움직임(거래되고 있는 카드)과 불완전한 정보(다른 플레이어가 몰래 갖고 있는 카드)를 모두 가지고 있다. (Binmore 2007, 2장)

완벽하고 완벽한 정보

완전한 광범위한 형태 표현은 다음을 명시한다.

1. 경기의 선수들
2. 기회가 있을 때마다 움직여야 한다.
3. 각각의 선수들이 각각의 동작에서 할 수 있는 것
4. 선수 개개인이 모든 움직임에 대해 알고 있는 것
5. 가능한 모든 움직임의 조합에 대해 모든 플레이어가 받는 성과금

오른쪽 경기는 1과 2의 두 선수가 있다. 모든 비터미널 노드별 숫자는 해당 의사결정 노드가 속한 플레이어를 나타낸다. 모든 터미널 노드별 숫자는 선수에 대한 보답을 나타낸다(예: 2,1은 선수 1에 대한 보상과 선수 2에 대한 보답을 나타낸다). 그래프의 모든 가장자리별 레이블은 가장자리가 나타내는 동작의 이름이다.

초기 노드는 플레이어 1에 속하며, 플레이어 1이 먼저 움직인다는 것을 나타낸다. 나무에 따라 플레이하라: 플레이어 1은 U와 D 중 하나를 선택하라; 플레이어 2는 플레이어 1의 선택을 관찰한 다음 U와 D 중 하나를 선택하라. 보상은 트리에 명시된 대로 한다. 트리의 4개의 터미널 노드로 대표되는 4가지 결과가 있다: (U,U', (U,D,'), (D,D') 각 결과와 관련된 보상은 각각 (0,0), (2,1), (1,2) 및 (3,1)과 같다.

1번 선수가 D를 하면 2번 선수가 U'를 해서 그들의 보수가 극대화되므로 1번 선수는 1번만 받는다. 단, 1번 선수가 U를 할 경우 2번 선수는 D'로, 1번 선수는 2번을 받는다. 1번 플레이어는 2대 1을 선호하기 때문에 U와 2번 플레이어는 D를 플레이한다. 이것이 서브게임 퍼펙트 밸런스다.

불완전한 정보

이런 식으로 경기를 대표할 수 있는 장점은 경기 순서가 명확하다는 점이다. 트리는 플레이어 1이 먼저 움직이고 플레이어 2가 이 동작을 관찰하는 것을 명확히 보여준다. 그러나 일부 게임에서는 플레이가 이렇게 일어나지 않는다. 한 플레이어가 항상 다른 플레이어의 선택을 관찰하는 것은 아니다(예를 들어, 이동이 동시에 발생하거나 이동이 숨겨질 수 있음). 정보 집합은 다음과 같은 의사결정 노드의 집합이다.

1. 세트의 모든 노드는 한 플레이어의 것이다.
2. 게임이 정보 집합에 도달하면 이동하려는 플레이어는 정보 집합 내의 노드를 구분할 수 없다. 즉, 정보 집합에 두 개 이상의 노드가 포함된 경우 해당 집합이 속한 플레이어는 집합의 어느 노드에 도달했는지 알지 못한다.

광범위한 형태에서 정보 집합은 해당 집합의 모든 노드를 연결하는 점선으로 표시되거나 때로는 해당 집합의 모든 노드 주위에 그려진 루프에 의해 표시된다.

한 게임에 한 명 이상의 회원과 함께 설정된 정보가 있다면 그 게임은 불완전한 정보를 가지고 있다고 한다. 완벽한 정보를 가진 게임은 모든 플레이어가 게임 초반에 무슨 일이 일어났는지 정확히 알 수 있는 게임이다. 즉, 모든 정보 세트는 싱글톤 세트다.^[1][2] 완벽한 정보가 없는 어떤 게임도 불완전한 정보를 가지고 있다.

오른쪽 게임은 2번 선수가 1번 선수가 경기하러 왔을 때 무엇을 하는지 모른다는 점을 제외하면 위의 경기와 같다. 묘사된 첫 번째 게임은 완벽한 정보를 가지고 있다; 오른쪽 게임은 그렇지 않다. 만약 두 선수 모두 이성적이고 두 선수 모두 이성적이라는 것을 알고 있고 어느 선수에 의해서 알려진 모든 것이 모든 선수에 의해 알려진다면(즉, 선수 1은 선수 1이 이성적이라는 것을 알고 있고 선수 2는 이를 알고 있다), 첫 번째 게임에서의 플레이는 다음과 같다: 선수 1은 U, 선수 2를 하면 다음과 같다. 'D'를 플레이한다(플레이어 2의 경우 1의 보수가 0의 보상으로 선호되기 때문에). 따라서 플레이어 1은 2를 받는다. 다만 1번 선수가 D를 하면 2번 선수가 U' (2번 선수에게 1번 선수보다 2번 선수가 더 좋기 때문에)를 하고 1번 선수가 1번을 받는다. 따라서 1번 선수가 2대 1로 받는 것을 선호하기 때문에 1번 선수가 2대 1로 받는 것을 선호하기 때문에 2번 선수가 D'를 하기 때문에 1번 경기에서는 평형이 (U, D')가 될 것이다.

두 번째 게임에서는 2번 선수가 1번 선수의 움직임을 관찰할 수 없다는 것이 명확하지 않다. 1번 선수는 2번 선수가 D를 하고 1번 선수가 3번을 받도록 실제 D를 했을 때 U를 한 것으로 착각하고 싶어한다. 실제로 두 번째 게임에서는 1번 선수가 D를 하고 2번 선수가 U'를 하고 2번 선수가 1번 선수가 반드시 D를 할 것이라는 믿음을 갖는 완벽한 베이시안 평형이 있다. 이 평형에서, 모든 전략은 보유된 신념과 모든 신념이 행해진 전략과 일치한다는 것을 고려할 때 합리적이다. 정보의 불완전함이 게임의 결과를 어떻게 변화시키는지 주목하라.

내시 평형을 위해 이 게임을 더 쉽게 풀기 위해, 그것은 정상적인 형태로 전환될 수 있다.^[3][4] 이것이 동시/시퀀스 게임임을 감안할 때, 1번 선수와 2번 선수는 각각 두 가지 전략을 가지고 있다.^[5]

• 플레이어 1의 전략: {U , D}
• 플레이어 2의 전략: {U' , D'}

2번 선수 플레이어 1	Up' (U'	다운' (D')
위(U)	(0,0)	(2,1)
다운(D)	(1,2)	(3,1)

우리는 각각의 움직임의 조합에 대해 독특한 보상이 있는 2x2 매트릭스를 가질 것이다. 정상적인 폼 게임을 활용하면 이제 게임을 해결하고 두 선수의 우세한 전략을 파악할 수 있게 됐다.

• 선수 1이 업(U)을 플레이하면 선수 2가 다운(D') 플레이를 선호한다(페이오프 1>0).
• 1번 선수가 다운(D)을 플레이하면 2번 선수가 업(U') 플레이를 선호한다(페이오프 2>1)
• 2번 선수가 UP(U')을 플레이할 경우, 1번 선수가 Down(D)을 플레이하는 것을 선호한다(페이오프 1>0).
• 2번 선수가 다운(D')을 플레이할 경우, 1번 선수가 다운(D) 플레이를 선호한다(3>2).

이러한 선호도는 매트릭스 내에서 표시할 수 있으며, 두 플레이어가 모두 선호하는 박스는 나시 평형을 제공한다. 이 특정 게임은 (D,U')의 단일 솔루션과 (1,2)의 보수가 있다.

무한 액션 공간과 불완전한 정보가 있는 게임에서는, 필요에 따라 위에서 설명한 호 뒤에 (비노달) 엔드포인트를 연결하는 점선을 삽입하거나 호 자체를 도킹하여 비싱글톤 정보 세트를 나타낸다. 위에서 설명한 Stackelberg 경기에서는, 두 번째 선수가 첫 번째 선수의 움직임을 관찰하지 않았다면, 경기는 더 이상 Stackelberg 모델에 맞지 않을 것이다. 그것은 Cournot 경기일 것이다.

불완전한 정보

플레이어가 게임의 이익이 무엇인지, 상대가 어떤 유형인지 정확히 알지 못하는 경우일 수 있다. 이런 종류의 게임은 불완전한 정보를 가지고 있다. 광범위한 형태에서 그것은 소위 Harsani 변환을 사용하는 완전하지만 불완전한 정보를 가진 게임으로 표현된다. 이러한 변신은 게임에 자연의 선택 또는 신의 선택이라는 개념을 도입한다. 구직자를 채용할지 여부를 고려하여 고용주로 구성된 게임을 고려한다. 구직자의 능력은 높거나 낮거나 둘 중 하나일 수 있다. 그들의 능력 수준은 무작위적이다; 그들은 확률 1/3로 낮은 능력을 가지고 있거나 확률 2/3으로 높은 능력을 가지고 있다. 이 경우, 그 확률에 따라 지원자의 능력을 선택하는 또 다른 종류의 선수로 자연을 모델링하는 것이 편리하다. 그러나 자연은 어떠한 보상도 가지고 있지 않다. 자연의 선택은 게임 트리에 채워지지 않은 노드로 표현된다. 자연의 선택 노드에서 나오는 가장자리는 그것이 발생한다고 나타내는 사건의 확률을 라벨로 표시한다.

왼쪽 게임은 완전한 정보(모든 선수와 보수는 모든 사람에게 알려져 있다) 중 하나이지만 불완전한 정보(고용주는 자연의 움직임이 무엇이었는지 모른다)이다. 초기 노드는 중앙에 있고 채워지지 않기 때문에 자연이 먼저 움직인다. 네이처는 같은 확률로 선수 1의 유형(이 게임에서는 플레이된 서브게임에서 보답을 선택하는 것과 같다)을 t1 또는 t2 중 하나로 선택한다. 플레이어 1은 이들을 위한 구별되는 정보 세트를 가지고 있다. 즉, 플레이어 1은 그들이 어떤 유형인지 알고 있다(이럴 필요는 없다). 그러나 2번 선수는 자연의 선택을 관찰하지 않는다. 그들은 1번 선수의 유형을 알지 못하지만, 이 게임에서 그들은 1번 선수의 행동을 관찰한다. 즉, 완벽한 정보가 있다. 실제로, 이제 위의 완전한 정보의 정의를 바꾸는 것이 적절하다: 게임의 모든 단계에서, 모든 플레이어는 다른 플레이어가 무엇을 했는지 안다. 개인 정보의 경우, 모든 플레이어는 자연이 어떤 플레이를 했는지 알고 있다. 정보 세트는 끊어진 선으로 이전과 같이 표현된다.

이 게임에서 자연이 t1을 플레이어 1의 타입으로 선택한다면, 플레이된 게임은 2 플레이어가 그것을 모른다는 것(그리고 이것이 그들의 정보를 가로지른다는 바로 그 사실은 하위 게임 상태에서 그것을 실격시킨다)을 제외하고, 설명된 바로 첫 번째 게임과 같을 것이다. 완벽한 베이시안 평형, 즉 다른 유형이 다른 일을 하는 평형을 분리하는 것이 있다.

두 유형이 동일한 작용(풀링)을 하는 경우 평형을 유지할 수 없다. 두 플레이어가 모두 D를 플레이한다면, 플레이어 2는 확률 1/2로 설정된 정보에서 어느 한 노드에 있다는 믿음을 형성할 수 있을 뿐이다(이것은 두 유형 중 하나를 볼 수 있는 기회이기 때문이다). 플레이어 2는 D'를 플레이함으로써 그들의 보답을 극대화한다. 그러나 만약 그들이 D'를 플레이한다면, 타입 2는 U를 플레이하는 것을 선호한다. 이것은 평형일 수 없다. 만약 두 타입 모두 U를 플레이한다면, 플레이어 2는 그들이 확률 1/2을 가진 어느 한 노드에 있다는 믿음을 다시 형성한다. 이 경우 2번 플레이어는 D'를 재생하지만, 1번 유형은 D를 재생하는 것을 선호한다.

만약 1타입이 U를 하고 2타입이 D를 한다면, 2타입은 그들이 관찰하는 어떤 행동이든 D를 하게 되지만, 1타입은 D를 선호한다. 따라서 유일한 평형은 1타입 D, 2타입 U, 2타입 U'로 D를 관찰하고 U를 관찰할 경우 무작위로 처리한다. 그들의 행동을 통해 1타입은 2타입에게 자신의 유형을 알렸다.

형식 정의

Formally, a finite game in extensive form is a structure ${\displaystyle \Gamma =\langle {\mathcal {K}},\mathbf {H} ,[(\mathbf {H} _{i})_{i\in {\mathcal {I}}}],\{A(H)\}_{H\in \mathbf {H} },a,\rho ,u\rangle }$ where:

• ${\displaystyle {\mathcal {K}}=\langle V,v^{0},T,p\rangle }$ is a finite tree with a set of nodes ${\displaystyle V}$, a unique initial node ${\displaystyle v^{0}\in V}$, a set of terminal nodes ${\displaystyle T\subset V}$ (let ${\displaystyle D=V\setminus T$$}$ 의사결정 노드의 집합이어야$$ 함) 및 즉시 이전 $함수{\displaystyle }$p :${\displaystyle V}$ → D ${\displaystyle$ p$:$게임의$$ 규칙이 표시된 $V\rightarrow D},$
• ${\displaystyle \mathbf{H}}$ ${\$은(는) $정보{\displaystyle }$ 파티션이라고 하는$$ D ${\displaystyle D}$의 파티션이다$$.
• ${\displaystyle A}$( ${\displaystyle H}$) ${\displaystyle A(H)}$은${\displaystyle (}$는) $모든{\displaystyle }$ 작업 $A{\displaystyle \mathcal{}}$ ${\$ $H$${\$$displaybf$ {$H$$}}$의$$집합에 $파티션$을 구성하는 각$정보$ 집합에 대해 사용 가능한 작업 집합이다$.$
• ${\$$V\setminus \{v^{0}\}\오른쪽$ 화살표 ${\mathcal {A}}$은(는) 각 노드 $v{\displaystyle }$ ${\displaystyle v}$을(를) 단일 작업 $a{\displaystyle }$( )${\displaystyle a(v)}$에 연결하는 작업 파티션으로$,$ 다음을$$ 충족한다.

${\displaystyle \forall H\in \mathbf {H} ,\forall v\in H}$, the restriction ${\displaystyle a_{v}:s(v)\rightarrow A(H)}$ of ${\displaystyle a}$ on ${\displaystyle s(v)}$ is a bijection, with ${\displaystyle s(v)}$ the set of successor nodes of ${\$$디스플레이$ 스타일 $v}$.

• ${\displaystyle {\mathcal {I}=\{1,...,$$I\}}$ is a finite set of players, ${\displaystyle 0}$ is (a special player called) nature, and ${\displaystyle (\mathbf {H} _{i})_{i\in {\mathcal {I}}\cup \{0\}}}$ is a player partition of information set ${\displaystyle \mathbf {H} }$. Let ${\displaystyle \iota (v)$$=\iota(H)}$는 노드 $v{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle H}${\$displaystyle v\in H}$에서 이동하는 단일 플레이어임$.$
• ${\displaystyle \rho =\{\rho _{H}:A(H)\rightarrow [0,1] H\in \mathbf {H} _{0}\}}$ is a family of probabilities of the actions of nature, and
• ${\displaystyle u=(u_{i})_{i\in {\mathcal {I}}}:T\rightarrow \mathbb {R} ^{\mathcal {I}}}$ is a payoff profile function.

Infinite action space

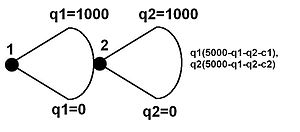
It may be that a player has an infinite number of possible actions to choose from at a particular decision node. The device used to represent this is an arc joining two edges protruding from the decision node in question. If the action space is a continuum between two numbers, the lower and upper delimiting numbers are placed at the bottom and top of the arc respectively, usually with a variable that is used to express the payoffs. The infinite number of decision nodes that could result are represented by a single node placed in the centre of the arc. A similar device is used to represent action spaces that, whilst not infinite, are large enough to prove impractical to represent with an edge for each action.

The tree on the left represents such a game, either with infinite action spaces (any real number between 0 and 5000) or with very large action spaces (perhaps any integer between 0 and 5000). This would be specified elsewhere. Here, it will be supposed that it is the former and, for concreteness, it will be supposed it represents two firms engaged in Stackelberg competition. The payoffs to the firms are represented on the left, with ${\displaystyle q_{1}}$ and ${\displaystyle q_{2}}$ as the strategy they adopt and ${\displaystyle c_{1}}$ and ${\displaystyle c_{2}}$ as some constants (here marginal costs to each firm). The subgame perfect Nash equilibria of this game can be found by taking the first partial derivative^{[citation needed]} of each payoff function with respect to the follower's (firm 2) strategy variable (${\displaystyle q_{2}}$) and finding its best response function, ${\displaystyle q_{2}(q_{1})={\tfrac {5000-q_{1}-c_{2}}{2}}}$. The same process can be done for the leader except that in calculating its profit, it knows that firm 2 will play the above response and so this can be substituted into its maximisation problem. It can then solve for ${\displaystyle q_{1}}$ by taking the first derivative, yielding ${\displaystyle q_{1}^{*}={\tfrac {5000+c_{2}-2c_{1}}{2}}}$. Feeding this into firm 2's best response function, ${\displaystyle q_{2}^{*}={\tfrac {5000+2c_{1}-3c_{2}}{4}}}$ and ${\displaystyle (q_{1}^{*},q_{2}^{*})}$ is the subgame perfect Nash equilibrium.

See also

• Axiom of determinacy
• Perfect information
• Combinatorial game theory
• Self-confirming equilibrium
• Sequential game
• Signalling
• Solution concept

References

• Hart, Sergiu (1992). "Games in extensive and strategic forms". In Aumann, Robert; Hart, Sergiu (eds.). Handbook of Game Theory with Economic Applications. 1. Elsevier. ISBN 978-0-444-88098-7.
• Binmore, Kenneth (2007). Playing for real: a text on game theory. Oxford University Press US. ISBN 978-0-19-530057-4.
• Dresher M. (1961). The mathematics of games of strategy: theory and applications (Ch4: Games in extensive form, pp74–78). Rand Corp. ISBN 0-486-64216-X
• Fudenberg D and Tirole J. (1991) Game theory (Ch3 Extensive form games, pp67–106). MIT press. ISBN 0-262-06141-4
• Leyton-Brown, Kevin; Shoham, Yoav (2008), Essentials of Game Theory: A Concise, Multidisciplinary Introduction, San Rafael, CA: Morgan & Claypool Publishers, ISBN 978-1-59829-593-1. An 88-page mathematical introduction; see Chapters 4 and 5. Free online at many universities.
• Luce R.D. and Raiffa H. (1957). Games and decisions: introduction and critical survey. (Ch3: Extensive and Normal Forms, pp39–55). Wiley New York. ISBN 0-486-65943-7
• Osborne MJ and Rubinstein A. 1994. A course in game theory (Ch6 Extensive game with perfect information, pp. 89–115). MIT press. ISBN 0-262-65040-1
• Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations, New York: Cambridge University Press, ISBN 978-0-521-89943-7. A comprehensive reference from a computational perspective; see Chapter 5. Downloadable free online.

Further reading

• Horst Herrlich (2006). Axiom of choice. Springer. ISBN 978-3-540-30989-5., 6.1, "Disasters in Game Theory" and 7.2 "Measurability (The Axiom of Determinateness)", discusses problems in extending the finite-case definition to infinite number of options (or moves)

Historical papers

• Neumann, J. (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen. 100: 295–320. doi:10.1007/BF01448847.
• Harold William Kuhn (2003). Lectures on the theory of games. Princeton University Press. ISBN 978-0-691-02772-2. contains Kuhn's lectures at Princeton from 1952 (officially unpublished previously, but in circulation as photocopies)