메커니즘 설계
Mechanism design메커니즘 설계는 참가자들이 합리적으로 행동하는 전략적 환경에서 원하는 목표를 향해 경제 메커니즘 또는 인센티브를 설계하기 위한 목표 우선 접근법을 취하는 경제학 및 게임 이론 분야입니다.게임이 끝날 때 시작해서 뒤로 가기 때문에, 그것은 역게임 이론이라고도 불린다.시장 설계, 경매 이론 및 사회적 선택 이론과 같은 분야의 경제 및 정치에서 네트워크 시스템(인터넷 도메인 간 라우팅, 후원 검색 경매)에 이르기까지 광범위한 응용 분야를 보유하고 있습니다.
메커니즘 설계는 개인 정보 게임 클래스의 솔루션 개념을 연구합니다.Leonid Hurwicz는 '설계 문제에서 목표 함수는 주요 "주어진" 반면 메커니즘은 알려지지 않은 것이라고 설명한다.그러므로, 설계 문제는 전통적인 경제 이론의 "역전"이며, 이것은 전형적으로 주어진 메커니즘의 성능 분석에 전념한다.'[1]이러한 게임의 두 가지 특징은 다음과 같습니다.
- 게임이 게임 구조를 계승하는 것이 아니라 게임 구조를 선택하는 것이다.
- 디자이너가 게임의 결과에 관심이 있다는 것을
2007년 노벨 경제학상은 메커니즘 설계 이론의 기초를 [2]다진 레오니드 후르비츠, 에릭 마스킨, 로저 마이어슨에게 수여되었다.
직감
베이지안 게임의 흥미로운 클래스에서, "원칙"이라고 불리는 한 플레이어는 다른 플레이어에 의해 개인적으로 알려진 정보에 따라 자신의 행동을 조절하고 싶어합니다.예를 들어, 교장은 판매원이 피칭하는 중고차의 실제 품질을 알고자 합니다.진실을 왜곡하는 것이 판매원에게 이익이 되기 때문에 그는 단순히 판매원에게 물어보는 것만으로 아무것도 배울 수 없다.그러나 메커니즘 설계에서 주체는 한 가지 장점이 있다.그는 다른 사람들이 그가 원하는 방식으로 행동하도록 영향을 줄 수 있는 규칙을 가진 게임을 설계할 수 있다.
메커니즘 설계 이론이 없다면, 교장의 문제는 해결하기 어려울 것이다.그는 가능한 모든 경기를 고려하고 다른 선수들의 전술에 가장 영향을 미치는 경기를 선택해야 할 것이다.또한 교장은 자신에게 거짓말을 할 수 있는 요원들로부터 결론을 도출해야 할 것이다.메커니즘 설계, 특히 폭로 원칙 덕분에, 주계약자는 에이전트가 자신의 개인 정보를 진실하게 보고하는 게임만 고려하면 된다.
기초
메커니즘
메커니즘 설계 게임은 주체라고 불리는 대리인 중 한 명이 보상 구조를 선택하는 개인 정보 게임입니다.Harsanyi(1967년)에 이어 에이전트는 성과에 관한 정보를 포함한 자연으로부터의 비밀 메시지(secret 'messages)를 받습니다.예를 들어, 메시지는 선호도 또는 판매용 상품의 품질에 대한 정보를 포함할 수 있습니다.이 정보를 에이전트의 "유형"이라고 부릅니다(통상은 라고 기재되어 있으며, 이에 따라 의 공간)). 다음 담당자는 전략적인 거짓말일 수 있는 유형을 교장( 모자에게 보고합니다보고 후, 본인과 대리인은 본인이 선택한 보수 구조에 따라 보수를 받는다.
게임의 타이밍은 다음과 같습니다.
- 주계약자는 를 보고유형의 함수로 하는 메커니즘 y)({ y에 커밋합니다.
- 요원들이 부정한 유형 프로파일을 요 { } {\ }}
- 메커니즘이 실행됩니다(는 y ( ) { y ( { \ { \ }) 。
누가 무엇을 얻을 수 있는지 이해하기 위해, 결과(\ y를 상품 할당과 송금, )) { )) () ) T y {ta로 나누는 것이 일반적입니다.t는 type의 함수로 화폐이체를 나타냅니다.
벤치마크로 설계자는 종종 완전한 정보 하에서 어떤 일이 일어날지 정의합니다.() 유형 프로파일을 수령 또는 제공된 상품의 할당에 직접 매핑하는 사회적 선택 f f(\를 정의합니다.
이와는 대조적으로 메커니즘은 보고된 유형 프로파일을 결과에 매핑합니다(상품 x(\x및 t(\t)
계시 원리
제안된 메커니즘은 베이지안 게임(개인 정보의 게임)을 구성하며, 그것이 잘 동작한다면 게임은 베이지안 내쉬 평형을 갖는다.평형 에이전트에서는 유형 함수로 전략적으로 보고서를 선택한다.
이러한 상황에서 베이지안 평형을 해결하기란 어렵다. 왜냐하면 베이지안 평형은 에이전트의 최선의 대응 전략과 가능한 전략적 거짓말로부터 최선의 추론을 위한 해결을 포함하기 때문이다.계시 원리라고 불리는 압도적인 결과 덕분에, 설계자는[3] 어떤 메커니즘이 있든 간에 에이전트가 유형을 진실하게 보고하는 균형에 주의를 집중할 수 있습니다.계시의 원칙은 다음과 같다: "모든 베이지안 내쉬 균형에는 같은 평형 결과를 가진 베이지안 게임이 있지만 플레이어는 유형을 진실하게 보고한다."
이것은 매우 유용합니다.이 원칙은 모든 참가자가 유형을 진실하게 보고한다고 가정함으로써 베이지안 평형을 해결할 수 있게 한다(유인 호환성 제약에 따라).단번에 전략적 행동이나 거짓말을 고려할 필요가 없어집니다.
그 증거는 꽤 직설적이다.에이전트의 전략과 보수가 그 타입의 함수이며, 다른 사람의 은 ( ) , - ( -) , i )( style _ { } \ ( _ { } , s _ { i } , s _ { } , s _ { i ( _ } \ ta _ i } \ _ right ) , s _ ta 。 s _는 예상 유틸리티의 내쉬입니다.
에이전트가 동일한 평형을 선택하도록 유도하는 메커니즘을 정의하기만 하면 됩니다.가장 쉽게 정의할 수 있는 것은 에이전트의 평형 전략을 실행하는 메커니즘입니다.
이러한 메커니즘 하에서 에이전트는 메커니즘이 최적이라고 판단한 전략을 실행하므로 당연히 유형을 밝히는 것이 최적임을 알게 됩니다.정식으로 y( ) { y ( \ ) } 를 합니다.
구현 가능성
메커니즘의 설계자는 일반적으로 다음 중 하나를 희망합니다.
- 사회적 선택 기능을 "실행" y를 설계한다.
- 일부 가치 기준(예: 이익)을 극대화하는 y)(\ y를 찾는다.
To implement a social choice function is to find some transfer function that motivates agents to pick . Formally, if the equilibrium strategy profile under the mechanism maps to the same goods allocation as a social choice기능.
우리는 그 메커니즘이 사회적 선택 기능을 실행한다고 말한다.
계시원칙 덕분에 디자이너는 일반적으로 t를 찾을 수 있으며, 관련 진실게임으로 사회적 선택을 구현할 수 있습니다.에이전트가 유형을 정확하게 보고하는 것이 최선이라고 판단되면
우리는 그러한 메커니즘이 진실하게 구현될 수 있다고 말한다(또는 단지 "불가능").그 후 과제는 진실하게 구현 한 t t를 해결하고 이 전송 함수를 원래 게임으로 돌리는 것입니다.다음과 같이 전송 t ) { x ( \) } { t ( \ )} 가 존재하는 경우, ( ) { display style t ( \theta)} 가 올바르게 실장됩니다.
인센티브 호환성(IC) 제약이라고도 합니다.
응용 프로그램에서는 IC 이 t( ) \ t ( \ )의 을 알기 쉽게 기술하는 열쇠입니다.특정 상황에서는 전송 기능을 분석적으로 분리할 수도 있습니다.또한 에이전트가 재생하지 않는 옵션이 있는 경우 참여(개별 합리성) 제약이 추가될 수 있습니다.
필요성
모든 에이전트가 유형 일치 유틸리티 (x , , ) { u ( , , \)} 를 가지고 있는 설정을 고려합니다. 의 상품 x( ) \ x ( \ )(k\ k )개수의 상품을 표시할 수 .그 논거에 관해 연속적이다.
x( ){ x ( \) } 은 다음 경우에만 구현 가능합니다.
x ( ) { x ( \) t t t ( \ t ( \) } 및 x 가에서 연속될 마다 이는 필수 조건이며 에이전트 최적화 문제의 1차 조건과 2차 조건으로부터 도출됩니다.
그 의미는 두 조각으로 나눌 수 있다.첫 번째 부분은 대리인의 한계 대체율(MRS)이 유형의 함수로서 증가한다고 말한다.
즉, 이 메커니즘이 높은 에이전트유형을 보다 싸게 제공하지 않으면 에이전트는 진실을 말하지 않습니다.그렇지 않으면 높은 유형을 보고로 처벌하는 메커니즘에 직면한 상위 유형은 거짓말을 하고 하위 유형을 선언하여 진실을 말하는 IC 제약을 위반하게 된다.두 번째 조각은 단조로운 상태가 일어나기를 기다리고 있습니다.
긍정적이면, 높은 타입은 좋은 것을 더 많이 줘야 한다는 거죠.
두 조각이 상호작용할 가능성이 있습니다.If for some type range the contract offered less quantity to higher types , it is possible the mechanism could compensate by giving higher types a discount.그러나 이러한 계약은 낮은 유형의 에이전트에 대해 이미 존재하므로 이 솔루션은 병적인 것입니다.이러한 해결책은 메커니즘에 대한 해결 과정에서 종종 발생합니다.이 경우 다림질해야 합니다.다재다능한 환경에서는 설계자가 에이전트에게 더 적은 양의 다른 제품(예: 마가린 버터)을 대체할 수 있는 여러 가지 제품으로 보상할 수도 있습니다.복수의 양호한 메커니즘은 메커니즘 설계 이론에서 현재 진행 중인 문제입니다.
충분.
메커니즘 설계서에서는 일반적으로 구현 가능성을 확보하기 위해 다음 두 가지 가정을 합니다.
이는 단일 교차 조건, 정렬 조건 및 스펜스-미르레스 조건의 여러 이름으로 알려져 있습니다.즉, 유틸리티 함수가 에이전트의 MRS 유형이 증가하는 형상의 함수입니다.
이것은 MRS의 성장률을 제한하는 기술적 조건입니다.
전제조건은 로운x ( x ( \)}를 구현할 수 있는 것으로 충분합니다(( t ( \) ) 。또, 싱글 굿 설정에서는, 싱글 크로스 조건에서는, 의 x )(\ x)만이 실장 가능하기 때문에, 디자이너는 검색을 의 x))(\ x로 제한할 수 있습니다.
하이라이트된 결과
수익균등성정리
Vickrey(1961)는 대규모 경매의 모든 구성원이 판매자에게 동일한 예상 수익을 보장하고 예상 수익이 판매자가 할 수 있는 최선의 것이라는 유명한 결과를 제공한다.이 경우입니다.
- 구매자가 동일한 평가 함수(유형의 함수일 수 있음)를 가집니다.
- 구매자의 유형이 독립적으로 분포되어 있습니다.
- 구매자 유형은 연속 분포에서 추출됩니다.
- 유형 분포는 단조 위험률 특성을 갖는다.
- 이 메커니즘은 가장 높은 평가를 받는 구매자에게 상품을 판매한다.
마지막 조건은 그 정리에 매우 중요하다.즉, 판매자가 더 높은 수익을 얻기 위해서는 더 낮은 평가를 가진 대리인에게 그 아이템을 주는 기회를 가져야 한다는 것입니다.보통 이것은 그가 그 물건을 전혀 팔지 않는 위험을 감수해야 한다는 것을 의미합니다.
빅레이-클라크-그로브스 메커니즘
Vickrey(1961) 경매 모델은 후에 Clarke(1971)와 Groves에 의해 확장되어 공공 프로젝트의 비용이 모든 대리인이 부담하는 공공 선택 문제를 해결했다(예: 도시 다리 건설 여부).결과적으로 도출된 "빅리-클라크-그로브스" 메커니즘은 대리인이 개인적으로 알려진 평가를 가지고 있더라도 대리인이 공공재의 사회적 효율적인 배분을 선택하도록 동기를 부여할 수 있다.즉, 특정 조건, 특히 준선형 유틸리티 또는 예산 균형이 필요하지 않은 경우 "공통의 비극"을 해결할 수 있습니다.
t t가 선형으로 평가되는 개인 v의 준선형 유틸리티를가진 을 고려합니다.VCG 설계자는 진정한 유형 프로파일을 얻기 위해 인센티브 호환(따라서 진정으로 구현 가능한) 메커니즘을 설계하고, 설계자는 이를 통해 사회적으로 최적의 할당을 구현합니다.
VCG 메커니즘의 영리함은 그것이 진실한 폭로를 동기화하는 방법이다.그것은 어떠한 대리인이 야기하는 왜곡의 비용에 의해 처벌함으로써 잘못된 보고를 하는 동기를 제거한다.에이전트가 작성할 수 있는 보고서 중 VCG 메커니즘은 그가 공공의 이익에는 무관심하고 송금에만 관심이 있다는 '늘' 보고서를 허용한다.이렇게 하면 에이전트가 게임에서 효과적으로 제거됩니다.에이전트가 유형을 보고하기로 선택한 경우 VCG 메커니즘은 보고서가 중추적인 경우, 즉 보고서가 다른 에이전트에 해를 입히기 위해 최적의 할당x 를 변경하는 경우 에이전트에게 요금을 청구합니다.지불이 계산되었습니다.
이는 1개의 에이전트에 의한 보고서 작성으로 인해 발생한 (자신이 아닌) 다른 에이전트의 유틸리티 왜곡의 합계입니다.
지바르-새터트웨이트 정리
지바드(1973년)와 새터스웨이트(1975년)는 애로우의 불가능 정리처럼 정신적으로 불가능한 결과를 제시한다.매우 일반적인 게임 클래스에서는 "독재적인" 소셜 선택 기능만 구현할 수 있습니다.
소셜 선택 함수 f()는 한 에이전트가 항상 가장 선호하는 상품 할당을 받는 경우 독재적입니다.
이 정리는 다음과 같은 경우, 일반적인 조건 하에서 진실하게 실행될 수 있는 사회적 선택 함수는 독재적이어야 한다고 기술한다.
- X는 유한하며 최소 3개의 요소를 포함합니다.
- 선호도는 합리적이다.
마이어슨-새터스웨이트 정리
마이어슨과 새터스웨이트(1983)는 한 당사자가 손해를 보고 거래하도록 강요할 위험 없이, 두 당사자가 각각 비밀스럽고 확률적으로 다양한 가치를 가질 때 상품을 거래할 수 있는 효율적인 방법이 없음을 보여준다.그것은 경제에서 가장 주목할 만한 부정적인 결과들 중 하나이며, 복지 경제학의 근본적인 이론들에 대한 일종의 부정적인 거울이다.
섀플리 값
Phillips and Marden(2018)은 오목한 비용 함수를 가진 비용 분담 게임의 경우, 우선 게임 내 최악의 비효율성(무정부 상태 가격)을 최적화하고 다음으로 최상의 결과(안정성 가격)를 최적화하는 최적의 비용 분담 규칙이 정확히 Shapley 가치 분담 [4]규칙임을 입증했다.대칭 문장은 볼록 효용 함수를 가진 효용 공유 게임에도 마찬가지로 유효하다.
예
가격 차별
Mirrlees(1971)는 전송 함수 t()를 해결하기 쉬운 설정을 도입한다.관련성과 추적성 때문에 그것은 문헌에서 일반적인 설정이다.에이전트에 알 수 없는 타입 의 준선형 유틸리티가 있는 단일 양호한 단일 에이전트 설정을 고려합니다 \ }
주계약자가 에이전트의 P P보다 우선적인 CDF를 가지고 있는 경우.주계약자는 볼록한 한계비용 c(x)로 상품을 생산할 수 있으며 거래에서 예상되는 이익을 극대화하고자 한다.
IC 및 IR 조건에 따라
여기서 주계약자는 고객의 유형을 식별할 수 없는 이윤 극대화 가격 체계를 설정하려는 독점자이다.일반적인 예로는 비즈니스, 레저 및 학생 여행객에 대한 항공사의 요금 책정이 있다.IR 조건으로 인해 모든 유형에 참여를 유도할 수 있는 좋은 거래를 제공해야 합니다.IC 조건 때문에 모든 타입에 대해 다른 타입보다 더 좋은 거래를 선호할 정도로 좋은 거래를 선호합니다.
Mirriclees(1971)에 의해 주어진 트릭은 엔벨로프 정리를 사용하여 전달 함수를 최대화하려는 기대에서 제거하는 것이다.
통합 중,
여기서 0 \ _은 인덱스 유형입니다. 호환t ( ) (x () , ) - () \ t ( \ ) ( ( \) - ( \ )} 를 최대값으로 바꿉니다.
부품별 통합 후.이 함수는 점 단위로 최대화할 수 있습니다.
U는 인센티브 호환성이 있기 에 설계자는 IC 구속조건을 해제할 수 있습니다.유틸리티 함수가 Spence-Mirrlees 조건을 만족하는 경우 x ( )(\ x 함수가 존재합니다.IR 제약은 평형 상태에서 확인할 수 있으며 그에 따라 수수료 일정을 올리거나 내릴 수 있습니다.또한 식에 위험률의 존재에 유의하십시오.유형 분포가 단조 위험 비율 특성을 갖는 경우 FOC는 t()에 대해 해결하기에 충분하다.그렇지 않은 경우, 할당 및 수수료 일정에 따라 모든 부분에서 단조성 제약(위의 충분성 참조)이 충족되는지 확인해야 합니다.그렇지 않은 경우 설계자는 마이어슨 다리미를 사용해야 합니다.
마이어슨 다리미
일부 응용 프로그램에서는 설계자가 가격과 할당 일정에 대한 1차 조건을 해결할 수 있지만 단조롭지 않습니다.예를 들어 준선형 설정에서 이는 위험비 자체가 단조롭지 않을 때 종종 발생한다.스펜스-미러즈 조건에 따라 최적의 가격과 할당 일정은 단조로운 것이어야 하므로 설계자는 일정의 방향을 바꾸는 간격을 평평하게 하여 제거해야 한다.
직감적으로, 디자이너는 특정 유형을 묶어서 동일한 계약을 체결하는 것이 가장 적합하다고 생각합니다.일반적으로 디자이너는 더 나은 거래를 제공함으로써 더 높은 유형의 사람들이 자신을 구별하도록 동기를 부여합니다.마진에 상위 유형이 충분하지 않은 경우 설계자는 상위 유형에 유형별 계약을 부과하기 위해 하위 유형에게 양보(정보 임대라고 함)를 부여하는 것이 가치가 없다고 본다.
위의 예와 같이 준선형 효용을 가진 대리인에게 독점적인 주계약 판매를 고려해보자.1차 조건을 만족시키는 할당 ( )( \ x ( \ )의 내부 피크는 1 ( \ {} )이고 내부 트로프는 2> ( \ _ { } > \_ { )입니다.
- 마이어슨(1981)에 따라 x x를 하여 평탄하게 만듭니다.여기서 1( _ { (는 에 대한 x 매핑의 역함수이며, 2 (){ displaystyle _ {2} 는 의 역함수입니다style2에 x 매핑의 역함수입니다 _ 내부 피크 전에 를 반환하고, 내부 뒤에 _{2 "\ \를 반환합니다.
- x 의 비단조 (\displaystyle x이 유형 공간의 가장자리에 접하는 경우 적절한 \ \ 함수(또는 둘 다)를 경계 유형으로 설정합니다.여러 영역이 있는 경우 반복 절차에 대한 교과서를 참조하십시오. 두 개 이상의 수조를 함께 다림질해야 할 수 있습니다.
증명
그 증거는 최적 제어 이론을 사용한다. 영역 )( \ ( \ } )의 간격 \ displaystyle [ { \ \ } , { \\ } } )의 를 고려하여 일정을 평평하게 합니다.그런 다음 간격 내에 x( x에 필요한 조건을 얻기 위해 해밀턴을 씁니다.
- 단조로움을 만족시키는
- 단조성 제약이 구간의 경계에 구속되지 않는 경우
조건 2는 최적의 제어 문제를 만족시키는x ( )(\ x가 간격 경계(점프 없음)에서 원래 문제의 일정에 다시 연결되도록 합니다.한 조건을 충족하는 모든 ( x는 단조롭고 경계에서 다시 연결되어야 하므로 평탄해야 합니다.
이전과 마찬가지로 원금의 기대 수익을 극대화하지만, 이번에는 단조성 제약에 따릅니다.
프라이스 ( ) { ( \) }
서x(\ x는 상태 변수이고 / x 컨트롤입니다.최적 제어에서 항상 그렇듯이, 코스트레이트 진화 방정식은 다음을 충족해야 한다.
2를 이용하여 단조성 제약은§(\ 간격의 경계에서 구속되지 않습니다.
뜻은 늑골이 있는 가변 상태와 또한 0와 같은지 통합할 수 있다.
원금 잉여금의 평균 왜곡은 0이어야 한다.일정을 평탄하게 하려면x\x 를 찾습니다. x\displaystyle x 의 반전 이미지가 위의 조건을 시키는{\\ \theta 간격에 매핑됩니다.
「 」를 참조해 주세요.
메모들
- ^ L. Hurwicz & S. Repeater (2006) 경제 메커니즘 설계, 페이지 30
- ^ "The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2007" (Press release). Nobel Foundation. October 15, 2007. Retrieved 2008-08-15.
- ^ 특이한 환경에서 몇몇truth-telling 게임이 더 그들이 매핑 된 베이 시안 게임보다equilibria다.참고 Fudenburg-Tirole 상공 회의소 7.2증명서를.
- ^ Phillips, Matthew; Marden, Jason R. (July 2018). "Design Tradeoffs in Concave Cost-Sharing Games". IEEE Transactions on Automatic Control. 63 (7): 2242–2247. doi:10.1109/tac.2017.2765299. ISSN 0018-9286. S2CID 45923961.
레퍼런스
- Clarke, Edward H. (1971). "Multipart Pricing of Public Goods" (PDF). Public Choice. 11 (1): 17–33. doi:10.1007/BF01726210. JSTOR 30022651. S2CID 154860771.
- Gibbard, Allan (1973). "Manipulation of voting schemes: A general result" (PDF). Econometrica. 41 (4): 587–601. doi:10.2307/1914083. JSTOR 1914083.
- Groves, Theodore (1973). "Incentives in Teams" (PDF). Econometrica. 41 (4): 617–631. doi:10.2307/1914085. JSTOR 1914085.
- Harsanyi, John C. (1967). "Games with incomplete information played by "Bayesian" players, I-III. part I. The Basic Model". Management Science. 14 (3): 159–182. doi:10.1287/mnsc.14.3.159. JSTOR 2628393.
- Mirrlees, J. A. (1971). "An Exploration in the Theory of Optimum Income Taxation" (PDF). Review of Economic Studies. 38 (2): 175–208. doi:10.2307/2296779. JSTOR 2296779. Archived from the original (PDF) on 2017-05-10. Retrieved 2016-08-12.
- Myerson, Roger B.; Satterthwaite, Mark A. (1983). "Efficient Mechanisms for Bilateral Trading" (PDF). Journal of Economic Theory. 29 (2): 265–281. doi:10.1016/0022-0531(83)90048-0. hdl:10419/220829.
- Satterthwaite, Mark Allen (1975). "Strategy-proofness and Arrow's conditions: Existence and correspondence theorems for voting procedures and social welfare functions". Journal of Economic Theory. 10 (2): 187–217. CiteSeerX 10.1.1.471.9842. doi:10.1016/0022-0531(75)90050-2.
- Vickrey, William (1961). "Counterspeculation, Auctions, and Competitive Sealed Tenders" (PDF). The Journal of Finance. 16 (1): 8–37. doi:10.1111/j.1540-6261.1961.tb02789.x.
추가 정보
- 의 7장. 대학원 게임 이론의 표준 교재입니다.
- 의 23장. 대학원 미시경제학 표준 교재.
- 경매에 관한 메커니즘 설계 원칙의 적용Milgrom, Paul (2004), Putting Auction Theory to Work, New York: Cambridge University Press, ISBN 978-0-521-55184-7.
- 노암 니산.메커니즘 디자인에 대한 구글 기술 토크입니다.
- Legros, Patrick; Cantillon, Estelle (2007). "What is mechanism design and why does it matter for policy-making?". Centre for Economic Policy Research.
- 로저 B. 마이어슨(2008년)."기계 설계", 새로운 Palgrave 경제학 사전 온라인, 추상.
- 메카니즘 설계에 특화된 졸업 교재Diamantaras, Dimitrios (2009), A Toolbox for Economic Design, New York: Palgrave Macmillan, ISBN 978-0-230-61060-6.
외부 링크
- Eric Maskin "Nobel Prize 강연"은 2007년 12월 8일 스톡홀름 대학교 Aula Magna에서 강의되었습니다.
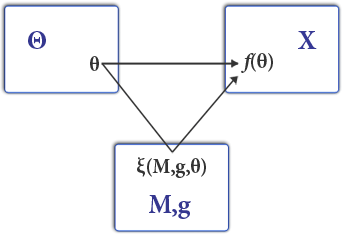
 유형 공간, 오른쪽 상단 공간 X는 결과 공간입니다.
유형 공간, 오른쪽 상단 공간 X는 결과 공간입니다. 타입 프로파일을 결과에 매핑합니다.메커니즘 설계 게임에서는 에이전트가 게임
타입 프로파일을 결과에 매핑합니다.메커니즘 설계 게임에서는 에이전트가 게임 
 보냅니다
보냅니다 균형은
균형은  기재되어 있으며, 이에 따라
기재되어 있으며, 이에 따라 
 보고유형의 함수로
보고유형의 함수로  커밋합니다.
커밋합니다.





 예상 유틸리티의 내쉬입니다.
예상 유틸리티의 내쉬입니다.


![{\displaystyle {\begin{aligned}\theta _{i}\in {}&\arg \max _{\theta '_{i}\in \Theta }\sum _{\theta _{-i}}\ p(\theta _{-i}\mid \theta _{i})\ u_{i}\left(y(\theta '_{i},\theta _{-i}),\theta _{i}\right)\\[5pt]&=\sum _{\theta _{-i}}\ p(\theta _{-i}\mid \theta _{i})\ u_{i}\left(s_{i}(\theta ),s_{-i}(\theta _{-i}),\theta _{i}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ddebc0c02e6a69987a230472f84db616382cc0c)
















 준선형 유틸리티를
준선형 유틸리티를





![\max _{{x(\theta ),t(\theta )}}{\mathbb {E}}_{\theta }\left[t(\theta )-c\left(x(\theta )\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9672a0138ebc8b76736cf959c80e418f2e66733)





 인덱스 유형입니다.
인덱스 유형입니다.
![{\displaystyle {\begin{aligned}&\mathbb {E} _{\theta }\left[V(x(\theta ),\theta )-{\underline {u}}(\theta _{0})-\int _{\theta _{0}}^{\theta }{\frac {\partial V}{\partial {\tilde {\theta }}}}d{\tilde {\theta }}-c\left(x(\theta )\right)\right]\\&{}=\mathbb {E} _{\theta }\left[V(x(\theta ),\theta )-{\underline {u}}(\theta _{0})-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial V}{\partial \theta }}-c\left(x(\theta )\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c51298829eb2b6333be4f860cab7d244d1bb8868)
 인센티브 호환성이 있기
인센티브 호환성이 있기 
 내부 트로프는
내부 트로프는 







![\left[\underline \theta ,\overline \theta \right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54d9753546a7597d8bc3ca0b2cd79ee786554c6)








