화살의 불가능성 정리

화살의 불가능성 정리, 일반가능성 정리 또는 화살의 역설은 사회선택이론에서 유권자가 3개 이상의 서로 다른 대안(옵션)을 가지고 있을 때, 어떤 순위 투표 선거 제도도 제한되지 않은 영역, 비독재권, 파레토 효율성 및 관련 없는 대안의 독립성과 같은 지정된 기준을 충족시키면서 개인의 순위 지정된 선호도를 공동체 전체(완전하고 과도기적인) 순위로 변환할 수 없습니다. 이 정리는 기바드-새터스웨이트 정리에 의해 더 해석되기 때문에 투표 이론의 논의에서 자주 인용됩니다. 이 정리는 경제학자이자 노벨상 수상자인 케네스 애로우(Kenneth Arrow)의 이름을 따서 지어졌는데, 그는 박사 논문에서 이 정리를 증명했고 1951년 저서인 사회적 선택과 개인의 가치에서 대중화했습니다. 논문의 제목은 '사회복지 개념의 어려움'이었습니다.^[1]

간단히 말해서, 이 정리는 항상 이 세 가지 "공정성" 기준을 만족시키는 어떤 순위제 선거제도도 설계될 수 없다는 것을 말합니다.

모든 유권자가 대안 Y보다 대안 X를 선호한다면, 집단은 Y보다 X를 선호합니다.
모든 유권자의 X와 Y 사이의 선호도가 변하지 않는다면, X와 Y 사이의 그룹의 선호도 또한 변하지 않을 것입니다. (유권자의 X와 Z, Y와 Z 또는 Z와 W와 같은 다른 쌍 사이의 선호도가 변하더라도).
"독재자"란 존재하지 않습니다. 어떤 유권자도 항상 그 집단의 선호도를 결정할 수 있는 권한을 가지고 있지 않습니다.

기본 투표 선거 제도는 순위 순서보다 더 많은 정보를 전달하기 때문에 이 정리에서는 다루지 않습니다.^[2]^[3] 기바드의 정리와 Duggan-Schwartz 정리는 전략적 투표가 여전히 문제임을 보여줍니다. Arrow가 채택한 공리적 접근 방식은 하나의 통합된 프레임워크 내에서 (선호도에 기반한) 생각할 수 있는 모든 규칙을 처리할 수 있습니다. 그런 점에서 규칙을 일일이 조사하던 투표 이론의 초기와는 접근 방식이 질적으로 다릅니다. 따라서 사회선택론의 현대적 패러다임은 이 정리에서 출발했다고 할 수 있습니다.^[4]

그 정리의 실제적인 결과는 논쟁의 여지가 있습니다. Arrow는 다음과 같이 말했습니다. "대부분의 시스템은 항상 제대로 작동하지 않을 것입니다. 제가 증명한 것은 모든 것이 때때로 잘못될 수 있다는 것입니다."^[5] 그는 미국 선거에 대해 무엇을 바꿀 것이냐는 질문에 "내가 가장 먼저 할 일은 모든 후보를 순위를 매기는 시스템으로 가는 것"이라고 말했습니다.^[6] 화살표의 불가능 정리는 비례대표와 같은 다승자 투표에는 적용되지 않습니다.

진술

선호를 종합할 필요성은 많은 분야에서 발생합니다: 허용되고 안정적인 경제적 결과를 찾으려고 시도하는 복지 경제학에서; 사람이 여러 기준에 근거하여 합리적인 선택을 해야 하는 결정 이론에서; 그리고 가장 자연스럽게 선거 제도에서, 그것은 다수의 유권자들의 선호로부터 통치와 관련된 결정을 추출하기 위한 메커니즘입니다.

화살표 정리의 틀은 주어진 옵션 집합(결과)에서 선호 순서를 추출해야 한다고 가정합니다. 사회의 각 개인(또는 동등하게, 각 결정 기준)은 결과 집합에 대한 특정 순서의 선호도를 제공합니다. 우리는 사회복지 기능(선호도 집계 규칙)이라고 불리는 순위 투표 선거 시스템을 찾고 있습니다. 이 시스템은 선호도 집합(선호도 프로파일)을 단일 글로벌 사회 선호도 순서로 변환합니다. 애로우의 정리는 의사결정기구가 최소 2명의 구성원과 최소 3개의 선택지를 가지고 있다면, 이 모든 조건(공정한 선거제도의 합리적인 요건으로 가정)을 충족하는 사회복지 기능을 한 번에 설계하는 것은 불가능하다는 것을 말합니다.

무독재

사회복지 기능은 다수 유권자의 바람을 고려해야 합니다. 그것은 단순히 단일 유권자의 선호를 모방할 수 없습니다.

제한 없는 도메인 또는 보편성

모든 유권자 선호도에 대해 사회복지 기능은 사회적 선택의 독특하고 완전한 순위를 산출해야 합니다. 따라서:

사회에 대한 선호도의 완전한 순위를 도출하는 방식으로 그렇게 해야 합니다.
유권자의 선호도가 동일한 방식으로 제시될 때마다 결정적으로 동일한 순위를 제공해야 합니다.

관련 없는 대안의 독립성(IIA)

x와 y 사이의 사회적 선호도는 x와 y 사이의 개인적 선호도(쌍별 독립성)에만 의존해야 합니다. 보다 일반적으로, 개인의 관련 없는 대안(특정 부분집합 밖의 대안) 순위의 변화는 부분집합의 사회적 순위에 영향을 미치지 않아야 합니다. 예를 들어, 후보 x가 후보 y보다 사회적 순위가 먼저라면, 세 번째 후보 z가 참여에서 제거되더라도 x가 y보다 사회적 순위가 먼저 되어야 합니다. (아래 비고 참조)

사회적 가치와 개인적 가치의 단일성 또는 긍정적 연관성

어떤 사람이 어떤 선택지를 홍보함으로써 자신의 선호 순서를 수정한다면, 사회적 선호 순서는 같은 선택지를 홍보하거나 변경하지 않아야 하며, 이전보다 더 낮게 두지 않아야 합니다. 개인은 옵션의 순위를 더 높게 매김으로써 옵션을 손상시킬 수 없어야 합니다.

비부과, 즉 시민주권

가능한 모든 사회적 선호 질서는 특정 개인 선호 질서에 의해 달성될 수 있어야 합니다. 이는 사회복지 기능이 객관적이라는 것을 의미합니다. 제한 없는 대상 공간이 있습니다.

이후의 (1963년)^[7] 버전의 애로우 정리는 단조성과 비부과 기준을 다음과 같이 대체했습니다.

파레토 효율성 또는 만장일치: 모든 사람이 다른 선택지보다 특정 선택지를 선호한다면, 그로 인한 사회적 선호 질서도 마찬가지여야 합니다. 이는 다시 사회복지 기능이 선호 프로파일에 최소한으로 민감할 것이라는 요구입니다.

이 후기 버전은 더 일반적이고 더 약한 조건을 가지고 있습니다. 단성, 비부과 및 IIA의 공리는 함께 파레토 효율성을 의미하는 반면, 파레토 효율성(자체가 비부과를 의미함)과 IIA는 함께 단성을 의미하지 않습니다.

정리의 수식

A를 결과 집합, N개의 유권자 또는 결정 기준으로 삼습니다. 우리는 $A$ 의 모든 선형 순서의 집합을 $L(A$ )로 표시할 것입니다 $.$

(엄격한) 사회복지 기능(선호도 집계 규칙)은 함수입니다.

F:\mathrm {L(A)} ^{N}\to \mathrm {L(A)}

유권자들의 $선호도$ 를 A에 대한 단일 선호도 순서로 집계합니다.^[9]

유권자가 $선호$ 하는 N쌍 $(R, \dots,$ $R)$ ∈ L(A)를 선호 프로파일이라고 합니다. 가장 강력하고 간단한 형태로, 화살의 불가능성 정리는 가능한 대안들의 집합 $A$ 가 2개 이상의 원소들을 가질 때마다, 다음의 세 조건들이 양립할 수 없게 된다고 말합니다.

만장일치 또는 약한 파레토 효율성: 대안 $a$ 가 모든 $순서 1$ R, $\dots,$ $R$ 에_N 대해 $b$ 보다 엄격하게 높은 순위를 차지하면, $F(R 1 2,$ R, $\dots,$ $R N)$ 에 $의해$ $a$ 가 b보다 엄격하게 높은 순위를 차지합니다. (단일성은 비부과를 의미합니다.)
무독재: 항상 엄격한 선호를 하는 $사람$ 은 없습니다. 즉 $,$ 모든( $R$ , …, R) ∈ L(A)와 모든 a와 b에 $대하여,$ a가 b보다 R에 의해 엄격하게 순위가 매겨질 때, a가 B보다 F(R, R, …, R)에 의해 엄격하게 순위가 높게 매겨지는 $i개$ 의∈ {1, …, N}가 없습니다.
무관한 대안의 독립성: 모든 개체 $i$ 에 대하여, 대안 $a$ 와 $b$ 가 $S$ 와_i 같은 순서를 $갖는 i$ 두 선호 프로파일(R, $\dots,$ $R N)$ 과 ( $S 11 N, \dots,$ S $)$ 의 경우, 대안 $a$ 와 $b$ 가 $F(S 1 N 1, \dots,$ $S N$ )와 같은 순서를 갖는 경우 $.$

결정적 연합에 의한 증명

애로우의 증명은 결정적인 연합의 개념을 사용했습니다.^[7]

정의:

유권자의 일부는 연합입니다.
연립의 모든 사람이 $x\succ _{i}y$ ≻ $iy$ ${\displaystyle$ x $\$ succ_{i}y}의 순위를 매기고 x ≻y {\displaystyle x\succy}를 전체적으로 매길 때에만 연립이 순서 쌍 $(x,y)$ ( $(x,y)$ y $(x,y)$ ${\displaystyle (x,$ y $)}$ 에 대해 결정됩니다.
연합은 모든 순서 쌍에 대해 결정적인 경우에만 결정적입니다.

다음 증명은 (Sen, 2014)^[10] 및 (Rubinstein, 2012)에서 가져온 단순화입니다.^[11] 단순화된 증명은 다음과 같은 추가 개념을 사용합니다.

A coalition is weakly decisive over $(x,y)$ if and only if when every voter $i$ in the coalition ranks $x\succ _{i}y$ , and every voter $j$ outside the coalition ranks $y\succ _{j}x$ , $그런$ 다음 x ≻ y ${\displaystyle$ x\succ y}.

따라서 사회적 선택 시스템은 제한되지 않은 영역, 파레토 효율성 및 IIA를 충족한다고 가정합니다. 또한 최소 3개의 서로 다른 결과가 있다고 가정합니다.

필드 확장 보조정리 - 어떤 $x\neq y$ ≠ $y$ {\ $displaystyle$ x\n에 대하여 연립 $G$ ${\displaystyle$ G $}$ 가 $(x,y)$ ( $(x,y)$ $(x,y)$ $(x, y)$ 보다 약하게 결정되는 경우 $eq$ 그러면 결정적입니다.

증명

$z {\displaystyle$ z $}$ 를 $z$ $x,$ $y$ ${\displaystyle$ x $,y$ 와 구별되는 결과라고 가정합니다.

청구항: $G {\displaystyle$ G $}$ 이 $G$ $(x,z)$ $(x,z)$ $(x,z)$ 보다 결정적입니다 $(x,z)$

$G$ $G$ 의 모든 사용자가 $z$ ${\displaystyle$ z $}$ 위에 $x$ $x$ ${\displaystyle$ $x$ $}$ 표를 $G$ 던지도록 합니다 $z$ IIA에 $의해$ y{\ $displaystyle$ y}의 표를 변경하는 $x,z$ 은 $x,$ z{\ $displaystyle$ x, $z}$ 에 중요하지 $y$ 않습니다 $x,z$ So change the votes such that $x\succ _{i}y\succ _{i}z$ in $G$ and $y\succ _{i}x$ and $z$ outside of $G$ .

Pareto $y\succ z$ 으로 $y\succ z$ ≻ z {\ $displaystyle$ y $x\succ y$ succz}. (x, y) {\displaystyle (x, y)}에 대해 약한 결정성을 연합하여 x ≻ y {\displaystyle x\succy}. $따라서$ $x\succ z$ ≻ z ${\displaystyle x$ \ succ z}. ◻ $\square$ displaystyle $\$ square}

마찬가지로 $G$ ${\displaystyle$ G $}$ 는 $(z,y)$ ( $(z,y)$ y $(z,y)$ ${\displaystyle (z,$ y $)}$ 보다 결정적입니다 $G$ $(z,y)$

위의 두 가지 주장을 반복함으로써(결정성이 약한 결정성을 의미한다는 점에 유의하십시오), $G$ 는G {\ $displaystyle G}$ 가 $\{x,y,z\}$ { $\{x,y,z\}$ $y$ $z$ ${\displaystyle \{x,$ y, z $\}$ 의 모든 순서 쌍에 대해 결정적임을 $G$ 알 수 있습니다 $\{x,y,z\}$ 그런 다음 이를 반복하여, $X$ 는 G ${\displaystyle$ G $}$ 가 X $X$ 의 모든 순서 쌍에 대해 결정적임을 $G$ 알 수 있습니다 $X$

군수축 보조정리 — 연합이 결정적이고 $크기가$ ≥ 2 {\ $displaystyle$ geq 2}인 경우, 연합은 결정적인 적절한 부분집합을 갖습니다.

증명

$G$ $G$ 를 $크기$ ≥ 2 ${\displaystyle$ \geq 2}인 연립이라 하자. 연립을 비어 있지 않은 $G_{1},G_{2}$ G $,$ G 2 {\ $displaystyle G_{$ 1 $G_{1},G_{2}$ G_{2}}로 분할합니다.

$고유$ 한 $x,$ y $,$ $z$ $x,y,z$ 를 고칩니다 $x,y,z$ 다음 투표 패턴을 설계합니다(Condorcet 패러독스를 유발하는 순환 투표 패턴임에 유의하십시오).

${\begin{aligned}{\text{voters in }}G_{1}&:x\succ _{i}y\succ _{i}z\\{\text{voters in }}G_{2}&:z\succ _{i}x\succ _{i}y\\{\text{voters outside }}G&:y\succ _{i}z\succ _{i}x\end{aligned}}$

( $x,$ $y,$ z $x,y,z$ 이외의 항목은 관련이 $x,y,z$ 없습니다.)

$G$ ${\displaystyle$ $G$ $}$ 가 결정적이므로 $x\succ y$ ≻ y {\ $displaystyle$ x $x\succ y$ succy}가 있습니다. 따라서 적어도 $x\succ z$ 는 $x\succ z$ 입니다 $:$ x ≻ $z {\$ $\$ succy} $또는$ z ≻ $y$ {\displaystyle z\succy}.

If $x\succ z$ , then $G_{1}$ is weakly decisive over $(x,z)$ . If $z\succ y$ , then $G_{2}$ is weakly decisive over $(z,y)$ . Now apply the field expansion lemma.

파레토에 의해 전체 유권자 집단이 결정적이고, 따라서 집단 수축 보조제에 의해 규모 1의 결정적 연합이 있습니다. 바로 독재자입니다.

중추적인 유권자에 의한 증명

중추적 유권자의 개념을 사용한 증명은 1980년 살바도르 바르베라에서 비롯되었습니다.^[12] 여기서 제시된 증명은 경제이론에 발표된 두 가지 증명을 바탕으로 단순화한 것입니다.^[13]^[14]

우리는 제한되지 않은 영역, 만장일치, 관련 없는 대안의 독립성(IIA)을 존중하는 모든 사회 선택 시스템이 독재라는 것을 증명할 것입니다. 핵심 아이디어는 투표가 사회적 결과를 좌우하는 중추적인 유권자를 찾는 것입니다. 그런 다음 우리는 이 유권자가 (특정한 기술적 의미에서, 아래에 설명된) 부분 독재자임을 증명합니다. 마지막으로 우리는 모든 부분 독재자들이 같은 사람이라는 것을 보여줌으로써 결론을 내립니다. 따라서 이 유권자는 독재자입니다.

단순화를 위해 모든 순위를 동점이 없는 것처럼 제시했습니다. 가능한 관계를 고려한 완전한 증명은 여기에 주어진 증명과 본질적으로 다르지 않습니다. 다만 어떤 경우에는 "아래" 또는 "아래" 대신 "위"라고 말해야 한다는 점을 제외하고는 말입니다. 자세한 내용은 원본 기사에 나와 있습니다.

1부: A보다 B가 더 "매우 중요한" 유권자가 있습니다.

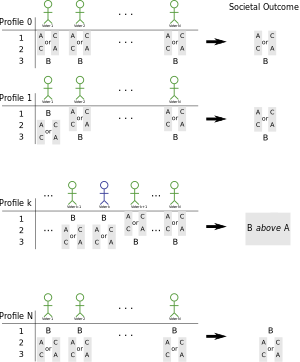
사회를 위한 세 가지 선택이 있다고 말하고, 그들을 A, B, C라고 부릅니다. 먼저 모든 사람이 옵션 B를 가장 덜 선호한다고 가정하자. 모든 사람은 B보다 A를 선호하고 모든 사람은 B보다 C를 선호합니다. 사회는 또한 만장일치로 B보다 A와 C 둘 다를 선호해야 합니다. 이 상황 프로파일을 0이라고 합니다.

반면에 모든 사람들이 다른 것보다 B를 더 선호한다면, 사회는 만장일치로 다른 것보다 B를 더 선호해야 할 것입니다. 이제 모든 유권자를 임의적이지만 고정된 순서로 정렬하고 각 ilet 프로필은 프로필 0과 동일하지만 B를 1부터 i까지의 유권자 투표의 맨 위로 이동시킵니다. 그래서 프로필 1은 유권자 1의 투표용지 맨 위에 B가 있지만, 다른 어떤 투표용지에도 B가 없습니다. 프로필 2는 유권자 1, 2위에 B가 있지만 다른 것들은 없습니다.

B는 결국 사회적 선호도 1위로 올라가기 때문에 사회적 순위에서 B가 먼저 A보다 위로 올라가는 프로필, 숫자 k가 있어야 합니다. 우리는 투표용지 변경으로 인해 A보다 B가 더 중요한 유권자라고 말합니다. A보다 B의 중추적인 유권자는 A보다 B보다 중추적인 유권자와 같은 선험적인 유권자가 아닙니다. 증명의 3부에서 우리는 이것들이 동일한 것으로 판명되었음을 보여줄 것입니다.

또한 IIA에 따르면 프로파일 0이 모든 유권자에 의해 A가 B보다 높은 순위를 차지하는 프로필인 경우에도 동일한 주장이 적용되며, A보다 B의 중추적인 유권자는 여전히 k입니다. 우리는 아래의 관찰을 사용할 것입니다.

2부: A보다 B의 중추적인 유권자는 C보다 B의 독재자입니다.

논쟁의 이 부분에서 우리는 A보다 B의 중추적인 유권자인 유권자 k를 단순화의 중추적인 유권자로 언급합니다. 우리는 중추적인 유권자가 C보다 B에 대한 사회의 결정을 결정한다는 것을 보여줄 것입니다. 즉, 우리는 사회의 나머지 사람들이 어떻게 투표하든, 중추적인 유권자가 C보다 B를 더 많이 투표한다면, 그것이 사회적 결과라는 것을 보여줍니다. C보다 B에 대한 독재자는 C보다 B에 대한 독재자와 같은 선험적인 독재자가 아니라는 것을 다시 한 번 주목하십시오. 증명의 3부에서 우리는 이것들도 동일한 것으로 판명되는 것을 볼 것입니다.

다음에서는 유권자 1~k - 1, 세그먼트 1, 유권자 k + 1~N, 세그먼트 2라고 부릅니다. 우선 투표용지가 다음과 같다고 가정해 보겠습니다.

한 세그먼트에 속한 모든 유권자는 C보다 B, A보다 C가 더 높습니다.
중추적인 유권자들은 A가 B보다 위에 있고 B가 C보다 위에 있습니다.
세그먼트의 모든 유권자는 A를 B보다 위에, B를 C보다 위에 두 순위를 매깁니다.

그런 다음 1부의 주장(그리고 그 부분의 마지막 관찰)에 의해 사회적 결과는 A를 B보다 높게 평가해야 합니다. 이 프로파일은 C의 위치를 변경하는 것을 제외하고는 파트 1의 프로파일 k - 1과 동일하기 때문입니다. 또한 사회적 결과는 만장일치로 B를 C보다 높게 평가해야 합니다. 따라서 저희는 이 경우의 결과를 완전히 알고 있습니다.

이제 중추적인 유권자가 B를 A보다 위로 이동시키지만 C를 같은 위치에 유지하고 A의 위치를 변경하지 않고 다른 유권자들 중 어떤 숫자(심지어 모두!)라도 B를 C보다 아래로 이동시키기 위해 투표용지를 변경한다고 가정해 보겠습니다. 그리고 C의 위치를 바꾸는 것 외에도 이것은 1부의 프로파일 k와 같기 때문에 사회적 결과는 A보다 B 위에 있습니다. 또한 IIA에 의해 사회적 결과는 이전 사례와 같이 A가 C보다 높은 순위를 차지해야 합니다. 특히, 비록 중추적 투표자가 유일하게 B를 C보다 높게 평가했을지라도, 사회적 결과는 B를 C보다 높게 평가합니다. IIA에 따르면, 이 결론은 A가 투표지에 위치하는 방식과 무관하게 유지되므로 중추적인 유권자는 C보다 B의 독재자입니다.

3부: 독재자가 있습니다.

논쟁의 이 부분에서 우리는 유권자들의 원래 순서를 다시 언급하고, 다른 중추적인 유권자들의 입장을 비교합니다(1부와 2부를 다른 후보 쌍에 적용함으로써 식별됨). 첫째, C보다 B의 중추적인 유권자는 C보다 더 일찍(또는 동일한 위치에) 등장해야 합니다. B와 C에 적용된 1부의 주장을 고려할 때, B를 유권자 투표의 1위로 연속적으로 이동시키기 때문에 사회가 C보다 높은 B 순위를 차지하는 회전점은 우리가 C보다 B의 독재자에게 도달하거나 도달하기 전에 와야 합니다. 마찬가지로, B와 C의 역할을 반대로, B보다 C의 중추적인 유권자는 C보다 B의 독재자보다 줄을 서거나 늦게 서야 합니다. 간단히 말해서, 만약 k가_X/Y Y에 대한 X의 중추적인 유권자의 위치를 나타낸다면(어떤 두 후보 X와 Y에 대해서도), 우리는 다음을 보여주었습니다.

k_B/C ≤ k_B/A ≤ k_C/B.

이제 위의 모든 논법을 B와 C로 바꾸어 반복하면, 우리는 또한

k_C/B_B/C≤ k

그래서 우리는

k = k = k

그리고 다른 쌍에 대한 동일한 주장은 모든 중추적인 유권자들(따라서 모든 독재자들)이 유권자 목록에서 동일한 위치에서 발생한다는 것을 보여줍니다. 이 유권자는 선거 기간 내내 독재자입니다.

해석

애로우의 정리는 수학적 결과이긴 하지만, 투표 방법이 공정하지 않다거나, 순위가 매겨진 투표 방법은 모두 흠이 있다거나, 흠이 없는 유일한 투표 방법은 독재라는 식의 진술로 비수학적으로 표현되는 경우가 많습니다.^[15] 이러한 문장은 일반적으로 사실로 간주되지 않는 Arrow의 결과를 단순화한 것입니다. 애로우의 정리가 말하는 것은 결정론적 우선 투표 메커니즘, 즉 선호 순서가 투표의 유일한 정보이고 가능한 투표 세트가 고유한 결과를 제공하는 메커니즘은 위에 주어진 모든 조건을 동시에 준수할 수 없다는 것입니다.

다양한 이론가들은 역설에서 벗어나는 방법으로 IIA 기준을 약화시킬 것을 제안했습니다. 순위 투표 방식을 지지하는 사람들은 IIA가 비합리적으로 강력한 기준이라고 주장합니다. 그것은 대부분의 유용한 선거 제도에서 위반된 것입니다. 이 입장을 지지하는 사람들은 표준 IIA 기준의 실패는 순환 선호의 가능성에 의해 사소한 것으로 암시된다고 지적합니다. 유권자가 다음과 같이 투표할 경우:

A > B > C 1표
B > C > A 1표
C > A > B 1표

그룹의 쌍대 선호도는 A가 B를 이기고, B가 C를 이기고, C가 A를 이기는 것입니다. 이러한 쌍대 비교는 가위바위보 선호도를 산출합니다. 이러한 상황에서 다수표를 얻은 후보가 선거에서 승리해야 한다는 기본적인 다수주의적 요건을 충족하는 모든 집계 규칙은 사회적 선호가 과도적(또는 비순환적)일 것을 요구한다면 IIA 기준에 실패하게 됩니다. 이를 확인하려면 이러한 규칙이 IIA를 만족한다고 가정합니다. 다수 선호가 존중되기 때문에 사회에서는 A를 B보다 선호합니다(A > B는 2표, B > A는 1표), B는 C, C는 A보다 C를 선호합니다. 따라서 주기가 생성되며, 이는 사회적 선호가 일시적이라는 가정과 모순됩니다.

따라서, 애로우의 정리가 실제로 보여주는 것은, 어떤 다수결 선거 제도든 사소하지 않은 게임이며, 그 게임 이론은 대부분의 투표 메커니즘의 결과를 예측하는 데 사용되어야 한다는 것입니다.^[16] 이것은 게임이 효율적인 균형을 가질 필요가 없기 때문에 실망스러운 결과로 보일 수 있습니다. 예를 들어, 투표는 애초에 아무도 원하지 않았지만 모두가 투표한 대안을 초래할 수 있습니다.

비고: 속성 및 IIA 속성 벡터로부터의 스칼라 순위

스칼라 선호 순위는 속성 벡터의 가중치(일반적으로 명시적이지 않음)에서 효과적으로 도출되기 때문에 현실적인 복잡성에 대한 인간의 의사 결정에서 IIA 속성이 충족되지 않을 수 있습니다(애로우 정리를 다루는 한 책은 독자가 다음에 대한 스칼라 척도를 만드는 관련 문제를 고려하도록 초대합니다). 육상 10종 경기(예: 원반던지기 경기에서 600점을 획득하고 1500m에서 600점을 획득하는 것으로 "상당할 수 있는" 점수를 얻는 방법)와 이 스칼라 순위는 다양한 속성의 가중치에 따라 민감하게 결정될 수 있습니다. 암묵적 가중치 자체가 명백하게 "관련성 있는" 선택에 의해 생성된 맥락 및 대비에 의해 영향을 받는 irre. 에드워드 맥닐(Edward MacNeal)은 그의 책 Math Semantics(1994)의 "Surveys" 장에서 "가장 살기 좋은 도시"의 순위와 관련하여 이 민감성 문제를 논의합니다.

선호 프로파일의 함수를 기반으로 한 대안

사회 선택 이론가들은 애로우 정리의 부정적인 결론에서 벗어나기 위해 다양한 가능성(ways out)을 조사했습니다. 이 섹션에는 다음을 다루는 접근 방식이 포함됩니다.

집계 규칙(각 선호 프로파일을 사회적 선호로 매핑하는 함수), 그리고
각 선호 프로파일을 대안으로 매핑하는 함수와 같은 다른 함수.

이 두 가지 접근법이 겹치는 경우가 많기 때문에 동시에 논의합니다. 이러한 접근 방식의 특징은 Arrow가 부과한 하나 이상의 조건(기준)을 제거 또는 약화시키거나 대체하여 다양한 가능성을 조사한다는 것입니다.

무한히 많은 개인들

몇몇 이론가들(예: Fishburn과^[17] Kirman and Sondermann^[18])은 개체가 무한히 많다는 가정을 버리면 애로우의 다른 조건들을 모두 만족시키는 집합 규칙을 찾을 수 있다고 지적합니다.

그러나 그러한 집계 규칙은 초필터, 고도로 비건설적인 수학적 객체를 기반으로 하기 때문에 실질적으로 관심이 제한적입니다. 특히 키르만과 손더만은 그러한 통치의 배후에 "보이지 않는 독재자"가 있다고 주장합니다.^[18] 미하라는^[19]^[20] 그러한 규칙이 알고리즘 계산 가능성을 위반한다는 것을 보여줍니다.^[21] 이러한 결과는 화살표 정리의 강건성을 확립하는 것으로 볼 수 있습니다.^[22]

반면, 울트라 필터(실제로 무한 모델로 구성하는 것은 선택 공리에 의존함)는 유한 모델에도 내재되어 있습니다(선택 공리가 필요 없음). 이들은 결정적 계층으로 해석될 수 있으며, 계층의 최상위 수준인 화살표의 독재자는 항상 유한한 모델로 존재하지만 무한한 계층에서 달성할 수 없는(= 누락) 유일한 차이점이 있습니다. 후자의 경우 '보이지 않는 독재자'는 무한한 결정적 위계질서 그 자체일 뿐입니다. 원하는 경우 한계점으로 보완할 수 있으며, 이를 통해 "보이는 독재자"가 됩니다. 독재자는 결정적 위계질서와 불가분의 관계에 있기 때문에 독재금지법은 결정적 위계질서를 자동적으로 금지하고 있는데, 이는 독재금지법보다 훨씬 자명하지 않습니다.^[23]^[24]^[25] "독재 금지 완화" 단락도 참조하십시오.

대안의 수 제한

선택할 수 있는 대안이 두 개뿐인 경우, 메이의 정리는 단순 다수결 원칙만이 특정 기준 세트를 만족한다는 것을 보여줍니다(예: 개인과 대안의 동등한 대우; 승리하는 대안에 대한 지지 증가가 패배하는 것으로 만들어서는 안 됩니다). 반면에 적어도 세 가지 대안이 있을 때, 애로우의 정리는 집단적 의사결정의 어려움을 지적합니다. 대안이 3개 미만인 경우와 최소 3개 이상인 경우의 차이가 이렇게 극명하게 나타나는 이유는 무엇일까요?

나카무라의 정리(단순한 게임의 핵심에 관한 것)는 좀 더 일반적인 답을 제공합니다. 그것은 대안의 수가 나카무라 수라고 불리는 특정 정수보다 적을 경우, 문제가 없는 규칙이 "최상의" 대안을 식별할 것이라는 것을 설정합니다. 대안의 수가 나카무라 수보다 크거나 같으면, 규칙이 항상 효과가 있는 것은 아닙니다. 일부 프로필의 경우 투표 역설(대안 B보다 사회적으로 선호되는 대안 A, 대안 B에서 C, C에서 A와 같은 순환)이 발생할 것입니다. 나카무라의 다수결 원칙의 수는 3이므로(4인의 경우는 제외) 나카무라의 정리로부터 다수결 원칙은 최대 2가지 대안을 합리적으로 다룰 수 있다고 결론지을 수 있습니다. (투표의 2/3을 요구하는 규칙과 같은) 일부 초다수 규칙은 나카무라 수가 3보다 클 수 있지만, 이러한 규칙은 애로우가 제공하는 다른 조건을 위반합니다.^[26]

쌍별투표

애로우의 역설을 "어라운드"하는 일반적인 방법은 대안 집합을 두 개의 대안으로 제한하는 것입니다. 따라서 두 가지 이상의 대안이 테스트에 투입되어야 할 때마다 쌍으로 짝을 지어 투표하는 메커니즘을 사용하는 것은 매우 유혹적인 것으로 보입니다. 이 메커니즘은 얼핏 보기에는 솔깃한 것처럼 보이지만 일반적으로 IIA는 말할 것도 없고 파레토 효율성을 충족시키는 것과는 거리가 있습니다. 쌍이 결정되는 특정 순서는 결과에 큰 영향을 미칩니다. 이것이 반드시 메커니즘의 나쁜 특징은 아닙니다. 많은 스포츠들이 토너먼트 메커니즘(본질적으로 페어링 메커니즘)을 사용하여 우승자를 선택합니다. 이는 약체팀이 우승할 수 있는 상당한 기회를 제공하여 대회 내내 관심과 긴장감을 더합니다. 이는 선택 사항이 짝을 이루는 순서를 통제하는 사람(의제 제작자)이 결과에 대한 통제력이 크다는 것을 의미합니다. 어쨌든 투표 전체 과정을 하나의 게임으로 볼 때, 애로우의 정리는 여전히 적용됩니다.

도메인 제한

또 다른 접근 방식은 보편성 조건을 완화하는 것인데, 이는 집계 규칙의 도메인을 제한하는 것을 의미합니다. 이 선을 따라 가장 잘 알려진 결과는 "단일 정점" 선호도를 가정한 것입니다.

던컨 블랙은 모든 개인이 "단일 정점" 선호도를 갖는 단 하나의 차원이 있다면, 애로우의 모든 조건은 다수결 원칙에 의해 충족된다는 것을 보여주었습니다. 대안 집합의 미리 결정된 선형 순서가 있다고 가정합니다. 개인의 선호도는 그 선을 따라 자신이 가장 좋아하는 특별한 장소가 있다면 이 순서와 관련하여 단일한 것이고, 그 대안에 대한 그의 반감은 그 지점에서 멀어질수록 더 커집니다(즉, 그 대안에 대한 그의 반감은 더 커집니다). 수평 축에 선형 순서에 따라 대안을 배치하면 그의 효용 함수의 그래프는 단일 피크를 갖습니다. 예를 들어, 유권자들이 음악 볼륨을 어디에 설정할지 투표했다면, 각 유권자는 자신의 이상적인 볼륨 선호도를 가지고 있으며 볼륨이 점차 너무 커지거나 너무 조용해질수록 점점 더 불만족스러워질 것이라고 가정하는 것이 합리적일 것입니다. 도메인이 선형 순서와 관련하여 모든 개인이 단일 정점 선호도를 갖는 프로파일로 제한되는 경우 다수 규칙을 포함하는 단순^[27] 집계 규칙은 비순환적(아래 정의된) 사회적 선호도를 가지므로 "최상의" 대안이 됩니다.^[28] 특히 홀수의 개인이 존재할 경우, 사회적 선호도는 추이적이 되며, 사회적으로 "최상의" 대안은 개인의 모든 피크의 중앙값과 같습니다(Black's median voteor theorem^[29]). 단일 정점 선호하에서 다수결 원칙은 어떤 면에서는 가장 자연스러운 투표 메커니즘입니다.

대안의 고차원 집합에 대한 "단일 피크" 선호도의 개념을 정의할 수 있습니다. 그러나 예외적인 경우에만 봉우리의 "중앙값"을 식별할 수 있습니다. 대신, 우리는 일반적으로 맥켈리의 혼돈 정리에 의해 제안된 파괴적인 상황을 가지고 있습니다:^[30] 임의의 x와 y에 대하여, x는 x에₁ 의해 과반수로, x는₁ x에₂ 의해, x는 y에 의해 최대로 이기는_k 일련의 대안들을 발견할 수 있습니다.

1977년 Ehud Kalai와 Eitan Muller는 영역 제한의 완전한 특성화를 통해 비독재적인 Arrow Social Welfare 기능을 인정했습니다.^[31]

편안한 감수성

사회적 선호의 전이성을 완화함으로써, 우리는 애로우의 다른 조건들을 만족시키는 집합 규칙들을 찾을 수 있습니다. 그러나 우리가 그러한 규칙에 중립성(대안의 동등한 대우)을 부과한다면, "베토"를 가진 개인이 존재합니다. 그래서 이 접근법이 제공하는 가능성도 매우 제한적입니다.

먼저, 사회적 선호도가 (일시적 대신) 준 일시적이라고 가정합니다. 이는 엄격한 $선호도$ ≻ {\ $displaystyle$ \succ}(" $better$ than")이 $x\succ z$ 일시적임을 의미합니다. 만약 $x$ ≻ y {\displaystyle x\succy}이고 y ≻ z {\displaystyle y\succz}이면, x ≻ z {\displaystyle x\succz}입니다. 그런 다음, Arrow의 조건을 만족시키는 비독재적 집합 규칙이 존재하지만, 그러한 규칙은 과두정적입니다.^[32] 이것은 L이 결정적이고(L의 모든 구성원이 y보다 x를 선호한다면 사회는 y보다 x를 선호한다), L의 각 구성원이 거부권을 갖는다는 것을 의미합니다(그녀가 y보다 x를 선호한다면 사회는 x보다 y를 선호할 수 없습니다).

둘째, 사회적 선호도가 비순환적(경향적 대신)이라고 가정합니다. 사이클( $x_{1}\succ x_{2},\;x_{2}\succ x_{3},\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}$ $x_{1}\succ x_{2},\;x_{2}\succ x_{3},\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}$ ≻ x $x_{1}\succ x_{2},\;x_{2}\succ x_{3},\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}$ $x_{1},\ldots ,x_{k}$ $x_{1}\succ x_{2},\;x_{2}\succ x_{3},\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}$ $2$ ≻ x $x_{1},\ldots ,x_{k}$ $x_{1}\succ x_{2},\;x_{2}\succ x_{3},\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}$ $,$ $x_{1}\succ x_{2},\;x_{2}\succ x_{3},\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}$ $x k$ - $1$ ≻ $x$ 1 {\ $display x_{1$ $},\ldots$ $,$ x_{k})을 형성하는 대안 x 1 $x_{1},\ldots ,x_{k}$ …, x k ≻ x 1 {\display $x_{$ 1}\succ x_{2},\; $x_{1},\ldots ,x_{k}$ {2}\succ x_{3}, $\;\ldots ,\;x_{k-1}\succ x_{k},\;x_{k}\succ x_{1}}$ ). 그렇다면, 적어도 개인만큼 많은 대안이 있다면, 애로우의 다른 조건을 만족시키는 집합 규칙은 집단적입니다.^[33] 이것은 모든 결정적인 연합의 교집합("collegium")에 속하는 사람들이 있다는 것을 의미합니다. 거부권을 가진 사람이 있다면, 그는 대학에 속합니다. 규칙이 중립적이라고 가정하면 거부권을 가진 사람이 있습니다.

마지막으로 브라운의 정리는 대안의 수가 개인의 수보다 적은 비순환적인 사회적 선호의 경우를 열어두었습니다. 나카무라 번호를 사용하면 그 경우에 대해 확실한 답을 줄 수 있습니다. 대안의 수 제한을 참조하십시오.

편안한 가정 IIA

애로우의 조건을 만족하는 집계 규칙은 IIA를 제외한 수많은 예가 있습니다. 보르다 규칙도 그 중 하나입니다. 그러나 이러한 규칙은 개인의 전략적 조작에 취약합니다.^[34]

위의 정리의 해석도 참조하십시오.

Pareto 기준 완화

Wilson(1972)^[35]은 Arrow의 조건이 Pareto 이외의 조건들도 만족된다면, 집합 규칙이 비부과적이고 비무효적이라면, 독재자 또는 역독재자가 존재한다는 것을 보여줍니다. 여기서 역독재자는 개인 i이므로 제가 y보다 x를 선호할 때마다 사회는 x보다 y를 선호합니다.

Amartya Sen은 과도성의 완화와 파레토 원리의 제거를 모두 제공했습니다.^[36] 그는 "파라치 자유주의자의 불가능성"으로 알려진 또 다른 흥미로운 불가능 결과를 증명했습니다 (자세한 내용은 자유주의 역설 참조). 센은 이어 이것이 투표 메커니즘과 관련해 파레토 최적성을 요구하는 것의 무익함을 보여준다고 주장했습니다.

독재 금지를 완화하는 것

Andranik Tangian(2010)은 독재자의 "대표성"에 대한 측정치를 소개했는데, 예를 들어 "인기 지수"는 독재자가 쌍별 선호도를 공유(즉, 대표)하는 사회 집단의 평균 크기로 정의되며, 모든 대안 쌍과 모든 선호 프로파일에 대해 평균을 나타냈습니다. 평균적으로 대다수를 대표하는 "선한" 애로우의 독재자들이 항상 존재한다는 것을 보여주었습니다.^[37] 그들은 민주적으로 선출된 대통령들처럼 오히려 사회의 대표자들이기 때문에, 그들을 금지할 자명한 이유가 없습니다. 독재자의 개념을 "나쁜" 개념, 즉 평균적으로 소수를 대표하는 사람들로만 제한하면, 애로우의 공리는 일관된 것으로 증명되었습니다.^[24]^[25]

사회적 선호 대신 사회적 선택

사회적 의사 결정에서 모든 대안의 순위를 매기는 것은 일반적으로 목표가 아닙니다. 종종 어떤 대안을 찾는 것으로 충분합니다. 대안 선택에 초점을 맞춘 접근법은 사회적 선택 함수(각 선호 프로파일을 대안으로 매핑하는 함수) 또는 사회적 선택 규칙(각 선호 프로파일을 대안의 하위 집합으로 매핑하는 함수)을 조사합니다.

사회적 선택 함수의 경우, 범위가 최소 3개의 대안을 포함하는 사회적 선택 함수가 전략적으로 증명되면 독재적이라는 Gibbard-Satterthwaite 정리가 잘 알려져 있습니다.

사회적 선택 규칙의 경우, 우리는 그들 뒤에 사회적 선호가 있다고 가정해야 합니다. 즉, 우리는 어떤 규칙을 어떤 사회적 선호의 최대 요소("최상의" 대안")를 선택하는 것으로 간주해야 합니다. 사회적 선호도의 최대 요소 집합을 핵심이라고 합니다. 핵심에서 대안의 존재 조건은 두 가지 접근 방식으로 조사되었습니다. 첫 번째 접근 방식은 기본 설정이 적어도 비순환적이라고 가정합니다(기본 설정이 임의의 유한 부분 집합에 최대 요소를 갖는 데 필요하고 충분합니다). 이 때문에 과도성을 완화하는 것과 밀접한 관련이 있습니다. 두 번째 접근 방식은 비순환적 선호도의 가정을 떨어트립니다. 쿠마베와 미하라는^[38] 이 방식을 채택합니다. 그들은 개인의 선호도가 최대 요소를 가지고 있다고 보다 직접적인 가정을 하고, 사회적 선호도가 최대 요소를 가질 수 있는 조건을 조사합니다. 이 두 가지 접근 방식에 대한 자세한 내용은 나카무라 번호를 참조하십시오.

기타대안

애로우는 원래 사회복지를 표현하기 위한 의미 있는 도구로서 기본 효용을 거부했고, 그래서 ^[39]그의 정리를 선호 순위에 집중했지만, 나중에 3개 또는 4개의 등급으로 구성된 기본 점수 체계가 "아마도 최고일 것"이라고 말했습니다.^[2]

Arrow의 프레임워크는 개인 및 사회적 선호도가 대안 집합에 대한 "순서"(즉, 완전성과 과도성을 충족)라고 가정합니다. 이는 선호도가 효용 함수로 표현될 경우 값이 클수록 더 나은 대안을 나타내는 만큼 의미가 있다는 의미에서 그 값이 순서형 효용임을 의미합니다. 예를 들어, 대안 a, b, c, d에 대해 각각 4, 3, 2, 1의 순서 유틸리티를 갖는 것은 1000, 100.01, 100, 0을 갖는 것과 같고, 다시 99, 98, 1, .997을 갖는 것과 같습니다. 모두 a가 b에서 ct보다 선호되는 순서를 나타냅니다. 애로우 정리에서 중요한 부분은 유용성에 대한 대인 비교를 배제하는 순서적 선호의 가정입니다.

다양한 이유로 인해 효용이 단순히 대안의 순위를 부여하는 것을 넘어 의미를 갖는 기본효용에 기반한 접근은 현대 경제학에서 일반적이지 않습니다. 그러나 일단 그러한 접근법을 채택하면, 선호도의 강도를 고려할 수도 있고, (i) 효용의 손익 또는 (ii) 효용 수준을 서로 다른 개인 간에 비교할 수도 있습니다. 특히 Harsanyi(1955)^[40]는 제레미 벤담(Jeremy Bentham)에서 비롯된 공리주의(개별 효용의 합으로 대안을 평가하는)의 정당화를 제시합니다. Hammond(1976)^[41]는 John Rawls로부터 유래된 맥심 원리(최악의 개인의 효용 측면에서 대안을 평가하는 것)를 정당화합니다.

모든 투표 방법이 입력으로 모든 후보자의 순서만 사용하는 것은 아닙니다.^[42] 흔히 "등급" 또는 "카드"(등급", "순서" 또는 "우선" 선거 제도와 달리)라고 하지 않는 방법은 기본 유틸리티만이 전달할 수 있는 정보를 사용하는 것으로 볼 수 있습니다. 그렇다면, 그들 중 일부가 재구성된 애로우의 조건을 모두 만족한다면 놀라운 일은 아닙니다.^[43] 범위 투표가 그런 방법입니다.^[5]^[44] 그러한 주장이 정확한지 여부는 각 조건을 어떻게 재구성하느냐에 달려 있습니다.^[45] Arrow의 기준에 대한 특정 일반화를 통과하는 다른 등급의 선거 제도로는 승인 투표와 다수결 심판이 있습니다. 화살표의 정리는 이와 같은 단일승자 방법에는 적용되지 않지만 기버드의 정리는 여전히 적용됩니다. 결함이 없는 선거제도는 완전히 전략이 없기 때문에 "선거제도가 완벽하지 않다"는 비공식적인 격언은 여전히 수학적 기초를 가지고 있습니다.^[46]

마지막으로, 어떤 종류의 규칙을 조사하는 접근법은 아니지만, James M의 비판이 있습니다. 뷰캐넌, 찰스 플로트, 그리고 다른 사람들. 개인의 선호와 유사한 사회적 선호가 있을 수 있다고 생각하는 것은 어리석은 일이라고 주장합니다.^[47] 애로우(^[48]1963, 8장)는 적어도 부분적으로 오해에서 오는 초기에 볼 수 있는 이런 종류의 비판에 답합니다.

참고 항목

참고문헌

^ Arrow, Kenneth J. (1950). "A Difficulty in the Concept of Social Welfare" (PDF). Journal of Political Economy. 58 (4): 328–346. doi:10.1086/256963. JSTOR 1828886. S2CID 13923619. Archived from the original (PDF) on 2011-07-20.
^ ^a ^b "Interview with Dr. Kenneth Arrow". The Center for Election Science. October 6, 2012. CES: you mention that your theorem applies to preferential systems or ranking systems. ... But ... Approval Voting, falls within a class called cardinal systems. ... Dr. Arrow: And as I said, that in effect implies more information. ... I'm a little inclined to think that score systems where you categorize in maybe three or four classes ... is probably the best.
^ Sen, Amartya (1999). "The Possibility of Social Choice". American Economic Review. 89 (3): 349–378. doi:10.1257/aer.89.3.349. JSTOR 117024. Does Arrow's impossibility ... go away with the use of interpersonal comparisons in social welfare judgments? ... yes. The additional informational availability allows sufficient discrimination to escape impossibilities of this type. ... even weaker forms of comparability would still permit making consistent social welfare judgments, satisfying all of Arrow's requirements
^ Suzumura, Kōtarō (2002). "Introduction". In Arrow, Kenneth J.; Sen, Amartya K.; Suzumura, Kōtarō (eds.). Handbook of social choice and welfare. Vol. 1. Amsterdam, Netherlands: Elsevier. p. 10. ISBN 978-0-444-82914-6.
^ ^a ^b McKenna, Phil (12 April 2008). "Vote of no confidence". New Scientist. 198 (2651): 30–33. doi:10.1016/S0262-4079(08)60914-8.
^ Aaron, Hamlin (25 May 2015). "CES Podcast with Dr Arrow". Center for Election Science. CES. Retrieved 9 March 2023.
^ ^a ^b ^c Arrow, Kenneth Joseph Arrow (1963). Social Choice and Individual Values (PDF). Yale University Press. ISBN 978-0300013641. Archived (PDF) from the original on 2022-10-09.
^ Mas-Colell, Andreu; Whinston, Michael Dennis; Green, Jerry R. (1995). Microeconomic Theory. Oxford University Press. p. 794. ISBN 978-0-19-507340-9.
^ 정의에 따라 여기에 정의된 사회 복지 함수는 제한되지 않은 영역 조건을 만족합니다. 서로 다른 결과 사이에서 결코 무관심하지 않은 사회적 선호도로 범위를 제한하는 것은 아마도 매우 제한적인 가정일 것이지만, 여기서의 목표는 정리에 대한 간단한 진술을 제공하는 것입니다. 제한을 완화하더라도 불가능한 결과는 지속될 것입니다.
^ Sen, Amartya (2014-07-22). "Arrow and the Impossibility Theorem". The Arrow Impossibility Theorem. Columbia University Press. pp. 29–42. doi:10.7312/mask15328-003. ISBN 978-0-231-52686-9.
^ Rubinstein, Ariel (2012). Lecture Notes in Microeconomic Theory: The Economic Agent (2nd ed.). Princeton University Press. Problem 9.5. ISBN 978-1-4008-4246-9. OL 29649010M.
^ Barberá, Salvador (January 1980). "Pivotal voters: A new proof of arrow's theorem". Economics Letters. 6 (1): 13–16. doi:10.1016/0165-1765(80)90050-6. ISSN 0165-1765.
^ Geanakoplos, John (2005). "Three Brief Proofs of Arrow's Impossibility Theorem" (PDF). Economic Theory. 26 (1): 211–215. CiteSeerX 10.1.1.193.6817. doi:10.1007/s00199-004-0556-7. JSTOR 25055941. S2CID 17101545. Archived (PDF) from the original on 2022-10-09.
^ Yu, Ning Neil (2012). "A one-shot proof of Arrow's theorem". Economic Theory. 50 (2): 523–525. doi:10.1007/s00199-012-0693-3. JSTOR 41486021. S2CID 121998270.
^ Cockrell, Jeff (2016-03-08). "What economists think about voting". Capital Ideas. Chicago Booth. Archived from the original on 2016-03-26. Retrieved 2016-09-05. Is there such a thing as a perfect voting system? The respondents were unanimous in their insistence that there is not.
^ 그렇다고 해서 게임이론에서 균형 개념을 사용하면 다양한 규범적 기준이 충족되는 것은 아닙니다. 실제로 프로파일에서 평형 결과로의 매핑은 사회적 선택 규칙을 정의하며, 그 성능은 사회적 선택 이론에 의해 조사될 수 있습니다. Austen-Smith & Banks (1999) 섹션 7.2를 참조하십시오.
^ Fishburn, Peter Clingerman (1970). "Arrow's impossibility theorem: concise proof and infinite voters". Journal of Economic Theory. 2 (1): 103–106. doi:10.1016/0022-0531(70)90015-3.
^ ^a ^b Kirman, A.; Sondermann, D. (1972). "Arrow's theorem, many agents, and invisible dictators". Journal of Economic Theory. 5 (2): 267–277. doi:10.1016/0022-0531(72)90106-8.
^ Mihara, H. R. (1997). "Arrow's Theorem and Turing computability" (PDF). Economic Theory. 10 (2): 257–276. CiteSeerX 10.1.1.200.520. doi:10.1007/s001990050157. JSTOR 25055038. S2CID 15398169. Archived from the original (PDF) on 2011-08-12. Reprinted in Velupillai, K. V.; Zambelli, S.; Kinsella, S., eds. (2011). Computable Economics. International Library of Critical Writings in Economics. Edward Elgar. ISBN 978-1-84376-239-3.
^ Mihara, H. R. (1999). "Arrow's theorem, countably many agents, and more visible invisible dictators". Journal of Mathematical Economics. 32 (3): 267–277. CiteSeerX 10.1.1.199.1970. doi:10.1016/S0304-4068(98)00061-5.
^ 계산 가능한 집계 규칙에 대한 미하라의 정의는 간단한 게임의 계산 가능성을 기반으로 합니다(라이스의 정리 참조).
^ 무한한 사회를 위한 사회적 선택에 대한 간결한 논의는 의 6장을 참조하십시오.
^ Tanguiane (Tangian), Andranick (1994). "Arrow's paradox and mathematical theory of democracy". Social Choice and Welfare. 11 (1): 1–82. doi:10.1007/BF00182898. S2CID 154076212.
^ ^a ^b Tangian, Andranik (2014). Mathematical theory of democracy. Berlin-Heidelberg: Springer.
^ ^a ^b Tangian, Andranik (2020). Analytical theory of democracy. Vols. 1 and 2. Cham, Switzerland: Springer.
^ Austen-Smith & Banks(1999, 3장)는 대안의 수를 제한하려는 접근 방식에 대해 자세히 설명합니다.
^ Austen-Smith, David; Banks, Jeffrey S. (1999). Positive political theory I: Collective preference. Ann Arbor: University of Michigan Press. ISBN 978-0-472-08721-1. Retrieved 2016-02-16.
^ 실제로 많은 다양한 사회복지 기능이 이러한 영역의 제한 하에서 애로우의 조건을 충족시킬 수 있습니다. 그러나 그러한 제한 하에서 애로우의 기준에 부합하는 사회복지적 기능이 존재한다면 다수결 원칙은 애로우의 기준에 부합할 것임이 증명되었습니다. 참조
^ Black, Duncan (1968). The theory of committees and elections. Cambridge, Eng.: University Press. ISBN 978-0-89838-189-4.
^ McKelvey, Richard D. (1976). "Intransitivities in multidimensional voting models and some implications for agenda control". Journal of Economic Theory. 12 (3): 472–482. doi:10.1016/0022-0531(76)90040-5.
^ Kalai, Ehud; Muller, Eitan (1977). "Characterization of Domains Admitting Nondictatorial Social Welfare Functions and Nonmanipulable Voting Procedures". Journal of Economic Theory. 16 (2): 457–469.
^ Gibbard, Allan F. (2014) [1969]. "Intransitive social indifference and the Arrow dilemma". Review of Economic Design. 18 (1): 3–10. doi:10.1007/s10058-014-0158-1. S2CID 154682454.
^ Brown, D. J. (1975). "Aggregation of Preferences". Quarterly Journal of Economics. 89 (3): 456–469. doi:10.2307/1885263. JSTOR 1885263.
^ Blair, Douglas; Muller, Eitan (1983). "Essential aggregation procedures on restricted domains of preferences". Journal of Economic Theory. 30 (1): 34–53. doi:10.1016/0022-0531(83)90092-3.
^ Wilson, Robert (1972). "Social Choice Theory without the Pareto principle". Journal of Economic Theory. 5 (3): 478–486. doi:10.1016/0022-0531(72)90051-8.
^ Sen, Amartya (September 1979a). "Personal Utilities and Public Judgements: Or What's Wrong With Welfare Economics?". The Economic Journal. 89 (355): 537–558. doi:10.2307/2231867. JSTOR 2231867.
^ Tangian, Andranik (2010). "Application of the mathematical theory of democracy to Arrow's Impossibility Theorem (How dictatorial are Arrow's dictators?)". Social Choice and Welfare. 35 (1): 135–167. doi:10.1007/s00355-009-0433-1. S2CID 206958453.
^ Kumabe, M.; Mihara, H. R. (2011). "Preference aggregation theory without acyclicity: the core without majority dissatisfaction" (PDF). Games and Economic Behavior. 72: 187–201. arXiv:1107.0431. Bibcode:2011arXiv1107.0431K. doi:10.1016/j.geb.2010.06.008. S2CID 6685306. Archived (PDF) from the original on 2022-10-09.
^ "현대 경제 이론은 효용의 순서적 개념을 주장해 왔습니다. 즉, 순서만 관찰할 수 있으므로 이러한 순서와 무관한 효용의 측정은 의미가 없습니다. 소비자의 요구 이론 분야에서 순서주의적 입장은 문제를 일으키지 않는 것으로 밝혀졌습니다. 기본 효용은 순서 이상의 설명력이 없었습니다. 라이프니츠의 불식의 정체성에 대한 원리는 당시 우리의 사고 패턴으로부터 기본적인 효용을 제거할 것을 요구했습니다." 화살표 (1967), 33쪽에 인용된 바와 같이,
^ Harsanyi, John C. (1955). "Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility". Journal of Political Economy. 63 (4): 309–321. doi:10.1086/257678. JSTOR 1827128. S2CID 222434288.
^ Hammond, Peter J. (1976). "Equity, Arrow's Conditions, and Rawls' Difference Principle". Econometrica. 44 (4): 793–804. doi:10.2307/1913445. JSTOR 1913445.
^ 그런 방법들이 보편성 기준에 크게 실패할 수도 있다고 주장하기도 합니다. 그러나 선호 순서가 투표로 고유하게 변환될 수 없는 경우 이러한 방법은 애로우의 집계 규칙(또는 도메인이 선호 프로파일로 구성된 함수) 정의에 실패한다고 간주하는 것이 더 적절합니다.
^ 그러나 화살표 정리의 수정된 버전은 여전히 이러한 방법에 적용될 수 있습니다(예:
^ Smith, Warren D.; et al. "How can range voting accomplish the impossible?". Retrieved 2016-02-16.
^ 기본 유틸리티를 사용하지 않는 투표 방법은 Arrow의 IIA(선호 프로파일이 투표용지 목록 또는 유틸리티 목록으로 대체됨)를 만족하지 않습니다. 이러한 이유로, IIA의 약화된 개념이 제안됩니다(예: Sen (1979, p. 129). 이 개념은 두 대안의 사회적 순위가 두 대안에서 개인이 달성한 효용 수준에만 의존해야 함을 요구합니다. (보다 공식적으로, 사회 복지 함수 $F$ ${\displaystyle$ F $}$ 는 각 목록 $u=(u_{1},\ldots ,u_{n})$ = $u=(u_{1},\ldots ,u_{n})$ $…,$ un) {\display u = (u_{1},\ldots $,$ $유틸리티$ 기능 $u=(u_{1},\ldots ,u_{n})$ 중 $u_$ {n $}}$ 을(를) 사회적 기본 설정으로 사용합니다. $F$ $F$ 은 $F$ (는) 모든 목록 $u$ 에 $,$ u' {\ $displaystyle u,$ u'}이고 $u,u'$ 모든 대안 $x,y$ 에 대해 $,$ $y$ ${\displaystyle$ x $,y$ if $u_{i}(x)=u'_{i}(x)$ and $u_{i}(y)=u'_{i}(y)$ for all $i$ , then $xF(u)y{\text{ iff }}xF(u')y$ .) 많은 기본 투표 방법(범위 투표 포함)이 IIA의 약화된 버전을 만족시킵니다.
^ Poundstone, William (2009-02-17). Gaming the Vote: Why Elections Are not Fair (and What We Can Do About It). Macmillan. ISBN 9780809048922.
^ Feldman, Allan M.; Serrano, Roberto (2006). Welfare Economics and Social Choice Theory. Springer Science & Business Media. ISBN 9780387293684. It is quite silly in the first place to think that there might be social preferences that are analogous to individual preferences. It is nonsense to talk about social preferences since society itself is nothing more than a collection of individuals, each with his own interests. ... this first reaction to Arrow's Theorem is logically attractive, but it can lead to varieties of nihilism that are unappealing to some people, including us.
^ Arrow, Kenneth Joseph (1963). "Chapter VIII Notes on the Theory of Social Choice, Section III. What Is the Problem of Social Choice?". Social Choice and Individual Values. Yale University Press. pp. 103–109. ISBN 978-0300013641. these criticisms are based on misunderstandings of my position

외부 링크

[1] Arrow, Kenneth J. (1950). "A Difficulty in the Concept of Social Welfare" (PDF). Journal of Political Economy. 58 (4): 328–346. doi:10.1086/256963. JSTOR 1828886. S2CID 13923619. Archived from the original (PDF) on 2011-07-20.

[:0-2] "Interview with Dr. Kenneth Arrow". The Center for Election Science. October 6, 2012. CES: you mention that your theorem applies to preferential systems or ranking systems. ... But ... Approval Voting, falls within a class called cardinal systems. ... Dr. Arrow: And as I said, that in effect implies more information. ... I'm a little inclined to think that score systems where you categorize in maybe three or four classes ... is probably the best.

[3] Sen, Amartya (1999). "The Possibility of Social Choice". American Economic Review. 89 (3): 349–378. doi:10.1257/aer.89.3.349. JSTOR 117024. Does Arrow's impossibility ... go away with the use of interpersonal comparisons in social welfare judgments? ... yes. The additional informational availability allows sufficient discrimination to escape impossibilities of this type. ... even weaker forms of comparability would still permit making consistent social welfare judgments, satisfying all of Arrow's requirements

[4] Suzumura, Kōtarō (2002). "Introduction". In Arrow, Kenneth J.; Sen, Amartya K.; Suzumura, Kōtarō (eds.). Handbook of social choice and welfare. Vol. 1. Amsterdam, Netherlands: Elsevier. p. 10. ISBN 978-0-444-82914-6.

[ns12-5] McKenna, Phil (12 April 2008). "Vote of no confidence". New Scientist. 198 (2651): 30–33. doi:10.1016/S0262-4079(08)60914-8.

[6] Aaron, Hamlin (25 May 2015). "CES Podcast with Dr Arrow". Center for Election Science. CES. Retrieved 9 March 2023.

[Arrow_1963-7] Arrow, Kenneth Joseph Arrow (1963). Social Choice and Individual Values (PDF). Yale University Press. ISBN 978-0300013641. Archived (PDF) from the original on 2022-10-09.

[8] Mas-Colell, Andreu; Whinston, Michael Dennis; Green, Jerry R. (1995). Microeconomic Theory. Oxford University Press. p. 794. ISBN 978-0-19-507340-9.

[9] 정의에 따라 여기에 정의된 사회 복지 함수는 제한되지 않은 영역 조건을 만족합니다. 서로 다른 결과 사이에서 결코 무관심하지 않은 사회적 선호도로 범위를 제한하는 것은 아마도 매우 제한적인 가정일 것이지만, 여기서의 목표는 정리에 대한 간단한 진술을 제공하는 것입니다. 제한을 완화하더라도 불가능한 결과는 지속될 것입니다.

[10] Sen, Amartya (2014-07-22). "Arrow and the Impossibility Theorem". The Arrow Impossibility Theorem. Columbia University Press. pp. 29–42. doi:10.7312/mask15328-003. ISBN 978-0-231-52686-9.

[11] Rubinstein, Ariel (2012). Lecture Notes in Microeconomic Theory: The Economic Agent (2nd ed.). Princeton University Press. Problem 9.5. ISBN 978-1-4008-4246-9. OL 29649010M.

[12] Barberá, Salvador (January 1980). "Pivotal voters: A new proof of arrow's theorem". Economics Letters. 6 (1): 13–16. doi:10.1016/0165-1765(80)90050-6. ISSN 0165-1765.

[13] Geanakoplos, John (2005). "Three Brief Proofs of Arrow's Impossibility Theorem" (PDF). Economic Theory. 26 (1): 211–215. CiteSeerX 10.1.1.193.6817. doi:10.1007/s00199-004-0556-7. JSTOR 25055941. S2CID 17101545. Archived (PDF) from the original on 2022-10-09.

[14] Yu, Ning Neil (2012). "A one-shot proof of Arrow's theorem". Economic Theory. 50 (2): 523–525. doi:10.1007/s00199-012-0693-3. JSTOR 41486021. S2CID 121998270.

[15] Cockrell, Jeff (2016-03-08). "What economists think about voting". Capital Ideas. Chicago Booth. Archived from the original on 2016-03-26. Retrieved 2016-09-05. Is there such a thing as a perfect voting system? The respondents were unanimous in their insistence that there is not.

[16] 그렇다고 해서 게임이론에서 균형 개념을 사용하면 다양한 규범적 기준이 충족되는 것은 아닙니다. 실제로 프로파일에서 평형 결과로의 매핑은 사회적 선택 규칙을 정의하며, 그 성능은 사회적 선택 이론에 의해 조사될 수 있습니다. Austen-Smith & Banks (1999) 섹션 7.2를 참조하십시오.

[Fishburn1970-17] Fishburn, Peter Clingerman (1970). "Arrow's impossibility theorem: concise proof and infinite voters". Journal of Economic Theory. 2 (1): 103–106. doi:10.1016/0022-0531(70)90015-3.

[kirman-s72-18] Kirman, A.; Sondermann, D. (1972). "Arrow's theorem, many agents, and invisible dictators". Journal of Economic Theory. 5 (2): 267–277. doi:10.1016/0022-0531(72)90106-8.

[mihara97-19] Mihara, H. R. (1997). "Arrow's Theorem and Turing computability" (PDF). Economic Theory. 10 (2): 257–276. CiteSeerX 10.1.1.200.520. doi:10.1007/s001990050157. JSTOR 25055038. S2CID 15398169. Archived from the original (PDF) on 2011-08-12. Reprinted in Velupillai, K. V.; Zambelli, S.; Kinsella, S., eds. (2011). Computable Economics. International Library of Critical Writings in Economics. Edward Elgar. ISBN 978-1-84376-239-3.

[20] Mihara, H. R. (1999). "Arrow's theorem, countably many agents, and more visible invisible dictators". Journal of Mathematical Economics. 32 (3): 267–277. CiteSeerX 10.1.1.199.1970. doi:10.1016/S0304-4068(98)00061-5.

[21] 계산 가능한 집계 규칙에 대한 미하라의 정의는 간단한 게임의 계산 가능성을 기반으로 합니다(라이스의 정리 참조).

[22] 무한한 사회를 위한 사회적 선택에 대한 간결한 논의는 의 6장을 참조하십시오.

[Tanguiane1994-23] Tanguiane (Tangian), Andranick (1994). "Arrow's paradox and mathematical theory of democracy". Social Choice and Welfare. 11 (1): 1–82. doi:10.1007/BF00182898. S2CID 154076212.

[Tangian2014-24] Tangian, Andranik (2014). Mathematical theory of democracy. Berlin-Heidelberg: Springer.

[Tangian2020-25] Tangian, Andranik (2020). Analytical theory of democracy. Vols. 1 and 2. Cham, Switzerland: Springer.

[26] Austen-Smith & Banks(1999, 3장)는 대안의 수를 제한하려는 접근 방식에 대해 자세히 설명합니다.

[austensmith-b99-27] Austen-Smith, David; Banks, Jeffrey S. (1999). Positive political theory I: Collective preference. Ann Arbor: University of Michigan Press. ISBN 978-0-472-08721-1. Retrieved 2016-02-16.

[28] 실제로 많은 다양한 사회복지 기능이 이러한 영역의 제한 하에서 애로우의 조건을 충족시킬 수 있습니다. 그러나 그러한 제한 하에서 애로우의 기준에 부합하는 사회복지적 기능이 존재한다면 다수결 원칙은 애로우의 기준에 부합할 것임이 증명되었습니다. 참조

[29] Black, Duncan (1968). The theory of committees and elections. Cambridge, Eng.: University Press. ISBN 978-0-89838-189-4.

[30] McKelvey, Richard D. (1976). "Intransitivities in multidimensional voting models and some implications for agenda control". Journal of Economic Theory. 12 (3): 472–482. doi:10.1016/0022-0531(76)90040-5.

[31] Kalai, Ehud; Muller, Eitan (1977). "Characterization of Domains Admitting Nondictatorial Social Welfare Functions and Nonmanipulable Voting Procedures". Journal of Economic Theory. 16 (2): 457–469.

[32] Gibbard, Allan F. (2014) [1969]. "Intransitive social indifference and the Arrow dilemma". Review of Economic Design. 18 (1): 3–10. doi:10.1007/s10058-014-0158-1. S2CID 154682454.

[33] Brown, D. J. (1975). "Aggregation of Preferences". Quarterly Journal of Economics. 89 (3): 456–469. doi:10.2307/1885263. JSTOR 1885263.

[34] Blair, Douglas; Muller, Eitan (1983). "Essential aggregation procedures on restricted domains of preferences". Journal of Economic Theory. 30 (1): 34–53. doi:10.1016/0022-0531(83)90092-3.

[35] Wilson, Robert (1972). "Social Choice Theory without the Pareto principle". Journal of Economic Theory. 5 (3): 478–486. doi:10.1016/0022-0531(72)90051-8.

[36] Sen, Amartya (September 1979a). "Personal Utilities and Public Judgements: Or What's Wrong With Welfare Economics?". The Economic Journal. 89 (355): 537–558. doi:10.2307/2231867. JSTOR 2231867.

[Tangian2010-37] Tangian, Andranik (2010). "Application of the mathematical theory of democracy to Arrow's Impossibility Theorem (How dictatorial are Arrow's dictators?)". Social Choice and Welfare. 35 (1): 135–167. doi:10.1007/s00355-009-0433-1. S2CID 206958453.

[kumabe-m10geb-38] Kumabe, M.; Mihara, H. R. (2011). "Preference aggregation theory without acyclicity: the core without majority dissatisfaction" (PDF). Games and Economic Behavior. 72: 187–201. arXiv:1107.0431. Bibcode:2011arXiv1107.0431K. doi:10.1016/j.geb.2010.06.008. S2CID 6685306. Archived (PDF) from the original on 2022-10-09.

[39] "현대 경제 이론은 효용의 순서적 개념을 주장해 왔습니다. 즉, 순서만 관찰할 수 있으므로 이러한 순서와 무관한 효용의 측정은 의미가 없습니다. 소비자의 요구 이론 분야에서 순서주의적 입장은 문제를 일으키지 않는 것으로 밝혀졌습니다. 기본 효용은 순서 이상의 설명력이 없었습니다. 라이프니츠의 불식의 정체성에 대한 원리는 당시 우리의 사고 패턴으로부터 기본적인 효용을 제거할 것을 요구했습니다." 화살표 (1967), 33쪽에 인용된 바와 같이,

[40] Harsanyi, John C. (1955). "Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility". Journal of Political Economy. 63 (4): 309–321. doi:10.1086/257678. JSTOR 1827128. S2CID 222434288.

[41] Hammond, Peter J. (1976). "Equity, Arrow's Conditions, and Rawls' Difference Principle". Econometrica. 44 (4): 793–804. doi:10.2307/1913445. JSTOR 1913445.

[42] 그런 방법들이 보편성 기준에 크게 실패할 수도 있다고 주장하기도 합니다. 그러나 선호 순서가 투표로 고유하게 변환될 수 없는 경우 이러한 방법은 애로우의 집계 규칙(또는 도메인이 선호 프로파일로 구성된 함수) 정의에 실패한다고 간주하는 것이 더 적절합니다.

[43] 그러나 화살표 정리의 수정된 버전은 여전히 이러한 방법에 적용될 수 있습니다(예:

[warrensmith-44] Smith, Warren D.; et al. "How can range voting accomplish the impossible?". Retrieved 2016-02-16.

[45] 기본 유틸리티를 사용하지 않는 투표 방법은 Arrow의 IIA(선호 프로파일이 투표용지 목록 또는 유틸리티 목록으로 대체됨)를 만족하지 않습니다. 이러한 이유로, IIA의 약화된 개념이 제안됩니다(예: Sen (1979, p. 129). 이 개념은 두 대안의 사회적 순위가 두 대안에서 개인이 달성한 효용 수준에만 의존해야 함을 요구합니다. (보다 공식적으로, 사회 복지 함수 $F$ ${\displaystyle$ F $}$ 는 각 목록 $u=(u_{1},\ldots ,u_{n})$ = $u=(u_{1},\ldots ,u_{n})$ $…,$ un) {\display u = (u_{1},\ldots $,$ $유틸리티$ 기능 $u=(u_{1},\ldots ,u_{n})$ 중 $u_$ {n $}}$ 을(를) 사회적 기본 설정으로 사용합니다. $F$ $F$ 은 $F$ (는) 모든 목록 $u$ 에 $,$ u' {\ $displaystyle u,$ u'}이고 $u,u'$ 모든 대안 $x,y$ 에 대해 $,$ $y$ ${\displaystyle$ x $,y$ if $u_{i}(x)=u'_{i}(x)$ and $u_{i}(y)=u'_{i}(y)$ for all $i$ , then $xF(u)y{\text{ iff }}xF(u')y$ .) 많은 기본 투표 방법(범위 투표 포함)이 IIA의 약화된 버전을 만족시킵니다.

[46] Poundstone, William (2009-02-17). Gaming the Vote: Why Elections Are not Fair (and What We Can Do About It). Macmillan. ISBN 9780809048922.

[47] Feldman, Allan M.; Serrano, Roberto (2006). Welfare Economics and Social Choice Theory. Springer Science & Business Media. ISBN 9780387293684. It is quite silly in the first place to think that there might be social preferences that are analogous to individual preferences. It is nonsense to talk about social preferences since society itself is nothing more than a collection of individuals, each with his own interests. ... this first reaction to Arrow's Theorem is logically attractive, but it can lead to varieties of nihilism that are unappealing to some people, including us.

[48] Arrow, Kenneth Joseph (1963). "Chapter VIII Notes on the Theory of Social Choice, Section III. What Is the Problem of Social Choice?". Social Choice and Individual Values. Yale University Press. pp. 103–109. ISBN 978-0300013641. these criticisms are based on misunderstandings of my position

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

v t 일반적인 역설
철학적	분석. 부리단 다리 꿈논쟁 에피쿠리아어 픽션 피치의 알 수 있는 능력 자유의지 굿맨즈 쾌락주의 리버럴 메노즈 덧셈 무어의 뉴컴즈 허무주의 전능 서문 규칙준수 소리꾼 테세우스의 배 백마 제논의
논리적	이발사 베리 Bhartrhari's Burali-Forti 법원. 악어 카레스 에피메니데스 자유선택 역설 그렐링-넬슨 크린-로저 거짓말쟁이 카드 노노 피노키오 퀸즈 야블로의 정반대의 날 집합론의 역설 리차드의 러셀의 소크라테스적 힐베르트 호텔 온도 패러독스 이발소 캐치-22 닭이나 달걀 애주가 수반 복권. 플라톤의 수염 레이븐 로스의 예기치 않은 매달림 "거북이 아킬레우스에게 한 말" 열사병 역설 올버스의 역설
경제의	알라이스 반독점 화살표정보 베르트랑 브레이스의 경쟁. 소득과 출산력 다운스톰슨 이스털린 에지워스 엘스버그 유럽의 깁슨의 기펜굿 이카루스 제본스 레온티에프 러너 루카스 만데빌의 메이필드의 메츨러 충분한 양의 생산성 번영 스키토프스키 서비스복구 상트페테르부르크 절약 토일 툴록 가치
결정론	빌렌 할당 앨라배마 주 뉴스테이트 주 인구. 애로우즈 부리단 엉덩이 체인스토어 Condorcet's 의사결정 다운스 엘스버그 펜노의 프레드킨즈 초록의 고슴도치의 발명가의 카브카의 독소 퍼즐 모튼 포크 네비게이션 뉴컴즈 파론도의 준비성 예방 죄수의 딜레마 관용 윌파워
목록. 카테고리

v t 게임이론의 주제
정의들	혼잡 게임 협동 게임 결정성 확약의 확대 광범위한 형태의 게임 첫번째 선수와 두번째 선수의 승리 게임 복잡도 그래픽 게임 신념의 위계 정보 집합 노멀폼 게임 선호 순차 게임 동시게임 동시실행선택 해결게임 간결한 게임
평형 개념들	베이지안 내쉬 균형 베르게 평형 코어 상관균형 엡실론 평형 진화적으로 안정된 전략 깁스 평형 메르텐스 안정 평형 마르코프 완전 평형 내쉬균형 파레토 효율 완전 베이즈 균형 적정평형 양자반응평형 준완전 평형 위험지배력 만족평형 자기확정형평형 순차평형 샤플리값 강한 내시 평형 서브게임 완성도 떨리는 손
전략들	후진유도 입찰 차양 공모 순방향유도 그림 방아쇠 마르코프 전략 지배적 전략 순수전략 혼합전략 전략 훔치기 논법 티트포타트
반 게임의	교섭문제 싸구려 토크 글로벌 게임 인트랜시티브 게임 평균 필드 게임 기구설계 n-플레이어 게임 완벽한 정보 라지 푸아송 게임 포텐셜 게임 반복게임 스크리닝 게임 시그널링 게임 슈타켈베르크 대회 엄격하게 결정된 게임 확률적 게임 대칭 게임 제로섬 게임
게임.	가세요 체스 무한 체스 체커즈 틱택토 죄수의 딜레마 선물교환 게임 선택적 죄수의 딜레마 여행자의 딜레마 코디 게임 치킨. 지네게임 루이스 신호 게임 자원봉사자의 딜레마 달러경매 성별의 전투 사슴사냥 매칭 페니 최후통첩 게임 가위 바위 보 해적게임 독재자 게임 공공재 게임 블로토 게임 소모전 엘파롤 바 문제 공정분할 페어 케이크 커팅 쿠르노 게임 교착상태 다이너의 딜레마 평균의 2/3을 맞혀보세요. 쿤 포커 내쉬 바게닝 게임 유도퍼즐 신뢰게임 공주와 괴물게임 랑데부 문제
정리	화살의 불가능성 정리 아우만 합의 정리 민속정리 미니맥스 정리 내쉬 정리 네가막스 정리 정화정리 폭로원칙 스프라그-그룬디 정리 제르멜로 정리
열쇠 수치	앨버트 W. 터커 아모스 트버스키 앙투안 오귀스트 인 쿠르노 아리엘 루빈스타인 클로드 샤넌 다니엘 카네만 데이비드 케이. 레빈 데이비드 M. 크렙스 도널드 B. 길리스 드류 푸덴베르크 에릭 매신 해럴드 W. 쿤 허버트 사이먼 Hervé Moulin 존 콘웨이 장 티롤 장 프랑수아 메르텐스 제니퍼 투어 채이스 존 하르사니 존 메이너드 스미스 존 내쉬 존 폰 노이만 케네스 애로우 케네스 빈모어 레오니드 후르비츠 로이드 샤플리 멜빈 드레셔 메릴엠. 홍수. 올가 본다레바 오스카르 모르겐슈테른 폴 밀그롬 페이튼 영 라인하르트 셀텐 로버트 액셀로드 로베르트 아우만 로버트 B. 윌슨 로저 마이어슨 새뮤얼 보울스 수잔 스카치머 토머스 셸링 윌리엄 비키
여러가지 종류의	올페이옥션 알파베타 가지치기 베르트랑 역설 유계 합리성 조합 게임 이론 대립분석 코페티션 진화게임이론 체스에서 일진일퇴의 이점 게임 설명 언어 게임 역학 게임이론 용어집 게임 이론가 목록 게임 이론의 게임 목록 무승상황 체스 풀기 위상 게임 공유지의 비극 작은 결정의 횡포

Search