그래프(이산수학)

이산수학에서, 더 구체적으로 그래프 이론에서, 그래프는 어떤 의미에서 객체의 일부 쌍이 "관련"된 객체의 집합에 해당하는 구조입니다.객체는 정점(노드 또는 점이라고도 함)이라고 불리는 수학적 추상화에 해당하며, 각 관련 정점 쌍을 에지(링크 또는 ^[1]선이라고도 함)라고 합니다.일반적으로 그래프는 꼭짓점에 대한 점 또는 원의 집합으로 다이어그램 형태로 표시되며, 가장자리에 대한 선 또는 곡선으로 연결됩니다.그래프는 이산수학의 연구 대상 중 하나입니다.

가장자리는 방향이 있을 수도 있고 방향이 없을 수도 있습니다.예를 들어, 정점들이 파티에서 사람들을 나타내고, 그들이 악수를 한다면 두 사람 사이에 간선이 존재한다면, B도 A와 악수를 해야만 A가 B와 악수를 할 수 있기 때문에 이 그래프는 무방향입니다.반대로, 어떤 사람 A가 어떤 사람 B에게 돈을 빚지고 있다는 것을 의미한다면, 빚지는 돈이 반드시 왕복할 필요는 없기 때문에 이 그래프는 지시된 것입니다.

그래프는 그래프 이론에 의해 연구되는 기초 과목입니다.그래프라는 단어는 1878년 J. J. 실베스터(J. J. Sylvester)가 수학과 화학 구조 ^[2][3]사이의 직접적인 관계 때문에 처음 사용했습니다.

정의들

그래프 이론의 정의는 다양합니다.다음은 그래프 및 관련 수학적 구조를 정의하는 보다 기본적인 방법입니다.

그래프

그래프(방향 그래프와 구별하기 위해 무방향 그래프 또는 다중 그래프와 구별하기 위해 단순 그래프라고도 함)는 G = 쌍(V, E)이며, 여기서 V는 원소를 정점(π: 정점)이라고 하는 집합이고, E는 원소를 에지(링크 또는 선)라고 하는 쌍을 이룬 정점의 집합입니다.

가장자리 {x, y}의 정점 x와 y를 가장자리의 끝점이라고 합니다.가장자리는 x와 y를 결합하고 x와 y에 입사한다고 합니다.정점은 가장자리에 속하지 않을 수 있으며, 이 경우 다른 정점에 결합되지 않습니다.

다중 그래프는 여러 모서리가 동일한 끝점 쌍을 가질 수 있도록 하는 일반화입니다.일부 텍스트에서는 다중 그래프를 단순히 ^[6][7]그래프라고 합니다.

그래프에 정점을 연결하는 가장자리인 루프를 포함할 수도 있습니다.루프를 허용하려면 E의 정점 쌍이 동일한 노드를 두 번 갖도록 허용해야 합니다.이러한 일반화된 그래프를 루프가 있는 그래프 또는 루프가 허용되는 상황이 명확할 때 단순한 그래프라고 합니다.

일반적으로 정점 V의 집합은 유한한 것으로 간주되며, 이는 간선의 집합도 유한하다는 것을 의미합니다.무한 그래프는 때때로 고려되지만 유한 그래프에 대한 대부분의 결과가 무한한 경우로 확장되지 않거나 다소 다른 증명이 필요하기 때문에 특별한 종류의 이항 관계로 간주되는 경우가 더 많습니다.

빈 그래프는 빈 정점 집합(따라서 빈 간선 집합)을 갖는 그래프입니다.그래프의 순서는 정점 V의 개수입니다. 그래프의 크기는 간선 E의 개수입니다. 그러나 알고리즘의 계산 복잡도를 표현하기 위한 것과 같은 일부 맥락에서 크기는 V + E입니다(그렇지 않으면 비어 있지 않은 그래프의 크기는 0이 될 수 있습니다).꼭짓점의 정도 또는 원자가는 꼭짓점에 결합된 모서리의 개수입니다. 루프가 있는 그래프의 경우, 루프가 두 번 카운트됩니다.

순서 n의 그래프에서 각 정점의 최대 차수는 n - 1(루프가 허용되면 n + 1)이고, 최대 간선 수는 n(n - 1)/2(루프가 허용되면 n(n + 1)/2(또는 n(n + 1)/2)입니다.

그래프의 가장자리는 정점에서 인접 관계라고 하는 대칭 관계를 정의합니다.특히, {x, y}이(가) 에지인 경우 두 꼭짓점 x와 y가 인접합니다.그래프는 n × n 제곱 행렬인 인접 행렬 A에 의해 완전히 지정될 수 있으며, A는_ij 정점 i에서 정점 j로의 연결 수를 지정합니다.단순 그래프의 경우 A는 연결을 나타내는 0 또는 연결을 나타내는 1입니다. 또한 단순 그래프의 가장자리는 동일한 정점에서 시작하여 끝날 수 없기 때문에 A = 0입니다.자가 루프가 있는 그래프는 일부 또는 모든_ii A가 양의 정수와 동일한 것으로, 다중 그래프(꼭짓점 사이에 여러 모서리가 있는 것)는 일부 또는 모든_ij A가 양의 정수와 동일한 것으로 특징지어집니다.무방향 그래프는 대칭 인접 행렬(A = A를 의미함)을 갖습니다.

방향 그래프

방향 그래프 또는 디그래프는 가장자리가 방향을 갖는 그래프입니다.

제한적이지만 매우 상식적인 용어에서 방향 그래프는 다음을 포함하는 쌍 G = (V, E)입니다.

• V, 꼭짓점 집합(노드 또는 점이라고도 함);
• E, 서로 다른 꼭짓점의 순서 쌍인 모서리 집합(방향 모서리, 방향 링크, 방향 선, 화살표 또는 호라고도 함):${\displaystyle E}$ ${\displaystyle \subseteq }$ {${\displaystyle }$( ${\displaystyle x,y}$ ${\displaystyle )}$ ${\displaystyle \mid }$ ${\displaystyle \in }$(${\displaystyle x}$, ${\displaystyle y}$ ) ≠ ${\displaystyle V^{}}$ ${\displaystyle 2}$ ${\displaystyle \mathrm{an}d}$ x${\displaystyle }$} y$$} {\$displaystyle E\$subseteq$\{(x,y)\mid (x,y)\in$ V$^{2}\;{\textrm$ {$and}\;x\neqy$

모호함을 방지하기 위해, 이러한 유형의 객체를 정확하게 방향 단순 그래프라고 부를 수 있습니다.

x에서 y로 향하는 모서리 (x, y)에서 꼭짓점 x와 y는 모서리의 끝점, x는 모서리의 꼬리, y는 모서리의 머리라고 불립니다.가장자리는 x와 y를 결합하고 x와 y에 입사한다고 합니다.꼭지점이 그래프에 존재할 수 있으며 가장자리에 속하지 않습니다.가장자리 (y, x)를 (x, y)의 반전 가장자리라고 합니다.위 정의에 따라 허용되지 않는 다중 모서리는 꼬리와 머리가 모두 같은 두 개 이상의 모서리입니다.

다중 에지를 허용하는 용어의 하나의 더 일반적인 의미에서, 방향 그래프는 다음을 포함하는 순서 삼중 G = (V, E, ϕ)입니다.

• V, 꼭짓점 집합(노드 또는 점이라고도 함);
• E, 모서리 집합(방향 모서리, 방향 링크, 방향 선, 화살표 또는 호라고도 함)
• ◦, 모든 에지를 순서화된 정점 쌍에 매핑하는 입사 함수(즉, 에지는 두 개의 서로 다른 정점과 연결됨):$}$$E\to \{(x,y)\mid (x,y)\in$ V$^{2}\;{\textrm {and}}\;x\neqy$

모호함을 방지하기 위해, 이러한 유형의 객체를 정확하게 방향 멀티그래프라고 부를 수 있습니다.

루프는 정점을 자신에 연결하는 가장자리입니다.정점 x {\displaystyle x}를 자신에 연결하는 루프는 (방향 단순 그래프의 경우) 가장자리이거나 (방향 다중 그래프의 경우) { (x, y) ∣ (x, y) ∈ V 2 및 x ≠ y } {\displaystyle \{(x,y)\mid (x,y)\"에 결합되지 않는 (방향 다중 그래프의 경우) {\displaystyle (x,y)}에 결합되므로 위의 두 정의에서 정의된 방향 그래프는 루프를 가질 수 없습니다$V^{2}\;{\textrm {and}}\;x\neqy$ 루프를 허용하려면 정의를 확장해야 합니다.방향이 지정된 단순 그래프의 경우, E {\displaystyle E}의 정의를 E ∈ { (x, y ) ∣ (x, y ) ∈ V 2 } {\displaystyle E\subseteq \{(x,y)\mid (x,y)\in V^{2}\}로 수정해야 합니다. 방향이 지정된 다중 그래프의 경우, ϕ {\displaystyle \phi }의 정의를 ϕ : E → { (x, y ) ∣ (x, y ) ∈ V 2 } {\displaystyle \phi :E$\to \{(x,y)\mid (x,y)\in$ V$^{2$ 모호함을 방지하기 위해, 이러한 종류의 객체를 각각 루프를 허용하는 방향 단순 그래프와 루프를 허용하는 방향 다중 그래프(또는 진동자)라고 정확하게 부를 수 $있습니다$.

고리 G를 허용하는 방향 단순 그래프의 가장자리는 G의 인접 관계라고 불리는 G의 꼭짓점에 대한 균질 관계입니다. 구체적으로 각 가장자리 (x, y)에 대해 끝점 x와 y가 서로 인접해 있다고 하며, 이는 x ~ y로 표시됩니다.

혼합 그래프

혼합 그래프는 일부 에지는 방향을 지정하고 일부는 방향을 지정하지 않을 수 있는 그래프입니다.위와 같이 정의된 V, E(무방향 에지), A(방향 에지), θ, θ가 있는 혼합 멀티그래프의 경우 순서대로 된 삼중 G = (V, E, A, θ, θ)이고, 혼합된 멀티그래프의 경우 G = (V, E, A, θ, θ)입니다.방향 그래프와 방향 그래프는 특수한 경우입니다.

가중치 그래프

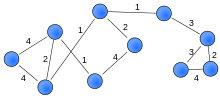
가중치 그래프 또는 네트워크는^[9][10] 숫자(가중치)가 각 ^[11]에지에 할당된 그래프입니다.이러한 가중치는 당면한 문제에 따라 예를 들어 비용, 길이 또는 용량을 나타낼 수 있습니다.그러한 그래프는 많은 맥락에서 발생합니다. 예를 들어, 판매원 여행 문제와 같은 최단 경로 문제에서 발생합니다.

그래프의 종류

방향 그래프

방향 그래프의 한 가지 정의는 (x, y) 및 (y, x) 중 최대 하나가 그래프의 가장자리가 될 수 있는 방향 그래프라는 것입니다.즉, 무방향(단순) 그래프의 방향으로 형성할 수 있는 방향 그래프입니다.

어떤 저자들은 "방향 그래프"를 "방향 그래프"와 같은 의미로 사용하기도 합니다.어떤 저자들은 "방향 그래프"를 사용하여 주어진 무방향 그래프 또는 멀티그래프의 방향을 의미합니다.

정규 그래프

정규 그래프는 각 정점이 동일한 수의 이웃을 갖는 그래프입니다. 즉, 모든 정점이 동일한 차수를 갖는 그래프입니다.꼭짓점이 k인 정규 그래프를 k 정규 그래프 또는 k 정규 그래프라고 합니다.

완전그래프

완전 그래프는 각 정점 쌍이 가장자리로 연결된 그래프입니다.완전한 그래프는 가능한 모든 가장자리를 포함합니다.

유한 그래프

유한 그래프는 꼭짓점 집합과 모서리 집합이 유한 집합인 그래프입니다.그렇지 않으면 무한 그래프라고 합니다.

그래프 이론에서 가장 일반적인 것은 논의된 그래프가 유한하다는 것입니다.그래프가 무한이면 일반적으로 구체적으로 설명됩니다.

연결그래프

무방향 그래프에서 경로가 x에서 y로 이어지는 경우, 순서가 없는 정점 쌍 {x, y}을(를) 연결이라고 합니다.그렇지 않으면 순서가 없는 쌍을 연결 끊김이라고 합니다.

연결된 그래프는 그래프의 모든 순서가 없는 정점 쌍이 연결된 무방향 그래프입니다.그렇지 않으면 연결 끊김 그래프라고 합니다.

방향 그래프에서, 방향 경로가 x에서 y로 이어진다면, 꼭짓점 (x, y)의 순서 쌍을 강하게 연결이라고 합니다.그렇지 않으면 방향이 없는 경로가 모두 방향이 없는 에지로 바꾼 후 x에서 y로 이어지는 경우 순서 쌍을 약하게 연결이라고 합니다.그렇지 않으면 순서 쌍을 연결 끊김이라고 합니다.

강하게 연결된 그래프는 그래프의 모든 순서가 있는 정점 쌍이 강하게 연결된 방향 그래프입니다.그렇지 않으면 그래프의 모든 정렬된 정점 쌍이 약하게 연결되어 있으면 약하게 연결된 그래프라고 합니다.그렇지 않으면 연결 끊김 그래프라고 합니다.

k-vertex 연결 그래프(k-vertex-connected graph) 또는 k-edge-connected graph(k-edge-connected graph)는 k - 1개의 정점 집합(각각 에지)이 존재하지 않는 그래프로, 제거 시 그래프를 연결 해제합니다.k-정점 연결 그래프는 종종 단순히 k-연결 그래프라고 불립니다.

이분 그래프

이분 그래프는 W의 두 정점이 동일한 에지를 공유하지 않고 X의 두 정점이 동일한 에지를 공유하지 않도록 정점 집합을 W와 X의 두 집합으로 분할할 수 있는 간단한 그래프입니다.또는 색수가 2인 그래프입니다.

완전한 이분 그래프에서 꼭짓점 집합은 W와 X의 두 개의 서로소 집합의 결합이므로 W의 모든 꼭짓점은 X의 모든 꼭짓점에 인접하지만 W 또는 X 내에는 간선이 없습니다.

경로그래프

경로 그래프 또는 n≥ 2의 선형 그래프는 정점들이 i = 1, 2, …, n - 1일 때 간선이 {v, v}이 되도록 v, v, …, v 순서로 나열될 수 있는 그래프입니다. 경로 그래프는 두 정점을 제외한 모든 정점의 차수가 2이고 나머지 두 정점의 차수가 1인 연결 그래프로 특징지어질 수 있습니다.경로 그래프가 다른 그래프의 하위 그래프로 발생하면 해당 그래프의 경로가 됩니다.

평면 그래프

평면 그래프는 두 모서리가 교차하지 않도록 꼭짓점과 모서리를 평면에 그릴 수 있는 그래프입니다.

순환 그래프

n ≥ 3차의 순환 그래프 또는 원형 그래프는 간선이 i = 1, 2, …, n - 1일 때 {v, v}이고 간선이 {v, v}이 되도록 정점을 v, v, …, v 순으로 나열할 수 있는 그래프입니다.순환 그래프는 모든 정점의 차수가 2인 연결 그래프로 특징지을 수 있습니다.순환 그래프가 다른 그래프의 하위 그래프로 발생하면 해당 그래프의 순환 또는 회로입니다.

나무

트리는 임의의 두 정점이 정확히 하나의 경로로 연결된 무방향 그래프 또는 이와 동등하게 연결된 비순환 무방향 그래프입니다.

포리스트는 최대 하나의 경로로 두 꼭짓점이 연결된 무방향 그래프 또는 이와 동등하게 비순환 무방향 그래프 또는 이와 동등하게 트리의 서로소 결합인 무방향 그래프입니다.

폴리트리

폴리트리(또는 방향 트리 또는 방향 트리 또는 단일 연결 네트워크)는 방향 비순환 그래프(DAG)로, 기본 무방향 그래프가 트리입니다.

폴리포레스트(또는 방향이 지정된 포리스트 또는 방향이 지정된 포리스트)는 방향이 지정된 비순환 그래프로, 기본 무방향 그래프는 포리스트입니다.

고급반

보다 고급 그래프 종류는 다음과 같습니다.

• Petersen 그래프 및 그 일반화
• 완벽한 그래프
• 코그라피;
• 초달 그래프
• 큰 오토모피즘 그룹이 있는 다른 그래프: 정점-전이, 호-전이 및 거리-전이 그래프;
• 강력한 정규 그래프와 그 일반화 거리-정규 그래프.

그래프의 속성

그래프의 두 모서리가 동일한 꼭지점을 공유하는 경우 인접이라고 합니다.첫 번째 그래프의 머리 부분이 두 번째 그래프의 끝 부분인 경우 두 개의 가장자리를 연속이라고 합니다.마찬가지로 두 꼭짓점이 공통 모서리를 공유하는 경우(첫 번째 꼭짓점이 꼬리이고 두 번째 꼭짓점이 모서리의 머리인 경우 연속) 인접이라고 하며, 이 경우 공통 모서리는 두 꼭짓점을 결합한다고 합니다.가장자리와 해당 가장자리의 정점을 인시던트(incident)라고 합니다.

꼭짓점이 하나만 있고 가장자리가 없는 그래프를 사소한 그래프라고 합니다.꼭짓점만 있고 모서리가 없는 그래프를 무 모서리 그래프라고 합니다.꼭짓점이 없고 가장자리가 없는 그래프를 귀무 그래프 또는 빈 그래프라고 부르기도 하지만 용어가 일치하지 않으며 모든 수학자가 이 대상을 허용하는 것은 아닙니다.

일반적으로, 그래프의 정점들은 집합의 원소로서의 성질상 구별할 수 있습니다.이런 종류의 그래프를 꼭짓점 레이블이라고 부를 수 있습니다.그러나 많은 질문의 경우 정점을 구별할 수 없는 것으로 취급하는 것이 더 좋습니다. (물론 정점은 그래프 자체의 속성, 예를 들어 입사 에지의 수에 의해 여전히 구별될 수 있습니다.)동일한 주석이 에지에 적용되므로 레이블이 지정된 에지가 있는 그래프를 에지 레이블이라고 합니다.가장자리 또는 꼭짓점에 레이블이 부착된 그래프는 일반적으로 레이블이 부착된 것으로 지정됩니다.따라서 정점이 구별되지 않고 가장자리가 구별되지 않는 그래프를 레이블 없는 그래프라고 합니다.(문헌에서 라벨링된 용어는 다른 꼭짓점이나 모서리를 구별하는 역할만 하는 다른 종류의 라벨링에도 적용될 수 있습니다.)

모든 그래프의 범주는 쉼표 범주 세트 ↓ D이며 여기서 D: 세트 → 세트는 s × s로 집합을 취하는 함수입니다.

예

• 이 다이어그램은 $정점$ V = {${\displaystyle 1,}$ ${\displaystyle 2,}$ ${\displaystyle 3,}$ ${\displaystyle 4,}$ ${\displaystyle 5,}$ $}$ {\$displaystyle$ V =$\{1, 2, 3, 4, 5,$ 6\}, $간선$ E =${\displaystyle }${{${\displaystyle 1,}$ ${\displaystyle 2\},}$ {${\displaystyle 1,}$ ${\displaystyle 5}$ ${\displaystyle \},}$ {${\displaystyle 2,}$ ${\displaystyle 3\},}$ {${\displaystyle 2,}$ ${\displaystyle 5\},}$ {${\displaystyle 3,}$ ${\displaystyle 4\},}$ {${\displaystyle 4,}$ ${\displaystyle 5\},}$ {${\displaystyle 4,}$ ${\displaystyle 6\},}$ ${\displaystyle$ E =\{$1, 2\},\{2, 5\},\{2, 5\},\{3, 4\},\{4,$6\},\{$4, 6\},.$
• 컴퓨터 과학에서 방향 그래프는 지식(예: 개념 그래프), 유한 상태 기계 및 기타 많은 이산 구조를 나타내는 데 사용됩니다.
• 집합 X의 이항 관계 R은 방향 그래프를 정의합니다.X의 원소 x는 xRy인 경우에만 X의 원소의 직접적인 전신입니다.
• 지시 그래프는 한 사용자가 다른 ^[12][13]사용자를 따라다니면서 트위터와 같은 정보 네트워크를 모델링할 수 있습니다.
• 유향 그래프의 특히 규칙적인 예는 유한 생성된 그룹의 케일리 그래프와 슈라이어 코셋 그래프에 의해 제공됩니다.
• 범주 이론에서 모든 작은 범주에는 정점이 범주의 개체이고 가장자리가 범주의 화살표인 기본 방향 다중 그래프가 있습니다.범주 이론의 언어에서는 작은 범주의 범주에서 떨림의 범주로 망각 기능자가 있다고 말합니다.

그래프 연산

초기 그래프에서 새 그래프를 생성하는 여러 작업이 있으며 다음 범주로 분류할 수 있습니다.

• 단항 연산: 다음과 같이 초기 그래프에서 새 그래프를 만듭니다.
  • 가장자리 수축,
  • 선 그래프,
  • 이중 그래프,
  • 상보 그래프,
  • 그래프 다시 쓰기;
• 다음과 같은 두 개의 초기 그래프에서 새 그래프를 생성하는 이진 연산:
  • 그래프의 분리 결합,
  • 그래프의 데카르트 곱,
  • 텐서곱 그래프,
  • 그래프의 강력한 산물,
  • 그래프 사전생성물,
  • 직렬-병렬 그래프

일반화

하이퍼그래프에서 모서리는 두 개 이상의 꼭짓점을 결합할 수 있습니다.

무방향 그래프는 1-단순(가장자리)과 0-단순(꼭짓점)으로 구성된 단순 복합체로 볼 수 있습니다.따라서 복합체는 고차원 단순화를 허용하기 때문에 그래프의 일반화입니다.

모든 그래프는 매트로이드를 생성합니다.

모델 이론에서 그래프는 구조일 뿐입니다.그러나 이 경우 모서리의 개수에는 제한이 없습니다. 임의의 기수가 될 수 있습니다. 연속형 그래프를 참조하십시오.

계산 생물학에서 검정력 그래프 분석은 무방향 그래프의 대안적 표현으로 검정력 그래프를 도입합니다.

지리 정보 시스템에서 기하학적 네트워크는 그래프를 면밀하게 본떠서 만들어지며, 그래프 이론에서 많은 개념을 빌려 도로망이나 유틸리티 그리드에 대한 공간 분석을 수행합니다.

참고 항목

• 개념 그래프
• 그래프(추상 데이터 유형)
• 그래프 데이터베이스
• 그래프도면
• 그래프 이론 주제 목록
• 그래프 이론의 출판물 목록
• 네트워크 이론

메모들

참고문헌

• Balakrishnan, V. K. (1997). Graph Theory (1st ed.). McGraw-Hill. ISBN 978-0-07-005489-9.
• Bang-Jensen, J.; Gutin, G. (2000). Digraphs: Theory, Algorithms and Applications. Springer.
• Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability.
• Berge, Claude (1958). Théorie des graphes et ses applications (in French). Paris: Dunod.
• Biggs, Norman (1993). Algebraic Graph Theory (2nd ed.). Cambridge University Press. ISBN 978-0-521-45897-9.
• Bollobás, Béla (2002). Modern Graph Theory (1st ed.). Springer. ISBN 978-0-387-98488-9.
• Diestel, Reinhard (2005). Graph Theory (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-3-540-26183-4.
• Graham, R.L.; Grötschel, M.; Lovász, L. (1995). Handbook of Combinatorics. MIT Press. ISBN 978-0-262-07169-7.
• Gross, Jonathan L.; Yellen, Jay (1998). Graph Theory and Its Applications. CRC Press. ISBN 978-0-8493-3982-0.
• Gross, Jonathan L.; Yellen, Jay (2003). Handbook of Graph Theory. CRC. ISBN 978-1-58488-090-5.
• Harary, Frank (1995). Graph Theory. Addison Wesley Publishing Company. ISBN 978-0-201-41033-4.
• Iyanaga, Shôkichi; Kawada, Yukiyosi (1977). Encyclopedic Dictionary of Mathematics. MIT Press. ISBN 978-0-262-09016-2.
• Zwillinger, Daniel (2002). CRC Standard Mathematical Tables and Formulae (31st ed.). Chapman & Hall/CRC. ISBN 978-1-58488-291-6.

추가열람

• Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication. ed.). New York: Dover Publications. ISBN 978-0-486-67870-2. Retrieved 8 August 2012.

외부 링크

라이브러리 리소스정보 그래프(수학)

라이브러리의 리소스

• Wikimedia Commons의 그래프(discrete mathematics) 관련 매체
• Weisstein, Eric W. "Graph". MathWorld.