스트라텔베르크 대회

Stackelberg 리더십 모델은 경제학의 전략 게임으로 리더 기업이 먼저 움직인 다음 팔로어 기업이 순차적으로 움직이는 게임이다. 이 모델을 기술한 1934년 마켓 구조와 평형(Market Structure and Balance, Marktform und Gleicgewicht)을 출간한 독일의 경제학자 하인리히 프리허르 폰 스트라텔베르크의 이름을 따서 지은 것이다.

게임이론적으로 보면 이 게임의 플레이어는 리더와 팔로워로 양으로 승부를 겨룬다. Stackelberg의 리더는 때때로 시장 리더라고 불린다.

Stackelberg 평형 유지에 몇 가지 추가 제약조건이 있다. 리더는 추종자가 자신의 행동을 관찰한다는 것을 알아야 한다. 추종자는 미래의 비 Stackelberg 리더의 행동에 전념할 수단이 없어야 하며 리더는 이것을 알아야 한다. 실제로 '팔로워'가 스택엘버그 리더 액션을 맡기고 '리더'가 이를 안다면 리더의 최선의 대응은 스택엘버그의 팔로워 액션을 연기하는 것이 될 것이다.

Stackelberg가 먼저 움직일 수 있는 장점이 있다면 기업들은 Stackelberg 경쟁에 참여할 수 있다. 더 일반적으로, 리더는 헌신적인 힘을 가져야 한다. 관찰할 수 있게 먼저 움직이는 것이 가장 분명한 헌신의 수단이다. 리더가 일단 움직임을 하면, 그것을 되돌릴 수 없다. 그것은 그 행동에 전념한다. 리더가 산업의 현재 독과점이고 추종자가 새로운 진입자라면 먼저 움직이는 것이 가능할 수 있다. 과잉 수용력을 보유하는 것도 헌신의 또 다른 수단이다.

서브게임 퍼펙트 나시 평형

Stackelberg 모델은 서브게임 퍼펙트 Nash 평형 또는 평형(SPNE)을 찾기 위해 풀릴 수 있다. 즉, 다른 플레이어의 전략을 고려할 때 각 플레이어에 가장 적합한 전략 프로파일로, 서브게임마다 모든 플레이어가 내시 평형을 이루도록 한다.

매우 일반적인 용어로, (이중) 산업의 가격 함수를 P $P$ 로 하자 $P$ 가격은 단순히 총 (산업) 산출물의 함수에 불과하며, 첨자 1은 리더를 나타내고, 2는 추종자를 $P(q_{1}+q_{2})$ P $P(q_{1}+q_{2})$ ( $P(q_{1}+q_{2})$ $P(q_{1}+q_{2})$ + $P(q_{1}+q_{2})$ ) ${\displaysty P(q_{1$ }+ $q_{2$ })도 마찬가지다 $.$ 기업 $i$ $i$ 이(가) $C_{i}(q_{i})$ 구조 C $C_{i}(q_{i})$ ( $C_{i}(q_{i})$ $C_{i}(q_{i})$ ) ${\displaystyle C_{i}(q_{i})$ 를 가지고 $i$ 있다고 가정합시다 $C_{i}(q_{i})$ 그 모델은 역유도법으로 해결된다. 리더는 추종자의 최선의 대응, 즉 리더의 양을 관찰한 후에 어떻게 대응할 것인가를 고려한다. 그런 다음 리더는 그 보상을 극대화하는 수량을 선택하여 팔로워의 예측된 반응을 예측한다. 팔로워는 실제로 이것을 관찰하고 평형상태에서 반응으로 예상되는 양을 선택한다.

SPNE를 계산하려면 먼저 추종자의 최상의 응답 기능을 계산해야 한다(추적 유도로 인해 계산이 '뒤로' 이동).

기업 2의 이익은 수익에서 원가를 뺀 것이다. Revenue is the product of price and quantity and cost is given by the firm's cost structure, so profit is: $\Pi _{2}=P(q_{1}+q_{2})\cdot q_{2}-C_{2}(q_{2})$ . $\Pi _{2}$ ${\$ $displaystyle q_{2$ }} $q_{2}$ q $q_{2}$ $\Pi _{2}$ 1{\ $displaystyle \Pi_{2$ }}: $\Pi _{2}$ $q_{1}$ $q_{1}$ ${\$ 즉 리더(펌 1)의 출력을 감안하면 팔로어의 이익을 극대화하는 산출물을 찾는 것이 최선의 대응이다. 따라서 $q_{2}$ $q_{2}$ ${\$ $\Pi$ $_{2$ }에 대한 $\Pi _{2}$ 최대 $\Pi _{2}$ {1 $}{$ 2}를 찾을 수 있다 $q_{2}$ . 먼저 $\Pi _{2}$ $q_{2}$ 2 $q_{2}$ ${\$ $displaystyle$ $\Pi _{2}$ \ $Pi_{2$

{\frac {\partial \Pi _{2}}{\partial q_{2}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot q_{2}+P(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}.

최대화를 위해 0으로 설정:

{\frac {\partial \Pi _{2}}{\partial q_{2}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot q_{2}+P(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}=0.

이 방정식을 만족하는 $q_{2}$ $q_{2}$ ${\$ }}의 값이 가장 좋은 반응이다. 이제 리더의 최선의 대응 기능이 고려된다. 이 함수는 방금 계산한 바와 같이 리더의 출력 함수로 추종자의 출력을 고려하여 계산한다.

기업 1(리더 $)$ 의 이익은 $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ 1 $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ = P $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ ( $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ + $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ 2 $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ ( $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ ) . $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ - C $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ ( $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ 1 $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$ ) ${\displaystyle \Pi _{1}=P(q_{1}+q_{2}(q_{1$ }){1}. $q_{1$ }- $C_{1}(q_{1}}),$ 여기서 $q_{2}(q_{1})$ 2 ( $q_{2}(q_{1})$ 1 $q_{2}(q_{1})$ ) ${\displaystyle q_{2$ }( $q_{1})$ 는 리더 $q_{2}(q_{1})$ 수량의 함수로서 추종자의 수량, 즉 위에서 계산한 함수다. ${\$ $displaystyle q_{1}}{$ $1$ } $q_{2}(q_{1})$ 2 $q_{2}(q_{1})$ ( $q_{2}(q_{1})$ 1 $){\displaystyle$ $\$ $Pi _{1}}$ 을 $\Pi _{1}$ $q_{2}(q_{1})$ 를) $q_{1}$ 하는 $q_{1}$ $q_{2}(q_{1})$ 의 값을 찾는 것이 최선의 대응이다. 즉, 추종자( $follower$ )의 최선의 대응 기능을 부여하면 리더의 이익을 극대화하는 산출물이 발견된다. 따라서 $q_{1}$ $q_{1}$ ${\$ $\$ $Pi_{1$ }에 $q_{1}$ 대한 최대 $\Pi _{1}$ ${$ 1}을 찾을 수 있다 $q_{1}$ . 먼저 $q_{1}$ $q_{1}$ ${\$ $displaystyle \Pi _{$ $1$ }에 대해 $\Pi _{1}$ q 1 {\ $displaystyle$ q_{1 $}$ :

{\frac {\partial \Pi _{1}}{\partial q_{1}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot {\frac {\partial q_{2}(q_{1})}{\partial q_{1}}}\cdot q_{1}+{\frac {\partial P(q_{1}+q_{2})}{\partial q_{1}}}\cdot q_{1}+P(q_{1}+q_{2}(q_{1}))-{\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}.

최대화를 위해 0으로 설정:

{\frac {\partial \Pi _{1}}{\partial q_{1}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot {\frac {\partial q_{2}(q_{1})}{\partial q_{1}}}\cdot q_{1}+{\frac {\partial P(q_{1}+q_{2})}{\partial q_{1}}}\cdot q_{1}+P(q_{1}+q_{2}(q_{1}))-{\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}=0.

예

다음의 예는 매우 일반적이다. 일반화된 선형 수요 구조를 가정한다.

p(q_{1}+q_{2}}={\bigg(}a-b(q_{1}+q_{2}}{\bigg )}}}}

그리고 문제를 해결할 수 있도록 비용 구조에 약간의 제한을 가한다.

{\frac {\partial ^{2}C_{i}(q_{i})}{\partial q_{i}\cdot \partial q_{j}}}=0,\forall j

and

{\frac {\partial C_{i}(q_{i})}{\partial q_{j}}}=0,j\neq \ i

계산하기 쉽도록

팔로워의 이익은 다음과 같다.

\pi _{2}={\bigg (}a-b(q_{1}+q_{2}){\bigg )}\cdot q_{2}-C_{2}(q_{2})

최대화 문제는 (일반 사례에서) 다음과 같이 해결된다.

{\frac {\partial {\bigg (}a-b(q_{1}+q_{2}){\bigg )}}{\partial q_{2}}}\cdot q_{2}+a-b(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}=0,

\Rightarrow \ -bq_{2}+a-b(q_{1}+q_{2}-{\frac {\partial C_{2}(q_{2}){\partial q_{2}=0,

\Rightarrow \ \q_{2}={\frac {a-bq_{1}-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}:{2b}}}.

리더의 문제를 고려하십시오.

\Pi _{1}={\bigg (}a-b(q_{1}+q_{2}(q_{1}){\bigg )}\cdot q_{1}-C_{1}(q_{1}).

다음 $q_{2}(q_{1})$ $q_{2}(q_{1})$ $q_{2}(q_{1})$ 에서 $q_{2}(q_{1})$ 2 $q_{2}(q_{1})$ ( $q_{2}(q_{1})$ q 1 ) {\ $displaystyle q_$ {2}(q_ ${1})$ 로 대체:

\Pi _{1}={\bigg (}a-b{\bigg (}q_{1}+{\frac {a-bq_{1}-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2b}}{\bigg )}{\bigg )}\cdot q_{1}-C_{1}(q_{1}),

\Rightarrow \Pi _{1}={\bigg (}{\frac {a-b)q_{1}+{{1}+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}:}{\partial q_{2}}){\bigg )}\cdot q_{1}-C_{1}(q_{1}).

최대화 문제는 (일반 사례에서) 다음과 같이 해결된다.

{\frac {\partial \pi _{1}}{\partial q_{1}}}={\bigg (}{\frac {a-2bq_{1}+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2}}{\bigg )}-{\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}=0.

이제 $q_{1}$ ${\$ $displaystyle q_{$ $1}{$ $1}^{*}}}{$ 1}}}}}{1}}}}}}}{1}}}}}}}}을 $q_{1}$ (를) 통해 리더의 최적의 작업 수행 $q_{1}^{*}$

q_{1}^{*}={\frac {a+{\frac {\partial c_{2}(q_{2})}{\partial q_{2}}:}}{\partial q_{1}{1}}}}}{partial q_{2b}}}.

이것은 평형 상태에서 추종자의 반응에 대한 리더의 최선의 대응이다. 이제 팔로워의 실제는 앞서 계산한 반응 함수에 이를 공급함으로써 찾을 수 있다.

q_{2}^{*}={\frac {a-b\cdot {\frac {a+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}-2\cdot {\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}}{2b}}-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2b}},

\Rightarrow q_{2}^{*}={\frac {a-3\cdot {\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}+2\cdot {\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}}{4b}}.

나시 평형도는 모두 $(q_{1}^{*},q_{2}^{*})$ $(q_{1}^{*},q_{2}^{*})$ ∗, $(q_{1}^{*},q_{2}^{*})$ $(q_{1}^{*},q_{2}^{*})$ $(q_{1}^{*},q_{2}^{*})$ ) ${\displaystyle (q_{1}^{*},q_{2}^{*}}}.$ (소요 비용이 0으로 가정되는 경우) 리더가 유의미한 이점을 갖는 것은 분명하다. 직관적으로 리더가 팔로워보다 나을 것이 없다면, 그것은 단순히 쿠르노 경쟁 전략을 채택할 것이다.

리더의 최상의 응답 기능에 팔로어의 수량 $q_{2}$ $displaystyle q_{2$ }}을 다시 꽂아도 $q_{1}$ ${\$ }가 생성되지 않는다 $q_{1}$ 이는 리더가 한 번 산출물에 전념하고 팔로워를 관찰한 결과 항상 생산량을 감소시키고자 하기 때문이다. 그러나 그것이 그렇게 할 수 없는 것은 쿠르노 밑에서보다 더 높은 이익을 얻을 수 있게 하는 것이다.

경제분석

광범위한 형태 표현은 Stackelberg 리더-팔로워 모델을 분석하는 데 종종 사용된다. "결정 트리"라고도 불리는 이 모델은 두 회사가 Stackelberg 게임에서 가지고 있는 산출물과 보상의 조합을 보여준다.

광범위한 형태로 대표되는 Stackelberg 게임

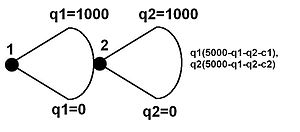
왼쪽의 이미지는 Stackelberg 게임을 광범위하게 묘사하고 있다. 보수는 오른쪽에 표시된다. 이 예는 꽤 간단하다. 한계비용만을 포함하는 기본원가구조가 있다(고정비용은 없다). 수요함수는 선형이고 수요의 가격탄력성은 1이다. 그러나 지도자의 장점을 잘 보여준다.

The follower wants to choose $q_{2}$ to maximise its payoff $q_{2}\times (5000-q_{1}-q_{2}-c_{2})$ . Taking the first order derivative and equating it to zero (for maximisation) yields ${\displaystyle$ $q_{2}={\frac {na-q_{1}-c_{2$ }}:{ $2}}:}}}}$ 을(를) $q_{2}$ $q_{2}$ ${\$ }}의 최대값으로 $q_{2}={\frac {5000-q_{1}-c_{2}}{2}}$ 한다 $q_{2}$

리더는 $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ ( $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ - $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ - $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ - q - $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ - $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ 1) {\ $displaystyle q_{1}\time$ ( $5000-q_{1}-q_{2}-c_{1}}}}}$ 을 최대화하기 위해 q $q_{1}$ 1 ${\$ $displaysty$ q_{1}을 $선택$ 하려고 $하지만,$ 평형 상태에서는 팔로워가 $q_{2}$ $q_{2}$ ${\{$ 1}을 선택할 것임을 $q_{2}$ 알고 있다 $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$ So in fact the leader wants to maximise its payoff $q_{1}\times (5000-q_{1}-{\frac {5000-q_{1}-c_{2}}{2}}-c_{1})$ (by substituting $q_{2}$ for the follower's best response function). 차별화에 의해 최대 보수는 $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$ $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$ = $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$ - 2 $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$ 1 $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$ + c $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$ ${\$ }에 의해 주어진다. $}}{2}}}$ . Feeding this into the follower's best response function yields $q_{2}={\frac {5000+2c_{1}-3c_{2}}{4}}$ . Suppose marginal costs were equal for the firms (so the leader has no market advantage other than first move) and in particular ${\displ$ $aystyle c_{1}=c_{2}=1000}$ . 리더는 2000을 생산하고 추종자는 1000을 생산한다. 이렇게 하면 리더는 200만, 팔로워는 100만 원의 이익을 얻을 수 있을 것이다. 단순히 먼저 움직인다고 해서 리더가 팔로워의 두 배의 이익을 챙겼다. 그러나 여기서 쿠르노트의 이익은 각각 178만 개(엄정, $(16/9)10^{6}$ ) $(16/9)10^{6}$ $(16/9)10^{6}$ ${\$ 스타일 $(16/9)10^{6}}}$ 개당 $(16/9)10^{6}$ 1백 7십8만 개)이므로 리더는 별로 얻지 못했지만 팔로워는 손해를 보았다. 그러나 이것은 예에 따라 다르다. Stackelberg 리더가 독점 이익에 접근하는 Cournot 이익 이상의 막대한 이익을 얻는 경우가 있을 수 있다(예를 들어, 리더 역시 더 나은 생산 기능 때문에 비용 구조상의 이점이 큰 경우). 실제로 리더보다 팔로워가 더 높은 수익을 누리는 사례도 있을 수 있지만, 단지 말하자면 비용이 훨씬 적기 때문일 뿐이다. 이러한 행동은 비록 회사들이 비대칭적이긴 하지만, 양립 시장에서 지속적으로 작용한다.

추종자의 신뢰할 수 있고 신뢰할 수 없는 위협

만약 리더가 평형량을 선택한 후에 추종자가 평형에서 이탈하여 최적하지 않은 양을 선택한다면, 그것은 자신뿐만 아니라 리더에게도 해를 끼칠 수 있다. 추종자가 최선의 대응보다 훨씬 더 많은 양을 선택한다면, 시장 가격은 낮아지고 리더의 이익은 쏘이게 될 것이고, 아마도 쿠르노 수준의 이익에는 미치지 못할 것이다. 이 경우 팔로워는 경기 시작 전에 리더에게 리더가 쿠르노 평형량을 선택하지 않으면 리더의 이익을 타격할 일탈 수량을 선택한다고 발표할 수 있다. 결국 평형 상태에서 리더가 선택한 양은 추종자도 평형 상태에서 플레이해야 최적이다. 그러나 지도자는 위험하지 않다. 일단 리더가 평형량을 선택했다면, 그 평형량도 다치게 되므로 추종자가 일탈하는 것은 비이성적일 것이다. 일단 리더가 선택했으면, 팔로워는 평형길에서 놀음으로써 더 잘 살 수 있다. 따라서 추종자의 그러한 위협은 신뢰할 수 없을 것이다.

그러나 (무제한) 스트라텔베르크 게임을 반복하는 경우, 팔로워가 현 시기의 비최적 전략을 선택하지 않는 한 다음 시기의 리더를 처벌하겠다고 위협하는 처벌 전략을 채택할 수도 있다. 이 위협은 추종자가 다음 기간에 처벌하는 것이 합리적일 수 있기 때문에 신뢰할 수 있으며, 따라서 리더가 쿠르노 수량을 선택할 수 있기 때문이다.

쿠르노와 비교한 Stackelberg

Stackelberg와 Cournot 모델은 두 가지 경쟁 모두 양에 관한 것이기 때문에 유사하다. 그러나, 보시다시피, 첫 번째 움직임은 Stackelberg의 리더에게 결정적인 이점을 준다. 또한 Stackelberg 게임에는 완벽한 정보에 대한 중요한 가정이 있다: 추종자는 리더가 선택한 양을 관찰해야 한다. 그렇지 않으면 게임은 쿠르노로 줄어든다. 불완전한 정보로 위에서 설명한 위협은 믿을 수 있다. 만약 추종자가 지도자의 움직임을 관찰할 수 없다면, 추종자가 코르노의 양 수준(사실 평형 작용)을 선택하는 것은 더 이상 비합리적이지 않다. 그러나 일단 지도자가 움직이면 될 수 있는지 없는지 관찰하지 않는 것은 비이성적이기 때문에 불완전한 정보가 있고 추종자가 지도자의 움직임을 관찰할 수 없다는 것이 틀림없었다. 관측할 수 있다면 최적의 결정을 내릴 수 있도록 할 것이다. 위와 같이 보정할 수 없더라도 관찰하지 않을 것이라고 주장하는 팔로워의 모든 위협. 너무 많은 정보가 선수에게 피해를 준 사례다. 쿠르노 경기에서는 어느 선수도 불리하지 않게 되는 것은 게임의 동시성(지식의 불완전성)이다.

게임 이론적 고려사항

앞서 언급한 바와 같이 리더쉽 게임에서 불완전한 정보는 쿠르노 경쟁으로 전락한다. 단, 일부 Cournot 전략 프로파일은 Nash 평형주의로 지속되지만 서브게임 완성도의 솔루션 개념을 적용하면 (위에서 설명한 바와 같이) 믿을 수 없는 위협으로 제거될 수 있다. 실제로, 그것은 스토텔버그 게임에서 쿠르노 전략의 프로필을 내시 평형으로 만들어 서브게임 완벽을 막는 바로 그것이다.

어떤 이유에서든 리더는 어떤 행동을 취하든 쿠르노트 수량을 선택할 것이라고 믿는 Stackelberg 게임(즉, Stackelberg 평형 유지에 대해 위에서 설명한 요건을 충족하는 게임)을 생각해 보십시오(아마 리더는 추종자가 비합리적이라고 믿고 있을 것이다). 리더가 스트라텔베르크 액션을 했다면, (그것은) 팔로워가 쿠르노를 연기할 것이라고 믿는다. 따라서 리더가 Stackelberg를 연기하는 것은 최적이 아니다. 사실, (쿠르노 평형 정의에 의한) 그것의 최선의 대응은 쿠르노트의 양을 연주하는 것이다. 일단 이렇게 되면 팔로어의 가장 좋은 반응은 쿠르노를 연기하는 것이다.

다음과 같은 전략 프로필을 고려하십시오. 리더는 쿠르노를, 리더는 쿠르노를, 리더는 Stackelberg를, 리더는 다른 것을 플레이하면 추종자는 임의의 전략을 구사한다(이것이 실제로 여러 프로필을 설명한다). 이 프로필은 내시 평형이다. 위에서 주장했듯이 평형 경로 놀이는 최상의 반응에 대한 최선의 반응이다. 그러나 쿠르노를 연기하는 것이 리더의 최선의 반응은 아닐 터였다. 만일 그 (리더)가 스트라텔베르크를 연기한다면 추종자가 스트라텔베르크를 연기할 것이라는 것이었다. 이 경우 리더의 최선의 대응은 스트라텔버그를 연기하는 것이 될 것이다. 따라서 이 프로파일(또는 이 프로파일)을 내시 평형(또는 오히려 내시 평형)으로 만드는 것은 리더가 스토텔버그를 플레이한다면 추종자가 비스테이켈버그를 플레이할 것이라는 사실이다.

그러나 바로 이 사실(리더만 Stackelberg를 한다면 추종자가 비Stackelberg를 한다는 것)은 리더가 이미 Stackelberg(평형 경로를 벗어난 서브게임)를 했을 때 시작되는 서브게임의 Nash 평형이 이 프로파일이 아님을 의미한다. 리더가 이미 Stackelberg를 플레이했다면, 추종자의 최선의 반응은 Stackelberg를 플레이하는 것이다(따라서 이 서브 게임에서 Nash 평형을 산출하는 유일한 액션이다). 따라서 Cournot인 전략 프로파일은 하위 게임에서 완벽하지 않다.

다른 과점 모델과의 비교

다른 과점 모델과 비교했을 때,

애그리게이트 Stackelberg 출력은 애그리게이트 Cournot 출력보다 크지만 애그리게이트 Bertrand 출력보다 작다.
Stackelberg 가격은 Cournot 가격보다 낮지만, Bertrand 가격보다 크다.
Stackelberg 소비자잉여금은 Cournot 소비자잉여금보다 크지만, Bertrand 소비자잉여금보다는 낮다.
Stackelberg의 총 생산량은 순수 독점이나 카르텔보다 크지만, 완벽하게 경쟁적인 생산량보다는 적다.
Stackelberg 가격은 순수 독점 가격이나 카르텔 가격보다 낮지만, 완벽한 경쟁 가격보다 더 크다.

적용들

Stackelberg 개념은 역동적인 Stackelberg 게임으로 확장되었다.^[1]^[2] 시간이 차원으로 추가되면서 리더에 의한 최적성 원칙을 위반하는 등 정적 게임에서는 발견되지 않는 현상이 발견되었다.^[2]

최근 몇 년 동안, Stackelberg 게임은 보안 영역에 적용되었다.^[3] 이 맥락에서 수비수(리더)는 공격자(팔로워)가 채택한 전략과 관계없이 자원이 안전하게 유지되도록 자원을 보호하기 위한 전략을 설계한다. Stackelberg 차등 게임은 공급망과 마케팅 채널의 모델로도 사용된다.^[4] Stackelberg 게임의 다른 응용 프로그램으로는 이기종 네트워크,^[5] 로봇공학,^[6]^[7] 자율 주행 ^[8]^[9]및 전기 그리드가 있다.^[10]^[11]

참고 항목

참조

^ Simaan, M.; Cruz, J. B. (May 1973). "On the Stackelberg strategy in nonzero-sum games". Journal of Optimization Theory and Applications. 11 (5): 533–555. doi:10.1007/BF00935665. ISSN 0022-3239.
^ ^a ^b Simaan, M.; Cruz, J. B. (June 1973). "Additional aspects of the Stackelberg strategy in nonzero-sum games". Journal of Optimization Theory and Applications. 11 (6): 613–626. doi:10.1007/BF00935561. ISSN 0022-3239.
^ Brown, Gerald (2006). "Defending critical infrastructure". Interfaces. 36 (6): 530–544. doi:10.1287/inte.1060.0252. hdl:10945/36732.
^ He, Xiuli; Prasad, Ashutosh; Sethi, Suresh P.; Gutierrez, Genaro J. (December 2007). "A survey of Stackelberg differential game models in supply and marketing channels". Journal of Systems Science and Systems Engineering. 16 (4): 385–413. CiteSeerX 10.1.1.727.2952. doi:10.1007/s11518-007-5058-2. ISSN 1004-3756.
^ Ghosh, Subha; De, Debashis (2021-04-28). "E²M³: energy-efficient massive MIMO–MISO 5G HetNet using Stackelberg game". The Journal of Supercomputing. doi:10.1007/s11227-021-03809-1. ISSN 0920-8542.
^ Koh, Joewie J.; Ding, Guohui; Heckman, Christoffer; Chen, Lijun; Roncone, Alessandro (2020-10-24). "Cooperative Control of Mobile Robots with Stackelberg Learning". 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas, NV, USA: IEEE: 7985–7992. arXiv:2008.00679. doi:10.1109/IROS45743.2020.9341376. ISBN 978-1-7281-6212-6.
^ Ranjbar-Sahraei, Bijan; Stankova, Katerina; Tuyls, Karl; Weiss, Gerhard (2013-09-02). "Stackelberg-based Coverage Approach in Nonconvex Environments". Advances in Artificial Life, ECAL 2013. MIT Press: 462–469. CiteSeerX 10.1.1.650.4481. doi:10.7551/978-0-262-31709-2-ch066. ISBN 978-0-262-31709-2.
^ Yoo, Jehong; Langari, Reza (2020). "A Stackelberg Game Theoretic Model of Lane-Merging". arXiv:2003.09786. Cite 저널은 필요로 한다. journal= (도움말)
^ Cooper, Matt; Lee, Jun Ki; Beck, Jacob; Fishman, Joshua D.; Gillett, Michael; Papakipos, Zoë; Zhang, Aaron; Ramos, Jerome; Shah, Aansh (2019), Salichs, Miguel A.; Ge, Shuzhi Sam; Barakova, Emilia Ivanova; Cabibihan, John-John (eds.), "Stackelberg Punishment and Bully-Proofing Autonomous Vehicles", Social Robotics, Cham: Springer International Publishing, 11876, pp. 368–377, arXiv:1908.08641, doi:10.1007/978-3-030-35888-4_34, ISBN 978-3-030-35887-7, retrieved 2021-05-03
^ Qiu, Haifeng; Gu, Wei; Wang, Lu; Pan, Guangsheng; Xu, Yinliang; Wu, Zhi (June 2021). "Trilayer Stackelberg Game Approach for Robustly Power Management in Community Grids". IEEE Transactions on Industrial Informatics. 17 (6): 4073–4083. doi:10.1109/TII.2020.3015733. ISSN 1551-3203.
^ An, Lu; Chakrabortty, Aranya; Duel-Hallen, Alexandra (2020-12-14). "A Stackelberg Security Investment Game for Voltage Stability of Power Systems". 2020 59th IEEE Conference on Decision and Control (CDC). Jeju, Korea (South): IEEE: 3359–3364. arXiv:2006.11665. doi:10.1109/CDC42340.2020.9304301. ISBN 978-1-7281-7447-1.

H. von Stackelberg, 시장구조 및 평형: 제1판 영어, 바진, 어치 & 힐, 스프링어 2011, XIV, 134 p, ISBN 978-3-642-1285-0
Fudenberg, D. and Tirole, J. (1993) 게임 이론, MIT 프레스. (제3장 제1장 참조)
기븐스, R. (1992) 게임 이론의 입문자, 하베스터-휠라체프. (제2장 제1B절 참조)
M.J. 오스본과 루벤스타인 A. (1994) MIT 프레스 게임 이론 강좌 (97-98 페이지 참조)
헉 딕슨의 서핑경제학 제6장 '간단하게 만든 과점 이론'

[1] Simaan, M.; Cruz, J. B. (May 1973). "On the Stackelberg strategy in nonzero-sum games". Journal of Optimization Theory and Applications. 11 (5): 533–555. doi:10.1007/BF00935665. ISSN 0022-3239.

[:0-2] Simaan, M.; Cruz, J. B. (June 1973). "Additional aspects of the Stackelberg strategy in nonzero-sum games". Journal of Optimization Theory and Applications. 11 (6): 613–626. doi:10.1007/BF00935561. ISSN 0022-3239.

[3] Brown, Gerald (2006). "Defending critical infrastructure". Interfaces. 36 (6): 530–544. doi:10.1287/inte.1060.0252. hdl:10945/36732.

[4] He, Xiuli; Prasad, Ashutosh; Sethi, Suresh P.; Gutierrez, Genaro J. (December 2007). "A survey of Stackelberg differential game models in supply and marketing channels". Journal of Systems Science and Systems Engineering. 16 (4): 385–413. CiteSeerX 10.1.1.727.2952. doi:10.1007/s11518-007-5058-2. ISSN 1004-3756.

[5] Ghosh, Subha; De, Debashis (2021-04-28). "E²M³: energy-efficient massive MIMO–MISO 5G HetNet using Stackelberg game". The Journal of Supercomputing. doi:10.1007/s11227-021-03809-1. ISSN 0920-8542.

[6] Koh, Joewie J.; Ding, Guohui; Heckman, Christoffer; Chen, Lijun; Roncone, Alessandro (2020-10-24). "Cooperative Control of Mobile Robots with Stackelberg Learning". 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas, NV, USA: IEEE: 7985–7992. arXiv:2008.00679. doi:10.1109/IROS45743.2020.9341376. ISBN 978-1-7281-6212-6.

[7] Ranjbar-Sahraei, Bijan; Stankova, Katerina; Tuyls, Karl; Weiss, Gerhard (2013-09-02). "Stackelberg-based Coverage Approach in Nonconvex Environments". Advances in Artificial Life, ECAL 2013. MIT Press: 462–469. CiteSeerX 10.1.1.650.4481. doi:10.7551/978-0-262-31709-2-ch066. ISBN 978-0-262-31709-2.

[8] Yoo, Jehong; Langari, Reza (2020). "A Stackelberg Game Theoretic Model of Lane-Merging". arXiv:2003.09786. Cite 저널은 필요로 한다. journal= (도움말)

[9] Cooper, Matt; Lee, Jun Ki; Beck, Jacob; Fishman, Joshua D.; Gillett, Michael; Papakipos, Zoë; Zhang, Aaron; Ramos, Jerome; Shah, Aansh (2019), Salichs, Miguel A.; Ge, Shuzhi Sam; Barakova, Emilia Ivanova; Cabibihan, John-John (eds.), "Stackelberg Punishment and Bully-Proofing Autonomous Vehicles", Social Robotics, Cham: Springer International Publishing, 11876, pp. 368–377, arXiv:1908.08641, doi:10.1007/978-3-030-35888-4_34, ISBN 978-3-030-35887-7, retrieved 2021-05-03

[10] Qiu, Haifeng; Gu, Wei; Wang, Lu; Pan, Guangsheng; Xu, Yinliang; Wu, Zhi (June 2021). "Trilayer Stackelberg Game Approach for Robustly Power Management in Community Grids". IEEE Transactions on Industrial Informatics. 17 (6): 4073–4083. doi:10.1109/TII.2020.3015733. ISSN 1551-3203.

[11] An, Lu; Chakrabortty, Aranya; Duel-Hallen, Alexandra (2020-12-14). "A Stackelberg Security Investment Game for Voltage Stability of Power Systems". 2020 59th IEEE Conference on Decision and Control (CDC). Jeju, Korea (South): IEEE: 3359–3364. arXiv:2006.11665. doi:10.1109/CDC42340.2020.9304301. ISBN 978-1-7281-7447-1.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

v t 게임 이론의 주제
정의들	혼잡 게임 협동 게임 결정성 약속의 에스컬레이션 포브스폼 게임 1번과 2번 우승 게임 복잡성 게임 설명 언어 그래픽 게임 믿음의 위계 정보 세트 노멀 폼 게임 선호 순차 게임 동시 게임 동시 동작 선택 해결된 게임 간결한 게임
평형 개념	나시 평형 서브게임 완성도 메르텐스-안정성 평형 베이시안 나시 평형 완벽한 베이시안 평형 떨리는 손 적정 평형 엡실론 평형화 상관평형 순차 평형 준완벽 평형 진화적으로 안정된 전략 위험 우위 코어 샤플리 값 파레토 효율 깁스 평형 양자 반응 평형 자기 확인 평형 강한 나시 평형 마르코프 완전 평형
전략들	우세한 전략 순수전략 혼합 전략 전략-스틸링 인수 Tit for tat 그림 트리거 공모 후진 유도 전진 유도 마르코프 전략 입찰 셰이딩
반 사냥감의	협상문제 싸구려 말씨 글로벌 게임 자동 게임 평균 필드 게임 메커니즘 설계 n-플레이어 게임 완벽한 정보 대형 포아송 게임 포텐셜 게임 반복 게임 스크리닝 게임 신호 게임 엄격하게 결정된 게임 확률 게임 대칭 게임 제로섬 게임
게임.	가다 체스 무한 체스 체커스 틱택토 죄수의 딜레마 선물 교환 게임 선택형수의 딜레마 여행자의 딜레마 코디네이션 게임 치킨 지네 게임 루이스 시그널 게임 자원봉사자의 딜레마 달러 경매 성 전투 사슴 사냥 매칭 페니 얼티메이텀 게임 가위바위보 해적 게임 독재자 게임 공공재 게임 블로토 게임 소모전 엘 파롤 바 문제 공정분할 페어 케이크 커팅 쿠르노 게임 교착 상태 다이너의 딜레마 평균의 2/3을 추측하라. 쿤 포커 나시 흥정 게임 유도 퍼즐 트러스트 게임 공주와 괴물 게임 랑데부 문제
정리	화살의 불가능 정리 오만의 합의 정리 민속 정리 미니맥스 정리 내시의 정리 정화 정리 계시의 원리 제르멜로의 정리
키 수치	앨버트 W. 터커 아모스 트베르스키 앙투안 아우구스틴 쿠르노 아리엘 루빈스타인 클로드 섀넌 대니얼 카너 데이비드 K. 레빈 데이비드 M. 크렙스 도널드 B. 길리스 드루 푸덴베르크 에릭 마신 해럴드 쿤 허버트 사이먼 헤르베 물랭 존 콘웨이 장 티롤 장프랑수아 메르텐스 제니퍼 투어 체이스 존 하사니 존 메이너드 스미스 존 나시 존 폰 노이만 케네스 애로우 케네스 빈모어 레오니드 후르비츠 로이드 샤플리 멜빈 드레스허 메릴 M. 홍수 올가 본다레바 오스카르 모겐스턴 폴 밀그롬 페이턴 영 라인하르트 셀턴 로버트 액슬로드 로버트 아우만 로버트 B. 윌슨 로저 마이어슨 새뮤얼 보울스 수잔 스카치머 토머스 셸링 윌리엄 비크리
잡다한	올페이 경매 알파-베타 가지치기 베르트랑 역설 한정적 합리성 콤비네이터 게임 이론 대립분석 쿠페티션 진화 게임 이론 체스의 첫 동작의 이점 게임 설명 언어 게임 역학 게임 이론 용어집 게임 이론가 목록 게임 이론의 게임 목록 승리가 없는 상황 체스 풀기 위상 게임 공동체의 비극 작은 결정의 횡포

Search