일반 폴리토페스 및 화합물 목록

일반 폴리토페스 예제

일반(2D) 다각형
볼록스	별
{5}	{5/2}
일반(3D) 다면체
볼록스	별
{5,3}	{5/2,5}
일반 2D 테셀레이션
유클리드 주	쌍곡선
{4,4}	{5,4}
일반 4D 폴리토페스
볼록스	별
{5,3,3}	{5/2,5,3}
일반 3D 테셀레이션
유클리드 주	쌍곡선
{4,3,4}	{5,3,4}

이 글에는 유클리드, 구형, 쌍곡선 공간에 있는 일반 폴리토페와 일반 폴리토페 화합물이 나열되어 있다.

Schléfli 기호는 n-sphere, 유클리드 및 쌍곡선 공간의 모든 규칙적인 다듬기를 설명한다. n-폴리토프를 설명하는 Schléfli 기호는 (n - 1)-sphere의 다듬기를 동등하게 설명한다. 또 일반 폴리토프나 테셀레이션의 대칭은 콕시터 그룹으로 표현되는데, 콕시터는 콕시터 표기법이라고 하는 표기법인 대괄호로 구분하는 것을 제외하고는 슐레펠리 기호와 동일하게 표현했다. 또 다른 관련 기호는 고리 없는 대칭 그룹을 나타내는 Coxeter-Dynkin 다이어그램이며, 는 첫 번째 노드에 링이 있는 일반 폴리토프 또는 테셀레이션을 나타낸다. 예를 들어, 큐브에는 Schléfli 기호 {4,3}이(가) 있으며, 팔면 대칭인 [4,3] 또는 , Coxeter 다이어그램으로 표시된다.

일반 폴리토프는 치수별로 분류되며 볼록형, 비콘벡스형, 무한형 등으로 분류된다. 비콘벡스 형태는 볼록 형태와 같은 정점을 사용하지만 교차하는 면을 가지고 있다. 무한은 1차원 유클리드 공간을 테셀레이트로 만든다.

무한의 형태는 쌍곡선 공간을 테셀레이트로 확장될 수 있다. 쌍곡선 공간은 작은 규모의 정상 공간과 같지만 평행선은 멀리 떨어져 있다. 이를 통해 정점 수치는 7개의 등각 삼각형으로 정점을 만들고 평평하게 눕게 하는 등 음의 각도 결함을 가질 수 있다. 일반 평면에서는 할 수 없지만 쌍곡면에서는 적절한 스케일이 될 수 있다.

단순한 Schléfli 기호가 없는 일반 폴리탑에 대한 보다 일반적인 정의는 일반 스큐 폴리탑과 비 평면 면 또는 정점 형상을 가진 정규 스큐 아페이로탑을 포함한다.

개요

이 표는 치수별 정규 폴리토프 카운트를 요약한 것이다.

유클리드 및 쌍곡선 기울기는 예상되는 것보다 한 차원 더 많이 주어지는 것에 유의한다. 이는 유한 폴리탑과의 유사성 때문이다: 볼록한 규칙적인 n폴리토프는 (n-1)차원 구면 공간의 테셀레이션으로 볼 수 있다. 따라서 유클리드 평면의 세 가지 정규 기울기(삼각형, 정사각형 및 육각형)는 2가 아닌 치수 3 아래에 나열된다.

Dim.	유한한			유클리드 주	쌍곡선			화합물
					작은		파라콤팩트
	볼록스	별	스큐	볼록스	볼록스	별	볼록스	볼록스	별
1	1	없는	없는	1	없는	없는	없는	없는	없는
2	$\displaystyle \infit }$	$\displaystyle \infit }$	$\displaystyle \infit }$	1	1	없는	없는	$\displaystyle \infit }$	$\displaystyle \infit }$
3	5	4	?	3	$\displaystyle \infit }$	$\displaystyle \infit }$	$\displaystyle \infit }$	5	없는
4	6	10	?	1	4	없는	11	26	20
5	3	없는	?	3	5	4	2	없는	없는
6	3	없는	?	1	없는	없는	5	없는	없는
7	3	없는	?	1	없는	없는	없는	3	없는
8	3	없는	?	1	없는	없는	없는	6	없는
9+	3	없는	?	1	없는	없는	없는	[a]	없는

유클리드 정규 스타 테셀레이션은 어떤 차원에서도 존재하지 않는다.

원차원

Coxeter 다이어그램은 거울 "플레인"을 노드로 나타내며, 점이 평면에 없을 경우 노드 주위에 링을 끼운다. 디온 { }, 는 점 p와 그 거울 영상 포인트 p'이며, 그들 사이의 선 세그먼트이다.

1차원 폴리토프 또는 1 폴리토프는 닫힌 선 세그먼트로, 두 개의 끝점으로 경계를 이룬다. 1 폴리토프는 정의상 규칙적이며 슐레플리 기호 {},^[1][2] 또는 단일 링 노드가 있는 콕시터 도표로 표현된다.노먼 존슨은 이를 디온이라고^[3] 부르며 슐레플리 기호 {}을 부여한다.

폴리토프처럼 사소하지만 폴리곤과 다른 고차원 폴리토페의 가장자리로 나타난다.^[4] 선 세그먼트와 일반 폴리곤의 데카르트 산물로서 Schléfli 기호 {}×{p} 또는 Coxeter 다이어그램과 같은 균일한 프리즘의 정의에 사용된다.^[5]

2차원(폴리곤)

2차원 폴리에스테르는 폴리곤이라고 불린다. 일반 다각형은 등각형이고 순환형이다. p-곤 정규 다각형은 Schléfli 기호 {p}로 표현된다.

보통 볼록한 폴리곤만 규칙적인 것으로 간주되지만, 별 폴리곤은 펜타그램과 마찬가지로 규칙적인 것으로도 간주될 수 있다. 그들은 볼록한 형태와 같은 정점을 사용하지만, 완성되기 위해 원을 두 번 이상 통과하는 대체 연결로 연결된다.

항성 다각형은 교차하는 가장자리가 새로운 정점을 생성하지 않고 모든 정점이 원 경계 위에 존재하기 때문에 오목한 것이 아니라 비콘벡스라고 해야 한다.

볼록스

Schléfli 기호 {p}은(는) 일반 p-곤을 나타낸다.

이름	삼각형 (2-510x)	사각형 (2정형) (2개)	펜타곤 (2-팔폴리토프 )	육각형	헵타곤	팔각형
슐레플리	{3}	{4}	{5}	{6}	{7}	{8}
대칭	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	D8, [8]
콕시터
이미지
이름	논아곤 (에네아곤)	데카곤	헨데카곤	도데카곤	삼각형	테트라데카곤
슐레플리	{9}	{10}	{11}	{12}	{13}	{14}
대칭	D9, [9]	D10, [10]	D11, [11]	D12, [12]	D13, [13]	D14, [14]
딘킨
이미지
이름	펜타데카곤	육각형	헵타데카곤	팔각형	에네아데카곤	이코사곤	...p-곤
슐레플리	{15}	{16}	{17}	{18}	{19}	{20}	{p}
대칭	D15, [15]	D16, [16]	D17, [17]	D18, [18]	D19, [19]	D20, [20]	Dp, [p]
딘킨
이미지

구면

정규 digon {2}은(는) 퇴행성 일반 다각형이라고 볼 수 있다. 그것은 구체나 토러스 표면과 같은 일부 비유클리드 공간에서 비파괴적으로 실현될 수 있다.

이름	모노곤	디곤
슐레플리 기호	{1}	{2}
대칭	D1, [ ]	D2, [2]
콕시터 다이어그램	또는
이미지

별들

슐레플리 기호는 합리적인 숫자 {n/m}(으)로 구성되는 2차원에는 무한히 많은 일반 항성 폴리탑이 존재한다. 그것들은 별 다각형이라고 불리며 볼록한 일반 다각형의 정점 배열을 공유한다.

일반적으로, 자연수 n의 경우, m < n/2(엄정히 말해서 {n/m}={n/(n-m)))와 m과 n이 동시임(따라서, 가장 많은 면수를 가진 폴리곤의 모든 스텔레이션은 정규 항성이 될 것이다)과 같은 모든 m에 대해 슐레플리 기호가 {n/m}인 n-pointed 항성이 있다. m과 n이 복사되지 않는 경우를 복합 폴리곤이라고 한다.

이름	펜타그램	헵타그램		옥타그램	엔네아그램		디카그램	...n그램
슐레플리	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{p/q}
대칭	D5, [5]	D7, [7]		D8, [8]	D9, [9]		D10, [10]	Dp, [p]
콕시터
이미지

최대 20면까지 일반 항성 다각형

{11/2}	{11/3}	{11/4}	{11/5}	{12/5}	{13/2}	{13/3}	{13/4}	{13/5}	{13/6}
{14/3}	{14/5}	{15/2}	{15/4}	{15/7}	{16/3}	{16/5}	{16/7}
{17/2}	{17/3}	{17/4}	{17/5}	{17/6}	{17/7}	{17/8}	{18/5}	{18/7}
{19/2}	{19/3}	{19/4}	{19/5}	{19/6}	{19/7}	{19/8}	{19/9}	{20/3}	{20/7}	{20/9}

구면 틸팅으로만 존재할 수 있는 항성 다각형은 모노곤, 디곤과 유사하게 존재할 수 있지만(예: {3/2}, {5/3}, {5/4}, {7/4}, {9/5}) 자세히 연구되지는 않은 것으로 보인다.

원 표면이 여러 번 미세하게 덮이지 않는 파이앵글과 같은 실패한 항성 다각형도 존재한다.^[6]

스큐 폴리곤

3차원 공간에서는 일반 스큐 폴리곤을 항정신병 폴리곤이라고 하는데, 항정신병 정점 배열이 있고, 가장자리의 부분집합으로 상하의 폴리곤과 하부의 폴리곤 사이에 지그재깅이 있다.

일반 스큐 지그재그 폴리곤 예제

육각형	팔각형	디카곤
D3d, [2+,6]	D4d, [2+,8]	D5d, [2+,10]
{3}#{ }	{4}#{ }	{5}#{ }	{5/2}#{ }	{5/3}#{ }

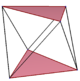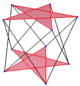4차원에서는 일반 스큐 폴리곤이 클리포드 토러스 위에 정점을 가질 수 있으며 클리포드 변위와 관련이 있다. 항정신병적 꼬치 다각형과 달리 이중 회전 시 꼬치 다각형은 변이 홀수일 수 있다.

그것들은 Coxeter 평면 투영의 둘레에서 일반 평면 폴리곤으로 보이는 볼록형 4 폴리곤의 페트리 폴리곤에서 볼 수 있다.

펜타곤	팔각형	도데카곤	트라이아콘타곤
5세포	16 셀	24셀	600셀

3차원(폴리헤드라)

3차원에서는 폴리토프를 폴리헤드라라고 부른다.

Schléfli 기호가 {p,q}이고 Coxeter 다이어그램이 있는 일반 다면체에는 정규 얼굴형 {p}과(와) 정규 정점 그림 {q}이(가) 있다.

(다면체의 정점)은 폴리곤으로, 주어진 정점에서 한 쪽 가장자리 떨어져 있는 정점을 연결함으로써 볼 수 있다. 정규 다면체의 경우 이 꼭지점 그림은 항상 정규(및 평면) 다각형이다.

정규 다면체 {p,q}의 존재는 정점 그림의 각도 결함과 관련된 불평등에 의해 제한된다.

${\displaystyle {\frac{1}&{\frac {1}{p}+{\frac {1}{q}}{\frac {1}{2}}:{\text{폴리헤드론(유클리드 3-공간에 있음)}}\\[6pt]&#{\frac {1}{1}:{p}+{\frac {1}{q}={\frac {1}{1}:{2}}:{\text{유클리드 평면 타일링}\\[6pt]&#{\frac {1}{p}+{\frac{1}{1}{q}<{\frac {1}{2}}:{\text{Hyperbolic Plane tiling}\end{arged}}$

순열을 열거하면 5개의 볼록 형태, 4개의 별 모양, 3개의 평면 기울기를 찾을 수 있는데, 모두 {3}, {4}, {5/2}, {6}로 제한된 다각형 {p} 및 {q}을(를) 찾을 수 있다.

유클리드 공간 너머에는 규칙적인 쌍곡선 기울기가 무한히 놓여 있다.

볼록스

5개의 볼록한 일반 다면체를 플라토닉 고형분이라고 부른다. 정점 수치는 각 정점 카운트와 함께 주어진다. 이 모든 다면체는 오일러 특성( ()이 2이다.

이름	슐레플리 {p,q}	콕시터	이미지 (솔리드)	이미지 (Sphere)	얼굴 {p}	가장자리	정점 {q}	대칭	이중
사면체 (3-630x)	{3,3}				4 {3}	6	4 {3}	Td [3,3] (*332)	(셀프)
육면체 큐브 (3개)	{4,3}				6 {4}	12	8 {3}	Oh [4,3] (*432)	팔면체
팔면체 (3정맥)	{3,4}				8 {3}	12	6 {4}	Oh [4,3] (*432)	큐브
도데카헤드론	{5,3}				12 {5}	30	20 {3}	Ih [5,3] (*532)	이코사헤드론
이코사헤드론	{3,5}				20 {3}	30	12 {5}	Ih [5,3] (*532)	도데카헤드론

구면

구면 기하학에서는 그렇지 않으면 폴리토페스로 퇴보될 정규 구면 다면체(구체의 기울기)가 존재한다. 이들은 호소헤드라 {2,n}과(와) 이중 디헤드라 {n,2}이다. Coxeter는 이러한 경우를 테셀레이션의 "악화"라고 부른다.^[7]

처음 몇 가지 사례(n 2부터 6까지)는 아래에 열거되어 있다.

호소헤드라

이름	슐레플리 {2,p}	콕시터 도표를 만들다	이미지 (Sphere)	얼굴 {2}π/p	가장자리	정점 {p}	대칭	이중
디지날 호소헤드론	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	셀프
삼각음소헤드론	{2,3}			3 {2}π/3	3	2 {3}	D3h [2,3] (*322)	삼면체
정사각형 호소헤드론	{2,4}			4 {2}π/4	4	2 {4}	D4h [2,4] (*422)	정방면체
오각형 호소헤드론	{2,5}		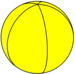	5 {2}π/5	5	2 {5}	D5h [2,5] (*522)	펜타곤 디헤드론
육각양수면체	{2,6}			6 {2}π/6	6	2 {6}	D6h [2,6] (*622)	육각다이헤드론

디헤드라

이름	슐레플리 {p,2}	콕시터 도표를 만들다	이미지 (Sphere)	얼굴 {p}	가장자리	정점 {2}	대칭	이중
디지온 다이헤드	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	셀프
삼면체	{3,2}			2 {3}	3	3 {2}π/3	D3h [3,2] (*322)	삼각음소헤드론
정방면체	{4,2}			2 {4}	4	4 {2}π/4	D4h [4,2] (*422)	정사각형 호소헤드론
펜타곤 디헤드론	{5,2}			2 {5}	5	5 {2}π/5	D5h [5,2] (*522)	오각형 호소헤드론
육각다이헤드론	{6,2}			2 {6}	6	6 {2}π/6	D6h [6,2] (*622)	육각양수면체

항성-다이헤드라 및 호소헤드라 {p/q,2} 및 {2,p/q}도 모든 항성 폴리곤 {p/q}에 대해 존재한다.

별들

일반 항성 다면체는 케플러-푸인소 다면체라고 불리며, 도면체 {5,3} 및 이면체 {3,5}의 정점 배열을 기준으로 4개가 있다.

구면 기울기로서 이들 항성 형태는 그 밀도라고 불리는 구체와 여러 번 겹쳐지며, 이러한 형태에 대해서는 3 또는 7이 된다. 타일링 이미지는 노란색으로 단일 구형 다각형 면을 보여준다.

이름	이미지 (알파벳어	이미지 (솔리드)	이미지 (Sphere)	스텔레이션 도표를 만들다	슐레플리 {p,q} 및 콕시터	얼굴 {p}	가장자리	정점 {q} 말벌의	χ	밀도	대칭	이중
소절개도면체					{5/2,5}	12 {5/2}	30	12 {5}	−6	3	Ih [5,3] (*532)	대두면체
대두면체					{5,5/2}	12 {5}	30	12 {5/2}	−6	3	Ih [5,3] (*532)	소절개도면체
그레이트 스틸 도데카헤드론					{5/2,3}	12 {5/2}	30	20 {3}	2	7	Ih [5,3] (*532)	대이코사면체
대이코사면체					{3,5/2}	20 {3}	30	12 {5/2}	2	7	Ih [5,3] (*532)	그레이트 스틸 도데카헤드론

실패한 별 다면체는 무한히 많다. 이것들은 또한 슐레플리 기호에 별 폴리곤이 있는 구형 틸링이지만 구를 여러 번 정밀하게 덮지는 않는다. 일부 예로는 {5/2,4}, {5/2,9}, {7/2,3}, {5/2,5/2}, {7/2,7/3}, {4,5/2}, {3,7/3} 등이 있다.

스큐 다면체

정규 스큐 폴리헤드라는 일반 다면체 집합에 대한 일반화로서, 비 평면 정점 그림의 가능성을 포함한다.

4차원 스큐 폴리헤드라의 경우, 콕시터는 이러한 수치들에 대해 수정된 Schléfli 기호 {l,m n}을 제공했는데, 이 기호들은 정점 수치를 암시하는 {l,m}, 정점 주위의 m l-곤과 n-곤홀을 의미한다. 그들의 꼭지점 수치는 두 평면 사이를 지그재그하는, 꼬불꼬불한 다각형이다.

{l,m n}(으)로 표현되는 일반 스큐 폴리헤드라는 다음 방정식을 따른다.

2 sin(π/l) sin(π/m) = cos(π/n)

4차원에서는 4개의 정점 배열과 가장자리 배열을 공유하는 4개의 일반 4폴리탑 면의 부분 집합체로 볼 수 있다.

{4, 6 3}	{6, 4 3}	{4, 8 3}	{8, 4 3}

4차원

Regular 4-polytopes with Schläfli symbol ${\displaystyle \{p,q,r\}}$ have cells of type ${\displaystyle \{p,q\}}$, faces of type ${\displaystyle \{p\}}$, edge figures ${\displaystyle \{r\}}$, and vertex figures ${\displaystyle \{q,r\}}$.

• 정점 그림(4 폴리토프의 정점)은 다면체로서, 주어진 정점 주위에 인접한 정점의 배열로 볼 수 있다. 정규 4폴리탑의 경우, 이 꼭지점은 정규 다면체다.
• 가장자리 그림은 가장자리 주위의 얼굴 배열로 볼 수 있는 다각형이다. 일반 4폴리탑의 경우, 이 가장자리 그림은 항상 일반 다각형이 될 것이다.

정규 4폴리토프${\displaystyle }${${\displaystyle p,}$ ${\displaystyle q,}$ ${\displaystyle r}$ ${\displaystyle \}}$ ${\displaystyle \{p,$${\displaystyle q}$$,r\}}$의 존재는 정규 다면체${\displaystyle }${p,${\displaystyle \{p,q,r\}}}$의 존재에 의해 제약된다$.$ 4폴리토프의 제안된 이름은 "폴리초론"^[8]이다.

각각은 다음 표현식에 따라 공간에 존재할 것이다.

${\displaystyle \sin \left\frac {}{p}\pi \right)\sin \refac\{r}\cos \left({\frac {}{q}\right)}$

${\displaystyle >0}$ : 초심 3공간 벌집 또는 4폴리토프

${\displaystyle =}$ ${\displaystyle 0}$ ${\displaystyle =0}$ $$: 유클리드 3-공간 벌집

${\displaystyle <0}$ : 쌍곡 3공간 벌집형

이러한 제약조건은 21개의 형태를 허용한다: 6개는 볼록, 10개는 비콘벡스, 1개는 유클리드 3칸 벌집, 4개는 쌍곡 벌집이다.

볼록 4폴리탑의 오일러$$ 특성 $\chi {\displaystyle }$ ${\displaystyle$\chi}은$($는) $0{\displaystyle }$: :${\displaystyle }$= ${\displaystyle V}$+ ${\displaystyle F}$- ${\displaystyle E}$- ${\displaystyle C}$= ${\displaystyle 0}$ ${\displaystyle \chi$ = $V+F-E-C=0}$

볼록스

6개의 볼록한 정규 4폴리탑은 아래 표에 나와 있다. 이 4폴리토프는 모두 오일러 특성(χ)이 0이다.

이름	슐레플리 {p,q,r}	콕시터	세포 {p,q}	얼굴 {p}	가장자리 {r}	정점 {q,r}	이중 {r,q,p}
5세포 (4-980x)	{3,3,3}		5 {3,3}	10 {3}	10 {3}	5 {3,3}	(셀프)
8셀 (4-11) (테서랙트)	{4,3,3}		8 {4,3}	24 {4}	32 {3}	16 {3,3}	16 셀
16 셀 (4인칭)	{3,3,4}		16 {3,3}	32 {3}	24 {4}	8 {3,4}	테세락트
24셀	{3,4,3}		24 {3,4}	96 {3}	96 {3}	24 {4,3}	(셀프)
120 셀	{5,3,3}		120 {5,3}	720 {5}	1200 {3}	600 {3,3}	600셀
600셀	{3,3,5}		600 {3,3}	1200 {3}	720 {5}	120 {3,5}	120 셀

5세포	8셀	16 셀	24셀	120 셀	600셀
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
와이어프레임(페트리 폴리곤) 스큐 직교 투영
솔리드 직교 투영
사방면체 (세포/세포) 꼭지점 중심)	세제곱 봉투 (세포 중심)	세제곱 봉투 (세포 중심)	육면체의 봉투 (세포 중심)	잘린 롬브릭 삼권면체 봉투 (세포 중심)	펜타키스 이코시다데카헤드랄 봉투 (제곱 중심)
와이어프레임 슐레겔 도표(내성 투영)
(세포 중심)	(세포 중심)	(세포 중심)	(세포 중심)	(세포 중심)	(제곱 중심)
와이어프레임 스테레오 투영(하이퍼시픽션

구면

Di-4-topes와 hoso-4-topes는 3-sphere의 일반 테셀레이션으로 존재한다.

Regular di-4-topes (2 facets) include: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2}, and their hoso-4-tope duals (2 vertices): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. 4-polytopes of the form {2,p,2} are the same as {2,2,p}. 또한 이면세포와 음면정점 형상을 가진 사례 {p,2,q}도 있다.

3-sphere 허니컴으로서의 일반 호소-4-톱

슐레플리 {2,p,q}	콕시터	세포 {2,p}π/q	얼굴 {2}π/p,π/q	가장자리	정점	정점수 {p,q}	대칭	이중
{2,3,3}		4 {2,3}π/3	6 {2}π/3,π/3	4	2	{3,3}	[2,3,3]	{3,3,2}
{2,4,3}		6 {2,4}π/3	12 {2}π/4,π/3	8	2	{4,3}	[2,4,3]	{3,4,2}
{2,3,4}		8 {2,3}π/4	12 {2}π/3,π/4	6	2	{3,4}	[2,4,3]	{4,3,2}
{2,5,3}		12 {2,5}π/3	30 {2}π/5,π/3	20	2	{5,3}	[2,5,3]	{3,5,2}
{2,3,5}		20 {2,3}π/5	30 {2}π/3,π/5	12	2	{3,5}	[2,5,3]	{5,3,2}

별들

슐레플리-헤스 4폴리토페스라고 불리는 10개의 일반 별 4폴리토페스가 있다. 그들의 정점은 볼록 120 셀 {5,3,3}과 600 셀 {3,3,5}에 기초한다.

루트비히 슐레플리는 세포나 정점 수치에 오일러 특성을 실패한 형태를 허용하지 않기 때문에 그 중 4개를 찾아내고 마지막 6개를 건너뛰었다. F+V−E=2). 에드먼드 헤스(1843–1903)는 자신의 독일 책 '아인레이퉁(Einleitung in die Lehre von der Kougelteilung mithor Beruksichigung Ihrer Anwendung auf die Theory der Gleichflichen und der 1883)'에서 10개의 전체 목록을 완성했다.

직교 투영으로 표시된 이들 10개의 일반 별 4-폴리탑에서 4개의 고유한 가장자리 배열과 7개의 고유한 얼굴 배치가 있다.

이름	와이어프레임	고체	슐레플리 {p,q,r} 콕시터	세포 {p,q}	얼굴 {p}	가장자리 {r}	정점 {q,r}	밀도	χ	대칭군	이중 {r,q,p}
이코사헤드랄120세포 (면적 600 셀)			{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480	H4 [5,3,3]	소형강관 120셀
소형강관 120셀			{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480	H4 [5,3,3]	이코사헤드랄120세포
그레이트 120 셀			{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0	H4 [5,3,3]	셀프듀얼
그랜드 120 셀			{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0	H4 [5,3,3]	그레이트 스틸 120 셀
그레이트 스틸 120 셀			{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0	H4 [5,3,3]	그랜드 120 셀
그랜드 스틸 120 셀			{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0	H4 [5,3,3]	셀프듀얼
대그랜드 120 셀			{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480	H4 [5,3,3]	대이심면 120세포
대이심면 120세포 (대단한 면 600 셀)			{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480	H4 [5,3,3]	대그랜드 120 셀
그랜드 600 셀			{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0	H4 [5,3,3]	대그랜드 스티어 120셀
대그랜드 스티어 120셀			{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0	H4 [5,3,3]	그랜드 600 셀

4개의 잠재적 일반 별 4-폴리토페 순열 실패가 있다: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. 그들의 세포와 정점 수치는 존재하지만, 그들은 한정된 반복 횟수로 하이퍼스피어를 덮지 않는다.

5차원 이상

In five dimensions, a regular polytope can be named as ${\displaystyle \{p,q,r,s\}}$ where ${\displaystyle \{p,q,r\}}$ is the 4-face type, ${\displaystyle \{p,q\}}$ is the cell type, ${\displaystyle \{p\}}$ is the face type, and ${\displaystyle \{s\}}$ is the face figure,${\displaystyle }${ ${\displaystyle r}$, ${\displaystyle s}$ ${\displaystyle \}}$ ${\displaystyle \{r$${\displaystyle ,s}$$\}$이(가) 가장자리 그림이고$,{\displaystyle }$ {${\displaystyle q,r}$,s\}${\displaystyle \{q,r,s\}}$이(가) 꼭지 그림이다$$.

정점 그림(5 폴리토프의 정점)은 4 폴리토프로, 각 정점에 대한 인접 정점의 배열로 볼 수 있다.

가장자리 그림(5 폴리토프)은 다면체로서, 각 가장자리 주위에 면의 배열로 볼 수 있다.

얼굴 모양(5폴리토프)은 폴리곤으로, 각 얼굴 주위에 세포가 배열되어 있는 것으로서 볼 수 있다.

일반 5-폴리토프$\{{\displaystyle }$$p$${\displaystyle }$,$$${\displaystyle q}$, ${\displaystyle r}$, ${\displaystyle s}$ ${\displaystyle \}}$ ${\디스플레이$ 스타일 $\{p,q,r,s\}}$ {${\displaystyle p,q}$,$\}$ $\{\backslash {\displaystyle }$$디스플레이$ 스타일 $\{$이$({\displaystyle }$가$)$ 일반 4-폴리토프인 경우에만 존재한다$$.

이 장치가 맞는 공간은 다음 표현식에 기반한다.

${\displaystyle {\frac {\cos ^{2}\왼쪽 사진\frac {\pi }{q}\오른쪽)}}{\sin ^{2}\왼쪽 사진\frac {\pi }{p}\오른쪽)}}}+{\frac {\cos ^{2}\왼쪽 사진\frac {\pi }{r}\오른쪽)}}{\sin ^{2}\왼쪽 사진\frac {\pi }{s}}\오른쪽)}}}$

${\displaystyle <1}$ : 구형 4칸 테셀레이션 또는 5칸 폴리토프

${\displaystyle =}$ ${\displaystyle 1}$ $[\displaystyle =1}$ $$: 유클리드 4공간 테셀레이션

$[\displaystyle >1}$ : 쌍곡선 4공간 테셀레이션

이러한 제약조건을 열거하면 볼록폴록 3개, 비콘벡스폴리토페 0개, 4칸테셀레이션 3개, 쌍곡 4칸테셀레이션 5개가 발생한다. 5차원 이상의 비콘벡스 일반 폴리토페스는 없다.

볼록스

치수 5 이상에서는 볼록한 일반 폴리토프의 종류가 3종류밖에 없다.^[9]

이름	슐레플리 기호 {p1,...,pn−1}	콕시터	k-sness	면 타자를 치다	꼭지점 형상을 나타내다	이중
n-제곱스	{3n−1}	...	${\displaystyle {{n+1} \{k+1} 선택$	{3n−2}	{3n−2}	셀프듀얼
n-sness	{4,3n−2}	...	${\displaystyle 2^{n-k}{n \선택 k}}$	{4,3n−3}	{3n−2}	n-정통주의
n-정통주의	{3n−2,4}	...	${\displaystyle 2^{k+1}{n \선택 {k+1}$	{3n−2}	{3n−3,4}	n-sness

슐래플리 기호의 일부 숫자가 2인 경우도 있다. 예를 들어, {p,q,r,...{p,q,r...에 따라 {p,q,r...}이(가) 부적절한 일반 구형 폴리토프다.{}은(는) 정규 구형 폴리토프이며, {...p,q,r}은(는) 정규 구형 폴리토프일 때마다 부적절한 정규 구형 폴리토프다. 그러한 폴리토프는 면으로도 사용될 수 있으며, {p,q, ...2...y,z}과 같은 형태를 산출한다.

5차원

이름	슐레플리 기호 {p,q,r,s} 콕시터	면 {p,q,r}	세포 {p,q}	얼굴 {p}	가장자리	정점	면 형상을 나타내다 {s}	가장자리 형상을 나타내다 {r,s}	꼭지점 형상을 나타내다 {q,r,s}
5와섹스	{3,3,3,3}	6 {3,3,3}	15 {3,3}	20 {3}	15	6	{3}	{3,3}	{3,3,3}
5시 15분	{4,3,3,3}	10 {4,3,3}	40 {4,3}	80 {4}	80	32	{3}	{3,3}	{3,3,3}
5형식	{3,3,3,4}	32 {3,3,3}	80 {3,3}	80 {3}	40	10	{4}	{3,4}	{3,3,4}

5와섹스

5시 15분

5형식

6차원

이름	슐레플리	정점	가장자리	얼굴	세포	4시 15분	5시 15분	χ
6-630x	{3,3,3,3,3}	7	21	35	35	21	7	0
6시 15분	{4,3,3,3,3}	64	192	240	160	60	12	0
6형식	{3,3,3,3,4}	12	60	160	240	192	64	0

6-630x

6시 15분

6형식

7차원

이름	슐레플리	정점	가장자리	얼굴	세포	4시 15분	5시 15분	6시 15분	χ
7시 15분	{3,3,3,3,3,3}	8	28	56	70	56	28	8	2
7시 15분	{4,3,3,3,3,3}	128	448	672	560	280	84	14	2
7형식	{3,3,3,3,3,4}	14	84	280	560	672	448	128	2

7시 15분

7시 15분

7형식

8차원

이름	슐레플리	정점	가장자리	얼굴	세포	4시 15분	5시 15분	6시 15분	7시 15분	χ
8시 15분	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	0
8시 15분	{4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	0
8인조	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256	0

8시 15분

8시 15분

8인조

9차원

이름	슐레플리	정점	가장자리	얼굴	세포	4시 15분	5시 15분	6시 15분	7시 15분	8시 15분	χ
9시 15분	{38}	10	45	120	210	252	210	120	45	10	2
9시 15분	{4,37}	512	2304	4608	5376	4032	2016	672	144	18	2
9형식	{37,4}	18	144	672	2016	4032	5376	4608	2304	512	2

9시 15분

9시 15분

9형식

10차원

이름	슐레플리	정점	가장자리	얼굴	세포	4시 15분	5시 15분	6시 15분	7시 15분	8시 15분	9시 15분	χ
10센트짜리	{39}	11	55	165	330	462	462	330	165	55	11	0
10시 30분	{4,38}	1024	5120	11520	15360	13440	8064	3360	960	180	20	0
십중팔구	{38,4}	20	180	960	3360	8064	13440	15360	11520	5120	1024	0

10센트짜리

10시 30분

십중팔구

...

논콘벡스

저차원 비콘벡스 일반 폴리토페스로 형성된 호소토페스를 제외한 5차원 이상의 비콘벡스 일반 폴리토페스는 없다.

일반 투영 폴리토페스

원래 n구형 정규 테셀레이션 {p,q, ...}이(가) 중심 대칭일 때 투영 정규(n+1)-폴리토프가 존재한다. 그러한 폴리토프는 헤미-{p,q,...}라고 이름 붙여지고 절반의 원소를 포함하고 있다. 콕시터는 {p,q,...}}/2, McMullen이 {p,q,...}(_h/2h)를 콕시터 번호로 지정함.^[10]

짝측 일반 폴리곤에는 헤미-2n곤 투영 폴리곤, {2p}/2가 있다.

플라톤 고형분 5개 중 4개와 관련된 4개의 정규 투영 다면체가 있다.

헤미-큐브와 헤미-옥타헤드론은 어떤 차원에서도 헤미-n-큐브와 헤미-정맥으로 일반화된다.

정규투영다면체

3차원 일반 헤미토프

이름	콕시터 맥멀런	이미지	얼굴	가장자리	정점	χ
헤미큐브	{4,3}/2 {4,3}3		3	6	4	1
헤미옥타헤드론	{3,4}/2 {3,4}3		4	6	3	1
헤미도데카헤드론	{5,3}/2 {5,3}5		6	15	10	1
헤미이코사면체	{3,5}/2 {3,5}5		10	15	6	1

일반 투영형 4폴리토프

4차원 6개의 볼록형 4폴리탑 중 5개는 투영형 4폴리탑을 생성한다. 특례 3건은 헤미-24셀, 헤미-600셀, 헤미-120셀이다.

4차원 일반 헤미토프

이름	콕시터 심볼	맥멀런 기호	세포	얼굴	가장자리	정점	χ
헤미테세락트	{4,3,3}/2	{4,3,3}4	4	12	16	8	0
헤미-16 셀	{3,3,4}/2	{3,3,4}4	8	16	12	4	0
헤미-24 셀	{3,4,3}/2	{3,4,3}6	12	48	48	12	0
헤미-120 셀	{5,3,3}/2	{5,3,3}15	60	360	600	300	0
헤미-600 셀	{3,3,5}/2	{3,3,5}15	300	600	360	60	0

일반 투영 5폴리토프

치수 5 이상에는 볼록한 정규 투영 헤미폴리탑이 2개만 있다.

이름	슐레플리	4시 15분	세포	얼굴	가장자리	정점	χ
헤미펜터액트	{4,3,3,3}/2	5	20	40	40	16	1
헤미펜타크로스	{3,3,3,4}/2	16	40	40	20	5	1

아페이로토페스

아페이로토프 또는 무한 폴리토프는 무한히 많은 면을 가진 폴리토프다. n-아페이로토프는 무한대 n-폴리토프: 2-아페이로토프 또는 아페이로곤은 무한대 다각형, 3-아페이로프 또는 아페이로헤드론은 무한대 다면체 등이다.

아페이로토프에는 두 가지 주요 기하학적 등급이 있다.^[11]

• n차원 공간을 완전히 채우는 n차원의 일반 허니컴.
• 더 높은 공간에 있는 n차원 다지관을 구성하는 일반 스큐 아페이로톱.

원차원(아페이로곤)

직선 아페이로곤은 선을 규칙적으로 다듬은 것으로, 선을 무한히 많은 동등한 부분으로 세분화한다. 그것은 정점과 가장자리가 무한히 많다. Schléfli의 기호는 {∞}이고 Coxeter 도표는 입니다.

......

p가 무한성을 지향함에 따라 p-곤의 한계로서 다음과 같이 존재한다.

이름	모노곤	디곤	삼각형	사각형	펜타곤	육각형	헵타곤	p-곤	아페이로곤
슐레플리	{1}	{2}	{3}	{4}	{5}	{6}	{7}	{p}	{∞}
대칭	D1, [ ]	D2, [2]	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	[p]
콕시터	또는
이미지

쌍곡면에 있는 아페이로곤, 가장 두드러지는 정규 아페이로곤, {∞}은 유클리드 평면의 유한 폴리곤과 마찬가지로 곡률을 가질 수 있으며, 정점은 원이 아닌 호로사이클이나 하이퍼사이클에 의해 제한된다.

무한대로 수렴하기 위해 크기가 조정되는 일반 아페이로곤은 {}} 기호를 가지고 있고 호로사이클에 존재하는 반면, 보다 일반적으로 하이퍼사이클에 존재할 수 있다.

{∞}	{πi/λ}
아페이로곤을 탄 아페이로곤	하이퍼사이클의 에이페이로곤

위는 푸앵카레 디스크 모델에서 두 개의 규칙적인 쌍곡선 아페이로곤이며, 오른쪽은 길이 λ으로 구분된 서로 다른 기본 영역의 수직 반사선을 보여준다.

꼬챙이 아페이로곤

2차원의 꼬챙이 아페이로곤은 비행기에서 지그재그 선을 형성한다. 만약 지그재그가 고르고 대칭이라면, 아페이로곤은 규칙적이다.

꼬챙이 아페이로곤은 어떤 치수든 만들 수 있다. 3차원에서는 보통 꼬챙이 아페이로곤이 나선형 나선형을 추적하며 왼손 또는 오른손잡이일 수 있다.

2시 30분	3시 30분
지그재그 아페이로곤	헬릭스 아페이로곤

2차원(아페이로헤드라)

유클리드 기울기

그 비행기의 정기 테셀레이션은 세 가지 있다. 세 개 모두 오일러 특성(χ)이 0이다.

이름	사각 타일링 (실제)	삼각 타일링 (델티유)	육각 타일링 (헥스티유)
대칭	p4m, [4,4], (*442)	p6m, [6,3], (*632)
슐래플리 {p,q}	{4,4}	{3,6}	{6,3}
콕시터 다이어그램
이미지

두 가지 부적절한 규칙적인 기울기가 있다: {196,2}, apirogonal dihedron, 각각 두 개의 apirogon으로 만들어졌고 각각 평면의 절반을 채웠다. 그리고 두 번째로, 무한 평행선의 집합으로 보이는 그것의 이중, {2,370].

{∞,2},

{2,∞},

유클리드 항성 기울기

항성 다각형의 일반적인 평면 기울기는 없다. {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12} 등 평면에 맞는 열거(1/p + 1/q = 1/2)가 많지만 주기적으로 반복되는 것은 없다.

쌍곡 틸팅

쌍곡선 2공간의 테셀레이션은 쌍곡선 기울기이다. H에는² 무한히 많은 규칙적인 기울기가 있다. 위에서 설명한 것처럼 모든 양의 정수 쌍 {p,q}이(가) 1/p + 1/q < 1/2이 쌍곡선 타일링을 준다. 실제로 일반 슈바르츠 삼각형(p, q, r)의 경우 1/p + 1/q + 1/r < 1에 대해서도 동일하게 유지된다.

쌍곡면을 표시하는 방법에는 다음과 같이 비행기를 원형으로 매핑하는 푸앵카레 디스크 모델을 포함하여 여러 가지가 있다. 아래 틸팅에 있는 모든 폴리곤 면은 크기가 같고 적용된 투영으로 인해 가장자리 근처만 작아지는 것으로 나타나며 카메라 피시아이 렌즈의 효과와 매우 유사하다는 점을 인식해야 한다.

쌍곡면(ppp,q})의 정기 기울기로서 p+q<pq/2(이전에는 테셀레이션으로 나열됨)와 함께 무한히 많은 평평한 정규 3-apeirotopes(apeirohedra)가 있다.

• {3,7}, {3,8}, {3,9} ... {3,∞}
• {4,5}, {4,6}, {4,7} ... {4,∞}
• {5,4}, {5,5}, {5,6} ... {5,∞}
• {6,4}, {6,5}, {6,6} ... {6,∞}
• {7,3}, {7,4}, {7,5} ... {7,∞}
• {8,3}, {8,4}, {8,5} ... {8,∞}
• {9,3}, {9,4}, {9,5} ... {9,∞}
• ...
• {∞,3}, {∞,4}, {∞,5} ... {∞,∞}

샘플링:

일반 쌍곡선 타일링 테이블 v t
구면(향상/원형)/유클리드/하이퍼볼릭(Poincaré 디스크: 컴팩트/파라콤팩트/비컴팩트) 테셀레이션(Schléfli 기호 포함)
p \ q	2	3	4	5	6	7	8	...	∞	...	이스트/이스트
2	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}		{2,∞}		{2,ihost/message}
3	{3,2}	(삼면체) {3,3}	(옥타헤드론) {3,4}	(이코사면체) {3,5}	(델티유) {3,6}	{3,7}	{3,8}		{3,∞}		{3,i6/190}
4	{4,2}	(iii) {4,3}	(실제) {4,4}	{4,5}	{4,6}	{4,7}	{4,8}		{4,∞}		{4,iiju/message}
5	{5,2}	(도면체) {5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}		{5,∞}		{5,i6/190}
6	{6,2}	(헥스티유) {6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}		{6,∞}		{6,i19/190}
7	{7,2}	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}		{7,∞}		{7,i19/190}
8	{8,2}	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}		{8,∞}		{8,i19/190}
...
∞	{∞,2}	{∞,3}	{∞,4}	{∞,5}	{∞,6}	{∞,7}	{∞,8}	{∞,∞}	{message,ihost/message}
...
이스트/이스트	{iπ/limits,2}	{iπ/limits,3}	{iπ/limits,4}	{iπ/limits,5}	{iπ/limits,6}	{iπ/limits,7}	{iπ/limits,8}	{iπ/limits,properties}	{iπ/limit,iπ/limit}

쌍곡선 항성 기울기

얼굴이나 정점 수치가 별 다각형인 쌍곡선 기울기의 무한 형태는 2가지가 있다: {m/2, m}과(m = 7, 9, 11, ....)와 그 이중 형태는 {m, m/2}이다. {m/2, m} 기울기는 {m, 3} 기울기의 스텔링이고, {m, m/2} 이중 기울기는 {m, 3} 기울기의 면과 {m, 3} 기울기의 그레이팅이다.

{m/2, m}, {m, m/2} 패턴은 다면체로서 홀수 m < 7에 대해 계속된다: m = 5일 때, 우리는 작은 스티드 도면체 및 큰 도면체를 얻으며, m = 3일 때 사례가 사면체로 변질된다. 다른 두 개의 케플러-푸인소트 다면체(대단백질 도데카헤드론과 대단백질)는 규칙적인 쌍곡선 타일링 유사체를 가지고 있지 않다. m이 짝수라면 {m/2}을(를) 어떻게 정의하느냐에 따라 다른 틸팅의 퇴행 이중 커버나 복합 틸팅을 얻을 수 있다.

이름	슐레플리	콕시터 다이어그램	이미지	얼굴형 {p}	정점수 {q}	밀도	대칭	이중
순서 7 헵타그램 타일링	{7/2,7}			{7/2}	{7}	3	*732 [7,3]	헵타그램 순서 헵타곤 타일링
헵타그램 순서 헵타곤 타일링	{7,7/2}			{7}	{7/2}	3	*732 [7,3]	순서 7 헵타그램 타일링
순서 9 에니어그램 타일링	{9/2,9}			{9/2}	{9}	3	*932 [9,3]	엔네아그램 순서 엔네오각 타일링
엔네아그램 순서 엔네오각 타일링	{9,9/2}			{9}	{9/2}	3	*932 [9,3]	순서 9 에니어그램 타일링
오더-11 헨데카그램 타일링	{11/2,11}			{11/2}	{11}	3	*11.3.2 [11,3]	Hendecagramic-order hendecangular tiling
Hendecagramic-order hendecangular tiling	{11,11/2}			{11}	{11/2}	3	*11.3.2 [11,3]	오더-11 헨데카그램 타일링
오더-p-그래믹 타일링	{p/2,p}			{p/2}	{p}	3	*p32 [p,3]	p-grammic-order p-gonal tiling
p-grammic-order p-gonal tiling	{p,p/2}			{p}	{p/2}	3	*p32 [p,3]	오더-p-그래믹 타일링

유클리드 3공간의 아페이로헤드라 꼬치

유클리드 3공간에 3개의 정규 스큐 아페이로헤드라가 있으며, 규칙적인 스큐 폴리곤 정점 형상이 있다.^[12][13][14] 그들은 3개의 볼록한 균일한 벌집들의 정점 배열과 가장자리 배열을 공유한다.

• 각 꼭지점 주위에 6개의 정사각형: {4,6 4}
• 각 꼭지점 주위에 4개의 16진수: {6,4 4}
• 각 꼭지점 주위의 6진수: {6,6 3}

일반 꼬치 다면체
{4,6 4}	{6,4 4}	{6,6 3}

유클리드 3공간에 30개의 정규 아페이로헤드라가 있다.^[16] 여기에는 위에 나열된 8개의 다른 "순수" 아페이로헤드라뿐만 아니라 모든 것이 입방체 벌집, {4,6},₄ {6,6}, {6,4}, 기타 스큐 폴리곤 면: {6,6,6}, {6,₆^a6}, {6,^b.*3_6,44,46}, {6,6,6}, {6,₄6},6,6,_6,36,} 등이 포함된다.

쌍곡선 3공간에 아페이로헤드라 꼬기

쌍곡선 3공간에 31개의 일반 스큐 아페이로헤드라가 있다.^[17]

• 14는 콤팩트: {8,10 3}, {10,8 3}, {10,4 3}, {4,10 3}, {6,4 5}, {4,6,6 5}, {10 3}, {8,8,6 3}, {8,83,}, {10 3,},{6,6,3},{8,3}.
• 17 are paracompact: {12,10 3}, {10,12 3}, {12,4 3}, {4,12 3}, {6,4 6}, {4,6 6}, {8,4 4}, {4,8 4}, {12,6 3}, {6,12 3}, {12,12 3}, {6,6 6}, {8,6 4}, {6,8 4}, {12,8 3}, {8,12 3}, and {8,8 4}.

3차원(4에이피로톱)

유클리드 3공간의 테셀레이션

3-공간(허니컴), {4, 3, 4}^[18]의 비퇴행 정기 테셀레이션이 단 하나 있다.

이름	슐레플리 {p,q,r}	콕시터	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	가장자리 형상을 나타내다 {r}	꼭지점 형상을 나타내다 {q,r}	χ	이중
큐빅 벌집	{4,3,4}		{4,3}	{4}	{4}	{3,4}	0	셀프듀얼

유클리드 3공간의 부적절한 테셀레이션

세 개의 규칙적인 유클리드 기울기를 바탕으로 한 짝을 이루는 여섯 개의 부적절한 규칙적인 테셀레이션이 있다. 그들의 세포와 꼭지점 수치는 모두 정규 호소헤드라 {2,n}, 디헤드라 {n,2}, 유클리드 기울기들이다. 이러한 부적절한 규칙적인 기울기는 절단 수술에 의한 프리즘적 균일 벌집과 건설적으로 관련이 있다. 그것들은 순서-2 아페이로겐 타일링과 아페이로겐 호소헤드론의 고차원적 유사점이다.

슐레플리 {p,q,r}	콕시터 도표를 만들다	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	가장자리 형상을 나타내다 {r}	꼭지점 형상을 나타내다 {q,r}
{2,4,4}		{2,4}	{2}	{4}	{4,4}
{2,3,6}		{2,3}	{2}	{6}	{3,6}
{2,6,3}		{2,6}	{2}	{3}	{6,3}
{4,4,2}		{4,4}	{4}	{2}	{4,2}
{3,6,2}		{3,6}	{3}	{2}	{6,2}
{6,3,2}		{6,3}	{6}	{2}	{3,2}

쌍곡선 3공간의 테셀레이션

쌍곡선 3-공간에는 10개의 평평한 일반 꿀콤이 있다:^[19] (이전에는 테셀레이션으로 나열되어 있다)

• 4는 소형: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
• 반면 6은 파라콤팩트: {3,6,6}, {6,3,3}, {3,4,4,4}, {4,6,3}, {3,3,3}, {4,3,6,6}, {4,4,4}, {5,3,6}, {6,6},6},6}.

소형 일반 벌집 4개 {5,3,4} {5,3,5} {4,3,5} {3,5,3}

보통 꿀벌통 11개 중 4개 {3,4,4} {3,6,3} {4,4,3} {4,4,4}

쌍곡선 3공간의 테셀레이션은 쌍곡선 벌집이라고 불릴 수 있다. H에는³ 쌍곡선 허니콤 15개, 콤팩트 4개, 파라콤팩트 11개가 있다.

소형 일반 벌집 4개

이름	슐레플리 기호 {p,q,r}	콕시터	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	가장자리 형상을 나타내다 {r}	꼭지점 형상을 나타내다 {q,r}	χ	이중
이코사헤드랄 벌집	{3,5,3}		{3,5}	{3}	{3}	{5,3}	0	셀프듀얼
오더-5입방 벌집	{4,3,5}		{4,3}	{4}	{5}	{3,5}	0	{5,3,4}
순서-4 도두면 벌집	{5,3,4}		{5,3}	{5}	{4}	{3,4}	0	{4,3,5}
주문-5도면체 벌집	{5,3,5}		{5,3}	{5}	{5}	{3,5}	0	셀프듀얼

There are also 11 paracompact H³ honeycombs (those with infinite (Euclidean) cells and/or vertex figures): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, and {6,3,6}.

11개의 파라콤팩트 일반 꿀벌집

이름	슐레플리 기호 {p,q,r}	콕시터	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	가장자리 형상을 나타내다 {r}	꼭지점 형상을 나타내다 {q,r}	χ	이중
순서 6 사면 벌집	{3,3,6}		{3,3}	{3}	{6}	{3,6}	0	{6,3,3}
육각 타일링 벌집	{6,3,3}		{6,3}	{6}	{3}	{3,3}	0	{3,3,6}
순서-4 팔면 벌집	{3,4,4}		{3,4}	{3}	{4}	{4,4}	0	{4,4,3}
사각 타일링 벌집	{4,4,3}		{4,4}	{4}	{3}	{4,3}	0	{3,3,4}
삼각 타일링 벌집	{3,6,3}		{3,6}	{3}	{3}	{6,3}	0	셀프듀얼
오더-6입방 벌집	{4,3,6}		{4,3}	{4}	{4}	{3,6}	0	{6,3,4}
순서-4 육각형 타일링 벌집	{6,3,4}		{6,3}	{6}	{4}	{3,4}	0	{4,3,6}
순서-4 사각 타일링 벌집	{4,4,4}		{4,4}	{4}	{4}	{4,4}	0	{4,4,4}
주문-6도면체 벌집	{5,3,6}		{5,3}	{5}	{5}	{3,6}	0	{6,3,5}
순서-5 육각 타일링 벌집	{6,3,5}		{6,3}	{6}	{5}	{3,5}	0	{5,3,6}
오더-6 육각형 타일링 벌집	{6,3,6}		{6,3}	{6}	{6}	{3,6}	0	셀프듀얼

비컴팩트 솔루션은 로렌츠 콕시터 그룹으로 존재하며 쌍곡선 공간의 열린 도메인(인피니티 이상으로 접근이 불가능한 일부 부품이 있는 기본 사면체)으로 시각화할 수 있다. 쌍곡선 세포나 정점 수치가 있고 슐래플리 기호에 2개가 없는 모든 꿀콤은 비합법적이다.

구형(이상/원형)/유클리드/하이퍼볼릭(컴팩트/파라콤팩트/비컴팩트) 벌집 {p,3,r}

{p,3} \ r	2	3	4	5	6	7	8	... ∞
{2,3}	{2,3,2}	{2,3,3}	{2,3,4}	{2,3,5}	{2,3,6}	{2,3,7}	{2,3,8}	{2,3,∞}
{3,3}	{3,3,2}	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	{3,3,∞}
{4,3}	{4,3,2}	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	{4,3,∞}
{5,3}	{5,3,2}	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	{5,3,∞}
{6,3}	{6,3,2}	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	{6,3,∞}
{7,3}	{7,3,2}	{7,3,3}	{7,3,4}	{7,3,5}	{7,3,6}	{7,3,7}	{7,3,8}	{7,3,∞}
{8,3}	{8,3,2}	{8,3,3}	{8,3,4}	{8,3,5}	{8,3,6}	{8,3,7}	{8,3,8}	{8,3,∞}
... {∞,3}	{∞,3,2}	{∞,3,3}	{∞,3,4}	{∞,3,5}	{∞,3,6}	{∞,3,7}	{∞,3,8}	{∞,3,∞}

{p,4,r} {p,4} \ r 2 3 4 5 6 ∞ {2,4} {2,4,2} {2,4,3} {2,4,4} {2,4,5} {2,4,6} {2,4,∞} {3,4} {3,4,2} {3,4,3} {3,4,4} {3,4,5} {3,4,6} {3,4,∞} {4,4} {4,4,2} {4,4,3} {4,4,4} {4,4,5} {4,4,6} {4,4,∞} {5,4} {5,4,2} {5,4,3} {5,4,4} {5,4,5} {5,4,6} {5,4,∞} {6,4} {6,4,2} {6,4,3} {6,4,4} {6,4,5} {6,4,6} {6,4,∞} {∞,4} {∞,4,2} {∞,4,3} {∞,4,4} {∞,4,5} {∞,4,6} {∞,4,∞}

{p,5,r} {p,5} \ r 2 3 4 5 6 ∞ {2,5} {2,5,2} {2,5,3} {2,5,4} {2,5,5} {2,5,6} {2,5,∞} {3,5} {3,5,2} {3,5,3} {3,5,4} {3,5,5} {3,5,6} {3,5,∞} {4,5} {4,5,2} {4,5,3} {4,5,4} {4,5,5} {4,5,6} {4,5,∞} {5,5} {5,5,2} {5,5,3} {5,5,4} {5,5,5} {5,5,6} {5,5,∞} {6,5} {6,5,2} {6,5,3} {6,5,4} {6,5,5} {6,5,6} {6,5,∞} {∞,5} {∞,5,2} {∞,5,3} {∞,5,4} {∞,5,5} {∞,5,6} {∞,5,∞}

{p,6,r} {p,6} \ r 2 3 4 5 6 ∞ {2,6} {2,6,2} {2,6,3} {2,6,4} {2,6,5} {2,6,6} {2,6,∞} {3,6} {3,6,2} {3,6,3} {3,6,4} {3,6,5} {3,6,6} {3,6,∞} {4,6} {4,6,2} {4,6,3} {4,6,4} {4,6,5} {4,6,6} {4,6,∞} {5,6} {5,6,2} {5,6,3} {5,6,4} {5,6,5} {5,6,6} {5,6,∞} {6,6} {6,6,2} {6,6,3} {6,6,4} {6,6,5} {6,6,6} {6,6,∞} {∞,6} {∞,6,2} {∞,6,3} {∞,6,4} {∞,6,5} {∞,6,6} {∞,6,∞}

{p,7,r} {p,7} \ r 2 3 4 5 6 ∞ {2,7} {2,7,2} {2,7,3} {2,7,4} {2,7,5} {2,7,6} {2,7,∞} {3,7} {3,7,2} {3,7,3} {3,7,4} {3,7,5} {3,7,6} {3,7,∞} {4,7} {4,7,2} {4,7,3} {4,7,4} {4,7,5} {4,7,6} {4,7,∞} {5,7} {5,7,2} {5,7,3} {5,7,4} {5,7,5} {5,7,6} {5,7,∞} {6,7} {6,7,2} {6,7,3} {6,7,4} {6,7,5} {6,7,6} {6,7,∞} {∞,7} {∞,7,2} {∞,7,3} {∞,7,4} {∞,7,5} {∞,7,6} {∞,7,∞}

{p,8,r} {p,8} \ r 2 3 4 5 6 ∞ {2,8} {2,8,2} {2,8,3} {2,8,4} {2,8,5} {2,8,6} {2,8,∞} {3,8} {3,8,2} {3,8,3} {3,8,4} {3,8,5} {3,8,6} {3,8,∞} {4,8} {4,8,2} {4,8,3} {4,8,4} {4,8,5} {4,8,6} {4,8,∞} {5,8} {5,8,2} {5,8,3} {5,8,4} {5,8,5} {5,8,6} {5,8,∞} {6,8} {6,8,2} {6,8,3} {6,8,4} {6,8,5} {6,8,6} {6,8,∞} {∞,8} {∞,8,2} {∞,8,3} {∞,8,4} {∞,8,5} {∞,8,6} {∞,8,∞}

{p,190,r} {p,properties} \ r 2 3 4 5 6 ∞ {2,∞} {2,∞,2} {2,∞,3} {2,∞,4} {2,∞,5} {2,∞,6} {2,∞,∞} {3,∞} {3,∞,2} {3,∞,3} {3,∞,4} {3,∞,5} {3,∞,6} {3,∞,∞} {4,∞} {4,∞,2} {4,∞,3} {4,∞,4} {4,∞,5} {4,∞,6} {4,∞,∞} {5,∞} {5,∞,2} {5,∞,3} {5,∞,4} {5,∞,5} {5,∞,6} {5,∞,∞} {6,∞} {6,∞,2} {6,∞,3} {6,∞,4} {6,∞,5} {6,∞,6} {6,∞,∞} {∞,∞} {∞,∞,2} {∞,∞,3} {∞,∞,4} {∞,∞,5} {∞,∞,6} {∞,∞,∞}

H에는³ 규칙적인 쌍곡선 별-허니콤이 없다: 모든 형태는 세포, 정점, 또는 둘 다 구형이 된다.

4차원(5apeirotopes)

유클리드 4공간의 테셀레이션

유클리드 4차원 공간을 테셀레이팅할 수 있는 무한 레귤러 테셀레이션(허니콤)은 세 종류가 있다.

유클리드 꿀콤 3종

이름	슐레플리 기호 {p,q,r,s}	면 타자를 치다 {p,q,r}	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	면 형상을 나타내다 {s}	가장자리 형상을 나타내다 {r,s}	꼭지점 형상을 나타내다 {q,r,s}	이중
큐테라틱 벌집	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{4}	{3,4}	{3,3,4}	셀프듀얼
벌집 16셀	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,4,3,3}
24셀 벌집	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{4,3,3}	{3,3,4,3}

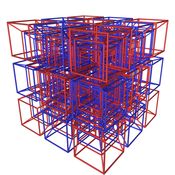{4,3,3,4}의 예상 부분 (계측 벌집)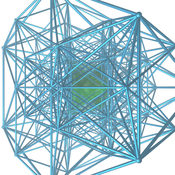

{3,3,4,3}의 예상 부분 (16셀 벌집)

{3,4,3,3}의 예상 부분 (24셀 벌집)

또한 두 가지 부적절한 사례가 있다.

유클리드 4공간의 평평한 일반 꿀콤은 다음과 같이 세 가지가 있다.^[18]

• {4,3,4}, {3,3,4,3}, {3,4,3}, {3,4,3}.

쌍곡선 4공간의 7개의 평평한 정규 볼록 꿀콤이 있다.^[19]

• 5는 소형: {3,3,3,5}, {5,3,3,3}, {4,3,3,5}, {5,3,3,4}, {5,3,3,5}
• 2는 파라콤팩트: {3,4,3,4} 및 {4,3,4,3}.

쌍곡선 4-공간에는 네 개의 평평한 일반 별 꿀콤이 있다.^[19]

• {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5}, {5,5/2,5,3}.

쌍곡선 4공간의 테셀레이션

H⁴ 공간에는 볼록형 일반 벌꿀컴 7개와 별꿀컴 4개가 있다.^[20] 5개의 볼록한 것은 콤팩트하고, 2개는 파라콤팩트다.

소형⁴ 일반 벌집 5개 H:

소형 일반 벌집 5개

이름	슐레플리 기호 {p,q,r,s}	면 타자를 치다 {p,q,r}	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	면 형상을 나타내다 {s}	가장자리 형상을 나타내다 {r,s}	꼭지점 형상을 나타내다 {q,r,s}	이중
순서-5 5셀 벌집	{3,3,3,5}	{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
벌집 120셀	{5,3,3,3}	{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
오더-5 테서틱 벌집	{4,3,3,5}	{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
순서-4 120셀 벌집	{5,3,3,4}	{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
순서-5 120셀 벌집	{5,3,3,5}	{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	셀프듀얼

두 개의 파라콤팩트⁴ 일반 H 허니컴은 다음과 같다: {3,4,3,4}, {4,3,4,3}.

파라콤팩트 일반 꿀컴 2개

이름	슐레플리 기호 {p,q,r,s}	면 타자를 치다 {p,q,r}	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	면 형상을 나타내다 {s}	가장자리 형상을 나타내다 {r,s}	꼭지점 형상을 나타내다 {q,r,s}	이중
순서-4 24셀 벌집	{3,4,3,4}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{4,3,4}	{4,3,4,3}
큐빅 벌집형 벌집형	{4,3,4,3}	{4,3,4}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,4,3,4}

비컴팩트 솔루션은 로렌츠 콕시터 그룹으로 존재하며, 쌍곡선 공간의 열린 도메인(인피니티 이상으로 접근 불가능한 일부 부품이 있는 기본 5-셀)으로 시각화할 수 있다. 아래 표 집합에 표시되지 않고 슐레플리 기호에 2개가 없는 모든 허니컴은 비컴팩트하다.

구형/유클리드/하이퍼볼릭(compact/paracompact/noncompact) 벌집 {p,q,r,s}
q=3, s=3 p \ r 3 4 5 3 {3,3,3,3} {3,3,4,3} {3,3,5,3} 4 {4,3,3,3} {4,3,4,3} {4,3,5,3} 5 {5,3,3,3} {5,3,4,3} {5,3,5,3}	q=3, s=4 p \ r 3 4 3 {3,3,3,4} {3,3,4,4} 4 {4,3,3,4} {4,3,4,4} 5 {5,3,3,4} {5,3,4,4}	q=3, s=5 p \ r 3 4 3 {3,3,3,5} {3,3,4,5} 4 {4,3,3,5} {4,3,4,5} 5 {5,3,3,5} {5,3,4,5}
q=4, s=3 p \ r 3 4 3 {3,4,3,3} {3,4,4,3} 4 {4,4,3,3} {4,4,4,3}	q=4, s=4 p \ r 3 4 3 {3,4,3,4} {3,4,4,4} 4 {4,4,3,4} {4,4,4,4}	q=4, s=5 p \ r 3 4 3 {3,4,3,5} {3,4,4,5} 4 {4,4,3,5} {4,4,4,5}
q=5, s=3 p \ r 3 4 3 {3,5,3,3} {3,5,4,3} 4 {4,5,3,3} {4,5,4,3}

쌍곡선 4공간의 별 테셀레이션

H⁴ 공간에는 4개의 일반 별 꿀벌이 있는데, 모두 콤팩트하다.

콤팩트한 일반 스타 허니컴 4개

이름	슐레플리 기호 {p,q,r,s}	면 타자를 치다 {p,q,r}	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	면 형상을 나타내다 {s}	가장자리 형상을 나타내다 {r,s}	꼭지점 형상을 나타내다 {q,r,s}	이중	밀도
소형 용접 120셀 벌집	{5/2,5,3,3}	{5/2,5,3}	{5/2,5}	{5/2}	{3}	{3,3}	{5,3,3}	{3,3,5,5/2}	5
펜타그램 주문 600셀 벌집	{3,3,5,5/2}	{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}	5
순서-5 이코사면 120셀 벌집	{3,5,5/2,5}	{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}	10
거대 120셀 벌집	{5,5/2,5,3}	{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}	10

5차원(6에이피로톱)

유클리드 5공간의 평평한 정기 벌집 하나: (이전에는 테셀레이션으로 나열되어 있음)^[18]

• {4,3,3,3,4}

쌍곡선 5-공간에는 5개의 평평한 일반 꿀콤이 있으며, 모든 파라콤팩트: (이전에는 테셀레이션으로 나열되어 있다)^[19]

• {3,3,3,4,3}, {3,4,3,3}, {3,3,3,3}, {3,4,3,3}, {3,3,3,4}, {4,3,3}, {4,3,3,3}, {4,3,3,3}, {4,3,3}

유클리드 5공간의 테셀레이션스

하이퍼큐브 허니콤은 각 능선을 중심으로 4개의 하이퍼큐브 면에 의해 형성된 5개 이상의 각 차원을 테셀링할 수 있는 유일한 일반 허니콤 계열이다.

이름	슐레플리 {p1, p2, ..., pn−1}	면 타자를 치다	꼭지점 형상을 나타내다	이중
사각 타일링	{4,4}	{4}	{4}	셀프듀얼
큐빅 벌집	{4,3,4}	{4,3}	{3,4}	셀프듀얼
큐테라틱 벌집	{4,32,4}	{4,32}	{32,4}	셀프듀얼
5개짜리 벌집	{4,33,4}	{4,33}	{33,4}	셀프듀얼
6-모양의 벌집	{4,34,4}	{4,34}	{34,4}	셀프듀얼
7인치 벌집	{4,35,4}	{4,35}	{35,4}	셀프듀얼
8인치 벌집	{4,36,4}	{4,36}	{36,4}	셀프듀얼
n-자궁 벌집	{4,3n−2,4}	{4,3n−2}	{3n−2,4}	셀프듀얼

E에서는⁵ 또한 부적절한 경우 {4,3,4,2}, {2,4,3,3,3,3,3,3,3}, {3,3,3,3}, {3,3,3}, {3,3,3,3}, {3,3,3}, {3,3,3,3}, {2,3,3,4,3}이 있다. E에서ⁿ {4,3ⁿ⁻³,4,2}, {2,4,3ⁿ⁻³,4}은(는) 항상 부적절한 유클리드 테셀레이션이다.

쌍곡선 5공간의 테셀레이션

H에는⁵ 5개의 정기적인 꿀벌이 있는데, 모든 파라콤팩트에는 무한(유클리드) 면이나 정점 수치가 포함되어 있다: {3,4,3,3,3}, {3,4,3,3}, {3,4,3}, {3,4,3}, {4,3,3}, {4,3,3},3},3}.

치수 5 이상의 쌍곡선 공간의 소형 정규 테셀레이션이 없고 치수 6 이상의 쌍곡선 공간에는 파라콤팩트 정규 테셀레이션이 없다.

5개의 파라콤팩트 일반 꿀컴

이름	슐레플리 기호 {p,q,r,s,t}	면 타자를 치다 {p,q,r,s}	4면체 타자를 치다 {p,q,r}	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	셀 형상을 나타내다 {t}	면 형상을 나타내다 {s,t}	가장자리 형상을 나타내다 {r,s,t}	꼭지점 형상을 나타내다 {q,r,s,t}	이중
5정형 벌집	{3,3,3,4,3}	{3,3,3,4}	{3,3,3}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,3}
24셀 벌집형 벌집	{3,4,3,3,3}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{3,3,3}	{4,3,3,3}	{3,3,3,4,3}
벌집 16셀	{3,3,4,3,3}	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{3,3}	{4,3,3}	{3,4,3,3}	자화자기의
주문-4 24셀 벌집형 벌집	{3,4,3,3,4}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{3,3,4}	{4,3,3,4}	{4,3,3,4,3}
큐셀틱 벌집형 벌집형	{4,3,3,4,3}	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,4}

잠재 세포나 정점 수치가 될 수 있는 n ≥ 5에 대한 정규 항성 n-폴리탑이 없기 때문에 n ≥ 5에 대한 H에는ⁿ 더 이상 쌍곡성 허니콤이 없다.

6차원 이상 (7 apeirotopes+)

쌍곡선 6공간 이상 테셀레이션

치수 6 이상의 쌍곡선 공간의 정규 컴팩트 또는 파라콤팩트 테셀레이션은 없다. 하지만, {p,q,r,s, 형식의 Schléfli 기호는...위에서 다루지 않는 }(p,q,r,s,s... 2 이상의 자연수 또는 무한수)는 쌍곡 n공간의 비복합적 테셀레이션을 형성한다.

복합폴리토페스

2차원 화합물

자연수 n에 대해서는 m < n/2(엄밀히 말하면 {n/m}={n/(n-m)})와 m과 n이 동일시되는 모든 m에 대해 Schléfli 기호가 {n/m}인 n점 항성 정규 다각형 항성이 있다. m과 n이 동일시되지 않을 때 얻은 별 폴리곤은 n/m 면이 있는 일반 폴리곤이 된다. 회전 정점의 수가 n/m - 1이 될 때까지 이러한 규칙적인 n/m-gon을 원래의 폴리곤에서 왼쪽으로 한 꼭지점 회전시켜 새로운 수치를 얻는다. 극단적인 경우는 n/m이 2인 경우로, n/2 직선 세그먼트로 구성된 수치를 생성하는데, 이를 퇴행성 폴리곤이라고 한다.

그 밖에 n과 m이 공통인자를 갖는 경우에는 하의 n에 대한 별 다각형을 구하여 회전판을 조합할 수 있다. 이러한 형상을 별 모양, 부적절한 별 다각형 또는 복합 다각형이라고 한다. Grünbaum(1994)과 같은 당국에서는 형식 k{n}이 더 정확하다고 간주하지만, 일반적으로 k = m이 그것들에 대해 동일한 표기법 {n/m}이(가) 종종 사용된다.

우리가 두 개 이상의 별 폴리곤을 혼합할 때 더 복잡한 문제가 발생한다. 예를 들어 두 개의 오각형은 36°의 회전으로 달라지며, 데카곤에 새겨져 있다. 이는 일반적으로 사용되는 {10/4}이(가) 아닌 2{5/2} 형식으로 k{n/m} 형식으로 올바르게 기록되어 있다.

Coxeter의 화합물 확장 표기법은 c{m,n,... 형식이다.}}[d{p,q,...}}e{s,t,...} d 구별 {p,q,...}을(를) 나타냄}}의 합은 {m,n,...의 정점을 커버한다.} c회 및 {s,t,...의 면.} e times. 일반 {m,n,n이 없는 경우...{}이(가) 존재하며, 표기법의 첫 부분이 제거되어 [d{p,q,...}}e{s,t,...{}; 정반대의 {s,t,...{}이(가) 존재한다. c{m,n,의 이중...}}[d{p,q,...}}e{s,t,...{}은(는) e{{t,s,...}}[d{q,p,...}}]c{n,m,...}.c 또는 e가 1이면 생략할 수 있다. 복합 폴리곤의 경우 이 표기법은 {nk}[k{n/m}]{nk}: 예를 들어, 육각형을 {6}[2{3}]{6}로 쓸 수 있다.

n=2..10, nk≤30의 예

2{2}

3{2}

4{2}

5{2}

6{2}

7{2}

8{2}

9{2}

10{2}

11{2}

12{2}

13{2}

14{2}

15{2}

2{3}

3{3}

4{3}

5{3}

6{3}

7{3}

8{3}

9{3}

10{3}

2{4}

3{4}

4{4}

5{4}

6{4}

7{4}

2{5}

3{5}

4{5}

5{5}

6{5}

2{5/2}

3{5/2}

4{5/2}

5{5/2}

6{5/2}

2{6}

3{6}

4{6}

5{6}

2{7}

3{7}

4{7}

2{7/2}

3{7/2}

4{7/2}

2{7/3}

3{7/3}

4{7/3}

2{8}

3{8}

2{8/3}

3{8/3}

2{9}

3{9}

2{9/2}

3{9/2}

2{9/4}

3{9/4}

2{10}

3{10}

2{10/3}

3{10/3}

2{11}

2{11/2}

2{11/3}

2{11/4}

2{11/5}

2{12}

2{12/5}

2{13}

2{13/2}

2{13/3}

2{13/4}

2{13/5}

2{13/6}

2{14}

2{14/3}

2{14/5}

2{15}

2{15/2}

2{15/4}

2{15/7}

일반적인 스큐 폴리곤은 또한 다음과 같은 항정신병 프리즘 화합물의 가장자리에서 볼 수 있는 화합물을 만든다.

일반 복합 스큐 폴리곤

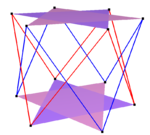
화합물 네모꼴을 꼬다		화합물 육각형을 꼬다	화합물 데카곤을 꼬다
두 {2}#{ }	세 {2}#{ }	두 {3}#{ }	두 {5/3}#{ }

3차원 화합물

일반 다면 화합물은 일반 다면체와 마찬가지로 정점-변환, 가장자리-변환, 얼굴-변환성 화합물로 정의할 수 있다. 이 정의로 5개의 정규 화합물이 있다.

대칭	[4,3] Oh	[5,3]+ I	[5,3] Ih
이중성	셀프듀얼			듀얼 페어
이미지
구면
폴리헤드라	2 {3,3}	5 {3,3}	10 {3,3}	5 {4,3}	5 {3,4}
콕시터	{4,3}[2{3,3}]{3,4}	{5,3}[5{3,3}]{3,5}	2{5,3}[10{3,3}]2{3,5}	2{5,3}[5{4,3}]	[5{3,4}]2{3,5}

일반 화합물에 대한 콕세터의 표기법은 슐레플리 기호를 통합하여 위의 표에 제시되어 있다. 대괄호 안의 재료인 [d{p,q}]는 화합물의 성분: d 별개의 {p,q}을(를) 나타낸다. 대괄호 앞의 재료는 화합물의 꼭지점 배열을 나타낸다. c{m,n}[d{p,q}]는 {m,n} 카운트 c의 정점을 공유하는 d {p,q}의 화합물이다. 대괄호 뒤에 있는 재료는 화합물의 전면 배열을 나타낸다. [d{p,q}]e{s,t}는 {s,t}의 얼굴을 e회수로 나눈 d {p,q}의 합성물이다. 이러한 것들은 결합될 수 있다: 따라서 c{m,n}[d{p,q}]e{s,t}는 {m,n} c의 정점과 {s,t}의 얼굴이 e회 계수된 정점을 공유하는 d {p,q}의 합성어다. 이 표기법은 여러 치수의 화합물에 일반화할 수 있다.^[21]

및

유클리드 평면의 정규 복합 테셀레이션의 2-모수 계열이 18개 있다. 쌍곡면에서는 1변수 가족 5명, 고립 사례 17명이 알려져 있지만 이 상장의 완전성은 아직 입증되지 않았다.

유클리드 및 쌍곡성 화합물 패밀리 2 {p,p} (4 ≤ p ≤ ∞, p 정수)는 구형 스텔라 옥탄굴라, 2 {3,3}과 유사하다.

유클리드 및 쌍곡성 정규화합물의 몇 가지 예

셀프듀얼	듀얼스		셀프듀얼
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}
{{4,4}} 또는 a{4,4} 또는 {4,4}[2{4,4}]{4,4}} + 또는	[2{6,3}]{3,6}	a{6,3} 또는 {6,3}[2{3,6}] + 또는	{{∞,∞}} 또는 a{∞,∞} 또는 {4,∞}[2{∞,∞}]{∞,4} + 또는
	3 {6,3}	3 {3,6}	3 {∞,∞}
	2{3,6}[3{6,3}]{6,3}	{3,6}[3{3,6}]2{6,3} + +	+ +

직교영

75 {4,3,3}	75 {3,3,4}

콕시터는 그의 저서 '레귤러 폴리토페스'에 일반 4폴리토페의 32가지 일반 화합물을 나열하고 있다.^[22] 맥뮬런은 자신의 논문 '4-폴리토페스의 새로운 정규 화합물'에 6개를 추가했는데, 이 역시 이 리스트가 이제 완성되었다는 것을 증명한다.^[23] 다음 표에서 위첨자(var)는 라벨로 표시된 화합물이 동일한 기호를 가진 다른 화합물과 구별됨을 나타낸다.

쟈가이이물물물물

화합물	구성 요소		정점열	세포열열
120 {3,3,3}	5세포	[5,3,3], 14400개[22] 주문	{5,3,3}	{3,3,5}
120 {3,3,3}(var)	5세포	1200을[23] 주문하다	{5,3,3}	{3,3,5}
720 {3,3,3}	5세포	[5,3,3], 14400개[23] 주문	6{5,3,3}	6{3,3,5}
5 {3,4,3}		[5,3,3], 14400개[22] 주문	{3,3,5}	{5,3,3}

이중 쌍으로 정규 화합물

화합물 1	화합물 2		정점 배열(1)	세포배열(1)	정점 배열(2)	2 세포배열(2)
3 {3,3,4}[24]	3 {4,3,3}	[3,4,3], 1152번[22] 주문	{3,4,3}	2{3,4,3}	2{3,4,3}	{3,4,3}
15 {3,3,4}	15 {4,3,3}	[5,3,3], 14400개[22] 주문	{3,3,5}	2{5,3,3}	2{3,3,5}	{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], 14400개[22] 주문	5{3,3,5}	10{5,3,3}	10{3,3,5}	5{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], 14400개[22] 주문	{5,3,3}	2{3,3,5}	2{5,3,3}	{3,3,5}
75 {3,3,4}	75 {4,3,3}	600개를[23] 주문하다	{5,3,3}	2{3,3,5}	2{5,3,3}	{3,3,5}
300 {3,3,4}	300 {4,3,3}	[5,3,3],+ 7200개[22] 주문	4{5,3,3}	8{3,3,5}	8{5,3,3}	4{3,3,5}
600 {3,3,4}	600 {4,3,3}	[5,3,3], 14400개[22] 주문	8{5,3,3}	16{3,3,5}	16{5,3,3}	8{3,3,5}
25 {3,4,3}	25 {3,4,3}	[5,3,3], 14400개[22] 주문	{5,3,3}	5{5,3,3}	5{3,3,5}	{3,3,5}

75개의 큐세르텍트에는 두 가지 다른 화합물이 있는데, 하나는 120셀의 정점을 공유하는 반면, 다른 하나는 600셀의 정점을 공유하는 것이다. 따라서 75개의 16-셀의 해당 이중 화합물도 서로 다르다는 것이 바로 뒤따라온다.

자기 이중 항성 화합물

화합물		정점열	세포열열
5 {5,5/2,5}	[5,3,3],+ 7200개[22] 주문	{5,3,3}	{3,3,5}
10 {5,5/2,5}	[5,3,3], 14400개[22] 주문	2{5,3,3}	2{3,3,5}
5 {5/2,5,5/2}	[5,3,3],+ 7200개[22] 주문	{5,3,3}	{3,3,5}
10 {5/2,5,5/2}	[5,3,3], 14400개[22] 주문	2{5,3,3}	2{3,3,5}

이중쌍체로서의 일반 항성 화합물

화합물 1	화합물 2		정점 배열(1)	세포배열(1)	정점 배열(2)	2 세포배열(2)
5 {3,5,5/2}	5 {5/2,5,3}	[5,3,3],+ 7200개[22] 주문	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {3,5,5/2}	10 {5/2,5,3}	[5,3,3], 14400개[22] 주문	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5,5/2,3}	5 {3,5/2,5}	[5,3,3],+ 7200개[22] 주문	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5,5/2,3}	10 {3,5/2,5}	[5,3,3], 14400개[22] 주문	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5/2,3,5}	5 {5,3,5/2}	[5,3,3],+ 7200개[22] 주문	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5/2,3,5}	10 {5,3,5/2}	[5,3,3], 14400개[22] 주문	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}

또한 14개의 부분 정규 화합물이 있는데, 정점 변환 또는 세포 변환이지만 둘 다 아니다. 7개의 정점-전환 부분 정규 화합물은 7개의 세포-전환 부분 정규 화합물의 이중성이다.

이중 쌍으로 부분적으로 정규 화합물

화합물 1 변환	화합물 2
16-182로[25] 2	2 큐세렌트	[4,3,3] 주문 384[22]
24(var) 셀 25	24(var) 셀 25	600개를[23] 주문하다
100 24 셀	100 24 셀	[5,3,3],+ 7200개[22] 주문
200 24 셀	200 24 셀	[5,3,3], 14400개[22] 주문
600 셀 5	120 셀 5	[5,3,3],+ 7200개[22] 주문
600 셀 10	120 셀 10	[5,3,3], 14400개[22] 주문

이중 쌍으로 부분적으로 정규 항성 화합물

화합물 1 정점 변환	화합물 2 세포전환	대칭
5 {3,3,5/2}	5 {5/2,3,3}	[5,3,3],+ 7200개[22] 주문
10 {3,3,5/2}	10 {5/2,3,3}	[5,3,3], 14400개[22] 주문

비록 5세포와 24세포가 모두 자가이중이지만, 그들의 이중 화합물(두 개의 5세포의 화합물과 두 개의 24세포의 화합물)은 정점정기도 세포정기도 아니기 때문에 두 개의 사면체 및 여러 가지 이중 폴리곤 화합물의 화합물과는 달리 규칙적인 것으로 간주되지 않는다.ular 4-blacktope.

유클리드 3-공간 화합물

유일한 일반 유클리드 복합 허니콤은 큐빅 허니콤의 무한한 화합물군이며, 모든 정점과 얼굴을 다른 큐빅 허니콤과 공유한다. 이 화합물에는 얼마든지 입방형 벌집합이 있을 수 있다. Coxeter 표기법은 {4,3,4}[d{4,3,4}]{4,3,4}이다.

5차원 이상 화합물

5, 6차원의 일반 화합물은 없다. 알려진 7차원 화합물은 3개(16개, 240개, 480개)이며, 알려진 8차원 화합물은 6개(16개, 240개 또는 480개의 8-Cube 또는 8-정형 화합물)이다. n이 2의 힘보다 1이 적다는 전제하에 n차원 공간에는 n-심플라이스의 화합물이 1개 있고, n이 2의 힘이라면 n-차원 공간에는 2개의 화합물(n-cube와 n-orthope의 이중 화합물)도 있다.

이러한 화합물에 대한 Coxeter 표기법은 다음과 같다ⁿ(αⁿ⁻¹ = {3ⁿ}, βⁿ⁻² = {3,4_n}, { = {4,3ⁿ⁻²}).

• 7-105xes: cγ₇[16cα₇]cβ₇, 여기서 c = 1, 15 또는 30
• 8형식: c c₈[16cβ₈]
• 8-102: [16c³₈]cβ₈

일반 사례(n = 2, d^k = 2, k^{2k − k − 1} = 2, 3, 4, ...):

• 심플렉스: γ_n−1[dα_n−1]β_n−1
• 정형외과목: γ_n[dβ_n]
• 하이퍼큐브: [dγ_n]β_n

유클리드 벌집 화합물

5개 이상의 차원으로 구성된 일반 유클리드 화합물 꿀콤의 알려진 집단은 다른 하이퍼큐빅 벌컴과 정점과 얼굴을 공유하는 하이퍼큐빅 벌컴의 무한한 화합물이다. 이 화합물에는 고농축 꿀콤이 얼마든지 있을 수 있다. Coxeter 표기법은 Δ_n[dΔ_n]Δ인데_n 여기서 n = 2일 때는 Δ_n = {³}이고 n n 3일 때는 {4,3ⁿ⁻³,4}이다.

추상 폴리토페스

추상적인 폴리토페스는 그들이 내장된 기하학적 공간과는 별개로 폴리토페스를 연구하려는 시도에서 생겨났다. 구면, 유클리드 및 쌍곡 공간의 테셀레이션, 다른 다지관의 테셀레이션, 그리고 위상이 잘 정의되어 있지 않지만 대신 "로컬" 위상에 의해 특징지어질 수 있는 많은 다른 물체를 포함한다. 모든 차원에 무한히 많다. 샘플은 이 지도책을 참조하십시오. 이 목록의 다른 곳에 나타나지 않는 추상적인 일반 다면체의 몇 가지 주목할 만한 예로는 11세포, {3,3}과 57세포, {5,3,5}이 있으며, 세포와 꼭지점 형상으로 규칙적인 투영 다면체를 가지고 있다.

추상적인 다면체의 원소는 그 몸체(최대 원소), 그 얼굴, 가장자리, 정점, 그리고 null polytope 또는 빈 집합이다. 이 추상적인 요소들은 평범한 공간에 매핑되거나 기하학적 숫자로 실현될 수 있다. 어떤 추상적인 다면체들은 잘 형성되어 있거나 충실한 깨달음을 가지고 있지만, 다른 것들은 그렇지 않다. 국기는 신체, 얼굴, 얼굴의 가장자리, 가장자리의 꼭지점, 그리고 무효 폴리토프인 다면체에 대해 각 차원의 연결된 원소의 집합이다. 추상적인 폴리토프는 결합 대칭이 깃발에 전이되는 경우 즉, 모든 깃발은 다면체의 대칭 아래에 다른 깃발로 매핑될 수 있는 경우 규칙적이라고 한다. 추상적인 일반 폴리토페스는 여전히 연구 활동 영역으로 남아 있다.

충실하게 실현될 수 없는 그런 규칙적인 추상적인 다면체 5개는 그의 저서 <레귤러 폴리토페스>(1977년)에서 H. S. M. Coxeter에 의해, 그리고 J. M. Wills는 <인덱스 2의 결합적으로 정규 다면체라>(1987년)에서 다시 확인되었다.^[26] 그것들은 모두 토로이드와 토폴로이드와 동등하다. 각각의 꼭지점 주위에 n개의 면들을 배열함으로써 그들의 구조는 쌍곡면의 기울기로 무한정 반복될 수 있다. 아래 다이어그램에서 쌍곡선 타일링 이미지는 다면체의 이미지와 일치하는 색상을 가진다.

다면체	중합성삼정면체	도데카데카헤드론	중삼면체	직교 도데코데카헤드론	발굴된 도데면체
정점수	{5}, {5/2}	(5.5/2)2	{5}, {5/2}	(5.5/3)3
얼굴	30롬비	펜타곤 12개 5행 12문자	육각형 20개	펜타곤 12개 5행 12문자	육각 20자
타일링	{4, 5}	{5, 4}	{6, 5}	{5, 6}	{6, 6}
χ	−6	−6	−16	−16	−20

이는 다음과 같은 이중 쌍으로 발생한다.

• 내측심삼면체(medial rombic triacontahedron)와 도데코데카헤드론은 서로 이중이다.
• 내측삼면체(medial triambic icosaheadron)와 dittrigonal dodecadecacescahedron은 서로 이중이다.
• 발굴된 도두면체는 자가이중이다.

참고 항목

• 폴리곤
  • 정규 다각형
  • 별 폴리곤
• 다면체
  • 일반 다면체(일반 플라톤 고형분 5개, 케플러-푸인소 고형분 4개)
    • 균일다면체
• 4칸짜리
  • 정규 4폴리토프(정규 4폴리토프 16개, 볼록 4개, 별 10개(슐레플리-헤스))
  • 제복4폴리토프
• 테셀레이션
  • 일반 다각형의 기울기
  • 볼록 균일 벌집
• 일반 폴리토프
  • 균일 폴리토프
• 정규지도(그래프 이론)

메모들

참조

외부 링크

• 플라토닉 솔리드
• 케플러-푸인소트 폴리헤드라
• 일반 4d 폴리토프 접이식
• 다차원 용어집(Hexacosichoron 및 Hecatonicosachoron 검색)
• 폴리토프 뷰어
• n차원 구체에서 p점 폴리탑과 최적 패킹
• 작은 일반 폴리토페스로 된 지도책
• 정규 다면체 시간 I. Hubard, Polytopes, Maps 및 해당 대칭
• 일반별 폴리토페스, 난마

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A을n	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	122 • 221
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	132 • 231 • 321
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	142 • 241 • 421
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1k2 • 2k1 • k21	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록

v t 치수 2-9의 기본 볼록 정규 및 균일한 벌집
공간	가족	${\displaystyle {\tilde{A}_{n-1}$	${\displaystyle {\tilde{C}_{n-1}$	${\displaystyle {\tilde{B}_{n-1}$	${\displaystyle {\tilde{D}_{n-1}$	${\displaystyle {\stackrel{}{G}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$G}$$${\displaystyle {\_}_{\mathrm{}}}$2}}$$/ F ~ 4 {\$displaystyle {\tilde{F}_{4}}$ $$/ $E{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{}}$ ${\$}
E2	균일 타일링	{3[3]}	δ3	Δ3	Δ3	육각형
E3	균일볼록 벌집	{3[4]}	δ4	Δ4	Δ4
E4	제복4벌집	{3[5]}	δ5	Δ5	Δ5	24셀 벌집
E5	제복5벌집	{3[6]}	δ6	Δ6	Δ6
E6	제복6벌집	{3[7]}	δ7	Δ7	Δ7	222
E7	제복7허니콤	{3[8]}	δ8	Δ8	Δ8	133 • 331
E8	제복8벌집	{3[9]}	δ9	Δ9	Δ9	152 • 251 • 521
E9	제복9벌집	{3[10]}	δ10	Δ10	Δ10
E10	제복10벌집	{3[11]}	δ11	Δ11	Δ11
En-1	제복(n-1)-벌집합	{3[n]}	δn	Δn	Δn	1k2 • 2k1 • k21