일반 폴리토프
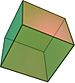
Regular polytope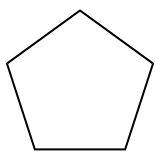 정규 오각형은 폴리곤으로, 가장자리가 5개인 2차원 폴리토프(Polytope)로 슐레플리 기호 {5} 기호로 표현된다. | 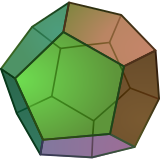 일반 도데카헤드론은 다면체(多面體)로, 3차원 폴리토프(polytope)로, 12개의 오각형 얼굴을 가지고 있으며, 슐레플리 기호 {5,3}로 표현된다. |
 일반 120 셀은 폴리초론(polychoron), 4차원 폴리토프(polytope)로 120개의 도데카헤드(deadechal cell)를 가지고 있으며, 슐레플리 기호 {5,3,3}(여기 슐레겔 다이어그램으로 표시됨) |  정규 입방형 벌집합은 테셀레이션으로, 슐레플리 기호 {4,3,4}로 대표되는 무한 3차원 폴리토프다. |
 8-큐브의 256 꼭지점과 1024 가장자리는 이 직교 투영(Petrie polygon)에서 볼 수 있다. | |
수학에서 일반 폴리토프는 그 깃발에 대칭군이 전이적으로 작용하여 가장 높은 대칭도를 주는 폴리토프다.그것의 모든 요소 또는 j-페이스 (여기서 n은 폴리토프의 치수인 0 ≤ j ≤ n에 대하여) - 세포, 면 등은 폴리토프의 대칭에서도 전이적이며, 치수 ≤ n의 규칙적인 폴리토페이다.
일반 다면체는 일반 다면체(예: 정사각형 또는 정사각형)와 일반 다면체(예: 정육면체)의 모든 치수에서 일반화된 아날로그다.일반 폴리토페스의 강한 대칭성은 비수체학자와 수학자 모두에게 흥미가 있는 미적 질을 부여한다.
고전적으로, n차원의 정규 폴리토프는 정규 면[(n - 1)-faces]과 정규 정점 수치를 갖는 것으로 정의할 수 있다.이 두 가지 조건은 모든 얼굴이 비슷하고 정점이 모두 비슷함을 보증하기에 충분하다.그러나 이 정의는 추상적인 폴리토페즈에는 적용되지 않는다는 점에 유의한다.
정규 폴리토프는 {a, b, c, ...., y, z} 형식의 Schléfli 기호로 나타낼 수 있으며, 정규 면은 {a, b, c, ..., y}이고, 정규 꼭지점 수치는 {b, c, ..., y, z}이다.
분류 및 설명
일반 폴리토페스는 주로 그 치수성에 따라 분류된다.
그것들은 대칭에 따라 더 분류될 수 있다.예를 들어, 정육면체와 정육면체는 정육면체 및 정육면체처럼 대칭을 공유한다.실제로 대칭군들은 때때로 4면체 대칭과 2면체 대칭과 같은 규칙적인 다면체의 이름을 따서 명명된다.
모든 차원에는 세 가지 종류의 일반 폴리토프가 존재한다.
2차원에서는, 무한히 많은 규칙적인 다각형이 있다.3차원과 4차원으로 이 세 가지 외에 몇 개의 일반 다면체와 4-폴리탑이 더 있다.5차원 이상에서는 이것밖에 없다.일반 폴리토페스의 목록도 참조하십시오.
폴리토프의 아이디어는 때때로 관련 종류의 기하학적 물체를 포함하도록 일반화된다.이들 중 일부는 아래의 역사적 발견에 관한 섹션에서 논의된 바와 같이 정기적인 예를 가지고 있다.
슐레플리 기호
19세기 루드비히 슐레플리에 의해 일반 폴리토페스에 대한 간결한 상징적 표현이 개발되었고, 약간 변형된 형태가 표준이 되었다.표기법은 한 번에 하나의 차원을 추가함으로써 가장 잘 설명된다.
- 면이 n개인 볼록한 일반 폴리곤은 {n}(으)로 표시된다.그래서 정삼각형은 {3}, 정사각형 {4} 등 무한정이다.중심 주위를 m번 감는 일반 별 폴리곤은 부분 값 {n/m}로 표시되며, 여기서 n과 m은 공동 프라임이므로 일반 펜타그램은 {5/2}이다.
- 정점 주위에 p면이 연결된 {n} 면의 일반 다면체는 {n, p}로 표시된다.9개의 정규 다면체는 {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 3/2} {5/2, 3} {5, 5/2}, {5/2}, {p}. {p}은 다면체의 정점이다.
- 가장자리 주위에 q셀이 결합되는 셀 {n, p}이(가) 있는 일반 4폴리토프는 {n, p, q}로 표시된다.4폴리토프의 꼭지점은 {p, q}이다.
- 일반 5폴리토프는 {n, p, q, r}이다.등등.
일반 폴리탑의 이중성
일반 폴리토프의 이중도 역시 일반 폴리토프다.이중 폴리토프의 슐래플리 기호는 거꾸로 쓰여진 원래의 기호일 뿐이다: {3, 3}은(는) 자기 이중이고 {3, 4}은(는) {4, 3, {4, 3, 3}에서 {3, 4}까지 이중이다.
일반 폴리토프의 꼭지점은 이중 폴리토프 면의 이중이다.예를 들어, {3, 3, 4}의 정점 수치는 {3, 4}이고 이중은 {4, 3}이며, {4, 3, 3} 셀이다.
어떤 차원에서도 측정치와 교차 폴리토프는 서로 이중적이다.
슐래플리 기호가 팔린드로믹(Palindromic)인 경우, 즉 동일한 앞뒤를 읽으면 다면체는 자가이중이다.자가이중 일반 폴리토판은 다음과 같다.
- 모든 일반 다각형, {a}.
- 모든 일반 n단순, {3,3,...,3}
- 4차원의 일반 24 셀, {3,4,3}.
- 위대한 120셀({5,5/2,5})과 웅장한 120셀({5/2,5/2})을 4차원으로 표현했다.
- 모든 일반 n차원 입방체 벌집, {4,3,...3,4}.이것들은 무한 폴리토페스로 취급될 수 있다.
- 쌍곡선 기울기 및 허니컴(p>4가 있는 틸팅 {p,p}, 2차원은 {4,4,4}, {5,3,5}, 3차원은 {3,5,3}, 3차원은 {3,5,3}, 4차원은 {5,3,6}, 5차원은 {3,4,3},3})
규칙적인 단순화
 |  |  |  |
| 라인 세그먼트 | 삼각형 | 사면체 | 펜타코론 |
 |  |  |
점 A로 시작하라.점으로부터 r 거리에 B를 표시하고 결합하여 선 세그먼트를 형성한다.1초 안에 C 점을 직교, 둘 다에서 r 거리에 치수를 표시하고 A와 B에 결합하여 정삼각형을 형성한다.세 번째 점 D를 직교로 표시하고, 세 가지 모두로부터 r을 치수화하고, 결합하여 정규 사면체를 형성한다.더 높은 차원을 위해.
이것들은 규칙적인 단순화 혹은 단순화들이다.이들의 이름은 차원성의 순서로 다음과 같다.
- 0. 포인트
- 1. 라인 세그먼트
- 2. 정삼각형(정삼각형)
- 3. 정사면체
- 4. 일반 펜타초론 또는 4-심플렉스
- 5. 일반 육각형 또는 5-심플렉스
- …n-심플렉스에는 n+1 정점이 있다.
폴리탑(하이퍼큐브) 측정
 |  |  |
| 사각형 | 큐브 | 테세락트 |
 |  |  |
점 A로 시작하라.거리 r에서 B 지점까지 선을 확장하고 결합하여 선 세그먼트를 형성하십시오.AB에 직교하는 두 번째 길이 r을 B에서 C로, 그리고 마찬가지로 A에서 D로 확장하여 정사각형 ABCD를 형성한다.각 코너에서 길이 r의 선을 각각 연장하여 AB와 BC 모두에 직교한다(즉, 위).큐브 ABCDEFGH를 형성하려면 새 점을 E,F,G,H로 표시하십시오.더 높은 차원을 위해.
이것들은 폴리토페스나 하이퍼큐브 측정법이다.이들의 이름은 차원성의 순서로 다음과 같다.
- 0. 포인트
- 1. 라인 세그먼트
- 2. 정사각형(정규 테트라곤)
- 3. 정육면체(일반 육면체)
- 4. 테세락트(정규옥타초론) 또는 4큐브
- 5. 펜터액트(일반 디카테론) 또는 5큐브
- n-큐브에는 정점이 2개n 있다.
교차다각류(정맥류)
 |  |  |
| 사각형 | 팔면체 | 16 셀 |
 |  |  |
점 O로 시작하라.O와 2r 사이의 거리 r에서 A와 B 지점까지 반대 방향으로 선을 연장한다.길이 2r의 선 COD를 O를 중심으로 그리고 AB에 직교한다.정사각형 ACBD를 형성하려면 끝을 연결하십시오.AB 및 CD에 직교하는 'O'를 중심으로 같은 길이의 선 EOF를 그리십시오(즉, 위아래).끝부분을 정사각형에 맞추어 고정된 팔면체를 형성한다.더 높은 차원을 위해.
이것들은 교차 폴리오페 또는 정형외과의 입니다.이들의 이름은 차원성의 순서로 다음과 같다.
- 0. 포인트
- 1. 라인 세그먼트
- 2. 정사각형(정규 테트라곤)
- 3. 정팔면체
- 4.정형 육각카초론(16셀) 또는 4정형
- 5. 규칙적인 트라이아콘타카이디테론(펜타크로스) 또는 5정맥
- n-정맥류는 정점이 2n이다.
발견의 역사
볼록 폴리곤과 폴리헤드라
일반 폴리곤과 폴리헤드라의 가장 초기 생존 수학적 치료법은 고대 그리스 수학자들로부터 우리에게 온다.그들에게는 다섯 개의 플라토닉 고체가 알려져 있었다.피타고라스는 그들 중 적어도 세 명을 알고 있었고 테에토스(기원전 417년 – 기원전 369년)는 다섯 가지를 모두 묘사했다.후에 유클리드는 수학에 대한 체계적인 연구를 저술하여 '원소'라는 제목으로 출판하여 기하학과 수 이론의 논리적 이론을 구축하였다.그의 작품은 다섯 가지 플라토닉 고형물에 대한 수학적인 서술로 끝을 맺었다.
별 다각형 및 다면체
우리의 이해는 유클리드 이후 수 세기 동안 정적인 상태를 유지했다.일반 폴리토페스의 후속 이력은 기본 개념의 점진적인 확대에 의해 특징지어질 수 있으며, 그 수에서 점점 더 많은 사물을 고려할 수 있다.토마스 브래드워딘(Bradwardinus)은 별 다각형에 대한 진지한 연구를 최초로 기록했다.다양한 별의 다면체들이 르네상스 예술에 등장하지만, 요하네스 케플러가 1619년 작은 도마뱀붙이와 큰 도마뱀붙이를 연구한 후에야 그는 이 두 개가 규칙적이라는 것을 깨달았다.루이 푸인소트는 1809년에 위대한 도데카헤드론과 위대한 이코사헤드론을 발견했고, 아우구스틴 카우치는 1812년에 그 리스트가 완성되었음을 증명했다.이 다면체들은 집합적으로 케플러-푸인소트 다면체라고 알려져 있다.
| 케플러-푸인소트 다면체 | |||
 |  |  |  |
| 소염전 도데면체 | 그레이트 스티어드 도데면체 | 대두면체 | 대이코사면체 |
고차원 폴리토페스
스위스 수학자인 루드비히 슐레플리가 일반 폴리토페스를 보다 높은 차원으로 검사하고 특성화한 것은 19세기에 이르러서였다.그의 노력은 처음에는 슐레플리(1855년)와 슐레플리(1858년)에 발표되었지만, 사후에 6년이 되는 슐레플리(1901년)에 완간되었다.1880년과 1900년 사이에 Schléfli의 결과는 적어도 9명의 다른 수학자들에 의해 독립적으로 재발견되었다. 자세한 내용은 Coxeter(1948, 페이지 143–144) (을 참조하라.슐레플리는 그런 인물을 '폴리슈켐'(영어로는 '폴리슈메' 또는 '폴리슈마'라고 불렀다.폴리토페(Polytope)라는 용어는 1882년 슐레플리의 재발견자 중 한 명인 라인홀드 호페(Linhold Hope)에 의해 도입되었고, 약 20년 후 알리샤 불레 스토트가 처음으로 영어로 사용하였다.폴리헤드로이드라는 용어는 초기 문헌에서도 사용되었다(Hilbert, 1952).
Coxeter (1948) 오류:(은 아마도 Schléfli의 결과를 가장 포괄적으로 인쇄한 치료법일 것이며 지금까지와 유사한 결과일 것이다.슐래플리는 4차원의 6개의 규칙적인 볼록 폴리스토페가 있다는 것을 보여주었다.Five of them can be seen as analogous to the Platonic solids: the 4-simplex (or pentachoron) to the tetrahedron, the hypercube (or tesseract) to the cube, the 4-orthoplex (or hexadecachoron or 16-cell) to the octahedron, the 120-cell to the dodecahedron, and the 600-cell to the icosahedron.여섯 번째, 24세포는 입방체와 팔면체 사이의 과도기적 형태로서 큐빅과 팔면체 사이의 과도기적 형태와 유사하게 볼 수 있다.
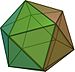
5개 이상의 차원에서는 4면체, 입방체, 8면체에 해당하는 정확히 3개의 일반 다면체가 있는데, 이것들은 규칙적인 단순화, 측정 다면체, 교차 다면체다면체다.이에 대한 설명은 일반 폴리토페즈 목록에서 찾을 수 있다.또한 슐래플리에 의해 부분적으로 발견되는 일반 4폴리탑 별도 관심사다.
19세기 말까지 아서 케일리, 루트비히 슐레플리 같은 수학자들은 테세락트나 24세포와 같은 4차원 이상의 일반 다상체 이론을 발전시켰다.
후자는 시각화하기는 어렵지만(불가능하지는 않지만) 여전히 그들의 저차원적 사촌들의 미적으로 보기 좋은 대칭을 유지하고 있다.큐빅은 8개의 큐빅 세포를 포함하고 있다.그것은 8개의 교차 모서리가 길이가 같고 각 큐브에 위치한 12+12 가장자리와 직교하도록 교차 연결된 정점이 있는 평행 하이퍼플레인으로 2개의 정사각형으로 구성된다.두 개의 정육면체의 상응하는 면은 연결되어 큐빅의 나머지 6개의 정육면체를 형성한다.24-셀은 각 정사각형 면의 8 정점을 추가 정점에 결합하여 피라미드의 4차원 아날로그를 형성함으로써 큐빅트에서 파생될 수 있다.두 인물은 물론 다른 4차원 인물들도 4차원 입체화면을 이용해 직접 시각화하고 묘사할 수 있다.[1]
아직도 상상하기 어려운 것은 57세포나 11세포와 같은 보다 현대적인 추상적인 일반 다세포들이다.그러나 수학적 관점에서 볼 때 이들 물체는 더욱 친숙한 2차원적, 3차원적 친족과 같은 미적 성질을 지니고 있다.
20세기 초에 일반 폴리토프의 정의는 다음과 같았다.
- 일반 다각형은 가장자리가 모두 같고 각도가 모두 같은 다각형을 말한다.
- 정다면체(正多面體)는 얼굴이 모두 합체 정다면체(正多面體)이며, 정점형상은 모두 합체 정다면체(正體面體)이다.
- 따라서, 규칙적인 n-폴리토프는 n-차원 폴리토프인데, (n - 1)차원 얼굴은 모두 규칙적이고 일치하며, 정점 형상은 모두 규칙적이고 일치한다.
이것은 "재발적"의 정의다.더 낮은 차원의 정규적인 수치 측면에서 더 높은 차원 수치의 정규성을 정의한다.등가(비복귀) 정의가 있는데, 폴리토프가 충분한 대칭도를 가지고 있으면 규칙적이라고 명시하고 있다.
- n-폴리토프는 정점, 이를 포함하는 가장자리, 가장자리를 포함하는 2차원 면 등으로 구성된 집합이 폴리토프의 대칭에 의해 다른 집합에 매핑될 수 있다면 규칙적이다.
예를 들어, 큐브는 정규적인데, 왜냐하면 큐브의 꼭지점 중 하나를 선택하고, 그 위에 있는 세 개의 가장자리 중 하나와 가장자리를 포함하는 두 개의 면 중 하나를 선택하면, 이 트리플트, 즉 플래그(Vertex, 엣지, 면)는 큐브의 적절한 대칭에 의해 다른 어떤 깃발에도 매핑될 수 있기 때문이다.따라서 우리는 매우 간결하게 규칙적인 폴리토프를 정의할 수 있다.
- 일반 폴리토프는 깃발에 대칭 그룹이 전이되는 것을 말한다.
20세기에는 몇 가지 중요한 발전이 이루어졌다.고전적인 일반 폴리토페스의 대칭 그룹은 현재 Coxeter 그룹이라고 불리는 그룹으로 일반화되었다.또한 콕시터 그룹은 공간 또는 평면의 규칙적인 테셀레이션의 대칭 그룹을 포함한다.예를 들어, 무한 체스 보드의 대칭 그룹은 Coxeter 그룹[4,4]이 될 것이다.
아페이로토페스 - 무한 폴리토페스
20세기 1부에 콕시터와 페트리는 무한구조물 {4,6}, {6,4}, {6,6}, {6,6}을(를) 발견했다.그들은 그것들을 규칙적인 다면체라고 불렀는데, 왜냐하면 그들은 모든 정점, 가장자리, 그리고 얼굴들이 비슷하고, 모든 각도가 같으며, 그림에는 자유 가장자리가 없기 때문이다.오늘날에는 무한 다면체 또는 아페이로헤드라라고 불린다.{4,4}, {3,6}, {6,3}, {6,3} 평면의 규칙적인 기울기는 무한 다면체라고도 볼 수 있다.
1960년대에 브란코 그룬바움(Branko Grünbaum)은 기하학계에 그가 폴리스트로마타라고 부르는 보다 추상적인 형태의 일반 폴리토페스를 고려하라는 요청을 발표했다.그는 폴리스트로마타 이론을 발전시켜, 그가 일반 아페이로토페스라고 부르는 새로운 물체의 예, 즉 무한히 많은 얼굴을 가진 일반 폴리토페스의 예를 보여주었다.꼬챙이 아페이로곤의 간단한 예는 지그재그일 것이다.그것은 정규 다각형의 정의를 만족시키는 것 같다. 모든 가장자리는 길이가 같고, 모든 각도는 같으며, 그림에는 느슨한 끝이 없다(그 이유는 결코 도달할 수 없기 때문이다).더 중요한 것은 아마도 어떤 꼭지점과 부착된 가장자리 쌍을 다른 것에 매핑할 수 있는 지그재그 대칭이 있을 것이다.이후 다른 일반 아페이로곤과 더 높은 아페이로토페스가 계속 발견되고 있다.
일반 복합 폴리토페스
복잡한 숫자는 우리가 모두 잘 알고 있는 비트인 실제 부분과 마이너스 1의 제곱근의 배수인 상상의 부분을 가지고 있다.복잡한 힐버트 공간은 복잡한 숫자로 x, y, z 등의 좌표를 가지고 있다.이것은 효과적으로 치수의 두 배가 된다.그러한 단일 공간에 만들어진 폴리토프를 복합 폴리토프라고 한다.[2]
추상 폴리토페스

그룬바움은 또한 이코사헤드라가 아닌 "헤미-아이코사헤드라"인 4차원 자기 이중 물체인 11-셀을 발견했는데, 이는 이코사헤드라의 반대쪽 얼굴을 실제로 같은 얼굴이라고 생각하면 얻게 되는 형상이다(Grünbaum 1976).헤미-icosaheadron은 20과 12를 가진 icosaheadron과 달리 10개의 삼각형 면과 6개의 정점만을 가지고 있다.
이 개념은 큐브와 헤미큐브의 관계를 생각한다면 독자들이 이해하기 더 쉬울 수 있다.일반적인 큐브는 8개의 모서리를 가지고 있으며, A에서 H로 라벨을 붙일 수 있으며, A는 H, B는 G로 반대편이다.헤미큐브에서는 A와 H를 같은 구석으로 취급할 것이다.B, G, 등등.가장자리 AB는 GH와 같은 가장자리가 되고, 얼굴 ABEF는 CDGH와 같은 얼굴이 된다.새로운 형태는 세 개의 면, 여섯 개의 가장자리, 네 개의 모서리에 불과하다.
11-셀은 평면(유클리드) 하이퍼스페이스에서는 정규 기하학적 구조를 형성할 수 없고, 양수 곡선(엘립틱) 하이퍼스페이스에서만 형성된다.
그룬바움이 11셀을 발견한 지 몇 년 후, H. S. M. 콕시터는 독립적으로 같은 모양을 발견했다.그는 일찍이 유사한 폴리토프인 57세포(Coxeter 1982, 1984년)를 발견했었다.
1994년까지 Grünbaum은 복합적인 점이나 정점 집합으로 추상적으로 폴리토페스를 고려하고 있었고, 얼굴이 평면적인지 여부에 대해서는 무관심했다.그와 다른 사람들이 이러한 사상을 다듬으면서 그러한 세트들은 추상적인 폴리토페스라고 불리게 되었다.추상적인 폴리토프는 부분적으로 순서가 정해진 세트(포셋)로 정의되며, 그 요소들은 격납에 의해 순서가 정해진 폴리토프의 얼굴(수직, 가장자리, 면 등)이다.고전적인 일반 폴리토페(Platonic solides 포함)에 의해 충족되는 속성과 유사한 세트에 일정한 제한이 가해진다.그러나 이 제한은 규칙적인 테셀레이션, 헤미큐브, 심지어 11세포나 이방인처럼 이상한 물체까지 모두 일반 다상체의 예일 정도로 느슨하다.
기하학적 폴리토프는 추상적 요소에서 기하학적 요소까지 일대일 매핑이 있는 것처럼 추상적 폴리토프의 실현으로 이해된다.따라서 모든 추상적 폴리토페가 적절한 추상적 포셋으로 설명될 수 있지만, 모든 추상적 폴리토페가 적절한 기하학적 실현을 가지는 것은 아니다.
이 이론은 이후 맥멀런&슐트(2002)에 의해 더욱 발전해 왔지만, 다른 연구자들 역시 기여를 했다.
추상 폴리에스테르의 규칙성
가장자리의 각도와 길이는 의미가 없기 때문에 규칙성은 추상적인 폴리토피에 대해서는 다르지만 관련이 있다.
도입부에 제시된 기의 과도성 측면에서 규칙성의 정의는 추상적인 다층화에 적용된다.
어떤 고전적인 일반 폴리토프는 얼굴 세트를 취함으로써 얻은 규칙적인 추상적인 등가물을 가지고 있다.그러나 예를 들어, 추상적인 폴리토페스는 각도와 가장자리 길이에 신경을 쓰지 않기 때문에, 비정규적인 고전적인 폴리토페스는 규칙적인 추상적 등가물을 가질 수 있다.그리고 보통의 추상적인 폴리토프는 고전적인 폴리토프로서 실현 가능하지 않을 수도 있다.
예를 들어, 모든 다각형은 추상적인 세계에서는 규칙적인 반면, 고전 세계에서는 동일한 각도와 길이가 같은 가장자리를 가진 것만이 규칙적인 것이다.
추상 폴리토페스의 꼭지점 그림
추상적인 폴리토프에 대해서도 정점 도형의 개념이 다르게 정의된다.주어진 정점 V에서 주어진 추상 n-폴리토프의 정점 수치는 V 자체를 포함하여 V를 포함하는 모든 추상적인 면의 집합이다.좀 더 형식적으로 말하면 추상적인 부분이다.
- Fn / V = {F V ≤ F ≤ Fn}
여기서 F는n 최대 얼굴, 즉 다른 모든 얼굴을 포함하는 n-얼굴이다.각 i-face, i ≥ 0 오리지널 폴리토페는 정점 그림의 (i - 1)면이 된다.
유클리드 폴리토페스의 경우와 달리, 규칙적인 면과 정점 형상을 가진 추상적인 폴리토페는 규칙적일 수도 있고 아닐 수도 있다. 예를 들어, 정사각형 피라미드와 같은, 모든 면과 정점 형상이 규칙적인 추상적인 폴리곤이다.
그러나 고전적인 꼭지점 수치는 추상적인 것의 실현이 될 것이다.
시공
폴리곤
일반적인 다각형 또는 실제로 비행기의 다른 어떤 형상을 만드는 전통적인 방법은 나침반과 직선이다.이런 식으로 어떤 규칙적인 다각형을 만드는 것은 매우 간단하다(아마도 가장 쉬운 것은 정삼각형일 것이다), 어떤 것은 더 복잡하고, 어떤 것은 불가능하다("구성이 불가능하다").구성할 수 없는 가장 간단한 몇 개의 일반 폴리곤은 n이 7, 9, 11, 13, 14, 18, 19, 21, n인 n면 폴리곤이다.
이 의미에서의 구성성은 이상적인 도구를 가진 이상적인 구성만을 가리킨다.물론 합리적으로 정확한 근사치는 다양한 방법으로 구성할 수 있지만 이론적으로 가능한 구조는 비현실적일 수 있다.
폴리헤드라
유클리드 원소는 다섯 개의 플라토닉 고형물에 대한 지배자와 공차 구조에 얼마만큼의 양을 주었다.[3]그러나 어떻게 하면 자로라도 우주에서 직선을 그릴 수 있는지에 대한 단순한 실용적인 질문은 일반 다면체를 "구축"하는 것이 정확히 무엇을 의미하는지 질문하게 할 수 있다.(물론 다면체에 대해서도 같은 질문을 할 수 있다.)
영어 단어 "construct"는 구성된 것을 체계적으로 만든다는 의미를 가지고 있다.일반 다면체를 만들기 위해 제시되는 가장 일반적인 방법은 접힌 그물을 통해서이다.다면체의 접이식 그물을 얻기 위해서는 다면체의 표면을 취하여 표면이 평평하게 펴질 수 있도록 가장자리를 따라 자른다.이것은 펼쳐진 다면체의 그물에 대한 계획을 준다.플라토닉 고형물은 얼굴을 위한 삼각형, 사각형, 펜타곤만 가지고 있고, 이것들은 모두 자와 나침반으로 구성 가능하기 때문에, 이러한 접힌 그물을 그리는 지배자와 주변적인 방법이 존재한다.여기서 우리는 겉으로 보이는 표면에만 그물을 만들도록 주의해야 하지만, 항성 다면체도 마찬가지다.
이 네트가 판지 또는 유사한 접이식 재료(예: 판금)에 그려진 경우, 그물을 잘라낼 수 있고, 자르지 않은 가장자리를 따라 접을 수 있으며, 적절한 절단 가장자리를 따라 결합할 수 있으며, 따라서 그물이 설계된 다면체를 형성할 수 있다.주어진 다면체의 경우 접힌 그물이 많을 수 있다.예를 들어, 큐브에는 11개가 있고, 도데체에는 900,000개가 넘는다.[4]
일반적으로 10대 또는 10대 이전 연령층을 대상으로 하는 수많은 어린이 장난감은 일반 다각형과 다면체 실험을 할 수 있다.예를 들어, Klikkko는 많은 다른 방법으로 가장자리 대 가장자리로 결합될 수 있는 플라스틱 삼각형, 사각형, 펜타곤 및 육각형 삼각형 세트를 제공한다.그러한 장난감을 가지고 노는 어린이는 특히 지식이 풍부한 어른으로부터 약간의 지도를 받는다면 플라토닉 고형물(또는 아르키메데스 고형물)을 재발견할 수 있을 것이다.
이론적으로, 거의 모든 물질은 규칙적인 다면체를 구성하는 데 사용될 수 있다.[5]그것들은 나무로 조각될 수도 있고, 철사로 모형화 될 수도 있고, 스테인드글라스로 만들어질 수도 있다.상상력이 한계다.
상위 치수


더 높은 차원에서는 사물을 "구축"함으로써 무엇을 의미하는지 말하기가 더 어려워진다.분명히 3차원 우주에서는 4차원 이상의 차원을 가진 물체의 물리적 모델을 만드는 것이 불가능하다.이 문제를 극복하기 위해 일반적으로 취해지는 몇 가지 접근법이 있다.
4차원에 적합한 첫 번째 접근방식은 4차원 입체화면을 사용한다.[1]3차원의 깊이는 수평 상대적 변위, 4차원의 깊이는 스테레오그래프의 왼쪽과 오른쪽 영상 사이에 수직 상대적 변위를 나타낸다.
두 번째 접근법은 평면상에 3차원 물체가 그려지는 방식과 유사한 방법을 사용하여 고차원 물체를 3차원 공간에 내장하는 것이다.예를 들어 앞 절에서 언급한 접이식 그물은 고차원적 등가물을 가지고 있다.[6]사람들은 다면체의 접힌 그물을 종이 위에 그리면서 이 접힌 그물의 모형을 만드는 것을 상상할 수도 있다.안타깝게도, 우리는 물리적 우주의 제약 때문에 4차원 폴리토프를 얻기 위해 필요한 3차원 구조의 접기를 결코 할 수 없었다.3차원의 고차원 형상을 "그리기"하는 또 다른 방법은 예를 들어, 직교 또는 원근 투영의 아날로그를 통한 것이다.Coxeter의 유명한 폴리토페스에 관한 책 (Coxeter 1948) (에는 그러한 정자 투영의 몇 가지 예가 있다.[7]4차원 폴리초라조차 직접 2차원에 담그는 것은 상당히 혼란스러운 일이다.이해하기 쉬운 것은 투영의 3-d 모델이다.그러한 모델들은 때때로 대학의 과학 박물관이나 수학 학과에서 발견된다.
3차원 하이퍼플레인이 있는 4차원(또는 더 높은) 차원의 일반 폴리토프의 교차점은 폴리토프(필수 정규적인 것은 아님)가 될 것이다.하이퍼플레인이 형상을 통해 이동하면 3차원 슬라이스를 결합하여 4차원 물체로 애니메이션화하여 4차원이 시간인 것으로 간주할 수 있다.이렇게 해서 4차원 일반 폴리탑의 전체 4차원 구조를 (완전히 파악하지 못하면) 이렇게 잘라낸 단면을 통해서 볼 수 있다.이는 CAT 스캔이 2차원 영상을 재조립해 스캔 중인 장기의 3차원 표현을 형성하는 방식과 유사하다.이상적인 것은 어떤 종류의 애니메이션 홀로그램이 될 것이지만, 보여지는 것과 같은 단순한 애니메이션이라도 이미 폴리토프의 구조에 대한 제한된 통찰력을 줄 수 있다.
3차원 시청자가 4차원 폴리토프의 구조를 이해할 수 있는 또 다른 방법은 아마도 어떤 형태의 가상현실 기술을 통해 사물에 '몰입'되는 것이다.이것이 어떻게 작동하는지 이해하기 위해서, 만약 공간이 큐브들로 채워진다면 무엇을 볼 수 있을지 상상해 보라.관람자는 정육면체 중 하나에 들어가 자신의 왼쪽과 오른쪽 앞, 뒤, 위, 아래, 정육면체를 볼 수 있을 것이다.만약 이런 방향으로 여행할 수 있다면, 정육면체의 배열을 탐색하고 기하학적 구조를 이해할 수 있을 것이다.정육면체의 무한 배열이 전통적 의미에서는 폴리토프가 아니다.사실 3차원(유클리드) 공간의 테셀레이션이다.그러나 4 폴리토프는 3차원 비유클리드 공간의 테셀레이션, 즉 4차원 구체 표면의 테셀레이션(4차원 구형 타일링)으로 볼 수 있다.

국지적으로, 이 공간은 우리가 익숙한 공간처럼 보인다. 따라서, 가상 현실 시스템은 원칙적으로 4차원 일반 폴리토페의 이러한 "테셀링" 즉, 탐사를 허용하도록 프로그램될 수 있다.UIUC의 수학과에는 도데카헤드라로 쌍곡선 공간을 다듬어 놓으면 어떤 것을 볼 수 있는지 여러 장의 그림이 있다.그러한 테셀레이션은 무한 추상적인 일반 폴리토프의 예를 형성한다.
일반적으로 추상적인 일반 다항체의 경우 수학자는 그 대칭 그룹의 구조가 알려져 있다면 그 물체가 "구축"된다고 생각한다.이것은 추상적인 정규 폴리토페스의 연구에서 중요한 정리 때문에, 추상적인 정규 폴리토페를 그 대칭 그룹에서 표준적이고 직접적인 방법으로 구성할 수 있는 기법을 제공한다.
자연 속의 규칙적인 폴리토페스
자연에서 다각형의 예는 다음을 참조하십시오.
플라토닉 고형물은 한 가지 또는 다른 형태로 자연적으로 발생한다.
참고 항목
참조
메모들
- ^ a b Brisson, David W. (2019) [1978]. "Visual Comprehension in n-Dimensions". In Brisson, David W. (ed.). Hypergraphics: Visualizing Complex Relationships In Arts, Science, And Technololgy. AAAS Selected Symposium. Vol. 24. Taylor & Francis. pp. 109–145. ISBN 978-0-429-70681-3.
- ^ 콕시터(1974)
- ^ 예를 들어 유클리드 원소를 참조하십시오.
- ^ 정육면체, 팔면체, 도데면체, 이코사면체의 흥미로운 접이식 그물 몇 개를 여기서 구할 수 있다.
- ^ 예를 들어 종이접기 모델을 제작하기 위한 지침은 여기에서 찾을 수 있다.
- ^ 이들 중 일부는 [1]에서 볼 수 있다.
- ^ 다른 예는 웹에서 찾을 수 있다(예: [2] 참조).
참고 문헌 목록
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover. ISBN 0-486-61480-8.
- — (1974). Regular Complex Polytopes. Cambridge University Press. ISBN 052120125X.
- — (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. ISBN 978-0-521-39490-1.
- Cromwell, Peter R. (1999). Polyhedra. Cambridge University Press. ISBN 978-0-521-66405-9.
- Euclid (1956). Elements. Translated by Heath, T. L. Cambridge University Press.
- Grünbaum, B. (1976). Regularity of Graphs, Complexes and Designs. Problèmes Combinatoires et Théorie des Graphes, Colloquium Internationale CNRS, Orsay. Vol. 260. pp. 191–197.
- Grünbaum, B. (1993). "Polyhedra with hollow faces". In Bisztriczky, T.; et al. (eds.). POLYTOPES: abstract, convex, and computational. Mathematical and physical sciences, NATO Advanced Study Institute. Vol. 440. Kluwer Academic. pp. 43–70. ISBN 0792330161.
- McMullen, P.; Schulte, S. (2002). Abstract Regular Polytopes. Cambridge University Press.
- Sanford, V. (1930). A Short History Of Mathematics. The Riverside Press.
- Schläfli, L. (1855). "Réduction d'une intégrale multiple, qui comprend l'arc de cercle et l'aire du triangle sphérique comme cas particuliers". Journal de Mathématiques. 20: 359–394.
- Schläfli, L. (1858). "On the multiple integral ∫^ n dxdy... dz, whose limits are p_1= a_1x+ b_1y+…+ h_1z> 0, p_2> 0,..., p_n> 0, and x^ 2+ y^ 2+…+ z^ 2< 1". Quarterly Journal of Pure and Applied Mathematics. 2: 269–301. 3 페이지 54–68, 97–197.
- Schläfli, L. (1901). "Theorie der vielfachen Kontinuität". Denkschriften der Schweizerischen Naturforschenden Gesellschaft. 38: 1–237.
- Smith, J. V. (1982). Geometrical and Structural Crystallography (2nd ed.). Wiley. ISBN 0471861685.
- Van der Waerden, B. L. (1954). Science Awakening. Translated by Dresden, Arnold. P Noordhoff.
- D.M.Y. Sommerville (2020) [1930]. "X. The Regular Polytopes". Introduction to the Geometry of n Dimensions. Courier Dover. pp. 159–192. ISBN 978-0-486-84248-6.
외부 링크
- Olshevsky, George. "Regular polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- 작은 일반 폴리토페스의 아틀라스 - 추상 일반 폴리토페스의 목록.
| 가족 | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정규 다각형 | 삼각형 | 사각형 | p-곤 | 육각형 | 펜타곤 | |||||||
| 균일다면체 | 사면체 | 옥타헤드론 • 큐브 | 데미큐브 | 도데카헤드론 • 이코사헤드론 | ||||||||
| 균일 폴리초론 | 펜타코론 | 16-셀 • 테세락트 | 데미테세락트 | 24셀 | 120 셀 • 600 셀 | |||||||
| 제복5폴리토프 | 5와섹스 | 5정형 • 5정형 | 5데미큐브 | |||||||||
| 제복6폴리토프 | 6-630x | 6-정통 • 6-118 | 6데미큐브 | 122 • 221 | ||||||||
| 제복7폴리토프 | 7시 15분 | 7정맥 • 7정맥 | 7데미큐브 | 132 • 231 • 321 | ||||||||
| 제복8폴리토프 | 8시 15분 | 8정형 • 8정형 | 8데미큐브 | 142 • 241 • 421 | ||||||||
| 제복9폴리토프 | 9시 15분 | 9-정통 • 9-11 | 9데미큐브 | |||||||||
| 균일 10폴리토프 | 10센트짜리 | 10정형 • 10정형 | 10데미큐브 | |||||||||
| 균일 n폴리토프 | n-제곱스 | n-직관 • n-직관 | n-데미큐브 | 1k2 • 2k1 • k21 | n-자갈 폴리토프 | |||||||
| 주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록 | ||||||||||||