헤미큐브(지오메트리)
Hemicube (geometry)| 헤미큐브 | |
|---|---|
 | |
| 유형 | 추상 정다면체 전지구 투영 다면체 |
| 얼굴 | 정사각형 3개 |
| 가장자리 | 6 |
| 정점 | 4 |
| 꼭지점 구성 | 4.4.4 |
| 슐레플리 기호 | {4,3}/2 또는 {4,3}3 |
| 대칭군 | S4, 주문 24 |
| 이중 다면체 | 헤미옥타헤드론 |
| 특성. | 방향성이 없는 오일러 특성 1 |
추상 기하학에서 헤미큐브는 추상적인 정규 다면체로서 큐브 면의 절반을 포함하고 있다.
실현
그것은 투사성 다면체(진짜 투사면의 3개 사변측정감시선에 의한 테셀레이션)로서 실현될 수 있는데, 투사면을 경계선을 따라 반대 지점이 연결되어 있는 반구로 구성하고 반구를 3등분하여 시각화할 수 있다.
그것은 세 개의 사각형 면, 여섯 개의 가장자리, 네 개의 꼭지점을 가지고 있다.모든 얼굴이 두 가장자리에 있는 다른 모든 얼굴과 접촉하고, 모든 얼굴에는 정점이 모두 들어 있어 정점에 의해 얼굴이 결정되지 않는 추상적인 폴리토프의 예가 된다.
그래프 이론의 관점에서 해골은 투영 평면에 K4(정점 4개가 있는 전체 그래프)를 내장한 사면 그래프다.
헤미큐브는 투사성 다면체인 데미큐브와 혼동해서는 안 되며 데미큐브는 일반적인 다면체(유클리드 공간)이다.둘 다 정점의 절반을 갖는 반면, 헤미큐브는 정점의 몫인 반면, 데미큐브의 정점은 정점의 부분집합이다.
관련 폴리토페스
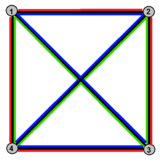
혈관은 일반 사면체에 대한 페트리 이중이며, 4면체의 4 정점, 6면 가장자리, 3면 Petrie polygon 4면이다.얼굴은 사면 그래프에서 빨간색, 녹색 및 파란색 가장자리 색상으로 볼 수 있다.
참고 항목
각주
참조
- McMullen, Peter; Schulte, Egon (December 2002), "6C. Projective Regular Polytopes", Abstract Regular Polytopes (1st ed.), Cambridge University Press, pp. 162–165, ISBN 0-521-81496-0