Domino 타일링

기하학에서 유클리드 평면에서 한 지역의 도미노 타일링은 도미노에 의해 그 지역을 다듬는 것으로, 가장자리에서 가장자리로 만나는 두 개의 단위 사각형의 결합에 의해 형성된 형상이다. 마찬가지로, 정점을 지역의 각 사각형 중심에 배치하고 정점 두 개를 인접한 사각형에 해당할 때 연결함으로써 형성된 격자 그래프에서 완벽하게 일치한다.

높이 함수

2차원의 일반 그리드에 있는 일부 기울기 클래스의 경우 그리드의 정점에 정수를 연결하는 높이 함수를 정의할 수 있다. 예를 들어, 체스보드를 그려 높이 ${\displaystyle 0_{}}$의 $노드{\displaystyle {}_{}}$ A ${\$를 수정한 다음, 모든 노드에 $대해{\displaystyle {}_{}}$ A ${\displaystyle {0\mathrm{}}_{}}$ ${\$까지의 경로가 있다. On this path define the height of each node ${\displaystyle A_{n+1}}$ (i.e. corners of the squares) to be the height of the previous node ${\displaystyle A_{n}}$ plus one if the square on the right of the path from ${\displaystyle A_{n}}$ to ${\displaystyle A_{n+1}}$ is black, and min우리 둘 다 그렇지

자세한 내용은 케년&오쿤코프(2005)에서 확인할 수 있다.

서스턴의 높이 상태

윌리엄 서스턴(William Thurston, 1990)은 비행기의 단위 사각형의 결합으로 형성된 단순 연결 영역에 도미노 타일링이 있는지 여부를 결정하기 위한 시험을 설명한다. He forms an undirected graph that has as its vertices the points (x,y,z) in the three-dimensional integer lattice, where each such point is connected to four neighbors: if x + y is even, then (x,y,z) is connected to (x + 1,y,z + 1), (x − 1,y,z + 1), (x,y + 1,z − 1), and (x,y − 1,z − 1), while if x + y is odd, then (x,y,z) is connected to (x + 1,y,z - 1), (x - 1,y,z - 1), (x,y + 1,z + 1) 및 (x,y - 1,z + 1) (x,y) 평면에서 정수 점의 시퀀스로 간주되는 영역의 경계는 이 3차원 그래프의 경로로 고유하게(시작 높이를 선택한 경우) 들어 올린다. 이 지역이 타일이 가능한 데 필요한 조건은 이 경로가 3차원의 단순 폐쇄 곡선을 형성하기 위해 닫아야 한다는 것이지만, 이 조건으로는 충분하지 않다. Thurston은 경계 경로에 대한 보다 세심한 분석을 사용하여 필요한 만큼 충분한 기와성 기준을 제공했다.

지역의 기울기 개수

${\displaystyle \frac{\mathrm{}}{}}$ ×${\displaystyle n}$ {\$displaystyle {\frac {mn}{2$}}개의$$도미노가$$ 있는 직사각형을$$ 커버하는 $방법$의 수는 템플리 & 피셔(1961년)와 Kastleyn(1961)에 의해 독립적으로 계산된다.

${\displaystyle \prod _{j=1}^{\lceil {\frac {m}{2}}\rceil }\prod _{k=1}^{\lceil {\frac {n}{2}}\rceil }\left(4\cos ^{2}{\frac {\pi j}{m+1}}+4\cos ^{2}{\frac {\pi k}{n+1}}\right).}$

m과 n이 모두 홀수일 경우 공식은 0의 도미노 기울기로 정확하게 감소한다.

$2{\displaystyle \mathrm{}}$ ${\displaystyle \times }$ ${\displaystyle n}$ ${\displaystyle 2\time n}$ 사각형을$$ n 도미노로 타일링할 때 특별한 경우가 발생하며, 이는 시퀀스가 피보나치 시퀀스로 감소한다.^[1]

m = n = 0, 2, 4, 6, 8, 10, 12, ...의 제곱에 대해 발생하는 또 다른 특별한 경우는 다음과 같다.

1, 2, 36, 6728, 12988816, 258584046368, 53060477521960000, ...(OEIS의 경우 시퀀스 A004003).

이 숫자는 고유값을 명시적으로 찾을 수 있는 m ${\displaystyle n}$ ${\displaystyle \times }$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle mn\times mn}$ 스큐 대칭$$ 행렬의 Pafeian으로 쓰면 찾을 수 있다. 이 기법은 많은 수학 관련 과목에 적용될 수 있는데, 예를 들어 통계 역학에서 조광기-다이머 상관 함수의 고전적 2차원 계산에 적용될 수 있다.

한 지역의 기울기 수는 경계 조건에 매우 민감하며, 그 지역의 모양에 있어 명백히 보잘것없는 변화로 극적으로 변할 수 있다. 이는 순서가 n인 아즈텍 다이아몬드의 기울기 수로 설명되며, 여기서 기울기 수는 2이다^{(n + 1)n/2}. 만약 이것이 2가 아니라 중간에 3개의 긴 열을 가진 n 순서의 "증강된 아즈텍 다이아몬드"로 대체된다면, 틸팅 수는 훨씬 적은 수인 D(n,n), 즉 델라노이 숫자로 감소하는데, 이는 n에서 초우수성장이 아니라 지수성장에 불과하다. 긴 가운데 행이 하나만 있는 n 오더 n의 "축소된 아즈텍 다이아몬드"의 경우 타일링이 하나만 있다.

• 

  1024개의 도미노 기울기가 있는 순서 4의 아즈텍 다이아몬드

• 

  하나의 가능한 타일링

다다미

다다미는 도미노 모양의 일본식 바닥 매트(1×2 사각형)이다. 그것들은 방들을 타일로 묶는 데 익숙하지만, 어떻게 배치될 수 있는지에 대한 추가적인 규칙들이 있다. 특히 전형적으로 3개의 다다미가 만나는 접점은 상서로운 것으로 간주되는 반면, 4개가 만나는 접점은 불명확하기 때문에 적당한 다다미타일링은 어느^[2] 모퉁이에서나 3개만 만나는 접점. 3개 구석에 만나는 다다미로 불규칙한 방을 타일링하는 문제는 NP완전이다.^[3]

퇴보된 공간 채우기 곡선

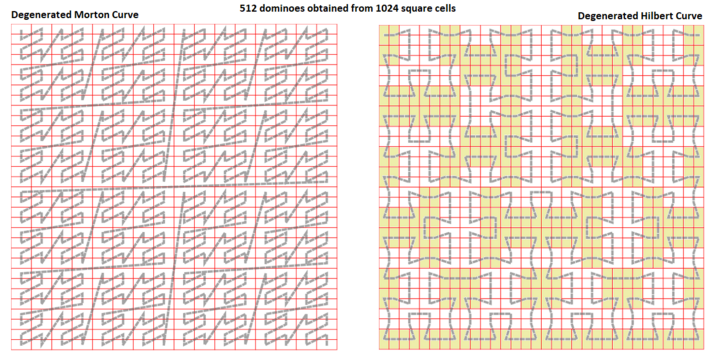
정규 제곱 격자 n×n을 형성하는 모든 유한한 집합의 셀은 지수 i가 0부터 n-1까지인² 정사각형(사면 단위 격자의 재귀적 4분할을 수행하는)과 일치하는 선택된 공간 채우기 곡선에 의해 색인화될 수 있다. 기하학적으로, 곡선은 사각 셀의 중심을 통과하는 경로로 그려질 수 있다. 도미노 타일링은 이웃 세포들을 합쳐서 얻는다. 각 도미노의 인덱스 j는 원래 그리드 인덱스의 함수 j=플로어(i ÷ 2)를 통해 얻는다. 새로운 프랙탈 곡선은 또 다른 프랙탈이기 때문에 "감속된 곡선"이다. 예:

"감소된 모튼 공간 채우기 곡선"은 수평 지향의 도미노 타일링을 정기적으로 생산하며, 이 곡선은 지오하쉬 지수화와 관련이 있으며, 여기서 Z자형 곡선은 и자형 곡선으로 변환된다.

'탈진 힐버트 공간 채우기 곡선'은 각 방향의 50%인 수평과 수직 지향 도미노를 혼합한 주기적 타일링 시스템을 생산한다. 퇴보한 힐버트 곡선은 뮌크레스의 프랙탈과 이형성이 있다.^[4]

통계물리학에서의 응용

2차원 주기율 격자 위에 완전 박리된 Ising 모델의 주기적인 도미노 타일링과 지상 상태 구성 사이에는 일대일 일치성이 있다.^[5] 이를 확인하기 위해 접지 상태에서 스핀 모델의 각 격자에는 정확히 하나의 좌절된 상호작용이 포함되어야 한다는 점에 주목한다. 따라서 이중 격자에서 볼 때, 각 좌절된 가장자리는 직사각형이 전체 격자에 걸쳐서 겹치지 않도록 1x2 직사각형으로 "덮어"져야 한다.

참고 항목

• 가우스 자유장, 일반 상황에서 높이 함수의 스케일링 한계(예: 큰 아즈텍 다이아몬드의 새겨진 원반 내부)
• 훼손된 체스판 문제, 62제곱의 체스판 부분집합 도미노 타일링에 관한 퍼즐
• 통계역학

메모들

참조

추가 읽기