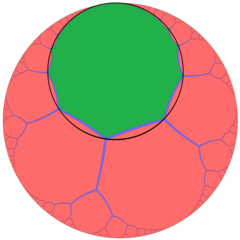
주문-3 a페이로건 타일링

주문-3 a페이로건 타일링
쌍곡면의 푸앵카레 디스크 모델
유형	쌍곡선 정규 타일링
꼭지점 구성	∞³
슐레플리 기호	{∞,3} t{{propert,properties} t(수,수,수,수)
와이토프 기호	3 ∞ 2 2 ∞ ∞ ∞ ∞ ∞
콕시터 다이어그램
대칭군	[∞,3], (∞32) [∞,∞], (∞∞2) [(∞,∞,∞)], (*∞∞∞)
이중	무한순 삼각 타일링
특성.	정점-변환, 에지-변환, 얼굴-변환

기하학에서 순서-3 apeirogonal tiling은 쌍곡면의 정규 타일링이다. 슐레플리 기호 { {,3}로 표현되며, 각 꼭지점 주위에 3개의 정규 아페이로곤이 있다. 각각의 아페이로곤은 호모시에 새겨져 있다.

순서 2 apeirogonal tiling은 유클리드 평면의 무한 다이헤드론(infinite dihedron)을 {1992,2}로 나타낸다.

이미지들

각각의 아페이로곤 면은 포앵카레 디스크 모델에서 원처럼 보이는 호로사이클에 의해 제한되며, 내부적으로는 투영 원 경계와 접한다.

균일 배색

유클리드 육각 타일링과 마찬가지로 각각 다른 반사 삼각형 그룹 도메인에서 나오는 오더-3 a페이로겐 타일링의 3가지 균일한 색상이 있다.

정규	잘라내기
{∞,3}	t_0,1{{propert,properties}	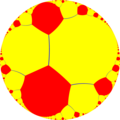t_1,2{{propert,properties}	t{{∞}^[3]
쌍곡선 삼각형 그룹
[∞,3]	[∞,∞]		[(∞,∞,∞)]

대칭

이 타일링에 대한 이중은 [(∞, ,, ∞, ))](*∞∞) 대칭의 기본 영역을 나타낸다. 거울 제거와 교대로 [((, ∞, ∞, ∞)]로 구성된 15개의 작은 지수 부분군(7개 고유)이 있다. 거울은 가지 주문이 모두 균등하면 제거할 수 있고, 주변 가지 주문을 절반으로 줄일 수 있다. 거울 두 개를 제거하면 제거된 거울이 만나는 곳에 반차량의 회전 지점이 남게 된다. 이러한 이미지에서 기본 도메인은 흑백으로 번갈아 가며 색상의 경계에는 거울이 존재한다. 대칭은 기본 영역을 이등분하는 거울을 추가하면 by∞2 대칭으로 배가될 수 있다. 기본 영역을 거울 3개로 나누면 ∞32 대칭이 생성된다.

더 큰 부분군이 구성되면 [(∞, ^*∞, ∞, ∞)], ( 8*∞)^∞가 제거되면 지수 8은 (*∞)^∞이 된다.

[(∞,∞,,,∞)](*∞∞)의 부분군
색인	1	2			4
도표
콕시터	[(∞,∞,∞)]	[(1⁺,∞,∞,∞)] =	[(∞,1⁺,∞,∞)] =	[(∞,∞,1⁺,∞)] =	[(1⁺,∞,1⁺,∞,∞)]	[(∞⁺,∞⁺,∞)]
오비폴드	*∞∞∞	*∞∞∞∞			∞*∞∞∞	∞∞∞×
도표
콕시터		[(∞,∞⁺,∞)]	[(∞,∞,∞⁺)]	[(∞⁺,∞,∞)]	[(∞,1⁺,∞,1⁺,∞)]	[(1⁺,∞,∞,1⁺,∞)] =
오비폴드		∞*∞			∞*∞∞∞
직접 부분군
색인	2	4			8
도표
콕시터	[(∞,∞,∞)]⁺	[(∞,∞⁺,∞)]⁺ =	[(∞,∞,∞⁺)]⁺ =	[(∞⁺,∞,∞)]⁺ =	[(∞,1⁺,∞,1⁺,∞)]⁺ =
오비폴드	∞∞∞	∞∞∞∞			∞∞∞∞∞∞
급진적 부분군
색인	∞			∞
도표
콕시터	[(∞,∞*,∞)]	[(∞,∞,∞*)]	[(∞*,∞,∞)]	[(∞,∞*,∞)]⁺	[(∞,∞,∞*)]⁺	[(∞*,∞,∞)]⁺
오비폴드	∞*∞^∞			∞^∞

관련 다면체 및 틸팅

이 타일링은 슐래플리 기호 {n,3}이(가) 있는 일반 폴리헤드라의 시퀀스의 일부로서 위상학적으로 관련이 있다.

*n32 일반 틸팅의 대칭 돌연변이: {n,3} v t
구면				유클리드 주	콤팩트 하이퍼브.		파라코.	비대칭 쌍곡선

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

[1968,3] 패밀리의 파라콤팩트 유니폼 틸팅 v t
대칭: [∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= 또는	= 또는	=

{∞,3}	t{{{propert,3}	r{{{195,3}	t{3,7}	{3,∞}	rr{reas,3}	tr{propert,3}	sr{sr,3}	h{{{no,3}	h₂{{{no,3}	s{3,7}
균일 듀얼


V∞³	V3.1987.1987	V(3.²19)	V6.6.1987	V3^∞	V4.3.4.1987	V4.6.1987	V3.3.3.3.1987	V(3.³19)		V3.3.3.3.3.1987

[직렬,직렬] 계열의 파라콤팩트 유니폼 틸팅 v t
= =	= =	= =	= =	= =	=	=

{∞,∞}	t{{propert,properties}	r{{{propert,properties}	2t{t{time,properties}=t{time,properties}	2r{{{190,190}={190,190}	rr{reas,reas}	tr{propert,properties}
이중 틸팅


V∞^∞	V∞.∞.∞.∞	V (1998.18)²	V∞.∞.∞.∞	V∞^∞	V4.1984.4.1987	V4.4.1987
교대
[1⁺,∞,∞] (*∞∞2)	[∞⁺,∞] (∞*∞)	[∞,1⁺,∞] (*∞∞∞∞)	[∞,∞⁺] (∞*∞)	[∞,∞,1⁺] (*∞∞2)	[(∞,∞,2⁺)] (2*∞∞)	[∞,∞]⁺ (2∞∞)


h{{{now,properties}	s{{proper,properties}	hr{hrp,properties}	s{{proper,properties}	h₂{{{now,properties}	흐르{{∞,∞}	sr{sr,properties}
교류 듀얼


V (1998.18)^∞	V(3.³19)	V (1998.4)⁴	V(3.³19)	V∞^∞	V(4.168.4)²	V3.3.1983.3.1987

[(수,수,수)] 계열의 파라콤팩트 균일 기울기 v t



(∞,∞,∞) h{{{now,properties}	r(∞, ∞, ∞) h₂{{{now,properties}	(∞,∞,∞) h{{{now,properties}	r(∞, ∞, ∞) h₂{{{now,properties}	(∞,∞,∞) h{{{now,properties}	r(∞, ∞, ∞) r{{{propert,properties}	t(수,수,수,수) t{{propert,properties}
이중 틸팅

V∞^∞	V∞.∞.∞.∞.∞.∞.∞	V∞^∞	V∞.∞.∞.∞.∞.∞.∞	V∞^∞	V∞.∞.∞.∞.∞.∞.∞	V∞.∞.∞.∞
교대
[(1⁺,∞,∞,∞)] (*∞∞∞∞)	[∞⁺,∞,∞)] (∞*∞)	[∞,1⁺,∞,∞)] (*∞∞∞∞)	[∞,∞⁺,∞)] (∞*∞)	[(∞,∞,∞,1⁺)] (*∞∞∞∞)	[(∞,∞,∞⁺)] (∞*∞)	[∞,∞,∞)]⁺ (∞∞∞)


교류 듀얼

V (1998.18)^∞	V (1998.4)⁴	V (1998.18)^∞	V (1998.4)⁴	V (1998.18)^∞	V (1998.4)⁴	V3.1987.3.1987.3.1987

참고 항목

참조

존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭, ISBN978-1-56881-220-5 (19장, 쌍곡선 아르키메데스 테셀레이션)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

외부 링크

Search