잘린 순서-4 반각 타일링

잘린 순서-4 반각 타일링
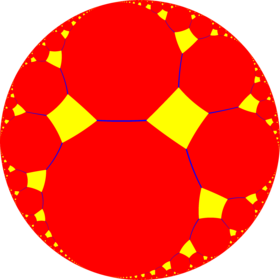쌍곡면의 푸앵카레 원반 모형
유형	쌍곡선 균일 타일링
정점 구성	4.∞.∞
슐레플리 기호	t{buffic,4} tr {displaystyle t${\begin{Bmatrix}\infty \\infty$\end {$Bmatrix}}$ $또는{\displaystyle }$t $displaystyle$t{\begin{Bmatrix$}}}$
위토프 기호	2 4 ∞ 2 ∞ ∞
콕서터 다이어그램	또는
대칭군	[∞,4], (*∞42) [∞,∞], (*∞∞2)
듀얼	무한차 테트라키스 정사각형 타일링
특성.	정점-이행

기하학에서 잘린 순서 4의 편각 타일링은 쌍곡면의 균일한 타일링이다.t{ symbol,4}의 Schléfli 기호가 있습니다.

균일한 착색

반대칭 색소는 tr{,, },}이며, 여기에 빨강과 노랑을 나타내는 2종류의 아페이로곤을 가진다.아페이로곤의 곡률이 너무 크면 오른쪽 그림과 같이 하나의 이상적인 점으로 수렴되지 않습니다. 아래의 빨간색 아페이로곤입니다.콕서터 다이어그램은 이러한 발산 초평행 미러에 대해 점선으로 표시됩니다.

(버텍스 중심)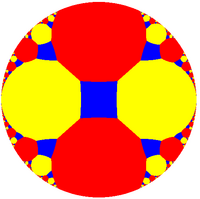

(사각형 중심)

대칭

[,,]] 대칭에서 거울 제거 및 교대로 15개의 작은 지수 부분군이 있다.거울은 지점 주문이 모두 짝수일 경우 제거할 수 있으며 주변 지점 주문을 절반으로 줄인다.미러 2개를 제거하면 제거된 미러가 만나는 반차 회전 지점이 남습니다.이러한 이미지에서 기본 도메인은 검은색과 흰색으로 번갈아 표시되고, 색상 사이의 경계에 거울이 존재합니다.대칭은 기본 영역을 이등분하는 거울을 추가함으로써 θ42 대칭으로 두 배가 될 수 있다.부분군 지수-8 그룹 [1⁺, ,, 1⁺, ,, ], ], ]1⁺]은 [,, ∞]의 정류자 부분군이다.

[,,]](*∞)2)의 작은 지수 부분군

색인	1	2			4
도표
콕서터	[∞,∞] =	[1+,440,160] =	[마음껏, 마음껏+, 마음껏, 1 。 =	[1명+, 1명, 1명] =	[1+,440,1+] =	[++마음껏, 마쉬움]
오르비폴드	*∞∞2	*∞∞∞		*∞2∞2	*∞∞∞∞	∞∞×
반직접 서브그룹
도표
콕서터		[+마음껏, 마쉬움]	[+마음껏, 마쉬움]	[(사기, 사기, 2+)]	[1번+, 1번, 2번+, 1번] = = = =	[1+,240,1+,240] = = = =
오르비폴드		∞*∞		2*∞∞	∞*∞∞
직접 부분군
색인	2	4			8
도표
콕서터	[+마음껏, 마쉬움] =	[++마음껏, 마쉬움] =	[++마음껏, 마쉬움] =	[1명+, 1명,+ 1명] =	[+++control,control] = [1,control+,1+,control,1+] = = =
오르비폴드	∞∞2	∞∞∞		∞2∞2	∞∞∞∞
급진 부분군
색인		∞		∞
도표
콕서터		[∞,∞*]	[∞*,∞]	[+이행, 이행*]	[+오디오*,오디오]
오르비폴드		*∞외부		∞∞

관련 다면체 및 타일링

*n42 잘린 타일링 대칭 돌연변이: 4.2n.2n v t
대칭 *n42 [n,4]	구면		유클리드	콤팩트 쌍곡선				파라콤프
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
잘렸다 수치
설정.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n개 수치
설정.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.★★

[,,4] 패밀리의 파라콤팩트 균일한 타일링 v t
{∞,4}	t{buffic,4}	r{syslog,4}	2t{buff,4}=t{4,4}	2r{br,4}={4,4}	rr{param,4}	tr {syslog, 4}
2자리 숫자
V★4	V4.★★	V(4.★)2	V8.8.★	V4∞	V43.★	V4.8.★
대체품
[1+,440,4] (*44∞)	[+4] (∞*2)	[1개+,4개] (*2∞2∞)	[4+] (4*∞)	[네, 네+, 하나] (*∞∞2)	[(고정, 4+, 2)] (2*2∞)	[4]+ (∞42)
=				=
h{param,4}	s{control,4}	hr{param,4}	s{4,190}	h{4,190}	hrr{param,4}	s{control,4}
교대 이중화
V(∞.4)4	V3.(3.★)2	V(4.14.4)2	V3 . 00 . ( 3 . 24 )	V★∞	V†.44	V3.3.4.3.★

[,,]] 계열의 파라콤팩트 균일한 타일링 v t
= =	= =	= =	= =	= =	=	=
{∞,∞}	t{contract,contract}	r{syslog,syslog}	2t{contract,contract}=t{contract,contract}	2r{buffic,buffic}={buffic,buffic}	rr{syslog,syslog}	tr {syslog, syslog}
듀얼 타일링
V★∞	V★★★★★★	V(∞.))2	V★★★★★★	V★∞	V4.★★★	V4.4.★
대체품
[1+,440,160] (*∞∞2)	[+마음껏, 마쉬움] (∞*∞)	[1명+, 1명, 1명] (*∞∞∞∞)	[+마음껏, 마쉬움] (∞*∞)	[마음껏, 마음껏+, 마음껏, 1 。 (*∞∞2)	[(사기, 사기, 2+)] (2*∞∞)	[+마음껏, 마쉬움] (2∞∞)
h{오디오,오디오}	s {syslog, syslog}	hr{syslog,syslog}	s {syslog, syslog}	h2{오디오,오디오}	hrr {syslog,syslog}	sr {various, svarious}
교대 이중화
V(∞.))∞	V(3.★)3	V(∞.4)4	V(3.★)3	V★∞	V(4.14.4)2	V3.3.3.

「 」를 참조해 주세요.

• 쌍곡면에서의 균일한 타일링
• 일반 폴리토프 목록

레퍼런스

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN978-1-56881-220-5(19장, 쌍곡 아르키메데스 테셀레이션)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

외부 링크

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
• 쌍곡선 및 구형 타일링 갤러리