볼록 균일 벌집

대체입방형 벌집모형은 유클리드 3공간에 있는 28개의 공간충전 균일 테셀레이션 중 하나로 노란색 테트라헤드라와 빨간색 옥타헤드라가 번갈아 가며 구성되어 있다.

기하학에서 볼록한 균일 벌집형(bolckx coniform honeycomb)은 3차원 유클리드 공간을 비과대칭된 균일 다면세포로 채우는 균일 테셀레이션이다.

그러한 꿀벌 28개는 다음과 같이 알려져 있다:

익숙한 입방형 벌집 및 그 7개의 잘림.
대체 입방형 벌집 및 벌집 4개.
균일한 평면 기울기에 기초한 10개의 프리즘 형태(입방형 벌집을 포함할 경우 11개)
연장 및/또는 교정을 통해 위의 일부 사항을 5번 수정한다.

그것들은 평면의 균일한 기울기에 대한 3차원 아날로그로 간주될 수 있다.

어떤 격자의 보로노이 도표는 세포가 조노헤드라인 볼록한 균일한 벌집을 형성한다.

역사

1900: 소럴드 고셋은 그의 저서 『n 치수공간의 정규 및 반정기적 도형에 관하여』에서 정규 입방 벌집 하나와 사면체 및 옥타헤드라를 포함한 2개의 반정형 형태의 다면체 목록을 열거하였다.
1905: 알프레도 안드레이니는 이 테셀링 중 25개를 열거했다.
1991: 노먼 존슨의 원고 Uniform Polytopes는 28개의 목록을 확인했다.^[1]
1994: Branko Grünbaum, 3-space의 유니폼 기울기 논문에서도 안드레이니의 출판에서 오류를 발견한 후 28개 모두를 독립적으로 열거했다. 그는 25개를 나열한 1905년 논문이 1개가 틀렸고, 4개가 누락된 것을 발견했다. Grünbaum은 이 논문에서 1991년에 같은 열거형을 달성한 노먼 존슨이 우선시되어야 한다고 말한다. 그는 또한 나를 언급한다. 러시아의 알렉세예프는 이 서식의 서술적 열거에 관해 그와 접촉했으나, 그룬바움이 당시 이것을 검증할 수 없었다고 한다.
2006년: 조지 올셰프스키는 그의 원고에서 11개의 볼록한 균일 기울기와 28개의 볼록한 균일 꿀콤의 파생 리스트를 반복하면서 143개의 볼록한 균일 테트라콤의 추가 파생 리스트를 확대한다.^[2]

볼록한 균일 다면체 중 오직 14개만이 이러한 패턴으로 나타난다.

다섯 개의 플라토닉 고형분 중 세 개는
13개의 아르키메데스 고형물 중 6개는
프리즘의 무한 5가지 가족

이름

이 세트는 일반 허니컴과 반정형 허니컴이라고 할 수 있다. 흔히 아르키메데스 고형물이라고 불리는 볼록한 제복(비정규) 다면체와 유추하여 아르키메데스 벌집이라고 불려왔다. 최근 콘웨이는 세트를 건축가 테셀레이션으로, 듀얼 허니컴을 캐터픽 테셀레이션으로 명명할 것을 제안했다.

개별 허니컴은 노먼 존슨(Norman Johnson)이 부여한 이름과 함께 나열된다. (아래에 사용된 용어 중 일부는 46개의 비prismatic Wythoffian 유니폼 4-폴리토페에 대한 Geometric 파생법에 정의되어 있다.)

상호 참조의 경우, 그것들은 안드레이니(1-22), 윌리엄스(1-2,9-19), 존슨(11-19, 21–25, 31–34, 41–49, 51–52, 61–65) 및 그룬바움(1-28)의 목록 지수로 제공된다. Coxeter는 입방형 벌집에는 Δ₄, 대체 입방형 벌집에는 Δ₄, 4분의 1 입방형 벌집에는 Δ를₄ 사용하며, Coxeter 다이어그램의 고리 패턴을 바탕으로 한 다른 형태에는 첨자를 사용한다.

컴팩트 유클리드 유니폼 테셀레이션(무한한 Coxeter 그룹 제품군별)

세 그룹의 세제곱 요소에 있는 기본 도메인.

가족 서신

3-공간을 위한 기본 무한 Coxeter 그룹은 다음과 같다.

$C$ ~ ${\tilde {C}}_{3}$ ${\$ [4,3,4], 입방체, (8개의 고유 형식과 1개의 교체 형태)
${\tilde {B}}_{3}$ ~ ${\tilde {B}}_{3}$ ${\$ [4,3^1,1], 대체 입방체, (11자형, 3자형)
${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ 주기 ${\tilde {A}}_{3}$ 그룹, [(3,3,3,3)] 또는 [3^[4]], (5개의 형식, 1개의 새로운 형식)

세 가족 모두 서신 왕래가 있다. Removing one mirror from ${\tilde {C}}_{3}$ produces ${\tilde {B}}_{3}$ , and removing one mirror from ${\tilde {B}}_{3}$ produces ${\tilde {A}}_{3}$ . This allows multiple constructions of the same 꿀벌들 각 Wythoff 구성 내에서 고유한 위치를 기준으로 셀에 색상을 입히면 이러한 다른 대칭이 나타날 수 있다.

또한 순수한 반사 대칭성을 가지지 않고 신장 및 집열 연산을 가진 반사형 형태로 구성된 5개의 특별한 꿀콤이 있다.

위의 독특한 꿀벌은 모두 18개다.

3-공간을 위한 무한 Coxeter 그룹의 프리즘 스택은 다음과 같다.

${\tilde {C}}_{2}$ ~ ${\tilde {C}}_{2}$ ${\$ }} ${\tilde {C}}_{2}$ ${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${\$ [4,4,2,16] 프리즘 그룹, (2가지 새로운 형태)
${\tilde {G}}_{2}$ ~ ${\tilde {G}}_{2}$ ${\$ }} ${\tilde {G}}_{2}$ ${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${\$ [6,3,2,16] 프리즘 그룹, (7개의 고유한 형태)
${\tilde {A}}_{2}$ ~ ${\tilde {A}}_{2}$ ${\$ }} ${\tilde {A}}_{2}$ ${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${\$ 1 ${\tilde {I}}_{1}$ [(3,3,3,3,3,2,3] 프리즘 그룹, (새로운 형식 없음)
${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${{\$ ${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${\$ 1} ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\$ [ [, ∞, prism] 프리즘 그룹, (이 모두 입방형 벌집이 된다)

또한 삼각 프리즘 벌집모양의 특별한 길쭉한 형태가 있다.

위의 총 고유 프리즘 꿀콤(앞서 계산한 입방체를 제외함)은 10이다.

이 숫자를 합치면, 18과 10은 우리에게 총 28개의 균일한 벌집을 준다.

C̃,₃ [4,3,4] 그룹(큐빅)

슐래플리 기호 {4,3,4}로 대표되는 일반 입방형 벌집합은 잘림 작업을 통해 7개의 고유한 파생 균일한 벌집을 제공한다. (하나의 중복 형태인 런케이트 입방 벌집합은 입방 벌집합과 동일하지만 완전성을 위해 포함된다.) 반사 대칭은 아핀 콕시터 그룹[4,3,4]이다. 교체를 생성하는 지수 2 하위그룹에는 4개의 인덱스 2 하위그룹이 있는데, 처음 생성된 2개의 반복 형태와 함께 [1⁺,4,3,4⁺], [4,3⁺,4], [4,3,4],⁺ 그리고 마지막 2개는 균일하지 않다.

C3 허니컴
공간 무리를 짓다	피브리폴드	확장됨 대칭	확장됨 도표를 만들다	주문	허니컴스
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	절반	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		하프 × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	쿼터 × 2	₁₀,
임3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

[4,3,4], 공간 그룹 Pm3m(221개)

참조 지수	벌집 이름 콕시터 다이어그램 슐래플리 기호	셀 카운트/버텍스 입방형 벌집형식의 위치						프레임 (내성적인)	정점수	이중세포
참조 지수	벌집 이름 콕시터 다이어그램 슐래플리 기호	(0)	(1)	(2)	(3)	알트	고체 (부분)	프레임 (내성적인)	정점수	이중세포
J_11,15 A을₁ W₁ G₂₂ δ₄	세제곱(촌) t₀{4,3,4} {4,3,4}				(8) (4.4.4)				팔면체	큐브,
J_12,32 A을₁₅ W₁₄ G₇ O₁	수정 입방체(부유한) t₁{4,3,4} r{4,3,4}	(2) (3.3.3.3)			(4) (3.4.3.4)		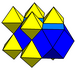		입방체의	사각형 bipyramid
J₁₃ A을₁₄ W₁₅ G₈ Δ₁₄ O₁₅	잘린 입방체(티치) t_0,1{4,3,4} t{4,3,4}	(1) (3.3.3.3)			(4) (3.8.8)				사각 피라미드	이소셀레 네모난 피라미드
J₁₄ A을₁₇ W₁₂ G₉ Δ_0,2₄ O₁₄	알 수 있는 입방체(srich) t_0,2{4,3,4} rr{4,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.4.4)				사선 삼각 프리즘	삼각비피라미드
J₁₇ A을₁₈ W₁₃ G₂₅ Δ_0,1,2₄ O₁₇	캔트런치 큐빅(회색) t_0,1,2{4,3,4} tr{4,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.8)				불규칙 사면체	삼각피라미드유
J₁₈ A을₁₉ W₁₉ G₂₀ Δ_0,1,3₄ O₁₉	런커런드 큐빅(프리치) t_0,1,3{4,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.8)	(1) (3.8.8)				사다리꼴 피라미드	사각 사방 피라미드
J_21,31,51 A을₂ W₉ G₁ Δ₄ O₂₁	대체 입방체(옥텟) h{4,3,4}				(8) (3.3.3)	(6) (3.3.3.3)			큐옥타헤드론	도데카헤드리유
J_22,34 A을₂₁ W₁₇ G₁₀ Δ₂₄ O₂₅	캔틱 큐빅(타토) ↔	(1) (3.4.3.4)		(2) (4.6.6)	(2) (3.6.6)				직사각형 피라미드	반쯤 지워진 옥타헤드리유
J₂₃ A을₁₆ W₁₁ G₅ Δ₃₄ O₂₆	런치 큐빅(래토) ↔	(1) 정육면체		(3) (3.4.4.4)	(1) (3.3.3)				테이퍼형 삼각 프리즘	쿼터 큐빌
J₂₄ A을₂₀ W₁₆ G₂₁ Δ_2,3₄ O₂₈	런시칸틱 큐빅 (환영) ↔	(1) (3.8.8)		(2) (4.6.8)	(1) (3.6.6)				불규칙 사면체	하프 피라미드유
통일형_b	정류된 세제곱을 스너브 sr{4,3,4}	(1) (3.3.3.3.3)	(1) (3.3.3)		(2) (3.3.3.3.4)	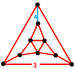(4) (3.3.3)			관개 삼면체
통일형	삼정화 비스무브 입방체 2s₀{4,3,4}	(3.3.3.3.3)	(4.4.4)	(4.4.4)	(3.4.4.4)
통일형	런치 캔티트런드 큐빅 sr₃{4,3,4}	(3.4.4.4)	(4.4.4)	(4.4.4)	(3.3.3.3.4)

[[4,3,4]] 허니컴, 우주군 임3m(229개)

참조 지수	벌집 이름 콕시터 다이어그램 슐래플리 기호	셀 카운트/버텍스 입방형 벌집형식의 위치			고체 (부분)	프레임 (내성적인)	정점수	이중세포
참조 지수	벌집 이름 콕시터 다이어그램 슐래플리 기호	(0,3)	(1,2)	알트	고체 (부분)	프레임 (내성적인)	정점수	이중세포
J_11,15 A을₁ W₁ G₂₂ δ₄ O₁	런케이트 입방체 (일반 세제곱으로 표시됨) (촌) t_0,3{4,3,4}	(2) (4.4.4)	(6) (4.4.4)				팔면체	큐브
J₁₆ A을₃ W₂ G₂₈ Δ_1,2₄ O₁₆	입방체(입방체)를 얇게시브(입방체) t_1,2{4,3,4} 2t{4,3,4}	(4) (4.6.6)		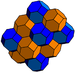			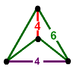(disphenoid	테트라헤드릴 주
J₁₉ A을₂₂ W₁₈ G₂₇ Δ_0,1,2,3₄ O₂₀	전분량 입방체(오치) t_0,1,2,3{4,3,4}	(2) (4.6.8)	(2) (4.4.8)				불규칙 사면체	여덟 번째 피라미드
J_21,31,51 A을₂ W₉ G₁ Δ₄ O₂₇	쿼터 큐빅 벌집 ht₀ht₃{4,3,4}	(2) (3.3.3)	(6) (3.6.6)				길쭉한 삼각 반감	큐빌 주
J_21,31,51 A을₂ W₉ G₁ Δ₄ O₂₁	대체 런케이티드 큐빅 (교체 입방체로 표시됨) ht_0,3{4,3,4}	(4) (3.3.3)	(4) (3.3.3)	(6) (3.3.3.3)			큐옥타헤드론
통일형	2s_0,3{(4,2,4,3)}
통일형_a	교번 비트롤드 큐빅 h2t{4,3,4}	(4) (3.3.3.3.3)		(4) (3.3.3)
통일형	2s_0,3{4,3,4}
통일형_c	대체된 전분해 입방 ht_0,1,2,3{4,3,4}	(2) (3.3.3.3.4)	(2) (3.3.3.4)	(4) (3.3.3)

B̃,₃ [4,3^1,1]그룹

${\tilde {B}}_{3}$ ~ ${\tilde {B}}_{3}$ ${\$ [4,3] 그룹은 잘림 작업을 통해 11개의 파생 양식을 제공하며, 4개는 고유한 균일한 벌집형이다. 교체를 생성하는 3개의 인덱스 2 하위그룹이 있다: [1⁺,4,3^1,1], [4,(3)],⁺ [4^1,1,3^1,1].⁺ 첫 번째는 벌집합을 반복적으로 생성하며, 마지막 두 개는 균일하지 않지만 완전성을 위해 포함되어 있다.

이 집단의 벌집들은 대체 정점이 제거된 입방형 벌집형으로 볼 수 있기 때문에 대체 입방체라고 불리며 입방 세포를 사면체 세포를 감소시키고 틈새에 팔면체 세포를 생성한다.

노드는 좌측에서 우측으로 색인화되며, 3은 0이 아래이고, 0은 0과 교환할 수 있다. 주어진 대체 입방체 이름은 이 주문에 기초한다.

B3 허니컴
공간 무리를 짓다	피브리폴드	확장됨 대칭	확장됨 도표를 만들다	주문	허니컴스
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁, ₂, ₃, ₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎, ₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅, ₆, ₇, ₍₆₎, ₉, ₁₀, ₁₁

[4,3^1,1] 균일한 벌집, 우주군 Fm3m(225)

참조됨 지수	벌집 이름 콕시터 도표	위치별 셀 (각 꼭지점 주위로 카운트)				고체 (부분)	프레임 (내성적인)	꼭지점 모양
참조됨 지수	벌집 이름 콕시터 도표	(0)	(1)	(0')	(3)	고체 (부분)	프레임 (내성적인)	꼭지점 모양
J_21,31,51 A을₂ W₉ G₁ Δ₄ O₂₁	대체입방체(옥텟) ↔			(6) (3.3.3.3)	(8) (3.3.3)			큐옥타헤드론
J_22,34 A을₂₁ W₁₇ G₁₀ Δ₂₄ O₂₅	캔틱 큐빅(타토) ↔	(1) (3.4.3.4)		(2) (4.6.6)	(2) (3.6.6)			직사각형 피라미드
J₂₃ A을₁₆ W₁₁ G₅ Δ₃₄ O₂₆	런치 큐빅(래토) ↔	(1) 정육면체		(3) (3.4.4.4)	(1) (3.3.3)			테이퍼형 삼각 프리즘
J₂₄ A을₂₀ W₁₆ G₂₁ Δ_2,3₄ O₂₈	런시칸틱 큐빅 (환영) ↔	(1) (3.8.8)		(2) (4.6.8)	(1) (3.6.6)			불규칙 사면체

<[4,3^1,1]> 균일 벌집, 우주군 Pm3m(221개)

참조됨 지수	벌집 이름 콕시터 도표 ↔	위치별 셀 (각 꼭지점 주위로 카운트)				고체 (부분)	프레임 (내성적인)	꼭지점 모양
참조됨 지수	벌집 이름 콕시터 도표 ↔	(0,0')	(1)	(3)	알트	고체 (부분)	프레임 (내성적인)	꼭지점 모양
J_11,15 A을₁ W₁ G₂₂ δ₄ O₁	큐빅(촌) ↔	(8) (4.4.4)						팔면체
J_12,32 A을₁₅ W₁₄ G₇ Δ₁₄ O₁₅	수정입방체(부유) ↔	(4) (3.4.3.4)		(2) (3.3.3.3)				입방체의
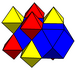J_12,32 A을₁₅ W₁₄ G₇ Δ₁₄ O₁₅	수정입방체(부유) ↔	(2) (3.3.3.3)		(4) (3.4.3.4)				입방체의
J₁₃ A을₁₄ W₁₅ G₈ Δ_0,1₄ O₁₄	잘린 입방체(티치) ↔	(4) (3.8.8)		(1) (3.3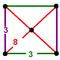.3.3)				사각 피라미드
J₁₄ A을₁₇ W₁₂ G₉ Δ_0,2₄ O₁₇	캔터링 큐빅(srich) ↔	(2) (3.4.4.4)	(2) (4.4.4)	(1) (3.4.3.4)				삼각 프리즘
J₁₆ A을₃ W₂ G₂₈ Δ_0,2₄ O₁₆	비트런드 큐빅(batch) ↔	(2) (4.6.6)		(2) (4.6.6)				이소체 사면체
J₁₇ A을₁₈ W₁₃ G₂₅ Δ_0,1,2₄ O₁₈	캔티트런드 큐빅(회색) ↔	(2) (4.6.8)	(1) (4.4.4)	(1) (4.6.6)				불규칙 사면체
J_21,31,51 A을₂ W₉ G₁ Δ₄ O₂₁	대체입방체(옥텟) ↔	(8) (3.3.3)			(6) (3.3.3.3)			큐옥타헤드론
J_22,34 A을₂₁ W₁₇ G₁₀ Δ₂₄ O₂₅	캔틱 큐빅(타토) ↔	(2) (3.6.6)		(1) (3.4.3.4)	(2) (4.6.6)			직사각형 피라미드
통일형_a	교번 비트롤드 큐빅 ↔	(2) (3.3.3.3.3)		(2) (3.3.3.3.3)	(4) (3.3.3)
통일형_b	교번식 캔티트런드 큐빅 ↔	(2) (3.3.3.3.4)	(1) (3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)			관개 삼면체

ANG₃^[4], [3

${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ [3^[4]] Coxeter 그룹으로 구성된 형태는^[3] 5가지가 있으며, 이 중 쿼터 큐빅 벌집만 독특하다. 스너브 폼을 생성하는 하나의 인덱스 2 하위 그룹[3^[4]]⁺이 있으며, 이는 균일하지는 않지만 완전성을 위해 포함되어 있다.

A3 허니컴
공간 무리를 짓다	피브리폴드	사각형 대칭	확장됨 대칭	확장됨 도표를 만들다	확장됨 무리를 짓다	허니콤 도표
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde{A}_{3}$	(없음)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 2₁ £ ${\tilde {B}}_{3}$ ~ ${\$ {\ $tild{B}_{3}}}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] 또는 [2⁺[3^[4]]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 4₁ 파운드 ${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ 8 파운드 ${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$ ${\tilde {C}}_{3}$ 2	_(*)
임3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ×8 파운드 ${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$ ${\tilde {C}}_{3}$ 2	₅

[[3^[4]] 균일한 벌집, 우주군 Fd3m(227)

참조됨 지수	벌집 이름 콕시터 도표	위치별 셀 (각 꼭지점 주위로 카운트)		고체 (부분)	프레임 (내성적인)	꼭지점 모양
참조됨 지수	벌집 이름 콕시터 도표	(0,1)	(2,3)	고체 (부분)	프레임 (내성적인)	꼭지점 모양
J_25,33 A을₁₃ W₁₀ G₆ Δ₄ O₂₇	쿼터 큐빅(바타토) ↔ q{4,3,4}	(2) (3.3.3)	(6) (3.6.6)			삼각 항정신병

<[3^[4]] £ [4,3^1,1] 균일 벌집, 우주군 Fm3m(225)

참조됨 지수	벌집 이름 콕시터 도표 ↔	위치별 셀 (각 꼭지점 주위로 카운트)			고체 (부분)	프레임 (내성적인)	꼭지점 모양
참조됨 지수	벌집 이름 콕시터 도표 ↔	0	(1,3)	2	고체 (부분)	프레임 (내성적인)	꼭지점 모양
J_21,31,51 A을₂ W₉ G₁ Δ₄ O₂₁	대체 입방체(옥텟) ↔ ↔ h{4,3,4}		(8) (3.3.3)	(6) (3.3.3.3)			큐옥타헤드론
J_22,34 A을₂₁ W₁₇ G₁₀ Δ₂₄ O₂₅	캔틱 큐빅(타토) ↔ ↔ h₂{4,3,4}	(2) (3.6.6)	(1) (3.4.3.4)	(2) (4.6.6)			직사각형 피라미드

[2[3^[4]] £ [4,3,4] 균일 벌집, 우주군 Pm3m(221)

참조됨 지수	벌집 이름 콕시터 도표 ↔	위치별 셀 (각 꼭지점 주위로 카운트)		고체 (부분)	프레임 (내성적인)	꼭지점 모양
참조됨 지수	벌집 이름 콕시터 도표 ↔	(0,2)	(1,3)	고체 (부분)	프레임 (내성적인)	꼭지점 모양
J_12,32 A을₁₅ W₁₄ G₇ Δ₁₄ O₁	수정 입방체(부유한) ↔ ↔ ↔ r{4,3,4}	(2) (3.4.3.4)	(1) (3.3.3.3)			입방체의

[4[3^[4]] £ [4,3,4] 균일 벌집, 우주군 임3m(229)

참조됨 지수	벌집 이름 콕시터 도표 ↔ ↔	위치별 셀 (각 꼭지점 주위로 카운트)		고체 (부분)	프레임 (내성적인)	꼭지점 모양
참조됨 지수	벌집 이름 콕시터 도표 ↔ ↔	(0,1,2,3)	알트	고체 (부분)	프레임 (내성적인)	꼭지점 모양
J₁₆ A을₃ W₂ G₂₈ Δ_1,2₄ O₁₆	입방체(입방체)를 얇게시브(입방체) ↔ ↔ 2t{4,3,4}	(4) (4.6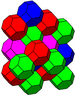.6)				이소체 사면체
통일형_a	교번식 캔티트런드 큐빅 ↔ ↔ h2t{4,3,4}	(4) (3.3.3.3.3)	(4) (3.3.3)

비와이토피아 양식(계량화 및 연장)

위의 허니컴 중 하나 또는 다른 하나를 얼굴이 연속면을 이루는 곳에서 깨트린 다음, 60도 또는 90도씩 번갈아 층을 회전시키거나 프리즘 층을 삽입하여 3개의 균일한 허니콤이 더 생성된다.

길쭉하고 길쭉한 교차 입방 기울기는 꼭지점 모양은 같지만 비슷하지는 않다. 길쭉한 형태에서, 각 프리즘은 한 삼각형 끝에서 사면체, 다른 쪽 끝에서 팔면체를 만난다. 길쭉한 형태에서 양쪽 끝에서 사방체를 만나는 프리즘은 양쪽 끝에서 팔방아를 만나는 프리즘과 번갈아 나타난다.

길쭉한 삼각 프리즘 타일링은 평형 프리즘 기울기 중 하나와 같은 꼭지점을 가지고 있다. 두 가지는 정육면체 층을 삽입하여 각각 평형 삼각 프리즘 기울기와 평형 삼각 프리즘 기울기에서 도출될 수 있다.

참조됨 지수	심볼	벌집 이름	셀 유형(각 꼭지점에서의 #)	꼭지점 모양
J₅₂ A을_2' G₂ O₂₂	h{4,3,4:g	Gyrated 교류 입방체(gytoh)	사면체(8) 팔면체(6)	삼각형 오르토스포폴라
J₆₁ A을_? G₃ O₂₄	h{4,3,4:ge	교번 대체 입방체(계토)	삼각 프리즘(6) 사면체(4) 팔면체 (3)
J₆₂ A을_? G₄ O₂₃	h{4,3,4:e	길쭉한 교번 세제곱(etoh)	삼각 프리즘(6) 사면체(4) 팔면체 (3)
J₆₃ A을_? G₁₂ O₁₂	{3,6:g × {message}	계량형 삼각 프리즘(계단)	삼각 프리즘(12)
J₆₄ A을_? G₁₅ O₁₃	{3,6:ge × {message}	길쭉한 삼각 프리즘(계타프리즘(계타프)	삼각 프리즘(6) 입방체(4)

프리즘 스택

11개의 프리즘적 기울기는 아래에 나타낸 11개의 균일한 평면 기울기를 평행한 층으로 쌓음으로써 얻는다.(이 중 하나는 위와 같은 입방체) 각각의 꼭지점 모양은 이등변 삼각형인 불규칙한 쌍곡선이다.

C̃×₂ĩ₁(∞), [4,4,2,∞], 프리즘 그룹

스퀘어 타일링의 독특한 꿀콤은 3개뿐이지만, 타일링의 6개 조각이 모두 아래에 나열되어 있어 완성도가 높으며, 타일링 이미지는 각 형태에 해당하는 색상으로 표시된다.

지수	콕시터딘킨 그리고 슐레플리 기호	벌집 이름	평면 타일링
J_11,15 A을₁ G₂₂	{4,4}×{∞}	큐빅 (제곱 프리즘) (촌)	(4.4.4.4)
	r{4,4}×{∞}
	rr{4,4}×{{∞}}
J₄₅ A을₆ G₂₄	t{4,4}×{{4}}	잘림/빗줄임 사각 프리즘(타시프)	(4.8.8)
J₄₅ A을₆ G₂₄	tr{4,4}×{{propert}	잘림/빗줄임 사각 프리즘(타시프)	(4.8.8)
J₄₄ A을₁₁ G₁₄	sr{4,4}×{5}	스너브 사각 프리즘(sassiph)	(3.3.4.3.4)
통일형	ht_0,1,2,3{4,4,2,190}

G̃₂Xĩ(∞),₁ [6,3,2,3] 프리즘 그룹

지수	콕시터딘킨 그리고 슐레플리 기호	벌집 이름	평면 타일링
J₄₁ A을₄ G₁₁	{3,6} × {∞}	삼각 프리즘(tiph)	(3⁶)
J₄₂ A을₅ G₂₆	{6,3} × {∞}	육각 프리즘(힙)	(6³)
J₄₂ A을₅ G₂₆	t{3,6} × {message}	육각 프리즘(힙)	(6³)
J₄₃ A을₈ G₁₈	r{6,3} × {∞}	삼각 프리즘(thiph)	(3.6.3.6)
J₄₆ A을₇ G₁₉	t{6,3} × {message}	잘린 육각 프리즘(타프)	(3.12.12)
J₄₇ A을₉ G₁₆	rr{6,3} × {∞}	Rhombi-trihexangular 프리즘(로타프)	(3.4.6.4)
J₄₈ A을₁₂ G₁₇	sr{6,3} × {message}	육각 프리즘 스너브(스나타프)	(3.3.3.3.6)
J₄₉ A을₁₀ G₂₃	tr{6,3} × {message}	잘린 3헥사형 프리즘(오타프)	(4.6.12)
J₆₅ A을_11' G₁₃	{3,6:e × {message}	길쭉한 삼각 프리즘(etoph)	(3.3.3.4.4)
J₅₂ A을_2' G₂	h3t{3,6,2,190}	Gyrated 사면체-옥타면체(gytoh)	(3⁶)
J₅₂ A을_2' G₂	s2r{3,6,2,3}	Gyrated 사면체-옥타면체(gytoh)	(3⁶)
통일형	ht_0,1,2,3{3,6,2,190}

와이토프 양식 열거

콕시터 그룹에 의한 모든 비prismatic Wythoff 건설은 그들의 교체와 함께 아래에 제공된다. 균일한 솔루션은 Branko Grünbaum의 상장과 함께 색인화된다. 녹색 배경은 반복되는 허니컴에 나타나며, 관계는 확장된 대칭도도로 표현된다.

콕시터군	확장됨 대칭	허니컴스		치랄 연장된 대칭	교대 벌집
[4,3,4]	[4,3,4]	6	₂₂ ₇ ₈ ₉ ₂₅ ₂₀	[1⁺,4,3⁺,4,1⁺]	(2)	₁ _b
	[2⁺[4,3,4]] =	(1)	₂₂	[2⁺[(4,3⁺,4,2⁺)]]	(1)	₁ ₆
	[2⁺[4,3,4]]	1	₂₈	[2⁺[(4,3⁺,4,2⁺)]]	(1)	_a
	[2⁺[4,3,4]]	2	₂₇	[2⁺[4,3,4]]⁺	(1)	_c
[4,3^1,1]	[4,3^1,1]	4	₁ ₇ ₁₀ ₂₈
	[1[4,3^1,1]]=[4,3,4] =	(7)	₂₂ ₇ ₂₂ ₇ ₉ ₂₈ ₂₅	[1[1⁺,4,3^1,1]]⁺	(2)	₁ ₆ _a
	[1[4,3^1,1]]=[4,3,4] =	(7)	₂₂ ₇ ₂₂ ₇ ₉ ₂₈ ₂₅	[1[4,3^1,1]]⁺ =[4,3,4]⁺	(1)	_b
[3^[4]]	[3^[4]]	(iii)
	[2⁺[3^[4]]]	1	₆
	[1[3^[4]]]=[4,3^1,1] =	(2)	₁ ₁₀
	[2[3^[4]]]=[4,3,4] =	(1)	₇
	[(2⁺,4)[3^[4]]]=[2⁺[4,3,4]] =	(1)	₂₈	[(2⁺,4)[3^[4]]]⁺ = [2⁺[4,3,4]]⁺	(1)	_a

예

이 28개의 테셀레이션은 모두 크리스탈 배열에서 찾을 수 있다.^{[citation needed]}

대체 입방형 벌집모양의 정점은 입방형 근접 구를 형성하기 때문에 특히 중요하다. 포장된 옥타헤드라와 사트라헤드라의 공간을 채우는 트러스들은 분명히 알렉산더 그레이엄 벨에 의해 처음 발견되었고 벅민스터 풀러에 의해 독립적으로 재발견되었다(그 트러스들은 그것을 옥타드 트러스라고 불렀고 1940년대에 특허를 얻었다. [3] [4] [5] [6]. 옥텟 트러스는 현재 건설에 사용되는 가장 일반적인 유형의 트러스에 속한다.

프리즈가 형성되다.

셀이 균일한 기울기를 허용하면 더 균일한 벌집을 정의할 수 있다.

패밀리:

${\tilde {C}}_{2}$ ~ ${\tilde {C}}_{2}$ ${\$ ${$ $2$ }} x A 1 {\ $displaystyle$ A_ ${$ 1} : [4,4,2]입방 슬래브 허니컴(3가지 형태)
${\tilde {G}}_{2}$ ~ ${\tilde {G}}_{2}$ ${\$ } ${2}}$ x A 1 {\ $displaystyle$ A_{1} : [6,3,2] 3헥사각 슬래브 허니컴(8종류)
${\tilde {A}}_{2}$ $A_{1}$ ${\tilde {A}}_{2}$ ~ ${\tilde {A}}_{2}$ ${\$ }} ${\tilde {A}}_{2}$ A 1 {\ $displaystyle$ A_ ${$ 1} $A_{1}$ : [(3,3,3)] 삼각 슬래브 허니컴(새 양식 없음)
${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${\$ x $A_{1}$ $A_{1}$ ${\$ $A_{1}$ A $A_{1}$ ${\$ } $A_{1}$ : [12,2] = 큐빅 칼럼 허니콤(1 형태)
$I_{2}(p)$ $I_{2}(p)$ ( p $I_{2}(p)$ ) $I_{2}(p)$ $I_{2}(p)$ ${\tilde {I}}_{1}$ ~ ${\tilde {I}}_{1}$ ${\$ } ${\tilde {I}}_{1}$ : [p,2,3] 다각형 기둥 허니컴프
${\tilde {C}}_{2}$ ~ ${\tilde {C}}_{2}$ ${\$ }} ${\tilde {C}}_{2}$ ${\tilde {C}}_{2}$ ~ 2 ${\$ }} x ${\tilde {C}}_{2}$ $A_{1}$ ${\$ } $A_{1}$ : [4,4,2] = (입방 슬래브 벌집합 계열과 동일)

예제(부분적으로 그려짐)
큐빅 슬래브 벌집	교류 육각 슬래브 벌집	삼헥사각 슬래브 벌집

(4) 4³: 입방체 (1) 4⁴: 사각 타일링	(4) 3³: 사면체 (3) 3⁴: 팔면체 (1) 3⁶: 삼각 타일링	(2) 3.4.4: 삼각 프리즘 (2) 4.4.6: 육각 프리즘 (1) (3.6):² 3헥사각 타일링

스칼리폼 벌집

신장형 벌집은 균일한 벌집처럼 정점 변환성이며, 일반적인 폴리곤 얼굴을 가지고 있는 반면, 세포와 상위 원소들은 정점이 하이퍼스피어 위에 놓여 있는 등각형, 등각형만 있으면 된다. 3D 허니컴의 경우, 이것은 존슨의 고형분의 부분집합과 균일한 다면체를 허용한다. 일부 메스폼은 교대 과정에 의해 생성될 수 있으며, 예를 들어 피라미드와 큐폴라 간극을 남긴다.^[4]

유클리드 벌집형 메스폼
프리제 슬래브			프리즘 스택
s₃{2,6,3},	s₃{2,4,4},	s{2,4,4},	3s₄{4,4,2,3}


(1) 3.4.3.4: 삼각 큐폴라 (2) 3.4.6: 삼각 큐폴라 (1) 3.3.3.3: 팔면체 (1) 3.6.3.6: 3헥사형 타일링	(1) 3.4.4.4: 사각 큐폴라 (2) 3.4.8: 사각 큐폴라 (1) 3.3.3: 사면체 (1) 4.8.8: 잘린 사각 타일링	(1) 3.3.3.3: 사각 피라미드 (4) 3.3.4: 사각 피라미드 (4) 3.3.3: 사면체 (1) 4.4.4.4: 사각 타일링	(1) 3.3.3.3: 사각 피라미드 (4) 3.3.4: 사각 피라미드 (4) 3.3.3: 사면체 (4) 4.4.4: 큐브

쌍곡선 형태

주문-4 도데카헤드허니콤, {5,3,4} 원근법

파라콤팩트 육각 타일링 벌집, {6,3,3} 원근법

쌍곡선 3-공간에 9개의 콤팩트한 균일 벌집형 벌집형 집단이 있으며, Wythoff 시공사로 생성되며 각 패밀리에 대한 Coxeter-Dynkin 도표의 링 순열로 표현된다.

이들 9개 제품군에서 생성된 독특한 꿀벌은 총 76개다.

[3,5,3] : - 9개 서식
[5,3,4] : - 15개 서식
[5,3,5] : - 9개 서식
[5,3^1,1] : - 11가지 형태([5,3,4] 계열과 7가지 중첩, 4가지가 고유)
[(4,3,3)] : - 9개 서식
[(4,3,4,3)] : - 6개 서식
[(5,3,3,3)] : - 9개 서식
[(5,3,4,3)] : - 9개 서식
[(5,3,5,3)] : - 6개 서식

쌍곡선 유니폼의 전체 목록은 증명되지 않았고 알려지지 않은 수의 비 위트피안 형태들이 존재한다. 알려진 예로는 {3,5,3}개 패밀리가 있다.

파라콤팩트 쌍곡선 형태

4등급의 파라콤팩트 콕시터 그룹도 23개나 된다. 이러한 패밀리는 무한대의 이상적인 정점을 포함하여 한이 없는 면이나 정점 모양을 가진 균일한 벌집을 생산할 수 있다.

심플렉틱 쌍곡선 파라콤팩트 그룹 요약
유형	콕시터 그룹	고유 벌집 수
선형 그래프		4×15+6+8+8 = 82
삼차 그래프		4+4+0 = 8
순환 그래프		4×9+5+1+4+1+0 = 47
반복-n-테일 그래프		4+4+4+2 = 14

참조

^ "A242941 - OEIS". oeis.org. Retrieved 2019-02-03.
^ 조지 올셰프스키, (2006년, 균일 파노플로이드 테트라콤, 원고 (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤 목록) [1]
^ [2], A000029 6-1건, 0 표시가 있는 1건 건너뛰기
^ "Polytope-tree".

John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292–298, includes all the nonprismatic forms)
브란코 그룬바움, (1994) 3공간의 균일한 기울기. 검비네이터 4, 49 - 56
노먼 존슨(1991) 제복 폴리탑스, 원고
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (5장: 폴리헤드라 패킹 및 공간충전)
Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [7]
- (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술] Zeit. 46 (1940) 380–407, MR 2,10](1.9 균일한 공간 채우기)
A. 안드레이니, (1905) 설레 레티디 리골라리 e semiregolari e sulle corrisponti retiative (폴리헤드라의 정규 및 반정형 그물 및 그에 상응하는 상관 그물에 대하여), 멤. 소시에타 이탈리아 델라 스키엔제, 세르.3, 14 75–129. PDF [8]
D. M. Y. Sommerville, (1930) n차원의 기하학 소개. 뉴욕, E. P. Dutton, . 196 페이지 (Dover Publications Edition, 1958)장 X장: 일반 폴리토페즈
Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. 제5장. 다면체 결합
Quasicrystals의 결정학: Walter Steurer, Sofia Deloudi(2009) 페이지 54-55. 12개 이상의 입방 대칭의 균일한 폴리헤드라 포장

외부 링크

Weisstein, Eric W. "Honeycomb". MathWorld.
3-Space VRML 모델의 균일한 Honeycombs
초급 허니콤은 꿀컴을 불균일 세포로 채우는 정점 전이 공간이다.
3-공간, 그 친척 및 임베딩의 균일한 파티션, 1999년
균일 폴리헤드라
가상현실 폴리헤드라 폴리헤드라 백과사전
옥텟 트러스 애니메이션
검토: A. F. Wells, 3차원 그물 및 다면체, H. S. M. Coxeter(출처: 황소. 아머. 수학. Soc. 제84권, 제3호(1978년), 제466-470호)
Klitzing, Richard. "3D Euclidean tesselations".
(OEIS에서 시퀀스 A242941)

v t 치수 2-9의 기본 볼록 정규 및 균일한 벌집
공간	가족	${\tilde{A}_{n-1$	${\tilde{C}_{n-1$	${\tilde{B}_{n-1$	${\tilde{D}_{n-1$	${\tilde {G}}_{2}$ ~ ${\tilde {G}}_{2}$ ${\$ G} ${\tilde {G}}_{2}$ ${\tilde {F}}_{4}$ 2}} ${\tilde {F}}_{4}$ / F ~ 4 {\ $displaystyle {\tilde{F}_{4}}$ ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$ ~ ${\tilde {E}}_{n-1}$ ${\$ }
E²	균일 타일링	{3^[3]}	δ₃	Δ₃	Δ₃	육각형
E³	균일볼록 벌집	{3^[4]}	δ₄	Δ₄	Δ₄
E⁴	제복4벌집	{3^[5]}	δ₅	Δ₅	Δ₅	24셀 벌집
E⁵	제복5벌집	{3^[6]}	δ₆	Δ₆	Δ₆
E⁶	제복6벌집	{3^[7]}	δ₇	Δ₇	Δ₇	2₂₂
E⁷	제복7허니콤	{3^[8]}	δ₈	Δ₈	Δ₈	1₃₃ • 3₃₁
E⁸	제복8벌집	{3^[9]}	δ₉	Δ₉	Δ₉	1₅₂ • 2₅₁ • 5₂₁
E⁹	제복9벌집	{3^[10]}	δ₁₀	Δ₁₀	Δ₁₀
E¹⁰	제복10벌집	{3^[11]}	δ₁₁	Δ₁₁	Δ₁₁
E^n-1	제복(n-1)-벌집합	{3^[n]}	δ_n	Δ_n	Δ_n	1_k2 • 2_k1 • k₂₁

[1] "A242941 - OEIS". oeis.org. Retrieved 2019-02-03.

[2] 조지 올셰프스키, (2006년, 균일 파노플로이드 테트라콤, 원고 (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤 목록) [1]

[3] [2], A000029 6-1건, 0 표시가 있는 1건 건너뛰기

[4] "Polytope-tree".

[1]

[2]

[3]

[4]

Search

볼록 균일 벌집

네임스페이스

더

목차

역사

이름

컴팩트 유클리드 유니폼 테셀레이션(무한한 Coxeter 그룹 제품군별)

C̃,₃ [4,3,4] 그룹(큐빅)

B̃,₃ [4,3^1,1]그룹

ANG₃^[4], [3

비와이토피아 양식(계량화 및 연장)

프리즘 스택

C̃×₂ĩ₁(∞), [4,4,2,∞], 프리즘 그룹

G̃₂Xĩ(∞),₁ [6,3,2,3] 프리즘 그룹

와이토프 양식 열거

예

프리즈가 형성되다.

스칼리폼 벌집

쌍곡선 형태

파라콤팩트 쌍곡선 형태

참조

외부 링크

Search

볼록 균일 벌집

역사

이름

컴팩트 유클리드 유니폼 테셀레이션(무한한 Coxeter 그룹 제품군별)

C̃,3 [4,3,4] 그룹(큐빅)

B̃,3 [4,31,1]그룹

ANG3[4], [3

비와이토피아 양식(계량화 및 연장)

프리즘 스택

C̃×2ĩ1(∞), [4,4,2,∞], 프리즘 그룹

G̃2Xĩ(∞),1 [6,3,2,3] 프리즘 그룹

와이토프 양식 열거

예

프리즈가 형성되다.

스칼리폼 벌집

쌍곡선 형태

파라콤팩트 쌍곡선 형태

참조

외부 링크

C̃,₃ [4,3,4] 그룹(큐빅)

B̃,₃ [4,3^1,1]그룹

ANG₃^[4], [3

C̃×₂ĩ₁(∞), [4,4,2,∞], 프리즘 그룹

G̃₂Xĩ(∞),₁ [6,3,2,3] 프리즘 그룹