페트리 듀얼

도데카헤드론의 페트리 폴리곤은 꼬치 데카곤이다.고체의 5배 대칭 축에서 볼 때, 그것은 보통의 데카곤처럼 보인다.한 쌍의 연속된 면은 모두 하나의 오각형에 속한다(그러나 세 쌍이 하는 것은 없다).

위상 그래프 이론에서 내장 그래프의 페트리 듀얼(모든 면 디스크가 있는 2-manifold에 있음)은 첫 번째 내장 그래프의 페트리 폴리곤을 면으로 하는 또 다른 내장 그래프다.^[1]

페트리 듀얼은 페트리얼이라고도 하며, 임베디드 그래프 G $G$ 의 페트리 듀얼은 $G^{\pi }$ $G^{\pi }$ ${\$ G $^{\pi }}}}}}$ 로 표기할 수 $G$ 있다 $G^{\pi }$ ^[2] 임베딩의 모든 모서리를 비틀어 임베디딩의 서명된 회전 시스템이나 리본 그래프 표현에서 얻을 수 있다.

특성.

일반적인 듀얼 그래프와 마찬가지로 페트리 듀얼 작동을 두 번 반복하면 원래 표면 임베딩으로 돌아간다.일반적인 이중 그래프(동일한 표면에 일반적으로 다른 그래프를 내장한 그래프)와는 달리, 페트리 듀얼은 일반적으로 다른 표면에 동일한 그래프를 내장한 것이다.^[1]

표면 이중성과 페트리 이중성은 윌슨 6개 작업 중 2개 작업이며, 함께 이러한 작업 그룹을 생성한다.^[3]

정다면체

페트리 듀얼을 일반 다면체에 적용하면 일반 지도가 생성된다.^[2]skew h-gonal 면의 수는 g/2h이며, 여기서 g는 그룹 순서, h는 그룹의 coxeter 수입니다.

예를 들어, 큐브의 페트리 듀얼(정점 8개와 12개의 가장자리가 있는 초당적 그래프, 6개의 사각면이 있는 구체에 내장됨)은 큐브의 등각자인 4개의^[4] 육각면을 가지고 있다.토폴로지로는 동일한 그래프를 토러스 위에 내장한다.^[1]

이렇게 해서 얻은 정규지도는 다음과 같다.

페트리얼 사면체, {3,3}^$π$은(는) 꼭지점 4개, 가장자리 6개, 꼬치 사각형 3개를 가지고 있다.오일러 특성 χ이 1인 경우, 위상학적으로 헤미큐브 {4,3}/2와 동일하다.
페트리얼 큐브인 {4,3}^$π$은(는) 8개의 꼭지점, 12개의 가장자리, 4개의 꼬치 육각형(빨간색, 녹색, 파란색, 주황색)을 가지고 있다.오일러 특성이 0인 경우 유형 {6,3}_(2,0)인 육각 타일링의 4개의 육각형 면에서도 볼 수 있다.
페트리얼 옥타헤드론 {3,4}^$π$은(는) 6개의 꼭지점, 12개의 가장자리, 4개의 꼬치 육각면을 가지고 있다.오일러 특성은 -2이며, 유형 {6,4}₃인 쌍곡 순서-4 육각 타일링에 대한 매핑을 가지고 있다.
페트리얼 도데카헤드론, {5,3}^$π$은(는) 정점 20개, 가장자리 30개, 꼬치 10각형 면 6개를 가지며, 유형 {10,3}₅의 쌍곡선 타일링과 관련된 -4의 오일러 특성을 가진다.
페트리아 아이코사헤드론 {3,5}^$π$은(는) 꼭지점 12개, 가장자리 30개, 꼬치 10각형 면 6개를 가지며 오일러 특성은 -12로 유형 {10,5}₃의 쌍곡선 타일링과 관련이 있다.

일반 애완동물
이름	페트리얼 사면체	페트리얼 정육면체	페트리얼 팔면체	페트리얼 도데면체	페트리얼 이코사헤드론
기호	{3,3}^$π$ , {4,3}₃	{4,3}^$π$ , {6,3}₄	{3,4}^$π$ , {6,4}₃	{5,3}^$π$ , {10,3}	{3,5}^$π$ , {10,5}
(v,e,f), χ	(4,6,3), χ = 1	(8,12,4), χ = 0	(6,12,4), χ = −2	(20,30,6), χ = −4	(12,30,6), χ = −12
얼굴	꼬치 사각형 3개	꼬치 6각형 4개		꼬치 데카곤 6개
얼굴	꼬치 사각형 3개
이미지
애니메이션
관련 수치	{4,3}₃ = {4,3}/2 = {4,3}_(2,0)	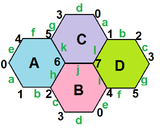{6,3}₃ = {6,3}_(2,0)	{6,4}₃ = {6,4}_(4,0)	{10,3}₅	{10,5}₃

케플러-푸인소 다면체의 4가지 꽃잎도 있다.

페트리얼 대두면체(petrial great dedecheadron, {5,5/2})^$π$는 12정점, 30개의 가장자리, 10개의 꼬치 육각면을 가지며 오일러 특성은 -8이다.
{5/2,5}^$π$의 페트리얼 소형 스티커드 도데카헤드론은 정점이 12개, 가장자리가 30개, 꼬치 육각면이 10개 있으며, χ은 -8이다.
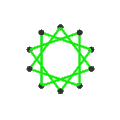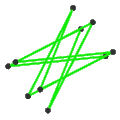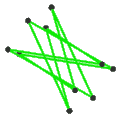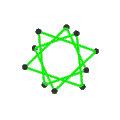
페트리얼 대 아이코사헤드론 {3,5/2}^$π$은(는) -12의 χ으로 정점 12개, 가장자리 30개, 꼬치 데카그램 6개를 가지고 있다.
페트리얼 그레이트 스틸 도데카헤드론, {5/2,3}^$π$은(는) 20개의 정점, 30개의 가장자리, 6개의 꼬치 데카그램 면(-4)을 가지고 있다.

일반별 꽃잎
이름	페트리얼 대단하다 도데면체	페트리얼 소염의 도데면체	페트리얼 대단하다 이코사헤드론	페트리얼 대단한 기질을 가진 도데면체
기호	{5,5/2}^$π$ , {6,5/2}	{5/2,5}^$π$ , {6,5}	{3,5/2}^$π$ , {10/3,5/2}	{5/2,3}^$π$ , {10/3,3}
(v,e,f), χ	(12,30,10), χ = -8	(12,30,10), χ = -8	(12,30,6), χ = -12	(20,30,6), χ = -4
얼굴	꼬치 6각형 10개		6개의 스큐 데카그램(파란색 데카그램 윤곽)
얼굴
이미지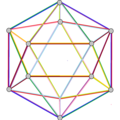
애니메이션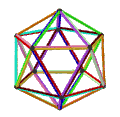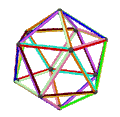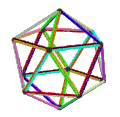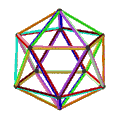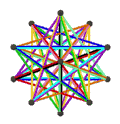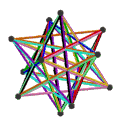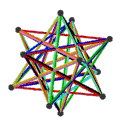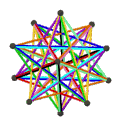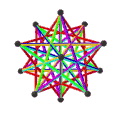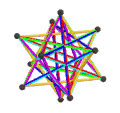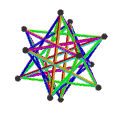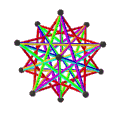

참조

^ ^a ^b ^c Gorini, Catherine A. (2000), Geometry at Work, MAA Notes, vol. 53, Cambridge University Press, p. 181, ISBN 9780883851647
^ ^a ^b McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge University Press, p. 192, ISBN 9780521814966
^ Jones, G. A.; Thornton, J. S. (1983), "Operations on maps, and outer automorphisms", Journal of Combinatorial Theory, Series B, 35 (2): 93–103, doi:10.1016/0095-8956(83)90065-5, MR 0733017
^ 팔면 대칭은 순서 48, Coxeter 번호는 6, 48/(2×6)=4

[gorini-1] Gorini, Catherine A. (2000), Geometry at Work, MAA Notes, vol. 53, Cambridge University Press, p. 181, ISBN 9780883851647

[arp-2] McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge University Press, p. 192, ISBN 9780521814966

[jt-3] Jones, G. A.; Thornton, J. S. (1983), "Operations on maps, and outer automorphisms", Journal of Combinatorial Theory, Series B, 35 (2): 93–103, doi:10.1016/0095-8956(83)90065-5, MR 0733017

[4] 팔면 대칭은 순서 48, Coxeter 번호는 6, 48/(2×6)=4

[1]

[2]

[3]

[4]

Search

페트리 듀얼

네임스페이스

더

특성.

정다면체

참조