원형

원형
원형
	원을 둘레 C 지름D 반지름 R 중심 또는 원점 O
유형	원추형 단면
대칭군	O(2)
지역	◦R2
둘레	C = 2πR

원은 주어진 점, 중심으로부터 주어진 거리에 있는 평면의 모든 점으로 구성된 모양입니다.원의 어떤 점과 중심 사이의 거리를 반지름이라고 합니다.

이 원은 기록된 역사가 시작되기 전부터 알려져 왔습니다.보름달이나 둥근 과일 조각과 같은 자연적인 원들은 흔합니다.원은 기어와 같은 관련 발명품으로 현대 기계의 많은 부분을 가능하게 하는 바퀴의 기초입니다.수학에서 원의 연구는 기하학, 천문학 그리고 미적분학의 발전에 영감을 주었습니다.

용어.

고리: 고리 모양의 물체로, 두 개의 동심원으로 경계를 이루는 고리 모양의 물체.
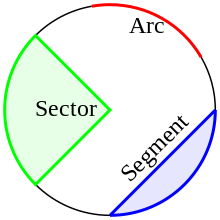
호(arc): 원의 연결된 모든 부분.호와 중심의 두 끝점을 지정하면 두 개의 호가 함께 전체 원을 구성할 수 있습니다.
중심: 원 위의 모든 점에서 등거리에 있는 점.
코드: 끝점이 원 위에 놓여 있으므로 원을 두 개의 세그먼트로 나눕니다.
원둘레: 원을 따라가는 한 회로의 길이 또는 원 주위의 거리.
지름: 끝점이 원 위에 있고 중앙을 지나는 선분 또는 선분의 길이.원 위의 두 점 사이의 거리가 가장 큽니다.그것은 코드의 특별한 경우, 즉 주어진 원에 대해 가장 긴 코드이며, 그것의 길이는 반지름의 두 배입니다.
디스크: 원으로 경계를 이루는 평면의 영역.엄격한 수학적 사용에서 원은 원반의 경계일 뿐인 반면, 일상에서는 원과 원반이라는 용어를 혼용하여 사용할 수 있습니다.
렌즈(Lens): 두 개의 중첩된 디스크의 (교차)에 공통되는 영역.
반지름: 원 자체 위의 한 점이 있는 원의 중심을 잇는 선분 또는 지름의 절반(길이)인 선분의 길이.일반적으로 반지름은 ${\displaystyle$ r $}$ 로 $r$ $r$ 되며 양수여야 합니다. $r=0$ = $r=0$ {\ $displaystyle$ r = 0 $}$ 인 원은 단일 점으로 구성된 축퇴 케이스입니다.
섹터: 동일한 길이의 두 반지름과 공통 중심을 가진 두 개의 가능한 두 개의 호 중 하나로 경계를 이루는 영역으로, 이 중심과 반지름의 끝점에 의해 결정됩니다.
세그먼트(segment): 코드와 코드의 끝을 연결하는 호들 중 하나로 경계를 이루는 영역.코드의 길이는 가능한 호의 지름에 더 낮은 경계를 부여합니다.때때로 세그먼트라는 용어는 아크가 속한 원의 중심을 포함하지 않는 영역에만 사용됩니다.
세컨트: 확장된 화음, 공면 직선, 원을 두 점으로 교차하는 것.
반원: 지름의 끝점에 의해 결정되는 가능한 두 개의 호 중 하나로, 중간점을 중심으로 합니다.비기술적인 일반적인 용도에서, 그것은 직경과 그것의 호들 중 하나로 경계지어지는 2차원 영역의 내부를 의미할 수 있는데, 이것은 엄밀히 말하면 하프 디스크라고 불립니다.하프 디스크는 세그먼트의 특수한 경우, 즉 가장 큰 경우입니다.
접선: 원과 공통으로 하나의 점이 있는 공면 직선("이 지점에서 원과 접촉").

지정된 모든 영역은 열린 영역, 즉 경계를 포함하지 않는 영역, 또는 각 경계를 포함한 닫힌 영역으로 간주될 수 있습니다.

어원

원(circle)이라는 단어는 그리스어의 π/π(키르코스/쿠클로스)에서 유래했으며, 그 자체는 호메로스 그리스어의 π(krikos)의 혼성어로 "후프" 또는 "반지"^[1]를 의미합니다.서커스와 서킷이라는 단어의 기원은 밀접한 관련이 있습니다.

역사

선사시대 사람들은 돌 원과 목재 원을 만들었고, 암각화나 동굴 ^[2]벽화에서는 원형의 요소가 일반적입니다.원반 모양의 선사시대 유물로는 네브라 하늘 원반과 비(Bi)라고 불리는 옥 원반이 있습니다.

기원전 1700년까지 거슬러 올라가는 이집트의 린드 파피루스는 원의 넓이를 찾는 방법을 제공합니다.결과는 다음과 같습니다.256/81(3.16049...)을 ^[3] $λ$ 의 근사값으로 합니다.

유클리드의 원소 3권은 원의 성질을 다루고 있습니다.유클리드는 원을 다음과 같이 정의합니다.

원은 하나의 곡선으로 경계를 이루는 평면 도형이며, 원 안의 특정 점에서 경계 선으로 그려지는 모든 직선이 동일합니다.경계선은 원둘레라고 하고 점, 중심이라고 합니다.
— Euclid, Elements, Book I^[4]^{: 4}

플라톤의 일곱 번째 편지에는 원에 대한 상세한 정의와 설명이 있습니다.플라톤은 완벽한 원을 설명하고, 그것이 어떤 그림, 단어, 정의 또는 설명과 어떻게 다른지 설명합니다.초기 과학, 특히 기하학과 점성학과 천문학은 대부분의 중세 학자들에게 신과 연결되어 있었고, 많은 사람들은 ^[5]^[6]원에서 찾을 수 있는 본질적으로 "신" 또는 "완벽한" 것이 있다고 믿었습니다.

서기 1880년, 페르디난트 폰 린데만은 $π$ 가 초월적이라는 것을 증명했고, 원을 제곱하는 천년 전의 문제는 직선과 ^[7]나침반으로는 수행될 수 없다는 것을 증명했습니다.

분석결과

둘레

원의 둘레와 지름의 비율은 $π$ (pi)이며, 비합리적인 상수는 대략 3.141592654와 같습니다.따라서 원둘레 C는 다음과 같이 반지름 r과 지름 d와 관련이 있습니다.

C=2\pir=\pid.

봉입면적

아르키메데스가 증명한 바와 같이, 원으로 둘러싸인 넓이는 밑면이 원둘레의 길이를 가지고, 높이가 원의 ^[8]반지름과 같은 삼각형의 넓이와 같고, 반지름의 $제곱$ 에 π를 곱하면 다음과 같습니다.

\mathrm {Area} =\pir^{2}

이와 동등하게 직경을 d로 표시하면,

\mathrm {Area} = {\frac {\pid^{2}}{4}}\n0.7854d^{2}

즉, 외접 사각형의 약 79%(외접 변의 길이는 d)입니다.

원은 주어진 원호 길이의 최대 면적을 둘러싸는 평면 곡선입니다.이것은 원을 변동의 미적분학의 문제, 즉 등거리 부등식과 연관시킵니다.

방정식

직각좌표

원의 방정식

x-y 데카르트 좌표계에서, 중심 좌표 (a, b)와 반지름 r이 있는 원은 다음과 같은 모든 점 (x, y)의 집합입니다.

{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}.

원의 방정식으로 알려진 이 방정식은 원 위의 모든 점에 적용되는 피타고라스 정리에서 따온 것입니다. 인접한 도표에서 볼 수 있듯이, 반지름은 다른 변의 길이가 x - a와 y - b인 직각 삼각형의 빗변입니다. 원이 원점 (0, 0)에서 중심을 잡으면 방정식은 다음과 같이 단순해집니다.

x^{2}+y^{2}=r^{2}

파라메트릭 폼

방정식은 삼각함수 사인과 코사인을 사용하여 파라메트릭 형태로 작성할 수 있습니다.

{\display{aligned}x&=a+r\,\cost,\y&=b+r\,\sint,\end{aligned}

여기서 t는 0 ~ 2π 범위의 모수 변수이며, 기하학적으로 (a, b)에서 (x, y)까지의 광선이 양의 x 축과 이루는 각도로 해석됩니다.

원의 대안적인 매개변수화는 다음과 같습니다.

{\display{aligned}x&=a+r{\frac {1-t^{2}},\y&=b+r{\frac {2t}{1+t^{2}}}.\end{aligned}

이 매개 변수화에서 t 대 t의 비율은 기하학적으로 x 축과 평행한 중심을 지나는 선의 입체 투영으로 해석할 수 있습니다(접선 반각 치환 참조).그러나 이 매개 변수화는 모든 실수뿐만 아니라 무한대의 한 점까지 범위를 지정하는 경우에만 작동합니다. 그렇지 않으면 원의 가장 왼쪽 점이 생략됩니다.

3점식

세 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 점 ( $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 1 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 1 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ ) $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ , ( $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 2 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ ) $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ , ( $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 3 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 3 ) ${\displaystyle (x_{1}, y_{1}),$ ( $x_{2}, y_{2}),$ ( $x_{3}, y_{3})$ 로 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ 결정된 원의 방정식은 원 방정식의 3점 형태의 변환으로 얻어집니다.

{\color {green}x}-x_{1}({\color {green}x}-x_{2})+({\color {red}y}-y_{1}){({\color {red}y}-y_{2})}{({\color {red}y}-y_{1}){({\color {x}x_{2})--({\color {red}y}-y_{2})({\color {green}x}-x_{1})}={\frac {(x_{3}-x_{1})+(y_{3}-y_{1}){(y_{3}-y_{2}){(y_{3}-y_{1}){(y_{3}-y_{1}){(x_{3}-y_{2})}{(x_{3}-y_{2})}{(x_{3}-(x_x_{1}}}

동형

동차좌표에서 원의 방정식을 갖는 각 원뿔곡선은 다음과 같은 형태를 갖습니다.

x^{2}+y^{2}-2axz-2byz+limit^{2}=0.

원뿔형 단면이 I(1: i: 0)점과 J(1: -i: 0)점을 포함할 때 원뿔형 단면이 원임을 증명할 수 있습니다.이 점들을 무한대의 원형 점이라고 합니다.

극좌표

극좌표에서 원의^[vague] 방정식은

r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2}

여기서 a는 원의 반지름 $(r,\theta )$ ( $(r,\theta )$ θ $(r,\theta )$ $(r,\theta)$ 은 원 위의 일반적인 점의 극좌표, ( $(r_{0},\phi )$ 0, $(r_{0},\phi )$ ϕ $(r_{0},\phi )$ ${\displaystyle$ (r_{ $0},\phi)}$ 은 원 중심의 극좌표입니다(즉, r은 원점에서 원 중심까지의 거리,그리고 θ는 원점과 원의 중심을 연결하는 선에 대한 양의 x축에서 반시계 방향 각도입니다.)원점을 중심으로 하는 원, 즉 r = 0의 경우 r = a로 줄어듭니다.r = a일 때 또는 원점이 원 위에 있을 때, 방정식은

r=2a\cos(\theta -\phi)

일반적인 경우에 방정식은 r 에 대해 풀 수 있으며, 다음을 줍니다.

r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\theta -\phi )}}

± 기호가 없으면 방정식은 경우에 따라 반원만 설명할 수 있습니다.

복소평면

복소평면에서 중심이 c이고 반지름이 r인 원은 방정식을 갖습니다.

z-c =r.

파라메트릭 형태로 다음과 같이 쓸 수 있습니다.

z=re^{it}+c.

약간 일반화된 방정식.

pz{\overline {z}}+gz+{\overline {gz}=q

실수 p, q, 복소수 g는 때때로 일반화된 원이라고 불립니다. $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ - $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ = $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ = z = z = $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ = - $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ ¯ $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ = $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ 2 - $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ 2 $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$ {\ $displaystyle$ p= $1,\g$ = - {\ $overline {c}},\$ q r r $^{2}$ - c $^{2$ 이므로 z $-$ c z $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ ¯ - $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ ¯ $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ z - $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ ^{2} z z {\ $displaystyle z-c ^{2$ } - {\ $overline {z}$ - {\ $overline {c}$ + c $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$ ¯ {\ $overline$ { $c$ 모든 일반화된 원이 실제로 원이 되는 것은 아닙니다. 일반화된 원은 (참인) 원 또는 선입니다.

접선

원 위의 점 P를 통과하는 접선은 P를 통과하는 지름과 수직입니다.만약 P = (x, y)이고 원의 중심 (a, b)와 반지름 r을 가진다면, 접선은 (a, b)에서 (x, y)까지의 선과 수직이므로 (x - a)x + (y – b)y = c의 형태를 갖습니다. (x, y)에서 계산하면 c의 값이 결정되고, 그 결과 접선의 방정식은

(x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1}

아니면

(x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}

만약₁ y ≥ b이면 이 선의 기울기는

{\frac {dy}{display}}=-{\frac {x_{1}-a}{y_{1}-b}}

이는 암시적인 차별화를 사용하여 찾을 수도 있습니다.

원의 중심이 원점에 있을 때, 접선의 방정식은

x_{1}x+y_{1}y=r^{2}

그리고 경사는

{\displaystyle {\frac {dy}{dy}}=-{\frac {x_{1}}{y_{1}}}.

특성.

원은 주어진 둘레 길이에 대해 가장 큰 면적을 갖는 모양입니다(등각 부등식 참조).
원은 매우 대칭적인 모양입니다: 중심을 지나는 모든 선은 반사 대칭의 선을 형성하고 모든 각도에 대해 중심을 중심으로 회전 대칭을 가집니다.대칭군은 직교군 O(2,R)입니다.회전 그룹만 원 그룹 T입니다.
모든 원은 ^{[citation needed]}다 비슷합니다.
- 원둘레와 반지름은 비례합니다.
- 둘러싸인 면적과 반지름의 제곱은 비례합니다.
- 비례 상수는 각각 2π와 $π$ 입니다.
원점에서 반지름이 1인 원을 중심으로 하는 원을 단위 원이라고 합니다.
- 단위구의 큰 원으로 생각하면 리만 원이 됩니다.
모든 것이 같은 선상에 있는 것이 아니라, 임의의 세 지점을 통해, 독특한 원이 있습니다.데카르트 좌표에서 원의 중심과 반지름의 좌표에 대해 주어진 세 점의 좌표로 명시적인 공식을 제공하는 것이 가능합니다.동그라미 참조.

코드

화음은 길이가 같을 경우에만 원의 중심에서 등거리입니다.
코드의 수직 이등분선은 원의 중심을 통과합니다. 수직 이등분선의 독특함에서 비롯된 동등한 문장은 다음과 같습니다.
- 원의 중심에서 수직선이 코드를 이등분합니다.
- 코드를 이등분하는 중앙을 통과하는 선분은 코드에 수직입니다.
만약 원의 중심각과 내접각이 같은 코드와 코드의 같은 면에 의해 감산된다면, 중심각은 내접각의 두 배가 됩니다.
만약 두 개의 각도가 같은 코드와 같은 쪽 코드에 새겨진다면, 그것들은 같습니다.
만약 두 개의 각도가 같은 코드와 코드의 반대쪽에 새겨져 있다면, 그것들은 보충적입니다.
- 순환 사각형의 경우 외부 각도는 내부 반대 각도와 같습니다.
지름에 의해 좌우되는 내접각은 직각입니다(탈레스 정리 참조).
지름은 원의 가장 긴 화음입니다.
- 코드 AB가 공통적으로 있는 모든 원 중에서, 반지름이 최소인 원이 직경 AB인 원입니다.
만약 어느 두 화음의 교집합이 하나의 화음을 길이 a와 b로 나누고 다른 화음을 길이 c와 d로 나눈다면, ab = cd.
만일 두 수직 화음의 교차점이 하나의 화음을 길이 a와 b로 나누고 다른 화음을 길이 c와 d로 나눈다면, a² + b² + c² + d는² ^[9]지름의 제곱과 같습니다.
주어진 지점에서 직각으로 교차하는 임의의 두 코드의 길이 제곱의 합은 동일한 지점에서 교차하는 임의의 다른 두 수직 코드의 길이와 동일하고 8r² - 4p에² 의해 주어집니다. 여기서 r은 원 반지름이고 p는 중심점에서 ^[10]교차점까지의 거리입니다.
원의 한 점에서 주어진 화음까지의 거리와 원의 지름을 곱한 값이 ^[11]^{: p.71}코드의 한 점에서 끝까지의 거리의 곱과 같습니다.

접선

원 위에 놓인 반지름의 끝점을 통해 반지름에 수직으로 그려진 선은 원과 접합니다.
원과의 접촉점을 통해 접선에 수직으로 그려진 선이 원의 중심을 통과합니다.
원 바깥의 모든 점에서 원에 항상 두 개의 접선을 그릴 수 있으며, 이 접선의 길이는 동일합니다.
A의 접선과 B의 접선이 외부 지점 P에서 교차하는 경우, 중심을 O로 표시하면 각도 θBOA와 θBPA는 보충적입니다.
AD가 A에서 원과 접하며 AQ가 원의 코드인 경우 ∠DAQ = 1/2arc(AQ)입니다.

정리

코드 정리는 CD와 EB 두 개의 코드가 A에서 교차하면 AC × AD = AB × AE가 된다고 말합니다.
AE와 AD 두 개의 시맨트가 각각 B와 C에서 원을 자를 경우 AC × AD = AB × AE (코드 정리의 따름).
접선은 끝이 일치하는 부분의 제한적인 경우로 간주될 수 있습니다.외부 점 A의 접선이 F의 원과 만나고 외부 점 A의 접선이 C와 D에서 각각 원과 만나는 경우 AF = AC × AD (원자-초단 정리).
코드와 그 끝점 중 하나에서 접선 사이의 각도는 코드의 반대쪽에서 원의 중심을 지나는 각도의 1/2과 같습니다.
중심에서 화음에 의해 지배되는 각도가 90°이면 θ = r θ2이고, 여기서 θ는 화음의 길이이고, r은 원의 반지름입니다.
오른쪽에 있는 것처럼 원에 두 개의 시맨트가 삽입된 경우 각도 A의 측정값은 포함된 원호의 측정값 차이의 절반과 같습니다( ${\overset {\frown }{BC}}$ ${\overset {\frown }{DE}}$ ⌢ {\ $overset {\frown}}},$ ${\overset {\frown }{BC}}$ ⌢ {\ $displaystyle$ {\ $overset$ {\ $frown}{BC}}).$ 즉, $2\angle {CAB}=\angle {DOE}-\angle {BOC}$ ∠ $2\angle {CAB}=\angle {DOE}-\angle {BOC}$ = ∠ $2\angle {CAB}=\angle {DOE}-\angle {BOC}$ - ∠ $2\angle {CAB}=\angle {DOE}-\angle {BOC}$ {\ $displaystyle$ 2 $\angle$ { $CAB$ }=\ $angle$ {DOE $}-\angle {B$ OC $2\angle {CAB}=\angle {DOE}-\angle {BOC}$ 여기서 O는 원의 중심(secant-secant 정리)입니다.

내접각

내접각(예: 그림의 파란색 및 녹색 각도)은 해당 중심각(빨간색)의 정확히 절반입니다.따라서 동일한 호(분홍색)를 나타내는 모든 내접각은 동일합니다.호(갈색)에 새겨진 각도는 보조적입니다.특히 지름을 제외한 모든 내접각은 직각입니다(중앙각은 180°이므로).

사기타

궁수(itt手, versine)는 코드의 중간점과 원의 호 사이에 코드에 수직으로 그려진 선분입니다.

코드의 길이 y와 궁수의 길이 x가 주어졌을 때, 피타고라스 정리를 사용하여 두 선 주위에 맞는 고유한 원의 반지름을 계산할 수 있습니다.

r={\frac {y^{2}}{8x}}+{\frac {x}{2}}

위에 제시된 두 가지 코드 특성에만 의존하는 이 결과에 대한 또 다른 증거는 다음과 같습니다.길이 y의 코드와 길이 x의 궁수가 있는 코드가 주어졌을 때, 궁수가 코드의 중간 지점과 교차하기 때문에, 우리는 그것이 원의 지름의 일부라는 것을 알고 있습니다.지름이 반지름의 두 배이므로 지름의 "누락" 부분의 길이는 (2r - x)입니다.한 코드의 한 부분과 다른 부분이 첫 번째 코드와 교차하는 코드를 따라 찍은 동일한 곱과 같다는 사실을 사용하면 (2r - x)x = (y / 2)를 알 수 있습니다.r을 해결하면 우리는 필요한 결과를 얻습니다.

나침반과 직선형 구조물

원을 만드는 나침반과 직선형의 구조물이 많이 있습니다.

가장 단순하고 기본적인 구성은 원의 중심과 원 위의 한 점이 주어집니다.나침반의 고정된 다리를 중심점에 놓고 이동 가능한 다리를 원 위의 지점에 놓고 나침반을 회전시킵니다.

소정의 직경을 갖는 구조

지름의 $중간점$ M을 만듭니다.
$중심$ M이 지름의 끝점 중 하나를 통과하도록 원을 구성합니다(다른 끝점도 통과함).

3개의 비공선점을 통한 시공

$점$ P, $Q$ , $R$ 의 이름을 대라.
$세그먼트$ PQ의 수직 이등분선을 구성합니다.
$세그먼트$ PR의 수직 이등분선을 구성합니다.
이 두 수직 $이등분선$ 의 교점을 M이라고 레이블을 지정합니다. (점들이 공선형이 아니기 때문에 이들은 서로 만납니다.
$중심$ M이 P, $Q$ $또는$ R $지점$ 중 하나를 통과하도록 원을 구성합니다(다른 두 지점도 통과함).

아폴로니오스 원

페르가의 폴로니우스는 원이 두 개의 고정 초점 A와 ^[12]^[13]B에 대한 거리의 일정한 비율(1이 아닌)을 갖는 평면의 점들의 집합으로도 정의될 수 있음을 보여주었습니다. (거리가 동일한 점들의 집합은 선분 AB의 수직 이등분선입니다.)그 원은 때때로 두 점 정도 그려진다고 합니다.

증거는 두 부분으로 나누어져 있습니다.먼저, 두 개의 초점 A와 B와 거리의 비율이 주어졌을 때, 거리의 비율을 만족하는 모든 점 P가 특정 원 위에 있어야 한다는 것을 증명해야 합니다.비율을 만족하고 세그먼트 AB에 놓여 있는 C를 또 다른 점으로 하겠습니다.각도 이등분 정리에 의해 선 세그먼트 PC는 내부 각도 APB를 이등분합니다.

{\displaystyle {\frac {AP}{BP}}={\frac {AC}{BC}}}.

유사하게, AB 확장된 일부 지점 D를 통한 선분 PD는 Q가 AP 확장된 해당 외부 각도 BPQ를 이등분합니다.내외각은 합이 180도이므로, 각도(CPD)는 정확히 90도, 즉 직각입니다.각도 CPD가 직각인 점 P의 집합은 원을 형성하며, 이 중 CD는 직경입니다.

둘째, 표시된 원의 모든 점이 주어진 비율을 만족한다는 증명을 참조하십시오^[14]^{: 15}.

교차비

원과 밀접하게 관련된 속성은 복소 평면에 있는 점들의 교차 비율의 기하학을 포함합니다.A, B, C가 위와 같다면, 이 세 점에 대한 아폴로니우스의 원은 교차비의 절대값이 1인 점 P의 집합입니다.

{\bigl}[A,B;C,P]{\bigr}=1.

다른 방법으로, P는 복소 평면에서 교차비 [A, B; C, P]가 단위 원 위에 있는 경우에만 아폴로니우스 원 위의 한 점입니다.

일반화된 원

C가 세그먼트 AB의 중간점인 경우, Apollonius 조건을 만족하는 점 P의 집합

{\frac { AP}{BP}}={\frac { AC}{BC}}

원이 아니라 선입니다.

따라서 A, B, C가 평면상에서 서로 다른 점들이 주어진다면 위의 방정식을 만족하는 점 P의 위치를 "일반화된 원"이라고 합니다.실제 원이나 선이 될 수 있습니다.이러한 의미에서 선은 무한반경의 일반화된 원입니다.

다른 수치에 대한 비문 또는 외접

모든 삼각형에서 인서클이라고 불리는 독특한 원은 ^[15]삼각형의 세 변에 각각 접하도록 새겨질 수 있습니다.

모든 삼각형에 대해 원둘레라고 불리는 독특한 원은 삼각형의 세 ^[16]꼭짓점을 각각 통과하도록 외접될 수 있습니다.

접선 다각형(tangential polygon)은 ^[17]다각형의 각 변에 접하는 원을 내접할 수 있는 볼록 다각형입니다.모든 정다각형과 모든 삼각형은 접선다각형입니다.

순환 다각형은 원이 각 꼭짓점을 통과하여 외접될 수 있는 볼록 다각형입니다.잘 연구된 예로는 순환 사각형이 있습니다.모든 정다각형과 모든 삼각형은 순환 다각형입니다.고리형이면서 접선형인 다각형을 쌍중심 다각형이라고 합니다.

하이포클로이드는 주어진 원 안에서 접하며 굴러가는 더 작은 원 위의 고정된 점을 추적하여 주어진 원 안에 새겨진 곡선입니다.

기타 수치의 제한 사례

원은 다양한 다른 그림들 각각의 제한적인 경우로 볼 수 있습니다.

데카르트 타원형은 점들 중 임의의 점에서 두 개의 고정점(포커스)까지의 거리의 가중 합이 상수인 점들의 집합입니다.타원은 무게가 같은 경우입니다.원은 이심률이 0인 타원으로, 두 초점이 원의 중심으로서 서로 일치한다는 것을 의미합니다.원은 무게 중 하나가 0인 직각 데카르트 타원형의 다른 특수한 경우이기도 합니다.
초구형은 $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ + $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ b $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ = $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ {\ $displaystyle \left$ {\ $frac {x}{a}}\right ^{n}\!$ $+\left {\frac {y}{b}}\right ^{n}\!$ $양$ 의 a, b 및 n에 대해 $=$ 1 $}.$ 초원은 b = a 입니다.원은 n = 2인 초원의 특수한 경우입니다.
카시니 타원형은 점들 중 하나에서 두 고정점까지의 거리의 곱이 상수인 점들의 집합입니다.두 고정점이 일치하면 원이 생성됩니다.
일정한 폭의 곡선은 한 점에서 경계와 교차하는 두 개의 다른 평행선 사이의 수직 거리로 정의되는 폭이 두 평행선의 방향에 관계없이 동일한 도형입니다.원은 이러한 유형의 그림 중 가장 간단한 예입니다.

상수 합의 위치

평면에서 n개의 ${\displaystyle$ n $}$ 개 $n$ 점으로 이루어진 $유한$ 집합을 고려합니다.주어진 점에 대한 거리의 제곱의 합이 일정한 점의 궤적은 중심이 주어진 ^[18]점의 중심에 있는 원입니다.n{\ $displaystyle$ n $}$ 점 $n$ 에서 $n$ $P_{n}$ $P_{n}$ ${\$ P_ ${n$ 의 꼭짓점을 ^[19]취하면 더 높은 거리의 힘에 대한 일반화를 얻을 수 있습니다. $원반지름$ R이 ${\displaystyle$ R $}$ 인 $R$ 주어진 정다각형의 꼭짓점에 $2m$ $d_{i}$ di {\ $displaystyle$ $2m$ d_ ${i}$ 의 $d_{i}$ 2m $2m$ {\ $displaystyle$ $2m$ }번째 $2m$ $d_{i}$ 의 합이 일정한 점의 궤적은 다음과 같습니다.

\sum _{i=1}^{n}d_{i}^{2m}>nR^{2m},\quad {\text{here}}~m=1,2,\n\text,n-1;

P_{n}

{\

의 중심이 되는 것.

정삼각형의 경우, 두 번째와 네 번째 거듭제곱의 상수 합의 로키는 원이고, 정사각형의 경우, 로키는 두 번째, 네 번째, 여섯 번째 거듭제곱의 상수 합을 나타내는 원입니다.일반 오각형의 경우 거리의 8제곱의 상수 합 등이 추가됩니다.

원의 사각형

원을 제곱하는 것은 고대 기하학자들이 제안한 문제로, 나침반과 직선으로 유한한 수의 계단만을 사용하여 주어진 원과 같은 면적의 정사각형을 만드는 것입니다.

1882년 린데만의 결과로 불가능한 것으로 판명되었습니다.파이( $π$ )가 대수적 무리수가 아닌 초월수임을 증명하는 바이어슈트라스 정리. 즉, 유리수를 갖는 다항식의 근이 아님을 증명합니다.불가능함에도 불구하고, 이 주제는 가짜 수학 애호가들에게 계속 관심의 대상이 되고 있습니다.

예술과 상징의 의의

아시리아인들과 고대 이집트인들, 인더스 계곡과 중국의 황하를 따라 있는 사람들과 같은 가장 초기의 문명의 시대부터,그리고 고전 고대 동안 고대 그리스와 로마의 서양 문명 – 이 원은 예술가의 메시지를 전달하고 특정한 생각을 표현하기 위해 시각 예술에서 직간접적으로 사용되었습니다.하지만 세계관(신념과 문화)의 차이는 예술가들의 인식에 큰 영향을 미쳤습니다.어떤 사람들은 원의 둘레를 강조하여 그들의 민주적인 표현을 보여주는 반면, 다른 사람들은 우주의 통합의 개념을 상징하기 위해 원의 중심에 초점을 맞췄습니다.신비주의 교리에서 원은 주로 존재의 무한하고 순환적인 성격을 상징하지만, 종교적 전통에서는 천상의 신체와 신성한 영혼을 나타냅니다.

원은 통일성, 무한성, 완전성, 우주, 신성성, 균형성, 안정성, 완벽성을 포함한 많은 신성하고 영적인 개념들을 의미합니다.그러한 개념은 상징의 사용, 예를 들어, 나침반, 후광, 베시카 피시스와 그것의 파생물들(물고기, 눈, 아우레올, 만돌라 등), 우로보로스, 달마바퀴, 무지개, 만다라, 장미창 ^[20]등을 통해 전세계 문화에 전달되었습니다.

일반화

다른 p-norms의 경우

원을 점에서 거리가 고정된 점의 집합으로 정의하면 거리의 정의가 다른 원으로 간주할 수 있습니다.p-norm에서 거리는 다음과 같이 결정됩니다.

\left\x\right\{p}=\left(\left x_{1}\right ^{p}+\left x_{2}\right ^{p}+\right x_{n}\right ^{p}\right)^{1/p}

유클리드 기하학에서 p = 2, 익숙한

\left\x\right\{2}={\sqrt {\left x_{1}\right ^{2}+\left x_{2}+\left x_{n}\right ^{2}}

택시 기하학에서 p = 1. 택시 원은 변이 좌표축에 대해 45° 각도로 향하는 정사각형입니다.각 변의 ${\sqrt {2}}r$ 는 ${\sqrt {2}}r$ 2r {\ $displaystyle$ {\ $sqrt {2}}$ r이며 ${\sqrt {2}}r$ , 여기서 r은 원의 반지름입니다. 택시 기하학에서 길이는 2r입니다.따라서 원의 원둘레는 8r입니다.따라서 이 기하학에서 $\pi$ $\pi$ 에 $\pi$ 대한 기하학적 유사체의 값은 4입니다.택시 기하학에서 단위 원에 대한 공식은 데카르트 좌표에서 x $|x|+|y|=1$ + $|x|+|y|=1$ = $|x|+|y|=1$ {\ $displaystyle$ x + y = $1}$ 이고

r={\frac {1}{\left \sin \theta \right +\left \cos \theta \right}}

극좌표로

(이 거리를 사용하여) 반지름 1의 원은 그 중심의 폰 노이만 근처입니다.

평면 상의 체비셰프 거리(L_∞ 메트릭)에 대한 반지름 r의 원도 측면 길이 2r이 좌표 축과 평행한 정사각형이므로, 평면 체비셰프 거리는 평면 택시 거리에 대한 회전 및 스케일링에 의해 동등한 것으로 볼 수 있습니다.그러나 L과 L_∞ 메트릭 간의₁ 이러한 동등성은 더 높은 차원으로 일반화되지 않습니다.

위상정의

위상수학에서 원은 기하학적 개념에만 국한되는 것이 아니라, 모든 동형에 한정됩니다.하나가 R의 변형을³ 통해 다른 하나로 변환될 수 있다면 두 개의 위상 원은 동일합니다(주변 동위 ^[21]원소로 알려져 있음).

특수하게 명명된

삼각형의

특정한 4각형의

정사각형의 8점 원

원추형 단면의

토러스의

비야르소 원

참고 항목

참고문헌

^ krikos 2013-11-06 Wayback Machine, Henry George Liddell, Robert Scott, 그리스-영어 렉시콘, Perseus에서 보관
^ Simek, Jan F.; Cressler, Alan; Herrmann, Nicholas P.; Sherwood, Sarah C. (1 June 2013). "Sacred landscapes of the south-eastern USA: prehistoric rock and cave art in Tennessee". Antiquity. 87 (336): 430–446. doi:10.1017/S0003598X00049048. ISSN 0003-598X.
^ 기원전 30000년 ~ 기원전 500년 연대기 Wayback Machine에서 2008-03-22년 보관.History.mcs.st-andrews.ac.uk .2012-05-03년 회수.
^ OL 7227282M
^ Arthur Koestler, The Sleepwalkers: 인류의 변화하는 우주관의 역사 (1959)
^ 플라톤의 신학에 관한 프로클로스, 플라톤 후계자 6권 웨이백 머신 Tr에서 보관 2017-01-23토마스 테일러(Thomas Taylor, 1816) 제2권, 2장, "플라톤의"
^ Wayback Machine에서 원형 사각형 보관 2008-06-24.History.mcs.st-andrews.ac.uk .2012-05-03년 회수.
^ Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, p. 108, ISBN 978-0-321-01618-8
^ Posamentier and Salkind, 기하학에서의 도전적 문제들, 도버, 제2판, 1996: pp. 104–105, #4–23
^ 대학수학저널 29(4), 1998년 9월, p. 331, 문제 635
^ 존슨, 로저 A., 고급 유클리드 기하학, 도버 출판사, 2007.
^ Harkness, James (1898). "Introduction to the theory of analytic functions". Nature. 59 (1530): 30. Bibcode:1899Natur..59..386B. doi:10.1038/059386a0. S2CID 4030420. Archived from the original on 7 October 2008.
^ 오길비, C. 스탠리, 기하학 여행, 도버, 1969, 14-17.
^ 알트실러-코트, 네이선, 대학 기하학, 도버, 2007 (원점. 1952)
^ 인써클 – Wolfram MathWorld Archived 2012-01-21에서 Wayback Machine으로.수학세계.wolfram.com (2012-04-26).2012-05-03년 회수.
^ 서클 – Wolfram MathWorld Archived 2012-01-20 Wayback Machine에서 제공.수학세계.wolfram.com (2012-04-26).2012-05-03년 회수.
^ Tangential Polygon – Wolfram MathWorld에서 Wayback Machine에서 2013-09-03 보관함.수학세계.wolfram.com (2012-04-26).2012-05-03년 회수.
^ Apostol, Tom; Mnatsakanian, Mamikon (2003). "Sums of squares of distances in m-space". American Mathematical Monthly. 110 (6): 516–526. doi:10.1080/00029890.2003.11919989. S2CID 12641658.
^ Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420 (inactive 1 August 2023). Archived from the original on 22 April 2021. Retrieved 17 May 2021.{{cite journal}}: CS1 메인 : 2023년 8월 기준 DOI 비활성화 (링크)
^ Abdullahi, Yahya (29 October 2019). "The Circle from East to West". In Charnier, Jean-François (ed.). The Louvre Abu Dhabi: A World Vision of Art. Rizzoli International Publications, Incorporated. ISBN 9782370741004.
^ Gamelin, Theodore (1999). Introduction to topology. Mineola, N.Y: Dover Publications. ISBN 0486406806.

추가열람

Pedoe, Dan (1988). Geometry: a comprehensive course. Dover. ISBN 9780486658124.
맥튜터 역사 수학 아카이브의 "Circle"

외부 링크

"Circle", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
플래닛 수학에서 원을 그리세요.
Weisstein, Eric W. "Circle". MathWorld.
"Interactive Java applets". for the properties of and elementary constructions involving circles
"Interactive Standard Form Equation of Circle". Click and drag points to see standard form equation in action
"Munching on Circles". cut-the-knot

[1] rikos 2013-11-06 Wayback Machine, Henry George Liddell, Robert Scott, 그리스-영어 렉시콘, Perseus에서 보관

[2] Simek, Jan F.; Cressler, Alan; Herrmann, Nicholas P.; Sherwood, Sarah C. (1 June 2013). "Sacred landscapes of the south-eastern USA: prehistoric rock and cave art in Tennessee". Antiquity. 87 (336): 430–446. doi:10.1017/S0003598X00049048. ISSN 0003-598X.

[3] 기원전 30000년 ~ 기원전 500년 연대기 Wayback Machine에서 2008-03-22년 보관.History.mcs.st-andrews.ac.uk .2012-05-03년 회수.

[4] OL 7227282M

[5] Arthur Koestler, The Sleepwalkers: 인류의 변화하는 우주관의 역사 (1959)

[6] 플라톤의 신학에 관한 프로클로스, 플라톤 후계자 6권 웨이백 머신 Tr에서 보관 2017-01-23토마스 테일러(Thomas Taylor, 1816) 제2권, 2장, "플라톤의"

[7] Wayback Machine에서 원형 사각형 보관 2008-06-24.History.mcs.st-andrews.ac.uk .2012-05-03년 회수.

[8] Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, p. 108, ISBN 978-0-321-01618-8

[9] Posamentier and Salkind, 기하학에서의 도전적 문제들, 도버, 제2판, 1996: pp. 104–105, #4–23

[10] 대학수학저널 29(4), 1998년 9월, p. 331, 문제 635

[11] 존슨, 로저 A., 고급 유클리드 기하학, 도버 출판사, 2007.

[12] Harkness, James (1898). "Introduction to the theory of analytic functions". Nature. 59 (1530): 30. Bibcode:1899Natur..59..386B. doi:10.1038/059386a0. S2CID 4030420. Archived from the original on 7 October 2008.

[13] 오길비, C. 스탠리, 기하학 여행, 도버, 1969, 14-17.

[14] 알트실러-코트, 네이선, 대학 기하학, 도버, 2007 (원점. 1952)

[15] 인써클 – Wolfram MathWorld Archived 2012-01-21에서 Wayback Machine으로.수학세계.wolfram.com (2012-04-26).2012-05-03년 회수.

[16] 서클 – Wolfram MathWorld Archived 2012-01-20 Wayback Machine에서 제공.수학세계.wolfram.com (2012-04-26).2012-05-03년 회수.

[17] Tangential Polygon – Wolfram MathWorld에서 Wayback Machine에서 2013-09-03 보관함.수학세계.wolfram.com (2012-04-26).2012-05-03년 회수.

[18] Apostol, Tom; Mnatsakanian, Mamikon (2003). "Sums of squares of distances in m-space". American Mathematical Monthly. 110 (6): 516–526. doi:10.1080/00029890.2003.11919989. S2CID 12641658.

[Mamuka-19] Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420 (inactive 1 August 2023). Archived from the original on 22 April 2021. Retrieved 17 May 2021.{{cite journal}}: CS1 메인 : 2023년 8월 기준 DOI 비활성화 (링크)

[20] Abdullahi, Yahya (29 October 2019). "The Circle from East to West". In Charnier, Jean-François (ed.). The Louvre Abu Dhabi: A World Vision of Art. Rizzoli International Publications, Incorporated. ISBN 9782370741004.

[gamelin-21] Gamelin, Theodore (1999). Introduction to topology. Mineola, N.Y: Dover Publications. ISBN 0486406806.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

원형
원을 둘레 C 지름D 반지름 R 중심 또는 원점 O
유형	원추형 단면
대칭군	$O(2)$
지역	$◦R 2$
둘레	$C = 2πR$

Search

원형

용어.

어원

역사