동위원소 다면체 및 기울기 목록

기하학에서 동위원소 다면체 및 기울기는 대칭이 다른 가장자리로 향하는 속성에 의해 정의된다.^[1] 이 속성을 가진 폴리헤드라는 "에지 변환"이라고도 할 수 있지만, 대칭이 기하학적이라기보다는 조합적인 에지 변환 그래프와 구별되어야 한다.

일반 다면체는 등면체(얼굴-변환), 이소곤체(Vertex-변환), 동위원소(에지-변환)이다.

Quasiregular polyhedra는 이등변과 동위원소이지만 등면체는 아니다; 그들의 이중은 이등변과 동위원소지만 이등변은 아니다.

동위원소 다면체의 이중도 역시 동위원소 다면체다.(이중 다면체 기사 참조)

볼록 동위원소 다면체

볼록 다면체의 이중도 역시 볼록 다면체다.^[2]

플라토닉 고형분에는 5개의 (정규) 플라토닉 고형분, 2개의 (정규) 플라토닉 고형분, 2개의 이중 코어 등 9개의 볼록 동위원소 다면체가 있다.

정점 형태는 정사각형이다. 정점 형태는 정삼각형과 정삼각형 또는 정삼각형과 정삼각형이다.

형태	정규	듀얼 레귤러	퀘이레굴라속	쿼이레겔러 이중
와이토프 기호	q2 p	p 2 q	2p q
꼭지점 구성	pq	qp	p.q.p.q.q.
p=3 q=3	사면체 {3,3} 3 2 3	사면체 {3,3} 3 2 3	사방면체 (옥타헤드론) 2 3 3	큐브 (롬 육면체)
p=4 q=3	큐브 {4,3} 3 2 4	팔면체 {3,4} 4 2 3	큐폭타헤드론 2 3 4	롬빅 도데카헤드론
p=5 q=3	도데카헤드론 {5,3} 3 2 5	이코사헤드론 {3,5} 5 2 3	이코시다데카헤드론 2 3 5	롬빅 삼권면체

동위원소 항성-폴리헤드라

비콘벡스 다면체의 이중도 역시 비콘벡스 다면체다.^[2] (대립에 의해)

quasiregular 옥타헤드론, quoctaheadron, icossidodechedron에 기반한 10개의 비콘벡스 동위원소 다면체(non-convoxal polyhedra)가 있다: quasiregular octaheadron, quoctaheadron, icoidron, icodecadron, ichedron, headron)에 기반한 5개의 headron:

형태	퀘이레굴라속	쿼이레겔러 이중
p=3 q=3	테트라헤미헥사헤드론	테트라헤미헥사크론
p=4 q=3	큐보헤미오크타헤드론	헥사헤미옥타크론
	옥타헤미오크타헤드론	옥타헤미오크타크론(Hexahemioctacron에서 잘 보이지 않음)*
p=5 q=3	소이코시헤미도데코헤드론	소형 아이코시헤미도드론(Small dodecahemidodacron에서 분명하지 않음)(*)
	소도데카헤미도데코헤드론	작은도데카헤미도데카크론

(*) 면, 가장자리 및 교차점은 동일하며, 무한대가 아닌 일부 다른 교차점만 정점으로 간주된다.

There are sixteen non-convex isotoxal polyhedra based on the Kepler–Poinsot polyhedra: the four (regular) Kepler–Poinsot polyhedra, the six (quasiregular) common cores of dual Kepler–Poinsot polyhedra (including four hemipolyhedra), and their six duals (including four (infinite) hemipolyhedron-duals):

형태	정규	듀얼 레귤러	퀘이레굴라속	쿼이레겔러 이중
와이토프 기호	q2 p	p 2 q	2p q
꼭지점 구성	pq	qp	p.q.p.q.q.
p=5/2 q=3	그레이트 스틸 도데카헤드론 {5/2,3} 3 2 5/2	대이코사면체 {3,5/2} 5/2 2 3	대이코시다데카헤드론 2 3 5/2	대범삼문자
			대이코시헤미도데코헤드론	대이코시헤미도데카크론
			대 도데카헤미도데코헤드론	그레이트 도데카헤미도데카크론
p=5/2 q=5	소절개도면체 {5/2,5} 5 2 5/2	대두면체 {5,5/2} 5/2 2 5	도데카데카헤드론 2 5 5/2	중합성삼정면체
			소이코시헤미도데코헤드론	소도데카헤미코사크론
			대 도데카헤미도데코헤드론	그레이트 도데카헤미코사크론

마지막으로 다른 6개의 비콘벡스 동위원소 다면체(non-convexal polyhedra)가 있다: 3개의 quasiregular ditrigonal(3 p q) 별 다면체 및 그 3개의 이중체:

퀘이레굴라속	쿼이레겔러 이중
3p q
대직류 이코시다데카헤드론 3/2 3 5	대삼면체
직교 도데코데카헤드론 3 5/3 5	중삼면체
소형 이코시다데카헤드론 3 5/2 3	작은삼각형 이코사면체

유클리드 평면의 동위원소 기울기

동위원소인 유클리드 평면의 최소 5개의 다각형 기울기가 있다. (자기 이중 사각 타일링은 네 가지 형태로 모두 재현된다.)

정규	듀얼 레귤러	퀘이레굴라속	쿼이레겔러 이중
육각 타일링 {6,3} 6 2 3	삼각 타일링 {3,6} 3 2 3	삼헥사각 타일링 2 3 6	롬빌 타일링
사각 타일링 {4,4} 4 2 4	사각 타일링 {4,4} 2 4 4	사각 타일링 {4,4} 4 2 4	사각 타일링 {4,4}

쌍곡면 동위원소 기울기

쌍곡면에는 정규 쌍곡선 기울기 {p,q} 및 비우측(p q r) 그룹의 Wythoff 시공을 포함하여 무한히 많은 동위원소 다각형 기울기가 있다.

여기 각각 2개의 정규형식과 1개의 준정형식을 가진 6개의 (p q 2)가족이 있다. 모두 quasiregular 형태의 rhombic 듀얼을 가지고 있지만, 오직 한 가지만 보여진다.

[p,q]	{p,q}	{q,p}	r{p,q}	이중 r{p,q}
콕시터딘킨
[7,3]	{7,3}	{3,7}	r{7,3}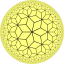
[8,3]	{8,3}	{3,8}	r{8,3}
[5,4]	{5,4}	{4,5}	r{5,4}
[6,4]	{6,4}	{4,6}	r{6,4}
[8,4]	{8,4}	{4,8}	r{8,3}
[5,5]	{5,5}	{5,5}	r{5,5}

여기 각각 3개의 quasiregular 형식을 가진 3개의 예(p q r)가 있다. 이중은 표시되지 않지만 동위원소 육각형 및 팔각형 면을 가지고 있다.

콕시터딘킨
(4 3 3)	3 4 3	3 4 3	4 3 3
(4 4 3)	4 4 3	3 4 4	4 4 3
(4 4 4)	4 4 4	4 4 4	4 4 4

구의 동위원소 기울기

위에 열거한 모든 동위원소 다면체는 구의 동위원소 기울기로 만들 수 있다.

구면 기울기 외에도 다면체로 퇴보하는 다른 두 가족이 있다. 주문된 호소헤드론도 반정형일 수 있고, 두 개의 LUN을 교대로 사용할 수 있으며, 따라서 동위원소:

• 호소헤드론 {2,q}
• 다이헤드론 {p,2}

참조

• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (6.4 동위원소 기울기, 309–321)
• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183