구면 다면체
Spherical polyhedron수학에서 구면 다면체 또는 구면 타일링은 표면이 큰 호에 의해 구면 다면체라고 불리는 경계 영역으로 분할되거나 분할되는 구의 타일링이다. 대칭적 다면체 이론의 대부분은 이런 방식으로 가장 편리하게 도출된다.
가장 친숙한 구형 다면체는 구면 잘린 이코사면이라고 생각되는 축구공이다. 다음으로 인기 있는 구면 다면체는 호소면이라고 생각되는 비치볼이다.
호소헤드라와 그들의 이중인 디헤드라와 같은 일부 "향상된" 다면체들은 구형 다면체로서 존재하지만 그들의 납작한 얼굴의 아날로그는 퇴보한다. 육각형 비치볼의 예인 {2, 6}은 호소헤드론이고, {6,2}은 이중다이헤드론이다.
역사
최초의 알려진 인공 다면체는 돌에 새겨진 구형 다면체다. 많은 것들이 스코틀랜드에서 발견되었고, 신석기 시대(신석기 시대)부터 현재까지 나타나고 있다.
10세기 동안 이슬람 학자인 아부 알 와파 부자냐(Abu'l Wafa)는 구형 다면체에 대한 최초의 진지한 연구를 저술하였다.
200년 전, 19세기 초 푸인소트는 구형 다면체를 사용하여 4개의 일반 별 다면체를 발견했다.
20세기 중반 콕세터는 이를 이용해 칼리디스코어(Wythoff 건설)의 건설을 통해 획일적인 다면체 중 하나를 제외한 모든 것을 열거했다.
예
모든 일반 다면체, 반정형 다면체 및 이중체를 구에 틸팅으로 투영할 수 있다.
| 슐레플리 심볼 | {p,q} | t{p,q} | r{p,q} | t{q,p} | {q,p} | rr{p,q} | tr{p,q} | sr{p,q} |
|---|---|---|---|---|---|---|---|---|
| 꼭지점 배열 | pq | Q.2p.2p | p.q.p.q.q. | 페이지 2q.2q | qp | Q.4.p.4 | 4.2q.2p | 3.3.q.3.p. |
| 사면체 대칭 (3 3 2) |  33 |  3.6.6 |  3.3.3.3 |  3.6.6 |  33 |  3.4.3.4 |  4.6.6 |  3.3.3.3.3 |
 V3.6.6 |  V3.3.3.3 |  V3.6.6 |  V3.4.3.4 |  V4.6.6 |  V3.3.3.3.3 | |||
| 팔면체 대칭 (4 3 2) |  43 |  3.8.8 |  3.4.3.4 |  4.6.6 |  34 |  3.4.4.4 |  4.6.8 |  3.3.3.3.4 |
 V3.8.8 |  V3.4.3.4 |  V4.6.6 |  V3.4.4.4 |  V4.6.8 |  V3.3.3.3.4 | |||
| 이코사헤드랄 대칭 (5 3 2) |  53 |  3.10.10 |  3.5.3.5 |  5.6.6 |  35 |  3.4.5.4 |  4.6.10 |  3.3.3.3.5 |
 V3.10.10 |  V3.5.3.5 |  V5.6.6 |  V3.4.5.4 |  V4.6.10 |  V3.3.3.3.5 | |||
| 디헤드랄 예시 p=6 (2 2 6) |  62 |  2.12.12 |  2.6.2.6 |  6.4.4 |  26 |  2.4.6.4 |  4.4.12 |  3.3.3.6 |
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | ... |
|---|---|---|---|---|---|---|---|---|---|
| n-프리즘 (2 2 p) |  |  |  |  |  |  | ... | ||
| n-비피라미드 (2 2 p) |  |  |  |  |  |  |  | ... | |
| n-안티프리즘 |  |  |  |  | ... | ||||
| n-트라페조헤드론 |  |  |  |  |  |  |  | ... |
부적절한 경우
구형 틸링은 다면체(hosohedra: {2,n}, dihedra: {n,2})가 아닌 경우를 허용한다. 일반적으로 일반 호소헤드라와 일반 디헤드라가 사용된다.
| 공간 | 구면 | 유클리드 주 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 타일링 이름 | (단조) 헤난각양소헤드론 | 디지날 호소헤드론 | (삼각형) 삼각음소헤드론 | (Tetrangle) 정사각형 호소헤드론 | 오각형 호소헤드론 | 육각양수면체 | 헵타곤양소헤드론 | 팔각양수면체 | 엔네오각형 호소헤드론 | 십각형 호소헤드론 | 황십각형 양수면체 | 도십각형 호소헤드론 | ... | 아페이로겐 호소헤드론 |
| 타일링 이미지 |  |  |  |  |  |  |  |  |  |  |  |  | ... |  |
| 슐레플리 기호 | {2,1} | {2,2} | {2,3} | {2,4} | {2,5} | {2,6} | {2,7} | {2,8} | {2,9} | {2,10} | {2,11} | {2,12} | ... | {2,∞} |
| 콕시터 다이어그램 | ... | |||||||||||||
| 면 및 모서리 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ |
| 정점 | 2 | ... | 2 | |||||||||||
| 정점 구성. | 2 | 2.2 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 | 211 | 212 | ... | 2∞ |
| 공간 | 구면 | 유클리드 주 | ||||||
|---|---|---|---|---|---|---|---|---|
| 타일링 이름 | (Hengonal) 단조 다이헤드론 | 디지온 다이헤드 | (삼각형) 삼면체 | (Tetrangle) 정방면체 | 펜타곤 디헤드론 | 육각다이헤드론 | ... | 아페이로겐 다이헤드론 |
| 타일링 이미지 |  |  | 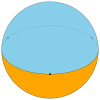 |  |  | 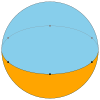 | ... |  |
| 슐레플리 기호 | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | {6,2} | ... | {∞,2} |
| 콕시터 다이어그램 | ... | |||||||
| 얼굴 | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} | ... | 2 {∞} |
| 모서리 및 정점 | 1 | 2 | 3 | 4 | 5 | 6 | ... | ∞ |
| 정점 구성. | 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 | ... | ∞.∞ |
투영 평면의 기울기와 관련
구면에 투영면의 2대 1 커버 맵이 있는 것처럼, 투영 폴리헤드라는 원점을 통해 반사되는 대칭인 구면 폴리헤드라와 2배 커버 아래 대응되는 최소 1배 이상의 반전 대칭을 갖는 구면 폴리헤드라는 투영 폴리헤드라[1](실제 투영면의 테셀레이션)와 관련이 있다.
투사성 다면체의 가장 잘 알려진 예로는 중심 대칭 플라토닉 고형분의 인용인 일반 투사성 다면체뿐만 아니라 두 가지 무한 등급의 디에드라와 호소헤드라가 있다.[2]
- 헤미큐브, {4,3}/2
- 헤미옥타헤드론, {3,4}/2
- 헤미도데카헤드론, {5,3}
- 헤미-icosaheadron, {3,5}/2
- 헤미다이헤드론, {2p,2}/2, p>=1
- 헤미호소헤드론, {2,p}/2, p>=1
참고 항목
| 위키미디어 커먼즈에는 구면 다면체 관련 미디어가 있다. |
참조
- ^ McMullen, Peter; Schulte, Egon (2002). "6C. Projective Regular Polytopes". Abstract Regular Polytopes. Cambridge University Press. pp. 162–5. ISBN 0-521-81496-0.
- ^ Coxeter, H.S.M. (1969). "§21.3 Regular maps'". Introduction to Geometry (2nd ed.). Wiley. pp. 386–8. ISBN 978-0-471-50458-0. MR 0123930.
추가 읽기
- Poinsot, L. (1810). "Memoire sur les polygones et polyèdres". J. De l'École Polytechnique. 9: 16–48.
- Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. (1954). "Uniform polyhedra". Phil. Trans. 246 A (916): 401–50. JSTOR 91532.
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover. ISBN 0-486-61480-8.







