다이헤드론
Dihedron| 일반 n-곤알 디헤드라 세트 | |
|---|---|
 구체의 육각 다이헤드론 예 | |
| 유형 | 일반 다면체 또는 구형 타일링 |
| 얼굴 | 2n-gon |
| 가장자리 | n |
| 정점 | n |
| 꼭지점 구성 | 엔 |
| 와이토프 기호 | 2n 2 |
| 슐레플리 기호 | {n,2} |
| 콕시터 다이어그램 | |
| 대칭군 | Dnh, [2,n], (*22n), 주문 4n |
| 회전군 | Dn, [2,n],+ (22n), 주문 2n |
| 이중 다면체 | 정규 n-곤 양수면체 |
다이헤드론은 다면체의 일종으로, 같은 n개의 가장자리 집합을 공유하는 두 개의 폴리곤 면으로 만들어졌다. 3차원 유클리드 공간에서는 얼굴이 평평하면 퇴화되는 반면, 3차원 구형 공간에서는 납작한 얼굴을 가진 다이드론을 렌즈로 생각할 수 있는데, 그 예가 렌즈 공간 L(p,q)의 기본 영역이다.[1] 디헤드라는 또한 비헤드라,[2] 평평한 다면체 [3]또는 이중으로 덮인 다각형이라고도 불린다.[3]
구면 타일링으로서, 다이헤드론은 비탈면 형태로 존재할 수 있는데, 구를 덮고 있는 두 개의 n면면이 있고, 각 면은 반구가 되며, 큰 원에는 정점이 있다. 꼭지점들이 같은 간격으로 있는 것은 규칙적이다.
n-곤 dihedron의 이중은 n-곤-호소헤드론이며, 여기서 n digon 면은 두 개의 정점을 공유한다.
납작한 얼굴의 다면체로서
다이헤드론은 두 개의 (평면) n측 폴리곤 베이스가 "뒤로" 연결되어 그 결과 물체의 깊이가 없는 퇴행성 프리즘으로 간주할 수 있다. 폴리곤은 응집력이 있어야 하지만, 한쪽이 다른 한쪽의 거울상일 정도로 접착되어 있어야 한다. 이는 두 얼굴 사이의 거리가 0일 경우에만 적용된다. 0보다 큰 거리에 대해 얼굴은 무한 폴리곤(아페이오날 호소헤드론의 디곤 면과 같은 약간은 0보다 큰 폭은 무한 줄무늬)이다.
디헤드라는 알렉산드로프의 고유성 정리에서 발생할 수 있는데, 이 정리에서는 볼록한 다면체의 표면상의 거리를 국소적으로 유클리드인 것으로 특징지으며, 단점은 4㎛에 이른다. 이 특성화는 다이헤드론 표면의 거리에도 적용되기 때문에 알렉산드로프 정리의 진술은 디헤드라를 볼록한 다면체로 간주할 것을 요구한다.[4]
일부 다이헤드라는 다른 다면체 집단의 하한선 구성원으로서 발생할 수 있다: 디곤 기단을 가진 프리즘은 사각 다이헤드론이고 디곤 기단을 가진 피라미드는 삼각 다이헤드론일 것이다.
슐래플리 기호가 {n,2}인 일반 다이헤드론은 각각 슐래플리 기호가 {n}[5]인 두 개의 일반 폴리곤으로 만들어진다.
구의 타일링으로서
구면 다이헤드론은 큰 원 적도에서 같은 정점 집합을 공유하는 두 개의 구면 폴리곤으로 만들어진다; 구면 다이헤드론의 각 폴리곤은 반구를 채운다.
일반 구면 다이헤드론은 큰 원 적도에 균등하게 간격을 두고 동일한 n 정점을 공유하는 두 개의 정규 구면 다각형으로 만들어진다.
일반 다면체{2,2}는 자가 이중이며, 호소면체와 다이면체 둘 다이다.
| 공간 | 구면 | 유클리드 주 | ||||||
|---|---|---|---|---|---|---|---|---|
| 타일링 이름 | (Hengonal) 단조 다이헤드론 | 디지온 다이헤드 | (삼각형) 삼면체 | (Tetrangle) 정방면체 | 펜타곤 디헤드론 | 육각다이헤드론 | ... | 아페이로겐 다이헤드론 |
| 타일링 이미지 |  |  | 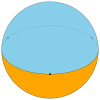 |  |  | 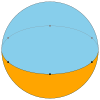 | ... |  |
| 슐레플리 기호 | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | {6,2} | ... | {∞,2} |
| 콕시터 다이어그램 | ... | |||||||
| 얼굴 | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} | ... | 2 {∞} |
| 모서리 및 정점 | 1 | 2 | 3 | 4 | 5 | 6 | ... | ∞ |
| 정점 구성. | 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 | ... | ∞.∞ |
아페이로겐 다이헤드론
n이 무한대로 되는 경향이 있기 때문에, n-곤알 디헤드론은 2차원 테셀레이션으로서 무페이로겐 디헤드론이 된다.
디토페스
일반 ditope는 diheadron의 n차원 아날로그로, Schléfli 기호가 {p,...,q,r,2}이다. {p, ..., q,r}이라는 두 개의 면을 가지고 있는데, 모든 능선을 공유하는 면은 {p, ..., q}이다.[6]
참고 항목
참조
- ^ Gausmann, Evelise; Roland Lehoucq; Jean-Pierre Luminet; Jean-Philippe Uzan; Jeffrey Weeks (2001). "Topological Lensing in Spherical Spaces". Classical and Quantum Gravity. 18 (23): 5155–5186. arXiv:gr-qc/0106033. Bibcode:2001CQGra..18.5155G. doi:10.1088/0264-9381/18/23/311. S2CID 34259877.
- ^ Kántor, S. (2003), "On the volume of unbounded polyhedra in the hyperbolic space" (PDF), Beiträge zur Algebra und Geometrie, 44 (1): 145–154, MR 1990989, archived from the original (PDF) on 2017-02-15, retrieved 2017-02-14.
- ^ a b O'Rourke, Joseph (2010), Flat zipper-unfolding pairs for Platonic solids, arXiv:1010.2450, Bibcode:2010arXiv1010.2450O
- ^ O'Rourke, Joseph (2010), On flat polyhedra deriving from Alexandrov's theorem, arXiv:1007.2016, Bibcode:2010arXiv1007.2016O
- ^ Coxeter, H. S. M. (January 1973), Regular Polytopes (3rd ed.), Dover Publications Inc., p. 12, ISBN 0-486-61480-8
- ^ McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, p. 158, ISBN 0-521-81496-0