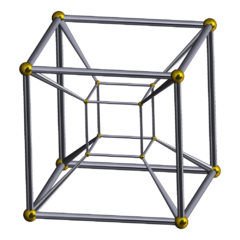
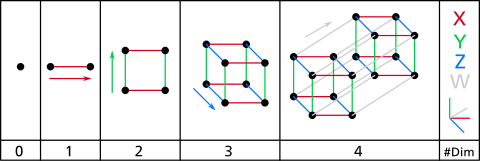테서랙트

테서랙트
8 셀
4큐브
테서랙트; 8 셀; 4큐브
	슐레겔도
유형	볼록정규4폴리토프
슐레플리 기호	{4,3,3}; t0,3{4,3,2} 또는 {4,3}×{ }; t0,2{4,2,4} 또는 {4}×{4}; t0,2,3{4,2,2} 또는 {4}×{}×{}; t0,1,2,3{2,2,2} 또는 { }×{ }×{ }×{ }×{ }
콕서터 다이어그램	; ; ; ;
셀	8 {4,3}
얼굴	24 {4}
가장자리	32
꼭지점	16
꼭지점 도형	; 사면체
페트리 폴리곤	팔각형
콕서터군	B4, [3,3,4]
듀얼	16 셀
특성.	볼록, 등각, 등각, 등각면
균일한 지수	10

달리 십자가, 정삼각형의 그물

큐브가 6개의 정사각형으로 펼쳐지는 것처럼 큐브는 8개의 큐브를 3D 공간으로 펼 수 있다.

기하학에서 정육면체는 정육면체의 4차원 유사체이다. 정육면체는 정육면체와 ^[1]정사각형과 같다.정육면체의 표면이 6개의 정사각형 면으로 구성되어 있는 것처럼, 정육면체의 초면체는 8개의 입방체 세포로 구성되어 있다.정삼각형은 6개의 볼록한 정사각형 중 하나이다.

정팔각형은 또한 8셀, C₈, (정팔각형) 옥타코론, 8면체,^[2] 큐빅 프리즘, 그리고 ^[3]테트라큐브라고 불립니다.4차원 하이퍼큐브 또는 4차원 하이퍼큐브 또는 측정 폴리톱의 ^[4]구성원으로서의 4-큐브입니다.Coxeter는 $\gamma _{4}$ 을 § $($ style $\display$ \ $gamma$ _ ${4})$ ^[5] 폴리토프라고 $\gamma _{4}$ 부른다.치수 참조가 없는 하이퍼큐브라는 용어는 종종 이 특정 폴리토프와 동의어로 취급됩니다.

옥스포드 영어 사전에 따르면, 테서랙트라는 단어는 찰스 하워드 힌튼이 1888년 그의 책 "생각의 새로운 시대"에서 그리스어 테사라와 아크티스에서 각각 꼭지점에서 서로 꼭지점까지의 네 모서리를 가리키며 처음 사용했다.힌튼의 후기 작품들뿐만 아니라 이 출판물에서도 가끔 이 단어는 테사랙트로 ^[6]쓰였다.

기하학.

각 모서리 주위에 3개의 큐브가 접힌 정다각형으로서 384차 초팔면체 대칭의 슐레플리 기호 {4,3,3}을 가진다.2개의 평행 입방체로 구성된 4D 하이퍼프리즘으로 구성되며 대칭 차수가 96인 복합 슐레플리 기호 {4,3} × {}로 명명할 수 있습니다.2개의 정사각형의 데카르트 곱인 4-4 이중 프리즘으로서 대칭 순서 64의 합성 슐레플리 기호 {4}×{4}로 명명할 수 있다.직교로는 합성 슐레플리 기호 { } × { } × { } × { } × { } 또는 { ⁴}, 대칭 순서 16으로 나타낼 수 있다.

정삼각형의 각 정점이 네 모서리에 인접하기 때문에 정삼각형의 정사면체는 정사면체이다.테서랙트의 이중 폴리토프는 슐레플리 기호 {3,3,4}을 가진 16셀이며, 이 셀과 결합하여 테서랙트와 16셀의 화합물을 형성할 수 있습니다.

정사각형의 각 모서리는 길이가 같다.이는 병렬 컴퓨팅에서 여러 프로세서를 링크하기 위한 네트워크토폴로지의 기초로서 테서랙트를 사용하는 경우에 중요합니다.두 노드 간의 거리는 최대 4로 웨이트 밸런싱을 가능하게 하는 다양한 경로가 있습니다.

좌표

유클리드 4공간의 표준 정삼각은 점(±1, ±1, ±1, ±1)의 볼록 선체로 주어진다.즉, 다음과 같은 포인트로 구성됩니다.

\displaystyle \{(x_{1},x_{2},x_{3},x_{4}\in \mathbb {R}^{4},:,-1\leq x_{i}\leq 1\}

이 데카르트 기준 프레임에서, 정삼각형의 반지름은 2이고 8개의 초평면에 의해 경계된다(x = ±1_i).평행하지 않은 초평면의 각 쌍이 교차하여 정삼각형 면 24개를 형성합니다.각 모서리에서 세 개의 큐브와 세 개의 정사각형이 교차합니다.각 정점에서 4개의 큐브, 6개의 정사각형 및 4개의 모서리가 만난다.총 8개의 큐브, 24개의 정사각형, 32개의 모서리, 16개의 꼭지점으로 구성됩니다.

그물

폴리포프의 전개를 그물이라고 한다.테서랙트에는 ^[7]261개의 뚜렷한 그물이 있다.정삼각형의 전개는 그물을 쌍으로 된 나무들에 매핑함으로써 셀 수 있다.

건설

차원 이동 애니메이션

하이퍼큐브의 구성은 다음과 같이 생각할 수 있습니다.

1차원:2개의 점 A와 B를 접속하면 선이 되어 새로운 선분 AB를 얻을 수 있다.
2차원:AB의 거리로 분리된 두 개의 평행선 세그먼트 AB와 CD를 연결하여 모서리가 ABCD로 표시된 정사각형으로 만들 수 있습니다.
3차원:AB의 거리로 분리된 두 개의 평행 정사각형 ABCD와 EFGH를 연결하여 모서리가 ABCDEFGH로 표시된 입방체가 될 수 있습니다.
4차원:AB의 거리로 분리된 두 개의 평행 큐브 ABCDEFGH와 IJKLMNOP를 연결하여 모서리가 ABCDEFGHIJKLMNOP로 표시된 정육면체가 될 수 있습니다.그러나 대응하는 8쌍의 정점이 각각 AB의 거리에 의해 분리되도록 2개의 큐브를 평행하게 배치하는 것은 4차원 이상의 공간에서만 가능하다.

정삼각형은 더 작은 4중합체로 분해될 수 있다.그것은 두 개의 반정맥(16셀) 화합물의 볼록한 껍질이다.정점과 정점을 공유하는 4차원 심플화(불규칙 5셀)로 삼각 측량할 수도 있습니다.이러한^[8] 삼각측량은 92487256개이며 그 중 가장 적은 4차원 단순도는 ^[9]16개로 알려져 있다.정삼각형의 특징적인 단순체(콕서터 다이어그램이 있는 특정 정삼각)의 24개로 분해하는 것은 가능한 정삼각형의 가장 기본적인 직접 구조이다.4-입방체의 특징적인 4-정격은 정삼각형의 정의 대칭군, 즉 B다양체를₄ 생성하는 그룹의 기본 영역이다.정삼각형의 특징인 심플렉스는 그룹의 작용을 통해 정삼각형을 직접 생성하며, 정삼각형의 경계면(거울 벽)에 반사한다.

반지름 등변 대칭

정삼각형의 긴 반지름(중앙에서 정점으로)은 가장자리 길이와 같기 때문에 중심을 통과하는 대각선(대각선에서 반대 정점으로)은 2개의 가장자리 길이입니다.4차원 정육면체와 24셀, 3차원 정육면체, 2차원 정육면체를 포함한 소수의 균일한 폴리톱만이 이러한 특성을 가지고 있습니다.특히, 정삼각형은 (0차원 점을 제외하고) 방사상으로 등변하는 유일한 하이퍼 큐브이다.단위 엣지 길이의 n차원 하이퍼큐브의 가장 긴 정점 대 버텍스 직경은 θn이므로 제곱의 경우 θ2, 입방체의 경우 θ3, 정방체의 경우 θ4, 정확히 2의 엣지 길이가 된다.

수식

Kuratowski 또는 Wagner의 이론을 사용하여 K(위) 또는_3,3 K(아래) 하위 그래프를₅ 찾아 하이퍼큐브 그래프가 평면이 아님을 단어 없이 증명한다.

측면 $길이$ 가 s인 정삼각형의 경우:

하이퍼볼륨: $($
표면적: $SV=8s^{3}$
면 $d_{\mathrm {2} }={\sqrt {2}}s$ : $d_{\mathrm {2} }={\sqrt {2}}s$ $d_{\mathrm {2} }={\sqrt {2}}s$ $d_{\mathrm {2} }={\sqrt {2}}s$ s {\ $displaystyle d_{\mathrm {2}$ } = $scsrt {$ 2}
셀 $d_{\mathrm {3} }={\sqrt {3}}s$ : $d_{\mathrm {3} }={\sqrt {3}}s$ $d_{\mathrm {3} }={\sqrt {3}}s$ $(\displaystyle d_{\mathrm {3}$ } = $scsrt {$ 3 $}s)$
4공간 $d_{\mathrm {4} }=2s$ : $d_{\mathrm {4} }=2s$ $d_{\mathrm {4} }=2s$ $(\displaystyle d_{\mathrm {4}$ = $2s})$

구성으로서

이 설정 매트릭스는 정삼각형을 나타냅니다.행과 열은 정점, 모서리, 면 및 셀에 해당합니다.대각선 숫자는 전체 정삼각형에서 각 요소가 얼마나 많이 발생하는지 나타냅니다.비대각 숫자는 행 요소 내에서 또는 행 ^[10]요소에서 발생하는 열 요소의 수를 나타냅니다.예를 들어, 두 번째 행의 첫 번째 열에 있는 2는 각 모서리에 두 개의 정점이 있음을 나타내고, 첫 번째 행의 두 번째 열에 있는 4는 4개의 모서리가 각 정점에서 만난다는 것을 나타냅니다.

$(\displaystyle {bmatrix}{\display{bmatrix}16&4&4&3&3\\4&24&2\8&6\end{bmatrix}}\end{bmatrix})$

투영

큐브를 2차원 공간에 투영하는 것과 유사하게 3차원 및 2차원 공간에 투영하는 것이 가능하다.

정삼각형의 평행 투영 엔벨로프(각 셀은 다른 색상으로 그려지고 반전 셀은 그려지지 않음)

마름모꼴 12면체는 정점-첫 번째 평행-투영의 볼록한 선체를 형성합니다.이 투영의 층에 있는 정점의 수는 파스칼 삼각형의 네 번째 행인 1 4 6 4 1입니다.

정삼각형의 3차원 공간에 대한 세포 최초의 평행 투영에는 입방체 외피가 있다.가장 가까운 셀과 가장 먼 셀은 큐브에 투영되고 나머지 6개의 셀은 큐브의 6개의 정사각형 면에 투영됩니다.

3차원 공간에 대한 정삼각형의 면 첫 평행 투영에는 정육면체 형태의 외피가 있다.두 쌍의 셀이 이 봉투의 상부와 하부에 투영되고 나머지 4개의 셀은 측면에 투영됩니다.

정삼각형의 가장자리를 3차원 공간에 평행하게 투영하는 것은 육각형 프리즘 모양의 외피를 가지고 있다.6개의 세포가 마름모꼴 프리즘에 투영되는데, 마름모꼴 프리즘은 3D 큐브의 면이 정점 첫 번째 투영 아래 육각 외피의 6개의 마름모꼴에 투영되는 것과 유사한 방식으로 배치됩니다.나머지 두 개의 세포는 프리즘 베이스에 투영됩니다.

3차원 공간에 대한 정점 첫 평행 투영 정점은 마름모꼴 12면체 외피를 가진다.정삼각형의 두 꼭지점이 원점에 투영되어 있다.마름모꼴 12면체를 4개의 합동 마름모꼴로 해부하는 방법은 정확히 두 가지가 있으며, 각각 정삼각형의 투영 입방체인 총 8개의 가능한 마름모꼴을 제공한다.이 투영도 최대 볼륨입니다.투영 벡터의 1세트는 u=(1, 1,-1,-1), v=θ1,1,-1, w=(1,-1,-1)이다.

테서랙트의 B 콕서터 평면₄ 투영 내의 각 개별 큐브를 보여주는 애니메이션입니다.

맞춤법 투영법
콕서터 평면	B₄.	B₃/D₄/A₂	B₂/D₃
그래프
이면체 대칭	[8]	[6]	[4]
콕서터 평면	다른.	에프₄	A₃.
그래프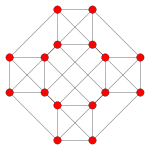
이면체 대칭	[2]	[12/3]	[4]

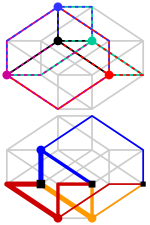
4차원 공간에서 평면을 중심으로 단순 회전을 수행하는 정삼각형의 3차원 투영법입니다.평면은 그림을 왼쪽에서 오른쪽 뒤로, 그리고 위에서 아래로 이등분합니다.	4차원 공간에서 2개의 직교 평면에 대해 이중 회전을 수행하는 정삼각형의 3D 투영입니다.

면 유무에 관계없이 3개의 정육면체의 3D 투영	숨겨진 볼륨을 배제하는 투시법.빨간색 모서리는 4D에서 가장 가깝고 주위에 4개의 입방체 셀이 모여 있습니다.

사면체는 정점 중심 투영법의 볼록한 선체를 형성한다.8개의 입방체 셀 중 4개가 표시되어 있습니다.16번째 정점은 무한대로 투영되고 4개의 가장자리는 표시되지 않습니다.	입체 투영 (에지는 3-sphere에 투영됩니다.)

정삼각형의 입체 3D 투영(평행 뷰)
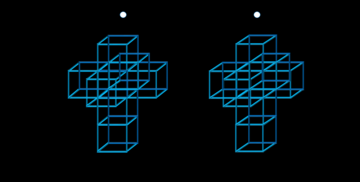입체 3D 무장 해제 Hypercube

테셀레이션

큐브는 모든 하이퍼큐브와 마찬가지로 유클리드 공간을 테셀레이트합니다.각 면 주위에 4개의 테서랙트로 구성된 자체 이중 테서랙틱 벌집에는 슐레플리 기호 {4,3,4}이 있습니다.따라서 정삼각은 90°^[11]의 이면각을 가진다.

정삼각형의 반지름 등변 대칭은 테셀레이션을 임의의 수의 차원으로 동일한 크기의 구체의 독특한 정육면체 중심 입방 격자로 만듭니다.

대중문화에서

그들의 발견 이후, 4차원 하이퍼큐브는 예술, 건축, 그리고 공상과학 소설에서 인기 있는 주제가 되었다.주목할 만한 예는 다음과 같습니다.

로버트 하인라인의 1940년 공상과학소설인 "그리고 그는 구부러진 집을 지었다"는 4차원 하이퍼큐브 ^[13]형태의 건물을 특징으로 한다.1946년에 출판된 마틴 가드너의 "무측 교수"는 뫼비우스 밴드, 클라인 병, 하이퍼 큐브(테서랙트)를 독자들에게 소개한 최초의 공상과학 소설 중 하나이다.
4차원 하이퍼큐브를 형상화한 살바도르 달리의 1954년 유화 십자가(Corpus Hypercubus)는 3차원 라틴 ^[14]십자가로 펼쳐졌다.
프랑스 파리 근교의 기념비이자 건물인 그란데 아케는 1989년에 완공되었다.이 기념비의 기술자인 에릭 레이첼에 따르면, 그란데 아케는 하이퍼큐브의 ^[15]투영을 닮도록 설계되었다고 한다.
다른 캐릭터가 볼 수 있는 2차원을 넘어 볼 수 있는 캐릭터를 플레이하여 플랫폼 퍼즐을 풀어야 하는 비디오 게임 Fez.플레이어가 세계를 탐색하고 능력을 사용하는 방법을 알려주는 테서랙트 "Dot"이 특징이며, 알려진 차원 ^[16]공간에 대한 인간의 인식 범위를 넘어 보는 테마에 부합합니다.

테서랙트라는 단어는 나중에 공상과학 소설 작품에서 플롯 장치로 사용되는 등 대중 문화에서 많은 다른 용도로 채택되었으며, 종종 이 기사의 4차원 하이퍼큐브와 거의 관련이 없거나 전혀 관련이 없다.'테서랙트'를 참조해 주세요.

「」를 참조해 주세요.

수학과 미술

메모들

^ "The Tesseract - a 4-dimensional cube". www.cut-the-knot.org. Retrieved 2020-11-09.
^ Matila Ghyka, 예술과 삶의 기하학(1977),
^ 이 용어는 또한 4개의 큐브로 만들어진 폴리큐브를 의미할 수 있다.
^ Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
^ Coxeter 1973, 페이지 122–123, § 7.2. 그림 7.2C.
^ "tesseract". Oxford English Dictionary (Online ed.). Oxford University Press. 199669. (가입 또는 참여기관 회원가입 필요)
^ "Unfolding an 8-cell". Unfolding.apperceptual.com. Retrieved 21 January 2018.
^ Pournin, Lionel (2013), "The flip-Graph of the 4-dimensional cube is connected", Discrete & Computational Geometry, 49 (3): 511–530, arXiv:1201.6543, doi:10.1007/s00454-013-9488-y, MR 3038527, S2CID 30946324
^ Cottle, Richard W. (1982), "Minimal triangulation of the 4-cube", Discrete Mathematics, 40: 25–29, doi:10.1016/0012-365X(82)90185-6, MR 0676709
^ Coxeter 1973, 페이지 12, § 1.8 구성.
^ 콕서터 1973, 페이지 293
^ Coxeter, H. S. M., Regular Complex Polytopes, 제2판, 케임브리지 대학 출판부, (1991)
^ Fowler, David (2010), "Mathematics in Science Fiction: Mathematics as Science Fiction", World Literature Today, 84 (3): 48–52, JSTOR 27871086
^ Kemp, Martin (1 January 1998), "Dali's dimensions", Nature, 391 (27): 27, Bibcode:1998Natur.391...27K, doi:10.1038/34063, S2CID 5317132
^ Ursyn, Anna (2016), "Knowledge Visualization and Visual Literacy in Science Education", Knowledge Visualization and Visual Literacy in Science Education, Information Science Reference, p. 91, ISBN 9781522504818
^ "Dot (Character) - Giant Bomb". Giant Bomb. Retrieved 21 January 2018.

레퍼런스

Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123.
F. 아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss(1995) 만화경: Wiley-Intercience 간행물 ISBN978-0-471-01003-6 [1] H.S.M. Coxeter 선정 논문
- (문서 22) H.S.M. Coxeter, 정규 및 준정규 폴리토피스 I, Mathemische Zeitschrift 46(1940) 380–407, MR 2,10]
- (페이퍼 23) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 II, [수학]Zeit. 188 (1985) 559-591]
- (문서 24) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 III, [수학]Zeit. 200 (1988) 3-45]
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass (2008) 사물의 대칭성, ISBN 978-1-56881-220-5 (26장 409쪽: Hemicubes: 1_n1)
T . Gosset(1900) 맥밀런, 수학 메신저, n차원 공간의 정칙 및 반규칙 도형에 대하여.
T. Proctor Hall (1893) "3평면에 4배 도형의 투영", 미국 수학 저널 15:179–89.
Norman Johnson Uniform Polytopes, 원고(1991)
- N.W. 존슨:균일한 폴리토프와 허니콤 이론 박사(1966년)
Victor Schlegel (1886) Uever Projectionsmodelle der Regelméssigen vier-dimensen Körper, Waren.

외부 링크

Weisstein, Eric W. "Tesseract". MathWorld.
Klitzing, Richard. "4D uniform polytopes (polychora) x4o3o3o - tes".
테서랙트 레이는 숨겨진 표면 제거로 이미지를 추적했습니다.이 사이트에서는 4D 솔리드를 시각화하는 방법을 자세히 설명합니다.
Der 8-Zeller(8셀) Marco Möller의 정규 폴리토피스(독일어⁴)
WikiChoron:테서랙트
HyperSolids는 Apple Macintosh(Mac OS X 이상)용 오픈 소스 프로그램으로, 3차원 공간의 5개의 정규 솔리드 및 4차원 공간의 6개의 정규 하이퍼로이드를 생성합니다.
Hypercube 98 Rudy Rucker 애니메이션 하이퍼큐브를 표시하는 Windows 프로그램
Ken Perlin의 홈페이지 하이퍼큐브를 시각화하는 방법, Ken Perlin의
4차원에 대한 일부 노트에는 데이비드 P의 테서랙트의 여러 다른 측면에 대한 애니메이션 튜토리얼이 포함되어 있습니다. 세르본
숨겨진 볼륨 제거 기능이 있는 테서랙트 애니메이션

v t 치수 2-10의 기본 볼록 정규 및 균일한 폴리토프
가족	A_n	B_n	I₂(p) / D_n	E₆/E₇/E₈/F₄/G₂	H_n
정다각형	삼각형	광장	p곤	육각형	펜타곤
균일한 다면체	사면체	8면체 • 큐브	데미큐브		12면체 • 이십면체
균일한 폴리코론	펜타코론	16 셀 • 테서랙트	데모테서랙트	24 셀	120 셀 • 600 셀
균일한 5 폴리토프	51200x	5 - ORTOPLEX • 5 - 큐브	5 데미큐브
균일한 6 폴리토프	61200x	6-정류 • 6-큐브	6-데미큐브	1₂₂ • 2₂₁
균일한 7 폴리토프	71200x	7-정류 • 7-큐브	7 데미큐브	1₃₂ • 2₃₁ • 3₂₁
균일한 8 폴리토프	8180x	8-정류 • 8-큐브	8개의 데미큐브	1₄₂ • 2₄₁ • 4₂₁
균일한 9-폴리토프	9169x	9-정류 • 9-입방체	9데미큐브
균일한 10 폴리토프	10-1996x	10 - ORTOPLEX • 10 - 큐브	10 데미큐브
균일한 n-폴리토프	n-1996x	n-ortoplex • n-입방체	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-오각형 폴리토프
주제: 폴리토프 패밀리 • 일반 폴리토프 • 일반 폴리토프 및 화합물 목록

[1] "The Tesseract - a 4-dimensional cube". www.cut-the-knot.org. Retrieved 2020-11-09.

[2] Matila Ghyka, 예술과 삶의 기하학(1977),

[3] 이 용어는 또한 4개의 큐브로 만들어진 폴리큐브를 의미할 수 있다.

[4] Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.

[FOOTNOTECoxeter1973122–123§7.2._illustration_Fig_7.2<small>C</small>-5] Coxeter 1973, 페이지 122–123, § 7.2. 그림 7.2C.

[6] "tesseract". Oxford English Dictionary (Online ed.). Oxford University Press. 199669. (가입 또는 참여기관 회원가입 필요)

[7] "Unfolding an 8-cell". Unfolding.apperceptual.com. Retrieved 21 January 2018.

[8] Pournin, Lionel (2013), "The flip-Graph of the 4-dimensional cube is connected", Discrete & Computational Geometry, 49 (3): 511–530, arXiv:1201.6543, doi:10.1007/s00454-013-9488-y, MR 3038527, S2CID 30946324

[9] Cottle, Richard W. (1982), "Minimal triangulation of the 4-cube", Discrete Mathematics, 40: 25–29, doi:10.1016/0012-365X(82)90185-6, MR 0676709

[FOOTNOTECoxeter197312§1.8_Configurations-10] Coxeter 1973, 페이지 12, § 1.8 구성.

[FOOTNOTECoxeter1973293-11] 콕서터 1973, 페이지 293

[12] Coxeter, H. S. M., Regular Complex Polytopes, 제2판, 케임브리지 대학 출판부, (1991)

[13] Fowler, David (2010), "Mathematics in Science Fiction: Mathematics as Science Fiction", World Literature Today, 84 (3): 48–52, JSTOR 27871086

[14] Kemp, Martin (1 January 1998), "Dali's dimensions", Nature, 391 (27): 27, Bibcode:1998Natur.391...27K, doi:10.1038/34063, S2CID 5317132

[15] Ursyn, Anna (2016), "Knowledge Visualization and Visual Literacy in Science Education", Knowledge Visualization and Visual Literacy in Science Education, Information Science Reference, p. 91, ISBN 9781522504818

[16] "Dot (Character) - Giant Bomb". Giant Bomb. Retrieved 21 January 2018.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

일반 볼록 4-폴리토피스
대칭군	A₄.	B₄.		에프₄	H₄
이름.	5셀 초정면체 5점	16 셀 초팔면체 8 포인트	8 셀 하이퍼 큐브 16 포인트	24 셀 24점	600셀 초이십면체 120점	120 셀 초이십이면체 600포인트
슐레플리 기호	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
콕서터 거울
거울면	𝝅/2 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2	𝝅/2 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2	𝝅/2 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2	𝝅/2 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2	𝝅/2 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2	𝝅/2 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2
그래프
꼭지점	5	8	16	24	120	600
가장자리	10	24	32	96	720	1200
얼굴	10개의 삼각형	32개의 삼각형	24 평방	96개의 삼각형	1200개의 삼각형	720 펜타곤
셀	5 사면체	16 사면체	8 큐브	24 팔면체	600 사면체	120 십이면체
토리	1 5면체	2 8면체	4 큐브×2	4 육팔면체	20 30면체	12 10-이십면체
내접	120 셀에 120	16 셀 × 1	16 소켓 × 2	8 소켓 × 3	24시간 365일	10 600파운드
뛰어난 폴리곤		2 µ/2 정사각형 x 3개	4µ/2개의 직사각형x 3	4 µ/3 헥사곤 x 4	12 µ/5 데카곤×6	50 µ/15 도데카곤×4
페트리 폴리곤	1 오각형	1 옥타곤	2 옥타곤	도데카곤 2개	30-gon×4	20 30-gon
등선 폴리곤		1 {8/2}=2{4} x {8/2}=2{4}	2 {8/2}=2{4} x {8/2}=2{4}	2 {12/2}=2{6} x {12/6}=6{2}	4 {30/2}=2 {15} x 30 {0}	20 {30/2}=2 {15} x 30 {0}
긴 반지름	$1$	$1$	$1$	$1$	$1$	$1$
가장자리 길이	$(\displaystyle\tfrac{5}{2}) 약 1.581$	$(\displaystyle\displaystyle{2}}\약 1.414)$	$1$	$1$	$(\displaystyle\tfrac{1}{\phi}}\약 0.120)$	${\displaystyle {1}{\phi ^{2}{\displayrt {2}}}}\약 0.140$
짧은 반지름	$(\displaystyle\tfrac{1}{4})$	${\displaystyle\tfrac{1}{2}}$	${\displaystyle\tfrac{1}{2}}$	$(\displaystyle\tfrac{1}{2}) 약 0.707$	$1-\left tfrac {2}}{2\phi {\phi {3}}}{2}\약 0.936$	$1-\leftfrac {1}{2\phi {3}}}\right)^{2}\약 0.968$
지역	$(\displaystyle 10\leftrt\tfrac {8}{9}\right) 약 9.428)$	$\ displaystyle 32 \ left \ tfrac { 3 } { 16 } \ right ) \ 13613.856 。$	$24$	$(\displaystyle 96\leftrt\tfrac {3}{16}\right) 약 41.569$	$1200\left tfrac}{8\phi ^{2}}\오른쪽) 약 99.238$	$\ displaystyle 720 \ tfrac { 25 + 10 {\ {rt { 5 } } { 8 \ phi ^ { 4 } \ right } \ 약 621 . 9}$
용량	$5\tfrac {5cfrt {5}}{24}\right}\약 2.329$	$(\displaystyle 16\tfrac {1}{3}}\right) 약 5.333}$	$8$	$(\displaystyle 24\leftrt\tfrac {2}{9}\right) 약 11.314}$	$600\left\tfrac {1}{3\phi ^{3}{\tftrt {8}}}\right}\약 16.693$	$120\leftfrac {2+\phi}{2\phi ^{3}{\displayrt {8}}}}\right}\약 18.19$
4-콘텐츠	${\displaystyle\tfrac{5}{24}\left\tfrac{5}{2}\right}^{4}\약 0.140$	$(\displaystyle\tfrac{2}{3}}\약 0.667)$	$1$	$2$	${\text{\text}Short}}\text{Vol}}{4}\약 3.907$	${\displaystyle {\text{\text}Short}}\text{Vol}}{4}\약 4.385$

Search

테서랙트

네임스페이스

더

목차

기하학.

좌표

그물

건설

반지름 등변 대칭

수식

구성으로서

투영

테셀레이션

관련 폴리토프 및 벌집

대중문화에서

「」를 참조해 주세요.

메모들

레퍼런스

외부 링크

직교	관점

₄{4}₂은(는) 16개의 정점과 8개의 4각형으로 구성되며, 8개의 4각형은 4개의 빨간색과 4개의 파란색 정사각형으로 표시됩니다.

Search

테서랙트

기하학.

좌표

그물

건설

반지름 등변 대칭

수식

구성으로서

투영

테셀레이션

관련 폴리토프 및 벌집

대중문화에서

「 」를 참조해 주세요.

메모들

레퍼런스

외부 링크

「」를 참조해 주세요.