플라톤 고체

기하학에서 플라톤 입체(Platonic solid)는 3차원 유클리드 공간에서 볼록하고 규칙적인 다면체입니다.정다각형이 된다는 것은 면이 합동(모양과 크기가 동일)인 정다각형(모든 각도가 합동이고 모든 모서리가 합동)이고 각 꼭짓점에서 동일한 수의 면이 만난다는 것을 의미합니다.다음과 같은 다면체는 5개뿐입니다.

사면체	큐브	팔면체	십이면체	정이십면체
포페이스	식스페이스	팔면	열두 얼굴	스무 얼굴
(애니메이션, 3D 모델)	(애니메이션, 3D 모델)	(애니메이션, 3D 모델)	(애니메이션, 3D 모델)	(애니메이션, 3D 모델)

기하학자들은 수천 년 동안 플라톤 고체를 연구해왔습니다.^[1]그들은 고대 그리스 철학자 플라톤의 이름을 따서 지어졌는데, 플라톤은 그의 대화록 중 하나인 티마이오스에서 고전적인 요소들이 규칙적인 고체로 이루어져 있다고 가정했습니다.^[2]

역사

플라톤 고체는 고대부터 알려져 왔습니다.스코틀랜드의 신석기 후기 사람들에 의해 만들어진 어떤 조각된 돌덩이들은 이러한 모양을 나타낸다고 제안되어 왔습니다; 그러나 이 공들은 다면체가 아닌 둥근 손잡이들을 가지고 있고, 손잡이들의 숫자는 플라톤 입체의 꼭짓점들의 숫자와 자주 달랐고, 손잡이들이 20개의 꼭짓점들과 일치하는 공은 없었습니다.십이면체와 노브의 배열이 항상 대칭적이지는 않았습니다.^[3]

고대 그리스인들은 플라톤 고체를 광범위하게 연구했습니다.프로클로스와 같은 몇몇 자료들은 피타고라스의 발견에 공을 돌립니다.다른 증거는 그가 사면체, 정육면체, 십이면체만 알고 있었을 수도 있고, 팔면체와 이십면체의 발견이 플라톤의 동시대 사람인 테아에테투스의 것이라는 것을 암시합니다.어쨌든, Theaetetus는 다섯 개 모두에 대한 수학적인 설명을 했고, 다른 볼록한 정다면체가 존재하지 않는다는 최초의 알려진 증거에 책임이 있었을지도 모릅니다.

플라톤의 고체는 그들의 이름과 같은 플라톤의 철학에서 두드러집니다.플라톤은 티마이오스 360 B.C.라는 대화에서 그것들에 대해 썼습니다. 그는 네 가지 고전적인 요소들 (지구, 공기, 물, 불) 각각을 규칙적인 고체와 연관시켰습니다.지구는 정육면체, 공기는 팔면체, 물은 정이십면체, 불은 정이십면체와 관련이 있었습니다.

플라톤은 다섯 번째 플라톤 고체인 십이면체에 대해 "신은 하늘 전체에 별자리를 배열하는 데 그것을 사용했다"고 모호하게 말했습니다.아리스토텔레스는 다섯 번째 원소를 추가했고, 하늘이 이 원소로 만들어졌다고 가정했지만, 그는 플라톤의 다섯 번째 고체와 일치시키는 데 관심이 없었습니다.^[4]

유클리드는 플라톤의 고체를 수학적으로 완전히 묘사했는데, 그 중 마지막 책(13권)은 그 성질에 전념하고 있습니다.제13권의 명제 13-17은 사면체, 팔면체, 정육면체, 정이십면체, 십이십면체 순서로 구성하는 것을 설명합니다.각 입체에 대해 유클리드는 외접 구의 지름과 모서리 길이의 비율을 구합니다.명제 18에서 그는 더 이상 볼록한 정다면체가 없다고 주장합니다.안드레아스 슈파이저는 5개의 정칙 고체의 구성이 요소에서 시성된 연역 체계의 주요 목표라는 견해를 주장했습니다.^[5]13권에 있는 많은 정보들은 아마도 Theaetetus의 작품에서 유래되었을 것입니다.

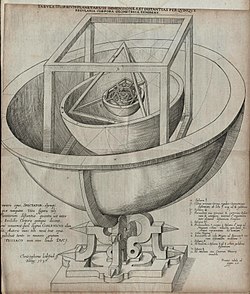
16세기 독일 천문학자 요하네스 케플러는 당시 알려진 외계 행성 다섯 개를 플라톤 고체 다섯 개와 연관시키려고 시도했습니다.1596년에 출판된 미스테리움 우주론에서 케플러는 태양계의 모델을 제안했는데, 그 모델은 다섯 개의 고체가 서로 내부에 설정되어 있고 일련의 내접구와 외접구에 의해 분리되어 있습니다.케플러는 당시 알려진 6개의 행성 사이의 거리 관계를 토성의 궤도를 나타내는 구 안에 포함된 5개의 플라톤 고체로 이해할 수 있다고 제안했습니다.여섯 개의 구체들은 각각 행성들 중 하나에 해당합니다 (수성, 금성, 지구, 화성, 목성, 토성).고체는 가장 안쪽이 팔면체, 그 다음이 정십면체, 십이면체, 정사면체, 그리고 마지막으로 정육면체 순으로 순서가 정해져서 플라톤 고체에 의해 태양계의 구조와 행성들 사이의 거리 관계를 결정하게 됩니다.결국 케플러의 독창적인 아이디어는 포기해야 했지만, 그의 연구에서 그의 궤도 역학의 세 가지 법칙이 나왔는데, 그 중 첫 번째 법칙은 행성의 궤도가 원이 아닌 타원이라는 것이었고, 이는 물리학과 천문학의 진로를 바꾸는 것이었습니다.그는 또한 두 개의 볼록하지 않은 정다면체인 케플러 고체를 발견했습니다.

직각좌표

원점에 중심을 둔 플라톤 입체의 경우 정점의 단순 직각좌표가 아래에 제공됩니다.그리스 문자 φ는 황금 비율을 나타내기 위해 사용됩니다. 1 + √5/2 ≈ 1.6180.

매개변수

피규어	사면체		팔면체	큐브	정이십면체		십이면체
얼굴들	4		8	6	20		12
꼭짓점	4		6 (2 × 3)	8	12 (4 × 3)		20 (8 + 4 × 3)
위치	1	2			1	2	1	2
꼭짓점 좌표들	(1, 1, 1) (1, −1, −1) (−1, 1, −1) (−1, −1, 1)	(−1, −1, −1) (−1, 1, 1) ( 1, −1, 1) ( 1, 1, −1)	(±1,0,0) (0, ±1, 0) (0, 0, ±1)	(±1, ±1, ±1)	(0, ±1, ±φ) (±1, ±φ, 0) (±φ, 0, ±1)	(0, ±φ, ±1) (±φ, ±1, 0) (±1,0,±φ)	(±1, ±1, ±1) (0, ±1/φ, ±φ) (±1/φ, ±φ, 0) (±φ, 0, ±1/φ)	(±1, ±1, ±1) (0, ±φ, ±1/φ) (±φ, ±1/φ, 0) (±1/φ, 0, ±φ)

사면체, 십이면체, 그리고 이십면체에 대한 좌표는 각각 다른 것으로부터 추론될 수 있도록 두 위치에 주어집니다: 사면체의 경우, 부호의 모든 좌표를 변경함으로써(중앙 대칭), 또는 다른 경우, 두 개의 좌표를 교환함으로써(세 개의 대각선 평면 중 하나에 대한 반사).

이 좌표들은 플라톤 입체 사이의 특정한 관계를 보여줍니다. 사면체의 꼭짓점은 정육면체의 꼭짓점의 절반을 {4,3} 또는 두 개의 쌍의 4개 꼭짓점 집합 중 하나를 h{4,3} 또는 h{4,3}로 나타냅니다. 두 사면체 위치 모두 화합물을 별이 있는 팔면체로 만듭니다.

정이십면체의 좌표는 s{3,4} 또는 s{3,4}로서 스너브 팔면체라고도 불리는 균일하지 않은 절단 팔면체의 두 개의 교대된 좌표 집합과 관련이 있으며, 두 개의 정이십면체의 화합물에서 볼 수 있습니다.

십이면체의 꼭짓점 중 8개가 정육면체와 공유됩니다.모든 방향을 완료하면 다섯 개의 정육면체 화합물이 생성됩니다.

조합 성질

볼록 다면체는 다음 세 가지 요건이 모두 충족되는 경우에만 플라톤 입체입니다.

• 모든 면은 합동 볼록 정다각형입니다.
• 가장자리를 제외하고는 어떤 면도 교차하지 않습니다.
• 각 꼭짓점에서 만나는 면의 수가 동일합니다.

따라서 각 플라톤 입체에는 정수 쌍 {p, q}이(가) 할당될 수 있으며, 여기서 p는 각 면의 모서리(또는 그와 동등한 꼭짓점)의 개수이고 q는 각 꼭짓점에서 만나는 면(또는 그와 동등한 모서리)의 개수입니다.슐레플리 기호라고 불리는 이 쌍 {p, q}은 다면체에 대한 조합적인 설명을 제공합니다.5개의 플라톤 입체의 슐레플리 기호는 아래 표에 나와 있습니다.

플라톤 고체의 특성

다면체		꼭짓점	모서리	얼굴들	슐레플리 기호	꼭지점구성
사면체의		4	6	4	{3, 3}	3.3.3
정육면체의		8	12	6	{4, 3}	4.4.4
팔면체		6	12	8	{3, 4}	3.3.3.3
십이면체		20	30	12	{5, 3}	5.5.5
정이십면체		12	30	20	{3, 5}	3.3.3.3.3

꼭짓점(V), 간선(E), 면(F)의 총 개수와 같은 입체에 대한 다른 모든 조합 정보는 p와 q로부터 결정할 수 있습니다. 임의의 간선은 두 개의 꼭짓점을 결합하고 두 개의 인접한 면을 가지므로 다음을 가져야 합니다.

${\displaystyle pF=2E=qV.\,}$

이 값들 사이의 다른 관계는 오일러 공식에 의해 주어집니다.

${\displaystyle V-E+F=2.\,}$

이것은 여러 가지로 증명될 수 있습니다.이 세 가지 관계를 통해 V, E, F가 완전히 결정됩니다.

${\displaystyle V={\frac {4p}{4-(p-2)(q-2)}},\quad E={\frac {2pq}{4-(p-2)(q-2)}},\quad F={\frac {4q}{4-(p-2)(q-2)}}}$

p와 q를 교환하면 F와 V가 바뀌며 E는 변하지 않습니다.이 특성에 대한 기하학적 해석은 § 이중 다면체를 참조하십시오.

구성으로

다면체의 요소는 구성 행렬로 표현할 수 있습니다.행과 열은 꼭짓점, 모서리 및 면에 해당합니다.대각선 숫자는 전체 다면체에서 각 원소가 얼마나 많이 발생하는지를 나타냅니다.비대각수는 열의 요소 중 몇 개가 행의 요소 안에서 발생하는지 또는 행의 요소에서 발생하는지 나타냅니다.다면체 쌍의 이중 구성 행렬은 서로 180도 회전합니다.^[6]

{p,q}	플라토닉 구성
그룹 순서: g = 8pq/(4 - (p - 2)(q - 2))	g = 24	g = 48		g = 120
v e f v g/2q q q e 2 g/4 2 f p p g/2p	{3,3} 4 3 3 2 6 2 3 3 4	{3,4} 6 4 4 2 12 2 3 3 8	{4,3} 8 3 3 2 12 2 4 4 6	{3,5} 12 5 5 2 30 2 3 3 20	{5,3} 20 3 3 2 30 2 5 5 12

분류

고전적인 결과는 볼록한 정다면체가 5개만 존재한다는 것입니다.아래의 두 가지 일반적인 주장은 플라톤 고체가 5개 이하로 존재할 수 없다는 것을 보여주지만, 주어진 고체의 존재를 긍정적으로 보여주는 것은 별개의 질문으로, 명백한 구성이 필요합니다.

기하학적 증명

꼭짓점 주위의 다각형

{3,3} 결함 180°	{3,4} 불량 120°	{3,5} 불량60°	{3,6} 불량 0°
{4,3} 결함 90°	{4,4} 불량 0°	{5,3} 불량 36°	{6,3} 불량 0°
꼭지점에는 면이 3개 이상 필요하고 각도 결점이 있습니다. 0°각 결함은 유클리드 평면에 규칙적인 타일링을 채웁니다. 데카르트 정리에 따르면 꼭짓점의 수는 720°/결함입니다.

다음의 기하학적 논변은 유클리드가 원소에서 제시한 논변과 매우 유사합니다.

위상 증명

순수한 위상학적 증명은 고체에 대한 조합 정보만을 사용하여 만들어질 수 있습니다.핵심은 오일러가 V - E + F = 2, 그리고 pF = 2E = qV라는 사실인데, 여기서 p는 각 면의 모서리의 개수를 의미하고 q는 각 꼭지점에서 만나는 모서리의 개수를 의미합니다.이 방정식들을 합하면 다음을 얻습니다.

${\displaystyle {\frac {2E}{q}}-E+{\frac {2E}{p}}=2.}$

간단한 대수적 조작은 다음을 제공합니다.

${\displaystyle {1 \over q} + {1 \over p}= {1 \over 2} + {1 \over E}}$

E가 엄밀하게 양성이기 때문에 우리는 다음을 가져야 합니다.

${\displaystyle {\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}}.$

p와 q가 둘 다 적어도 3이어야 한다는 사실을 이용하면 {p, q}에 대한 가능성이 5가지라는 것을 쉽게 알 수 있습니다.

{3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}.

기하학적 특성

각도

각 플라톤 입체와 관련된 여러 각도가 있습니다.다면체 각도는 두 면면 사이의 내부 각도입니다.입체 {p,q}의 이면체 각도, θ는 다음 공식으로 주어집니다.

${\displaystyle \sin \left ({\frac {\theta}{2}}\right)={\frac {\cos \left ({\frac {\pi}{q}\right)}{\sin \left ({\frac {\pi}{p}}\right)}}}.$

이는 때때로 다음과 같이 접선의 관점에서 보다 편리하게 표현됩니다.

${\displaystyle \tan \left ({\frac {\theta}{2}}\right)={\frac {\cos \left ({\frac {\pi}{q}\right)}{\sin \left ({\frac {\pi}{h}}\right)}}}.$

정사면체, 정육면체, 정팔면체, 십이면체, 정이십면체의 경우, h의 양은 각각 4, 6, 6, 10, 10입니다.

다면체의 꼭짓점에서의 각결핍은 꼭짓점에서의 면각의 합과 2 π의 차이입니다.플라톤 입체 {p,q}의 임의의 꼭짓점에서 결점인 δ는

${\displaystyle \delta =2\pi -q\pi \left(1-{2 \over p}\right)}$

데카르트 정리에 의해, 이것은 4 π를 정점의 수로 나눈 것과 같습니다(즉, 모든 정점의 총 결점은 4 π입니다).

평면 각도의 3차원 아날로그는 입체각입니다.플라톤 입체의 꼭짓점에 있는 입체각 ω는 다음과 같이 이면체각으로 주어집니다.

${\displaystyle \Omega = q\theta -(q-2)\pi .\,}$

이는 구면 다각형에 대한 구면 과잉 공식과 다면체 {p,q}의 꼭짓점 도형이 정칙 q-곤이라는 사실에서 따온 것입니다.

플라톤 입체의 중심에서 벗어난 면의 입체각은 완전 구(4 π 스테라디안)의 입체각을 면의 수로 나눈 값과 같습니다.이는 이중성의 각결핍과 같습니다.

플라톤 입체와 관련된 다양한 각도가 아래 표로 나와 있습니다.입체각의 수치는 스테라디안 단위로 제공됩니다.상수 φ = 1 + √5/2는 황금 비율입니다.

다면체	이면체 각 (θ)	황갈색 θ/2개	하자 (δ)	꼭지점 실선각 ( ω)	얼굴 단단한 각
사면체의	70.53°	${\displaystyle 1 \over {\sqrt {2}}}$	${\displaystyle \pi}$	${\displaystyle \arccos \left ({\frac {23}{27}}\right)\quad \approx 0.551286}$	${\displaystyle \pi}$
정육면체의	90°	${\displaystyle 1}$	${\displaystyle \pi \over 2}$	${\displaystyle {\frac {\pi}{2}}\quad \approx 1.57080}$	${\displaystyle 2\pi \over 3}$
팔면체	109.47°	${\displaystyle {\sqrt {2}}$	${\displaystyle {2\pi} \over 3}$	${\displaystyle 4\arcsin \left ({1 \over 3}\right)\quad \approx 1.35935}$	${\displaystyle \pi \over 2}$
십이면체	116.57°	${\displaystyle \varphi}$	${\displaystyle \pi \over 5}$	${\displaystyle \pi -\arctan \left ({\frac {2}{11}\right)\quad \approx 2.96174}$	${\displaystyle \pi \over 3}$
정이십면체	138.19°	${\displaystyle \varphi ^{2}}$	${\displaystyle \pi \over 3}$	${\displaystyle 2\pi -5\arcs in \left ({2 \over 3}\right)\quad \approx 2.63455}$	${\displaystyle \pi \over 5}$

반지름, 넓이, 부피

규칙성의 또 다른 장점은 플라톤 고체가 모두 세 개의 동심원을 가지고 있다는 것입니다.

• 모든 꼭짓점을 통과하는 외접구,
• 가장자리의 중간 지점에서 각 가장자리에 접하게 되는 중권(midsphere,
• 면 중앙의 각 면에 접하여 있는 내접구

이 구체들의 반지름을 원반지름, 중반지름, 인반지름이라고 합니다.이 거리는 다면체의 중심에서 꼭짓점, 모서리 중간점 및 면 중심까지의 거리입니다.가장자리 길이가 a인 고체 {p, q}의 원반지름 R과 내반지름은 다음과 같이 주어집니다.

${\displaystyle {\begin{aligned}R&={\frac {a}{2}}\tan \left ({\frac {\pi}{q}}\right)\tan \left ({\frac {\theta}{2}\right)\cot\left ({\frac {\pi}{p}\right)\tan \left ({\frac {\theta}{2}\right)\end{align}}$

여기서 θ는 이면체각입니다.미드라디우스 ρ는 다음과 같이 주어집니다.

${\displaystyle \rho = {\frac {a}{2}}\cos \left ({\frac {\pi}}\right)\,{\csc}{\biggl(}{\frac {\pi}{h}}{\biggr )}}$

여기서 h는 이면체각(h = 4, 6, 6, 10 또는 10)의 정의에서 위에서 사용된 양입니다.반지름과 반지름의 비는 p와 q에서 대칭입니다.

${\displaystyle {\frac {R}{r}=\tan \left ({\frac {\pi}{p}}\right)\tan \left ({\frac {\pi}{q}}\right)={\frac {\sqrt {\csc ^2}}{\Bigl(}{\frac {\theta}{2}}-{\cos ^2}}}-{\Bigl(}{\frac {\alpha}{2}}}{\sin {\bigl(}{\frac {\alpha}{2}}}{\bigr}}}}{\sin {\frac {\frac {\alpha}}}}.$

플라톤 고체 {p, q}의 표면적 A는 면의 수 F에 대한 정규 p-곤의 면적으로 쉽게 계산됩니다.이 내용은:

${\displaystyle A={\biggl (}{\frac {a}{2}}{\biggr )}^{2}Fp\cot \left ({\frac {\pi}{p}\right)}$

부피는 기저가 정칙 p-곤이고 높이가 반경 r인 피라미드의 부피의 F배로 계산됩니다.그것은,

${\displaystyle V={\frac {1}{3}}rA.}$

다음 표는 플라톤 고체의 다양한 반경을 표면적과 부피와 함께 나열한 것입니다.전체 크기는 모서리 길이 a를 2로 하여 고정됩니다.

다면체, a = 2	반지름			표면적, A	용량
	인-, r	미드, 미드.	원-, R		V	단위 모서리
사면체의	${\displaystyle 1 \over {\sqrt {6}}$	${\displaystyle 1 \over {\sqrt {2}}}$	${\displaystyle {\sqrt {3 \over 2}}}$	${\displaystyle 4{\sqrt {3}}$	${\displaystyle {\frac {\sqrt {8}}{3}}\approx 0.942809}$	${\displaystyle \approx 0.117851}$
정육면체의	${\displaystyle 1\,}$	${\displaystyle {\sqrt {2}}$	${\displaystyle {\sqrt {3}}$	${\displaystyle 24\,}$	${\displaystyle 8\,}$	${\displaystyle 1\,}$
팔면체	${\displaystyle {\sqrt {2 \over 3}}}$	${\displaystyle 1\,}$	${\displaystyle {\sqrt {2}}$	${\displaystyle 8{\sqrt {3}}$	${\displaystyle {\frac {\sqrt {128}}{3}}\approx 3.771236}$	${\displaystyle \approx 0.471404}$
십이면체	${\displaystyle {\frac {\varphi^{2}}{\xi}}$	${\displaystyle \varphi ^{2}}$	${\displaystyle {\sqrt {3}},\varphi }$	${\displaystyle 12{\sqrt {25+10{\sqrt {5}}}}$	${\displaystyle {\frac {20\varphi ^{3}}{\xi ^{2}}\approx 61.304952}$	${\displaystyle \approx 7.663119}$
정이십면체	${\displaystyle {\frac {\varphi ^{2}}{\sqrt {3}}}$	${\displaystyle \varphi}$	${\displaystyle \xi \varphi}$	${\displaystyle 20{\sqrt {3}}$	${\displaystyle {\frac {20\varphi ^{2}}{3}}\approx 17.453560}$	${\displaystyle \approx 2.181695}$

위의 상수 φ와 ξ는 다음과 같이 주어집니다.

${\displaystyle \varphi = 2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}{2}},\qquad \xi =2\sin {\pi \over 5}={\sqrt {5-{\sqrt {5}}{2}}={\sqrt {3-\varphi}}}}.$

플라톤 입체 중에서, 십이면체 또는 이십면체 중 하나가 구에 대한 가장 좋은 근사치로 보일 수 있습니다.정이십면체는 면의 수가 가장 많고 정이십면체 각도가 가장 크며, 내접하는 구를 가장 꽉 껴안고, 표면적 대 부피비는 같은 크기의 구와 가장 가깝습니다(즉, 동일한 표면적 또는 동일한 부피).반면, 십이면체는 가장 작은 각결함, 가장 큰 꼭지점 입체각을 가지며, 외접구를 가장 많이 채웁니다.

점 인 스페이스

플라톤 입체의 중심까지의 거리와 n개의 꼭짓점이 각각 L과 d인_i, 원반지름 R을 갖는 플라톤 입체의 공간에 있는 임의의 점에 대하여,

${\displaystyle S_{}^{}}$[ ${\displaystyle n_{}^{}}$] (${\displaystyle 2_{}^m}$ )${\displaystyle {}_{}^{}}$=${\displaystyle {}_{}^{}1}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}^{}\underset{}{\overset{}{}}}$ i =$1$ ${\displaystyle n_{}^{}}$ i 2 $m$ {\$displaystyle$S_{[n]}^{(2${\displaystyle {}_{}^{}}$m)} =${\frac$ {1}{$n}}\su$ _{i$=1}^{$n}$d_{$i$\}^\{$2 m},

가지고^[7] 있습니다

${\displaystyle {\begin{aligned}S_{[4]}^{(2)}=S_{[6]}^{(2)}=S_{[8]}^{(2)}=S_{[12]}^{(2)}=S_{[20]}^{(2)}&=R^{2}+L^{2},\[4px]S_{[4]}^{(4)} = S_{[6]}^{(4)} = S_{[8]}^{(4)} = S_{[12]}^{(4)} = S_{[20]}^{(4)}&=\left(R^{2}+L^{2}\right)^{2}+\frac {4}}R^{2},\[4px]S_{[6]}^{(6)}=S_{[8]}^{(6)}=S_{[12]}^{(6)}=S_{[20]}^{(6)}&=\left(R^{2}+L^{2}\right)^{3}+4R^{2}\left(R^{2}+L^{2}\right),\[4px]S_{[12]}^{(8)}=S_{[20]}^{(8)}&=\left(R^{2}+L^{2}\right)^{4}+8R^{2}L^{2}\left(R^{2}+L^{2}\right)^{2}+{\frac {16}{5}R^{4},\[4px]S_{[12]}^{(10)}=S_{[20]}^{(10)}&=\left(R^{2}+L^{2}\right)^{5}+{\frac {40}{3}}\left(R^{2}+L^{2}\right)^{3}+16R^{4}L^{4}\left(R^{2}+L^{2}\right).\end{aligned}}$

5개의 플라톤 고체 모두에 대해, 우리는^[7]

${\displaystyle S_{[n]}^{(4)}+{\frac {16}{9}}R^{4}=\left(S_{[n]}^{(2)}+{\frac {2}{3}}R^{2}\right)^{2}}}.$

만약_i d가 플라톤 입체의 n개의 꼭짓점에서 그것의 외접구 상의 임의의 점까지의 거리라면^[7],

${\displaystyle 4\left(\sum _{i=1}^{n}d_{i}^{2}\right)^{2}=3n\sum _{i=1}^{n}d_{i}^{4}}$

루퍼트 속성

다면체 P는 크기가 같거나 크고 P와 같은 모양의 다면체가 P의 구멍을 통과할 수 있다면 루퍼트 성질을 가진다고 합니다.^[8]플라톤 고체 다섯 개 모두 이 성질을 가지고 있습니다.^[8][9][10]

대칭성

이중 다면체

모든 다면체는 면과 꼭짓점이 서로 교환된 이중(또는 "극성") 다면체를 가지고 있습니다.모든 플라톤 고체의 이중성은 또 다른 플라톤 고체이므로 5개의 고체를 이중쌍으로 배열할 수 있습니다.

• 사면체는 자기이중(self-dual)입니다(즉, 그것의 이중은 다른 사면체입니다).
• 정육면체와 팔면체는 이중쌍을 형성합니다.
• 십이면체와 정이십면체는 이중쌍을 형성합니다.

다면체에 Schläfli 기호가 {p, q}이면 이중체에 기호가 {q, p}입니다.실제로, 하나의 플라톤 입체의 모든 조합 성질은 이중의 또 다른 조합 성질로 해석될 수 있습니다.

쌍대의 꼭짓점을 원래 도형의 면의 중심이 되도록 함으로써 쌍대 다면체를 구성할 수 있습니다.원본에서 인접한 면의 중심을 연결하면 듀얼의 모서리가 형성되며, 따라서 모서리의 수를 유지하면서 면의 수와 꼭짓점의 수를 변경할 수 있습니다.

보다 일반적으로, 플라톤 고체를 고체와 동심원인 반지름 d의 구와 관련하여 이원화할 수 있습니다.고체의 반지름(R, ρ, r)과 이중의 반지름(R*, ρ*, r*)은 다음과 같은 관계가 있습니다.

${\displaystyle d^{2}=R^{\ast}r=r^{\ast}R=\rho ^{\ast}\rho.}$

중간구(d = ρ)에 대한 이중화는 중간구가 두 다면체에 대해 동일한 관계를 가지므로 종종 편리합니다.d = Rr을 취하면 원반지름과 반지름이 같은 이중고체가 생성됩니다(즉, R* = R 및 r* = r).

대칭군

수학에서 대칭의 개념은 수학적 집단의 개념과 함께 연구됩니다.모든 다면체는 다면체를 불변하게 하는 모든 변환(유클리드 등각)의 집합인 관련 대칭 그룹을 갖습니다.대칭 그룹의 순서는 다면체의 대칭 개수입니다.흔히 반사를 포함하는 완전 대칭군과 회전만을 포함하는 적절한 대칭군을 구분합니다.

플라톤 입체의 대칭군은 다면체 군으로 알려진 3차원 점군의 특별한 부류입니다.플라톤 입체의 높은 대칭성은 여러 가지 방법으로 해석될 수 있습니다.가장 중요한 것은, 각 입체의 꼭짓점들이 대칭군의 작용 하에서 가장자리와 면들과 마찬가지로 모두 동등하다는 것입니다.하나는 대칭군의 작용이 꼭짓점, 모서리, 면에서 전이적이라고 말합니다.사실, 이것은 다면체의 규칙성을 정의하는 또 다른 방법입니다: 다면체는 꼭짓점이 균일하고, 모서리가 균일하고, 면이 균일한 경우에만 규칙적입니다.

플라톤 입체와 관련된 대칭군은 5개가 아니라 3개뿐인데, 이는 임의의 다면체의 대칭군이 이중체의 대칭군과 일치하기 때문입니다.이는 이중 다면체의 구조를 살펴봄으로써 쉽게 알 수 있습니다.원본의 어떤 대칭도 쌍대칭이어야 하며 그 반대도 마찬가지입니다.세 개의 다면체 군은 다음과 같습니다.

• 사면체군 T,
• 팔면체군 O(입방체의 대칭군이기도 함), 그리고
• 정이십면체의 대칭군이기도 한 정이십면체 그룹 I.

적절한(회전) 그룹의 차수는 각각 12, 24, 60으로 각 다면체의 모서리 개수의 정확히 두 배입니다.완전 대칭 그룹의 차수는 다시 두 배입니다(24, 48, 120).이러한 사실의 도출에 관해서는 (Coxeter 1973)을 참조하십시오.사면체를 제외한 모든 플라톤 입체는 중심 대칭이며, 원점을 통해 반사되어 보존됨을 의미합니다.

다음 표는 플라톤 입체의 다양한 대칭 특성을 보여줍니다.나열된 대칭 그룹은 괄호 안에 회전 부분군이 있는 전체 그룹입니다(대칭 개수의 경우와 마찬가지로).Withoff의 만화경 구성은 대칭군으로부터 직접 다면체를 구성하는 방법입니다.이들은 플라톤 고체 각각에 대한 위토프의 기호를 참조하기 위해 나열되어 있습니다.

다면체	슐레플리 기호.	위트호프 기호.	이중 다면체	대칭군(반사, 회전)
				다면체	쇤.	콕스.	오브.	주문
사면체의	{3, 3}	3 2 3	사면체의	사면체	Td T	[3,3] [3,3]+	*332 332	24 12
정육면체의	{4, 3}	3 2 4	팔면체	팔면체	Oh O	[4,3] [4,3]+	*432 432	48 24
팔면체	{3, 4}	4 2 3	정육면체의
십이면체	{5, 3}	3 2 5	정이십면체	정이십면체	Ih I	[5,3] [5,3]+	*532 532	120 60
정이십면체	{3, 5}	5 2 3	십이면체

자연과 기술에서

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 없는 자료에 이의를 제기하여 삭제할 수 있습니다. (2018년 10월) (본 템플릿 메시지 삭제 방법 및 시기 알아보기)

정사면체, 정육면체, 팔면체는 모두 결정 구조에서 자연적으로 발생합니다.이것들은 가능한 형태의 결정들의 수를 결코 다 소모하지 않습니다.그러나 정이십면체도 정이십면체도 아닙니다.파이리토헤드론이라고 불리는 형태들 중 하나는 일반적인 십이면체의 면들과 같은 패턴으로 배열된 12개의 오각형 면들을 가지고 있습니다.하지만, 다면체의 면들은 규칙적이지 않기 때문에, 다면체 또한 규칙적이지 않습니다.붕소와 탄화붕소와 같은 많은 붕소 화합물의 동소체는 결정 구조 내에 이산 비코셰드라를₁₂ 포함합니다.카르보란산은 또한 규칙적인 이코사헤드라에 가까운 분자 구조를 가지고 있습니다.

20세기 초, Ernst Haeckel은 Radiolaria의 많은 종들을 묘사했고(Haeckel, 1904), 그들 중 일부는 다양한 규칙적인 다면체 모양을 하고 있습니다.예를 들면 Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus, Circorrhegma dodechedra 등이 있습니다.이 생물들의 모양은 이름에서 분명해야 합니다.

헤르페스^[11] 바이러스와 같은 많은 바이러스들은 정이십면체 모양을 하고 있습니다.바이러스 구조는 반복되는 동일한 단백질 소단위로 만들어지며, 이 소단위를 사용하여 조립하기에 가장 쉬운 형태는 정이십면체입니다.일반 다면체는 반복적으로 사용되는 하나의 기본 단위 단백질로 만들 수 있기 때문에 사용됩니다. 이것은 바이러스 게놈의 공간을 절약합니다.

기상학과 기후학에서 지구 대기 흐름의 수치 모델은 일반적으로 사용되는 경도/위도 그리드 대신에 정이십면체(삼각형으로 정의됨)를 기반으로 하는 측지선 그리드를 사용하여 증가하는 관심사입니다.이는 다소 큰 수치적 난이도를 감수하면서 특이점(즉 극)이 없는 공간 해상도가 고르게 분포되어 있다는 장점이 있습니다.

우주 프레임의 기하학은 종종 플라톤 고체에 기초합니다.MERO 시스템에서 플라톤 고체는 다양한 공간 프레임 구성의 명명 규칙에 사용됩니다.예를 들어, 1/2O+T는 팔면체와 사면체의 절반으로 이루어진 구성을 말합니다.

테트라헤드로인이 아닌 큐베인 및 도데케드로인을 포함한 여러 플라톤 탄화수소가 합성되었습니다.

• 

  테트라헤란

• 

  쿠바네

• 

  도데카데란

플라톤 고체는 종종 주사위를 만드는데 사용되는데, 이 모양의 주사위는 공정하게 만들어질 수 있기 때문입니다.6면 주사위는 매우 흔하지만 다른 숫자들은 롤플레잉 게임에서 일반적으로 사용됩니다.이러한 주사위는 일반적으로 dn이라고 하며, 여기서 n은 면의 수(d8, d20 등)입니다. 자세한 내용은 주사위 표기법을 참조하십시오.

이런 모양들은 종종 다른 게임이나 퍼즐에 나타납니다.루빅스 큐브와 유사한 퍼즐은 다섯 가지 모양으로 모두 나옵니다. 마법 다면체를 참고하세요.

플라톤 고체의 대칭을 갖는 액정

액정이라고 불리는 중간 물질 상에 대해서, 그러한 대칭의 존재는 H. Kleinert와 K에 의해 1981년에 처음으로 제안되었습니다.마키.^[12][13] 알루미늄의 경우 이십면체 구조가 댄 셰흐트만에 의해 3년 뒤에 발견되어 2011년 노벨 화학상을 수상했습니다.

관련 다면체 및 다면체

균일 다면체

볼록하지 않은 4개의 정다면체가 존재하는데, 이를 케플러-포인소 다면체라고 합니다.이것들은 모두 정이십면체 대칭을 가지며 십이면체와 정이십면체의 별자리로 얻어질 수 있습니다.

정팔면체

정이십면체

플라톤 입체 다음으로 규칙적인 볼록 다면체는 정육면체와 정팔면체의 정류인 정팔면체와 정팔면체와 정팔면체의 정류인 정이십면체입니다(자이십면체의 정류는 정팔면체입니다).이것들은 모두 준규칙적이며, 꼭짓점과 모서리가 균일하고 규칙적인 면을 가지고 있지만, 면들이 모두 합동이 되는 것은 아닙니다(두 개의 다른 클래스에서 나타남).그들은 다면체 대칭을 가진 볼록한 균일 다면체인 13개의 아르키메데스 입체 중 2개를 형성합니다.그들의 쌍대인 마름모 십이면체와 마름모 삼이면체는 가장자리와 면전이형이지만, 그들의 면은 규칙적이지 않고 꼭짓점은 각각 두 가지 유형으로 나옵니다; 그것들은 13개의 카탈루냐 고체 중 두 개입니다.

균일한 다면체는 훨씬 더 넓은 다면체 종류를 형성합니다.이 도형들은 꼭짓점이 균일하며, 얼굴에 대해 일반 다각형 또는 별 다각형의 한 가지 이상의 유형을 가지고 있습니다.이것들은 무한한 프리즘 집합, 무한한 반 프리즘 집합, 그리고 53개의 다른 비볼록 형태와 함께 위에서 언급된 다면체를 포함합니다.

Johnson 입체는 볼록 다면체로, 일정한 면을 가지지만 균일하지 않습니다.이 중에는 볼록 삼각형 여덟 개 중 다섯 개가 있는데, 이들은 모두 정삼각형이지만 균일하지는 않습니다. (나머지 세 개의 볼록 삼각형은 플라톤 정사면체, 팔면체, 정이십면체입니다.)

정기 테셀레이션

규칙적인 구면 타일링

플라토닉
{3,3}	{4,3}	{3,4}	{5,3}	{3,5}
정이면체
{2,2}	{3,2}	{4,2}	{5,2}	{6,2}...
정호면체
{2,2}	{2,3}	{2,4}	{2,5}	{2,6}...

평면의 세 가지 규칙 테셀레이션은 플라톤 고체와 밀접한 관련이 있습니다.실제로 플라톤 고체를 구의 규칙적인 테셀레이션으로 볼 수 있습니다.이것은 각각의 고체를 동심원에 투영함으로써 이루어집니다.면들은 구체를 정확하게 덮고 있는 규칙적인 구면 다각형에 투영됩니다.구면 타일링은 극에 2개의 꼭짓점이 있는 호소헤드라 {2,n}와 반구면이 2개 있고 적도에 일정한 간격을 가진 꼭짓점이 있는 이중 다이헤드라 {n,2}의 무한한 추가 타일링 세트를 제공합니다.그러한 테셀레이션은 다면체로서 진정한 3D 공간에서 퇴화될 것입니다.

구의 모든 정규 테셀레이션은 1/p + 1/q > 1/2인 정수 {p, q} 쌍으로 특징지어진다는 것을 보여줄 수 있습니다.마찬가지로 평면의 정규 테셀레이션도 조건 1/p + 1/q = 1/2로 구성됩니다.세 가지 가능성이 있습니다.

유클리드 평면의 세 가지 규칙적인 타일링

{4, 4}	{3, 6}	{6, 3}

비슷한 방식으로 쌍곡면의 규칙적인 테셀레이션을 고려할 수 있습니다.이들은 조건 1/p + 1/q < 1/2에 의해 특징지어집니다.테셀레이션에는 무한한 가족이 있습니다.

쌍곡선 평면의 규칙적인 타일링 예제

{5, 4}	{4, 5}	{7, 3}	{3, 7}

고차원

치수수	볼록정규다포체수
0	1
1	1
2	∞
3	5
4	6
> 4	3

3차원 이상에서 다면체는 다면체로 일반화되며, 고차원 볼록 정다면체는 3차원 플라톤 입체와 동등합니다.

19세기 중반 스위스의 수학자 루트비히 슐레플리는 볼록한 정다각형이라고 불리는 플라톤 입체의 4차원 유사체를 발견했습니다.5개는 플라톤 고체와 유사합니다. 5개는 {3,3,3}, 16개는 {3,3,4}, 600개는 {3,3,5}, tesseract는 {4,3,3}, 120개는 {5,3,3}, 6번째는 자기 이중 24개는 {3,4,3,3}입니다.

4보다 높은 모든 차원에서 볼록 정다각형은 3개뿐입니다: {3,3,...,3}의 심플렉스, {4,3,...,3}의 하이퍼큐브, {3,3,...,4}^[14]의 크로스 폴리토프.3차원에서, 이것들은 사면체가 {3,3}, 정육면체가 {4,3}, 팔면체가 {3,4}인 것과 일치합니다.

참고 항목

인용문

일반 출처 및 인용 출처

• Atiyah, Michael; Sutcliffe, Paul (2003). "Polyhedra in Physics, Chemistry and Geometry". Milan J. Math. 71: 33–58. arXiv:math-ph/0303071. Bibcode:2003math.ph...3071A. doi:10.1007/s00032-003-0014-1. S2CID 119725110.
• Boyer, Carl; Merzbach, Uta (1989). A History of Mathematics (2nd ed.). Wiley. ISBN 0-471-54397-7.
• Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York: Dover Publications. ISBN 0-486-61480-8.
• Euclid (1956). Heath, Thomas L. (ed.). The Thirteen Books of Euclid's Elements, Books 10–13 (2nd unabr. ed.). New York: Dover Publications. ISBN 0-486-60090-4.
• 가드너, 마틴 (1987)시카고 대학 출판부, 제2회 미국 수학 퍼즐과 다양성 책, 1장: 다섯 개의 플라토닉 고체, ISBN 0226282538
• Haeckel, Ernst, E. (1904).쿤스트 포맨더 네이처.Haeckel, E. (1998)로서 이용가능; Art form in nature, Prestel USA. ISBN 3-7913-1990-6
• 케플러. 요하네스 스트렝스 드 니브 색각굴라(육각 눈송이 위에서), 1611년 케플러가 눈 결정의 육각형 모양과 자연의 형태와 대칭에 대해 논한 논문.플라톤 고체에 대해 이야기합니다.
• Kleinert, Hagen & Maki, K. (1981). "Lattice Textures in Cholesteric Liquid Crystals" (PDF). Fortschritte der Physik. 29 (5): 219–259. Bibcode:1981ForPh..29..219K. doi:10.1002/prop.19810290503.
• Lloyd, David Robert (2012). "How old are the Platonic Solids?". BSHM Bulletin: Journal of the British Society for the History of Mathematics. 27 (3): 131–140. doi:10.1080/17498430.2012.670845. S2CID 119544202.
• Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
• Weyl, Hermann (1952). Symmetry. Princeton, NJ: Princeton University Press. ISBN 0-691-02374-3.
• Wildberg, Christian (1988존 필로포누스의 아리스토텔레스의 에테르 이론에 대한 비판월터 드 그뤼터 11-12쪽ISBN 9783110104462입니다.

외부 링크

이 섹션에서 외부 링크를 사용하는 것은 위키백과의 정책이나 지침을 따르지 않을 수 있습니다. 과도하거나 부적절한 외부 링크를 제거하고, 필요한 경우 유용한 링크를 각주 참조로 변환하여 이 기사를 개선하십시오.(2019년 12월) (본 템플릿 메시지 제거 방법 및 시기 알아보기)

• 수학 백과사전의 플라톤 고체
• Weisstein, Eric W. "Platonic solid". MathWorld.
• Weisstein, Eric W. "Isohedron". MathWorld.
• 유클리드의 원소 13권.
• 자바에서의 대화형 3D 다면체
• 시각적 다면체에 있어서 플라토닉 고체
• Solid Body Viewer는 svg, stl 또는 obj 형식으로 모델을 저장할 수 있는 대화형 3D 다면체 뷰어입니다.
• 대화형 접이식 플라토닉 고체 Java 웨이백 머신에서 보관 2007-02-09
• Stella 소프트웨어에서 생성된 그물을 이용하여 생성된 Platonic 고체의 종이 모델
• 플라토닉 솔리드 프리 종이 모형 (그물)
• Grime, James; Steckles, Katie. "Platonic Solids". Numberphile. Brady Haran. Archived from the original on 2018-10-23. Retrieved 2013-04-13.
• 미대생이 만든 모형으로 수학 가르치기
• 미술 선생님과 함께 수학을 가르치는 모형 만들기 방법
• 대수면의 플라톤 입체영상 골조
• 몇 가지 공식 유도가 있는 플라톤 고체
• 정육면체에서 플라톤 고체 4개 만드는 법