모노곤

Monogon
모노곤
Monogon.svg
원 위에서 모노곤은 단정점, 360도 원호 가장자리 하나를 가진 테셀레이션이다.
유형정규 다각형
모서리 및 정점1
슐레플리 기호{1} 또는 h{2}
콕시터-딘킨 도표CDel node.png 또는
대칭군[ ], Cs

기하학에서 헤나곤이라고도 하는 모노곤은 하나의 가장자리와 하나의 꼭지점을 가진 다각형이다. 슐래플리 기호 {1}을(를)[1] 가지고 있다. 모노곤은 한쪽 면만 있고 꼭지점이 하나만 있기 때문에 모든 모노곤은 정의상 규칙적이다.

유클리드 기하학에서

유클리드 기하학에서 모노곤은 모든 유클리드 선 세그먼트와 달리 그것의 끝점이 일치해야 하기 때문에 퇴보된 다각형이다. 유클리드 기하학에서 폴리곤의 대부분의 정의는 모노곤을 인정하지 않는다.

구형 기하학에서

구형 기하학에서 모노곤은 큰 원(등분자)에 정점으로 구성될 수 있다. 이것은 하나의 360° 가장자리와 하나의 꼭지점을 공유하는 두 개의 반구형 단색 면을 가진 다이헤드론 {1,2}을(를) 형성한다. 그것의 이중, 호소헤드론, {2,1}은 극점에 두 개의 반정점, 360도 룬 면 하나, 그리고 두 정점 사이에 한 개의 에지(메리지안)를 가지고 있다.[1]

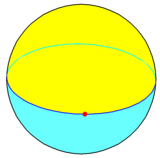Hengonal dihedron.png
단조 다이헤드론, {1,2} 		Henagonal hosohedron.png
단일 호소헤드론, {2,1}

참고 항목

참조

  1. ^ a b Coxeter, 기하학 입문, 1969년, 제2판, 제21.3절 일반 지도, 페이지 386-388
  • 헤르베르트 부세만, 지질학의 기하학. 뉴욕, 학술지, 1955년
  • 콕시터, H.S.M; 일반 폴리토페스 (제) 도버 출판사 ISBN0-486-61480-8