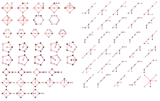
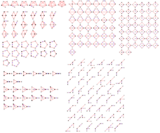콕시터-딘킨 도표

기하학에서 Coxeter-Dynkin 다이어그램(또는 Coxeter 다이어그램, Coxeter 그래프)은 거울 집합(또는 반사되는 하이퍼플레인) 사이의 공간 관계를 나타내는 숫자 레이블이 붙은 그래프다. 그것은 케일리드코픽 구조를 묘사하고 있다: 각 그래프 "노드"는 거울(도메인 면)을 나타내며 나뭇가지에 부착된 라벨은 두 거울 사이의 이음각 순서를 인코딩한다. 즉 반사면 사이의 각도를 곱하여 180도를 얻을 수 있는 양이다. 라벨이 부착되지 않은 가지는 암묵적으로 순서-3(60도)를 나타낸다.

각 다이어그램은 Coxeter 그룹을 나타내며, Coxeter 그룹은 관련 다이어그램에 의해 분류된다.

Dynkin 다이어그램은 두 가지 측면에서 Coxeter 다이어그램과 다른 밀접하게 연관된 개체로, 첫째, "4" 이상 라벨이 표시된 분기는 방향을 지시하는 반면, Coxeter 다이어그램은 방향을 조정하지 않은 반면, 둘째, Dynkin 다이어그램은 허용되는 분지 라벨만 2, 3, 4, 6이라는 추가적인 (결정) 제한을 충족해야 한다. Dynkin 다이어그램은 루트 시스템을 분류하는 데 사용되며, 따라서 리 알헤브라를 반시 구현한다.^[1]

설명

Coxeter-Dynkin 다이어그램의 가지에는 180°/p의 이음각도를 나타내는 합리적인 숫자 p가 라벨로 표시되어 있다. p = 2일 때 각도는 90°이고 미러는 교호작용이 없으므로 도표에서 분기를 생략할 수 있다. 나뭇가지에 라벨이 부착되지 않은 경우, 60°의 각도를 나타내는 p = 3을 가지는 것으로 가정한다. 두 개의 평행 미러는 "∞"로 표시된 가지를 가지고 있다. 원칙적으로 n 거울은 모든 n(n - 1) / 2가지 가지를 그리는 완전한 그래프로 나타낼 수 있다. 실제로 거의 모든 흥미있는 거울의 구성은 다수의 직각을 포함하고 있기 때문에 그에 상응하는 가지가 생략된다.

도표는 그래프 구조로 라벨을 붙일 수 있다. 루트비히 슐래플리가 연구한 첫 번째 형태는 규칙적인 폴리토피와 규칙적인 허니콤을 생성하는 선형 그래프를 가진 직교체들이다. Plagioschemes는 가지 그래프로 표현되는 단순함이고, cycloschemes는 순환 그래프로 표현되는 단순함이다.

슐레플리 행렬

모든 Coxeter 다이어그램에는 해당하는 Schléfli 행렬(Ludwig Schléfli의 이름을 딴 것)이 있으며, 행렬 요소 a_i,j = -2cos_j,i(-2cos)가 있다. 여기서 p는 미러 쌍 사이의 분기 순서다. 코사인의 행렬로서, 조르겐 페데르센 그램의 이름을 따서 그람의 행렬이라고도 한다. 모든 Coxeter 그룹 Schléfli 행렬은 루트 벡터가 정규화되기 때문에 대칭이다. 일반적으로 대칭이 아닌 p = 2,3,4,6의 제한된 사례에서 유사하지만 지시된 그래프 Dynkin 다이어그램에 사용되는 Cartan 행렬과 밀접하게 관련되어 있다.

슐래플리 행렬의 결정요인과 그 부호는 그룹이 유한(양), 아핀(0), 무한(음)인지를 결정한다. 이 규칙은 Schléfli의 기준이라고 불린다.^[2]

Schléfli 매트릭스의 고유값은 Coxeter 그룹이 유한 유형(모든 양성), 아핀 유형(모든 비음성, 적어도 하나 이상 0)인지 또는 무기한 유형(기타)인지를 결정한다. 무기한 유형은 쌍곡선 및 기타 Coxeter 그룹으로 더 세분되는 경우가 있다. 그러나 쌍곡선 Coxeter 그룹에 대해서는 여러 개의 비등호적 정의가 있다. 우리는 다음과 같은 정의를 사용한다: 연결된 도표를 가진 Coxeter 그룹은 그것이 유한하지 않거나 아핀 타입이 아니라면 쌍곡이지만, 모든 적절한 연결 서브 다이어그램은 유한하거나 아핀 타입이다. 쌍곡선 Coxeter 그룹은 모든 부분군이 유한할 경우(즉, 양의 결정 인자가 있음), 모든 부분군이 유한할 경우(즉, 음의 결정 인자가 아닌 경우) 소형이다.

유한집단과 아핀집단을 각각 타원형, 포물선형이라고도 한다. 쌍곡 그룹은 F의 이름을 따서 Lannér라고도 불린다. 1950년에 콤팩트한 쌍곡선 집단을 열거한 란네르와 파라콤팩트 집단을 위한 코스줄(또는 준란레르)이 있다.^[3]

순위 2 Coxeter 그룹

순위 2의 경우, Coxeter 그룹의 유형은 단순히 고유값의 산물이기 때문에 Schléfli 행렬의 결정요인에 의해 완전히 결정된다. 유한형(양성 결정인자), 아핀형(영(0) 또는 쌍곡선(음성 결정인자) Coxeter는 노드 브랜치 그래픽 다이어그램의 대체물로 분기 주문의 순서를 나열하는 등가 괄호 표기법을 사용한다. gcd(p,q)=1과 함께 합리적인 솔루션 [p/q]도 존재하는데, 이 솔루션은 중복되는 기본 도메인을 정의한다. 예를 들어 3/2, 4/3, 5/2, 5/3, 5/4 및 6/5.

유형	유한한					아핀	쌍곡선
기하학					...
콕시터	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
주문	2	4	6	8	2p	∞
미러 라인은 Coxeter 다이어그램 노드에 대응하도록 색상이 지정된다. 기본 도메인은 교대로 색칠된다.

순위 2 Coxeter 그룹도
주문 p	그룹	콕시터 다이어그램		슐레플리 행렬
				${\displaystyle \left[{\displaysty}2&a_{12}\\a_{21}&2\end{message}\right]}}$	결정인자 (4-a21*a12)
유한(결정)0
2	I2(2) = A1xA1		[2]	${\displaystyle \left[{\put{smallmatrix}2&0\0&2\end{smallmatrix}\오른쪽]}$	4
3	I2(3) = A2		[3]	${\displaystyle \left[{\\\smallmatrix}2&-1\-1&2\end{smallmatrix}\오른쪽]}$	3
3/2			[3/2]	${\displaystyle \left[{\\smallmatrix}2&1\1&2\end{smallmatrix}\오른쪽]}$
4	I2(4) = B2		[4]	${\displaystyle \left[{\\put{smallmatrix}2&-{\sqrt{2}&end{smallmatrix}\right]}}$	2
4/3			[4/3]	${\displaystyle \left[{\put{smallmatrix}2&#{\sqrt{2}}&end{smallmatrix}\right]}}$
5	I2(5) = H2		[5]	${\displaystyle \left[{\\physmatrix}2&-\phi \\\\end{smallmatrix}\오른쪽]}$	${\displaystyle(5-{\sqrt{5}})/2}$ ~1.38196601125
5/4			[5/4]	${\displaystyle \left[{\\smallmatrix}2&\phi \\\\end{smallmatrix}\오른쪽]}$
5/2			[5/2]	${\displaystyle \left[{\phod{smallmatrix}2-\phi \\\1-\phi &2\end{smallmatrix}\오른쪽]}$	${\displaystyle(5+{\sqrt{5}})/2}$ ~3.61803398875
5/3			[5/3]	${\displaystyle \left[{\\\smallmatrix}2&\phi -1\\\\phi -1&2\end{smallmatrix}\right]}$
6	I2(6) = G2		[6]	${\displaystyle \left[{\\put{smallmatrix}2&-{\sqrt{3}\\nd{smallmatrix}\right]}}$	1
6/5			[6/5]	${\displaystyle \left[{\\put{smallmatrix}2&{\sqrt{3}\}\\\\sqrt{3}&end{smallmatrix}\오른쪽]}$
8	I2(8)		[8]	${\displaystyle \left[{\\smallmatrix}2&-{\sqrt{2+{\sqrt{2}}~{\sqrt{2}}}\\\sqrt{2}}}}$	${\displaystyle 2-{\sqrt{2}}$ ~0.58578643763
10	I2(10)		[10]	${\displaystyle \left[{\\smallmatrix}2&-{\sqrt{5}}/2}}:\-{\sqrt{5}}}{5+{\sqrt{5}}}/2}{smallmatrix}\right]}$	${\displaystyle(3-{\sqrt{5}})/2}$ ~0.38196601125
12	I2(12)		[12]	${\displaystyle \left[{\\smallmatrix}2&-{\sqrt {2+{\sqrt{3}}\\\\sqrt{3}}}{\sqrt{3}}}}}}$	${\displaystyle 2-{\sqrt{3}}$ ~0.26794919243
p	아이2(p)		[p]	${\displaystyle \left[{\\pi}2\cos(\pi /p)\2\cos(\pi /p)&2\end{smallmatrix}\right]}}$	${\displaystyle 4\sin ^{2}(\pi /p)}$
아핀 (결정=0)
∞	I2(∞) = $I{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$} $$= $A{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$}}		[∞]	${\displaystyle \left[{\\\smallmatrix}2&-2\\-2\end{smallmatrix}\오른쪽]}$	0
쌍곡선(Decminantant0)
∞			[∞]	${\displaystyle \left[{\\\smallmatrix}2&-2\\-2\end{smallmatrix}\오른쪽]}$	0
∞			[iπ/λ]	${\displaystyle \left[{\\smallmatrix}2&-2cosh(2\smallda )\\\2cosh(2\smallda )&2\end{smallmatrix}\right]}}$	${\displaystyle -4\sinh ^{2}(2\buffda )\leq 0}$

기하학적 시각화

Coxeter-Dynkin 도표는 거울의 기본 영역에 대한 그래픽 설명으로 볼 수 있다. 거울은 주어진 치수 구형 또는 유클리드 또는 쌍곡선 공간 내의 하이퍼플레인이다. (2D 공간에서는 거울이 선이고, 3D 공간에서는 거울이 평면이다.)

이러한 시각화는 2D 및 3D 유클리드 그룹과 2D 구형 그룹에 대한 기본 도메인을 보여준다. 각 Coxeter 다이어그램은 90도 분음각(주문 2)을 무시한 채 하이퍼플레인 미러를 식별하고 연결 라벨을 표시하여 추론할 수 있다.

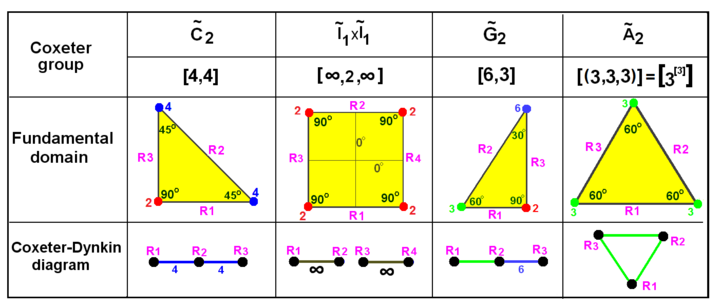등가 도표를 사용하여 유클리드 평면에서 콕시터를 그룹화한다. 반사는 그래프 노드 R1, R2 등으로 표시되며 반사 순서에 따라 색상이 지정된다. 90도에서의 반사는 비활성화되고 따라서 도표에서 억제된다. 평행 미러는 나뭇가지로 표시된 ∞로 연결된다. The prismatic group ${\displaystyle {\tilde {I}}_{1}}$x${\displaystyle {\tilde {I}}_{1}}$ is shown as a doubling of the ${\displaystyle {\tilde {C}}_{2}}$, but can also be created as rectangular domains from doubling the ${\displaystyle {\tilde {G}}_{2}}$ triangles. ${\displaystyle A_{\mathrm{}}}$~ 2 ${\$}}은 $G{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}개의$$ 삼각형을 곱한 것이다$$.
쌍곡선의 많은 Coxeter 그룹은 일련의 쌍곡선 해결책으로 유클리드 사례에서 확장될 수 있다.
3-공간에서 다이어그램과 함께 콕시터를 그룹화하십시오. 미러(삼각면)는 반대쪽 꼭지점 0..3으로 라벨이 표시된다. 나뭇가지들은 반사 순서에 따라 색을 입힌다. ${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ 큐브의 1/48을 채운다$$. $B$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ 큐브의 1/24를 채운다$$. ${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ 큐브의 1/12을 채운다$$.	구에서 등가 다이어그램으로 콕시터를 그룹화한다. 하나의 기본적인 영역은 노란색으로 윤곽이 드러나 있다. 도메인 정점(및 그래프 분지)은 반사 순서에 따라 색상이 지정된다.

유한 콕시터 군

이러한 그룹과 연관된 엔드 노드 균일한 폴리토페 표에 대한 폴리토페 패밀리를 참조하십시오.

• 동일한 그룹에 대해 세 개의 다른 기호가 주어진다. 문자/숫자로, 괄호로 묶인 숫자 집합으로, 그리고 Coxeter 도표로.
• 두 갈래로 갈라진 D_n 그룹은 일반 C_n 그룹의 절반 또는 대체 버전이다.
• 두 갈래로 갈라진 D와_n E_n 그룹도 위첨자 양식[3^a,b,c]으로 라벨을 붙인다. 여기서 a,b,c는 세 가지 분기의 각 분기의 세그먼트 수입니다.

연결된 유한 Coxeter-Dynkin 다이어그램(1~9위)

순위	단순 리 그룹			예외적인 Lie
	${\displaystyle {A}_{1+}}$	${\displaystyle {B}_{2+}}$	${\displaystyle {D}_{2+}}$	${\displaystyle {E}_{3-8}}$	${\displaystyle {F}_{3-4}}$	${\displaystyle {G}_{2}}$	${\displaystyle {H}_{2-4}}$	${\displaystyle {I}_{2}(p)}$
1	A1=[ ]
2	A2=[3]	B2=[4]	D2=A1A1			G2=[6]	H2=[5]	I2[p]
3	A3=[32]	B3=[3,4]	D3=A3	E3=A2A1	F3=B3		H3
4	A4=[33]	B4=[32,4]	D4=[31,1,1]	E4=A4	F4		H4
5	A5=[34]	B5=[33,4]	D5=[32,1,1]	E5=D5
6	A6=[35]	B6=[34,4]	D6=[33,1,1]	E6=[32,2,1]
7	A7=[36]	B7=[35,4]	D7=[34,1,1]	E7=[33,2,1]
8	A8=[37]	B8=[36,4]	D8=[35,1,1]	E8=[34,2,1]
9	A9=[38]	B9=[37,4]	D9=[36,1,1]
10+	..	..	..	..

균일한 폴리에스테르를 가진 어플리케이션

균일한 폴리토페스를 구성할 때, 발전기 포인트가 미러에서 벗어나면 노드가 링에 의해 활성으로 표시되어 발전기 포인트와 미러 이미지 사이에 새 에지를 만든다. 링이 없는 노드는 새로운 점을 생성하지 않는 비활성 미러를 나타낸다. 노드가 없는 고리를 구멍이라고 한다.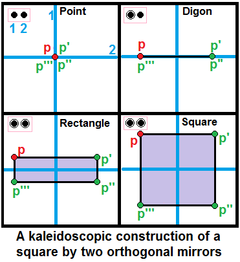

직교 미러 2개를 사용하여 사각형을 생성할 수 있으며, 여기에는 빨간색 제너레이터 포인트와 미러에 걸쳐 3개의 가상 복사본이 표시된다. 내부를 생성하려면 이 직교 케이스의 양쪽 미러에서 제너레이터를 꺼야 한다. 링 마크업은 활성 링에 모든 미러로부터 동일한 거리에 발전기가 있다고 가정하는 반면 사각형은 균일하지 않은 용액을 나타낼 수 있다.

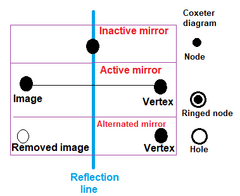
Coxeter-Dynkin 도표는 거의 모든 종류의 균일한 폴리토페와 균일한 테셀레이션을 명시적으로 열거할 수 있다. 순수 반사 대칭이 있는 모든 균일한 폴리토프(특수 사례를 제외하고 모두 순수한 반사 대칭을 가지고 있음)는 마크업 순열이 있는 Coxeter-Dynkin 도표로 나타낼 수 있다. 각각의 균일한 폴리토프는 그러한 미러와 단일 발생기 지점을 사용하여 생성될 수 있다: 미러 이미지는 반사로서 새로운 점을 생성하고, 그 다음 포인트와 미러 이미지 포인트 사이에 폴리토프 가장자리를 정의할 수 있다. 얼굴은 결국 원래의 발생기로 감싸는 가장자리의 반복적인 반사에 의해 생성된다. 최종 모양뿐만 아니라 고차원적인 면도 영역을 둘러싸기 위해 반사되는 얼굴에 의해 생성된다.

생성 정점을 지정하려면 하나 이상의 노드에 링이 표시되는데, 이는 링이 링이 있는 노드로 표시되는 미러에 정점이 없음을 의미한다. (두 개 이상의 거울이 표시된 경우, 꼭지점이 거울과 등거리인 경우) 거울은 거울 위에 있지 않은 점에 대해서만 활성(반사를 생성)한다. 다이어그램에는 폴리토프를 나타내려면 적어도 하나의 활성 노드가 필요하다. 연결되지 않은 다이어그램(주문-2 분기 또는 직교 미러로 구분된 하위 그룹)은 각 하위 그래프에 하나 이상의 활성 노드를 필요로 한다.

Schléfli 기호 {p, q, r, ...}로 대표되는 모든 일반 폴리토페는 첫 번째 노드가 링으로 된 상태에서 p, q, r, ...로 라벨을 붙인 노드와 가지 라인의 관련 Coxeter-Dynkin 도표를 가진 n 미러 집합으로 대표되는 기본 도메인을 가질 수 있다.

하나의 링을 가진 균일한 폴리토프는 기본 도메인 심플렉스 모서리의 발생기 점에 해당한다. 두 개의 링은 심플렉스 가장자리와 일치하며 자유도를 가지며, 가장자리 길이가 같은 경우 중간점만 균일한 솔루션으로 한다. 일반적으로 simplx의 (k-1)-faces는 simplx의 (k-1)-faces이며, 모든 노드가 ring되면 발전기 지점은 simplx 내부에 있다.

비반사 대칭이 있는 균일한 폴리탑의 특별한 경우는 링이 달린 노드의 중심점이 제거되는 2차 마크업(구멍이라고 함)으로 표현된다. 이러한 모양은 반사 대칭이 있는 폴리탑의 교대로, 다른 모든 꼭지점이 삭제됨을 의미한다. 그 결과 폴리토프는 원래의 Coxeter 그룹의 대칭성을 가질 것이다. 잘린 교대체를 스너브라고 한다.

• 단일 노드는 단일 거울을 나타낸다. 이것을₁ A그룹이라고 한다. 링이 연결된 경우 이는 미러에 수직인 선 세그먼트를 생성하며, {}(으)로 표시됨).
• 연결되지 않은 두 개의 노드는 두 개의 수직 미러를 나타낸다. 두 개의 노드가 모두 링으로 되어 있으면 직사각형을 만들 수 있고, 두 개의 미러로부터 동일한 거리에 점이 있을 경우 사각형을 만들 수 있다.
• 오더-n 분기에 의해 부착된 두 개의 노드는 포인트가 하나의 미러에 있는 경우 n-곤을 생성하고 포인트가 양쪽 미러에서 벗어난 경우 2n-곤을 생성할 수 있다. 이것은₁ I(n) 그룹을 형성한다.
• 두 개의 평행 미러는 ĩ라고도₁ 하는₁ 무한 폴리곤 I(∞) 그룹을 나타낼 수 있다.
• 삼각형의 세 개의 거울은 전통적인 칼리디스코프에서 보이는 이미지를 형성하며 세 개의 노드가 삼각형으로 연결되어 표현될 수 있다. 반복적인 예에는 (3 3 3 3), (2 4 4), (2 3 6)라는 라벨이 붙지만, 마지막 두 가지는 선으로 그릴 수 있다(두 가지 가지는 무시함). 이것들은 균일한 기울기를 발생시킬 것이다.
• 3개의 거울은 균일한 다면체를 생성할 수 있다; 합리적인 숫자를 포함하여 슈바르츠 삼각형 세트를 제공한다.
• 한 거울이 다른 거울과 수직인 거울 세 개는 균일한 프리즘을 형성할 수 있다.

기본 영역 내의 7개의 위상학적 발생기 위치에 기초하여 일반 삼각형 내에 7개의 반사 균일 구조가 있다. 모든 활성 거울은 가장자리를 생성하며, 두 개의 활성 미러에는 도메인 측에 생성기가 있고 세 개의 활성 미러에는 내부에 생성기가 있다. 결과 다면체 또는 타일링의 동일한 가장자리 길이에 대한 고유한 위치에 대해 1, 2도의 자유도를 해결할 수 있다.

예제 7개의 8번째 스너브 생성기를 교대로 사용하여 8번째 스너브 생성, 8번째 영역 대칭, 기본 영역 대칭에 대한 생성기

균일한 폴리탑의 이중은 링 노드를 대체하는 수직 슬래시와 스너브의 구멍 노드에 대한 슬래시 구멍으로 표시되기도 한다. 예를 들어, 직사각형(활성 직교 미러 두 개)을 나타내며, 이중 폴리곤인 Rhombus를 나타낸다.

다면체 및 기울기 예제

예를 들어 B₃ Coxeter 그룹에는 다음과 같은 다이어그램이 있다. 이것을 팔면대칭이라고도 한다.

이 대칭 그룹에서 구성할 수 있는 7개의 볼록한 균일한 폴리헤드라와 교대칭 하위대칭에서 3개가 있으며, 각각 Coxeter-Dynkin 도표로 고유하게 표시된다. 와이트오프 기호는 순위 2 지사를 억제하지 않고 3가지 지령 모두 이름을 붙인 순위 3 그래프에 대한 Coxeter 다이어그램의 특별한 경우를 나타낸다. Wythoff 기호는 스너브 폼을 처리할 수 있지만 모든 노드가 울리지 않으면 일반적인 교대형을 처리할 수 없다.

균일한 팔면체 다면체
대칭: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= 또는	= 또는	=
이중에서 균일한 폴리헤드라까지
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

동일한 구조는 균일한 프리즘과 같이 분리(직교) Coxeter 그룹에서도 만들어질 수 있으며, 구에 있는 디히드론과 호소헤드론의 기울임으로 보다 명확하게 볼 수 있다(이 [6]×[] 또는 [6,2] 계열:

균일한 육각형 이면구형 다면체
대칭: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
듀얼 투 유니폼
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

이에 비해 [6,3] 계열은 유클리드 평면의 7개의 균일한 기울기와 이중 기울기의 병렬 세트를 생산한다. 다시 3번의 교대조화와 일부 반대칭 버전이 있다.

균일한 육각/삼각형 틸팅 v t
대칭: [6,3], (*632)							[6,3]+ (632)	[6,3+] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}
63	3.122	(3.6)2	6.6.6	36	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
균일 듀얼
V63	V3.122	V(3.6)2	V63	V36	V3.4.6.4	V.4.6.12	V34.6	V36

쌍곡선 평면[7,3]에서 패밀리는 균일한 기울기와 이중 기울기의 병렬 세트를 생산한다. 모든 분기 주문이 홀수여서 교대(스너브)가 1개뿐입니다. 많은 다른 균일한 기울기의 쌍곡선 가족은 쌍곡선의 균일한 기울기에서 볼 수 있다.

균일한 헵탄/삼각형 틸팅 v t
대칭: [7,3], (*732)							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
균일 듀얼
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

아핀 콕시터 그룹

볼록한 제복 유클리드 테셀레이션의 가족은 아핀 콕시터 그룹에 의해 정의된다. 이 그룹들은 하나의 추가된 노드를 포함하는 유한 그룹과 동일하다. 편지 이름에서 그들은 편지 위에 "~"와 같은 문자를 받는다. 지수는 유한집단을 가리키므로 순위는 지수 플러스 1. (어네스트 위트(Ernst Witt) 기호는 어네스티네 그룹에 대해서도 다음과 같이 주어진다.)

1. ${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle n_{}}$- ${\displaystyle 1_{}}$ ${\$: 이런 유형의 다이어그램은 사이클이다. (또한_n P)
2. ${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle n_{}}$- ${\displaystyle 1_{}}$ ${\$}은$($는) 하이퍼큐브 정규 테셀레이션 {4, 3, ...., 4} 계열과 연관되어 있다$$. (또한_n R)
3. ${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle n_{}}$- ${\displaystyle 1_{}}$ ${\$ 거울 1개를 제거하여 C와 관련된$$ (또한_n S)
4. ${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle n_{}}$- ${\displaystyle 1_{}}$ ${\$두 개의 제거된 거울에 의해 C와 관련됨$$. (또한 Q_n)
5. ${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${{\$ ${\displaystyle E_{\mathrm{}}}$~ 7 ${\$${\displaystyle {\stackrel{}{}}_{}}E{\displaystyle {\stackrel{}{}}_{}}$ ~ ${\displaystyle 8_{\mathrm{}}}$ ${\$ (또한₇ T, T₈₉)
6. ${\displaystyle {\stackrel{}{F}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$은(는) {3,4,3,3}의 정기 테셀레이션을 형성한다$$. (또한₅ U)
7. ${\displaystyle {\stackrel{}{G}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}: 30-60-90 삼각형 기본 도메인을 형성한다$$. (또한₃ V)
8. ${\displaystyle {\stackrel{}{I}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$}는 두 개의 평행 거울이다$$. ( = $A{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$= $C{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$ (또₂ W)

복합 그룹은 직교 프로젝트로도 정의될 수 있다. $A{\displaystyle {\stackrel{}{}}_{}}$${\displaystyle {\stackrel{}{}}_{}^{}}$~ ${\displaystyle 1_{\mathrm{}}^{}}$ ${\$$displaystyle$ ${\$$tilde{A}_{1}^{2}}$과$$${\displaystyle {\mathrm{}}_{}^{}}$ 가장 많이 사용되는 용도는 유클리드 평면의 사각형 또는 직사각형 체커 보드 도메인을 나타낸다$.$ 그리고 $A{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\displaystyle {}_{}{\stackrel{}{}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}은 유클리드 3공간에 있는 삼각 프리즘 기본 영역을 나타낸다$$.

최대 (2~10개 노드)의 Affine Coxeter 그래프

순위	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$+ ${\$P2+)$$	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$+ ${\$S4+)	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$+ ${\$R2+)	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$+ ${\$4+}}($$Q5+)	${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle n_{}}$ ${\displaystyle {{E}_{n}}($Tn+1) / F${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$${\displaystyle U_{}}$5) / G$$~ 2 {\$displaystyle {\tilde{G}}_{2$}}($$V3)
2	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$} = [filename]$$		${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 1_{\mathrm{}}}$ ${\$} = [filename]$$
3	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}} $=[$3[3]] *		${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}} = $$[4,4] *		${\displaystyle {\stackrel{}{G}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}} = $$[6,3] *
4	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ =[$$3[4]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ =[$$4,31,1] *	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ =[$$4,3,4] *	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = $$[31,1,3−1,31,1] = $A{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$
5	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ =[$$3[5]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ =[$$4,3,31,1] *	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ =[$$4,32,4] *	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ = $$[31,1,1,1] *	${\displaystyle {\stackrel{}{F}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ =[$$3,4,3,3] *
6	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ =[$$3[6]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ =[$$4,32,31,1] *	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ =[$$4,33,4] *	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$ = $$[31,1,3,31,1] *
7	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ =[$$3[7]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ =[$$4,33,31,1]	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ =[$$4,34,4]	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ = $$[31,1,32,31,1]	${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ =[$$32,2,2]
8	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$ =[$$3[8]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$ = $$[4,34,31,1] *	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$ = [$$4,35,4]	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$ = $$[31,1,33,31,1] *	${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$ =[$$33,3,1] *
9	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 8_{\mathrm{}}}$ ${\$ =[$$3[9]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 8_{\mathrm{}}}$ ${\$ =[$$4,35,31,1]	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 8_{\mathrm{}}}$ ${\$ = $$[4,36,4]	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 8_{\mathrm{}}}$ ${\$ = $$[31,1,34,31,1]	${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle 8_{\mathrm{}}}$ ${\$ =[$$35,2,1] *
10	${\displaystyle {\stackrel{}{A}}_{}}$~ ${\displaystyle 9_{\mathrm{}}}$ ${\$ =[$$3[10]] *	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 9_{\mathrm{}}}$ ${\$ =[$$4,36,31,1]	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 9_{\mathrm{}}}$ ${\$ =[$$4,37,4]	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 9_{\mathrm{}}}$ ${\$ = $$[31,1,35,31,1]
11	...	...	...	...

쌍곡선 Coxeter 그룹

무한 쌍곡선 콕시터 그룹이 많다. 쌍곡선 그룹은 컴팩트 또는 그렇지 않은 그룹으로 분류되며, 컴팩트 그룹은 기본 도메인을 경계로 한다. 콤팩트한 심플렉스 쌍곡선 그룹(Lannér 단순화)이 3~5위로 존재한다. 파라콤팩트 심플렉스 그룹(Koszul simples)이 10위까지 존재한다. 하이퍼콤팩트(Vinberg polytopes) 그룹은 탐색되었지만 완전히 파악되지는 않았다. 2006년에 올콕은 최대 6까지 치수에 대한 소형 빈버그 폴리토페스가 무한히 많고, 최대 19까지 치수에 대한 유한 볼륨 빈버그 폴리토페스가 무한히 많음을 증명하여 완전한 열거는 불가능하다.^[4] 이러한 모든 기본 반사 영역, 즉 단순과 비반사 영역은 종종 Coxeter polytopes 또는 때로는 덜 정확하게 Coxeter polyhedra라고 불린다.

H의² 쌍곡선 그룹

기본 도메인 삼각형의 푸앵카레 디스크 모델

오른쪽 삼각형 예제 [p,q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
일반 삼각형 예제 [(p,q,r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

2차원 쌍곡선 삼각형 그룹은 순위 3 Coxeter 다이어그램으로 존재하며, 다음과 같은 경우 삼각형(p q r)으로 정의된다.

${\displaystyle {\frac {1}{p1}+{\frac {1}{q}+{\frac {1}{r}}<1.}$

선형 및 삼각형 그래프를 포함하여 매우 많은 소형 삼각형 쌍곡선 Coxeter 그룹이 있다. 선형 그래프는 직삼각형(r=2)에 대해 존재한다.^[5]

콤팩트 쌍곡선 Coxeter 그룹

선형	주기적
∞ [p,q], : 2(p+q)<pq ... ... ...	∞ [(p,q,r)], : p+q+r>9 ...

3등급의 파라콤팩트 콕시터 그룹은 소형 그룹의 한계로 존재한다.

선형 그래프	순환 그래프
[p,pi] [∞,∞]	[(p,q,cs)] [(p,p,page,properties)] [(∞,∞,∞)]

산술삼각형군

또한 산술 그룹인 쌍곡 삼각형 그룹은 유한 부분 집합을 형성한다. 컴퓨터 검색에 의해 전체 목록은 키사오 타케우치가 1977년 발표한 논문 '산술 삼각형'에서 정했다.^[6] 총 85개, 콤팩트 76개, 파라콤팩트 9개가 있다.

오른쪽 삼각형(p q 2)	일반 삼각형(p q r)
콤팩트 그룹: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 파라콤팩트 오른쪽 삼각형: (4) , , ,	일반 삼각형: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , 파라콤팩트 일반 삼각형: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), (2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

삼각형 위의 쌍곡선 코엑스미터 다각형

4각형 그룹의 기본 영역

또는 [∞,3,∞] [iπ/λ1,3,iπ/λ2] (*3222)	또는 [((3,∞,3)),∞] [(3,iπ/iλ1,3),iπ/iλ2] (*3322)	또는 [(3,∞)[2]] [(3,iπ/iλ1,3,i//iλ2) (*3232)	또는 [(4,∞)[2]] [(4,iπ/iλ1,4,iπ/iλ2)] (*4242)	(*3333)
이상적인 정점을 가진 도메인
[iπ/λ1,∞,iπ/λ2] (*∞222)	(*∞∞22)	[(iπ/λ1,∞,i,iπ/λ2,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

다른 H² 쌍곡선 케일리디스코어는 고차 다각형으로 제작할 수 있다. 삼각형 그룹과 마찬가지로 이 케일리디스코어들은 (b cd ...)로 기본 영역 주위의 거울 교차로 순서의 주기적 순서에 의해 식별될 수 있으며, 또는 *abcd....로 오비폴드 표기법에서 동등하게 구별될 수 있다. 이러한 다각측량경의 Coxeter-Dynkin 도표는 퇴행(n-1)-단순(simplex) 기본 영역으로 볼 수 있으며, 가지들의 주기적인 순서는 a,b,c...이고, 나머지 n*(n-3)/2가지 분기는 비절연 거울을 나타내는 무한(infinite)으로 표시된다. 유일한 비유동적 예로는, 유클리드 대칭 4개의 거울을 정사각형이나 직사각형으로, , [∞, 2, or] (orbifold *222)로 한다. 빈버그가 비절개 미러에 대해 표현한 또 다른 분기는 점선 또는 점선으로 무한 분기를 표시하므로, 이 도표는 둘레 주위에서 4개의 순서-2 분기를 억제하여 로 표시할 수 있다.

예를 들어, 사각형 영역(a b c d)은 초경량 미러를 연결하는 두 개의 무한 순서 분기를 가질 것이다. 가장 작은 쌍곡선 예로는 , [ ,,3,∞] 또는 [iπ/λ₁,3,iπ/λ₂](orbifold *3222)이며, 여기서 (λ₁₂,))는 초경사울 거울 사이의 거리이다. 대체 표현식은 , 둘레 주위에서 3개의 순서-2 분기가 억제되어 있다. 이와 유사하게 (2 3 2 3) (또는 생물체 *322)는 (3 3 3 3 3)으로 나타낼 수 있고, (또는 생물체 *3333)는 완전한 그래프로 나타낼 수 있다.

가장 높은 사각형 영역(∞ quad ∞ is)은 무한 사각형이며, 초경사선 미러에 대해 4개의 주변 분기를 이상적인 정점으로 하고 2개의 대각선 분기를 무한(점선으로 표시)으로 하는 완전한 사면 그래프로 표현된다.

소형(Lannér simplex 그룹)

콤팩트한 쌍곡선 집단은 1950년 처음 연구한 폴케 란네르(Folke Lannér)의 이름을 따서 란네르(Lannér) 집단으로 불린다.^[7] 그것들은 4위와 5위 그래프로만 존재한다. Coxeter는 1954년 논문 Regular Honeycombs in performbolic space에서 선형 쌍곡선 쌍곡선 응축기 그룹을 연구했는데,^[8] 여기에는 쌍곡선 4공간에 [5/2,5,3,3] = [5,5/2,3,3] = .

4~5위

두 개의 분기 그룹 중 하나인 [5^1,1,3]과 [5,3,3^1,1]의 기본 영역은 각각 [5,3,4]와 [5,3,4]의 두 배다. 편지 이름은 Johnson에 의해 확장된 Witt 기호로 주어진다.^[9]

콤팩트 쌍곡선 Coxeter 그룹

치수 Hd	순위	총계수	선형	분기화	주기적
H3	4	9	3: ${\$$$$H}_{3}}$ = [4,3,5]: ${\displaystyle {\stackrel{\text{'}}{K}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [5,3,5]: ${\displaystyle {\stackrel{\text{'}\text{'}}{J}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [3,5,3]:	${\displaystyle {\stackrel{}{D}}_{}}$의 ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [5,31,1]:	${\displaystyle {\stackrel{}{A}}_{}}$ ${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [(33,4)]: ${\displaystyle {\stackrel{}{A}}_{}}$ ${\displaystyle {\stackrel{}{H}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [(33,5)]: ${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [(3,4)]:[2] ${\$$H}_{3}}$ = [(3,4,3,5)]: ${\$$$$HH}_{3}}$ $$= [(3,5)]:[2]
H4	5	5	3: ${\displaystyle {\stackrel{}{}H}_{\mathrm{}}}$ 4 ${\$ $$= [33,5]: ${\$$H}}_{4}}$ = [4,3,3,5]: ${\displaystyle {\stackrel{}{}K}_{\mathrm{}}}$ 4 ${\$ $$= [5,3,3,5]:	${\displaystyle {\stackrel{}{D}}_{}}$ ${\displaystyle {\stackrel{}{H}4}_{\mathrm{}}}$ ${\$ = [5,3,31,1]:	${\displaystyle {\stackrel{}{A}}_{}}$ ${\displaystyle {\stackrel{}{F}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $$= [(34,4)]:

파라콤팩트(Koszul simplex 그룹)

파라콤팩트(비컴팩트라고도 함) 쌍곡선 Coxeter 그룹은 아핀 하위 그룹을 포함하고 있으며 점근성 단순 도메인을 가지고 있다. 가장 높은 파라콤팩트 쌍곡선 Coxeter 그룹은 10위다. 이 그룹들은 프랑스의 수학자 장 루이 코즐의 이름을 따서 지어졌다.^[10] 콤팩트한 란네르 그룹을 확장하는 준란네르 그룹이라고도 한다. 그 목록은 M에 의한 컴퓨터 검색에 의해 완전하게 결정되었다. Chein 그리고 1969년에 출판되었다.^[11]

빈버그에 따르면, 이 72개의 콤팩트하고 파라콤팩트 단순화 중 8개를 제외한 모든 것이 산술적이다. 비산술 그룹 중 두 개는 소형이다: 및 . 나머지 6개의 비산술 그룹은 모두 파라콤팩트인데, 5개의 3차원 그룹 , , , , , , 그리고 1개의 5차원 그룹이 있다.

이상적인 단순화

이상적인 단순성을 표현하는 5개의 쌍곡선 Coxeter 그룹이 있는데, 그래프는 하나의 노드를 제거하면 해당 Coxeter 그룹이 된다. 따라서 이 이상적인 심플렉스의 모든 정점은 무한대에 있다.^[12]

순위	이상군		아핀 부분군
3	[(∞,∞,∞)]		[∞]
4	[4[4]]		[4,4]
4	[3[3,3]]		[3[3]]
4	[(3,6)[2]]		[3,6]
6	[(3,3,4)[2]]		[4,3,3,4], [3,4,3,3]	,

4-10위

4위부터 10위까지 총 58개의 파라콤팩트 쌍곡선 Coxeter 그룹이 있다. 58개 모두 아래 5개 범주로 분류된다. 문자 기호는 Johnson에 의해 확장 Witt 기호로 주어지며, 첨부된 Witt 기호의 PQFIRSTWUV를 사용하고, LMNOXYZ를 추가한다. 이러한 쌍곡선 그룹에는 사이클로셰프를 위한 오버라인, 즉 모자가 주어진다. Coxeter의 괄호 표기법은 Coxeter 그룹의 선형화된 표현이다.

쌍곡선 포물선 그룹

순위	총계수	무리
4	23	${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{R}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [(3,3,4,4)]: ${\displaystyle {\stackrel{}{C}}_{}}$ ${\displaystyle {\stackrel{}{R}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [(3,43)]: ${\displaystyle {\stackrel{}{R}}_{}}$ ${\displaystyle {\stackrel{}{R}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [4[4]]: ${\displaystyle {\stackrel{}{A}}_{}}$ ${\displaystyle {\stackrel{}{V}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ = [(33,6)]: ${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{V}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [(3,4,3,6)]: ${\displaystyle {\stackrel{}{H}}_{}}$ ${\displaystyle {\stackrel{}{V}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\${HV$}_{3}}$ $$= [(3,5,3,6)]: ${\displaystyle {\stackrel{}{V}}_{}}$ ${\displaystyle {\stackrel{}{V}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [(3,6)]:[2]	${\displaystyle {\stackrel{}{}P}_{\mathrm{}}}$ 3 ${\$ $$= [3,3[3]]: ${\displaystyle {\stackrel{}{B}}_{}}$ ${\$ = [4,3[3]]: ${\displaystyle {\stackrel{}{H}}_{}}$ ${\displaystyle {\stackrel{}{P}3}_{\mathrm{}}}$ 3 ${\$HP$}_{3}}$ = [5,3[3]]: ${\displaystyle {\stackrel{}{V}}_{}}$ ${\displaystyle {\stackrel{}{P}}_{}}$} ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [6,3[3]]: ${\displaystyle {\stackrel{}{D}}_{}}$ ${\displaystyle {\stackrel{}{V}3}_{\mathrm{}}}$ 3 ${\$ $$= [6,31,1]: ${\displaystyle {\stackrel{}{}O}_{\mathrm{}}}$ 3 ${\$ = [3,41,1]: ${\displaystyle {\stackrel{\text{'}}{M}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [41,1,1]:	${\displaystyle {\stackrel{}{}R}_{\mathrm{}}}$ 3 ${\$ $$= [3,4,4]: ${\displaystyle {\stackrel{}{}N}_{\mathrm{}}}$ 3 ${\$ = [43]: ${\displaystyle {\stackrel{}{V}}_{}}$의${\$ $$= [3,3,6]: ${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{V}3}_{\mathrm{}}}$ 3${\$BV$}_{3$}} $$= [4,3,6]: ${\displaystyle {\stackrel{}{H}}_{}}$ ${\displaystyle {\stackrel{}{V}3}_{\mathrm{}}}$ 3 ${\$HV$}_{3}}$ $$= [5,3,6]: ${\displaystyle {\stackrel{\text{'}\text{'}}{Y}}_{}}$ ${\displaystyle 3_{\mathrm{}}}$ ${\$ $$= [3,6,3]: ${\$ = [6,3,6]:	${\displaystyle {\stackrel{}{D}}_{}}$ ${\displaystyle {\stackrel{}{P}3}_{\mathrm{}}}$ 3 ${\$ = [3[]x[]]: ${\displaystyle {\stackrel{}{P}}_{}}$ ${\displaystyle {\stackrel{}{P}3}_{\mathrm{}}}$ 3${\$ = [3[3,3]]:
5	9	${\displaystyle {\stackrel{}{}P}_{\mathrm{}}}$ 4 ${\$ $$= [3,3[4]]: ${\displaystyle {\stackrel{}{B}}_{}}$ ${\displaystyle {\stackrel{}{P}}_{}}$ ${\$ $$= [4,3[4]]: ${\displaystyle {\stackrel{}{F}}_{}}$ ${\displaystyle {\stackrel{}{R}}_{}}$ ${\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $$= [(3,42,3,4)]: ${\displaystyle {\stackrel{}{D}}_{}}$ ${\displaystyle {\stackrel{}{P}4}_{\mathrm{}}}$ 4 ${\$ $$= [3[3]x[]]:	${\displaystyle {\stackrel{}{}N}_{\mathrm{}}}$ 4 ${\$ $$= [4,3, (4,2,3)]: ${\displaystyle {\stackrel{}{}O}_{\mathrm{}}}$ 4 ${\$ $$= [3,4,31,1]: ${\displaystyle {\stackrel{}{S}}_{}}$의${\$ $$= [4,32,1]:	${\displaystyle {\stackrel{}{}R}_{\mathrm{}}}$ 4 ${\$ $$= [(3,4)]:2	${\displaystyle {\stackrel{}{}M}_{\mathrm{}}}$ 4 ${\$ $$= [4,31,1,1]:
6	12	${\displaystyle {\stackrel{\text{'}}{P}5}_{\mathrm{}}}$ ${\$ $$= [3,3[5]]: ${\displaystyle {\stackrel{}{A}}_{}}$ ${\displaystyle {\stackrel{}{U}}_{}}$^ ${\displaystyle 5_{\mathrm{}}}$ ${\${\$widehat {AU}_{5}}$ = [(35,4)]: ${\displaystyle {\stackrel{}{A}}_{}}$ ${\displaystyle {\stackrel{}{R}}_{}}$ ${\displaystyle 5_{\mathrm{}}}$ ${\$ {$AR}_{5}}$ = [(3,3,4)]:[2]	${\displaystyle {\stackrel{}{S}}_{}}$의${\$ $$= [4,3,32,1]: ${\displaystyle {\stackrel{}{}O}_{\mathrm{}}}$ 5 ${\$ $$= [3,4,31,1]: ${\displaystyle {\stackrel{\text{'}}{N}5}_{\mathrm{}}}$ ${\$ = [3,(3,4)]:1,1	${\displaystyle {\stackrel{\text{'}}{U}5}_{\mathrm{}}}$ ${\$ $$= [33,4,3]: ${\displaystyle {\stackrel{\text{'}}{X}}_{}}$ ${\displaystyle 5_{\mathrm{}}}$ ${\$ $$= [3,3,4,3,3]: ${\displaystyle {\stackrel{\text{'}}{R}5}_{\mathrm{}}}$ ${\$ $$= [3,4,3,3,4]:	${\displaystyle {\stackrel{\text{'}}{Q}}_{}}$ ${\displaystyle 5_{\mathrm{}}}$ ${\$ $$= [32,1,1,1]: ${\displaystyle {\stackrel{\text{'}}{M}5}_{\mathrm{}}}$ ${\$ $$= [4,3,31,1,1]: ${\displaystyle {\stackrel{\text{'}}{L}5}_{\mathrm{}}}$ ${\$ $$= [31,1,1,1,1]:
7	3	${\displaystyle {\stackrel{\text{'}}{P}}_{}}$ ${\displaystyle 6_{\mathrm{}}}$ ${\$ $$= [3,3[6]]:	${\displaystyle {\stackrel{\text{'}}{Q}}_{}}$ ${\displaystyle 6_{\mathrm{}}}$ ${\$ $$= [31,1,3,32,1]:	${\displaystyle {\stackrel{\text{'}}{S}}_{}}$ ${\displaystyle 6_{\mathrm{}}}$ ${\$ $$= [4,32,32,1]:
8	4	${\displaystyle {\stackrel{\text{'}}{P}}_{}}$ ${\displaystyle 7_{\mathrm{}}}$ ${\$ $$= [3,3[7]]:	${\displaystyle {\stackrel{\text{'}}{Q}}_{}}$ ${\displaystyle 7_{\mathrm{}}}$ ${\$ $$= [31,1,32,32,1]:	${\displaystyle {\stackrel{}{S}}_{}}$의${\$ $$= [4,33,32,1]:	${\displaystyle {\stackrel{}{}T}_{\mathrm{}}}$ 7 ${\$ $$= [33,2,2]:
9	4	${\displaystyle {\stackrel{}{}P}_{\mathrm{}}}$ 8 ${\$ $$= [3,3[8]]:	${\displaystyle {\stackrel{\text{'}}{Q}}_{}}$ ${\displaystyle 8_{\mathrm{}}}$ ${\$ $$= [31,1,33,32,1]:	${\displaystyle {\stackrel{\text{'}}{S}}_{}}$ ${\displaystyle 8_{\mathrm{}}}$ ${\$ $$= [4,34,32,1]:	${\displaystyle {\stackrel{}{}T}_{\mathrm{}}}$ 8 ${\$ $$= [34,3,1]:
10	4	${\displaystyle {\stackrel{}{}P}_{\mathrm{}}}$ 9 ${\$ $$= [3,3[9]]:	${\displaystyle {\stackrel{\text{'}}{Q}}_{}}$ ${\displaystyle 9_{\mathrm{}}}$ ${\$ $$= [31,1,34,32,1]:	${\displaystyle {\stackrel{}{}S}_{\mathrm{}}}$ 9 ${\$ $$= [4,35,32,1]:	${\displaystyle {\stackrel{}{}T}_{\mathrm{}}}$ 9 ${\$ $$= [36,2,1]:

파라콤팩트 쌍곡선 그룹의 부분군 관계

이 나무들은 파라콤팩트 쌍곡선 그룹의 부분군 관계를 나타낸다. 각 연결에 대한 부분군 지수는 빨간색으로 표시된다.^[13] 지수 2의 하위 그룹은 미러 제거 및 기본 영역 배열을 나타낸다. 다른 것들은 사면 영역에 대한 비례성(볼륨의 정수 비율)으로 추론할 수 있다.

부분군 트리
H3
H4
H5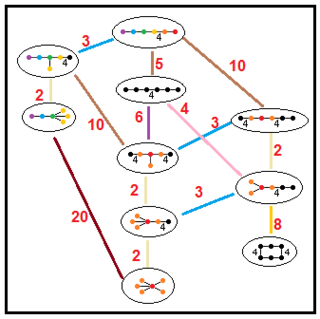

Hypercompact Coxeter 그룹(Vinberg polytopes)

쌍곡면 H가² 삼각형이 아닌 다각형 도메인을 갖는 것처럼, 고차원 반사 쌍곡선 도메인도 존재한다. 이러한 비임플렉스 영역은 무한 순서가 부여된 비 교차 미러 또는 Coxeter 다이어그램에서 그러한 분기에는 점선 또는 점선이 주어지는 퇴보적인 단순성으로 간주할 수 있다. 이러한 비임플렉스 도메인은 쌍곡 반사 그룹의 비임플렉스 기본 도메인을 찾는 어니스트 빈버그의 알고리즘을 따라 빈버그 폴리토페스라고 불린다. 기하학적으로 이러한 기본 영역은 n=2,3,4의 경우 hed/n으로 이면각을 갖는 두 거울의 교차점으로서 가장자리가 있는 4면 피라미드, 프리즘 또는 기타 폴리토페스로 분류할 수 있다.

심플렉스 기반 도메인에는 n차원 공간을 위한 n+1 거울이 있다. 단순하지 않은 도메인에는 n+1개 이상의 거울이 있다. 그 명단은 유한하지만 완전히 알려진 것은 아니다. 대신 부분 목록은 2,3,4로 k에 대한 n+k 미러로 열거되었다.

3차원 공간 이상의 하이퍼콤팩트 Coxeter 그룹은 하나의 본질적인 측면에서 2차원 그룹과 다르다. 동일한 주기적 순서로 동일한 각도를 갖는 두 쌍곡선 n-gon은 다른 가장자리 길이를 가질 수 있으며 일반적으로 일치하지는 않는다. 이와는 대조적으로 3차원 이상의 빈버그 폴리토페스는 이음각으로 완전히 결정된다. 이 사실은 n>=3에 대한ⁿ H의 반사에 의해 생성되는 2개의 이형성 그룹이 합치된 기본 영역(Vinberg polytopes)을 정의하는 모스토우 경성 정리에 기초한다.

n차원 공간에 대해 순위 n+2를 갖는 빈버그 폴리토페스

n-dimension용 n+2등급 미러를 가진 소형 쌍곡선 빈버그 폴리토페스의 전체 목록은 F에 의해 열거되었다. 1996년 에스셀만.^[14] 일부 목록은 I. M. 카플린스카야에 의해 1974년에 출판되었다.^[15]

파라콤팩트 솔루션의 전체 목록은 P에 의해 발표되었다. 2003년 투마킨, 치수 3~17.^[16]

H에서³ 가장 작은 파라콤팩트 형태는 , 또는 [1968,3,3,3,3]으로 나타낼 수 있으며, 파라콤팩트 쌍곡선 그룹 [3,4,4]을 [3,4,1⁺,4]로 거울 제거하여 구성할 수 있다. 두 배의 기본 영역은 사면체에서 사면체 피라미드로 바뀐다. Another pyramids include [4,4,1⁺,4] = [∞,4,4,∞], = . Removing a mirror from some of the cyclic hyperbolic Coxeter graphs become bow-tie graphs: [(3,3,4,1⁺,4)] = [((3,∞,3)),((3,∞,3))] or , [(3,4,4,1⁺,4)] = [((4,∞,3)),((3,∞,4))] or , [(4,4,4,1⁺,4)] = [((4,∞,4)),((4,∞,4))] or .

4각 피라미드 기본 영역을 갖는 다른 유효한 파라콤팩트 그래프에는 다음이 포함된다.

치수	순위	그래프
H3	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

또 다른⁺ 하위 그룹 [1^1,1,1,4] = [4,4,1⁺,4,4,4,4] = [1]^[6] = = . ^[17]

n차원 공간에 대한 n+3등급의 빈버그 폴리토페스

최대 8차원까지 존재하는 퇴보적인 근본적인 단순화의 수가 한정되어 있다. n-dimension용 n+3 미러를 가진 컴팩트 빈버그 폴리토페스의 전체 목록은 P에 의해 열거되었다. 2004년 투마르킨. 이러한 그룹은 초경사선에 대해 점선/파손선으로 레이블이 지정된다. 순위 n+3 미러와 n-dimensions에 대한 하나의 단순하지 않은 꼭지점이 있는 비 컴팩트 빈버그 폴리토페스의 전체 목록은 마이크 로버츠에 의해 열거되었다.^[18]

4~8차원의 경우 순위 7~11 Coxeter 그룹은 각각 44, 16, 3, 1, 1로 계산된다.^[19] 가장 높은 것은 1984년 부게엔코에 의해 11등급인 8등급으로 발견되었다.^[20]

치수	순위	경우들	그래프
H4	7	44	...
H5	8	16	..
H6	9	3
H7	10	1
H8	11	1

n차원 공간에 대해 순위 n+4를 갖는 빈버그 폴리토페스

최대 8차원까지 존재하는 퇴보적인 근본적인 단순화의 수가 한정되어 있다. n-dimension용 n+4 미러를 가진 콤팩트 빈버그 폴리토페스는 A가 탐구했다. 펠릭슨과 P. 2005년 투마킨.^[21]

로렌츠 그룹

로렌츠 그룹이 있는 일반 허니컴

푸앵카레 볼 모델 외부에서 본 {3,3,7}

푸앵카레 볼 모델 외부에서 본 {7,3,3}

심플렉스 도메인의 로렌츠 그룹은 파라콤팩트 쌍곡선 형태를 벗어난 그래프로 정의할 수 있다. 이것들은 때때로 초이상적 단순화라고 불리며, 특수 및 일반 상대성 공간-시간 분야에서 헨드릭 로렌츠의 이름을 딴 로렌츠 기하학과도 관련이 있는데, 자기 도트 산출물이 음수인 하나 이상의 시간 유사 치수 성분을 포함하고 있다.^[9] 대니 케일리가리는 n차원 쌍곡선 공간에서 이러한 볼록한 코코막트 콕시터 그룹을 부른다.^[22][23]

레벨 2

1982년 조지 맥스웰, 스피어패킹, 쌍곡반영그룹에 의해 발표된 논문은 로렌츠인의 유한한 5위부터 11위까지를 열거하고 있다. 그는 그것들을 레벨 2라고 부르는데, 이는 2개의 노드의 순열을 제거하면 유한 또는 유클리드 그래프가 남는다는 것을 의미한다.

순위 4의 모든 상위 분기 Coxeter 그룹은 Lorenzian으로, [ limit]^[3,3]로 표현할 수 있는 6개의 무한 순서 분기가 포함된 전체 그래프 3-simplex Coxeter-Dynkin 다이어그램으로 끝맺는다. 5-11등급은 각각 186개, 66개, 36개, 13개, 10개, 8개, 4개의 로렌츠 그룹을 제한적으로 가지고 있다.^[24]

H의 2013년 논문. 첸과 J.P.랩베, 로렌츠 콕시터 그룹, 보이드--맥스웰 볼패킹이 전체 순위 5,189의 3개 그룹을 새로 추가해 전체 리스트를 집계하고 발표했다.^[25]

5위부터 7위까지의 그래픽을 포함한 전체 목록이다.

로렌츠 콕시터 그룹

순위	그래프	패킹	무리
4	∞	∞	[3,3,7] ... [∞,∞,∞]: ... [4,3[3]] ... [∞,∞[3]]: ... [5,41,1] ... [∞1,1,1]: ... ... [(5,4,3,3)] ... [∞[4]]: ... ... ... [4[]×[]] ... [∞[]×[]]: ... ... [4[3,3]] ... [∞[3,3]]
5	186+3	95+	...[3[3,3,3]]:...
6	66	30	...[4,31,1,1,1]:
7	36	13	...[31,1,1,1,1,1]:
8	13	9	[3,3,3[6]]: [3,3[6],3]: [3,3[2+4],3]: [3,3[1+5],3]: [3[ ]e×[3]]:	[4,3,3,33,1]: [31,1,3,33,1]: [3,(3,3,4)1,1]: [32,1,3,32,1]:		[4,3,3,32,2]: [31,1,3,32,2]:
9	10	8	[3,3[3+4],3]: [3,3[9]]: [3,3[2+5],3]:	[32,1,32,32,1]:	[33,1,33,4]: [33,1,3,3,31,1]:	[33,3,2]: [32,2,4]: [32,2,33,4]: [32,2,3,3,31,1]:
10	8	7	[3,3[8],3]: [3,3[3+5],3]: [3,3[9]]:	[32,1,33,32,1]:	[35,3,1]: [33,1,34,4]: [33,1,33,31,1]:	[34,4,1]:
11	4	3		[32,1,34,32,1]:	[32,1,36,4]: [32,1,35,31,1]:	[37,2,1]:

매우 확장된 Coxeter 다이어그램

한 가지 용도는 아핀 그룹을 확장된 쌍곡선으로 간주하고 세 번째 노드를 확장된 단순 그룹으로 간주하는 직접 Dynkin 다이어그램 사용에서 매우 확장된 정의를 포함한다. 이러한 확장자는 일반적으로 확장된 노드 수에 대한 1,2, 또는 3 + 기호의 지수로 표시된다. 이 확장 영상 시리즈는 분기 노드를 제거한 후 프로세스가 중지되지만, 그래프의 동일한 위치에서 노드를 순차적으로 제거함으로써 뒤로 확장할 수 있다. E₈ 확장 패밀리는 E에서₃ 앞으로 뒤로 확장되어 E로₁₁ 확장되는 가장 일반적인 예다.

확장 프로세스는 유한에서 부연으로, 쌍곡선에서 로렌츠어로 진행되는 제한된 일련의 Coxeter 그래프를 정의할 수 있다. 카르탄 행렬의 결정 인자는 시리즈가 유한(양)에서 아핀(0)으로, 쌍곡(음)으로, 그리고 적어도 하나의 쌍곡 부분군을 포함하는 로렌츠 그룹으로 변하는 위치를 결정한다.^[26] 비결정형 H_n 그룹은 H가₄ 소형 쌍곡선으로 확장되고 로렌츠 그룹으로 과도하게 확장되는 확장 시리즈를 형성한다.

등급별 Schléfli 행렬의 결정 요인은 다음과 같다.^[27]

• det(A₁ⁿ=[2^n-1]) = 2ⁿ(모든 n에 대해 마무리)
• det(A_n=[3^n-1]) = n+1(모든 n에 대해 완료)
• det(B_n=[4,3^n-2]) = 2(모든 n에 대해 마무리)
• det(D_n=[3^n-3,1,1]) = 4(모든 n에 대해 마무리)

Schléfli 행렬의 예외적인 시리즈 결정 요인은 다음과 같다.

• det(E_n=[3^n-3,2,1]) = 9-n(E₃(=AA₂₁), E₄₅(=A₄), E(=D₅), E(=D), E₆₇, E, E, E는₈ E₉(E ~ 8${\displaystyle {\stackrel{}{)}}_{}}$에$$아핀(${\displaystyle {\stackrel{}{}}_{}}$ ~ 8 {\$displaystyle{\tilde}_{8}}),$ $$E에서는₁₀ 쌍곡선(E)
• det([3^n-4,3,1]) = 2(8-n) (n=4 ~ 7에 대한 마무리, appine(${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$ $$및 n=8에 쌍곡선.
• det([3^n-4,2,2]) = 3(7-n) (n=4 ~ 6, appine(${\displaystyle {\stackrel{}{}}_{}}$~ 6 ${\$ $$및 n=${\displaystyle 7_{}}$에서 쌍곡선.
• det(F_n=[3,4,3^n-3]) = 5-n(F₃(=B₃)에서 F로₄ 마무리, ${\displaystyle F_{}}$에서₅ 아핀(${\displaystyle {\stackrel{}{}}_{}}$~ 4 ${\$ $$F에서₆ 쌍곡선(F)
• det(G_n=[6,3^n-2]) = 3-n(G의₂ 경우 마무리, G의₃ 경우 아핀(${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}$$), $$G의₄ 쌍곡선)

소형 확장 시리즈

유한한	${\displaystyle A_{2}}:$	${\displaystyle C_{2}}$	${\displaystyle G_{2}}$	${\displaystyle A_{3}}$	${\displaystyle B_{3}}$	${\displaystyle C_{3}}$	${\displaystyle H_{4}}$
랭크 n	[3[3],3n-3]	[4,4,3n-3]	Gn=[6,3n-2]	[3[4],3n-4]	[4,31,n-3]	[4,3,4,3n-4]	Hn=[5,3n-2]
2	[3] A을2	[4] C2	[6] G2		[2] A을12	[4] C2	[5] H2
3	[3[3]] A2+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}	[4,4] C2+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}	[6,3] G2+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$}}	[3,3]=A3	[4,3] B3	[4,3] C3	[5,3] H3
4	[3[3],3] A2++=$$의${\displaystyle {\stackrel{}{}3}_{\mathrm{}}}$ ${\$	[4,4,3] C2++= $$의${\displaystyle {\stackrel{}{}3}_{\mathrm{}}}$ ${\$	[6,3,3] G2++= ${\displaystyle {\stackrel{}{}}_{}}$}' ${\displaystyle 3_{\mathrm{}}}$ ${\${\$overline{V}_{3}}}$	[3[4]] A3+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$	[4,31,1] B3+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$	[4,3,4] C3+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$	[5,3,3] H4
5	[3[3],3,3] A을2+++	[4,4,3,3] C2+++	[6,3,3,3] G2+++	[3[4],3] A3++= $$의${\displaystyle {\stackrel{}{}4}_{\mathrm{}}}$ ${\$	[4,32,1] B3++=$$의${\displaystyle {\stackrel{}{}4}_{\mathrm{}}}$ ${\$	[4,3,4,3] C3++= $$의${\displaystyle {\stackrel{}{}4}_{\mathrm{}}}$ ${\$	[5,33] H5= ${\displaystyle {\stackrel{}{}}_{}}$¯ ${\displaystyle 4_{\mathrm{}}}$ ${\$
6				[3[4],3,3] A을3+++	[4,33,1] B3+++	[4,3,4,3,3] C3+++	[5,34] H6
데트(Mn)	3(3-n)	2(3-n)	3-n	4(4-n)	2(4-n)

중간연장시리즈

유한한	${\displaystyle A_{4}}$	${\displaystyle B_{4}}$	${\displaystyle C_{4}}$	${\displaystyle D_{4}}$	${\displaystyle F_{4}}$	${\displaystyle A_{5}}$	${\displaystyle B_{5}}$	${\displaystyle D_{5}}$
랭크 n	[3[5],3n-5]	[4,3,3n-4,1]	[4,3,3,4,3n-5]	[3n-4,1,1,1]	[3,4,3n-3]	[3[6],3n-6]	[4,3,3,3n-5,1]	[31,1,3,3n-5,1]
3		[4,3−1,1] B2A1	[4,3] B3	[3−1,1,1,1] A을13	[3,4] B3		[4,3,3] C3
4	[33] A을4	[4,3,3] B4	[4,3,3] C4	[30,1,1,1] D4	[3,4,3] F4		[4,3,3,3−1,1] B3A1	[31,1,3,3−1,1] A3A1
5	[3[5]] A4+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	[4,3,31,1] B4+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	[4,3,3,4] C4+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	[31,1,1,1] D4+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	[3,4,3,3] F4+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	[34] A을5	[4,3,3,3,3] B5	[31,1,3,3] D5
6	[3[5],3] A4++=$$의${\displaystyle {\stackrel{}{}5}_{\mathrm{}}}$ ${\$	[4,3,32,1] B4++=$$의${\$	[4,3,3,4,3] C4++= $$의${\displaystyle {\stackrel{}{}5}_{\mathrm{}}}$ ${\$	[32,1,1,1] D4++= ${\displaystyle {\stackrel{\text{'}}{}}_{}}$ ${\displaystyle 5_{\mathrm{}}}$ ${\$	[3,4,33] F4++= ${\displaystyle {\stackrel{\text{'}}{}5}_{\mathrm{}}}$ ${\$	[3[6]] A5+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$	[4,3,3,31,1] B5+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$	[31,1,3,31,1] D5+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 5_{\mathrm{}}}$ ${\$
7	[3[5],3,3] A을4+++	[4,3,33,1] B4+++	[4,3,3,4,3,3] C4+++	[33,1,1,1] D4+++	[3,4,34] F4+++	[3[6],3] A5++= $$의${\$	[4,3,3,32,1] B5++=$$의${\displaystyle {\stackrel{}{}6}_{\mathrm{}}}$ ${\$	[31,1,3,32,1] D5++= ${\displaystyle {\stackrel{\text{'}}{}}_{}}$ ${\displaystyle 6_{\mathrm{}}}$ ${\$
8						[3[6],3,3] A을5+++	[4,3,3,33,1] B5+++	[31,1,3,33,1] D5+++
데트(Mn)	5(5-n)	2(5-n)		4(5-n)	5-n	6(6-n)	4(6-n)

더 높은 확장 시리즈

유한한	${\displaystyle A_{6}}$	${\displaystyle B_{6}}$	${\displaystyle D_{6}}$	${\displaystyle E_{6}}$	${\displaystyle A_{7}}$	${\displaystyle B_{7}}$	${\displaystyle D_{7}}$	${\displaystyle E_{7}}$	${\displaystyle E_{8}}$
랭크 n	[3[7],3n-7]	[4,33,3n-6,1]	[31,1,3,3,3n-6,1]	[3n-5,2,2]	[3[8],3n-8]	[4,34,3n-7,1]	[31,1,3,3,3,3n-7,1]	[3n-5,3,1]	En=[3n-4,2,1]
3									[3−1,2,1] E3=A2A1
4				[3−1,2,2] A을22				[3−1,3,1] A3A1	[30,2,1] E4=A4
5		[4,3,3,3,3−1,1] B4A1	[31,1,3,3,3−1,1] D4A1	[30,2,2] A을5				[30,3,1] A을5	[31,2,1] E5=D5
6	[35] A을6	[4,34] B6	[31,1,3,3,3] D6	[31,2,2] E6		[4,3,3,3,3,3−1,1] B5A1	[31,1,3,3,3,3−1,1] D5A1	[31,3,1] D6	[32,2,1] E6*
7	[3[7]] A6+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$	[4,33,31,1] B6+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$	[31,1,3,3,31,1] D6+= ${\displaystyle {\stackrel{~}{}6}_{\mathrm{}}}$ ${\$	[32,2,2] E6+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$	[36] A을7	[4,35] B7	[31,1,3,3,3,30,1] D7	[32,3,1] E7*	[33,2,1] E7*
8	[3[7],3] A6++=${\displaystyle P_{\mathrm{}}}$7 ${\$	[4,33,32,1] B6++=${\displaystyle S_{\mathrm{}}}$7 ${\$	[31,1,3,3,32,1] D6++= ${\displaystyle {\stackrel{\text{'}}{}7}_{\mathrm{}}}$ ${\$	[33,2,2] E6++= ${\displaystyle {\stackrel{}{}7}_{\mathrm{}}}$ ${\$	[3[8]] A7+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$	[4,34,31,1] B7+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$	[31,1,3,3,3,31,1] D7+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$	[33,3,1] E7+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$	[34,2,1] E8*
9	[3[7],3,3] A을6+++	[4,33,33,1] B6+++	[31,1,3,3,33,1] D6+++	[34,2,2] E6+++	[3[8],3] A7++=${\displaystyle P_{\mathrm{}}}$8 ${\$	[4,34,32,1] B7++=${\displaystyle {\stackrel{\text{'}}{}}_{}}$ ${\displaystyle 8_{\mathrm{}}}$ ${\$	[31,1,3,3,3,32,1] D7++= ${\displaystyle {\stackrel{\text{'}}{}}_{}}$ ${\displaystyle 8_{\mathrm{}}}$ ${\$	[34,3,1] E7++=${\displaystyle {\stackrel{\text{'}}{}}_{}}$ ${\displaystyle 8_{\mathrm{}}}$ ${\$	[35,2,1] E9=E8+= ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 8_{\mathrm{}}}$ ${\$
10					[3[8],3,3] A7+++*	[4,34,33,1] B7+++*	[31,1,3,3,3,33,1] D7+++*	[35,3,1] E7+++*	[36,2,1] E10=E8++=${\displaystyle {\stackrel{\text{'}}{}9}_{\mathrm{}}}$ ${\$
11									[37,2,1] E11=E8+++*
데트(Mn)	7(7-n)	2(7-n)	4(7-n)	3(7-n)	8(8-n)	2(8-n)	4(8-n)	2(8-n)	9-n

기하학적 폴딩

유한 및 부착형 접이식^[28]

φAΓ : A -> 유한형Γ' A
Γ	Γ'	폴딩 설명	콕시터-딘킨 도표
아이2(h)	γ(h)	디헤드럴 폴딩
Bn	A을2n	(I,sn)
	Dn+1, A2n-1	(A3,+/-)
F4	E6	(A3,±ε)
H4	E8	(A4,±ε)
H3	D6
H2	A을4
G2	A을5	(A5,±ε)
	D4	(D4,±ε)
φΓ+: A -> 아핀 타입에 대한Γ'+ A
${\displaystyle {\tilde{A}_{n-1}$	${\displaystyle {\tilde{A}_{kn-1}$	로컬 사소한
${\displaystyle {\tilde{B}_{n}}$	${\displaystyle {\tilde{D}_{2n+1}}$	(I,sn)
	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle {\mathrm{n}}_{}}$+ 1 ${\$ $D{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle {\mathrm{2n}}_{}}$ ${\$	(A3,±ε)
${\displaystyle {\tilde{C}_{n}}$	${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle {\mathrm{n}}_{}}$+ 1 ${\$ $C{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle {\mathrm{2n}}_{}}$ ${\$	(A3,±ε)
	${\displaystyle {\tilde{C}_{2n+1}}$	(I,sn)
${\displaystyle {\tilde{C}_{n}}$	${\displaystyle {\tilde{A}_{2n+1}}$	(I,sn) & (I,s0)
	${\displaystyle {\tilde{A}_{2n}}$	(A3,196) & (I,s0)
	${\displaystyle {\tilde{A}_{2n-1}$	(A3,190) & (A3,190')
${\displaystyle {\tilde{C}_{n}}$	${\displaystyle {\tilde{D}_{n+2}}$	(A3,-bask) & (A3,-bask')
${\displaystyle {\tilde{C}_{2}}:$	${\displaystyle {\tilde{D}_{5}}$	(I,s1)
${\displaystyle {\tilde{F}_{4}}$	${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ $E{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$	(A3,±ε)
${\displaystyle {\tilde{G}_{2}}$	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ E${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 7_{\mathrm{}}}$ ${\$	(A5,±ε)
	${\displaystyle {\stackrel{}{}}_{}}$$B{\displaystyle {\stackrel{}{}}_{}}$${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 3_{\mathrm{}}}$ ${\$ F${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	(B3,±ε)
	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ E${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$	(D4,±ε)

(단순 레이싱) 대칭성을 갖는 Coxeter-Dynkin 다이어그램(마인드, 아핀 또는 쌍곡선)은 대칭에 의해 인용될 수 있으며, "접기"라고 하는 공정과 함께 일반적으로 레이싱된 새 도표를 산출한다.^[29][30]

예를 들어, D₄ 폴딩에서 G의₂₂ 가장자리는 3개의 외부 노드의 클래스(밸런스 1)에서 중앙 노드의 클래스(밸런스 3)까지 가리킨다. 그리고 E는₈ H 2장으로₄ 접고, 2부는 τ로 축척한다.^[31]

기하학적으로 이것은 균일한 폴리토페와 테셀레이션의 직교 투영에 해당한다. 특히, 모든 유한 단순 레이싱 Coxeter-Dynkin 도표는 I₂(h)로 접을 수 있으며, 여기서 h는 Coxeter 평면에 대한 투영에 기하학적으로 해당하는 Coxeter 번호다.

쌍곡선 접기 몇 개

복합반사

Coxeter-Dynkin 다이어그램은 노드가 2보다 큰 기간의 단일 반사인 C라는ⁿ 복잡한 공간으로 확장되었다. 노드는 지수로 라벨을 표시하며, 억제된 경우 일반적인 실제 반사를 위해 2로 가정한다. Coxeter는 복잡한 그룹 p[q]r을 도표로 쓴다.^[32]

$C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$의 1차원 일반 복합 폴리토프는 , p 정점이 있는 로 표현된다$$. 그것의 실제 표현은 일반 다각형, {p}이다. 그것의 대칭은 [] 또는 , 순서 p이다. 에 대한 단일 연산자 ${\displaystyle {}^{}}$는 R$$2 {\$displaystyle \mathb{R}^{$2}} X$$ 2㎛/p 라디안 단위로 시계 반대 방향으로 회전하는 것으로 보이며, 단일 단일 유니터리 반사의 순차적 적용에 의해 에지가 생성된다. p 정점이 있는 1 폴리토프의 단일 반사 발생기는 e^2πi/p = cos(2㎛/p) + i sin(2㎛/p)이다. p = 2일 때 발전기는 e^πi = –1로 실제 평면의 점 반사와 동일하다.

상위 폴리토프에서 {} 또는 p-에지 요소를 나타내며, 2-에지, {} 또는 는 두 꼭지점 사이의 일반적인 실제 에지를 나타낸다.

일반복합1폴리탑

아간드 평면에서 p = 2, 3, 4, 5, 6의 정규 폴리곤으로 표현되는 복잡한 1 폴리탑, 검은색 정점. p 꼭지점의 중심은 빨간색으로 보인다. 다각형의 측면은 대칭 발생기의 한 가지 응용을 나타내며, 각 꼭지점을 다음 반시계방향 복사본에 매핑한다. 복합 1폴리토프는 가장자리가 없을 수 있고(복잡한 가장자리인 경우가 많으며) 꼭지 요소만 포함하기 때문에 이러한 다각측면은 폴리토프의 가장자리 요소가 아니다.

부분군 지수 관계를 가진 12개의 수정 불가능한 Shephard 그룹.[33] 부분군 지수 2는 실제 반사를 제거함으로써 관련된다. p[2q]2 --> [q],p 색인 2. p[4]q --> [q],p 색인 q.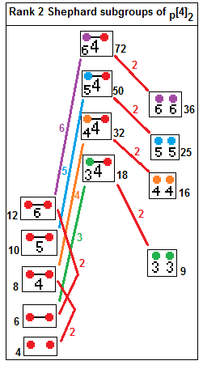

p[4]2 부분군: p=2,3,4... p[4]2 --> [p], 색인 p p[4]2 --> []×[],p 색인 2

$C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$의 정규 복합 폴리곤에는 {q}_r 또는 Coxeter 다이어그램이 있다$.$ 일반 복합 폴리곤의 대칭 집단을 콕시터 집단이 아니라 콤플렉스 반사 집단의 일종인 셰퍼드 집단으로 부른다. [q]_r의 $순서$는 8 /${\displaystyle q}$ ${\displaystyle \cdot }$ ${\displaystyle (1}$/ p${\displaystyle }$+ 2${\displaystyle }$/ ${\displaystyle \mathrm{q}}$+ ${\displaystyle 1}$ /${\displaystyle r}$- ${\displaystyle 1{}^{}}$)${\displaystyle {}^{}}$- ${\displaystyle 2^{}}$ ${\$^[34]

The rank 2 Shephard groups are: ₂[q]₂, _p[4]₂, ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂, and ₅[4]₃ or , , , , , , , , , , , , , of order 2q, 2p², 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200, and 1800 respectively.

대칭군[q]_p2은 2개의 발전기 R₁, R으로₂ 표시되며 여기서₁^p₁: R = R₂^p₂ = I. q가 짝수이면 (RR₂₁)^q/2 = (RR₁₂). ^q/2q가 홀수이면 (RR₂₁)^(q-1)/2R₂ = (RR₁₂)^(q-1)/2R₁. q가 홀수일 때는₁ p=p₂.

The ${\displaystyle \mathbb {C} ^{3}}$ group or [1 1 1]^p is defined by 3 period 2 unitary reflections {R₁, R₂, R₃}: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₁)^p = 1. The period p can be seen as a double rotation in real ${\displaystyle \mathbb {R} ^{4}}$.

유사한 $C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$ 그룹$$ 또는 [1 1]^(p)은 3주기 2 단일 반사 {R₁, R₂, R, R₃: R₁² = R₁²₃² = (RR₁₂₂₃)³³ = (RRR₃₁)³ = (RRRR) = (RRRR₁₂₃₂)^p = 1) = 1로 정의된다.

참고 항목

• 콕시터군
• 슈바르츠 삼각형
• 구르사트 사면체
• 딘킨 도표
• 균일 폴리토프
  • 와이토프 기호
  • 균일다면체
  • 균일한 다면체 목록
  • 균일 평면 기울기 목록
  • 제복4폴리토프
  • 볼록 균일 벌집
  • 쌍곡선 공간의 볼록 균일 벌집
• Wythoff 시공 및 Wythoff 기호

참조

추가 읽기

• 제임스 E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge 고급 수학 연구, 29 (1990)
• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[8], Googlebooks [9]
  • (용지 17) Coxeter, The Evolution of Coxeter-Dynkin 다이어그램, [Neyuw Archief voor Wiskunde 9(1991) 233-248]
• 콕시터, 기하학의 아름다움: 12편의 에세이, 도버 퍼블리셔스, 1999년 ISBN 978-0-486-40919-1 (제3장: 균일한 폴리토페스를 위한 와이토프의 건설)
• Coxeter, 일반 폴리토페스 (1963), 맥밀란 회사
  • 일반 폴리토페스, 제3판, (1973) 도버판, ISBN 0-486-61480-8 (제5장: 칼리도스코프 및 제11.3절 그래프별 표현)
• H.S.M. Coxeter와 W. O. J. Moser. 이산 그룹용 생성기 및 관계 4번째 에드 스프링어-버래그. 1980년 뉴욕
• Norman Johnson, Geometries and Transformations, 11,12,13장, 2011 사전 인쇄
• N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. T. Chantz, 쌍곡 콕시터 심플렉스 크기 1999, 변환 그룹 1999, 제4권, 제4권, 제4권, 페이지 329–353 [10] [11]
• Norman W. Johnson과 Asia Ivic Weiss Quadratic Integers and Coxeter Groups PDF Can. J. 수학. 제51권(6), 1999 페이지 1307–1336

외부 링크

위키미디어 커먼즈에는 콕시터-딘킨 도표와 관련된 미디어가 있다.

• Weisstein, Eric W. "Coxeter–Dynkin diagram". MathWorld.
• 1978년 10월 캐나다 토론토에서 Coxeter와 Dynkin의 Coxeter 다이어그램의 역사에 대한 토론; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library.