정육면체 5개 혼합물

정육면체 5개 혼합물
(애니메이션, 3D 모델)
유형	정규 화합물
콕시터 기호	2{5,3}[5{4,3}][1]
스텔레이션 코어	3면체
볼록 선체	도데카헤드론
색인	UC9
폴리헤드라	정육면체 5개
얼굴	30제곱(삼각형 360개로 표시)
가장자리	60
정점	20
이중	5옥타헤드라 화합물
대칭군	이코사헤드랄 (Ih)
하나의 구성 요소로 제한되는 부분군	피리토헤드랄(Th)

5개의 정육면체 화합물은 5개의 정규 다면체 화합물 중 하나이다. 1876년 에드먼드 헤스가 처음 묘사한 것이다.

5개의 정규 화합물 중 하나이며, 5개의 옥타헤드라의 화합물에는 이중이다. 그것은 보통의 도데카헤드론의 면모라고 볼 수 있다.

그것은 3면체 중 하나이다. 그것은 좌골 대칭(I_h)

기하학

이 화합물은 도데카헤드론(오각형 면과 상관되는 오각형을 볼 수 있다)의 면이다. 각 입방체는 도데카헤드론의 20개 정점 중 8개 정점의 선택을 나타낸다.

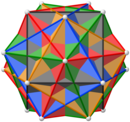	2-폴드, 5-폴드, 3-폴드 대칭 축의 뷰

5개 입방체의 조합으로 간주하여 자가 교차 표면이 없는 단순 비콘벡스 고체를 산출하는 경우 360면(모든 삼각형), 182 정점(60도 3, 30도, 12도, 12도, 60도, 8도, 20도, 12도), 540개의 가장자리를 가지며 182 - 540 + 360 = 2의 오일러 특성을 나타낸다.

모서리 배열

그것의 볼록한 선체는 보통의 도데카헤드론이다. 그것은 그것의 가장자리 배열을 작은 ditrigonal icodechadron, 큰 ditrigonal icodechadron, 그리고 ditrigonal decadodechadron과 추가로 공유한다. 이것들로, 그것은 퇴보하는 균일한 별인 다면체 화합물을 형성할 수 있다; 작은 복합 롬비코도데카헤드론, 거대한 복합 롬비코도데카헤드론, 그리고 복합 롬비도데카헤드론.

소형 이코시다데카헤드론	대직류 이코시다데카헤드론	직교 도데코데카헤드론
도데카헤드론(콘벡스 선체)	정육면체 5개 혼합물	구면 타일링으로

이 다섯 개의 정사각형을 각각 취하여 스텔라 옥탄굴라(입방체의 같은 정점 배열을 공유하는)의 두 개의 정사각형으로 대체함으로써 10개의 정사각형의 화합물을 형성할 수 있다.

기장으로서.

스텔레이션 면 노란색 영역은 하나의 큐브 면에 해당한다.

이 화합물은 롬빅 삼정면체의 단층으로서 형성될 수 있다. 30개의 롬빅 면은 5개의 정육면체 평면에 존재한다.

참고 항목

네 개의 큐브 화합물로 전환

5옥타헤드라 화합물 정육면체 3개 혼합물 네 개의 큐브 화합물 정육면체 6개 혼합물 균일다면 화합물

참조

• Cromwell, Peter R. (1997), Polyhedra, Cambridge. p 360
• Harman, Michael G. (c. 1974), Polyhedral Compounds, unpublished manuscript.
• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
• Cundy, H.와 Rollett, A. "도데카헤드론의 5 큐브." 수학 모델, 3차 개정의 제3.10.6조. 영국 스트래드브로크: 1989년 135-136페이지의 타킨 펍.
• H.S.M. Coxeter, 일반 폴리토페스, (3판, 1973), 도버판, ISBN 0-486-61480-8, 3.6 플라토닉 고형분, 6.2 스텔링, pp.96-104

외부 링크

• MathWorld: 큐브 5 컴파운
  • MathWorld: Rhombic Triacontahedron Stellations
• 조지 하트: 큐브 화합물
• Steven Dutch: Uniform Polyedra and The Duals
• VRML 모델: [1]^{[permanent dead link]}
• Klitzing, Richard. "3D compound".