잘린 사각 타일링
Truncated square tiling| 잘린 사각 타일링 | |
|---|---|
 | |
| 유형 | 반정형 타일링 |
| 꼭지점 구성 |  4.8.8 |
| 슐레플리 기호 | t{4,4} tr{4,4} 또는 { |
| 와이토프 기호 | 2 4 4 4 4 2 |
| 콕시터 다이어그램 | |
| 대칭 | p4m, [4,4], (*442) |
| 회전 대칭 | p4, [4,4]+, (442) |
| 보우어 약자 | 토스쿼트 |
| 이중 | 테트라키스 네모난 타일 |
| 특성. | 정점 변환 |
기하학에서 잘린 정사각형 타일링은 각 꼭지점에 정사각형 1개와 옥타곤 2개를 가진 유클리드 평면의 정규 다각형에 의한 반정형 타일링이다. 이것은 팔각형이 들어 있는 일반 볼록 폴리곤에 의한 유일한 가장자리 대 가장자리 타일링이다. 그것은 t{4,4}의 Schléfli 기호를 가지고 있다.
콘웨이는 이것을 네모난 타일링(쿼드릴)에 적용되는 잘린 쿼드릴이라고 부른다.
이 무늬에 사용된 다른 이름으로는 지중해식 타일링과 팔각 타일링이 있는데, 이것은 종종 작은 사각형으로 표현된다. 그리고 길고 짧은 모서리를 번갈아 쓰는 비정규적인 팔각형이 있다.
평면에 3개의 규칙적인 기울기와 8개의 반정형 기울기가 있다.
균일 배색
잘린 사각형 타일링에는 두 가지 뚜렷한 균일한 색상이 있다. (색상의 이름을 꼭지점 주변 지수로 지정: 122, 123).
 2가지 색상: 122 |  3가지 색상: 123 |
서클패킹
잘린 사각형 타일링은 원 패킹으로 사용할 수 있으며, 모든 점의 중심에 동일한 직경의 원을 배치할 수 있다. 모든 원은 패킹의 다른 원(키스 번호) 3개와 접촉한다.[1]
변형

흔히 지중해 패턴이라고 불리는 이 패턴의 한 변형은 작은 사각형의 돌 기와와 테두리에 대각선으로 정렬되어 나타난다. 다른 변화들은 정사각형이나 팔각형을 늘린다.
피타고라스 타일링은 크고 작은 사각형을 번갈아 가며, 잘린 사각 타일링과 토폴로지적으로 동일하다고 볼 수 있다. 정사각형은 45도 회전하고 옥타곤은 중간 정점을 가진 정사각형으로 변형된다.
직조 패턴은 또한 동일한 위상을 가지며, 옥타곤은 직사각형을 평평하게 만들었다.
| p4m(*442) | p4(442) | p4g (4*2) | pmm(*2222) | ||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |
| p4m(*442) | p4(442) | cmm(2*22) | pmm(*2222) | ||||
 |  |  |  |  |  |  |  |
| 지중해 | 피타고라스 | 플랑드르 본드 | 직조 | 뒤틀림 | 직사각형/롬브릭 | ||
관련 다면체 및 틸팅

잘린 사각형 타일링은 쌍곡면으로 확장되는 4.2n.2n 정점을 가진 균일한 다면 및 틸팅의 일부로서 위상학적으로 관련이 있다.
| *n42 잘린 틸팅의 대칭 돌연변이: 4.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭 *n42 [n,4] | 구면 | 유클리드 주 | 콤팩트 쌍곡선 | 파라콤. | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| 잘림 수치 |  |  |  |  |  |  |  |  | |||
| 구성. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| n-11 수치 |  |  |  |  |  |  |  |  | |||
| 구성. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.1987.12 | |||
평면에 투영된 3차원 비트런드 큐빅 벌집에는 잘린 타일링의 복사본 2개가 표시된다. 평면에서는 복합 타일링으로 나타낼 수 있고, 조합된 사각 타일링으로 볼 수 있다.
 |  | 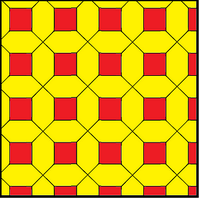 |
사각 타일링으로부터의 Wythoff 시공
원래 얼굴에는 붉은색으로, 원래 꼭지점에는 노란색, 원래 가장자리를 따라 파란색으로 칠해진 타일을 그리면 8가지 형태가 모두 구별된다. 그러나 얼굴을 동일하게 취급하는 것은 세 가지 독특한 형태, 즉 사각 타일링, 잘린 사각 타일링, 스너브 사각 타일링이다.
| 사각 타일링 대칭에 따른 균일한 기울기 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [4,4], (*442) | [4,4]+, (442) | [4,4+], (4*2) | |||||||||
 |  |  |  |  |  |  |  | ||||
| {4,4} | t{4,4} | r{4,4} | t{4,4} | {4,4} | rr{4,4} | tr{4,4} | sr{4,4} | s{4,4} | |||
| 균일 듀얼 | |||||||||||
 |  |  |  |  |  |  |  | ||||
| V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.4.4.4 | V4.8.8 | V3.3.4.3.4 | ||||
기타 대칭의 관련 기울기
| *n42 전분해 틸팅의 대칭 돌연변이: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 대칭 *n42 [n,4] | 구면 | 유클리드 주 | 콤팩트 쌍곡선 | 파라콤. | ||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | |
| 옴니트런어드 형상을 나타내다 |  4.8.4 |  4.8.6 |  4.8.8 |  4.8.10 |  4.8.12 |  4.8.14 |  4.8.16 |  4.8.∞ |
| 옴니트런어드 듀얼스 |  V4.8.4 |  V4.8.6 |  V4.8.8 |  V4.8.10 |  V4.8.12 |  V4.8.14 |  V4.8.16 |  V4.8.1987 |
| *n2 전위차단 틸팅의 대칭 돌연변이: 4.2n.2n | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭 *n2 [n,n] | 구면 | 유클리드 주 | 콤팩트 쌍곡선 | 파라콤. | ||||||||||
| *222 [2,2] | *332 [3,3] | *442 [4,4] | *552 [5,5] | *662 [6,6] | *772 [7,7] | *882 [8,8]... | *∞∞2 [∞,∞] | |||||||
| 피겨 |  |  |  |  |  |  |  |  | ||||||
| 구성. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | ||||||
| 이중 |  |  |  |  |  |  |  |  | ||||||
| 구성. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.1987.12 | ||||||
테트라키스 네모난 타일
테트라키스 사각 타일링은 잘린 사각 타일링에 이중인 유클리드 평면의 타일링이다. 각 정사각형을 중심점에서 4개의 이소셀 직삼각형으로 나누어 선의 무한 배열을 형성하여 정사각형 타일링을 구성할 수 있다. 또한 격자의 각 정사각형을 대각선으로 2개의 삼각형으로 세분화하여 대각선이 교대하고 대각선이 방향을 바꾸거나, 대각선이 2개의 사각 격자를 중첩시켜 형성할 수 있으며, 하나는 다른 사각 격자로부터 45도 회전하고 scaled2의 배수로 스케일링한다.
콘웨이는 이를 키스콰드리유라고 부르는데,[2] 정사각형 타일링(콰드리유)의 얼굴을 대신하기 위해 중앙점과 삼각형을 추가하는 키스 작전으로 대표된다. 그것은 그것의 8도 정점을 둘러싸고 있는 삼각형의 영국 국기와 유사하기 때문에 Union Jack 격자라고도 불린다.[3]
참고 항목
| 위키미디어 커먼즈에는 Uniform tiling 4-8-8 (Trunced square tiling)과 관련된 미디어가 있다. |
참조
- ^ 오더 인 스페이스: 디자인 소스 북, Keith Critchlow, p.74-75, 원 패턴 H
- ^ 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭, ISBN978-1-56881-220-5"Archived copy". Archived from the original on 2010-09-19. Retrieved 2012-01-20.
{{cite web}}: CS1 maint: 제목(링크)으로 보관된 복사본(제21장, Archimedeans and Catalan polyedra and tilings, p288 표) - ^ Stephenson, John (1970), "Ising Model with Antiferromagnetic Next-Nearest-Neighbor Coupling: Spin Correlations and Disorder Points", Phys. Rev. B, 1 (11): 4405–4409, doi:10.1103/PhysRevB.1.4405.
- 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭, ISBN 978-1-56881-220-5 [1]
- Grünbaum, Branko & Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (제2.1장: 규칙적이고 균일한 틸팅, 페이지 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 40. ISBN 0-486-23729-X.
- 데일 시모어와 질 브리튼 테셀레이션 소개, 1989년 ISBN 978-0866514613, 페이지 50-56
외부 링크
- Weisstein, Eric W. "Semiregular tessellation". MathWorld.
- Klitzing, Richard. "2D Euclidean tilings o4x4x - tosquat - O6".








