헵타데카곤

일반 헵타데카곤
일반 헵타데카곤
유형	정규 다각형
모서리 및 정점	17
슐레플리 기호	{17}
콕시터-딘킨 도표
대칭군	디헤드랄(D17), 2×17 주문
내부 각도(도)	≈158.82°
특성.	볼록, 주기, 등변, 이등변, 동위원소

기하학에서 헵타데카곤, 셉타데카곤 또는 17곤은 17면 다각형이다.

일반 헵타데카곤

정규 헵타데카곤은 슐레플리 기호 {17}로 표현된다.

건설

17은 페르마트 프라임이기 때문에, 정규 헵타데카곤은 구성 가능한 폴리곤이다(즉, 나침반과 표시되지 않은 직선자를 사용하여 구성할 수 있는 폴리곤). 이것은 1796년 카를 프리드리히 가우스가 19세의 나이로 보여주었다.^[1] 이 증거는 2000년 이상에 걸친 정기적인 다각형 건설의 첫 진전을 나타낸다.^[1] 가우스의 입증은 첫째, 구성성이 산술 연산 및 제곱근 추출 측면에서 공통 각도의 삼각함수의 표현가능성과 동일하다는 사실과 둘째, $N{\displaystyle }${\$displaystyle$N}의 홀수 주요 요소$,$ 즉 정수의 측수인 경우 이것이 가능하다는 그의 입증에 달려 있다. polygon, are distinct Fermat primes, which are of the form ${\displaystyle F_{n}=2^{2^{n}}+1}$ for some nonnegative integer ${\displaystyle n}$. Constructing a regular heptadecagon thus involves finding the cosine of ${\displaystyle 2\pi /17}$ in terms of square roots, which involves an equ17급—페르마트 전성기. 가우스의 저서 《산수학》에서는 다음과 같이 말하고 있다(현대 표기법에서).^[2]

${\displaystyle {\begin{aligned}16\,\cos {\frac {2\pi }{17}}=&-1+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}+\\&2{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}\\=&-1+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}+\\&2{\sqrt {17+3{\sqrt {17}}-{\sqrt {170+38{\sqrt {17}}}}}}.\end{정렬}}}$

유클리드에서는 면수가 2배인^h 정삼각형, 오각형, 오각형, 다각형의 건축물을 주었으나, 3번과 5번 이외의 페르마트 프리메이스를 바탕으로 한 건축물은 옛사람들에게는 알려지지 않았다. (만 알려져 있는 페르마트 프리타임은 n = 0, 1, 2, 3, 4에 대한_n F이다. 그들은 3, 5, 17, 257, 65537이다.)

헵타데카곤의 노골적인 건축은 1893년 허버트 윌리엄 리치몬드에 의해 이루어졌다. 다음의 시공 방법은 아래와 같이 칼라일 서클을 사용한다. 정규 17곤의 구성을 바탕으로 n은 3 또는 5(또는 둘 다)로 17의 제품이고 2의 검정력: 일반 51곤, 85곤 또는 255곤과 2배의^h 면수를 가진 일반 n곤으로 쉽게 구성할 수 있다.

직선 가장자리와 나침반을 이용한 일반 헵타데카곤의 또 다른 구조는 다음과 같다.

뉴욕 로체스터의 T. P. 스토웰은 W.E.의 Query에 응답했다. 1874년 분석가의 힐, 휠링, 인디애나:^[4]

"17개의 면으로 된 규칙적인 다각형을 원형으로 구성하기 위해서입니다. 직경 AB: OC와 OB에서 반경과 OQ를 반경과 같게 그리고 반경의 8번째 부분과 동일한 OD를 취한다. Make DE and DF each equal to DQ and EG and FH respectively equal to EQ and FQ; take OK a mean proportional between OH and OQ, and through K, draw KM parallel to AB, meeting the semicircle described on OG in M; draw MN parallel to OC, cutting the given circle in N – the arc AN is the seventeenth part of the whole circumference."

다음과 같은 간단한 디자인은 1893년 허버트 윌리엄 리치몬드에서 나왔다.^[5]

"LET OA, OB(그림 6)는 원의 두 수직 반지름이다. OB의 4분의 1로 OI를 만들고 OA의 4분의 1 각도에서 OIE를 찾으십시오. 또한 OA에서 발견하면 EIF가 45° AF에 있는 원을 지름 OB로 K에서 자르고, 중심이 E이고 반지름 EK인 원을₃ N과₅ N에서 OA로 자르게 하고, NP를₃₃₅₅ 서열하면 원주(原主)의₃ 원주(原主)의 원주(元主)의 원주(原主)인₅ 원주(原主)의 3/17과 5/17이 되게 하라."

• N₃ 지점은 탈레스의 AF에 대한 정리의 중심점에 매우 가깝다.

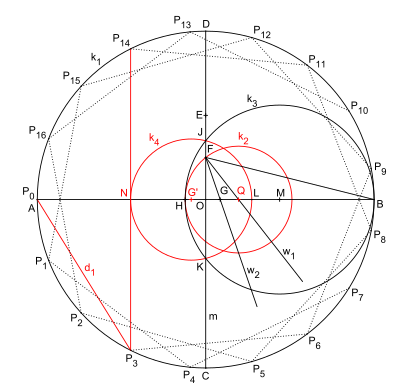
다음은 H. W. 리치몬드 공사의 변형이다.

원본과의 차이점:

• 원 k는₂ 이등분 w 대신₃ H점을 결정한다.
• G' 지점 주변의 원 k₄' (m에서 G 지점의 반사)는 접선 구성을 위해 더 이상 M에 가깝지 않은 N 지점을 산출한다.
• 몇몇 이름들은 바뀌었다.

또 다른 최근의 건설은 캘러지에 의해 주어진다.^[2]

대칭

일반 헵타데카곤은 Dih₁₇ 대칭, 순서 34이다. 17은 소수이기 때문에 치골 대칭을 가진 한 부분군이 있다. Dih₁ 및 2개의 순환 그룹 대칭: Z 및₁₇ Z₁.

이 4개의 대칭은 헵타데카곤의 4개의 뚜렷한 대칭에서 볼 수 있다. 존 콘웨이는 편지와 단체 주문으로 이것들에 라벨을 붙였다.^[6] 정규형식의 완전한 대칭은 r34이며 어떤 대칭도 a1로 표기되지 않는다. 이음 대칭은 정점(대각의 경우 d) 또는 가장자리(직각의 경우 p)를 통과하는지와 반사선이 양쪽 가장자리와 정점을 통과했을 때 i에 따라 구분된다. 중앙 열의 주기적 대칭은 중심 교량 순서에 대해 g로 표시된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. g17 부분군만 자유도는 없지만 지시된 가장자리로 볼 수 있다.

관련 다각형

헵타데카그램

헵타데카그램은 17면 별 다각형이다. 슐래플리 기호가 주는 정규 형식은 7가지로 되어 있는데, {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7}, {17/8}이다. 17이 황금수기 때문에, 이 모든 것은 일반 별이고 복합 형상이 아니다.

사진	{17/2}	{17/3}	{17/4}	{17/5}	{17/6}	{17/7}	{17/8}
실내각	≈137.647°	≈116.471°	≈95.2941°	≈74.1176°	≈52.9412°	≈31.7647°	≈10.5882°

페트리 폴리곤

정규 헵타데카곤은 고차원 정규 볼록 폴리토프용 페트리 폴리곤으로, 스큐 직교 투영으로 투영된다.

16-단순(16D)

참조

추가 읽기

• Dunham, William (September 1996). "1996—a triple anniversary". Math Horizons. 4: 8–13. doi:10.1080/10724117.1996.11974982. Retrieved 6 December 2009.
• 클라인, 펠릭스 외 유명한 문제들과 다른 모노그래프들. – Gauss에 의한 대수적 측면을 설명한다.

외부 링크

위키미디어 커먼즈는 17-gon과 관련된 미디어를 가지고 있다.

• Weisstein, Eric W. "Heptadecagon". MathWorld. 구성에 대한 설명을 포함한다.
• "Constructing the Heptadecagon". MathPages.com.
• 헵타데카곤 삼각함수
• 영국 BBC 방송의 태양열 연구 개발 센터영국
• Ghostarchive 및 Wayback Machine에 보관: