옥타곤

정팔각형
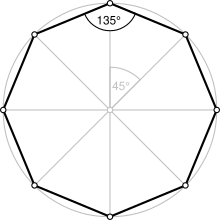정팔각형
유형	정다각형
모서리 및 정점	8
슐레플리 기호	{8}, t{4}
콕서터-딘킨 도표
대칭군	이면체(D8), 2×8 순서
내부 각도(도)	135°
특성.	볼록형, 순환형, 등변형, 등변형, 등변형, 등변형

기하학에서, 팔각형은 8면 다각형 또는 8각형이다.

정팔각형은 슐레플리 기호 {8}을(를) 가지며, 또한 두 가지 유형의 모서리를 번갈아 사용하는 준정사각형 t{4}로 구성될 수 있다.잘린 8각형 t{8}은(는) 16진수 {16}입니다.팔각형의 3D 유사체는 치환된 모서리처럼 삼각형 면이 있는 마름모꼴 정육면체가 될 수 있다.

일반 팔각형의 특성

8각형의 모든 내부 각도의 합은 1080°이다.모든 폴리곤과 마찬가지로 외부 각도는 총 360°입니다.

정사각형이 모두 8각형 변에 내부 또는 외부로 구성되는 경우, 반대쪽 정사각형의 중심을 연결하는 세그먼트의 중간점은 등각 및 정각(즉, ^{[2]: Prop. 9} 대각선이 서로 동일하고 직각인 사각형)을 형성합니다.

참조 팔각형의 중간점 팔각형은 참조 팔각형의 변의 중간점에 8개의 정점이 있습니다.정사각형이 모두 중간점 8각형 변에 내부 또는 외부로 구성되는 경우 반대쪽 정사각형의 중심을 연결하는 세그먼트의 중간점이 ^{[2]: Prop. 10} 정사각형의 정점을 형성합니다.

정팔각형

정팔각형은 길이가 같은 변과 크기가 같은 내각을 가진 닫힌 도형이다.8단계의 반사 대칭과 회전 대칭의 8줄을 가지고 있습니다.정팔각형은 슐레플리 기호 {8}로 표시됩니다.정팔각형의 각 정점에서의 내부 각도는 135°입니다(\$displaystyle\scriptstyle\frac {3\pi$}{4$$$}).$중심 각도는 45°( the ${\displaystyle \frac{4}{}}$\ $displaystyle \scriptstyle$\ $frac$ \$pi$} { $4$} radians$$ )입니다.

지역

변 길이 a의 정팔각형 면적은 다음과 같이 주어진다.

${\displaystyle A=2\cot {8}a^{2}=2(1+{\displayrt {2})a^{2}\displayq 4.828,a^{2}.}$

원반경 R의 관점에서 면적은

${\displaystyle A=4\sin {frac {pi }{4}R^{2}=2{\sqrt {2}\simeq 2.828,R^{2}}$

원점 r(내각 그림 참조)의 관점에서 면적은 다음과 같습니다.

${\displaystyle A=8\tan {frac {8}}r^{2}=8grt {2}r^{2}\displayq 3.314,r^{2}.}$

마지막 두 계수는 단위 원의 면적인 파이 값을 묶습니다.

영역은 다음과 같이 나타낼 수도 있습니다.

$디스플레이 스타일!A=S^{2}-a^{2}}$

여기서 S는 팔각형의 스팬 또는 두 번째로 짧은 대각선이며 a는 변 또는 밑면의 길이입니다.8각형으로 바깥쪽에 정사각형을 그린 다음 모서리 삼각형(이것들은 45~45~90개의 삼각형)을 안쪽으로 향하게 하여 정사각형을 형성하면 쉽게 입증된다.이 정사각형의 가장자리는 각각 밑면의 길이입니다.

변 a의 길이를 지정하면 스팬 S는

${\displaystyle S=syslogfrac {a}{\syslogrt {2}}+a+{\syslogrt {2}}=(1+{\syslogrt {2}})a\약 2.414a}$

즉, 스팬은 은 비율에 변을 곱한 a와 같습니다.

영역은 위와 같습니다.

${\displaystyle A=((1+{\sqrt {2})a)^{2}-a^{2}=2(1+{\sqrt {2})a^{2}\약 4.828a^{2}.}$

스팬으로 표현하면 면적은

$\displaystyle A=2({\sqrt {2}}-1)S^{2}\약 0.828S^{2}}$

이 영역의 또 다른 간단한 공식은

$(\displaystyle\A=2aS).}$

스판 S를 알고 있는 경우가 많아 정사각형 재료를 정팔각형으로 절단할 때처럼 변의 길이 a를 결정한다.위에서부터

$(\displaystyle a\approx S/2.414).}$

각 변의 두 끝 길이 e(사각형에서 녹색)는 e ${\displaystyle =a\sqrt{\mathrm{}}}$ /${\displaystyle }$2$$, \$displaystyle$ e$=a/{\displayrt {2}}$일 뿐만 아니라 다음과 같이 계산할 수 있습니다.

$\displaystyle \,\!e=(S-a)/2.}$

서클라디우스와 인라디우스

변 길이 a의^[3] 관점에서 정팔각형의 둘레 반지름은 다음과 같다.

${\displaystyle R=\left({\frac {4+2crt {2}}}}}{2}}\right)a,}$

그리고 인라디우스는

${\displaystyle r=\leftfrac {1+{\displayrt {2}}{2}}\right)a.}$

(이는 은 비율의 1/2에 측면 a 또는 스팬 S의 1/2을 곱한 값입니다.)

대각선

정팔각형은 변 길이 a에 대해 세 가지 다른 대각선이 있습니다.

• 짧은 대각선
• 중간 대각선(스판 또는 높이라고도 함)은 inradius 길이의 2배입니다.
• 긴 대각선, 이것은 원주경의 두 배 길이입니다.

각각의 공식은 기하학의 기본 원리에 따라 달라집니다.길이의 ^{[citation needed]}공식은 다음과 같습니다.

• 짧은 대각선: ${\displaystyle a\sqrt{\mathrm{}}}$2 +$$ ${\sqrt {2+{\sqrt {2}}};$
• 중간 대각선$:{\displaystyle }$ (${\displaystyle 1}$+${\displaystyle 2\sqrt{\mathrm{}}}$)$a$ ($1+{\sqrt {2}})$ a$;$ (실버 비율 곱하기 a)
• 긴 대각선: ${\displaystyle a\sqrt{\mathrm{}}}$4${\displaystyle \sqrt{}}$+ ${\displaystyle \sqrt{2\sqrt{\mathrm{}}}}${\$sqrt {4+2{\sqrt {2}}}.$

건축 및 기초 특성

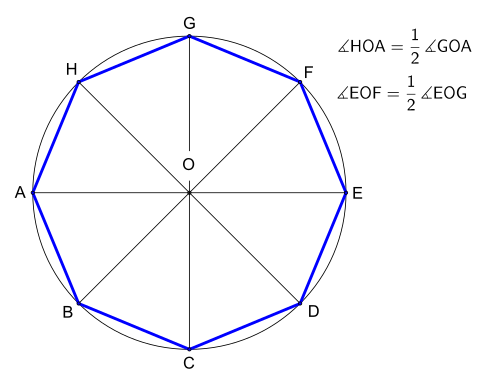
주어진 원의 정팔각형은 다음과 같이 구성할 수 있다.

1. 원과 직경의 AOE를 그립니다.여기서 O는 중심이고 A, E는 원의 점입니다.
2. AOE에 수직인 다른 직경의 GOC를 그립니다.
3. (A,C,E,G는 정사각형의 꼭지점임을 주의한다.)
4. 직경 GOA와 EOG의 이등분선을 그리면서 두 개의 직경을 더 HOD와 FOB로 만듭니다.
5. A, B, C, D, E, F, G, H는 8각형의 정점이다.

정팔각형은 직선 모서리와 나침반을 사용하여 구성할 수 있으며, 이는 8³ = 2의 거듭제곱이다.

일반 팔각형은 메카노 막대로 구성할 수 있습니다.사이즈 4의 12바, 사이즈 5의 3바, 사이즈 6의 2바가 필요합니다.

정팔각형의 각 변은 정점을 연결하는 원의 중심에서 반직각으로 기울어져 있다.따라서 면적을 8개의 이등변 삼각형의 합으로 계산할 수 있으며, 그 결과는 다음과 같습니다.

$({displaystyle {text {Area}}}=2a^{2}({\sqrt {2}}+1)})$

면 a의 8각형에 대해

표준 좌표

원점을 중심으로 하고 변 길이가 2인 정팔각형의 정점에 대한 좌표는 다음과 같습니다.

• (±1, ±(1+1602))
• (±(1+22), ±1).

절개요

8 입방체 투영	24 마름모 절단
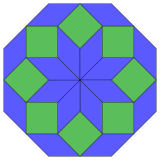	규칙적인.	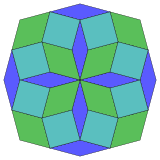아이소톡살

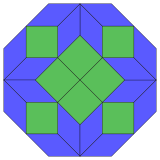Coxeter는 모든 조노곤(대면 평행하고 길이가 같은 2m-곤)을 m(m-1)/2개의 ^[4]평행사변형으로 해부할 수 있다고 말한다.특히 많은 변이 균등하게 있는 일반 다각형에 해당하며, 이 경우 평행사변형은 모두 마름모꼴입니다.정팔각형의 경우 m=4이며, 아래 예시와 같이 6로 나눌 수 있다.이 분해는 정삼각형의 페트리 폴리곤 투영 평면에서 24개의 면 중 6개로 볼 수 있다.목록(OEIS의 시퀀스 A006245)은 이 단면의 8가지 방향으로 솔루션의 수를 8로 정의한다.이 사각형과 로므브는 암만-빈커 타일링에 사용된다.

일반 팔각형 해부

테서랙트	4개의 로브와 2개의 정사각형

스큐 팔각형

스큐 팔각형은 8개의 정점과 모서리가 있지만 동일한 평면에 존재하지 않는 스큐 폴리곤입니다.이러한 8각형 내부는 일반적으로 정의되어 있지 않다.스큐 지그재그 팔각형은 2개의 평행평면을 번갈아 가며 정점을 가진다.

정규 스큐 팔각형은 동일한 가장자리 길이를 가진 정점 추이적입니다.3차원에서는 지그재그 스큐 8각형으로 D, [2⁺,8] 대칭이 같은_4d 정사각형 반비례의 정점과 변연에서 16차원으로 볼 수 있다.

페트리 폴리곤

A, B₄ 및 D₅ Coxeter 평면의 이러한₇ 스큐 직교 투영에 나타나는 이러한 고차원 정규 및 균일한 폴리토프에 대한 일반 스큐 8각형은 Petrie 폴리곤입니다.

A7.	D5.	B4.
71200x	5 데미큐브	16 셀	테서랙트

팔각형의 대칭

대칭

정팔각형의 11개 대칭.반사선은 정점을 지나 파란색, 모서리를 지나 보라색이며 중심에는 회전 순서가 지정됩니다.정점은 대칭 위치에 따라 색상이 지정됩니다.

정팔각형은 Dih 대칭을 가지며₈, 차수는 16입니다.3개의 이면체 부분군이 있습니다.Dih₄, Dih₂, Dih₁ 및 4개의 순환 부분군인 Z₈, Z₄₂, Z, Z, 그리고₁ 대칭이 없음을 나타내는 마지막 부분군입니다.

대칭에 의한 8진수 예제

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

정팔각형에는 11개의 뚜렷한 대칭이 있습니다.John Conway는 전체 대칭을 ^[5]r16으로 표시합니다.이면체 대칭은 꼭지점(대각선인 경우 d) 또는 모서리(수직인 경우 p)를 통과하느냐에 따라 분할됩니다. 가운데 열의 순환 대칭은 중심 회전 순서에 대해 g로 레이블이 지정됩니다.정규 형태의 전체 대칭은 r16이며 대칭은 a1로 표시되지 않습니다.

가장 일반적인 고대칭 팔각형은 p8이며, 4개의 거울로 구성된 등각 팔각형은 긴 모서리와 짧은 모서리를 번갈아 볼 수 있으며, d8은 같은 모서리 길이로 구성된 등각 팔각형이지만 두 개의 서로 다른 내부 각도를 교대로 하는 정점이다.이 두 가지 형태는 서로 쌍대칭이며 정팔각형과 대칭의 반을 가지고 있다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용합니다.g8 서브그룹에만 자유도가 없지만 방향 가장자리로 볼 수 있습니다.

옥타곤의 사용

팔각형 모양은 건축에서 디자인 요소로 사용됩니다.바위의 돔은 독특한 8각형 계획을 가지고 있다.아테네의 바람의 탑은 팔각형 구조의 또 다른 예이다.팔각형의 평면은 또한 St.와 같은 교회 건축에도 있어왔다. 조지 대성당, 아디스 아바바, 산 비탈레 대성당(이탈리아 라벤나의), 카스텔 델 몬테(아풀리아, 이탈리아), 플로렌스 침례교, 줌 프리데푸르스텐 교회(독일) 및 노르웨이의 여러 팔각형 교회.아헨 대성당의 중앙 공간인 카롤링거 팔라틴 채플은 규칙적인 8각형 평면도를 가지고 있습니다.교회에서 팔각형의 사용은 니다로스 대성당의 팔각형의 압세와 같은 덜 디자인적인 요소도 포함합니다.

John Andrews와 같은 건축가들은 빌딩 서비스와 사무실 영역을 기능적으로 분리하기 위해 건물 내 8각형 바닥 배치를 사용해 왔습니다.특히 워싱턴 D.C.의 Intelsat Headquarters, 캔버라의 Callam Office, 호주의 Parramatta의 Octagon Office가 그렇습니다.

기타 용도

• 

  우산은 종종 8각형의 윤곽을 가지고 있다.

• 

  유명한 부하라 융단 디자인은 8각형의 '코끼리 발'을 모티브로 하고 있다.

• 

  바르셀로나의 Eixample 지구의 스트리트 & 블록 레이아웃은 비정기적인 옥타곤을 기반으로 합니다.

• 

  장기는 팔각형을 사용해요.

• 

  일본의 복권 추첨기는 팔각형인 경우가 많습니다.

• 

  영어권 국가 및 대부분의 유럽 국가에서 사용되는 정지 표지판

• 

  중간에 손이 있는 정지 표시 아이콘입니다.

• 

  도교의 바구아는 종종 팔각형으로 배열된다.

• 

  벨리퉁호 난파선의 유명한 팔각형의 금잔

• 

  Shimer College의 수업은 전통적으로 팔각형 테이블 중심으로 진행된다

• 

  준팔각형 모양의 랭스 대성당의 미로.

• 

  Nintendo 64 컨트롤러, GameCube 컨트롤러, Wii Nunchuk 및 Classic 컨트롤러의 아날로그 스틱의 움직임은 회전하는 8각형 영역에 의해 제한되며 스틱은 8개의 다른 방향으로만 움직일 수 있습니다.

파생 수치

• 

  잘린 정사각형 타일링은 모든 정점 주위에 2개의 8각형을 가집니다.
  

• 

  팔각형 프리즘은 두 개의 팔각형 면을 포함한다.
  

• 

  팔각반대론은 두 개의 팔각면을 포함하고 있다.
  

• 

  잘린 정육면체는 6개의 팔각형 면을 포함하고 있다.
  

• 

  잡동사니 큐빅 벌집
  

관련 폴리토프

잘린 정사각형인 팔각형은 먼저 잘린 하이퍼큐브의 연속입니다.

잘린 하이퍼큐브

이미지								...
이름.	옥타곤	잘린 정육면체	잘린 정삼각형	잘린 5입방체	잘린 6입방체	잘린 7 입방체	잘린 8 입방체
콕서터 다이어그램
꼭지점 도형	( )v( )	( )v{ }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3}	( )v{3,3,3,3}

확장 정사각형으로서, 확장 하이퍼큐브의 순서에서도 첫 번째가 됩니다.

확장 하이퍼큐브

							...
옥타곤	마름모 육팔면체	룬케이티드 정삼각형	입체화 5입방체	펜텔레이티드 6입방체	헥시사이티드 세븐큐브	헵텔레이티드 8 큐브

「 」를 참조해 주세요.

• 범퍼풀
• 한센의 작은 팔각형
• 옥타곤 하우스
• 팔각수
• 옥타그램
• 팔면체, 8개의 면이 있는 3D 형태입니다.
• 헝가리 부다페스트의 주요 교차로 옥토곤
• 루브 엘 히즈브(Al Quds Star, Octa Star라고도 함)
• 매끄러운 팔각형

레퍼런스

외부 링크

• 옥타곤 계산기
• 인터랙티브 애니메이션을 사용한 8각형의 정의와 특성